Probing Inflation with Large-Scale Structure Data: The Contribution of Information at Small Scales †
Abstract
1. Introduction
- The nature of dark matter, which constitutes the bulk of the matter content.
- The component causing the accelerated expansion of the Universe. This may be a cosmological constant (, or some additional component known as dark energy, which may be dynamical, with a redshift-dependent equation of state (parametrized by some expression for w, e.g., or it may be a constant.
- Conditions in the very early Universe. The Theory of Inflation is well-established, and has been confirmed with remarkable precision by a succession of cosmic microwave background (CMB) probes. WMAP [1,2] provided conclusive evidence for inflation. Planck [3,4] conclusively excluded a scale-invariant primordial power spectrum. What is the form of this power spectrum beyond its main shape and amplitude? Does it contain features? If so, at which scales do they occur? What is the inflaton potential producing this power spectrum?
2. Primordial Physics
The Inflationary Potential
3. Method
- Simulated Planck CMB data alone (shown in red in the triangle plots);
- Joint Euclid Conservative galaxy clustering + Euclid Conservative cosmic shear + simulated Planck CMB data (shown in blue);
- Joint Euclid Realistic galaxy clustering + Euclid Realistic cosmic shear + simulated Planck CMB data (shown in green).
3.1. The Non-Linear Theoretical Uncertainty: ‘Conservative’ and ‘Realistic’ Setups
- Conservative galaxy clustering: We use a cut-off on large wavelengths at . This eliminates scales which are bigger than the bin width or which violate the small-angle approximation. On small wavelengths, we use a theoretical uncertainty with .
- Realistic galaxy clustering: The same formulation, but with
- Conservative cosmic shear: We include multipoles from up to a bin-dependent non-linear cut-off given by
- Realistic cosmic shear: the same, but with .
3.2. Fiducial Cosmology and WWI Models
4. Results
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CMB | Cosmic microwave background |
| CDM | cold dark matter |
| MCMC | Markov chain Monte Carlo |
| WMAP | Wilkinson Microwave Anisotropy Probe |
| WWI | Wiggly Whipped Inflation |
References
- Spergel, D.N.; Verde, L.; Peiris, H.V.; Komatsu, E.; Nolta, M.R.; Bennett, C.L.; Halpern, M.; Hinshaw, G.; Jarosik, N.; Kogut, A.; et al. First-year Wilkinson Microwave Anisotropy Probe (WMAP) observations: Determination of cosmological parameters. Astrophys. J. Supp. 2003, 148, 175–194. [Google Scholar] [CrossRef]
- Hinshaw, G.; Larson, D.; Komatsu, E.; Spergel, D.N.; Bennett, C.L.; Dunkley, J.; Nolta, M.R.; Halpern, M.; Hill, R.S.; Odegard, N.; et al. Nine-year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Cosmological parameter results. Astrophys. J. Supp. 2013, 208, 19. [Google Scholar] [CrossRef]
- Planck Collaboration VI. Planck 2018 results—VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6. [Google Scholar] [CrossRef]
- Planck Collaboration X. Planck 2018 results—X. Constraints on inflation. Astron. Astrophys. 2020, 641, A10. [Google Scholar] [CrossRef]
- Debono, I.; Hazra, D.K.; Shafieloo, A.; Smoot, G.F.; Starobinsky, A.A. Constraints on features in the inflationary potential from future Euclid data. Mon. Not. R. Astron. Soc. 2020, 496, 3448–3468. [Google Scholar] [CrossRef]
- Hazra, D.K.; Shafieloo, A.; Smoot, G.F.; Starobinsky, A.A. Wiggly whipped inflation. J. Cosmol. Astropart. Phys. 2014, 8, 48. [Google Scholar] [CrossRef]
- Kosowsky, A.; Turner, M.S. CBR anisotropy and the running of the scalar spectral index. Phys. Rev. D 1995, 52, 1739. [Google Scholar] [CrossRef]
- Bridle, S.L.; Lewis, A.M.; Weller, J.; Efstathiou, G. Reconstructing the primordial power spectrum. Mon. Not. R. Astron. Soc. 2003, 342, L72–L78. [Google Scholar] [CrossRef]
- Planck Collaboration XVI. Planck 2013 results. XVI. Cosmological parameters. Astron. Astrophys. 2014, 571, A16. [Google Scholar] [CrossRef]
- Planck Collaboration XIII. Planck 2015 results. XIII. Cosmological parameters. Astron. Astrophys. 2016, 594, A13. [Google Scholar] [CrossRef]
- Hannestad, S. Reconstructing the inflationary power spectrum from cosmic microwave background radiation data. Phys. Rev. D 2001, 63. [Google Scholar] [CrossRef]
- Tegmark, M.; Zaldarriaga, M. Separating the early universe from the late universe:Cosmological parameter estimation beyond the black box. Phys. Rev. D 2002, 66. [Google Scholar] [CrossRef]
- Mukherjee, P.; Wang, Y. Model-independent reconstruction of the primordial power spectrum from Wilkinson Microwave Anistropy Probe data. Astrophys. J. 2003, 599, 1–6. [Google Scholar] [CrossRef]
- Shafieloo, A.; Souradeep, T. Primordial power spectrum from WMAP. Phys. Rev. D 2004, 70. [Google Scholar] [CrossRef]
- Kogo, N.; Sasaki, M.; Yokoyama, J. Constraining Cosmological Parameters by the Cosmic Inversion Method. Progress Theor. Phys. 2005, 114, 555–572. [Google Scholar] [CrossRef][Green Version]
- Leach, S.M. Measuring the primordial power spectrum: Principal component analysis of the cosmic microwave background. Mon. Not. R. Astron. Soc. 2006, 372, 646–654. [Google Scholar] [CrossRef]
- Tocchini-Valentini, D.; Hoffman, Y.; Silk, J. Non-parametric reconstruction of the primordial power spectrum at horizon scales from WMAP data. Mon. Not. R. Astron. Soc. 2006, 367, 1095–1102. [Google Scholar] [CrossRef]
- Shafieloo, A.; Souradeep, T. Estimation of primordial spectrum with post-WMAP 3-year data. Phys. Rev. D 2008, 78. [Google Scholar] [CrossRef]
- Nicholson, G.; Contaldi, C.R. Reconstruction of the primordial power spectrum using temperature and polarisation data from multiple experiments. J. Cosmol. Astropart. Phys. 2009, 2009, 011. [Google Scholar] [CrossRef]
- Paykari, P.; Jaffe, A.H. Optimal binning of the primordial power spectrum. Astrophys. J. 2010, 711, 1–12. [Google Scholar] [CrossRef][Green Version]
- Gauthier, C.; Bucher, M. Reconstructing the primordial power spectrum from the CMB. J. Cosmol. Astropart. Phys. 2012, 2012, 050. [Google Scholar] [CrossRef]
- Hlozek, R.; Dunkley, J.; Addison, G.; Appel, J.W.; Bond, J.R.; Carvalho, C.S.; Das, S.; Devlin, M.J.; Dünner, R.; Essinger-Hileman, T.; et al. The Atacama Cosmology Telescope: A measurement of the primordial power spectrum. Astrophys. J. 2012, 749, 90. [Google Scholar] [CrossRef]
- Hazra, D.K.; Shafieloo, A.; Souradeep, T. Primordial power spectrum: A complete analysis with the WMAP nine-year data. J. Cosmol. Astropart. Phys. 2013, 2013, 031. [Google Scholar] [CrossRef]
- Dorn, S.; Ramirez, E.; Kunze, K.E.; Hofmann, S.; Enßlin, T.A. Generic inference of inflation models by non-Gaussianity and primordial power spectrum reconstruction. J. Cosmol. Astropart. Phys. 2014, 2014, 048. [Google Scholar] [CrossRef]
- Hazra, D.K.; Shafieloo, A.; Smoot, G.F.; Starobinsky, A.A. Ruling out the power-law form of the scalar primordial spectrum. J. Cosmol. Astropart. Phys. 2014, 2014, 061. [Google Scholar] [CrossRef][Green Version]
- Hazra, D.K.; Shafieloo, A.; Souradeep, T. Primordial power spectrum from Planck. J. Cosmol. Astropart. Phys. 2014, 2014, 011. [Google Scholar] [CrossRef]
- Hunt, P.; Sarkar, S. Reconstruction of the primordial power spectrum of curvature perturbations using multiple data sets. J. Cosmol. Astropart. Phys. 2014, 2014, 025. [Google Scholar] [CrossRef]
- Hazra, D.K.; Shafieloo, A.; Smoot, G.F.; Starobinsky, A.A. Inflation with whip-shaped suppressed scalar power spectra. Phys. Rev. Lett. 2014, 113, 071301. [Google Scholar] [CrossRef]
- Hazra, D.K.; Shafieloo, A.; Smoot, G.F.; Starobinsky, A.A. Primordial features and Planck polarization. J. Cosmol. Astropart. Phys. 2016, 9, 009. [Google Scholar] [CrossRef]
- Sprenger, T.; Archidiacono, M.; Brinckmann, T.; Clesse, S.; Lesgourgues, J. Cosmology in the era of Euclid and the Square Kilometre Array. J. Cosmol. Astropart. Phys. 2019, 2019, 047. [Google Scholar] [CrossRef]
- Hazra, D.K.; Sriramkumar, L.; Martin, J. BINGO: A code for the efficient computation of the scalar bi-spectrum. J. Cosmol. Astropart. Phys. 2013, 2013, 026. [Google Scholar] [CrossRef]
- Brinckmann, T.; Lesgourgues, J. MontePython 3: Boosted MCMC sampler and other features. Phys. Dark Universe 2019, 24, 100260. [Google Scholar] [CrossRef]
- Blas, D.; Lesgourgues, J.; Tram, T. The Cosmic Linear Anisotropy Solving System (CLASS). Part II: Approximation schemes. J. Cosmol. Astropart. Phys. 2011, 2011, 034. [Google Scholar] [CrossRef]
- Takahashi, R.; Sato, M.; Nishimichi, T.; Taruya, A.; Oguri, M. Revising the Halofit model for the nonlinear matter power spectrum. Astrophys. J. 2012, 761, 152. [Google Scholar] [CrossRef]
- Bird, S.; Viel, M.; Haehnelt, M.G. Massive neutrinos and the non-linear matter power spectrum. Mon. Not. R. Astron. Soc. 2012, 420, 2551–2561. [Google Scholar] [CrossRef]
- Audren, B.; Lesgourgues, J.; Bird, S.; Haehnelt, M.G.; Viel, M. Neutrino masses and cosmological parameters from a Euclid-like survey: Markov Chain Monte Carlo forecasts including theoretical errors. J. Cosmol. Astropart. Phys. 2013, 1301, 026. [Google Scholar] [CrossRef]
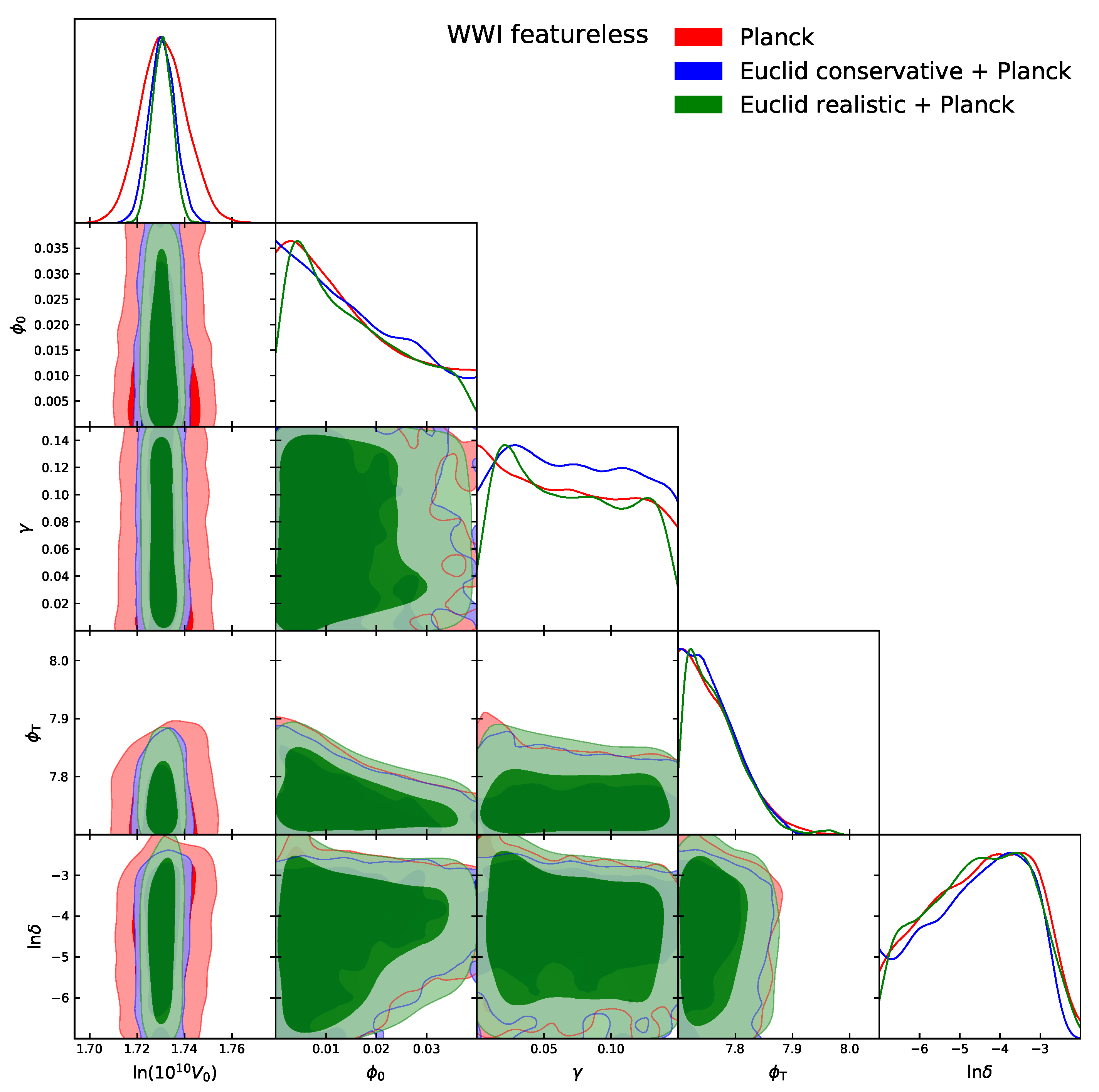
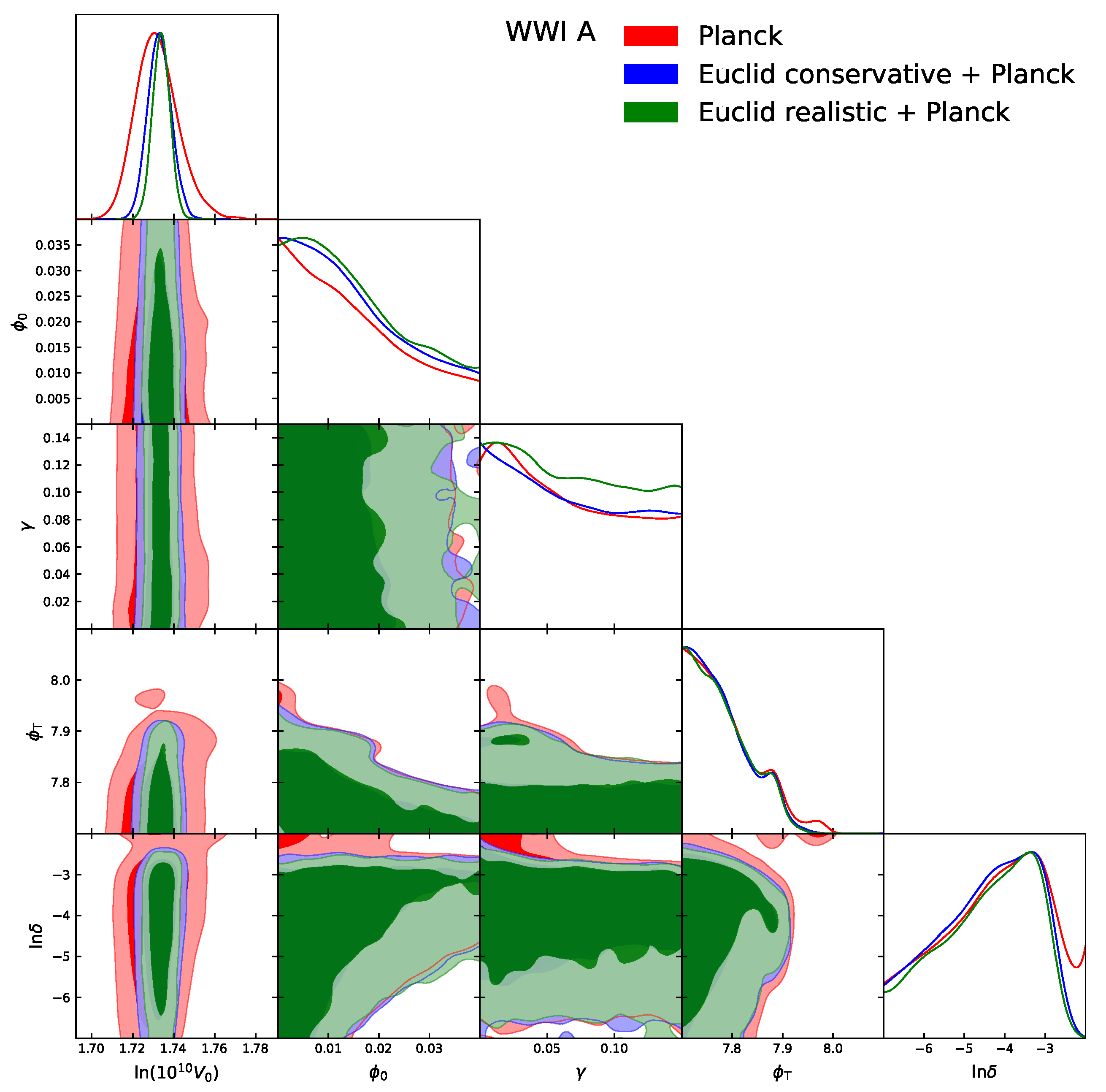
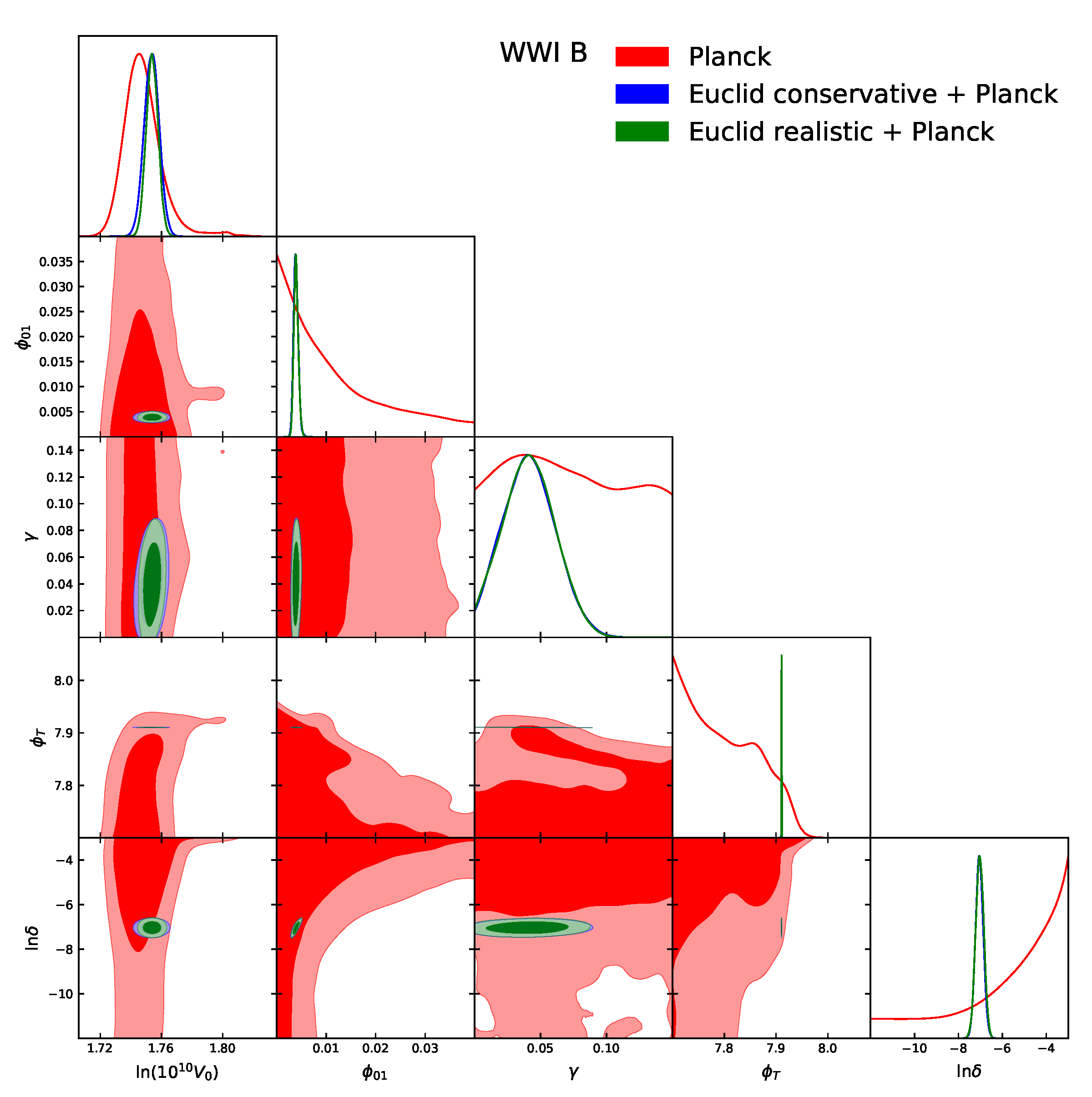

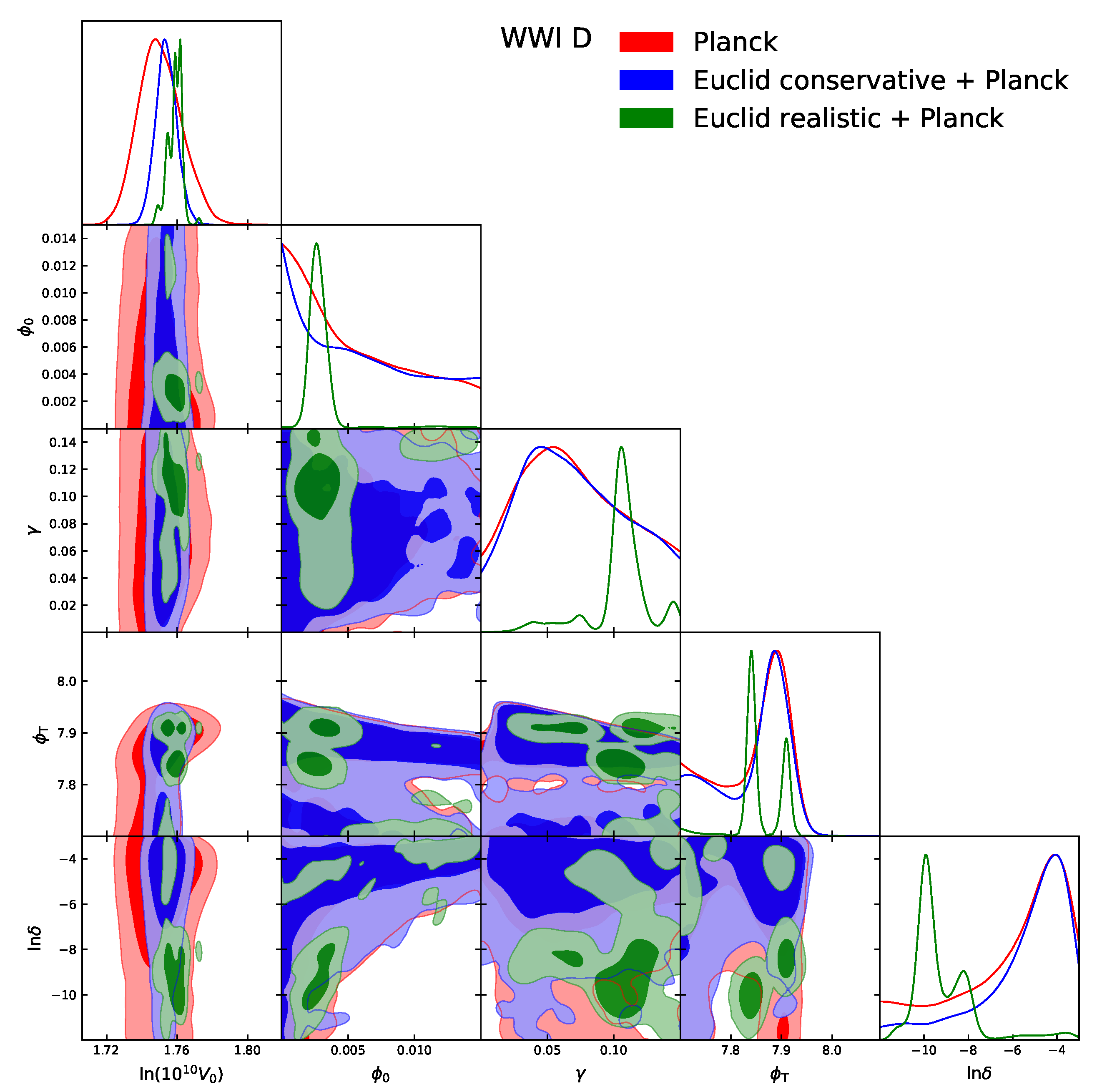
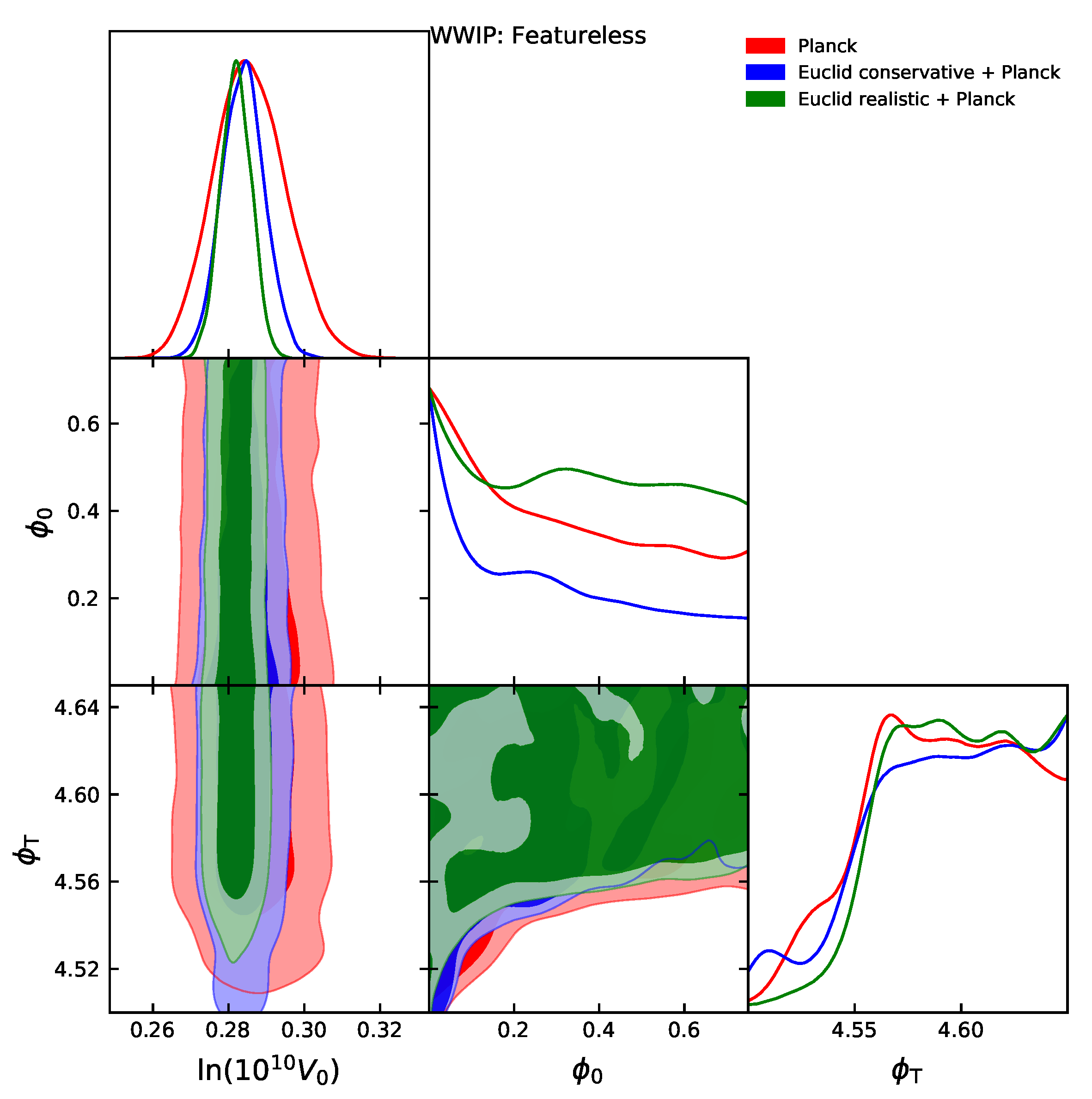
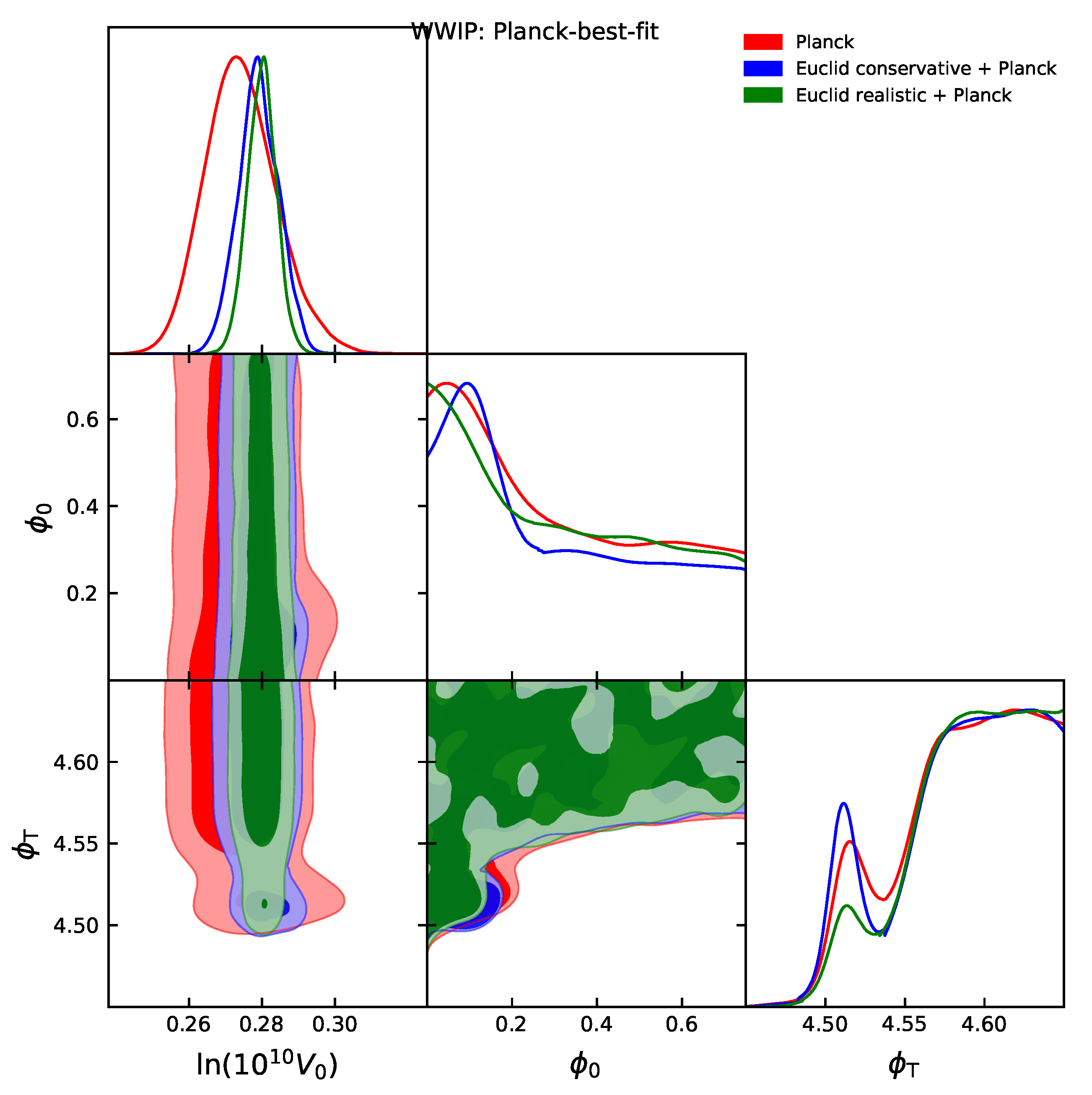
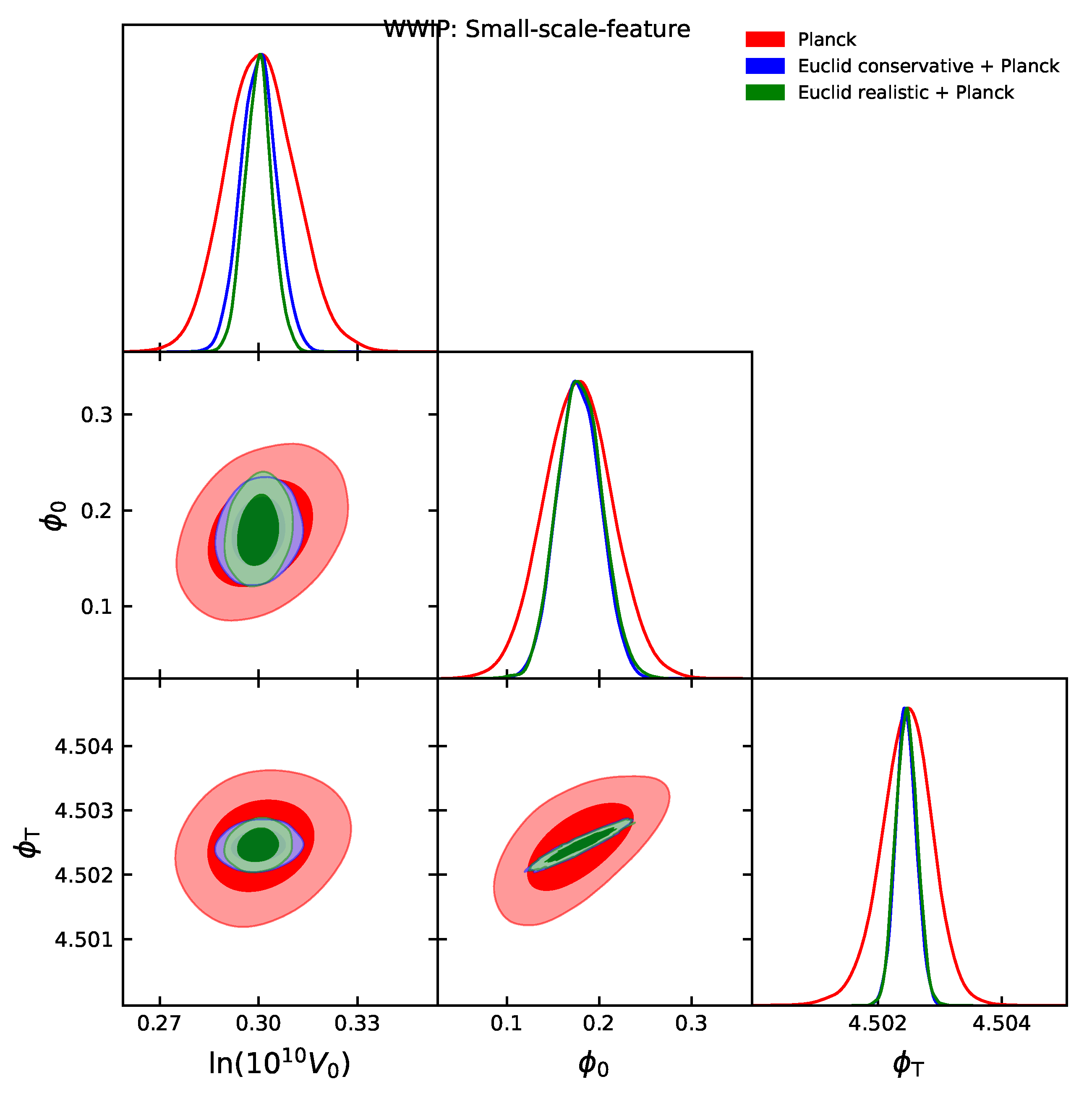
| Model | |||||
|---|---|---|---|---|---|
| WWI: Featureless | 0 | 0 | – | – | |
| WWI–A | |||||
| WWI–B | |||||
| WWI–C | |||||
| WWI–D | |||||
| WWIP: Featureless | 0 | – | – | – | |
| WWIP: Planck-best-fit | – | – | |||
| WWIP: Small-scale-feature | – | – |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Debono, I. Probing Inflation with Large-Scale Structure Data: The Contribution of Information at Small Scales. Phys. Sci. Forum 2021, 2, 45. https://doi.org/10.3390/ECU2021-09371
Debono I. Probing Inflation with Large-Scale Structure Data: The Contribution of Information at Small Scales. Physical Sciences Forum. 2021; 2(1):45. https://doi.org/10.3390/ECU2021-09371
Chicago/Turabian StyleDebono, Ivan. 2021. "Probing Inflation with Large-Scale Structure Data: The Contribution of Information at Small Scales" Physical Sciences Forum 2, no. 1: 45. https://doi.org/10.3390/ECU2021-09371
APA StyleDebono, I. (2021). Probing Inflation with Large-Scale Structure Data: The Contribution of Information at Small Scales. Physical Sciences Forum, 2(1), 45. https://doi.org/10.3390/ECU2021-09371






