A Survey of Effective Parameters in Biomass Separation Using Vacuum Membrane Filtering: A Case Study of Pectin Acidic Solution †
Abstract
:1. Introduction
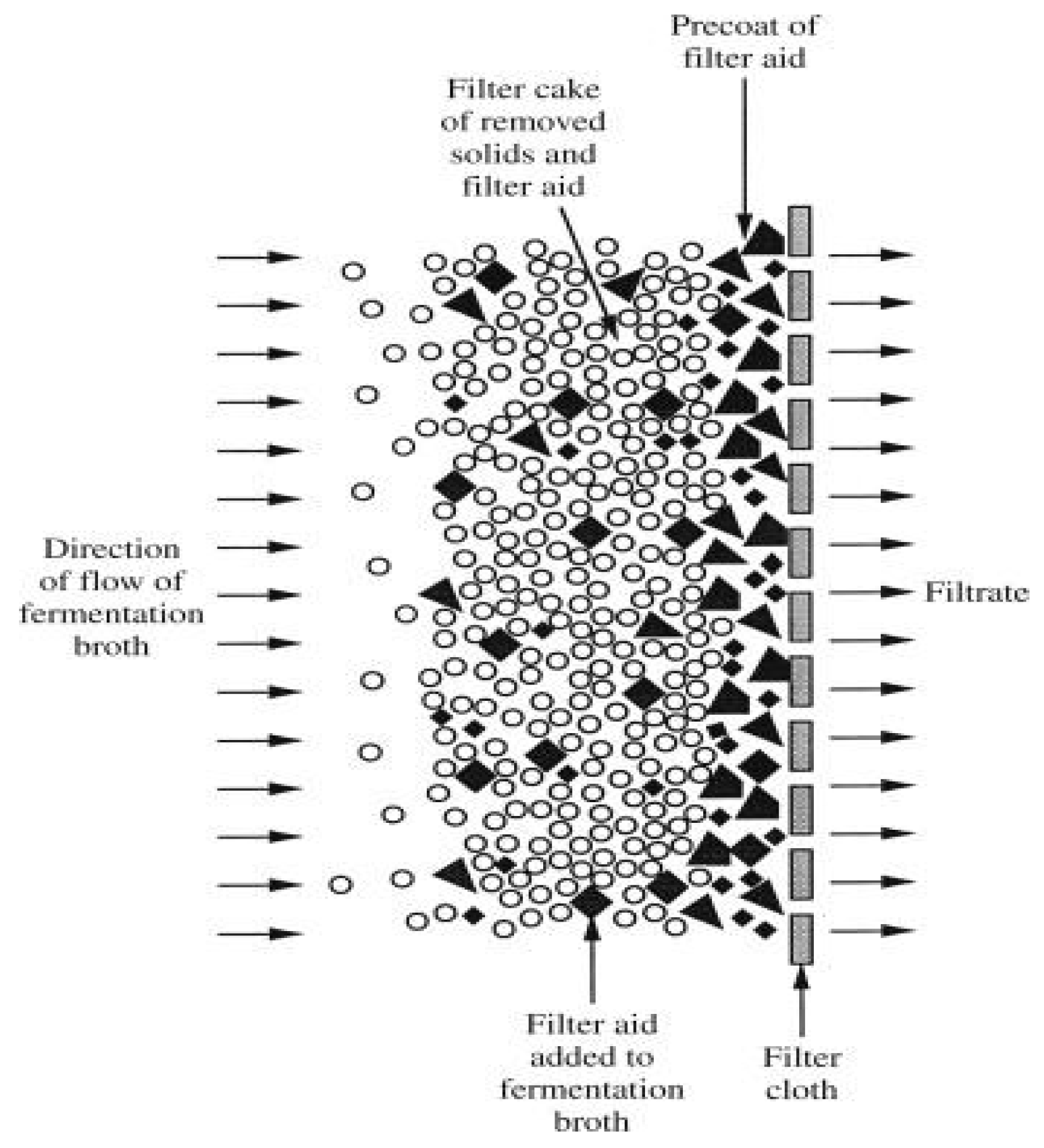
2. Methods and Materials
2.1. Design and Construction Method of a Vacuum Filter System
2.2. Method of Preparing Filtration Fluid
2.3. Method of Filtration Using a Vacuum Filtration System
2.4. Method of Measuring Energy Consumption
2.5. Method of Measuring Production Flow Rate
- Q = Volumetric flow rate (mL/s)
- v = Volume of fluid (mL)
- t = Time (s)
2.6. Method of Measuring Separation Efficiency
- Raf = Separation efficiency (%)
- mt = Amount of solid material in the control solution (g)
- mi = Amount of solid material in the filtered solution (g)
2.7. Statistical Analysis
3. Results and Analysis
3.1. Results of Variance Analysis of Energy Consumption Data by Vacuum Filtration System
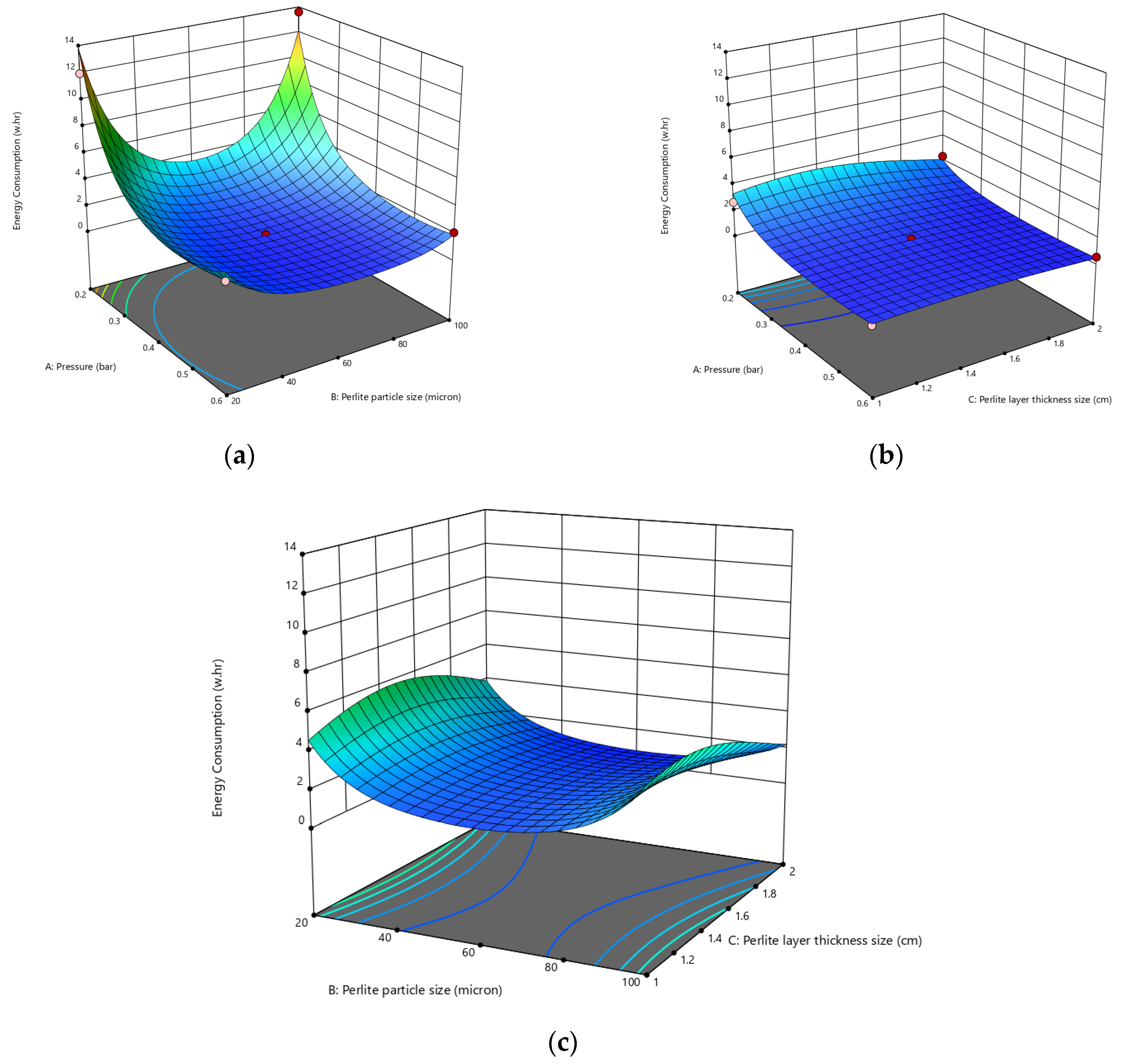
3.2. The Interaction Effect of Independent Variables on Energy Consumption
3.3. ANOVA Results for Fluid Flow Rate
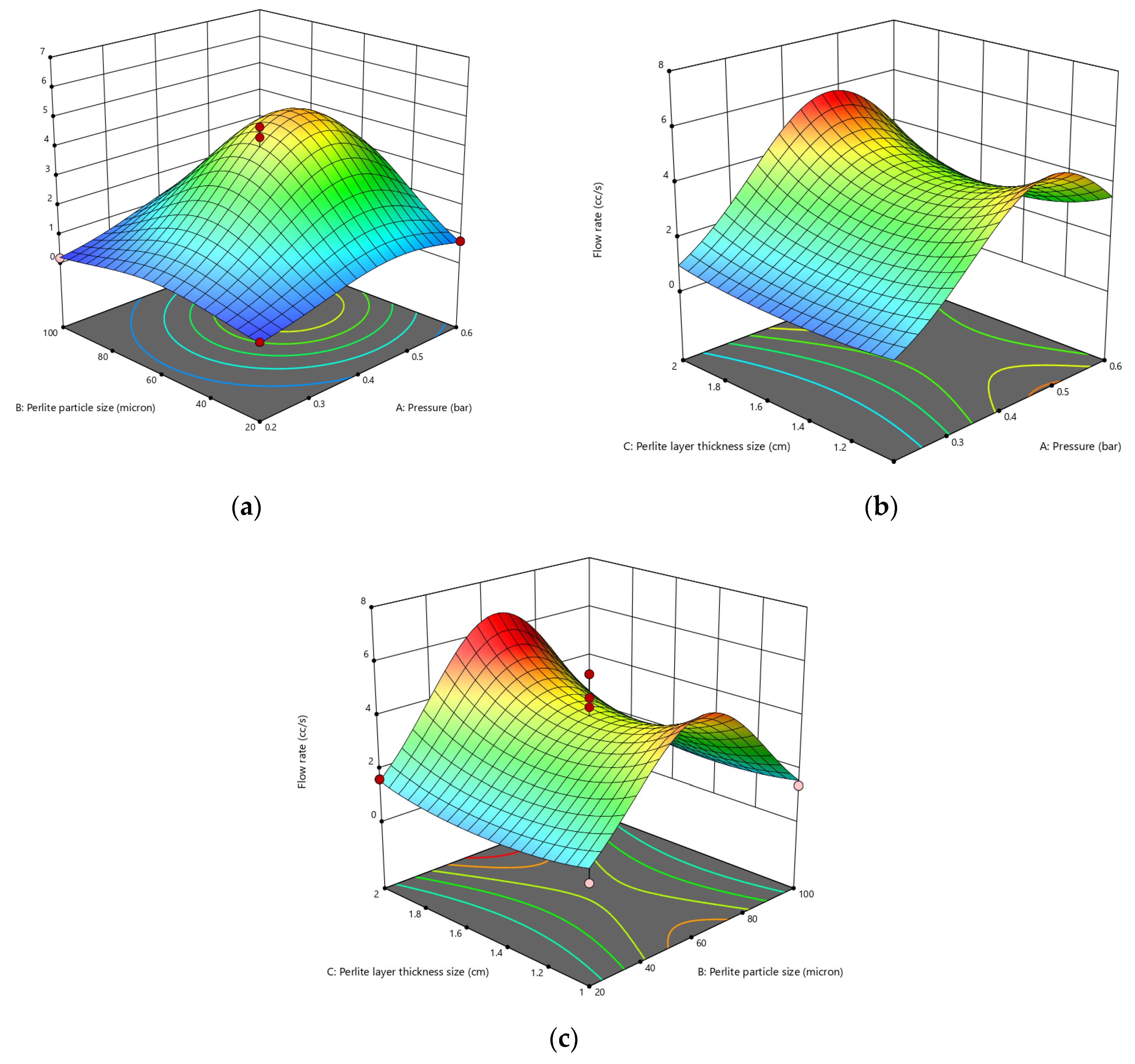
3.4. The Mutual Effect of Independent Changes on Discharge
3.5. Results of Analysis of Variance (ANOVA) for Separation Efficiency
3.6. The Interaction Effect of Independent Variables on Separation Efficiency
3.7. Determining the Minimum Points in the Evaluation Range of the Filtration Process Using the Vacuum Filter System
4. Conclusions
- A vacuum filtration membrane system can be used as an effective separation method in the pectin production process.
- The dependent variable, separation yield, indicates the purity of the separated fluid, and the evaluation showed that the vacuum level, perlite particle size, and thickness of the perlite layer have an effect on its changes. Increasing the vacuum level leads to more impurities being sucked into the fluid and decreases the separation yield from 41% to 30%. Increasing the particle size from 20 microns to 60 microns decreases the yield from 55% to 33%, but increasing the particle size from 60 microns to 100 microns has no significant effect on the separation yield. The thickness of the perlite layer has the most significant effect on the separation yield, and by increasing it from 1 to 2 cm, the yield increased by 2.5 times. The maximum separation yield was achieved at a vacuum level of 0.2 bar, a particle size of 20 microns, and a thickness of 2 cm.
- The level of vacuum and the size of the perlite particles affect the effective fluid flow changes. Increasing the vacuum level from 2.0 bar to 4.0 bar results in a 5.6 times increase in flow rate. However, with further increases in vacuum, the flow rate decreases. This trend is also observed for the size of perlite particles, indicating filter clogging and reduced flow rate at a vacuum level of 6.0 bar and perlite size of 100 microns.
- Evaluation of energy consumption of the filtration system showed that the effective variables on energy consumption are the vacuum level and the size of perlite particles. With an increase in vacuum level from 2.0 bar to 6.0 bar, the energy consumption decreased by 5 times. The energy consumption for perlite size of 60 microns was optimized to be 74.0 Wh, and coarser or finer perlite sizes had 5.4 times higher energy consumption.
- The optimal conditions were obtained by the RSM method using a computer at a vacuum level of 4.0 bar, perlite size of 60 microns, and perlite layer thickness of 2 cm.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pesch, G.R.; Du, F. A review of dielectrophoretic separation and classification of non-biological particles. Electrophoresis 2021, 42, 134–152. [Google Scholar] [CrossRef] [PubMed]
- Rao, S.R. Surface Chemistry of Froth Flotation: Volume 1: Fundamentals; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Uduman, N.; Qi, Y.; Danquah, M.K.; Forde, G.M.; Hoadley, A. Dewatering of microalgal cultures: A major bottleneck to algae-based fuels. J. Renew. Sustain. Energy 2010, 2, 12701. [Google Scholar] [CrossRef]
- Cheremisinoff, N.P. Industrial liquid filtration equipment. In Fibrous Filter Media; Elsevier: Amsterdam, The Netherlands, 2017; pp. 27–50. [Google Scholar]
- Shao, P.; Darcovich, K.; McCracken, T.; Ordorica-Garcia, G.; Reith, M.; O’Leary, S. Algae-dewatering using rotary drum vacuum filters: Process modeling, simulation and techno-economics. Chem. Eng. J. 2015, 268, 67–75. [Google Scholar] [CrossRef]
- Purchas, D.; Sutherland, K. Handbook of Filter Media; Elsevier: Amsterdam, The Netherlands, 2002. [Google Scholar]
- Svarovsky, L. Solid-Liquid Separation; Elsevier: Amsterdam, The Netherlands, 2000. [Google Scholar]
- Jadwani, V. Development of a Method to Prepare a Test Fluid with Soft Particles in Biodiesel Fuel Blends. 2020. Available online: http://www.diva-portal.org/smash/get/diva2:1463440/FULLTEXT01.pdf (accessed on 1 November 2023).
- Grassino, A.N.; Halambek, J.; Djaković, S.; Brnčić, S.R.; Dent, M.; Grabarić, Z. Utilization of tomato peel waste from canning factory as a potential source for pectin production and application as tin corrosion inhibitor. Food Hydrocoll. 2016, 52, 265–274. [Google Scholar] [CrossRef]
- Maran, J.P.; Sivakumar, V.; Thirugnanasambandham, K.; Sridhar, R. Microwave assisted extraction of pectin from waste Citrullus lanatus fruit rinds. Carbohydr. Polym. 2014, 101, 786–791. [Google Scholar] [CrossRef] [PubMed]
- Bagal-Kestwal, D.R.; Pan, M.H.; Chiang, B. Properties and applications of gelatin, pectin, and carrageenan gels. In Bio Monomers for Green Polymeric Composite Materials; Wiley: Hoboken, NJ, USA, 2019; pp. 117–140. [Google Scholar]
- Leclere, L.; Van Cutsem, P.; Michiels, C. Anti-cancer activities of pH-or heat-modified pectin. Front. Pharmacol. 2013, 4, 128. [Google Scholar] [CrossRef] [PubMed]
- Minjares-Fuentes, R.; Femenia, A.; Garau, M.C.; Meza-Velázquez, J.A.; Simal, S.; Rosselló, C. Ultrasound-assisted extraction of pectins from grape pomace using citric acid: A response surface methodology approach. Carbohydr. Polym. 2014, 106, 179–189. [Google Scholar] [CrossRef] [PubMed]
- Huttunen, M.; Nygren, L.; Kinnarinen, T.; Ekberg, B.; Lindh, T.; Ahola, J.; Karvonen, V.; Häkkinen, A. Specific energy consumption of vacuum filtration: Experimental evaluation using a pilot-scale horizontal belt filter. Dry. Technol. 2019, 38, 460–475. [Google Scholar] [CrossRef]
- Duarte, F.L.; Coimbra, L.; Baleiras-Couto, M. Filter media comparison for the removal of Brettanomyces bruxellensis from wine. Am. J. Enol. Vitic. 2017, 68, 504–508. [Google Scholar] [CrossRef]
- Fillaudeau, L.; Carrère, H. Yeast cells, beer composition and mean pore diameter impacts on fouling and retention during cross-flow filtration of beer with ceramic membranes. J. Memb. Sci. 2002, 196, 39–57. [Google Scholar] [CrossRef]






| Number | Pressure (bar) | Perlite Particle Size (micron) | Perlite Layer Thickness (cm) |
|---|---|---|---|
| 1 | 0.4 | 60 | 1.5 |
| 2 | 0.4 | 60 | 1.5 |
| 3 | 0.4 | 60 | 1.5 |
| 4 | 0.4 | 60 | 1.5 |
| 5 | 0.2 | 60 | 2 |
| 6 | 0.2 | 20 | 1.5 |
| 7 | 0.2 | 60 | 1 |
| 8 | 0.4 | 100 | 2 |
| 9 | 0.6 | 60 | 2 |
| 10 | 0.4 | 20 | 2 |
| 11 | 0.4 | 20 | 1 |
| 12 | 0.6 | 60 | 1 |
| 13 | 0.6 | 20 | 1.5 |
| 14 | 0.4 | 100 | 1 |
| 15 | 0.6 | 100 | 1.5 |
| 16 | 0.2 | 100 | 1.5 |
| 17 | 0.4 | 60 | 1.5 |
| Source | df | Sum of Squares | Mean Squares | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 9 | 3.01 | 0.3343 | 26.93 a | 0.0001 |
| A—Pressure | 1 | 0.8902 | 0.8902 | 71.72 b | 0.0001< |
| B—Perlite particle size | 1 | 0.0701 | 0.0701 | a 5.65 | 0.0491 |
| C—Perlite layer thickness | 1 | 0.0714 | 0.0714 | 1.46 a | 0.0476 |
| B × A | 1 | 0.0181 | 0.0181 | ns 1.08 | 0.2668 |
| C × A | 1 | 0.0004 | 0.0004 | ns 0.0327 | 0.8615 |
| C × B | 1 | 0.0169 | 0.0169 | ns 1.46 | 0.2820 |
| A × A | 1 | 0.4919 | 0.4919 | a 39.63 | 0.0004 |
| B × B | 1 | 1.33 | 1.33 | 106.96 b | 0.0001< |
| C × C | 1 | 0.0789 | 0.0789 | a 6.35 | 0.0398 |
| Residual | 7 | 0.0869 | 0.0124 | ||
| Lack of fit | 3 | 0.0706 | 0.0235 | ns 5.77 | 0.0617 |
| Pure error | 4 | 0.0163 | 0.0041 | ||
| Cor total | 16 | 3.1 |
| Source | df | Sum of Squares | Mean Squares | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 9 | 3.07 | 0.3414 | 17.96 a | 0.0005 |
| A—Pressure | 1 | 0.9039 | 0.9039 | 47.55 a | 0.0002 |
| B—Perlite particle size | 1 | 0.0196 | 0.0196 | ns 1.03 | 0.3442 |
| C—Perlite layer thickness | 1 | 0.0173 | 0.0173 | ns 0.9102 | 0.3718 |
| B × A | 1 | 0.021 | 0.021 | ns 1.1 | 0.3285 |
| C × A | 1 | 0.0001 | 0.0001 | ns 0.0044 | 0.9488 |
| C × B | 1 | 0.0065 | 0.0065 | ns 0.3415 | 0.5773 |
| A × A | 1 | 0.7255 | 0.7255 | a 37.17 | 0.0005 |
| B × B | 1 | 1.22 | 1.22 | b 64.03 | 0.0001< |
| C × C | 1 | 0.1203 | 0.1203 | a 6.33 | 0.0401 |
| Residual | 7 | 0.1331 | 0.019 | ||
| Lack of fit | 3 | 0.1103 | 0.0368 | 6.45 ns | 0.0518 |
| Pure error | 4 | 0.0228 | 0.0057 | ||
| Cor total | 16 | 3.21 |
| Source | df | Sum of Squares | Mean Squares | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 9 | 3332.33 | 370.26 | 132.24 b | 0.0001< |
| A—Pressure | 1 | 168.54 | 168.54 | 60.19 a | 0.0001 |
| B—Perlite particle size | 1 | 940.48 | 940.48 | 335.89 b | 0.0001< |
| C—Perlite layer thickness | 1 | 1609.71 | 1609.71 | b 574.9 | 0.0001< |
| B × A | 1 | 41.54 | 41.54 | a 14.84 | 0.0063 |
| C × A | 1 | 82.54 | 82.54 | a 29.48 | 0.0010 |
| C × B | 1 | 0.8742 | 0.8742 | ns 0.3122 | 0.5937 |
| A × A | 1 | 16.08 | 16.08 | a 6.00 | 0.0442 |
| B × B | 1 | 460.44 | 460.44 | b 164.44 | 0.0001< |
| C × C | 1 | 5.36 | 5.36 | ns 1.91 | 0.2092 |
| Residual | 7 | 19.6 | 2.8 | ||
| Lack of fit | 3 | 8.17 | 2.72 | 0.9531 ns | 49.54 |
| Pure error | 4 | 11.43 | 2.86 | ||
| Cor total | 16 | 3351.93 |
| Name | Goal | Lower Limit | Upper Limit | Lower Weight | Upper Weight |
|---|---|---|---|---|---|
| Pressure | is in range | 0.2 | 0.6 | 1 | 1 |
| Perlite particle size | is in range | 20 | 100 | 1 | 1 |
| Perlite layer thickness | is in range | 1 | 2 | 1 | 1 |
| Energy consumption | minimize | 0.54 | 13.6 | 1 | 1 |
| Flow rate | maximize | 0.17 | 5.62 | 1 | 1 |
| Extraction yield | maximize | 18.46 | 68 | 1 | 1 |
| Number | Pressure (bar) | Perlite Particle Size (micron) | Perlite Layer Thickness (cm) | Energy Consumption (Wh) | Flow Rate (mL/s) | Extraction Yield (%) |
|---|---|---|---|---|---|---|
| 1 | 0.379 | 56.174 | 2 | 0.498 | 5.865 | 50.216 |
| 2 | 0.380 | 55.798 | 1.999 | 0.499 | 5.864 | 50.257 |
| 3 | 0.380 | 55.857 | 1.999 | 0.499 | 5.865 | 50.240 |
| 4 | 0.383 | 55.188 | 1.995 | 0.500 | 5.864 | 50.220 |
| 5 | 0.392 | 53.352 | 1.983 | 0.503 | 5.864 | 50.052 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gholami, S.; Minaei, S.; Mahdavian, A.; Bazyar, P. A Survey of Effective Parameters in Biomass Separation Using Vacuum Membrane Filtering: A Case Study of Pectin Acidic Solution. Biol. Life Sci. Forum 2024, 30, 14. https://doi.org/10.3390/IOCAG2023-16340
Gholami S, Minaei S, Mahdavian A, Bazyar P. A Survey of Effective Parameters in Biomass Separation Using Vacuum Membrane Filtering: A Case Study of Pectin Acidic Solution. Biology and Life Sciences Forum. 2024; 30(1):14. https://doi.org/10.3390/IOCAG2023-16340
Chicago/Turabian StyleGholami, Shoaib, Saeid Minaei, Alireza Mahdavian, and Pourya Bazyar. 2024. "A Survey of Effective Parameters in Biomass Separation Using Vacuum Membrane Filtering: A Case Study of Pectin Acidic Solution" Biology and Life Sciences Forum 30, no. 1: 14. https://doi.org/10.3390/IOCAG2023-16340
APA StyleGholami, S., Minaei, S., Mahdavian, A., & Bazyar, P. (2024). A Survey of Effective Parameters in Biomass Separation Using Vacuum Membrane Filtering: A Case Study of Pectin Acidic Solution. Biology and Life Sciences Forum, 30(1), 14. https://doi.org/10.3390/IOCAG2023-16340








