Determination of Optimal Tilt and Orientation Angles for Fixed Photovoltaic Systems Using a Three-Dimensional Vector Analysis of Direct Normal Irradiance in Equatorial Regions

Abstract

Efficient utilization of solar energy in equatorial regions depends on accurately determining the optimal tilt and azimuth angles of fixed photovoltaic (PV) systems. This study presents a three-dimensional vector-based methodology that employs Direct Normal Irradiance (DNI) to estimate the mean direction of incident solar flux. Hourly DNI data from 2020–2024 for the city of Guayaquil, Ecuador, were transformed into spatial vectors and integrated to obtain a resultant vector representing the average orientation and elevation of direct solar radiation. The analysis yielded an optimal tilt angle of 5.73° and an azimuth of 59.15°, values consistent with Guayaquil’s equatorial latitude and previous studies conducted in tropical environments. The low tilt angle reflects the persistently high solar elevation typical of equatorial zones, while the slight northeastward orientation deviation corresponds to the asymmetric diurnal distribution of solar irradiance. The main contribution of this work lies in providing a geometrically rigorous and computationally efficient approach capable of synthesizing the directional behavior of solar flux without relying on complex transposition models. The proposed method enhances the optimization of PV system design, urban energy planning, and renewable microgrid modeling in data-scarce contexts, supporting the sustainable development of solar energy in equatorial regions.

1. Introduction

In regions located near the equatorial line, photovoltaic (PV) systems installed in residential, commercial, and institutional infrastructures often exhibit inclination angles defined empirically or by generalized standards without locally validated technical adjustment. This practice leads to significant losses in Direct Normal Irradiance (DNI) as the capture of incident radiation is not properly optimized [1,2]. In tropical environments, such as northeastern Brazil or equatorial areas of Africa characterized by high annual solar radiation availability, the lack of optimization criteria reduces energy-conversion efficiency and limits the economic and environmental impact of photovoltaic projects [3].

Several studies have shown that optimizing the tilt angle can increase the energy yield within a range between 8% and 20%, depending on local conditions and the applied technique [1]. Research conducted by Guler et al. [2] demonstrates that intelligent techniques based on fuzzy logic can improve the performance of fixed-tilt systems by up to 20%. In tropical climates, such as those analyzed by Lopes Júnior et al. [3], Direct Normal Irradiance exhibits high sensitivity to cloudiness conditions, directly influencing the angle selection. Similarly, Ashetehe et al. [4] developed a generalized approach for Ethiopia that allowed for the calculation of optimal angles without relying on local databases, while Arslan et al. experimentally confirmed how small variations in tilt angle significantly affect the fill factor (FF) and short-circuit current in PV systems. These improvements are particularly relevant in developing countries, where maximizing energy utilization is essential to ensure the financial sustainability of renewable-energy investments. Even at low latitudes, small changes in tilt can cause significant variations in key electrical parameters such as short-circuit current and module fill factor [5].

However, most methodologies applied to date are based on isotropic and anisotropic transposition models, which require extensive databases and local validation processes with high computational demand [6,7]. Other studies indicate that atmospheric dust also alters the optimal angle efficiency [8] as well as the performance differences between fixed-tilt systems and single-axis tracking configurations [9]. The need to assess the optimal tilt angle as a function of latitude, seasonality, cloud cover, and local conditions is reinforced by the work of González-González et al. [10], who even proposed solar climatic zones as predictive tools. Although these models have demonstrated robustness in specific contexts, they exhibit limitations when applied to equatorial regions with a restricted availability of high-resolution meteorological data. Additionally, such models tend to prioritize global radiation on an inclined plane, introducing uncertainties associated with the estimation of diffuse and reflected fractions.

In this context, the present research proposes an alternative approach based on a three-dimensional vector analysis DNI, capable of synthesizing the annual and multi-annual weighted mean direction of direct solar radiation. Unlike studies based on limited periods, this work incorporates a continuous five-year database (2020–2024), ensuring greater statistical representativeness and enabling the evaluation of the robustness of the optimal angle against interannual fluctuations. The central objective was to estimate the optimal tilt and orientation angles for fixed photovoltaic systems in Guayaquil, Ecuador, a representative case study due to its proximity to the equinoctial line, its high annual solar radiation, and its growing demand for sustainable energy solutions.

2. Methods

This research was conducted under an integrated approach combining meteorological data, solar geometry models, and the vector analysis of DNI with the purpose of estimating the optimal tilt angle for photovoltaic modules in regions near the equatorial line. The temporal extension of the database, covering a continuous five-year period from January 2020 to December 2024, incorporates the interannual variability of solar radiation, thereby enhancing the statistical robustness of the results and reducing the bias associated with limited single-year datasets.

2.1. Irradiance and Solar Position Data

Hourly series of DNI for the period from 1 January 2020 to 31 December 2024 were retrieved through the Open-Meteo API [11]. Complementarily, solar position parameters, specifically the azimuth angle (θ) and the altitude angle (α), were obtained from the SunEarthTools platform [12,13]. These parameters serve as the basis for the vector transformation of the solar resource, allowing for a high-precision representation of the solar trajectory across multiple years. 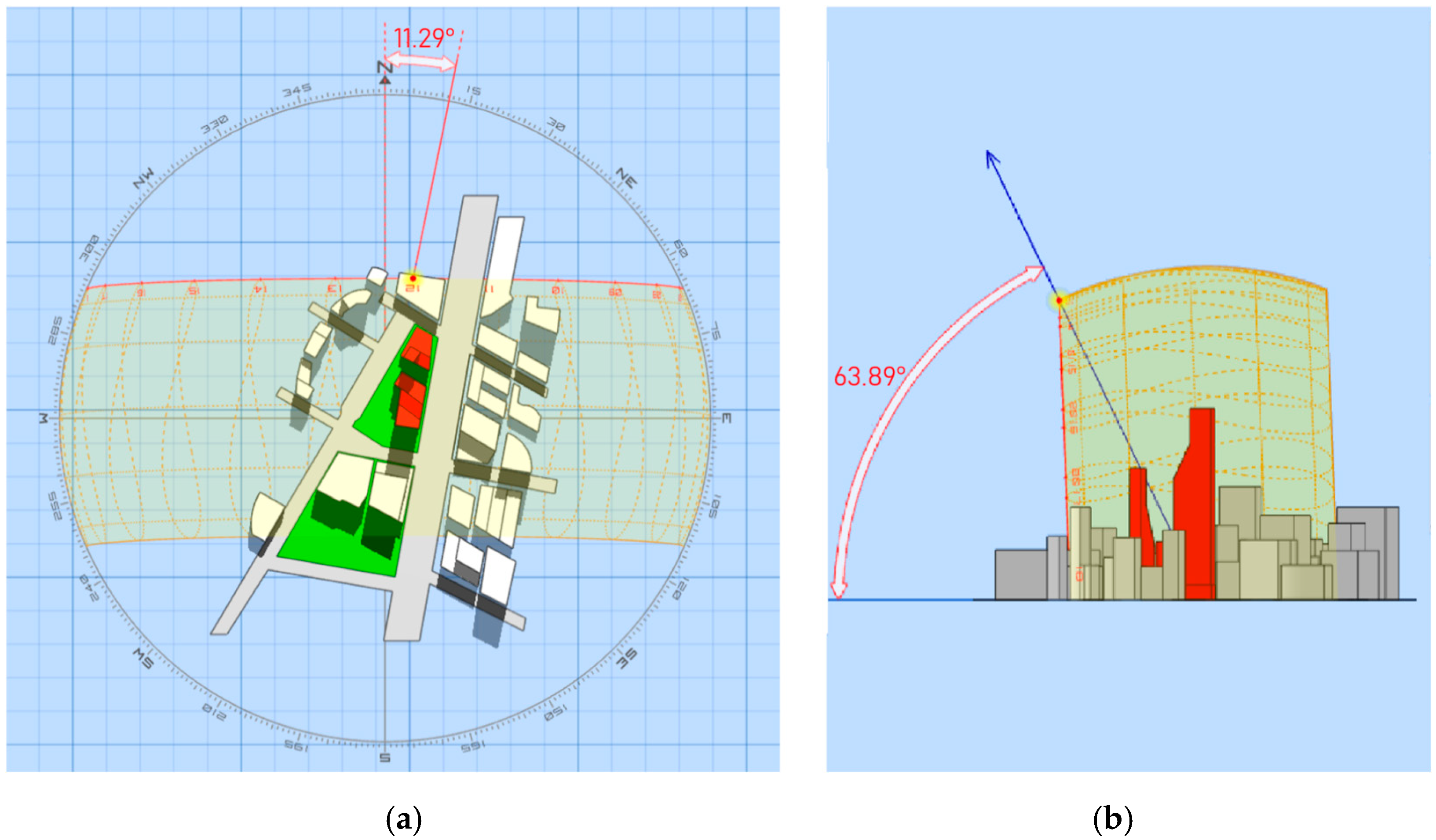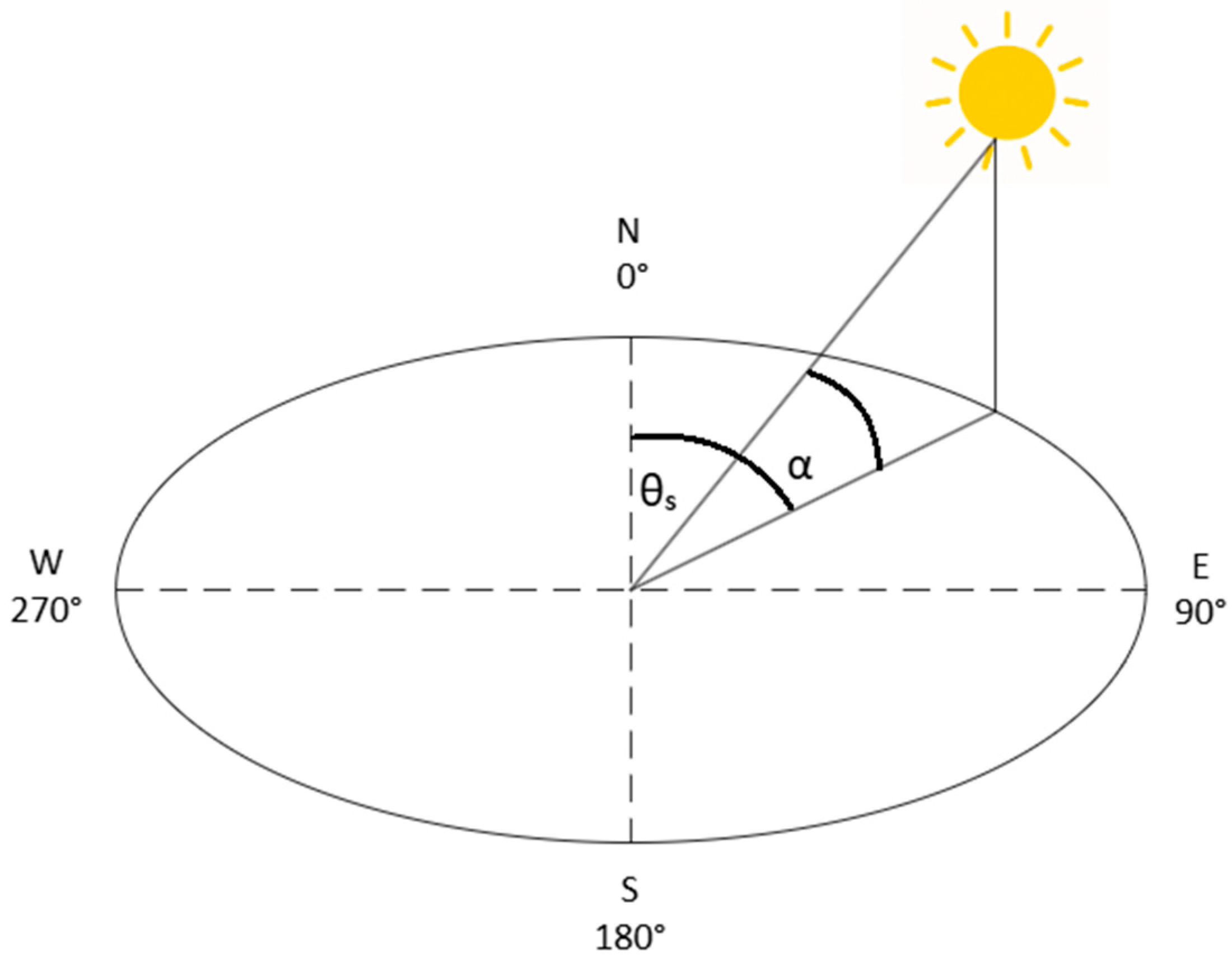Figure 1 illustrates the solar elevation and azimuth angles that define the apparent path of the Sun during a typical day at the study site.

Solar position is primarily described by two angles: the solar altitude (α) and the azimuth (θ). The solar altitude, also referred to as elevation, corresponds to the angle formed between the observer’s horizontal plane and the line connecting the observation point to the apparent position of the Sun [13]. Additionally, the Solar Position Algorithm (SPA), developed by the National Renewable Energy Laboratory (NREL), was employed to compute the zenith and azimuth angles with high accuracy. This algorithm is applicable over an extensive temporal range (from the year −2000 to 6000) with an approximate uncertainty of ±0.0003° [12], ensuring a precise representation of solar geometry throughout the entire analysis period from 2020 to 2024. Figure 1 shows the annual solar trajectory for Guayaquil, depicting the variation in the Sun’s position throughout the year, including solstices and equinoxes. The geographic location of the site corresponds to a latitude of −2.1475° and a longitude of −79.9139°, within the GMT−05:00 time zone. The simulation was conducted for 21 June 2025, at 12:00. Under these conditions, the sun exhibits an azimuth of 11.29° and an altitude of 63.89°, with sunrise occurring at 06:22 and sunset at 18:21, resulting in 12 h of daylight. Twilight times are as follows: civil twilight takes place between 05:59 and 18:44, nautical twilight between 05:33 and 19:10, and astronomical twilight between 05:07 and 19:36.

2.2. Study Sites

The reference area selected for this study was the city of Guayaquil, Ecuador, whose geographical characteristics are summarized in

Table 1. Characteristics of the selected study site.

City	Latitude (°)	Longitude (°)	Elevation (m)	Data Source
Guayaquil	−2.1475	−79.9139	15	TMY

. Guayaquil was chosen as the representative site due to its proximity to the Equator, its high annual solar irradiance, and its strategic relevance as one of Ecuador’s main urban and industrial centers. These conditions make it an ideal location for assessing the applicability and performance of photovoltaic systems under equatorial solar geometry.

2.3. Meteorological Database

The meteorological information used in this study corresponded to a Typical Meteorological Year (TMY) dataset with hourly resolution, extended to a continuous five-year range (2020–2024). Hourly series of DNI were obtained from the Open-Meteo API [11], which is based on climate reanalysis datasets. These datasets integrate observations from meteorological stations, aircraft, buoys, radars, and satellites, complemented through atmospheric assimilation models to generate continuous and high-quality historical records.

In particular, the ECMWF IFS dataset compiled and processed by Open-Meteo was employed. This dataset uses simulations with the latest version of the Integrated Forecasting System (IFS) model, ensuring high precision and spatiotemporal resolution in the reconstruction of meteorological conditions, even in areas with limited instrumental coverage such as rural regions or open oceanic zones.

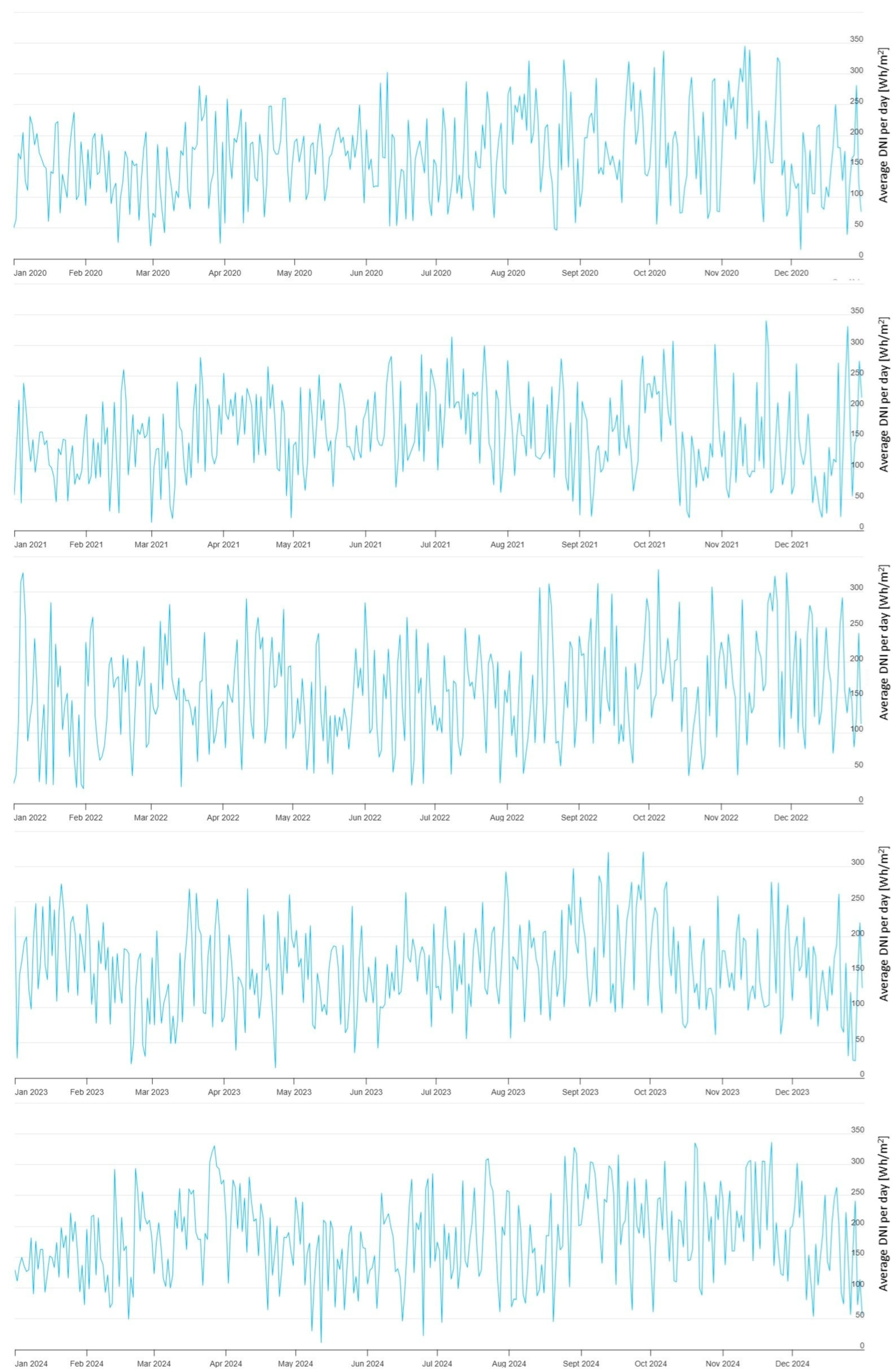
The extension to five consecutive years of meteorological records allowed for the assessment of the interannual stability of DNI and its influence on the determination of the optimal tilt angle, constituting a methodological contribution compared with studies that only used a single reference year.

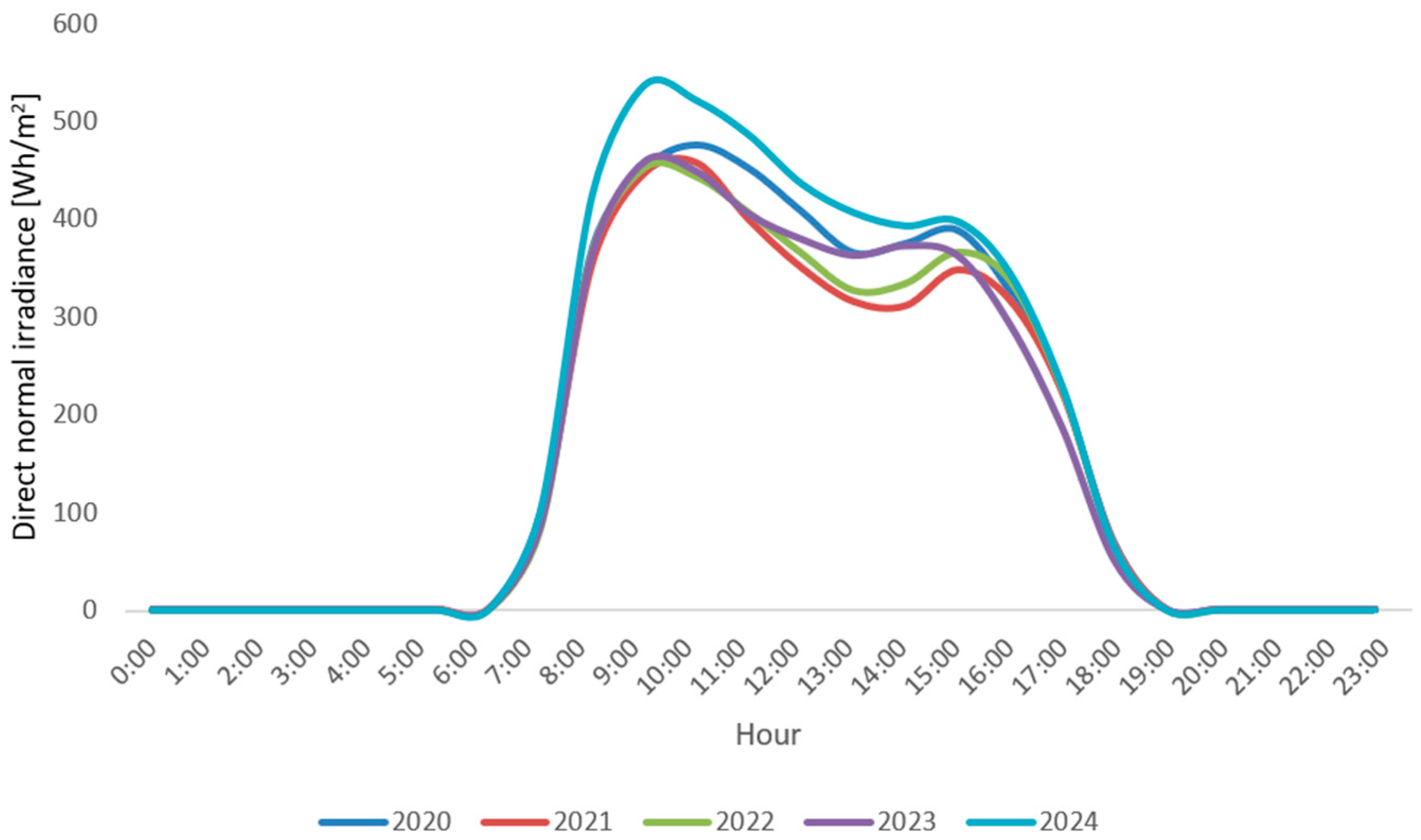
The temporal variability of DNI from 2020 to 2024 for Guayaquil is shown in Figure 2, where the fluctuations correspond to the characteristic patterns of solar availability in tropical regions. The annual uniform distribution of irradiance confirms the absence of marked seasonal differences near the Equator. Furthermore, the average hourly profiles of Direct Normal Irradiance (Wh/m²), illustrated in Figure 3, revealed a consistent diurnal trend with peak irradiance occurring between 09:00 and 15:00 for all analyzed years. This stability supports the robustness of the long-term solar potential assessment in equatorial locations.

The corresponding average hourly DNI values for each year are summarized in

Table 2. Average hourly values of Direct Normal Irradiance (Wh/m²) for the 2020–2024 period.

Hour	2020	2021	2022	2023	2024
7:00:00	97.9	89.6	82.9	85.5	101.0
8:00:00	370.4	355.1	368.0	364.7	425.4
9:00:00	451.1	446.7	453.6	458.3	536.8
10:00:00	475.3	456.9	443.6	447.7	520.8
11:00:00	451.2	398.6	407.0	404.3	485.6
12:00:00	407.5	349.8	365.8	378.9	436.1
13:00:00	365.0	315.0	327.5	362.2	406.5
14:00:00	374.5	310.6	334.5	372.0	392.7
15:00:00	387.9	347.4	366.7	361.9	397.4
16:00:00	325.1	316.3	338.2	291.8	344.5
17:00:00	223.0	223.2	228.1	186.4	229.4
18:00:00	67.8	66.7	64.1	50.4	64.8

, showing the magnitude of irradiance during representative daylight hours and highlighting that hours with the highest irradiance are between 9:00 and 10:00.

2.4. Mathematical Methodology

The mathematical modeling of solar radiation is a fundamental component for accurately estimating the energy incident on inclined surfaces. In photovoltaic applications, solar panels are rarely installed horizontally; therefore, it is necessary to transpose the radiation from a horizontal plane to an inclined plane. This process relies on models that describe the angular distribution of sky radiance, considering variations in luminous intensity across the celestial dome. Among the most widely used approaches in the literature are isotropic and anisotropic models.

The isotropic diffuse radiation model assumes that the sky emits radiation uniformly in all directions. Under this assumption, the diffuse component incident on an inclined surface is determined proportionally to the geometric factor between the horizontal and inclined planes. Its analytical simplicity and low computational cost have made it a recurrent tool in preliminary simulations, particularly when limited input data are available or when multiple angular configurations must be evaluated efficiently [6,7]. However, this model may introduce systematic errors under specific atmospheric conditions, such as clear or partially cloudy skies, where diffused radiation is not homogeneously distributed across the sky vault.

In contrast, the anisotropic model assumes that the distribution of diffuse radiance varies spatially, exhibiting regions of higher energy concentration. This approach incorporates three distinct components: (i) a homogeneous isotropic component; (ii) circumsolar brightening, representing the increased radiance near the solar disk; and (iii) horizon brightening, which accounts for the enhanced irradiance near the lower edge of the sky. Including these corrections improves the physical representation of atmospheric scattering, yielding more accurate results under high direct radiation and low turbidity conditions. Models proposed by Hay, Klucher, and Perez are widely adopted due to their balance between accuracy and computational efficiency [15,16,17]. These models mainly differ in how they handle the diffuse sky component, which is the largest potential source of computational error. While calculating the direct component is simple and nearly error-free, the ground reflected component can also introduce errors.

Within the framework of this study, the selection of the conceptual model was guided by the goal of achieving analytical simplification without compromising result reliability. Consequently, the isotropic model was adopted as the reference approach, considering the DNI as the principal variable. This choice allowed DNI to be employed as a robust proxy for the overall behavior of the solar resource, avoiding the explicit modeling of diffuse and reflected radiation. Under this assumption, it was considered that the angular variability of radiation was uniform in all directions, enabling a direct determination of the optimal tilt and orientation angles of fixed photovoltaic panels.

2.5. Three-Dimensional Vector Representation of Direct Normal Irradiance

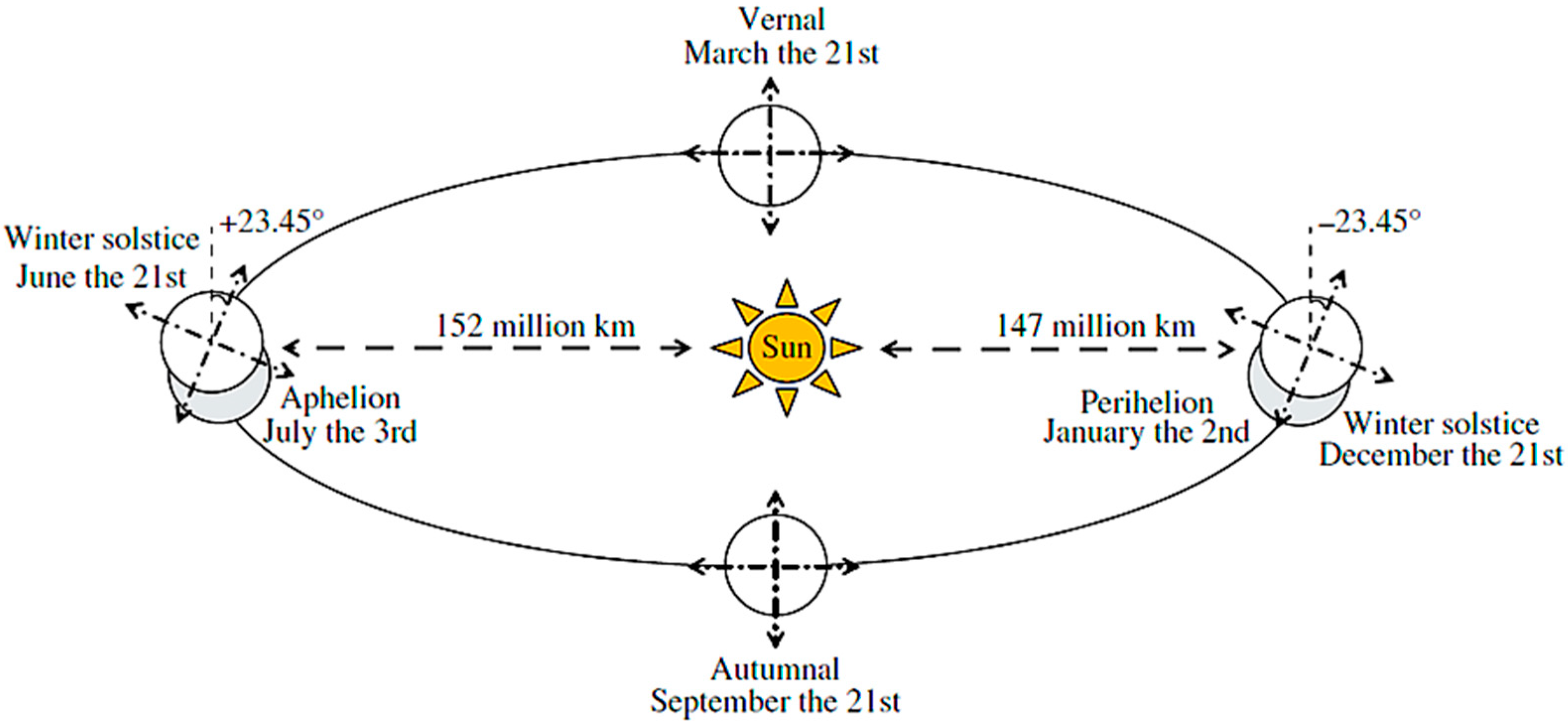
The determination of the solar position forms the basis of the geometric modeling of solar radiation. The Earth’s revolution around the Sun follows an elliptical orbit, characterized by a slight orbital eccentricity that induces periodic variations in the Earth–Sun distance. These variations directly affect the extraterrestrial irradiance, and consequently, the solar energy incident on the Earth’s surface. The principal orbital points defining these variations are the winter solstice on 21 December (approximately 147 million km), the summer solstice on 21 June (approximately 152 million km), the perihelion on 2 January (when the Earth is at its closest approach to the Sun, ~147 million km), and the aphelion on 3 July (when it is at its farthest distance, ~152 million km) [18].

As shown in Figure 4 [19], the elliptical trajectory of the Earth around the Sun and its axial tilt of 23.45° govern the annual distribution of solar irradiance received at different latitudes. This geometric configuration determines the variation in solar decline throughout the year and explains the seasonal asymmetry in the apparent solar path. The perihelion and aphelion distances, together with the solstitial and equinoctial positions, define the temporal limits of solar exposure, which are particularly relevant for modeling irradiance under equatorial conditions where seasonal fluctuations are minimal but geometrically significant.

The fundamental angles that describe the apparent position of the Sun relative to a terrestrial observer are:

The solar altitude angle (α), which represents the angular height of the Sun above the horizon.

The solar azimuth angle (θ_s), which defines the direction of the Sun with respect to the geographic north on the horizontal plane [20].

For a given geographic location, the solar position is fully determined by the altitude (α) and azimuth (θ_s) angles, which vary as a function of the true solar time, solar declination, and the site’s latitude, as illustrated in Figure 5.

2.6. Geometric and Astronomical Fundamentals

A three-dimensional vector-based approach was implemented to represent DNI and determine the mean direction of the solar energy flux over the analyzed period. Each hourly DNI value was transformed into a three-dimensional vector, with its components corresponding to the projections of solar radiation onto Cartesian axes: X (East–West), Y (North–South), and Z (Elevation) [21].

In accordance with previous geometric–radiometric modeling methodologies [22], the DNI is mathematically expressed through Equations (1)–(3), which define the vector components of the irradiance along the spatial coordinate system.

$$\mathrm{X}=\mathrm{D}\mathrm{N}\mathrm{I}\times \cos \left(\mathsf{\alpha }\right)\times \sin \left({\mathsf{\theta }}_{\mathrm{s}}\right)$$

(1)

$$\mathrm{Y}=\mathrm{D}\mathrm{N}\mathrm{I}\times \cos \left(\mathsf{\alpha }\right)\times \cos ({\mathsf{\theta }}_{\mathrm{s}})$$

(2)

$$\mathrm{Z}=\mathrm{D}\mathrm{N}\mathrm{I}\times \sin \left(\mathsf{\alpha }\right)$$

(3)

where:

DNI: Direct Normal Irradiance (W/m²);

α: Solar altitude angle (°);

θ_s: Solar azimuth angle (°).

The annual result of direct irradiance is obtained from the vector summation of all hourly records within the analyzed period, as defined in Equation (4). The magnitude of the resultant vector, representing the accumulated mean intensity of direct solar radiation, is calculated as follows:

$$|\mathrm{R}|=\sqrt{{\mathrm{R}}_{\mathrm{x}}^2+{\mathrm{R}}_{\mathrm{y}}^2+{\mathrm{R}}_{\mathrm{z}}^2}$$

(4)

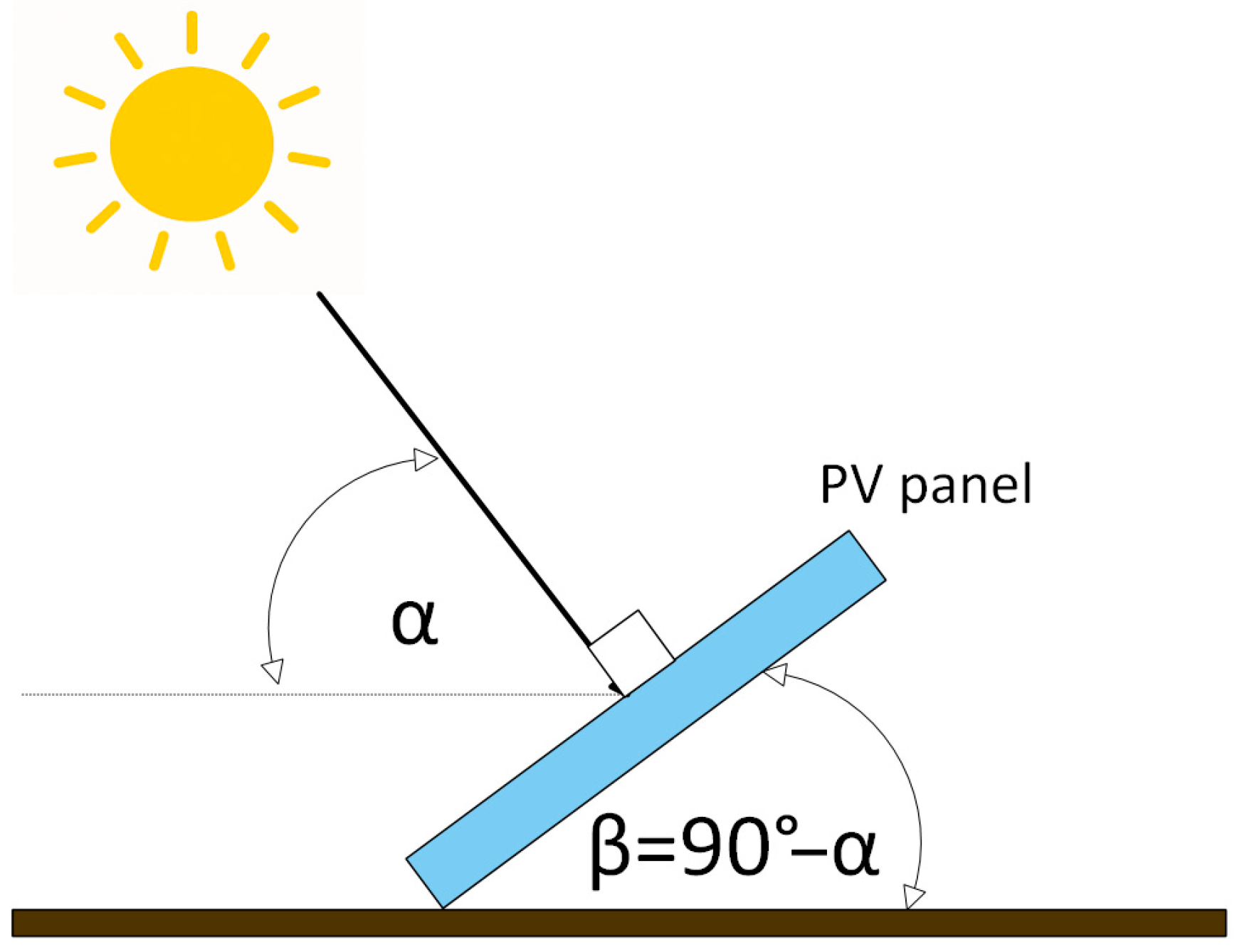
From the orientation of the resultant vector, the characteristic solar angles that define the optimal tilt and orientation of the photovoltaic panels are derived, as shown in Equations (5)–(7).

$$\mathrm{A}\mathrm{l}\mathrm{t}\mathrm{i}\mathrm{t}\mathrm{u}\mathrm{d}\mathrm{e}\left(\mathsf{\alpha }\right)=\arctan {\displaystyle \frac{{\mathrm{R}}_{\mathrm{z}}}{\sqrt{{\mathrm{R}}_{\mathrm{x}}^2+{\mathrm{R}}_{\mathrm{y}}^2}}}$$

(5)

$$\mathrm{A}\mathrm{z}\mathrm{i}\mathrm{m}\mathrm{u}\mathrm{t} ({\mathsf{\theta }}_{\mathrm{s}})=90°-\arctan {\displaystyle \frac{{\mathrm{R}}_{\mathrm{y}}}{{\mathrm{R}}_{\mathrm{x}}}}$$

(6)

$$\mathrm{T}\mathrm{i}\mathrm{l}\mathrm{t}\left(\mathsf{\beta }\right)=90°-\mathsf{\alpha }$$

(7)

This procedure enables the synthesis of the annual distribution of direct irradiance flux into a single representative vector (Figure 6), providing a geometric criterion for determining the optimal tilt angle (β_opt) and optimal orientation that maximize solar energy captured in fixed photovoltaic systems. In the developed analysis, the panel orientation angle and the solar azimuth angle (θ_s) are equivalent, as both describe the horizontal direction of the mean solar vector relative to true north.

3. Results

3.1. Determination of Optimal Tilt and Orientation Angles

Based on the resultant vector obtained through the weighted summation of the hourly DNI vectors, the altitude (α) and azimuth (θ_s) angles were determined, representing the annual mean direction of the direct solar radiation flux at the study site. These geometric parameters define the optimal orientation and inclination of fixed photovoltaic (PV) systems, whose surfaces must be arranged perpendicular to this resultant vector to maximize energy capture.

The implemented approach integrated all hourly records for the 2020–2024 period, generating a cumulative three-dimensional solar vector that synthesized both the magnitude and average direction of the solar resource. This procedure is conceptually analogous to constructing a cumulative sky model in tilt optimization methodologies [22], but offers the advantage of operating directly on the vectorial component of DNI, without relying on transposition models.

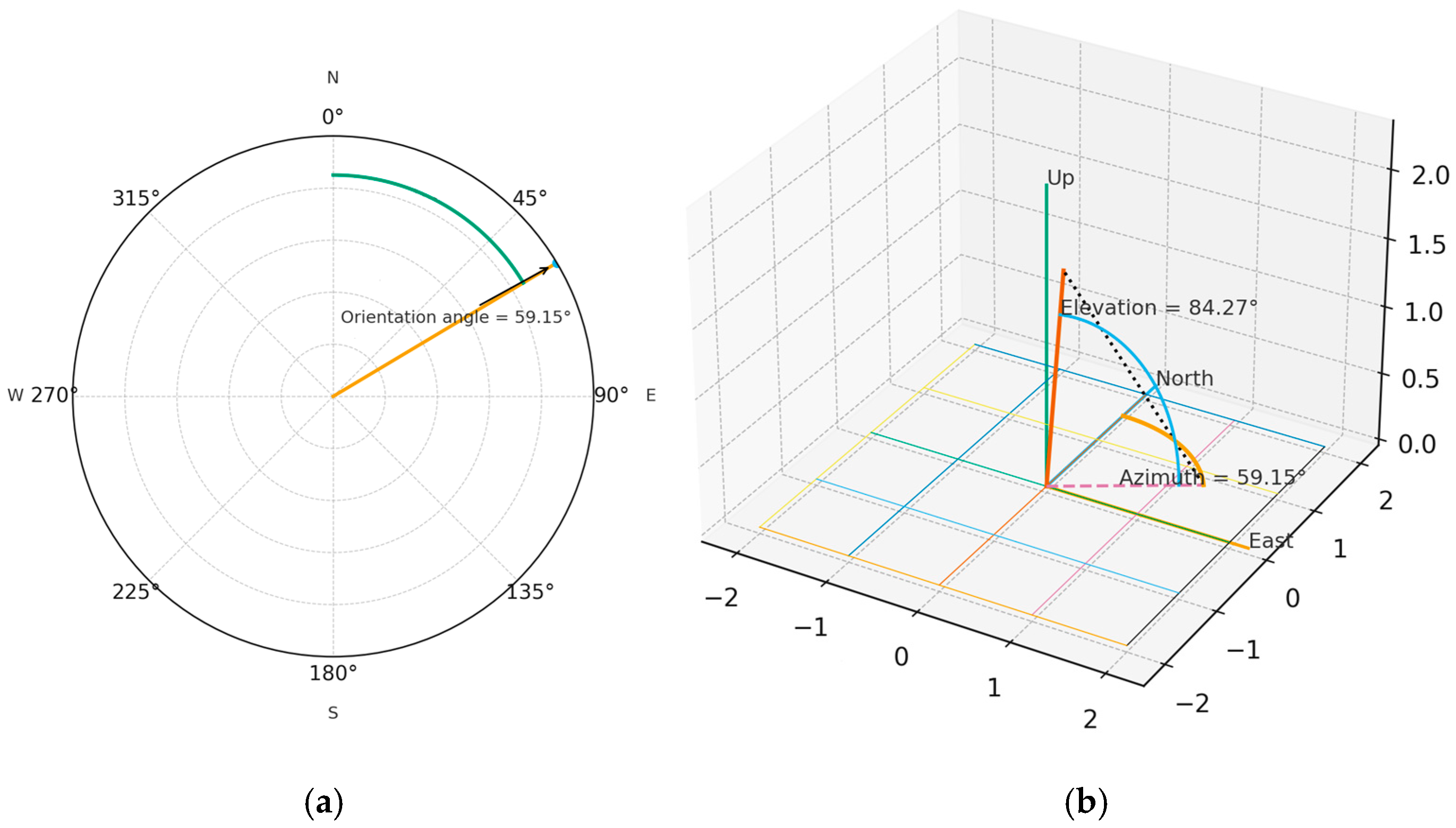
As a result, the optimal installation angles were obtained, corresponding to a tilt of 5.73° and an azimuth of 59.15°, as illustrated in Figure 7a,b. These values reflect the average direction toward which the highest annual energy density of direct radiation is concentrated over Guayaquil, Ecuador. The magnitude of the resultant vector therefore represents the net directional component of solar radiation, serving as an efficient tool for defining the optimal geometric configuration of fixed solar panel installations in equatorial latitudes.

The interannual variability of the solar geometry parameters is summarized in

Table 3. Angles obtained for each year.

	Altitude (°)	Azimuth (°)	Optimal Tilt (°)	Orientation (°)
2020	84.83	52.92	5.17	52.92
2021	82.83	44.15	7.17	44.15
2022	85.82	67.76	4.18	67.76
2023	83.78	64.63	6.22	64.63
2024	83.66	68.23	6.34	68.23

, which presents the elevation and azimuth angles obtained for each analyzed year. The results showed minimal deviation among years, confirming the temporal stability of solar directionality in equatorial conditions.

The results shown in Table 3, obtained from Equations (5)–(7), were used to determine the resultant vector per year through the proposed three-dimensional model. The overall results of this model are summarized in

Table 4. Angles obtained with the proposed model.

Ciudad	Altitude (°)	Azimuth (°)	Optimal Tilt (°)	Orientation (°)
Guayaquil	84.27	59.15	5.73	59.15

, which identifies the optimal tilt and azimuth orientation derived from the resultant vector analysis.

3.2. Methodological Validation with Previous Studies

The methodology developed in this study builds upon approaches used in prior research that optimized tilt angles for photovoltaic systems under diverse environmental and climatic contexts. Ferry et al. [22] demonstrated the usefulness of integrating meteorological databases with sky discretization techniques to determine the optimal tilt angles for bifacial systems in Europe. Following this principle, the present method extends these foundations by employing a three-dimensional vector analysis of DNI, capable of reproducing comparable results with reduced computational complexity and enhanced applicability in tropical and equatorial regions.

To validate the proposed approach, results were contrasted with the study by Warburg et al. [23], conducted near the equatorial line in Tanzania. Their research estimated global irradiance on inclined planes using extended time series (2000–2017) and a combination of isotropic and anisotropic transposition models to obtain monthly averages on tilted surfaces from horizontal records. The tilt angle of 5.73° obtained in this study fell well within the range reported by Warburg et al. for equatorial latitudes (annual β_opt between 2° and 11°, depending on the climatic zone analyzed). This narrow range is physically consistent with the near-perpendicular solar incidence characteristic of equatorial regions, which favors smaller tilt angles compared to mid- and high-latitude locations. These results reinforce the validity and physical coherence of the vector-based approach, which effectively synthesizes the annual mean direction of direct irradiance using hourly DNI data, achieving equivalence with conventional methods that maximize annual irradiance on inclined planes.

The methodology was further compared to the study by Serrano-Guerrero et al. [24] for Ecuador, which optimized the annual solar capture on inclined planes using five established radiative models (Isotropic Diffuse, Liu–Jordan, Temps–Coulson, Klucher, and Pérez). Based on TMY datasets (8760 h), their study reported annual tilt angles ranging from 12° to 19° and azimuth orientations between 20° and 60° relative to true north for the main Ecuadorian cities. The values obtained in the present study for tilt (β) = 5.73° and azimuth (θ_s) = 59.15° fell slightly below and within those ranges, respectively. This difference was expected since the proposed method optimizes the mean direction of DNI rather than the total plane-of-array irradiance, which includes both diffuse and reflected components. Thus, the resulting angles correspond to the direction of the maximum direct solar energy, not necessarily the configuration that maximizes the total irradiance.

Finally, our results aligned with those of Jacobson and Jadhav [25], who computed global optimal tilt angles using historical meteorological datasets and the PVWatts model. Their findings confirmed similar values for Quito, Ecuador (latitude ~0°), where the annual optimal tilt angle was approximately 3°, oriented toward the north. This agreement among radiometric, empirical, and vectorial methodologies supports the robustness and reliability of the proposed model as a rapid and accurate analytical tool for determining the optimal photovoltaic installation angles in equatorial regions.

4. Discussion

The results obtained through the three-dimensional vector representation of DNI provide a physically consistent interpretation of solar radiation behavior in equatorial environments. The derived tilt (5.73°) and azimuth (59.15°) angles represent the annual mean direction of maximum direct solar irradiance for fixed photovoltaic (PV) systems in Guayaquil, Ecuador. This approach effectively integrates the annual geometric behavior of the three-dimensional solar vector and translates it into an optimized configuration for energy capture.

The low optimal tilt angle is consistent with geographical proximity to the Earth’s equator, where the solar altitude remains high throughout most of the year and direct radiation is maximized under nearly horizontal configurations. This finding aligns with previous studies reporting optimal tilt angles between 0° and 10° for tropical latitudes, where the solar trajectory remains nearly perpendicular to the surface [23,24]. The azimuth orientation of 59.15° (approximately northeast) indicates a slight deviation from true north, attributable to the asymmetric hourly distribution of solar irradiance influenced by atmospheric conditions and seasonal variations.

When compared with well-established radiometric transposition models such as those of Hay, Klucher, and Perez [15,16,17], the proposed methodology demonstrated comparable accuracy while substantially reducing the computational demands associated with anisotropic modeling. Studies performed in similar latitudes, including those by Warburg et al. in Tanzania [23] and Serrano-Guerrero et al. in Ecuador [24], reported analogous results, reinforcing the physical validity of the present model. These works also confirm that in low-latitude regions, annual variability of the optimal tilt angle remains limited due to the near-vertical solar path, consistent with the present findings.

Beyond empirical consistency, the proposed methodology introduces conceptual advancement by treating DNI as a vector magnitude that simultaneously incorporates directional and intensity information. This enables the synthesis of the annual mean solar flux direction without explicitly modeling diffuse or reflected components, thereby reducing the reliance on high-resolution radiometric data and enhancing applicability in regions with limited meteorological infrastructure. Consequently, the method constitutes an efficient, geometrically grounded, and computationally lightweight tool for the preliminary estimation of optimal tilt and orientation angles for fixed PV systems in tropical and equatorial environments.

Furthermore, its analytical structure allows for potential applications in system design, calibration, and urban energy planning, as well as in renewable microgrid modeling. The vector representation can be extended to bifacial or tracking systems and integrated into artificial intelligence algorithms or digital twins for dynamic performance monitoring. Overall, the three-dimensional vector interpretation of solar irradiance represents a versatile approach that contributes to the sustainable development of solar technologies in data-limited or resource-constrained contexts.

Finally, future research should expand the scope of this model by incorporating diffuse and reflected radiation components, validating its performance under different climatic regimes, and conducting uncertainty analyses against conventional radiometric models.

5. Conclusions

Based on the three-dimensional vector representation methodology of DNI, the optimal installation angles for fixed photovoltaic (PV) systems in Guayaquil, Ecuador, were determined. The results indicate an optimal tilt angle of 5.73° and an azimuth orientation of 59.15° relative to true north, values that represent the average annual direction of the maximum direct solar irradiance capture at the study site.

The low tilt angle obtained is consistent with the geographical location near the equatorial line, where the solar trajectory exhibits high elevations throughout most of the year, favoring reduced inclinations for optimal incident radiation. The azimuth orientation of 59.15° (approximately northeast) reflects a specific correction derived from the vectorial approach, which accounts for the hourly and seasonal distribution of direct irradiance.

The results are consistent with previous studies conducted in tropical and equatorial regions, which recommend tilt angles between 0° and 10° to maximize solar radiation capture in fixed systems [26]. Therefore, the proposed methodology represents a simplified, geometrically rigorous, and computationally efficient alternative to conventional transposition-based methods, as it explicitly integrates the annual hourly behavior of irradiance in a vector form.

The main contribution of this study lies in offering a vector-based analytical framework that synthesizes the directional behavior of solar flux without relying on complex transposition models. This approach enhances the optimization of photovoltaic design, urban energy planning, and renewable microgrid modeling in contexts with limited meteorological data availability. Furthermore, its integration into simulation platforms or digital twin environments can support performance monitoring, predictive maintenance, and energy management strategies, strengthening the sustainable exploitation of solar resources in tropical regions.