Abstract
Bifacial photovoltaic (PV) modules have the advantage of using light reflected off of the ground to contribute to power production. Predicting the energy gain is challenging and requires complex models to do so accurately. Often, module degradation over time is neglected in models for the sake of simplicity or is underestimated. Comparing outdoor and indoor current–voltage (I–V) performance for bifacial modules is more challenging than for monofacial modules, as there are additional variables to consider such as rear albedo non-uniformity, cell mismatch, and their effects on temperature. This challenge is compounded when heterogeneous degradation modes occur, such as polarization-type potential-induced degradation (PID-p). To examine the effects of PID-p on I–V predictions using an empirical data-driven approach, 16 bifacial PERC modules are installed outdoors on racks with different albedo conditions. A subset is exposed to high-voltage biases of −1500 V or +1500 V. Outdoor data are traced at irradiance ranges of 150–250 W/m2, 500–600 W/m2, and 900–1000 W/m2. These curves are corrected using control module temperature, wire resistivity, and module resistance measured indoors. We examine several methods to transform indoor I–V curves to accurately, and more simply than existing methods, approximate outdoor performance for bifacial modules without and with varying levels of PID-p degradation. This way, bifacial performance modeling can be more accessible and informed by fielded, degraded modules. Distributions of percent errors between indoor and outdoor performance parameters and Mean Absolute Percent Errors (MAPEs) are used to assess method quality. Results including low-irradiance data (150–250 W/m2) are discussed but are filtered for quantifying method quality as these data introduce substantial errors. The method with the most optimal tradeoff between low MAPE and analysis simplicity involves measuring the front side of a module indoors at an irradiance equal to plane-of-array irradiance plus the product of module bifaciality and albedo irradiance. This method gives MAPE values of 1–6.5% for non-degraded and 1.6–5.9% for PID-p degraded module performance.
1. Introduction
1.1. Background and Motivation
The world market share of glass–glass modules is projected to grow to at least 50% by the year 2027 and was over 30% in 2022 [1]. This is due at least in part to the power gain from allowing light from the rear side to transmit to the photovoltaic (PV) cells. Passivated emitter and rear cell (PERC) technology has dominated the market share for several years but is expected to be displaced by tunnel oxide passivated contacts (TOPCons) in coming years. Regardless of cell technology, comparing outdoor to indoor performance is challenging, with efforts from several groups made to address it for monofacial and bifacial current–voltage (I–V) performance [2,3,4,5,6], with further challenges when accounting for module degradation. Characterizing bifacial modules is another challenge which requires the rear-side contribution to be carefully considered [7,8].
Traditionally, PV system degradation is assessed year over year by tracking the inverter power output. The challenges with this approach include inverter clipping due to increasing DC-to-AC ratios [9], curtailment, and operation and maintenance issues such as tracker failure. These often prevent an accurate assessment of the true degradation and even lead to greater degradation than what is typically observed at the module level. This has important implications for plant operators who would like to hold manufacturers accountable to their product and performance warranty. Indoor module characterization is the best-known approach to assess the degradation of a single module; however, for systems on the MW to GW scale with installations of hundreds of thousands if not millions of modules, it is not logistically possible nor financially viable to perform indoor characterization on every single module every year. In fact, best industry practice dictates that PV plant operators annually select a subset of 25–30 modules to be brought inside for characterization so that they can accurately track degradation.
There are changes coming to address this challenge. For example, modern string inverters are improving their capabilities and many now offer string level diagnostics like I–V curve tracing. Module-level electronics are also getting more traction as they are becoming more financially attractive and could offer an alternative to indoor module characterization. However, even in these scenarios, outdoor data is much noisier, especially in the case of bifacial modules (varying irradiance, albedo, temperature through the day) with respect to indoor data collected at a constant irradiance and temperature. Indoor data is easily comparable because conditions are kept constant and provide the advantage of being able to eliminate the contribution of light on the rear side, effectively making it a “monofacial” measurement. This allows both sides to be measured independently.
It is unclear today how to accurately compare indoor and outdoor I–V because of varying environmental conditions or how to decouple front and rear contributions if possible. This is an ongoing area of research. This work seeks to close that gap by comparing I–V curves taken outdoors (varying conditions, including albedo conditions due to installation configuration, sun elevation, time of the day, degradation types) with indoor data taken around the same time frame.
Comparing outdoor data to indoor data at standard test conditions (STCs) could also bring forth methods of modeling outdoor performance for accurate energy yield predictions and inform testing standards development on how to best test bifacial modules to correlate to reliability. This work is pertinent to industry (particularly for plant operators who have access to string or module level data) in accurately estimating not only energy production but also string or module level degradation in situ. Ultimately, this can significantly reduce uncertainties and costs associated with warranty and maintenance planning. This work is also pertinent to researchers involved in outdoor testing and in bifacial module performance modeling by providing a benchmark framework to build upon. This work considers both regular and degraded modules for completeness.
The common method of measuring front and rear I–V at STC may not always reflect how the module will perform in the field, especially for polarization-type potential-induced degradation (PID-p). One complication is accounting for module degradation and the relationship between the rear side and front side degradation. Most work that has been performed in this field is on analyzing bifacial performance apart from degradation, such as investigating the influence of environmental and installation conditions on bifacial gain [2,3,6,8,10,11,12,13]. Accounting for degradation complicates modeling bifacial performance, and to the authors’ knowledge, this has yet to be addressed in the literature. This is a necessary next step in improving performance modeling to ensure accurate reliability and cost–benefit analyses. Exceptional complications are expected to be present for PID-p.
PID-p is a degradation mode that is related to charge accumulation in the dielectric layers due to surface passivation degradation [14]. In the case of PERC cells, the rear side can experience PID-p when the cells experience high negative voltages, leading to positive charge accumulation on the passivation layer which increases minority carrier electron recombination [14]. Maximum power () loss occurs primarily due to a reduction in short-circuit current () and an increase of the first diode saturation current. Open-circuit voltage () degrades to a minor degree while fill factor () is typically intact or with minor degradation. Rear-side PID-p degradation is more strongly pronounced at low front and rear irradiances [14,15]. Cell to cell, PID-p is strongly heterogeneous as shown by representative electroluminescence (EL) images of the same module before and after PID-p degradation in Figure 1.

Figure 1.
Representative rear-side EL images at nameplate for a module (a) before and (b) after PID-p degradation.
1.2. Addressing Challenges
Standard methods for correcting or normalizing performance data for monofacial modules are mostly empirical methods. Some standard corrections blend theoretical physical principles (e.g., diode equations) with empirical data adjusted or calibrated through measured field or laboratory data.
We also consider empirical methods, specifically data-driven empirical normalization methods (no experimentally derived correction coefficients and equations here). In our case, we measured field and laboratory I–V data and applied various normalization adjustments to enable meaningful comparison between outdoor and indoor conditions. Several methods have been attempted to transform indoor I–V curves of bifacial PERC modules, with and without PID-p degradation, to outdoor I–V curves. The heterogeneous nature of PID-p degradation allows us to evaluate how well these methods match I–V performance based on varying levels of degradation. Models tend to be complex with many variables needed to properly account for rear-side contributions, with rear-side degradation neglected. The methods presented in this work are simple to implement and require indoor front and rear I–V curves at STC. A reliable method of predicting outdoor performance can be used to monitor outdoor I–V and transform to STC conditions for better comparisons, as transforming indoor I–V to predict outdoor performance can be reversed and applied to outdoor I–V.
2. Materials and Methods
2.1. Outdoor Testbed and Performance Measurements
A total of 16 bifacial PERC modules were installed on a high-voltage (HV) testbed at the Florida Solar Energy Center (FSEC) in Cocoa, FL. The testbed was designed with racks which simulate different installation conditions: one rack for simulated ground, one rack for residential rooftop, and two open racks, shown in Figure 2a, Figure 2b, and Figure 2c, respectively (only one open rack is shown). Ground installation was simulated using a rolling structure with an open box on the top for soil. For residential rooftop, a rolling structure covered with black ethylene propylene diene monomer shingles.

Figure 2.
Racks on the HV testbed for (a) simulated ground, (b) simulated residential rooftop, and (c) open rack installation conditions.
Each module was connected to a resistor to load the modules at approximately . Three modules from each rack were biased during the day while one module was not biased to act as the control. Three modules on one open rack, three modules on the simulated ground rack, and three modules on the simulated roof rack were biased during the day with the cells at −1500 V with respect to the grounded frame, giving a total of nine modules biased at −1500 V. Three modules were biased on an open rack with the cells at +1500 V with respect to the grounded frame. As shown in [15], the modules used in this experiment do not experience potential-induced degradation PID-p at +1500 V of bias, and therefore, are included in the non-degraded dataset.
Each of the 16 modules underwent I–V tracing. Three traces were measured per day in the following irradiance windows: 150–250 W/m2, 500–600 W/m2, 900–1000 W/m2.
Ambient temperature is obtained from a meteorological station located adjacent to the HV testbed. For each installation condition, the racks were each equipped with LI-COR LR-200R irradiance sensors for plane-of-array (POA) and albedo measurements. Albedo sensors are installed 180° to the POA sensors. Omega Engineering Type SA1-T thermocouples are placed on the back of two modules per installation condition: one on a control module, the other on a biased module.
HV testing started after three months of light exposure. All I–V curves measured before voltage was applied is included in the non-degraded dataset for analysis. Due to complications with the equipment, the simulated roof rack was exposed to bias (−1500 V) approximately 5.5 weeks after the other racks. The I–V curves measured on this rack during these 5.5 weeks are included in the non-degraded dataset. A positive reverse bias (+1500 V) was applied during 10 days on the same rack, resulting in performance recovery. A bias of −1500 V was applied after this. After two days of exposure to −1500 V, the modules returned to the degraded state prior to exposure to +1500 V. The curves during these 12 days are omitted from the analysis to prevent mixing non-degraded and degraded module data together, removing only 0.5% of the total dataset (2.4% of the degraded dataset). This study focuses on comparing indoor to outdoor I–V curves rather than degradation analysis, and therefore, this is not expected to significantly influence the analysis.
These modules were uninstalled and brought inside periodically for indoor measurements. Multi-irradiance I–V and as a function of irradiance (suns-) were measured using a Sinton FMT-350 module flash tester. EL images were obtained at different bias levels using a modified consumer DSLR camera and an optical 950 nm longpass filter. All indoor measurements were performed on each side with the back side of the module covered to block reflection and at STC (AM1.5G spectrum, module temperature 25 °C ± 2 °C).
2.2. Data Quality Assurance
Any data impacted by testbed maintenance or equipment failure has been removed from the analysis. A sky stability filter is applied such that the standard deviation of the POA irradiance () one minute before and 30 s after the trace does not exceed 3. Notably, the outdoor I–V curves show significantly . The minimum measured on the front side indoors using is ≈78.4%; for comparison, ≈57% of the outdoor I–V curves show before applying corrections. After applying corrections for wire resistivity, measurement resistance, and temperature, this percentage changed to ≈19%. The remaining discrepancy in is most likely due to resistive losses in the measurement circuit which are not accounted for, errors in wire resistivity corrections (particularly for approximating wire temperature as the module temperature), rear-side cell mismatch losses due to spectral mismatch, and non-uniformity of the albedo irradiance [7].
Indoor I–V measurements on the rear module side for irradiances below the maximum outdoor albedo () value () were of dubious quality. Therefore, indoor I–V curves on the rear side at are used. This work only uses the measured rear maximum power current (), and since is linear with irradiance, a ratio of the albedo irradiance to is used to scale the at to extrapolate the at albedo irradiance. Importantly, the cover for the side opposite to what was being measured indoors likely did not prevent all reflection. It is possible that even the minor reflection of the cover increased the measured performance. As the rear side is less efficient than the front, rear-side measurements (cover blocking the front glass side) likely observe a disproportionately higher gain than for measuring the front side due to reflection.
2.3. Analysis
2.3.1. Outdoor Data Preparation
Outdoor I–V curves were first corrected for wire resistivity in the measurement circuit. The voltage drop across the wire at current I, denoted as , is calculated using Equation (1):
where I is the measured current, is the wire resistivity at the module temperature, L is the wire length, and A is the wire cross-sectional area. is calculated using Equation (2):
where is the standard temperature at 20 °C, T is the wire temperature, is the conductor temperature coefficient of copper, is the resistivity at , and is the resistivity at T.
Wire length is measured on the outdoor testbed. The 10AWG PV wire A = 5.26 mm2, − mm2/m, . Wire temperature is approximated using module temperature, and since only representative control modules have temperature measured, T is approximated as the control module temperature.
Furthermore, a series resistance () value is measured on the module indoors via comparing front-side I–V at 1000 W/m2 and pseudo-I–V calculated from suns- [16]. We assume that the primary sources of error are due to the outdoor measurement circuit and environmental conditions rather than the PV modules themselves, so using an value measured indoors could shift the outdoor closer to what the modules themselves are producing. Equations (3) and (4) were used to correct the outdoor voltage data using indoor :
where is the voltage at maximum power and is the pseudo-voltage at the pseudo-current = point. is used in Ohm’s law to correct for voltage:
Outdoor data are temperature corrected only after resistive corrections as temperature corrections are proportional to voltage values and are related to the PV device properties, while the resistive values are related to the measurement circuit. This way, corrections are applied to first reduce measurement uncertainty and then apply corrections based on the device. Both indoor and outdoor data are corrected to 25 °C, though indoor data were obtained at 25 °C ± 2 °C, and therefore, they have small changes. Both voltage and current were corrected using the manufacturer specification sheet’s temperature correction coefficients for voltage and current.
On average, the wire resistivity corrections increased outdoor by 0.58 abs% and the indoor corrections increased outdoor by 6.6 abs% and temperature corrections by 0.49 abs%. Together, these corrections increased the outdoor by an average of 7.6 abs%.
2.3.2. Indoor Data Transformations
Several methods are attempted to approximate the outdoor performance using indoor measurements. Each outdoor I–V curve is linked to a rear-side and front-side indoor I–V curve measured within at most ±28 days from the outdoor trace to ensure indoor data are as representative to outdoor data as possible. The front-side curve is taken at and the rear-side curve at 200 W/m2.
Each method makes assumptions with some differences. The following list shows all possible assumptions and the descriptions below mention which are used:
- Rear-side efficiency is equal to that of the front (i.e., bifaciality = 1) and for all irradiances;
- Albedo non-uniformity = 0;
- Cell mismatch effects are negligible;
- Rear spectral mismatch losses are negligible;
- Rear-side gain contributes negligibly to voltage and primarily to current;
- is a non-zero constant at 0 W/m2 200 W/m2.
Assumption 1 is clearly untrue but provides simple methods for tracking potential improvements. Assumption 2 is required as there are no uniformity measurements and uniformity changes with the sun’s path (daily and seasonally). Assumption 3 is expected to be fair for modules with no degradation; however, this assumption becomes progressively untenable as PID-p progresses on the rear side. Assumption 4 is required as there are no measurements on albedo spectrum taken. Assumption 5 is expected to hold more consistently in high irradiance ranges (>400 W/m2) as current changes more strongly with irradiance than voltage at those ranges [17,18]. Assumption 6 is required as the indoor rear-side I–V data up to the maximum measured W/m2 were of poor quality. Table 1 summarizes which assumptions each method makes.

Table 1.
Summary table showing assumptions for each method. * This assumption is made for the voltage values.
The methods are described as follows:
- Method 1
- Outdoor data are directly compared to indoor front side at . This provides a baseline for comparing how other analyses change the indoor curve.
- Method 2
- The indoor curve is taken at and is used primarily to compare to Method 3.
- Method 3
- The front-side curve is taken at . This method is using the equivalent irradiance in the IEC TS 60904-1-2 standard [19] using a based on . is calculated using of the rear side at 200 W/m2 and dividing by the front-side at 200 W/m2. Using times attempts to account for cell mismatch effects since is calculated from rear-side measurements.
- Method 4
- The front-side curve is split into voltage and current, with current values added by the rear at to account for rear cell mismatch. Since the is taken directly from rear-side measurements, is naturally included and cell mismatch losses are more closely approximated.
- Method 5
- The front-side current from Method 4 is combined with the voltage from Method 2. This accounts for and cell mismatch effects on current but assumes those have no effect on rear voltage contributions. Despite being similar to Method 3, the current values for this method are expected to be more accurate since it is using direct rear-side current measurements.
2.4. Comparison Methods
Once all I–V curves are prepared from outdoor measurements and transformed indoor measurements, we calculate , FF, , , , and . The percent error () of a parameter X between the outdoor and indoor measurements are calculated using Equation (5):
such that is a parameter derived from an I–V curve i. Percent errors are used since the outdoor data are considered the true values. Comparison quality is defined using the Mean Absolute Percent Error (MAPE) between the outdoor and indoor I–V parameters using Equation (6):
where n is the number of points used. MAPE is used to evaluate the accuracy of predicted values compared to true values. The outdoor data are considered the true values against which the transformed indoor data are compared, as the transformation are attempting to predict what the outdoor values would be. The analysis is split between non-degraded and degraded modules, such that degradation is qualified by exposure to a voltage bias which is known to induce PID-p in this module technology under the installation conditions. This is performed to examine how or if the degree of PID-p degradation influences the quality of the comparisons. For each indoor data transformation method, 95% of the degraded or non-degraded values (e.g., , ) are used to ensure a statistically representative set of values are used. values are filtered using Z-scores which leave 95% of the data remaining. Outliers (Z-score ≥ 3) constitute 0.09–2.8% of the values, so both outliers and other exceptionally large values are removed while maintaining a statistically significant proportion of the data.
3. Results and Discussion
Figure 3 shows the probability distribution functions (PDFs) of the for each method of transforming indoor data for each of the analyzed parameters. Note that the number of non-degraded curves (>16,000) used for analysis is significantly higher than that of the degraded curves (>4500). The comparisons between methods are made for all curves and for a subset obtained when W/m2. i.e., removing curves within the irradiance range of 150–250 W/m2 and keeping those in 500–600 W/m2 and 900–1000 W/m2. This conveniently fits the recommended irradiance range (>400 W/m2) for comparing monofacial and bifacial performance found in [8]. Besides calculating for Method 3 and measuring rear for Methods 4 and 5, the front-side (monofacial) data are being compared to the bifacial (outdoor) data.
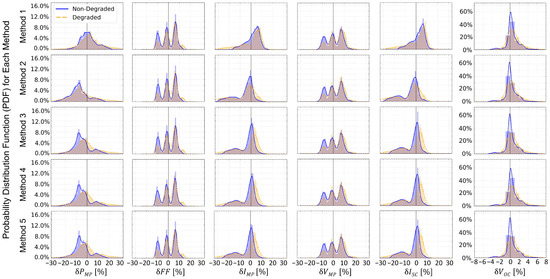
Figure 3.
Probability Distribution Functions (PDFs) for each parameter obtained for each method. Blue bars with solid blue lines represent non-degraded modules; orange bars with dashed orange lines represent degraded modules. Each bar represents a bin of 1%. Colored lines show kernel density estimations. The vertical black line is a visual guide for percent error of parameter , , equal to 0%. Each row shows the results for methods 1–5 from top to bottom. Each column shows the distribution of between the outdoor parameter and the transformed indoor I–V curve. Left to right, they show , FF, , , , and . Note the scaling for the x-axes and y-axes for all parameters is the same except for .
The filtered subset has >9200 non-degraded curves and >2100 degraded curves. For the dataset without filtering and for the filtered dataset, a random sample of non-degraded curves equal in number to the degraded curves were taken and the MAPE values were recalculated to assess validity in comparing subsets of different sample sizes. For data including all irradiances (i.e., without irradiance filtering), changes in MAPE ranged from −0.16 abs% to +0.12 abs% compared to the set of >16,000 curves; for the filtered subset, changes in MAPE ranged from −0.21 abs% to +0.09 abs% compared to the set of >9200 curves. The differences per MAPE are small compared to the MAPE values for each parameter.
We will focus mostly on the influence of each method on comparison quality using MAPE and distributions, and the impact of irradiance filtering and comparison quality. MAPE values for non-degraded and degraded modules are tabulated in Table 2 and Table 3, respectively, and distributions are shown in Figure 3. These MAPE values and distributions are separated to evaluate the impact of degradation (particularly, PID-p) on bifacial I–V predictions.

Table 2.
Mean Absolute Percent Error (MAPE) values between outdoor and indoor I–V parameters after transformation using each method on non-degraded modules. Values are shown for I–V curves obtained at all intensity ranges (150–1000 W/m2) and at a subset (500–1000 W/m2). Values in parentheses were taken from the subset. Left to right, columns show , FF, , , , , and the sum of MAPE values for each method.

Table 3.
Mean Absolute Percent Error (MAPE) values between outdoor and indoor I–V parameters after transformation using each method on degraded modules. Values are shown for I–V curves obtained at all intensity ranges (150–1000 W/m2) and at a subset (500–1000 W/m2). Values in parentheses were taken from the subset. Left to right, columns show , FF, , , , , and the sum of MAPE values for each method.
3.1. Impact of Low-Irradiance Data
For non-degraded and degraded modules, keeping data at W/m2 reduced the MAPE across all methods for (0.95–1.2 abs%), (0.96–4.9 abs%), and (0.59–4.6 abs%), while MAPE of slightly increased (0.04-0.11 abs%). MAPE of for degraded modules decreased across all methods, while it varied little across all methods for non-degraded modules. Degraded module MAPEs decreased more than the non-degraded after filtering (1.9–3.4 abs%), (2.1–7.7 abs%), and (1.0–6.7 abs%).
The degraded MAPE of increased more (0.28–0.34 abs%) than that of the non-degraded and the degraded PDF in Figure 3 tends to be more positive than for the non-degraded, suggesting over-correction of outdoor data. PID-p most notably reduces module , and consequently, [14,15], so the difference in temperature between degraded modules and non-degraded controls increases as PID-p progresses due to reduced Joule heating. Outdoor values were corrected using the representative control module temperature and nameplate temperature coefficients. Temperature coefficients have been observed to change depending on the degradation state of the module [20], though one study shows effectively no degradation in temperature coefficients over eight years of outdoor exposure, particularly when using data at >900 W/m2 irradiance [21]; however, the study in [21] uses monofacial modules without PID-p. This suggests that errors in temperature coefficients are lower for the non-degraded than the degraded modules. It is likely that the temperature discrepancy changes in the coefficient with respect to temperature and irradiance [22] and degradation state contribute to errors in outdoor corrections. At low irradiances, the control and degraded module temperatures will be closer in value since the front-side performance dominates, reducing the temperature correction error; removing the low-irradiance data consequently increases the MAPE of degraded for the benefit of reduced MAPE for the remaining parameters except .
For all modules, a notable increase in MAPE for (0.25–0.64 abs%) is shown after filtering low irradiance data (Table 2 and Table 3). Three distinct peaks appear in their PDFs in Figure 3. Comparing the values at different irradiances, these center most closely around zero for low irradiance, then diverge in greater degree as irradiance increases. Removing low-irradiance data shrinks the rightmost peak in from ≈10% to ≈2% and for , from ≈8% to ≈1%. MAPE was arbitrarily smaller for these parameters since the PDF was nearly centered around zero prior to filtering. After filtering, the low rightmost peak in is mostly eliminated and the left tail in and are completely removed, leading to narrower PDFs and smaller MAPEs. The overall reductions in MAPEs and narrowing PDFs comes at the cost of sample size reduction, consequently reducing the scope of what is considered useful I–V data.
Higher uncertainties in low-irradiance I–V tracing is partly due to rapid fluctuations in incident irradiance [23]. The effects are more pronounced in low-irradiance conditions and are expected to compound with the uncertainties introduced in bifacial modules, namely rear non-uniformity [24,25,26,27] and spectral mismatch [24,28]. Rear non-uniformity as high as 21.5% has been reported [24]. A decrease of rear non-uniformity from 12% to 5% was observed by elevating the module one meter but saw negligible improvements at higher elevations [25]. This is promising for the open rack modules, as they are approximately two meters above the ground, though the modules on the simulated roof and ground structures are much closer to the structures (<0.5 m) and are expected to suffer more from non-uniformity.
Non-uniformity, along with , are not static and are challenging to account for [27]. A constant calculated at 200 W/m2 is used in Method 3 due to dubious I–V quality on indoor measurements below <150 W/m2. Improved data quality at irradiance levels < 150 W/m2 would allow irradiance-dependent to be calculated. This is expected to improve the quality of Method 3 though errors due to variations in albedo spectrum and degradation states would remain. Spectral mismatch may introduce lower errors than expected, as the spectral mismatch for AM1.5G solar simulators is compared to that of reflected spectra on gravel at 135 W/m2 irradiance with negligible effect [24]; however, these modules were not installed above gravel, and other factors such as installation angle and time of day play a role.
The remainder of this discussion focuses on data with low irradiances filtered out.
3.2. Impact of Indoor Transformation Methods
We hypothesized that Method 5 would yield the closest comparisons between indoor and outdoor data, as it is the only method that uses both (1) directly measured rear performance and (2) accounts for impact on voltage. However, its performance is similar to Methods 3 and 4. This suggests that the impact of on module voltage is small or that the errors in are sufficiently large to overshadow the impact of on voltage. Both are likely, as in several studies, monofacial and bifacial modules are studied to examine performance gain from bifaciality and small differences are observed for [2,3,6] and [3]. Methods 3–5 have approximately equal MAPEs except Method 4 gives higher values for (non-degraded, 0.30–0.32 abs% higher; degraded, 0.22 abs% higher) than Methods 3 and 5.
Method 2 leads to the highest MAPE values in for both datasets. For degraded modules, the remaining MAPEs from Method 2 are the lowest of the other methods. For non-degraded modules, MAPEs for , , and are comparable to Methods 3–5. MAPEs for and are much lower than for Method 1 (1.9 abs% and 2.3 abs% lower, respectively) but still higher than for Methods 3–5 (0.80 abs% and 0.77 abs% higher, respectively). The reduced MAPE in current is clearly due to accounting for but without accounting for , Method 2 over-corrects current. Applying to reduces MAPE further and brings the distribution closer to zero (note how the PDFs in Figure 3 change from underestimating current in Method 1, to overestimation in Method 2, then slightly shifting towards zero).
Based on both non-degraded and PID-p degraded modules in this study, using data at W/m2, Method 3 is overall recommended as it provides the best tradeoff between low MAPE values and analysis simplicity. While MAPE of for non-degraded modules using Method 1 is the lowest, it is difficult to conclude that Method 1 is better since outdoor measurement resistance leads to substantially low measured . Method 3 is more realistic, as it factors both contributions and rear-side performance (). If accurate current values are prioritized, Method 3 is the most effective for non-degraded modules, but Method 2 is the most effective for modules with PID-p degradation. Method 2 gives the highest MAPE for PID-p degraded modules but one could use Method 3 for and Method 2 for the remaining parameters.
4. Conclusions
Outdoor bifacial I–V data were corrected for the resistivity of the wires in the measurement circuit, for measurement resistance using the indoor module , and temperature effects on current and voltage. Four simple methods of transforming indoor I–V curves, using measurements isolating the front and rear sides, were used to predict outdoor I–V performance. The comparison quality is quantified using the MAPE for each parameter. Degraded and non-degraded module data are analyzed separately to evaluate transformation methods for bifacial modules themselves and with added sources of error for degradation; however, based on both non-degraded and PID-p degraded module data at W/m2, Method 3 is recommended as it provides the best tradeoff between low MAPE values (i.e., closest fits between predicted and actual outdoor performance) and analysis simplicity (only need , and ). This method uses the indoor front-side I–V curve at an irradiance . Distributions of percent errors, , show that tended to be overestimated but this is attributed primarily to outdoor measurement resistance. MAPE of for non-degraded modules is lowest in Method 1 for this same reason. Method 2 can be used for modules with PID-p or other severe current losses if minimizing MAPE for and is most desired. Overall, Method 3 provides the best tradeoff between strong predictions and analysis simplicity.
The I–V curves within the range of 150–250 W/m2 introduced significant errors. Spectral mismatch between cells and albedo, non-uniformity of albedo, and cell mismatch (especially for degraded modules) likely contributed the most to these errors. Other errors include outdoor measurement circuit resistance, a cover for indoor measurements whose reflectivity is non-zero, and assumptions in module and wire temperatures.
Opportunities for improvement and expansion:
- Use EL image analysis to estimate degree of cell mismatch and calculate a metric to correct curves.
- Measure non-uniformity on the rear side for different installation conditions and different incident sunlight angles and calculate a metric to correct curves.
- Measure modules indoors with a nearly perfectly non-reflective cover and compare to outdoor curves on the same modules.
- Apply the model in [27] to account for changes in and non-uniformity throughout the day.
Author Contributions
Conceptualization and methodology D.J.C., C.M., P.H. and H.P.S.; software, D.J.C. (Python), C.M. and R.M.S. (JMP); validation, D.J.C. and C.M.; formal analysis, D.J.C., C.M., R.M.S. and H.P.S.; investigation, D.J.C., C.M., R.M.S., M.M., B.A.T., J.B. and H.P.S.; resources, D.J.C., C.M., R.M.S., M.M. and H.P.S.; data curation, D.J.C., C.M., R.M.S., M.M. and H.P.S.; writing—original draft preparation, D.J.C. and C.M.; writing—review and editing—D.J.C., C.M., R.M.S., M.M., P.H., F.L., B.A.T., J.B., G.T. and H.P.S.; visualization, D.J.C.; supervision, H.P.S.; project administration, D.J.C. and H.P.S.; funding acquisition, H.P.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the U.S. Department of Energy’s Solar Energy Technologies Office under grant number DE-EE0009345. The APC was graciously wavered by MDPI.
Data Availability Statement
Data available upon request.
Conflicts of Interest
Author Ryan M. Smith was employed by the company Pordis LLC. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AM1.5G | Air Mass 1.5 Global |
| FF | Fill Factor |
| G | Irradiance |
| HV | High-Voltage |
| Current at Maximum Power | |
| Short-Circuit Current | |
| I–V | Current–Voltage |
| MAPE | Mean Absolute Percent Error |
| PERC | Passivated Emitter and Rear Cell |
| PID | Potential-Induced Degradation |
| PID-p | Polarization-type Potential-Induced Degradation |
| Maximum Power, Power at the Maximum Power Point |
| POA | Plane of Array |
| PV | Photovoltaic |
| TOPCon | Tunnel Oxide Passivated Contact |
| Voltage at Maximum Power | |
| Open-Circuit Voltage |
References
- International Technology Roadmap for Photovoltaic (ITRPV), 14th ed.; Technical Report; Verband Deutscher Maschinen und Anlagenbau (German Engineering Federation): Frankfurt, Germany, 2023.
- García, M.A.; Quispe, G.R.; Zamudio, M.A.; Conde, L.A.; Angulo, J.R.; Berastain, A.E.; Töfflinger, J.A. Outdoor I-V characterization of tilted and vertical bifacial PV modules. J. Phys. Conf. Ser. 2023, 2538, 012002. [Google Scholar] [CrossRef]
- Dolara, A.; Leva, S.; Mazzeo, D.; Ogliari, E. Characterization of Bifacial Photovoltaic Modules Based on I-V Curves Outdoor Measurement. In Proceedings of the 2023 IEEE International Conference on Environment and Electrical Engineering and 2023 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Madrid, Spain, 6–9 June 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Kawagoe, K.; Hishikawa, Y.; Yamada, N. Outdoor Direct STC Performance Measurement of PV Modules Based on a Sun-Shading Technique. IEEE J. Photovoltaics 2017, 7, 1725–1730. [Google Scholar] [CrossRef]
- Polo, J.; Martín-Chivelet, N.; Alonso-García, M.C.; Zitouni, H.; Alonso-Abella, M.; Sanz-Saiz, C.; Vela-Barrionuevo, N. Modeling I-V curves of photovoltaic modules at indoor and outdoor conditions by using the Lambert function. Energy Convers. Manag. 2019, 195, 1004–1011. [Google Scholar] [CrossRef]
- Gu, W.; Li, S.; Liu, X.; Chen, Z.; Zhang, X.; Ma, T. Experimental investigation of the bifacial photovoltaic module under real conditions. Renew. Energy 2021, 173, 1111–1122. [Google Scholar] [CrossRef]
- Singh, J.P.; Aberle, A.G.; Walsh, T.M. Electrical characterization method for bifacial photovoltaic modules. Sol. Energy Mater. Sol. Cells 2014, 127, 136–142. [Google Scholar] [CrossRef]
- Baloch, A.A.; Hammat, S.; Figgis, B.; Alharbi, F.H.; Tabet, N. In-field characterization of key performance parameters for bifacial photovoltaic installation in a desert climate. Renew. Energy 2020, 159, 50–63. [Google Scholar] [CrossRef]
- Matam, M.; Smith, R.M.; Seigneur, H. PV Module Degradation Due to Frequent and Prolonged Inverter Clipping: A Preliminary Study. In Proceedings of the 2022 IEEE 49th Photovoltaics Specialists Conference (PVSC), Philadelphia, PA, USA, 5–10 June 2022; pp. 0596–0603. [Google Scholar] [CrossRef]
- González-Moreno, A.; Mazzeo, D.; Dolara, A.; Ogliari, E.; Leva, S. Outdoor Performance Comparison of Bifacial and Monofacial Photovoltaic Modules in Temperate Climate and Industrial-like Rooftops. Appl. Sci. 2024, 14, 5714. [Google Scholar] [CrossRef]
- Lee, S.; Nam, J.; Choi, D.; Jang, H.; Lee, Y.; Sohn, J.W.; Hong, K.K.; Kim, D.; Kang, Y.; Bae, S.; et al. Characterization of rear-side potential-induced degradation in bifacial p-PERC solar modules. Sol. Energy Mater. Sol. Cells 2024, 278, 113131. [Google Scholar] [CrossRef]
- Park, H.; Jeong, J.; Shin, E.; Kim, S.; Yi, J. A reliability study of silicon heterojunction photovoltaic modules exposed to damp heat testing. Microelectron. Eng. 2019, 216, 111081. [Google Scholar] [CrossRef]
- Patel, M.T.; Vijayan, R.A.; Asadpour, R.; Varadharajaperumal, M.; Khan, M.R.; Alam, M.A. Temperature-dependent energy gain of bifacial PV farms: A global perspective. Appl. Energy 2020, 276, 115405. [Google Scholar] [CrossRef]
- Molto, C.; Oh, J.; Mahmood, F.I.; Li, M.; Hacke, P.; Li, F.; Smith, R.; Colvin, D.; Matam, M.; DiRubio, C.; et al. Review of Potential-Induced Degradation in Bifacial Photovoltaic Modules. Energy Technol. 2023, 11, 2200943. [Google Scholar] [CrossRef]
- Mahmood, F.i.; Li, F.; Hacke, P.; Molto, C.; Colvin, D.; Seigneur, H.; TamizhMani, G. Susceptibility to polarization type potential induced degradation in commercial bifacial p-PERC PV modules. Prog. Photovoltaics Res. Appl. 2023, 31, 1078–1090. [Google Scholar] [CrossRef]
- Sinton, R.; Cuevas, A. A Quasi-Steady-State Open-Circuit Voltage Method for Solar Cell Characterization. In Proceedings of the 16th European Photovoltaic Solar Energy Conference, Glasgow, Scotland, 1–5 May 2000; pp. 1152–1155. [Google Scholar]
- Colvin, D.J.; Iqbal, N.; Yerger, J.H.; Li, F.; Sinha, A.; Vicnansky, G.; Brummer, G.; Zheng, N.; Schneller, E.J.; Barkaszi, J.; et al. Degradation of Monocrystalline Silicon Photovoltaic Modules from a 10-Year-Old Rooftop System in Florida. IEEE J. Photovoltaics 2023, 13, 275–282. [Google Scholar] [CrossRef]
- Colvin, D.J.; Schneller, E.J.; Davis, K.O. Impact of interconnection failure on photovoltaic module performance. Prog. Photovoltaics Res. Appl. 2021, 29, 524–532. [Google Scholar] [CrossRef]
- IEC TS 60904-1-2; Photovoltaic Devices—Part 1-2: Measurement of Current-Voltage Characteristics of Bifacial Photovoltaic (PV) Devices. IEC: Geneva, Switzerland, 2019.
- Piliougine, M.; Oukaja, A.; Sidrach-de Cardona, M.; Spagnuolo, G. Temperature coefficients of degraded crystalline silicon photovoltaic modules at outdoor conditions. Prog. Photovoltaics Res. Appl. 2021, 29, 558–570. [Google Scholar] [CrossRef]
- Paudyal, B.R.; Imenes, A.G. Investigation of temperature coefficients of PV modules through field measured data. Sol. Energy 2021, 224, 425–439. [Google Scholar] [CrossRef]
- Gasparin, F.P.; Kipper, F.D.; Oliveira, F.S.d.; Krenzinger, A. Assessment on the variation of temperature coefficients of photovoltaic modules with solar irradiance. Sol. Energy 2022, 244, 126–133. [Google Scholar] [CrossRef]
- Hishikawa, Y.; Doi, T.; Higa, M.; Yamagoe, K.; Ohshima, H. Precise Outdoor PV Module Performance Characterization Under Unstable Irradiance. IEEE J. Photovoltaics 2016, 6, 1221–1227. [Google Scholar] [CrossRef]
- Monokroussos, C.; Gao, Q.; Zhang, X.; Lee, E.; Wang, Y.; Zou, C.; Rimmelspacher, L.; Castro, J.B.; Schweiger, M.; Herrmann, W. Rear-side spectral irradiance at 1 sun and application to bifacial module power rating. Prog. Photovoltaics Res. Appl. 2020, 28, 755–766. [Google Scholar] [CrossRef]
- Ganesan, K.; Winston, D.P.; Sugumar, S.; Prasath, T.H. Performance investigation of n-type PERT bifacial solar photovoltaic module installed at different elevations. Renew. Energy 2024, 227, 120526. [Google Scholar] [CrossRef]
- Ozkalay, E.; Lopez-Garcia, J.; Pinero-Prieto, L.; Gracia-Amillo, A.; Kenny, R.P. Evaluation of the non-uniformity of rear-side irradiance in outdoor mounted bifacial silicon PV modules. AIP Conf. Proc. 2019, 2147, 020011. [Google Scholar] [CrossRef]
- Zhang, Q.; Peng, J.; Luo, Y.; Wang, M.; Wang, S.; Tan, Y.; Ma, T. Development of a novel power generation model for bifacial photovoltaic modules based on dynamic bifaciality. Energy Convers. Manag. 2025, 324, 119305. [Google Scholar] [CrossRef]
- Riedel-Lyngskær, N.; Ribaconka, M.; Pó, M.; Thorseth, A.; Thorsteinsson, S.; Dam-Hansen, C.; Jakobsen, M.L. The effect of spectral albedo in bifacial photovoltaic performance. Sol. Energy 2022, 231, 921–935. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).