Evaluation of a Hybrid Solar–Combined Heat and Power System for Off-Grid Winter Energy Supply

Abstract

The study investigates a hybrid energy system integrating photovoltaic (PV) panels, micro-CHP units, battery storage, and thermal storage to meet the winter energy demands of a residential building in Bacău, Romania. Using real-world experimental data from amorphous, polycrystalline, and monocrystalline PV panels, C++ Model 1 simulates building energy needs and PV system performance under varying irradiance levels. The results show that PV systems alone cannot meet the total winter demand, with polycrystalline slightly outperforming monocrystalline, yet still falling short. A second computational model (C++ Model 2) simulates hybrid energy flow, demonstrating how the CHP unit and storage systems can ensure off-grid autonomy. The model dynamically manages energy between components based on daily irradiance scenarios. The findings reveal critical thresholds for PV surplus, optimal CHP sizing, and realistic battery and thermal storage needs. This paper provides a practical framework for designing efficient, data-driven hybrid solar–CHP systems for cold climates. The novelty lies in the integration of real-world PV efficiency data with a dynamic irradiance-driven simulation framework, enabling precise hybrid system sizing for winter-dominant regions.

1. Introduction

Photovoltaic–CHP (Combined Heat and Power) hybrid systems have proven to be a reliable option for off-grid residential supply, especially in cold regions where solar output drops during winter. A simulation for a typical German home (temperate cold climate) shows that when irradiance is low, the micro-CHP unit shoulders the electric and thermal peak loads, raising self-consumption to 80% and cutting fossil fuel demand by 40–60% [1]. Likewise, a fully islanded setup combining PV, a SOFC (Solid Oxide Fuel Cell)-based micro-CHP, and seasonal heat storage covers 100% of the annual electricity needs, provides 95% of the winter heat demand, and lowers CO₂ emissions by 88.6% compared with conventional solutions [2]. These findings confirm that PV-CHP integration boosts overall energy yield, enhances self-sufficiency, and minimizes dependence on external energy sources under challenging climatic conditions.

Coupling rooftop PV panels with residential micro-CHP provides a highly efficient, low-carbon pathway for household energy supply. In a micro-grid composed of a 3.5 kWp PV array, a 1.3–4.7 kWe/4–12.5 kWth micro-CHP, and a 5 kWh battery, Cardoso et al. cut grid imports by about 45% and pushed the overall efficiency above 85%, all while delivering both hot water and electricity in island mode [3]. Complementing this, Pipicelli et al. showed that applying a prescient model-predictive control scheme to a battery-supported PV-CHP system boosted primary-energy savings by up to 12%, smoothed residual grid draws, and trimmed fuel use and CO₂ emissions, thereby increasing household self-sufficiency [4]. Together, these studies confirm that hybrid solar–CHP architectures outperform standalone PV by raising energy yield, flattening grid reliance, and further lowering carbon intensity.

A growing body of recent research underscores the technical and economic viability of PV–CHP hybrid systems in off-grid residential contexts, especially in cold climates. Control strategies are central to optimizing system performance: hierarchical and model predictive control schemes have been shown to reduce CO₂ emissions by up to 50% while substantially increasing energy self-sufficiency and robustness under variable weather conditions [5,6,7]. Seasonal performance is strongly influenced by the use and management of thermal energy storage, which has consistently demonstrated greater impact than batteries in maintaining winter efficiency, reducing CHP cycling, and stabilizing thermal output. Optimal system configurations typically involve sizing CHP units to meet 60–80% of the peak thermal demand and PV arrays to supply around 50% of the annual electrical consumption [8,9,10]. Both experimental and simulation-based studies report primary energy savings of 35–50%, CO₂ reductions of 30–60%, and self-sufficiency ratios exceeding 80% when advanced control strategies and appropriately dimensioned storage are implemented [11,12,13].

Recent advances in hybrid photovoltaic–thermal (PV/T) systems further reinforce their potential as high-efficiency alternatives or complements to PV–CHP configurations. PV/T collectors—designed to harvest both electrical and thermal energy—can achieve overall efficiencies exceeding 70%, making them suitable for residential heating, solar-assisted heat pumps, and even low-temperature industrial processes. Technological innovations such as heat pipes, low-emissivity coatings, and conductive polymer channels have enabled effective dual-energy extraction, while advanced working fluids (e.g., nanofluids) provide both cooling and spectral filtering. Despite persisting technical and economic challenges, widespread adoption of PV/T could reduce global CO₂ emissions by over 16% relative to 2030 baseline scenarios [14]. Furthermore, coupling PV/T systems with thermal storage or low-temperature heat pumps has been shown to improve self-consumption and reduce payback periods.

Additional performance enhancements are achievable through the integration of phase change materials (PCMs) and advanced heat exchanger architectures. The use of nano-PCM composites and structured flow geometries—such as twisted-tape or conical-leaf channels—can improve thermal efficiency by 20–30%, reduce exergy destruction, and shorten payback periods to under six years. Radiative cooling strategies, particularly effective at night, further enhance stability in cold-climate scenarios. Life cycle analyses suggest that PV/T–PCM systems can prevent up to 59 kg CO₂ emissions annually per square meter of collector area, although the selection and recyclability of PCMs and nanoparticles remain critical considerations [15].

Recovering waste heat from PV modules is increasingly recognized as an essential design strategy. Since over 70% of incident solar radiation is converted to heat, elevated module temperatures can reduce electrical efficiency by 0.2–0.5%/°C. Passive thermal management solutions—such as radiative coatings or PCM backing layers—can lower cell temperature by 5–15 °C and improve electrical efficiency by up to 15%, while active cooling strategies using liquids or nanofluids have demonstrated gains of 10–50% [16]. PV/T integration not only recovers this waste heat but also enhances winter thermal availability for domestic use or CHP supplementation.

Although PV–CHP systems remain the primary focus of off-grid hybrid energy design, PV–heat pump (PV–HP) configurations offer a valuable point of comparison. When properly dimensioned, these systems can achieve Seasonal Performance Factors (SPFs)—a combined efficiency metric for PV–HP setups—ranging from 2.8 to 6.9, with temperature-corrected performance ratios approaching 0.99. In optimized scenarios, SPF values can reach as high as 11.3, particularly when the nominal capacity of the PV array is sized between 60% and 200% of the heat pump’s rated capacity [17].

In addition to system-level integrations, several technologies focused on PV-side performance have been shown to enhance overall hybrid efficiency. Advanced maximum power point tracking (MPPT) algorithms—particularly fuzzy logic and neuro-fuzzy controllers—can increase primary energy yield by up to 50%. Dual-axis solar trackers provide gains of 20–50%, depending on latitude. Floating PV (FPV) systems offer output improvements of 11–20% and reduce water evaporation from associated storage reservoirs by up to 70%, a beneficial synergy when thermal storage or micro-hydro support is integrated [18].

Recent developments in PCM-based thermal storage have also shown promise, enabling compact system designs and prolonged heat delivery without increasing fuel consumption or storage volume [19].

Complementary evidence from high-latitude Canada highlights the benefits of winter-optimized hybridization strategies. Aghajani Delavar and Wang modeled a 30 m² parabolic-dish micro-gas-turbine Brayton cycle for Edmonton, showing that electrical output rises from 3.7 kW in January to 9.9 kW in July, with cycle efficiency increasing from 19% to 35%. Enhancing recuperator effectiveness from 60% to 80% alone yielded a 52% efficiency gain, although auxiliary firing remained necessary due to reduced winter solar yield [20]. Similarly, Yaïci et al. demonstrated that integrating an Organic Rankine Cycle (ORC) with a ground-source heat pump (GSHP) and using the ORC’s summer waste heat to recharge a borefield can reduce annual residential energy consumption by over 80%, cut heat pump operating hours by up to 57%, and maintain a long-term Coefficient of Performance (COP) near 3.8—even under Edmonton’s severe winter conditions [21]. These findings affirm the viability of solar–microturbine topping cycles and ORC-assisted thermal storage as valuable complements to PV–CHP architectures, offering significant performance benefits for autonomous dwellings in cold climates.

Taken together, findings across the literature—complemented by high-latitude field studies—validate the feasibility and resilience of hybrid PV–CHP systems as efficient, low-emission solutions for off-grid residential applications, particularly in regions with limited solar availability during the winter months.

This study evaluates whether CHP, thermal storage, or battery storage is required by analyzing PV system energy production under varying winter irradiance levels. Real-world efficiency values obtained from experimental tests are used to assess the system’s ability to meet electrical and thermal energy demands. The findings will guide optimal system configurations and energy management strategies for hybrid residential applications.

This study follows a progressive system design methodology grounded in empirical data and is structured into two interdependent phases. In the first phase, the performance of three different PV systems—amorphous, polycrystalline, and monocrystalline—is analyzed under winter conditions to evaluate their capacities to meet a building’s combined electrical and thermal energy demands. This evaluation is conducted using experimental data processed through C++ Model 1, which simulates solar power generation, building energy loads, and real-world system efficiency.

Based on the outcomes of the initial phase, the second phase investigates whether supplementary energy sources—such as CHP units, thermal storage, or battery systems—are necessary to enhance energy autonomy and performance stability. To this end, a second computational tool, C++ Model 2, is developed to simulate the optimal sizing and operation of these auxiliary components under variable weather and demand scenarios.

The residential building under investigation has specific thermal and electrical energy requirements, with distinct variations between daytime and nighttime consumption. Given the climatic conditions of the Bacău region in Romania, this study considers seasonal variations, solar irradiation levels, and the impact of panel orientation and tilt angle on system performance.

This study identifies optimal system configurations that maximize energy use and ensure stable power and heat supply under various operational scenarios. The results support a deeper understanding of solar–CHP hybrid solutions for off-grid residential applications, highlighting key challenges and benefits.

To ensure flexibility and adaptability, this study defines key parameters as variables, allowing the model to be applied to different building configurations. The input variables are divided into two phases, namely, Phase 1 (

Table 1. Phase 1: variables for PV systems and energy demand analysis used in C++ Model 1.

Category	Variable Name	Description	Unit	Input Type
Building characteristics	wallArea	Total wall area (after deducting windows and doors)	m2	External
	windowArea	Total window area	m2	External
	floorArea	Total floor area	m2	External
	roofArea	Total roof surface area	m2	External
Thermal properties	uWall	U-value of walls (thermal transmittance)	W/(m2K)	External
	uWindow	U-value of windows	W/(m2K)	External
	uFloor	U-value of the floor	W/(m2K)	External
	uRoof	U-value of the roof	W/(m2K)	External
	In_Out_DT_Day	Temperature difference inside/outside (daytime)	°C	External
	In_Out_DT_Night	Temperature difference inside/outside (nighttime)	°C	External
Time durations	day_Duration	Duration of daytime	hours	External
	night_Duration	Duration of nighttime	hours	External
Solar energy parameters	solarGainFactor	Solar gain factor	-	External
	G_Solar	Average solar irradiance for daytime in winter	W/m2	External
	reductionFactor	Reduction factor for vertical windows	-	External
Energy demand	electricalNeedsDay	Electrical energy demand (daytime)	kWh	External
	electricalNeedsNight	Electrical energy demand (nighttime)	kWh	External
Heating system	mWater	Mass of heating water per cycle	kg	External
	cWater	Specific heat capacity of water/constant	J/(kgK)	External
	deltaT_Cycle	Temperature difference per cycle	°C	External
Domestic hot water (DHW)	daily_DHW_Volume	Total daily hot water consumption	L	External
	DHW_Day_Ratio	Daytime hot water	%	External
	TCold	Temperature of cold water	°C	External
	THot	Desired temperature of hot water	°C	External
PV system	panelType	Type of PV panel	-	External
	amArea	Amorphous panel area	m2	External
	polyArea	Polycrystalline panel area	m2	External
	monoArea	Monocrystalline panel area	m2	External
	installedPowerPV	Installed PV power	kW	External
	efficiencyPV	Efficiency of PV panels	%	External
	costPV	Total cost of the PV system	USD	External
	areaPVsystem	Surface area occupied by PV panels	m2	External
Economic inputs	el_price_kWh	Price of electricity/kWh	USD/kWh	External

) and Phase 2, with Phase 2 being implemented based on the findings of Phase 1.

The limited roof area constrains PV capacity, making the system output dependent on panel efficiency and availability. In winter, standalone PV may not ensure a reliable supply. This study addresses this gap by proposing a validated experimental–computational framework for designing hybrid solar–CHP systems in cold climates. Using real PV data and a dynamic irradiance-based model, the approach enables the optimal sizing of CHP, battery, and thermal storage for off-grid autonomy.

2. Materials and Methods

2.1. Study Scope and Assumptions

This study follows a progressive system design approach based on real-world data.

Table 2. Variables calculated in C++ Model 1.

Category	Variable Name	Description	Unit
Solar heat gain	$Q_{sol}$	Solar heat gain through windows	kWh
Heat losses	$Q_{loss,d}$	Heat loss of the building during daytime	kWh
	$Q_{loss,n}$	Heat loss of the building during nighttime	kWh
Heating energy demand	$Q_{heat,cycle}$	Energy needed for heating system in one cycle	kWh
	$Q_{heat,d}$	Energy required for heating system (daytime)	kWh
	$Q_{heat,n}$	Energy required for heating system (nighttime)	kWh
	$Q_{DHW}$	Total energy demand for DHW	kWh
	$Q_{DHW,d}$	Daytime energy demand for DHW	kWh
	$Q_{DHW,n}$	Nighttime energy demand for DHW	kWh
	dayCycles	Number of heating water cycles/day	-
	nightCycles	Number of heating water cycles/night	-
Total energy demand	buildingEnergyDay	Total energy demand (daytime)	kWh
	buildingEnergyNight	Total energy demand (nighttime)	kWh
	totalBuildingEnergy	Total daily energy demand	kWh
PV system performance and cost analysis	${\eta }_{PV,real}$	Real-world PV efficiency	%
	$E_{PV}$	PV system power generation	kWh
	$E_{PV,lifetime}$	PV system lifetime energy production
	$C_{PV}$	Cost per unit energy produced by the PV system	USD/kWh
	$T_{payback}$	Investment payback period	years

summarizes the calculations performed in Phase 1.

C++ Model 1 performs the following key calculations, as presented in Table 2. First, it analyzes the performance of the PV system by computing solar electricity generation based on real irradiance data, comparing measured efficiencies with manufacturer-specified values, and determining the cost per unit of generated energy alongside the investment payback period. Second, the model calculates the building’s energy demand by estimating daytime and nighttime heat losses and by quantifying the thermal energy required for both space heating and DHW supply. Finally, it establishes a total energy balance by comparing the PV system’s output with the building’s energy demand, thereby assessing whether solar energy alone can meet consumption needs or if additional energy sources—such as CHP systems or thermal and battery storage—are necessary to ensure off-grid reliability.

Based on the results of these calculations, the second phase of the analysis evaluates the necessity of integrating additional energy sources to meet the building’s off-grid energy requirements. A micro-CHP unit is introduced in scenarios where PV electricity production alone is insufficient to satisfy the combined electrical and thermal demand. If the CHP unit generates excess thermal energy beyond the immediate heating needs, a thermal storage system is considered to capture and retain this surplus for later use. Battery storage is evaluated only in cases where PV production exceeds demand during daylight hours, making it advantageous to store excess electricity for consumption during periods of low or no solar availability, particularly at night.

The second phase requires C++ Model 2 to properly simulate the sizing and operation of CHP, thermal storage, and battery systems.

The full source codes for both C++ Model 1 and Model 2 used in this study are not included in this manuscript but are available from the authors upon reasonable request.

Because PV alone cannot meet winter energy demand, this study evaluates the need for CHP and storage integration based on data, rather than assuming it from the outset. This approach ensures a realistic assessment of hybrid system configurations. The key variables introduced in this phase are summarized in

Table 3. Phase 2: Additional variables for hybrid system expansion.

Category	Variable Name	Description	Unit
Battery Storage	batteryCapacity	Total battery capacity for electricity use	kWh
Micro-CHP System	CHP_Efficiency	Efficiency of the micro-CHP unit	%
	CHP_Electrical_Output	Electrical output of the CHP unit	kW
	CHP_Heat_Output	Thermal output of the CHP unit	kW
Thermal Storage (Puffer Tank)	pufferCapacity	Total capacity of the thermal storage tank	L
	pufferHeatLoss	Heat loss from the storage tank	kWh

.

2.2. Experimental Setup

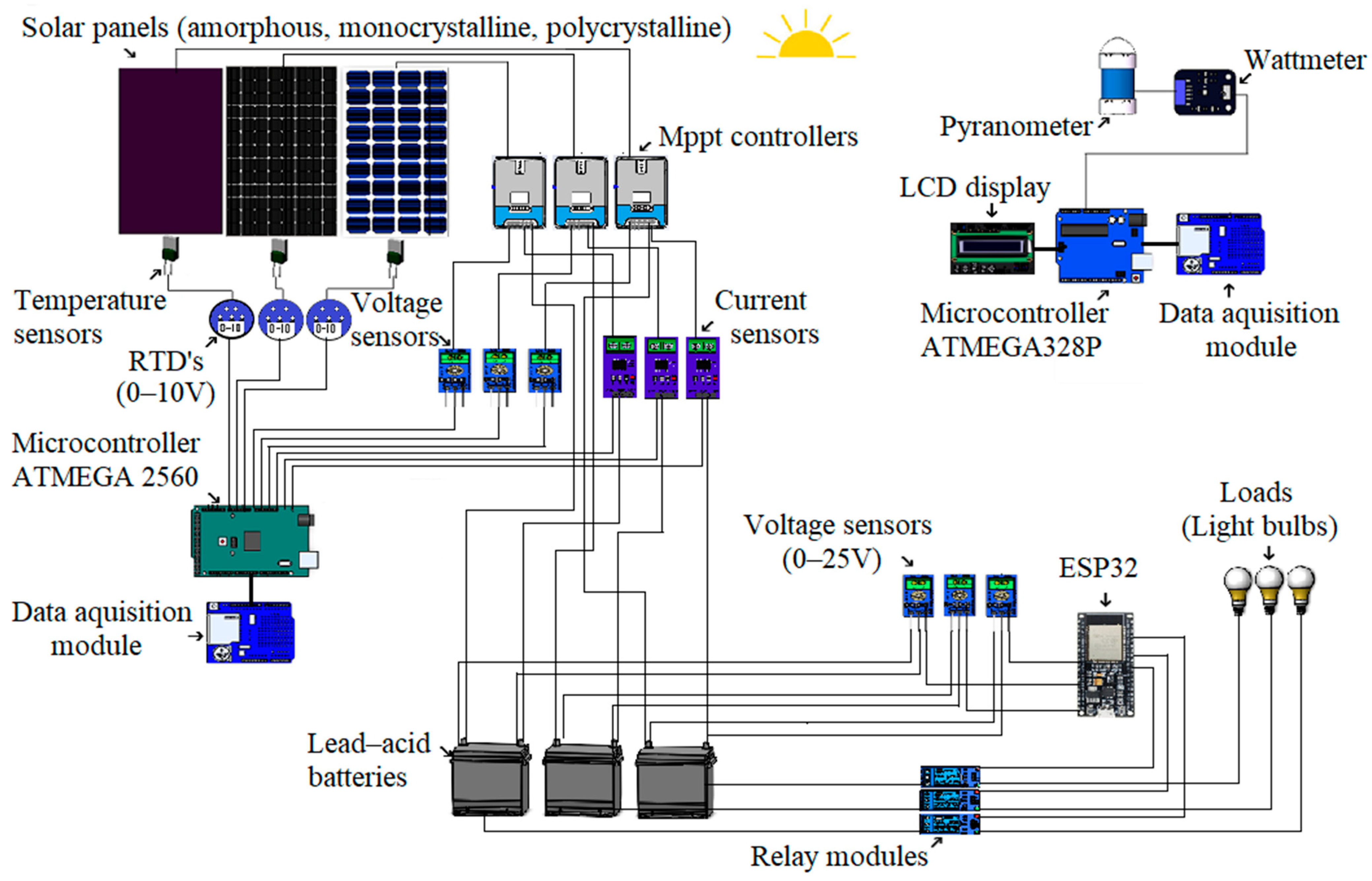
The experimental setup illustrated in Figure 1 was developed to measure and analyze the performance of three photovoltaic panel technologies—amorphous, polycrystalline, and monocrystalline—under real-world winter conditions. The system includes sensors, controllers, batteries, dynamic loads, and data acquisition modules for real-time monitoring of electrical, thermal, and environmental parameters.

Each PV panel is connected to a dedicated battery, along with voltage and current sensors and an MPPT charge controller to ensure optimal power conversion. An ESP32 microcontroller manages DC relays that activate 12 V resistive loads to prevent overcharging and maintain continuous energy flow. The setup is located in Bacău, Romania (46.43° N, 26.89° E). Based on prior studies [22,23], the optimal fixed tilt angle for PV systems approximates the local latitude [24,25], with seasonal adjustments—typically increasing tilt by 10–20° in winter and reducing it in summer—recommended to improve performance [26,27,28]. Following this guidance, the PV panels and pyranometer were installed at a 56° tilt to enhance winter energy capture.

2.2.1. Experimental System Components

The experimental setup includes three types of PV panels—amorphous, polycrystalline, and monocrystalline—selected for comparative performance evaluation under real-world winter conditions. The key specifications of each component are summarized in

Table 4. Summary of experimental system components and sensor specifications.

Component	Model/Manufacturer	Key Specifications
Amorphous PV panel	SN Solartechnics SN-50—SN Solartechnics GmbH & Co. KG (Osnabrück, Germany)	50 W, Voc 62 V, Isc 1.42 A, Vmp 43 V, Imp 1.17 A
Polycrystalline PV panel	Solar Jianbao SA-100—Changzhou Jianbo Solar Technology Co., Ltd. (Changzhou, China)	100 W, Voc 21 V, Isc 6.4 A, Vmp 17.6 V, Imp 5.71 A
Monocrystalline PV panel	Breckner BK87482—Breckner Germany (Berlin, Germany)	100 W, Voc 21.1 V, Isc 5.96 A, Vmp 17.6 V, Imp 5.71 A
Voltage sensor	Compatible with Arduino—Arduino AG (Turin, Italy)	5 V logic, 0–25 V range, 4.89 mV resolution
Current sensor	Gravity SEN-0291—DFRobot (Shanghai, China)	±8 A, 1 mA resolution, 3.3–5.5 V supply
Temperature sensor	Tewa PT100—TEWA Temperature Sensors (Lublin, Poland)	–70 °C to 400 °C, 100 Ω, 0–10 V analog output
MPPT controller	VOLT Polska MPPT 20A—Volt Polska Sp. z o.o. (Sopot, Poland)	12/24 V input, ≤100 V input, >99.9% tracking efficiency
Microcontroller 1	ATMEGA2560—Microchip Technology Inc. (Chandler, Arizona, USA)	16 MHz, 54 digital I/O, 16 analog inputs, SD + RTC
Microcontroller 2	ATMEGA328P + LCD—Microchip Technology Inc. (Chandler, Arizona, USA)	16 MHz, data logging and power display
Irradiance sensor	Pyranometer 485—Jiangsu Skyray Instrument Co., Ltd. (Jiangsu, China)	–0–10 V output, 1 W/m2 resolution, ±5% accuracy
Battery (per panel)	12 V, 55 Ah lead-acid—Rombat SA (Bistrița, Romania)	Dedicated to each PV panel
Load control	ESP32 Dev Module + relay—Espressif Systems (Shanghai, China)	Dual-core, 34 I/O pins, 12 V/100 W halogen bulbs

.

2.2.2. The Workflow of the System

The experimental setup includes three PV panels, each linked to a dedicated measurement and control circuit. Sensor arrays continuously collect voltage, current, and temperature data, which are transmitted to Arduino microcontrollers for real-time monitoring.

The Arduino Mega R3 records panel-specific electrical and thermal data, while the Arduino Uno R3 handles solar irradiance and power readings. All values are time-stamped and stored on SD cards for subsequent analysis. Data collection and control routines are implemented in C/C++.

Energy management is automated through a logic sequence that prioritizes efficient storage and protection. MPPT controllers regulate charging, and an ESP32 module monitors battery voltage, activating resistive loads when thresholds are exceeded to prevent overcharging.

This workflow ensures synchronized monitoring of generation, storage, and environmental parameters, enabling accurate input to the simulation models and supporting performance analysis under variable winter irradiance.

2.3. C++ Model 1: Simulation Code and Computational Methods

This section presents C++ Model 1, a computational framework developed to simulate the energy performance of a residential building under winter conditions. The model integrates real-world experimental data and theoretical calculations to evaluate solar power generation, thermal energy demand, and photovoltaic system efficiency.

To provide a structured overview,

Table 5. Complete list of methods used in C++ Model 1.

Class	Method Nr.	Function Name	Description
Building	1	calculateQSolar()	Computes solar heat gain through windows.
	2	calculateHeatLossDay()	Calculates heat loss during the day, considering solar gains.
	3	calculateHeatLossNight()	Computes heat loss during nighttime.
EnergyDemand	1	calculateEnergyForHeatingWaterDay()	Computes energy required for heating needs during the day.
	2	calculateEnergyForHeatingWaterNight()	Computes energy required for heating needs during the night.
	3	calculateDHWEnergy()	Computes total energy needed for DHW.
	4	calculateHeatingNeedsDay()	Calculates total heating energy needs during the day.
	5	calculateHeatingNeedsNight()	Calculates total heating energy needs during the night.
PVSystem	1	updateEfficiency()	Updates PV efficiency based on experimental data.
	2	dailyEnergyProduction()	Computes daily PV power generation based on efficiency.
	3	calculateCostPerEnergy()	Determines cost per unit energy produced by PV.
	4	calculateCostCoveragePeriod()	Calculates the payback period for PV investment.

summarizes the key methods implemented in C++ Model 1, detailing their role in heat loss analysis, solar gains, energy demand calculations, and PV system performance evaluation.

The computational model is organized into three interrelated components that collectively simulate the building’s off-grid energy performance. The first component is the building energy model, which estimates solar heat gain, thermal losses, and total heating energy requirements based on the structure’s thermal characteristics and prevailing environmental conditions. The second component, the energy demand model, quantifies the energy required for space heating and DHW supply, capturing variations in consumption between daytime and nighttime periods. The third component focuses on the photovoltaic system, analyzing PV panel efficiency, daily energy yield, and economic performance using experimentally derived efficiency data to evaluate cost-effectiveness under real-world operating conditions.

By integrating these modules, C++ Model 1 delivers a comprehensive assessment of the building’s energy requirements and the capability of various PV technologies to meet them. The code performs all key calculations related to energy demand, photovoltaic system performance, and economic viability, offering a detailed analysis of energy efficiency, solar heat gains, and the practical feasibility of PV integration in residential settings.

2.4. Mathematical Model and Equations Used

The computational framework consists of three principal models that collectively simulate the thermal and electrical behavior of the off-grid system. The building energy model estimates solar heat gains, heat losses through the envelope, and the resulting total heating demand based on external weather conditions and structural properties. The energy demand model calculates the specific energy requirements for space heating and DHW, aggregating these into the building’s total thermal load. The PV system model assesses the electrical efficiency of the PV panels, computes daily energy production, and evaluates the system’s cost-effectiveness under real operational conditions. The governing equations for each of these models are detailed in the following subsections.

For the calculation of the variables listed in Table 2, a simplified notation is employed throughout the mathematical formulation. This approach ensures clarity while maintaining a direct connection to the descriptive names of the variables. The following equations illustrate the key relationships used in C++ Model 1.

2.4.1. Building Energy Model Equations

Solar heat gain through windows, representing the amount of solar energy entering the building through glazed surfaces, is calculated as

$$Q_{sol}={\displaystyle \frac{A_{win}{G}_{sol}{F}_{red}{F}_{gain}t}{1000}},$$

(1)

where $Q_{sol}$ denotes the solar heat gain (kWh), $A_{win}$ is the total window area (m²), $G_{sol}$ represents the average solar irradiance (W/m²), $F_{red}$ is the dimensionless reduction factor accounting for the vertical window orientation, $F_{gain}$ is the dimensionless solar gain factor, and $t$ is the duration of solar exposure (h).

Heat loss through the building envelope is calculated separately for daytime ($Q_{loss,d}$) and nighttime ($Q_{loss,n}$), reflecting the varying temperature differences between indoor and outdoor environments over a 24 h period. During the day, solar gains reduce the net thermal losses. The daytime heat loss is calculated as

$$Q_{loss,d}={\displaystyle \frac{(U_w{A}_w+U_{win}{A}_{win}+U_f{A}_f+U_r{A}_r)\Delta T_{d}t}{1000}}-Q_{sol},$$

(2)

and the nighttime heat loss is given by

$$Q_{loss,n}={\displaystyle \frac{(U_w{A}_w+U_{win}{A}_{win}+U_f{A}_f+U_r{A}_r)\Delta T_{n}t}{1000}},$$

(3)

where $U_w$, $U_{win}$, $U_f$, and $U_r$, are the the thermal transmittances of the walls, windows, floor, and roof in watts per square meter kelvin, W/(m²K), $A_w$, $A_{win}$, $A_f$, and $A_r$ are their respective surface areas (m²), and $\Delta T_d$ and $\Delta T_n$ are the temperature differences between the inside and outside during daytime and nighttime (°C).

2.4.2. Energy Demand Model Equations

This section calculates the energy required for space heating and DHW. In this closed-loop heating system, the mass of water circulated per cycle is assumed constant. Minor variations due to expansion, inefficiencies, or thermal stratification are neglected to simplify the calculations. Therefore, the energy requirements depend only on the number of day/night cycles ($N_{cycle,d}$; $N_{cycle,n}$) and temperature differences. For a single heating cycle, the energy needed to heat the water $Q_{heat,cycle}$ is calculated as

$$Q_{heat,cycle}={\displaystyle \frac{m_{water}{c}_{water}\Delta T_{cycle}}{3.6\times {10}^6}},$$

(4)

in kilowatt-hours (kWh), where, $m_{water}$ is the mass of heating water per cycle (kg), $c_{water}$ is the specific heat capacity of water in J/(kgK), and $\Delta T_{cycle}$ is the temperature difference in one cycle.

The total daily heating demand during daytime and nighttime is then given by

$$Q_{heat,d}=Q_{heat,cycle}{N}_{cycle,d},$$

(5)

$$Q_{heat,n}=Q_{heat,cycle}{N}_{cycle,n}.$$

(6)

Energy required for DHW ($Q_{DHW}$) heating is calculated in kWh as

$$Q_{DHW}={\displaystyle \frac{m_{DHW}{c}_{water}\Delta T_{DHW}}{3.6\times {10}^6}},$$

(7)

where $m_{DHW}$ is the daily hot water consumption (L) (assuming a density of 1 kg/L) and $\Delta T_{DHW}$ is the temperature difference between cold and hot water.

The daytime and nighttime energy requirements ($Q_{DHW,d}$; $Q_{DHW,n}$) are then given by

$$Q_{DHW,d}=Q_{DHW}{f}_{day},$$

(8)

$$Q_{DHW,n}=Q_{DHW}(1-f_{day}),$$

(9)

with $f_{day}$ representing the fraction of hot water consumption during the day.

2.4.3. Photovoltaic System Model Equations

This section calculates the PV system’s energy output, real-world efficiency, and cost-effectiveness.

The real-world PV efficiency, ${\eta }_{PV,real}$, differs from the manufacturer-rated efficiency, which assumes optimal conditions, because it accounts for real operating factors such as irradiance, panel temperature, and environmental losses. Model 1 dynamically updates this efficiency based on measured data using the equation

$${\eta }_{PV,real}={\displaystyle \frac{{{10}^{3}E}_{PV,test}}{G_{solar}t{A}_{PV}}},$$

(10)

where $E_{PV,test}$ represents the electrical energy output (kWh) measured from the PV panels used in the testing setup, $G_{solar}$ is the average solar irradiance (W/m²), and $A_{PV}$ is the PV panel area (m²).

Using the updated efficiency, the daily energy production of the PV system, $E_{PV}$, is calculated as

$$E_{PV}={\displaystyle \frac{G_{solar}t{A}_{PV}{\eta }_{PV,real}}{1000}}.$$

(11)

This equation calculates the daily energy production of the PV system (in kWh) based on the updated real-world efficiency, providing an estimate of the system’s performance under actual environmental conditions.

To evaluate cost-effectiveness, the cost per unit of energy, in USD/kWh, produced by the PV system ($C_{PV}$) is calculated as

$$C_{PV}={\displaystyle \frac{C_{install}}{E_{PV,lifetime}}},$$

(12)

where $C_{install}$ is the total installation cost and $E_{PV,lifetime}$ is the lifetime energy production (kWh), computed as

$$E_{PV,lifetime}=365N_{years} E_{PV}.$$

(13)

In the above equation, $N_{years}$ is the expected operational lifetime of the PV system. This metric provides a basis for comparing the financial feasibility of different PV technologies.

The payback period, $T_{payback}$, which indicates the time required for the PV system’s savings to recover its initial investment, is given by

$$T_{payback}={\displaystyle \frac{C_{install}}{S_{year}}},$$

(14)

where $S_{year}$ is the annual savings from PV electricity (USD).

A shorter payback period reflects a more cost-effective system, with electricity price, system efficiency, incentives, and maintenance costs influencing the return on investment.

2.5. Building Characteristics and Energy Needs

The analyzed building is a two-story residential structure with a total floor area of 100 m² (50 m² per floor) and an internal volume of 250 m³. It has an 8 m × 6.25 m footprint and a pitched roof totaling 104 m², oriented east–west. For PV installation, only the south-facing roof section is considered, consistent with the experimental panel orientation. Accounting for mounting gaps and spacing, the effective available roof area is estimated at 50 m².

To isolate the impact of envelope-related thermal behavior, internal heat gains from occupants, lighting, and appliances are excluded from the analysis. The thermal model focuses solely on heat losses through the building envelope in response to external temperature conditions.

The off-grid energy system comprises photovoltaic generation, battery storage, a thermal buffer tank, and a micro-CHP unit to ensure an uninterrupted energy supply. Photovoltaic panels provide daytime electricity, with surplus stored in batteries for nighttime use. The CHP unit covers thermal and electrical demand during low-irradiance periods, and its excess thermal output is stored in the buffer tank. Supporting components such as pumps, controllers, piping, and an expansion vessel ensure safe and reliable system operation.

2.5.1. PV Surface Allocation and Installation Constraints

To ensure a fair comparison among different photovoltaic technologies, all systems were designed to occupy approximately the same usable roof surface of 43 m², corresponding to the south-facing section of the roof, accounting for panel gaps, mounting requirements, and edge clearance. Based on the dimensions and available configurations of commercial PV modules, the following system layouts were selected:

Amorphous silicon PV: Mitsubishi 100 W panels (1.414 m × 1.114 m), arranged in 9 columns × 3 rows, resulting in an installed power of 2.7 kW and an occupied surface of 42.53 m². Manufacturer-reported efficiency: 6.65%.

Polycrystalline PV: SUNCECO 300 W panels (0.992 m × 1.956 m), initially arranged as 2 columns × 10 rows. To match the surface used by the amorphous configuration, 2 additional panels were added, resulting in a total installed power of 6.6 kW on 42.7 m². Manufacturer-reported efficiency: 15.5%.

Monocrystalline PV: BLUESUN 600 W panels (2.384 m × 1.096 m), scaled to match the same surface area, allowing a maximum installed power of 9.6 kW over 42.7 m², consistent with the surface used for the other two configurations. Manufacturer-reported efficiency: 23%.

To maintain consistency, the same total panel surface (43 m²) was used in simulations for each PV technology. This allowed a balanced comparison of energy production capabilities under identical installation constraints. These configurations reflect both market availability and realistic installation feasibility for residential buildings, ensuring that the model reflects practical design choices.

2.5.2. Building Parameters

To ensure adaptability, the building characteristics are defined as variables, which can be adjusted for different scenarios.

Table 6. Building parameter used for simulation.

Category	Variable Name	Description	Unit	Input Value
Building dimensions	wallArea	Total wall area (excluding windows and doors)	m2	125
	windowArea	Total window area	m2	18
	floorArea	Total floor area	m2	50
	roofArea	Total roof surface area	m2	50
Thermal properties	uWall	U-value of walls (thermal transmittance)	W/(m2K)	0.21
	uWindow	U-value of windows	W/(m2K)	1.1
	uFloor	U-value of the floor	W/(m2K)	0.1
	uRoof	U-value of the roof	W/(m2K)	0.25
Temperature differences	In_Out_DT_Day	Temperature difference inside/outside (day)	°C	19
	In_Out_DT_Night	Temperature difference inside/outside (night)	°C	22
Time duration	day_Duration	Duration of daytime	hours	8
	night_Duration	Duration of nighttime	hours	16
Solar energy parameters	solarGainFactor	Solar gain factor	-	0.6
	G_Solar	Average solar irradiance for daytime in winter	W/m2	-
	reductionFactor	Reduction factor for vertical windows	-	0.3

summarizes the key building parameters used in this study.

Solar irradiance, $G_{solar}$, is a dynamic parameter in the model, varying throughout the day and across different weather conditions. Instead of a single predefined value, the model continuously updates $G_{solar}$ to reflect real-world variations in solar energy availability. This allows for an accurate assessment of PV system performance and heating energy contributions under different irradiance scenarios.

2.5.3. Energy Needs

The building’s total energy demand consists of electrical consumption, heating demand, and DHW requirements. The energy needs are categorized into daytime and nighttime consumption, reflecting variations in usage patterns and external temperature conditions.

Electrical energy demand—The electricity demand varies between daytime and nighttime, influenced by appliance usage, lighting, and heating system operation.

Table 7. Electrical energy demand variables of the building.

Variable Name	Description	Unit	Input Value
electricalNeedsDay	Electrical energy demand (daytime)	kWh	0.2
electricalNeedsNight	Electrical energy demand (nighttime)	kWh	0.05

lists the key electrical parameters used in the simulations. These values exclude heating system demand.

Heating energy demand of the building—Space heating demand is influenced by heat losses through walls, windows, floor, and roof, as well as the heating water cycle. The model calculates the energy needed to maintain indoor temperature using the variables listed in

Table 8. Heating energy demand variables.

Variable Name	Description	Unit	Input Value
mWater	Mass of heating water per cycle	kg	100
cWater	Specific heat capacity of water	J/(kgK)	4186
deltaT_Cycle	Temperature difference per cycle	°C	10
dayCycles	Number of heating water cycles per day	-	TBD
nightCycles	Number of heating water cycles/night	-	TBD

.

DHW energy demand—DHW energy demand is based on daily hot water consumption and the required temperature increase.

Table 9. Domestic hot water demand variables in C++ Model 1.

Variable Name	Description	Unit	Input Value
daily_DHW_Volume	Total daily hot water consumption	L	160
DHW_Day_Ratio	Percentage of hot water used during the day	%	60
TCold	Temperature of domestic cold water	°C	10
THot	Desired temperature of domestic hot water	°C	60

outlines the key parameters for the DHW calculations.

The building’s total energy demand includes electricity, space heating, and DHW, accounting for both daytime and nighttime usage. Electrical demand covers appliances, lighting, and system controls, while heating demand depends on envelope heat losses and the energy needed to maintain indoor temperatures. The heating system operates in cycles, heating a fixed water mass multiple times daily; the number of cycles varies with day–night temperature differences, allowing precise thermal load estimation. DHW demand is calculated separately, based on daily hot water use and temperature rise, and is distributed between day and night using a fixed ratio. The final energy balance evaluates whether PV production can meet total demand; if not, CHP, thermal storage, or batteries are used to ensure supply.

3. Results

3.1. Experiment Carried Out

The experimental phase was conducted to measure the real-world performance of three different PV panel technologies—amorphous, polycrystalline, and monocrystalline—under winter conditions. The goal was to collect irradiance, power output, and panel temperature data to validate the efficiency assumptions used in the computational model. The collected data serves as direct input for C++ Model 1, ensuring that the solar energy generation and efficiency calculations are based on measured values rather than theoretical estimates. Each panel was monitored individually under identical environmental conditions to ensure a direct comparison of its performance characteristics. To ensure accuracy, all the data was logged at fixed intervals throughout the day, capturing real-time variations in solar irradiance, voltage, current, and panel temperature.

To ensure realistic simulations, the experimental data collected over a period of 100 days (from 5 November 2024 to 14 February 2025) was processed and integrated into C++ Model 1.

The following methodology was used:

Sampling frequency: Each solar panel (amorphous, polycrystalline, monocrystalline) was continuously monitored for daytime, during which approximately 3600 samples were recorded per parameter (voltage, current, temperature).

Irradiance monitoring: In parallel, a system logged real-time solar irradiance data using a pyranometer, following the same sampling frequency.

Data processing: Raw data from the SD card was imported into Excel for preprocessing. The instantaneous power output for each PV panel was calculated using measured voltage and current values.

To determine the total daily energy production of the test panels, the instantaneous power values were summed over the 8 h solar exposure period and normalized by the total number of recorded samples. The resulting quantity, denoted $E_{PV,test}$, was used in Equation (10) to compute the real-world PV efficiency:

$$E_{PV,test}={\displaystyle \frac{\Sigma P_{samples}8h}{N_{samples}1000}},$$

(15)

where $P_{samples}$ is the recorded instantaneous power values (W) and $N_{samples}$ is the number of samples collected during the measurement period. This equation yields the average power over the sampling interval, converts it to kilowatt-hours, and accounts for the total exposure time. For example, under typical winter conditions with an average irradiance of approximately 330 W/m², the amorphous panel generated over 300 Wh, while the polycrystalline and monocrystalline panels produced about 140 Wh each.

These values were then used as input parameters in C++ Model 1, replacing predefined theoretical efficiencies with real-world experimental measurements.

While panel temperature can affect voltage drop and efficiency, the measured panel temperatures remained relatively low during the experiment and did not significantly impact performance. The maximum recorded temperatures during operation reached 42 °C for the amorphous panel, while both the polycrystalline and monocrystalline panels exhibited peak temperatures of approximately 35 °C.

However, these peaks were reached only for short intervals, and for most of the experimental period, panel temperatures remained below 20 °C. As a result, temperature-related efficiency degradation was negligible and was not included as a correction factor in the computational model.

By changing $G_{solar}$ and the experimental energy output values of the solar panels (amEnergyOut, polyEnergyOut, monoEnergyOut), the model dynamically adapts to different weather and solar conditions, allowing for a flexible and accurate simulation of hybrid system performance.

In Table 2, the variable $E_{PV}$ is defined generally under the PV system performance category. However, during simulation, this value is calculated separately for each panel type, namely, as dailyEnergyProduction_Am, dailyEnergyProduction_Poly, and dailyEnergyProduction_Mono, to reflect the distinct performance of amorphous, polycrystalline, and monocrystalline technologies under varying solar conditions.

Table 10. Input/output variables for selected winter irradiance scenarios (C++ Model 1).

Irradiance (W/m2)	40	100	150	235	280	300	330	415
Input variables
amEnergyOut (Wh)	46	108	180	241	267	300	320	410
polyEnergyOut (Wh)	26	54	81	118	129	130	140	175
monoEnergyOut (Wh)	24	54	64	84	100	110	137	155
Output variables
buildingEnergyDay (kWh)	15.1	13.9	11.6	10.4	9.3	8.1	6.9	5.8
dailyEnergyProduction_Am (kWh)	1.32	3.1	5.16	6.91	7.65	8.6	9.17	11.8
dailyEnergyProduction_Poly (kWh)	1.96	4.07	6.11	8.9	9.73	9.88	10.6	13.2
dailyEnergyProduction_Mono (kWh)	1.98	4.47	5.29	6.95	8.27	9.1	11.3	12.8

Note: The building’s nighttime energy demand remains constant at 27.03 kWh across all scenarios, as it is determined by internal temperature settings and external nighttime conditions, which were assumed constant during the simulation period.

presents the input and output variables from C++ Model 1 for selected winter days, highlighting the relationship between real-world solar conditions and the model’s energy simulations.

As shown in Table 10, daily PV output increases with irradiance, with polycrystalline panels consistently delivering the highest values. Even under the most favorable winter conditions (415 W/m²), the polycrystalline system produced only 13.2 kWh—well below the building’s total daily demand of 31.92 kWh. This confirms that PV alone cannot support full off-grid operation in winter. A notable surplus begins near 300 W/m², where all systems slightly exceed the 8.1 kWh daytime demand: 8.6 kWh (amorphous), 9.1 kWh (monocrystalline), and 9.88 kWh (polycrystalline). However, this margin is small and infrequent, limiting opportunities for battery charging and thermal storage. To evaluate seasonal scalability, a future model extension will consider higher irradiance scenarios typical of spring and autumn, where surplus energy could support nighttime use via storage. These dynamics are addressed in Phase 2 through C++ Model 2, which simulates the operation and sizing of a fully integrated hybrid system.

While the experimental setup was designed for high-resolution data acquisition, several limitations should be acknowledged. The pyranometer used for irradiance measurements has a declared accuracy of $\pm$5%, and the analog sensors for voltage, current, and temperature, although calibrated, are not certified to metrological laboratory standards. External conditions such as shading, dust accumulation, and ambient temperature fluctuations may also introduce variability in real-time measurements. Furthermore, the data was collected over a specific winter period in a single geographic location (Bacău, Romania), which may limit generalizability to other climatic regions or seasons. These uncertainties do not compromise the core findings but should be considered in future extensions of this study.

No thermal energy was extracted from the PV modules in this study. Although module temperature was continuously measured to assess its potential impact on electrical efficiency, the values remained low throughout the experiment (generally below 20 °C) and were therefore not used for any thermal application. All thermal energy simulations in this paper refer exclusively to the micro-CHP unit’s output, as modeled in C++ Model 2. The PV system served only as an electricity source, without any PV/T integration or waste heat recovery.

3.2. Daily Energy Balance and Hybrid System Requirements

To assess the need for additional energy sources, such as micro-CHP units, battery storage, or thermal storage, it is essential to evaluate the daily balance between photovoltaic energy production and the building’s energy demand under winter conditions. This comparison is based on values generated by C++ Model 1, using real-world experimental data for different irradiance levels.

The building’s energy demand was divided into daytime and nighttime periods. Some components remained constant across all irradiance scenarios, while others varied with solar gain.

The building’s daily energy demand was categorized into daytime and nighttime periods to reflect solar gain variability. While electrical and DHW loads remained constant within each interval, the heating demand varies during the day depending on solar irradiance, which offsets net heat loss. At night, in the absence of solar input, all loads were fixed and represent the maximum thermal and electrical requirements used for system design. Detailed values are provided in the sizing methodology (Section 3.2.1).

By comparing these constant and variable demands with the energy produced by each PV system, the model identifies whether a deficit exists. When solar production is insufficient, additional systems are required to cover the shortfall. The next sections of this paper use this energy gap analysis to define the role and sizing needs of hybrid system components such as micro-CHP units, batteries, and thermal storage.

3.2.1. Micro-CHP Unit Selection Methodology

Since the PV system alone cannot fully meet the demand, especially during low-irradiance days and nighttime periods, the CHP unit must be capable of independently covering the most demanding scenarios.

To ensure that the sizing methodology remains adaptable to other cases, it was built entirely around input variables. This way, the same logic can be applied even if the energy needs of another building differ from those used in this study.

Step 1. Determining maximum energy needs.

The building’s energy demand was divided into daytime (8 h) and nighttime (16 h) periods, with three key components identified in each interval: thermal energy for space heating, thermal energy for DHW, and electrical loads.

The corresponding energy values were obtained from the simulation results using C++ Model 1. In the case study analyzed, the daytime energy demand included 10.46 kWh for heating ($Q_{heat,d}$), 5.58 kWh for DHW ($Q_{DHW,d}$), and 0.2 kWh for electricity. At night, the demand increased to 23.26 kWh for heating ($Q_{heat,n}$), 3.72 kWh for DHW ($Q_{DHW,n}$), and 0.05 kWh for electricity.

Step 2. Thermal output requirement.

To define the minimum thermal output of the CHP unit ($P_{CHP,th}$), the nighttime period was considered critical, as it typically requires the highest thermal demand and receives no solar input. The required hourly thermal power was calculated as

$$P_{CHP,th}\ge max\left({\displaystyle \frac{Q_{heat,d}+Q_{DHW,d}}{t_{day}}},{\displaystyle \frac{Q_{heat,n}+Q_{DHW,n}}{t_{night}}}\right),$$

(16)

where $t_{day}$ and $t_{night}$ are the respective durations of the daytime and nighttime periods (h).

Applying the values from the model, $P_{CHP,th}$ has to be at least 2.005 kW to ensure both space heating and DHW supply during the coldest, least sunny periods.

Step 3. Electrical output requirement.

Although the electrical load is relatively small, it must still be covered by the CHP unit ($P_{CHP,el}$) when solar or battery sources are unavailable. The required electrical power was calculated as

$$P_{CHP,el}\ge max\left({\displaystyle \frac{E_{el,d}}{t_{day}}}, {\displaystyle \frac{E_{el,n}}{t_{night}}}\right),$$

(17)

where $E_{el,d}$ and $E_{el,n}$ are the daytime and nighttime electrical energy demands (kWh).

Based on the model, the minimum required electrical output of the CHP unit is 0.025 kW.

Built on the defined input variables, the minimum required thermal output of the CHP unit was calculated by identifying the period with the highest combined demand for space heating and domestic hot water, which occurs during nighttime. The resulting value of 2.005 kW represents the baseline thermal capacity needed to meet this demand over 16 h, assuming ideal conditions and no losses.

In practical applications, however, CHP systems operate with efficiencies below 100%. To reflect real-world performance, a thermal efficiency of 90% was assumed for the CHP unit. This means that only 90% of the input fuel energy is converted into useful thermal output, while the rest is lost as exhaust or mechanical waste.

To compensate for these losses and ensure the system can reliably cover building demand, the simulations assumed a gas-fired micro-CHP unit with a nominal thermal output of 2.5 kW and an electrical output of 0.05 kW, representative of commercially available residential cogeneration systems. This capacity ensured the system can meet both heating and electrical loads independently, even during the most demanding conditions when no solar input is available.

The thermal efficiency value of 90% is consistent with technical specifications for gas-fired micro-CHP systems designed for residential applications (e.g., WhisperGen, Baxi, Viessmann). This value represents steady-state efficiency under nominal load. To validate sizing robustness, simulations were conducted across a range of thermal outputs (1.8–3.0 kW), examining how well each size matched the calculated peak demand. While 2.0 kW was the theoretical minimum, it provided little buffer against transient shortfalls. Outputs above 2.7 kW led to increased unused capacity. A 2.5 kW thermal rating thus offered a balanced compromise between load coverage and cost-efficiency

These specifications form the foundation for the hybrid energy system simulations presented in C++ Model 2, where the CHP unit is integrated with battery and thermal storage to provide full off-grid functionality.

3.2.2. Hybrid System Logic and Operational Flow

To simulate the operation of a hybrid solar–CHP system and evaluate its performance under different winter irradiance conditions, a structured step-by-step logic is implemented in C++ Model 2. This model integrates the operation of photovoltaic panels, a micro-CHP unit, battery storage, and thermal storage, following a fixed energy management priority and dynamically adjusting to the energy balance for each scenario.

The algorithm follows a rule-based decision sequence designed to prioritize clean energy and minimize CHP usage. The daily irradiance level serves as the primary input to estimate daytime PV generation. The algorithm then applies the following logic: (1) daytime PV energy is first allocated to cover the building’s immediate electrical demand; (2) any PV surplus is directed to thermal storage (for DHW or heating) and then to battery charging; (3) if a daytime energy deficit exists, the CHP unit is activated to fill the shortfall, with its thermal and electrical output logged; and (4) at night, energy stored in the battery and thermal tank is consumed first; only if this is insufficient does the CHP unit reactivate to maintain full demand coverage.

Since the polycrystalline PV system demonstrated the highest daily energy output in almost all irradiance scenarios (as shown in Table 10), the following hybrid system simulations are based solely on the energy values obtained from the polycrystalline system. This allows for a focused and performance-based evaluation of the CHP, battery, and thermal storage integration.

To ensure full coverage of demand under off-grid conditions, the hybrid system follows the operational logic illustrated in Figure 2.

Building on the rule-based structure outlined above, the model simulates full daily energy flows by quantifying both generation and demand across daytime and nighttime periods. During the day, it calculates total energy needs by summing electrical consumption, DHW usage, and the heating load—each of which varies with irradiance. Simultaneously, real-world PV performance data are used to estimate solar energy production. The balance between generation and consumption determines whether a surplus is available for storage or whether a deficit must be met by activating the CHP unit. If CHP operation is required, its thermal and electrical outputs are recorded, and any excess energy is stored when capacity allows. For the nighttime period, where energy needs are constant and solar input is absent, the model prioritizes stored energy from the battery and thermal tank. If storage proves insufficient, the CHP unit is re-engaged to ensure an uninterrupted supply. For each irradiance scenario, the simulation tracks the contribution of PV, CHP, battery storage, and thermal storage, providing a complete energy balance and system performance profile.

The model analyzes representative daily scenarios to evaluate system autonomy under varying solar input, supporting optimal sizing and operation of hybrid components, as summarized in

Table 11. Energy flows for each irradiance scenario (polycrystalline PV system).

Irradiance (W/m2)	0	40	100	150	235	280	300	330	415
Daytime
PV system input (kWh)	0	1.96	4.07	6.11	8.9	9.73	9.88	10.6	13.2
Building daytime energy demand (kWh)	16.24	15.08	13.92	11.59	10.43	9.27	8.11	6.94	5.78
Daytime electric need from CHP (kWh)	0.2	0	0	0	0	0	0	0	0
Excess PV to thermal (kWh)	0	1.76	3.87	5.91	8.7	9.07	7.91	6.74	5.58
Excess PV to battery (kWh)	0	0	0	0	0	0.46	1.77	3.66	7.42
CHP ran for (h)	6.42	5.25	3.94	2.19	0.61	0	0	0	0
CHP thermal output (kWh)	16.04	13.12	9.85	5.48	1.53	0	0	0	0
CHP electrical output (kWh)	0.32	0.26	0.2	0.11	0.03	0	0	0	0
CHP electricity used for daytime (kWh)	0.2	0	0	0	0	0	0	0	0
CHP electricity stored in batteries (kWh)	0.12	0.26	0.2	0.11	0.03	0	0	0	0
Total batteries stored CHP+PV (kWh)	0.12	0.26	0.2	0.11	0.03	0.46	1.77	3.66	7.42
Nighttime—Building energy demand 27.03 kWh
From batteries for electricity	0.05	0.05	0.05	0.05	0.05	0.05	0.05	0.05	0.05
From batteries for heating	0.07	0.21	0.15	0.06	0.03	0.41	1.72	3.61	7.37
CHP ran for (h)	10.76	10.71	10.73	10.77	10.79	10.63	10.1	9.35	7.84
CHP thermal output (kWh)	26.91	26.77	26.83	26.92	26.98	26.57	25.26	23.37	19.61
CHP electrical output (kWh)	0.54	0.54	0.54	0.54	0.54	0.53	0.51	0.47	0.39
Batteries energy in the morning (kWh)	0.54	0.54	0.54	0.54	0.54	0.53	0.51	0.47	0.39

Note: From an irradiance of 280 W/m² onward, PV generation fully supplies the daytime load, so CHP operation is not required during the day.

. It can be observed that starting from an irradiance level of 280 W/m², the photovoltaic system becomes sufficient to fully cover the building’s daytime energy demand, eliminating the need for CHP operation during the day. This marks the transition to full daytime autonomy, with any surplus PV energy redirected to thermal or battery storage. The table illustrates how increasing solar input progressively reduces reliance on CHP and enhances overall system self-sufficiency.

4. Discussion

This study systematically evaluated the capacity of hybrid solar–CHP systems to meet the winter energy needs of a residential building in Bacău, Romania, under real-world operating conditions. The results highlight several critical observations regarding PV performance, energy demand dynamics, and the operational logic required to achieve full off-grid autonomy in winter.

Unlike previous studies based solely on theoretical PV outputs or steady-state models, this paper introduces a real-time, data-driven simulation that accounts for low-irradiance solar behavior and CHP–battery–thermal interactions under winter-only conditions.

A key finding is that none of the PV technologies alone—amorphous, polycrystalline, or monocrystalline—can meet the total daily energy demand of the building during winter, even under the highest recorded irradiance of 415 W/m². While polycrystalline panels showed the highest energy output across all irradiance levels, their maximum daily production (13.2 kWh) still fell short of the building’s combined demand of 31.92 kWh (5.78 kWh daytime and 27.03 kWh nighttime). This reinforces the necessity of integrating additional sources such as micro-CHP units and energy storage systems.

Another important insight is that the daytime energy balance begins to improve substantially as solar irradiance approaches 280 W/m². At this level, the building’s daytime energy demand is 9.27 kWh. The polycrystalline PV system just surpasses this, producing 9.73 kWh, while the monocrystalline and amorphous systems still fall short, delivering 8.27 kWh and 7.65 kWh, respectively. This means that only the polycrystalline system is capable of independently covering the full daytime load at this threshold. However, it is only from 300 W/m² upward that all three PV systems begin to consistently exceed the building’s daytime demand, marking the transition to full daytime autonomy. From this point onward, the CHP unit no longer needs to run during the day, significantly reducing fuel consumption and operational hours. This also enables surplus solar energy to be stored in batteries and thermal buffers, improving the overall efficiency and flexibility of the hybrid system.

Nighttime demand remains constant and substantial across all scenarios, totaling 27.03 kWh—comprising 23.26 kWh for space heating, 3.72 kWh for DHW, and 0.05 kWh for electricity. With no solar or thermal gains at night, this load must be covered by stored energy or the CHP unit. While batteries provide partial support, they are often insufficient under low irradiance conditions, when PV surplus is minimal or absent.

The hybrid energy management strategy implemented in C++ Model 2 proved highly effective in dynamically responding to each scenario.

The model is designed to prioritize the use of solar energy by first allocating PV generation to cover daytime electrical demand. Any surplus PV energy is subsequently directed toward thermal storage for space heating or DHW and to battery charging if capacity remains. The operation of the CHP unit is deferred until both PV production and available storage are insufficient, thereby minimizing CHP runtime and associated fuel consumption. At irradiance levels below 280 W/m², the CHP unit plays a key daytime role, often running over 6 h to supplement heating and electricity. On fully overcast days (0 W/m²), it operates for the longest durations—6.42 h during the day and 10.76 h at night—covering nearly all energy needs. This highlights its critical backup role under low-solar conditions.

A valuable side-effect of CHP operation is its electrical cogeneration, which can charge the battery and enhance system resilience overnight. For example, at 40 W/m², even limited CHP use stores 0.26 kWh—enough to fully cover the 0.05 kWh nighttime electrical load and partially offset heating demand.

Another key insight is that under high irradiance, the battery is not fully depleted overnight—not because PV alone covers nighttime demand, but because the CHP recharges it during night operation. At 415 W/m², 7.42 kWh are stored during the day, partially used overnight. By morning, 0.39 kWh remain, generated by the CHP, not leftover PV. This highlights the CHP’s dual role: meeting thermal demand and replenishing battery reserves. In multi-day high-irradiance scenarios, this synergy enhances stability and self-sufficiency, bringing full energy autonomy within reach.

The thermal storage tank acts as a short-term buffer, typically charged during the day with excess CHP or PV energy and depleted by the evening. When battery electricity is sufficient, it can be reheated overnight via resistance heating. Although the heat source shifts from thermal to electrical, the tank remains active over the full 24 h cycle. Still, only the battery enables true day-to-night shifting by storing electricity for both direct use and indirect thermal support.

A key experimental finding is the small difference in real-world efficiency between panel types under winter conditions. At 330 W/m², the measured efficiencies were 8.08% (amorphous), 9.3% (polycrystalline), and 9.97% (monocrystalline). These values, derived from experimental data and used in C++ Model 1, contrast with manufacturer ratings (6.65–23%) and highlight the need for site-specific evaluation. While polycrystalline and monocrystalline panels perform better at higher irradiance, their advantage narrows in low-light winter scenarios, making amorphous panels a cost-effective, space-efficient option where diffuse light tolerance is critical.

Storage Capacity Sizing Based on Maximum Surplus

The simulation results (Table 11) show that the maximum daily PV surplus occurs at 415 W/m², enabling 7.42 kWh of battery charging and 9.07 kWh of thermal energy for the storage tank. To capture this surplus and avoid energy waste, the hybrid system should include a battery bank of at least 7.5 kWh and a thermal tank of 9.1 kWh. These values reflect the building’s winter energy profile and serve as upper bounds for storage sizing. Oversizing offers little added benefit under winter conditions, while undersizing risks reduced autonomy and unused energy.

The results suggest that solar-only systems are not viable in winter without supplemental sources. The hybrid system proposed here provides a practical blueprint: pairing real-world PV output with CHP ensures full demand coverage, even under low irradiance. The energy flow logic also illustrates how thermal and battery storage must be proportioned based on surplus availability and nighttime loads. This helps avoid oversizing and improves overall efficiency in cold-climate deployments.

While this study provides detailed simulations of hybrid system behavior under varying winter irradiance levels, it does not include a full techno-economic analysis of the integrated system. Specifically, factors such as CHP fuel consumption, operational costs, and Levelized Cost of Energy (LCOE) are not assessed in detail. This omission was intentional to maintain focus on the core objective: identifying the performance limits of solar-only configurations and evaluating the necessary conditions for off-grid autonomy. Incorporating a complete economic model would require additional assumptions and significantly expand the scope. Nevertheless, future work will aim to extend the current framework by integrating cost models and fuel consumption dynamics to support comprehensive system optimization.

To highlight the practical contributions and relative performance of the proposed system,

Table 12. Comparative overview of recent PV–CHP studies for residential off-grid supply.

Study	Methodology	PV Input	CHP Model	Data Type	Storage Simulated	Key Results	Novelty
Kneiske and Braun [1]	Simulation	Theoretical	Gas-fired micro-CHP	Synthetic irradiance	No	80% self-consumption, 40–60% fossil fuel cut	Hierarchical control algorithm
Ghanem et al. [2]	Simulation	PV + SOFC	SOFC-based micro-CHP	Annual average	Seasonal thermal only	100% electricity, 95% winter heat, –88.6% CO2	Seasonal storage + SOFC
Cardoso et al. [3]	Real data + model	PV (3.5 kWp)	1.3–4.7 kWe	Real + control optimization	Battery only	45% grid reduction, 85% efficiency	Model predictive control
This study	Experiment + simulation	Amorphous, poly, mono (measured)	Gas-fired micro-CHP 2.5 kWth	Real irradiance, real PV efficiency	Battery + thermal	Full winter autonomy from 330 W/m2, optimal sizing of all components	Real-world data-driven hybrid design for cold-climate off-grid systems

compares the present study with several relevant works already cited in the literature review. The comparison includes key aspects such as modeling approach, system configuration, climatic conditions, PV performance treatment, and scope of integration. This study distinguishes itself by integrating real-world PV data into a dynamic irradiance-driven simulation framework focused exclusively on winter conditions. Unlike most existing studies relying on theoretical PV assumptions or averaged seasonal performance, the proposed model uses measured irradiance and panel-specific efficiency curves, allowing accurate daily simulations and sizing decisions for CHP, battery, and thermal storage components.

5. Conclusions

This study evaluated the performance of a hybrid solar–CHP system for residential off-grid energy supply under winter conditions in Bacău, Romania. A two-phase methodology was employed, combining experimental data with computational simulations using two custom-built C++ models.

The key findings include the following: (1) The best-performing PV system (polycrystalline) reached a maximum daily output of 13.2 kWh at 415 W/m², while the building’s total daily demand was 31.92 kWh (5.78 kWh daytime and 27.03 kWh nighttime); (2) PV-only systems failed to reach full energy autonomy in any winter scenario; (3) a CHP unit with 2.5 kW thermal and 0.05 kW electrical output ensured full coverage during low-irradiance conditions; (4) a battery bank sized at 7.5 kWh and a thermal storage tank of 9.1 kWh were sufficient to absorb the maximum solar surplus recorded; and (5) full daytime autonomy was achieved only at irradiance levels ≥300 W/m², with total off-grid autonomy realized from 330 W/m² upward using the hybrid system.

Phase 1 analyzed the real-world performance of amorphous, polycrystalline, and monocrystalline PV panels. Experimental efficiency values were integrated into C++ Model 1 to compute solar gains, heating and DHW demands, and PV output. The results showed that PV systems alone could not meet winter energy needs, with the best-performing system (polycrystalline) reaching only 13.2 kWh/day versus a 31.92 kWh demand. Phase 2, using C++ Model 2, demonstrated that adding a micro-CHP unit with battery and thermal storage ensures full off-grid autonomy. The CHP unit offsets heating shortfalls and co-generates electricity to support nighttime battery use.

From a practical standpoint, this study offers design benchmarks: (1) a thermal output of 2.5 kW ensures full nighttime heating coverage; (2) battery and puffer tank sizing should not exceed 7.5 kWh and 9.1 kWh, respectively, under the examined irradiance spectrum; and (3) irradiance-based control logic reduces unnecessary CHP runtime and fuel use, improving autonomy and operational efficiency.

This study concludes that a well-dimensioned hybrid system, guided by real data and scenario-specific simulations, can ensure a reliable winter energy supply in residential buildings. Optimal performance is achieved when PV surplus is stored efficiently, and CHP operation is minimized through smart energy management.

While this study focused on a real-world winter scenario in Bacău, Romania, the simulation framework developed here can be readily adapted for other geographic regions by integrating local irradiance and temperature datasets. Future work will explore the performance of hybrid PV–CHP systems under varying climatic conditions to assess the generalizability of sizing strategies and operational thresholds across multiple solar zones.