Modeling Cost-Effectiveness of Photovoltaic Module Replacement Based on Quantitative Assessment of Defect Power Loss
Abstract
1. Introduction
2. Module Degradation—A Brief Review
3. Experimental Section
- 2020: 27 August to 9 September, 1 to 8 October;
- 2021: 5 May to 9 September;
- 2022: 19 May to 8 June.
4. Methodology
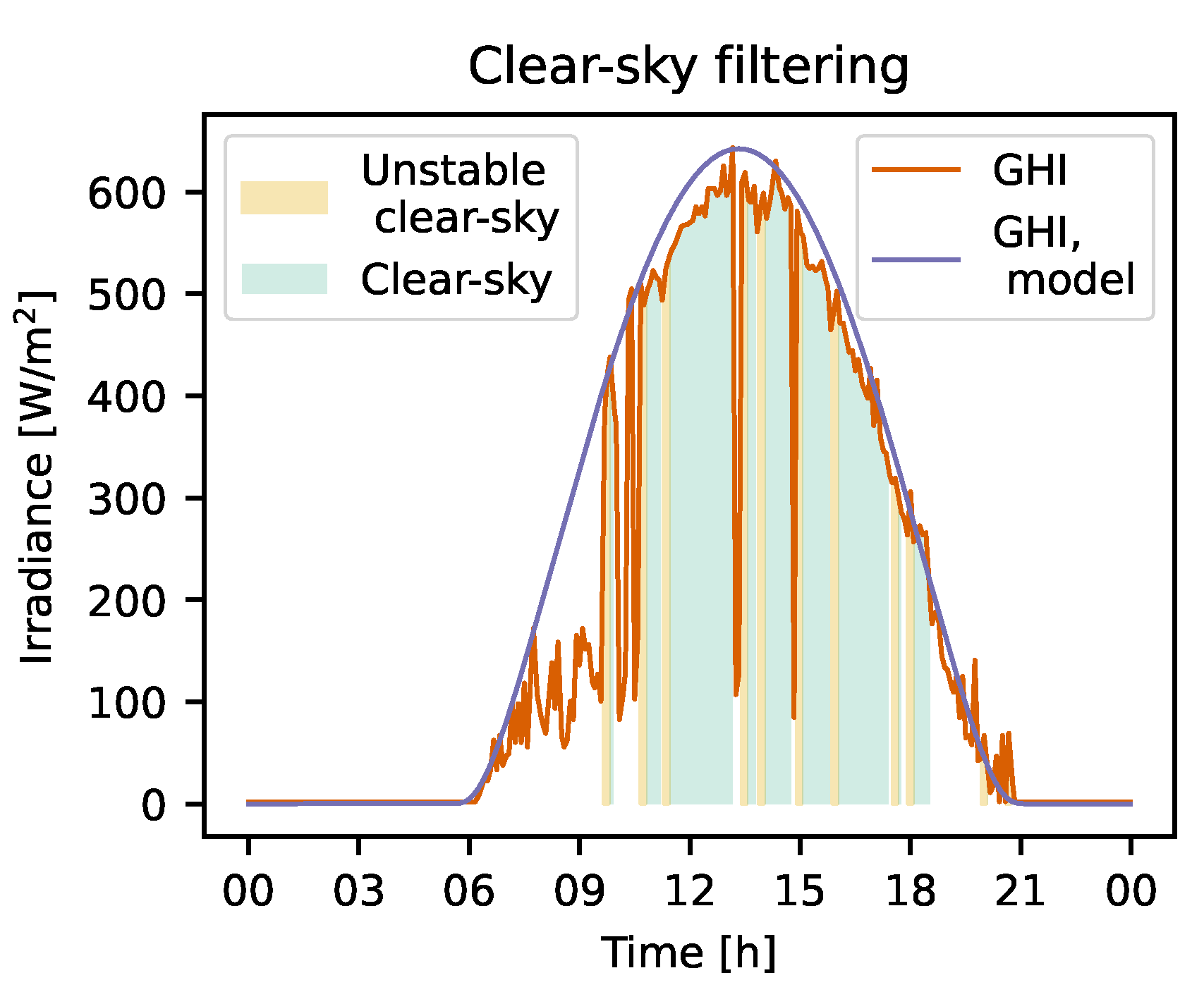
4.1. Clear-Sky Filtering of Thermography Images
4.2. Defect Heating and Power Loss
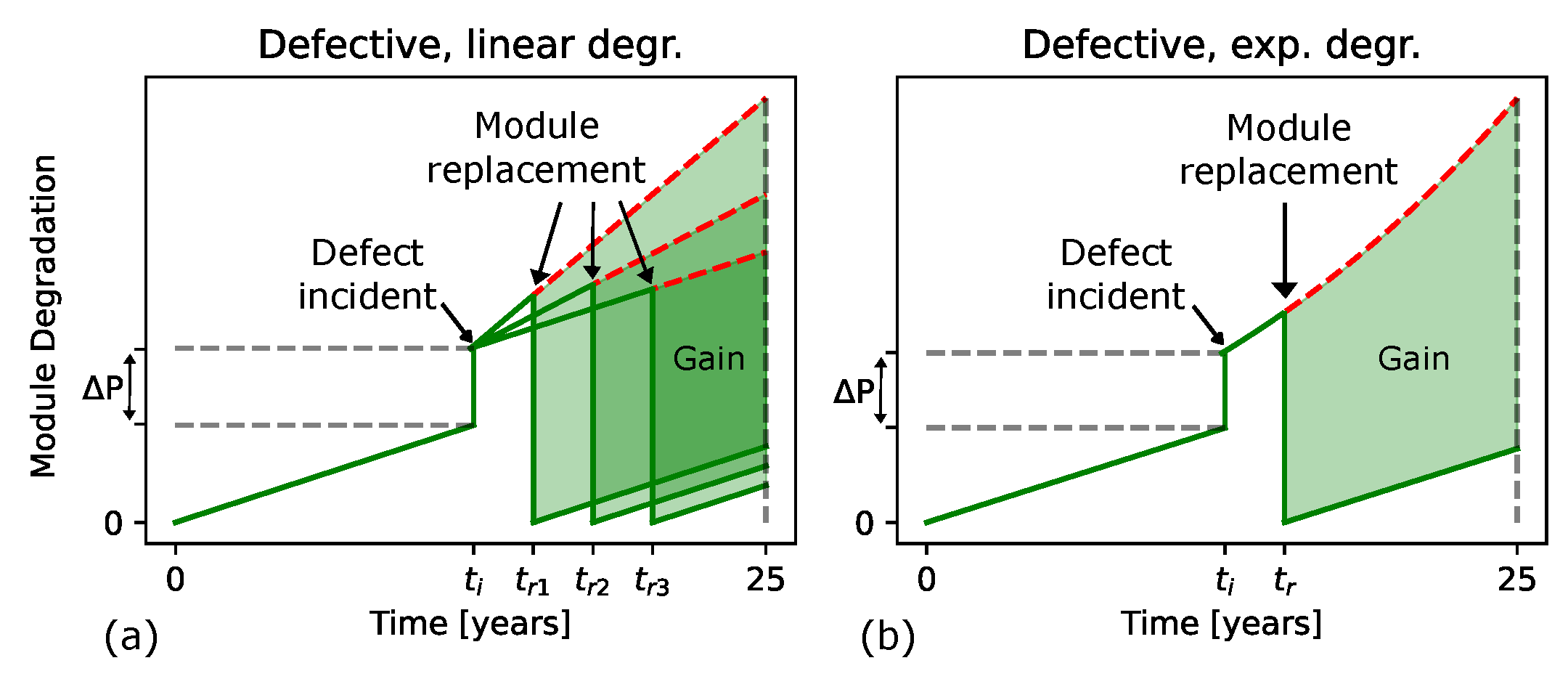
4.3. Cumulative Energy Loss from Defects and Degradation
4.4. Energy Gain from Module Replacement
5. Experimental Foundation
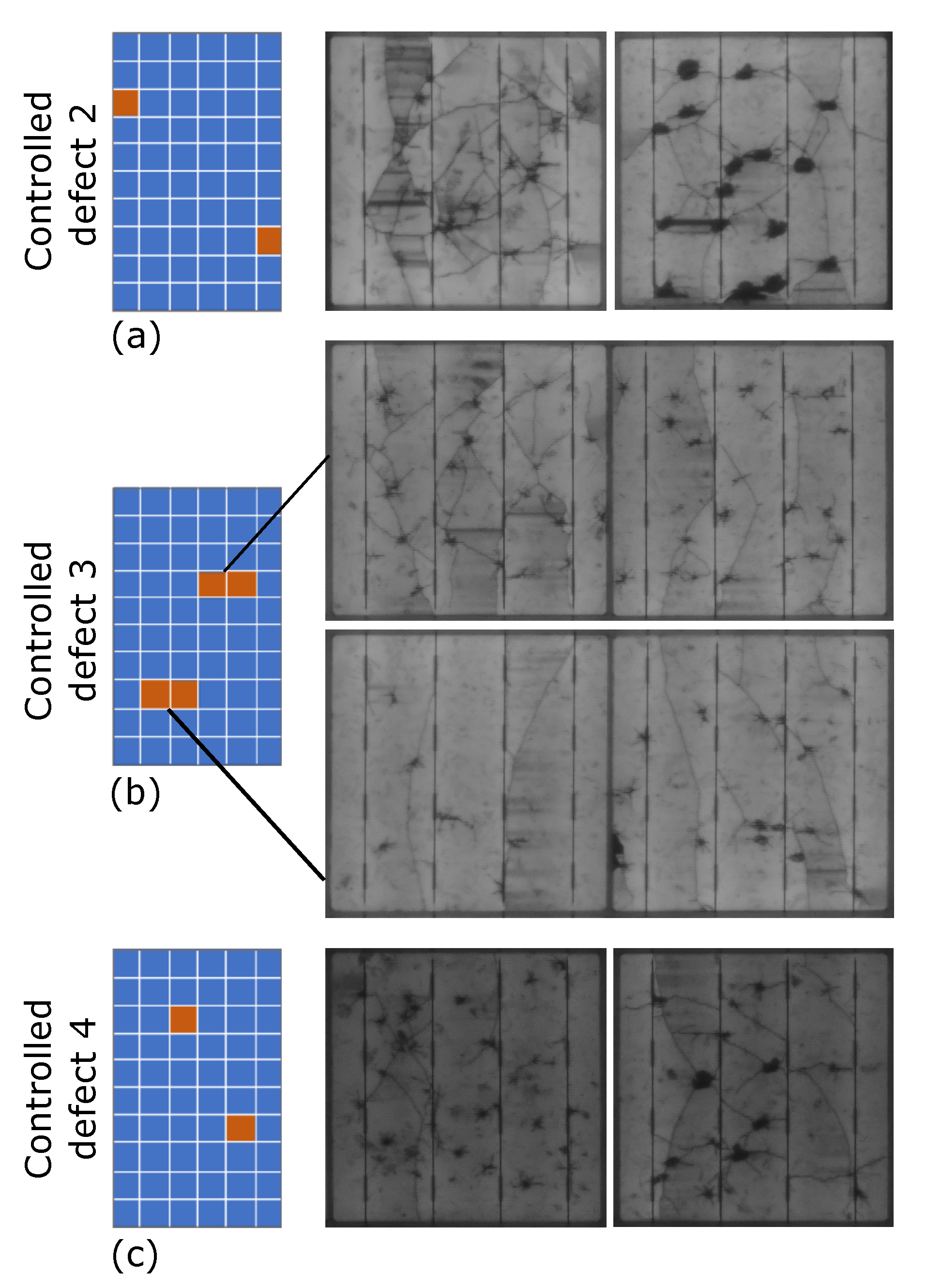
5.1. Characterization of Defects with Light IV and EL
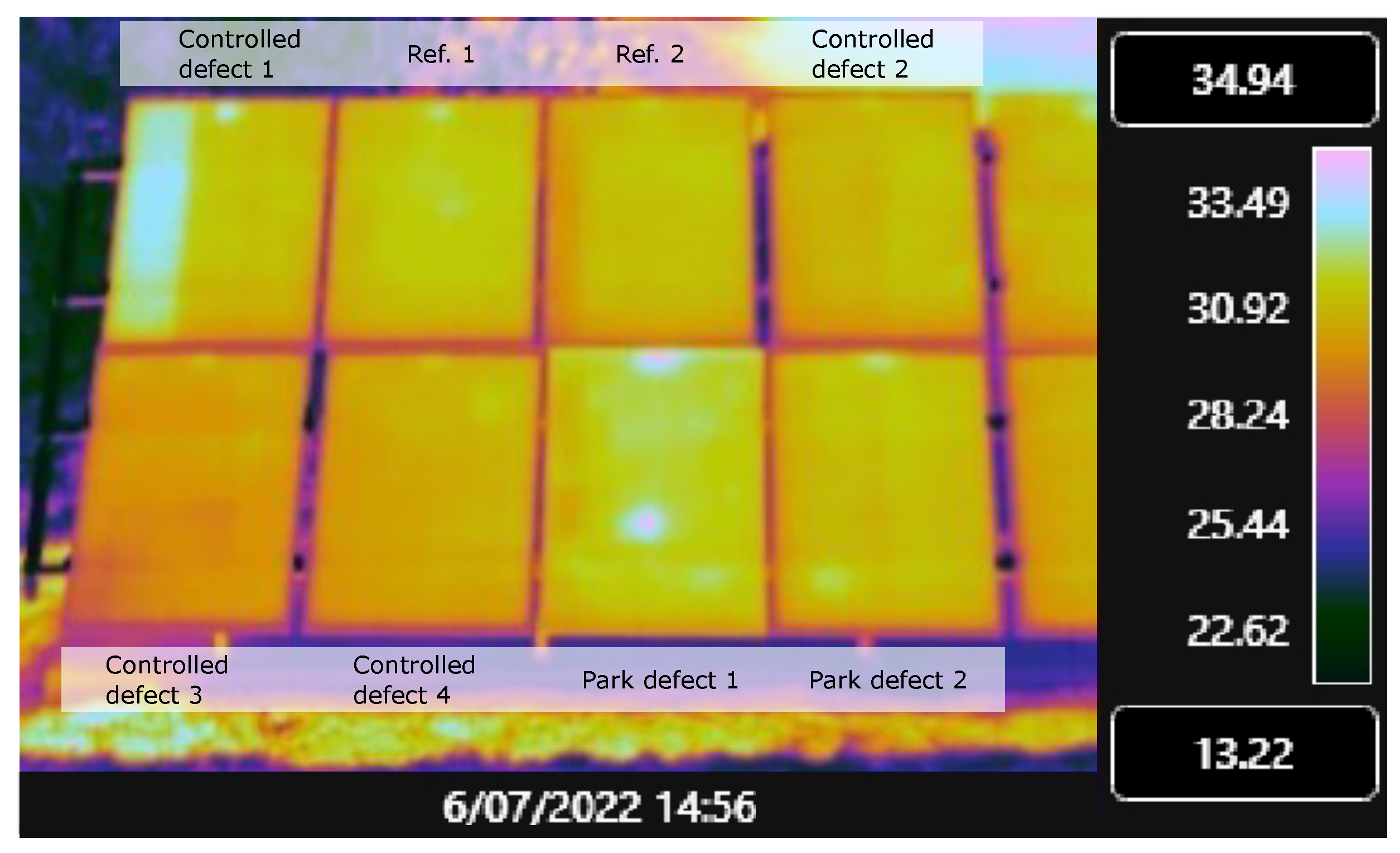
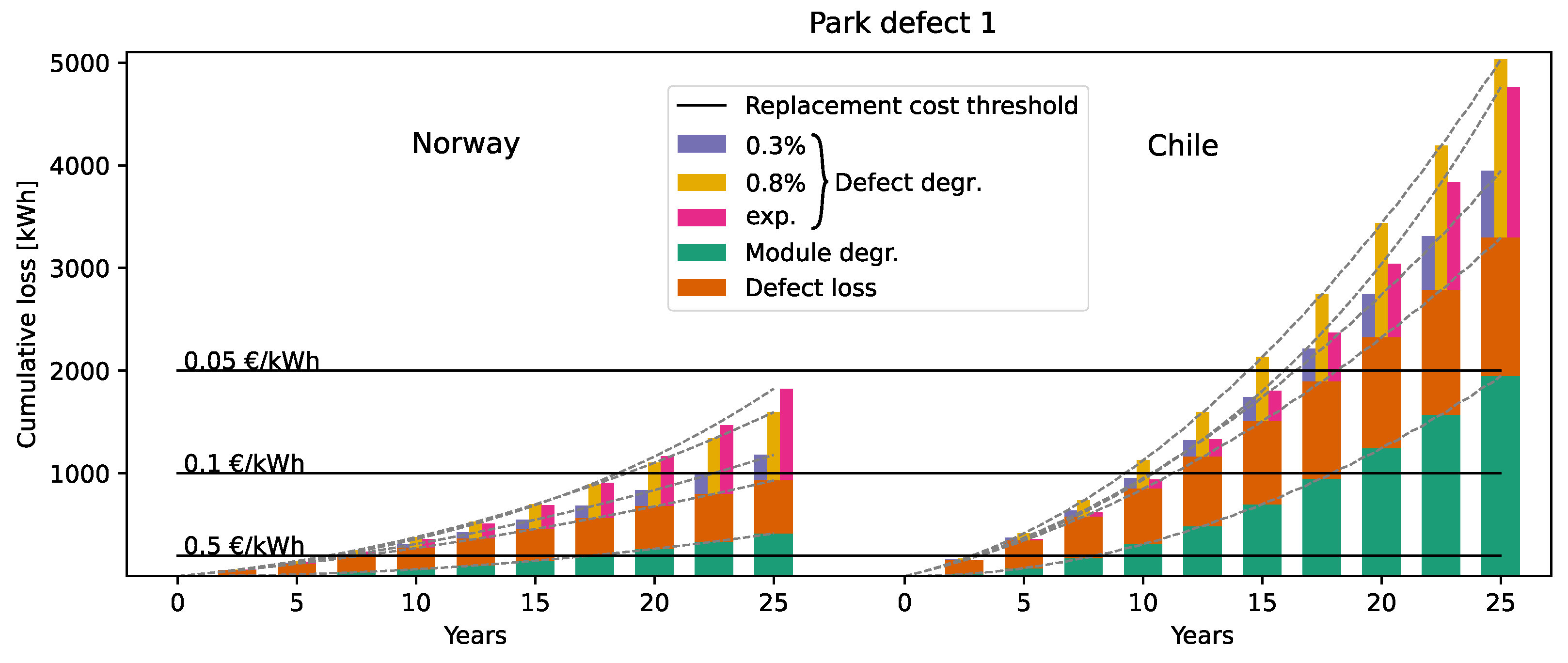
5.2. Power Loss from Park Defects
6. Calculations on the Economic Impact of Defects
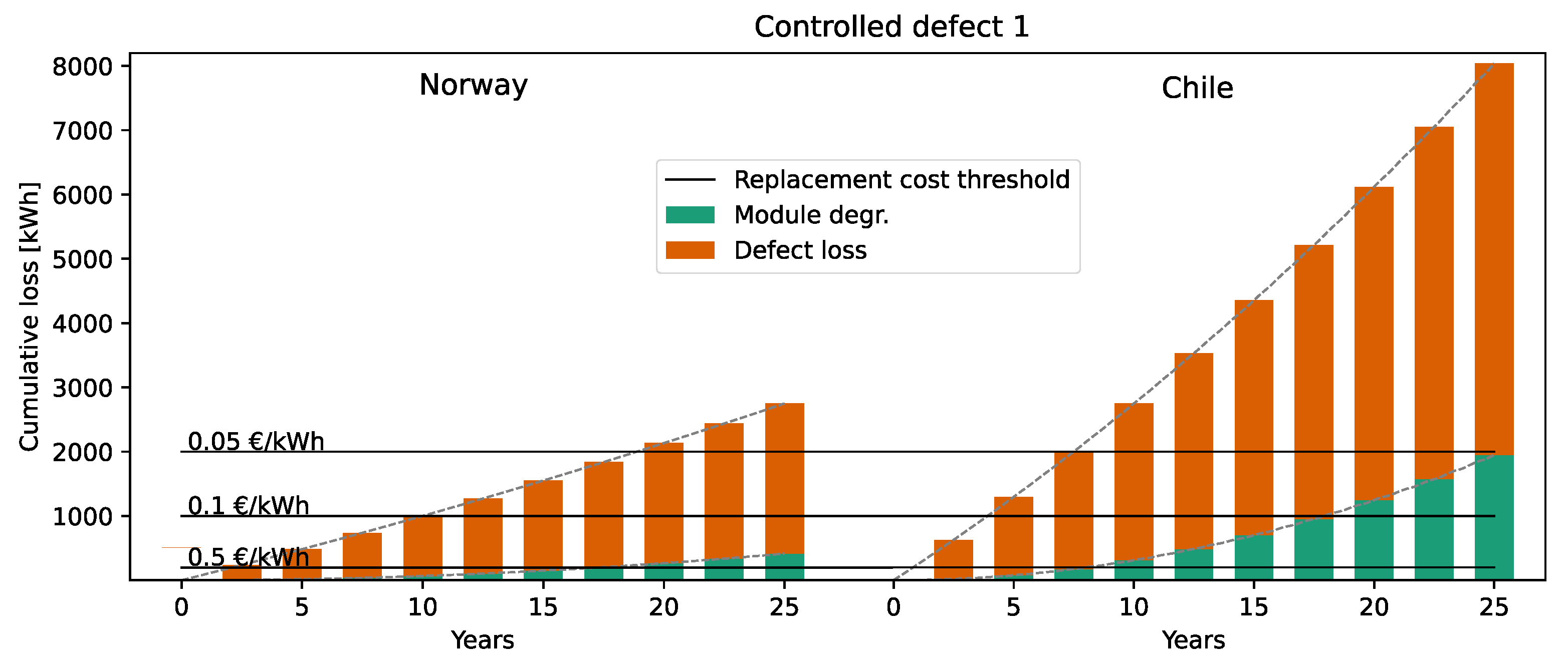
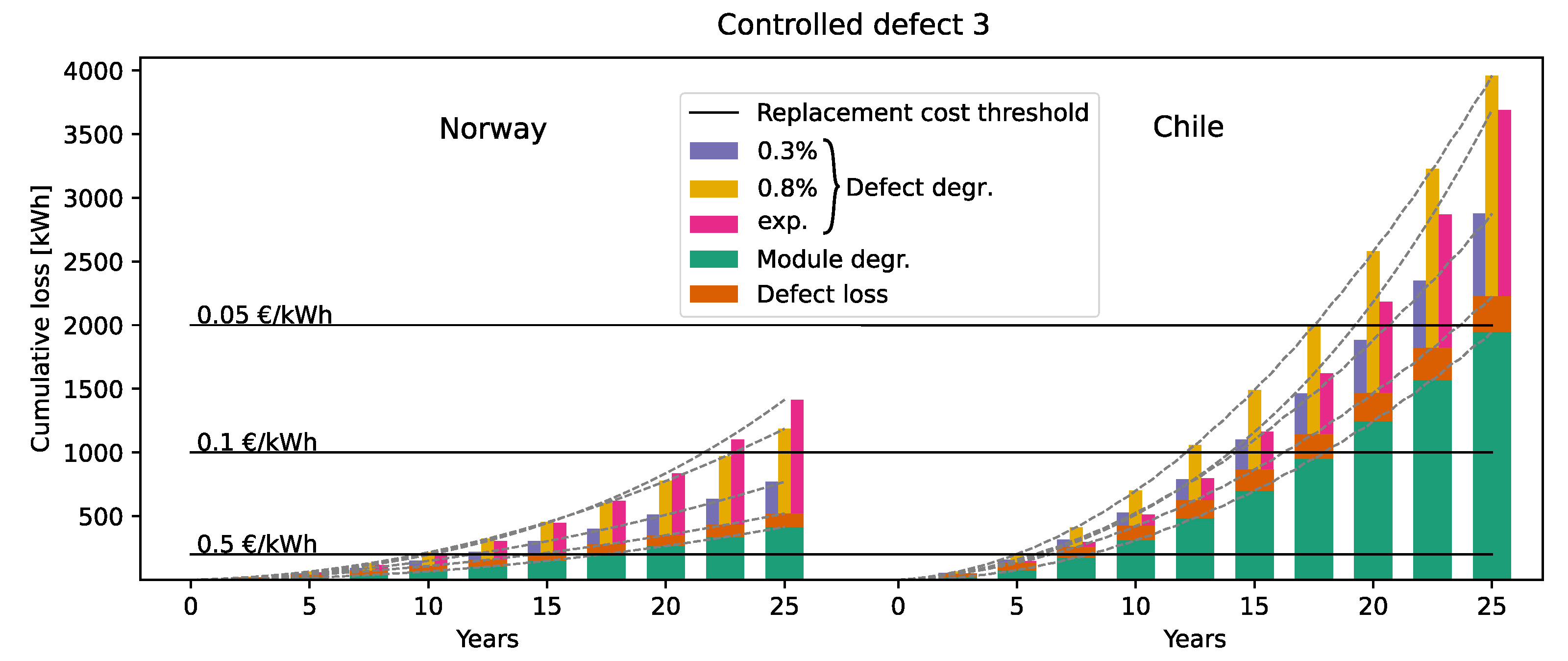
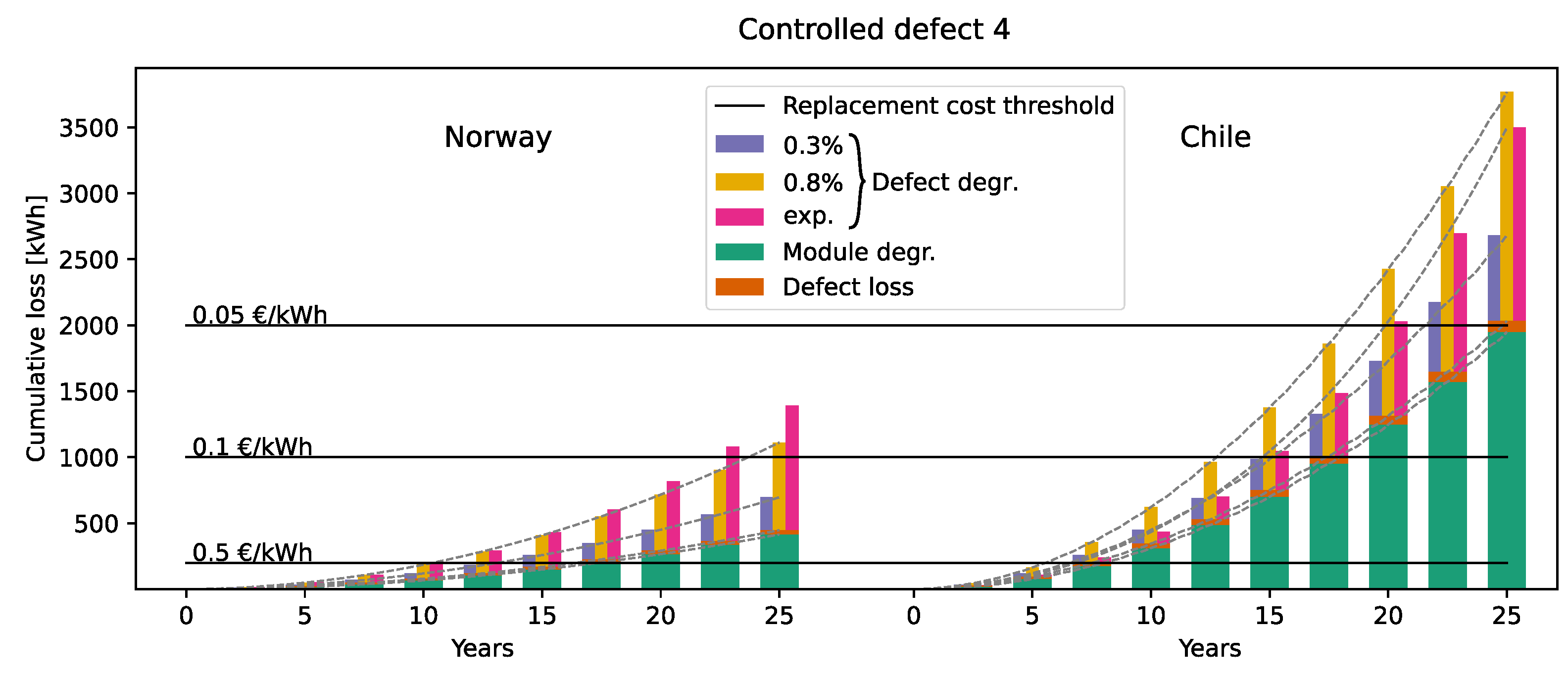
6.1. Cumulative Power Loss
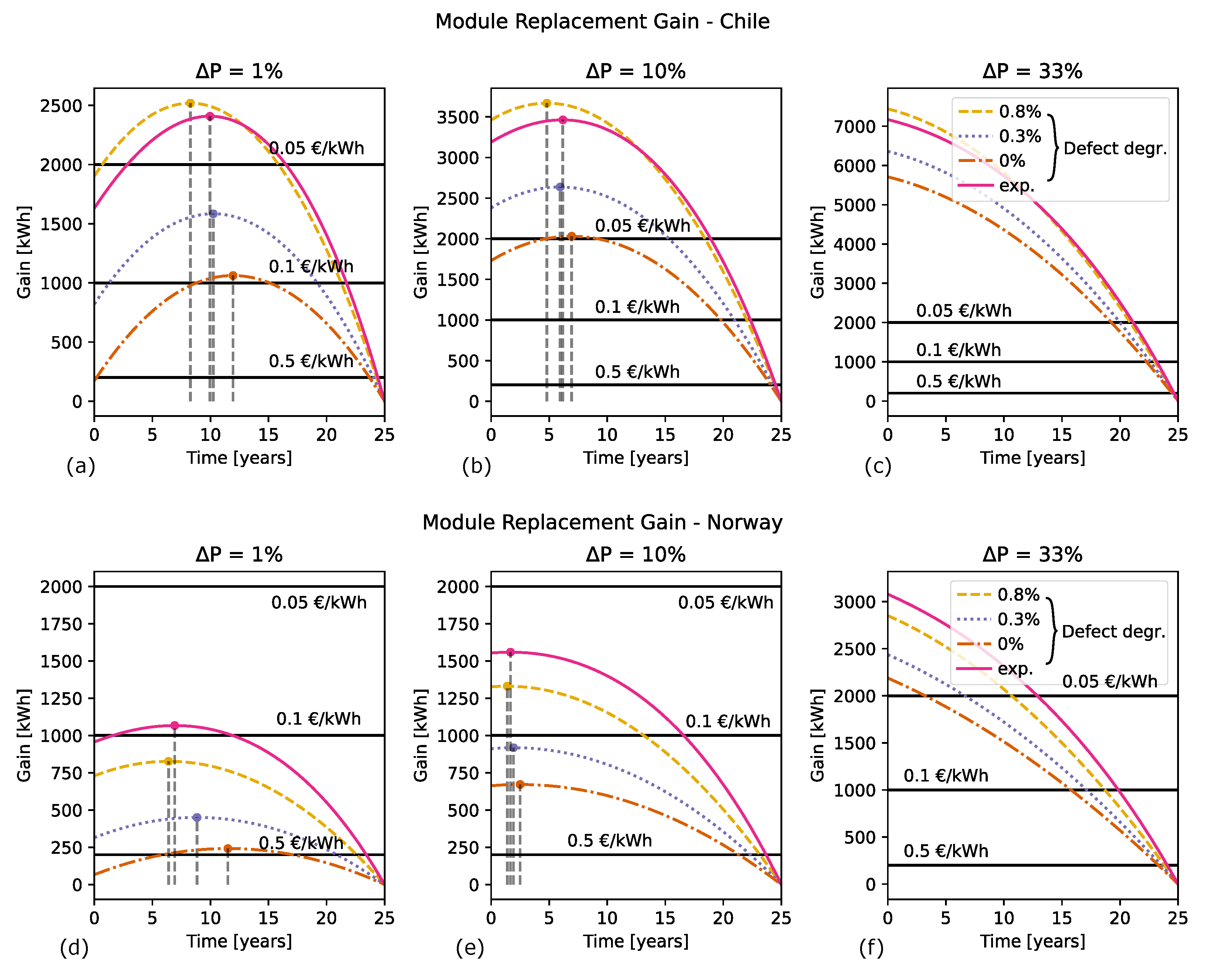
6.2. Module Replacement Gain
6.2.1. Infant-Life Failures
- The most cost-effective approach is not necessarily to replace a defective module immediately; for the less severe defects, the peak occurs after some years of degradation.
- The more significant the defects, the earlier the modules need to be replaced to ensure cost-effectiveness.
- The minor defect of P = 1% is most probably not cost-effective to replace in Norway unless the feed-in tariff prices are as high as EUR 0.5/kWh. For Chile, it can be beneficial to replace the module, but mainly if the module has sustained around 10 years of additional module degradation before it is replaced with a new module.
- The medium-size defect with a loss of P = 10% is cost-effective to replace in Chile, especially after around five years of additional module degradation, but it might not be cost-effective to replace in Norway.
- The bypassed substring with a defect loss of P = 33% is cost-effective to replace in both Norway and Chile, even if they are discovered late in the park life. This conclusion also extends to defects resulting in power losses greater than 33%.
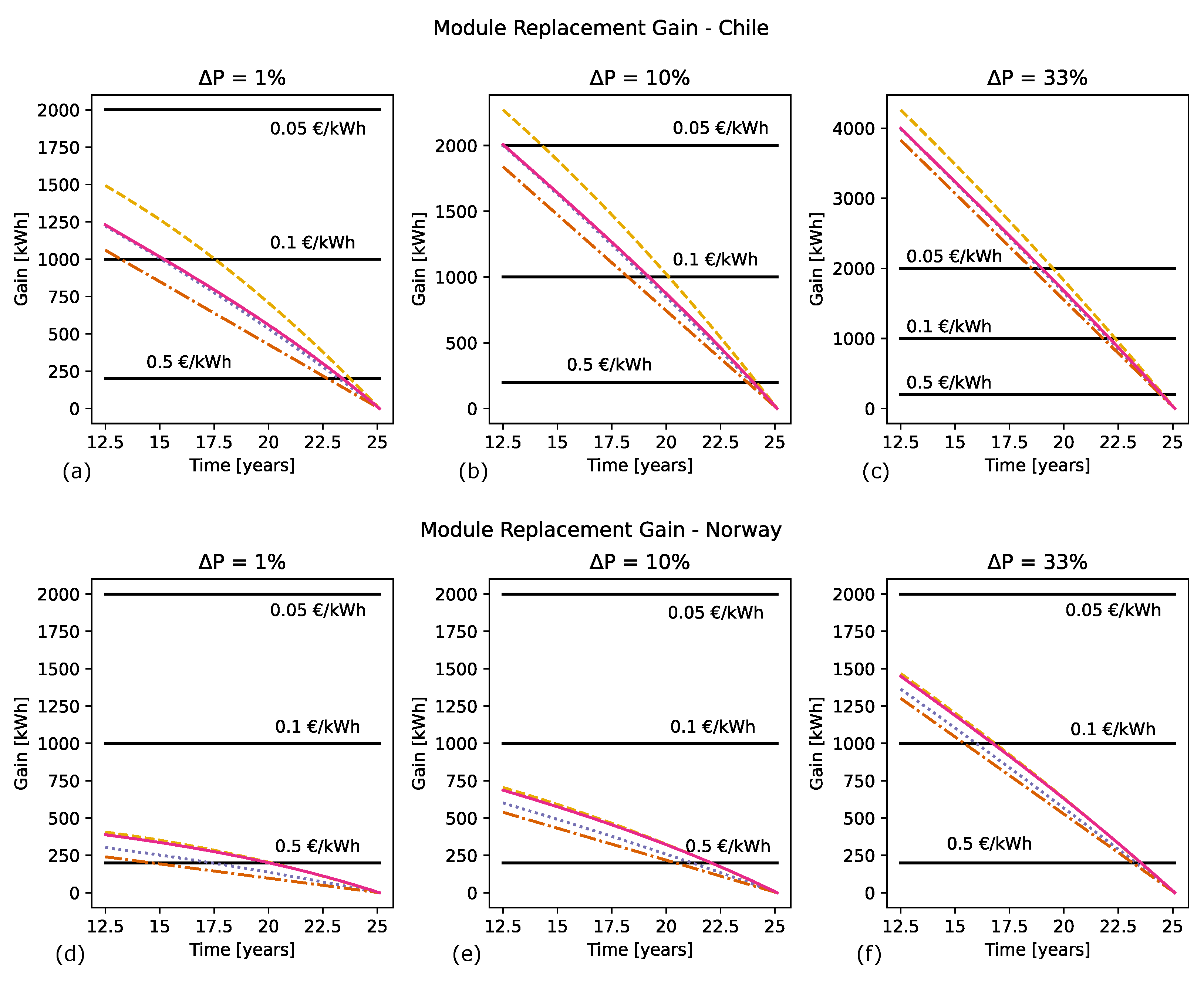
6.2.2. Mid-Life Failures
- Unlike the infant-life failures in Figure 13, mid-life failures are most cost-effective to replace immediately.
- Minor defects of 1% are most likely not cost-effective to replace, even in high-irradiation locations like Chile.
- Defects of 10% are likely beneficial to replace mid-life in high-irradiation conditions, but not in low-irradiation locations like Norway.
- For the more severe defect of 33%, there is a substantial gain from replacing the module in high-irradiation locations, even when they are not immediately detected. There might be a gain from replacing the 33% defects in low-irradiation conditions as well, given an early detection.
7. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Li, L.; Lin, J.; Wu, N.; Xie, S.; Meng, C.; Zheng, Y.; Wang, X.; Zhao, Y. Review and outlook on the international renewable energy development. Energy Built Environ. 2022, 3, 139–157. [Google Scholar] [CrossRef]
- International Renewable Energy Agency. Renewable Power Generation Costs in 2022; Technical Report; International Renewable Energy Agency (IRENA): Abu Dhabi, United Arab Emirates, 2023. [Google Scholar]
- Mahdi, A.; Leahy, H.; Alghoul, P.G.; Morrison, M.; Al Mahdi, H.; Leahy, P.G.; Alghoul, M.; Morrison, A.P. A Review of Photovoltaic Module Failure and Degradation Mechanisms: Causes and Detection Techniques. Solar 2024, 4, 43–82. [Google Scholar] [CrossRef]
- Rajput, P.; Singh, D.; Singh, K.Y.; Karthick, A.; Shah, M.A.; Meena, R.S.; Zahra, M.M.A. A comprehensive review on reliability and degradation of PV modules based on failure modes and effect analysis. Int. J. Low-Carbon Technol. 2024, 19, 922–937. [Google Scholar] [CrossRef]
- International Energy Agency (IEA). Review of Failures of Photovoltaic Modules; Technical Report; International Energy Agency (IEA): Paris, France, 2014. [Google Scholar]
- Buerhop, C.; Bommes, L.; Schlipf, J.; Pickel, T.; Fladung, A.; Peters, I.M. Infrared imaging of photovoltaic modules: A review of the state of the art and future challenges facing gigawatt photovoltaic power stations. Prog. Energy 2022, 4, 042010. [Google Scholar] [CrossRef]
- Kirsten Vidal de Oliveira, A.; Aghaei, M.; Rüther, R. Aerial infrared thermography for low-cost and fast fault detection in utility-scale PV power plants. Sol. Energy 2020, 211, 712–724. [Google Scholar] [CrossRef]
- Herz, M.; Friesen, G.; Jahn, U.; Koentges, M.; Lindig, S.; Moser, D. Identify, analyse and mitigate—Quantification of technical risks in PV power systems. Prog. Photovoltaics Res. Appl. 2023, 31, 1285–1298. [Google Scholar] [CrossRef]
- Moser, D.; Del Buono, M.; Jahn, U.; Herz, M.; Richter, M.; De Brabandere, K. Identification of technical risks in the photovoltaic value chain and quantification of the economic impact. Prog. Photovoltaics Res. Appl. 2017, 25, 592–604. [Google Scholar] [CrossRef]
- International Energy Agency (IEA). Quantification of Technical Risks in PV Power Systems Task 13 Performance, Operation and Reliability of Photovoltaic Systems Identify Analyse Mitigate; International Energy Agency (IEA): Paris, France, 2021. [Google Scholar]
- Kim, J.; Rabelo, M.; Padi, S.P.; Yousuf, H.; Cho, E.C.; Yi, J. A review of the degradation of photovoltaic modules for life expectancy. Energies 2021, 14, 4278. [Google Scholar] [CrossRef]
- Aghaei, M.; Fairbrother, A.; Gok, A.; Ahmad, S.; Kazim, S.; Lobato, K.; Oreski, G.; Reinders, A.; Schmitz, J.; Theelen, M.; et al. Review of degradation and failure phenomena in photovoltaic modules. Renew. Sustain. Energy Rev. 2022, 159, 112160. [Google Scholar] [CrossRef]
- Jordan, D.C.; Wohlgemuth, J.H.; Kurtz, S.R. Technology and climate trends in pv module degradation. In Proceedings of the 27th European Photovoltaic Solar Energy Conference and Exhibition, Frankfurt, Germany, 24–28 September 2012; pp. 3118–3124. [Google Scholar] [CrossRef]
- Dubey, R.; Chattopadhyay, S.; Kuthanazhi, V.; Kottantharayil, A.; Singh Solanki, C.; Arora, B.M.; Narasimhan, K.L.; Vasi, J.; Bora, B.; Singh, Y.K.; et al. Comprehensive study of performance degradation of field-mounted photovoltaic modules in India. Energy Sci. Eng. 2017, 5, 51–64. [Google Scholar] [CrossRef]
- Jordan, D.C.; Kurtz, S.R.; VanSant, K.; Newmiller, J. Compendium of photovoltaic degradation rates. Prog. Photovoltaics Res. Appl. 2016, 24, 978–989. [Google Scholar] [CrossRef]
- Singh, J.; Belmont, J.; TamizhMani, G. Degradation analysis of 1900 PV modules in a hot-dry climate: Results after 12 to 18 years of field exposure. In Proceedings of the 2013 IEEE 39th Photovoltaic Specialists Conference (PVSC), Tampa, FL, USA, 16–21 June 2013; pp. 3270–3275. [Google Scholar] [CrossRef]
- Deceglie, M.G.; Silverman, T.J.; Member, S.; Young, E.; Hobbs, W.B.; Member, S.; Libby, C. Field and Accelerated Aging of Cracked Solar Cells. IEEE J. Photovoltaics 2023, 13, 836–841. [Google Scholar] [CrossRef]
- Suleske, A.; Singh, J.; Kuitche, J.; Tamizh-Mani, G. Performance degradation of grid-tied photovoltaic modules in a hot-dry climatic condition. In Proceedings of the Reliability of Photovoltaic Cells, Modules, Components, and Systems IV, San Diego, CA, USA, 22–25 August 2011; Volume 8112, p. 81120P. [Google Scholar] [CrossRef]
- Jordan, D.C.; Silverman, T.J.; Sekulic, B.; Kurtz, S.R. PV degradation curves: Non-linearities and failure modes. Prog. Photovoltaics Res. Appl. 2017, 25, 583–591. [Google Scholar] [CrossRef]
- Buerhop, C.; Wirsching, S.; Bemm, A.; Pickel, T.; Hohmann, P.; Nieß, M.; Vodermayer, C.; Huber, A.; Glück, B.; Mergheim, J.; et al. Evolution of cell cracks in PV-modules under field and laboratory conditions. Prog. Photovoltaics Res. Appl. 2018, 26, 261–272. [Google Scholar] [CrossRef]
- IEC 60904-9; Photovoltaic Devices—Part 9: Solar Simulator Performance Requirements. International Electrotechnical Commission: Geneva, Switzerland, 2007.
- IEC TS 60904-13; Photovoltaic Devices—Part 13: Electroluminescence of Photovoltaic Modules. International Electrotechnical Commission: Geneva, Switzerland, 2018.
- Holmgren, W.F.; Hansen, C.W.; Mikofski, M.A. pvlib python: A python package for modeling solar energy systems. J. Open Source Softw. 2018, 3, 884. [Google Scholar] [CrossRef]
- Teubner, J.; Buerhop, C.; Pickel, T.; Hauch, J.; Camus, C.; Brabec, C.J. Quantitative assessment of the power loss of silicon PV modules by IR thermography and its dependence on data-filtering criteria. Prog. Photovoltaics Res. Appl. 2019, 27, 856–868. [Google Scholar] [CrossRef]
- Moretón, R.; Lorenzo, E.; Narvarte, L. Experimental observations on hot-spots and derived acceptance/rejection criteria. Sol. Energy 2015, 118, 28–40. [Google Scholar] [CrossRef]
- Dhimish, M.; Badran, G. Investigating defects and annual degradation in UK solar PV installations through thermographic and electroluminescent surveys. npj Mater. Degrad. 2023, 7, 14. [Google Scholar] [CrossRef]
- National Solar Radiation Database. 2024. Available online: https://nsrdb.nrel.gov/data-viewer (accessed on 12 August 2024).
- Solar Module Prices Increase for First Time in Years, Anza Reports—pv Magazine USA. 2014. Available online: https://pv-magazine-usa.com/2024/06/12/solar-module-prices-increase-for-first-time-in-years-anza-reports/ (accessed on 26 September 2024).
- Feed-in Tariffs (FITs) in Europe—pv Magazine International. 2024. Available online: https://www.pv-magazine.com/features/archive/solar-incentives-and-fits/feed-in-tariffs-in-europe/ (accessed on 26 September 2024).
- Aarseth, B.L.; Nygård, M.M.; Otnes, G.; Marstein, E.S. Combining Production Data Timeseries and Infrared Thermography to Assess the Impact of Thermal Signatures on Photovoltaic Yield Over Time. IEEE J. Photovoltaics 2024. early access. [Google Scholar] [CrossRef]



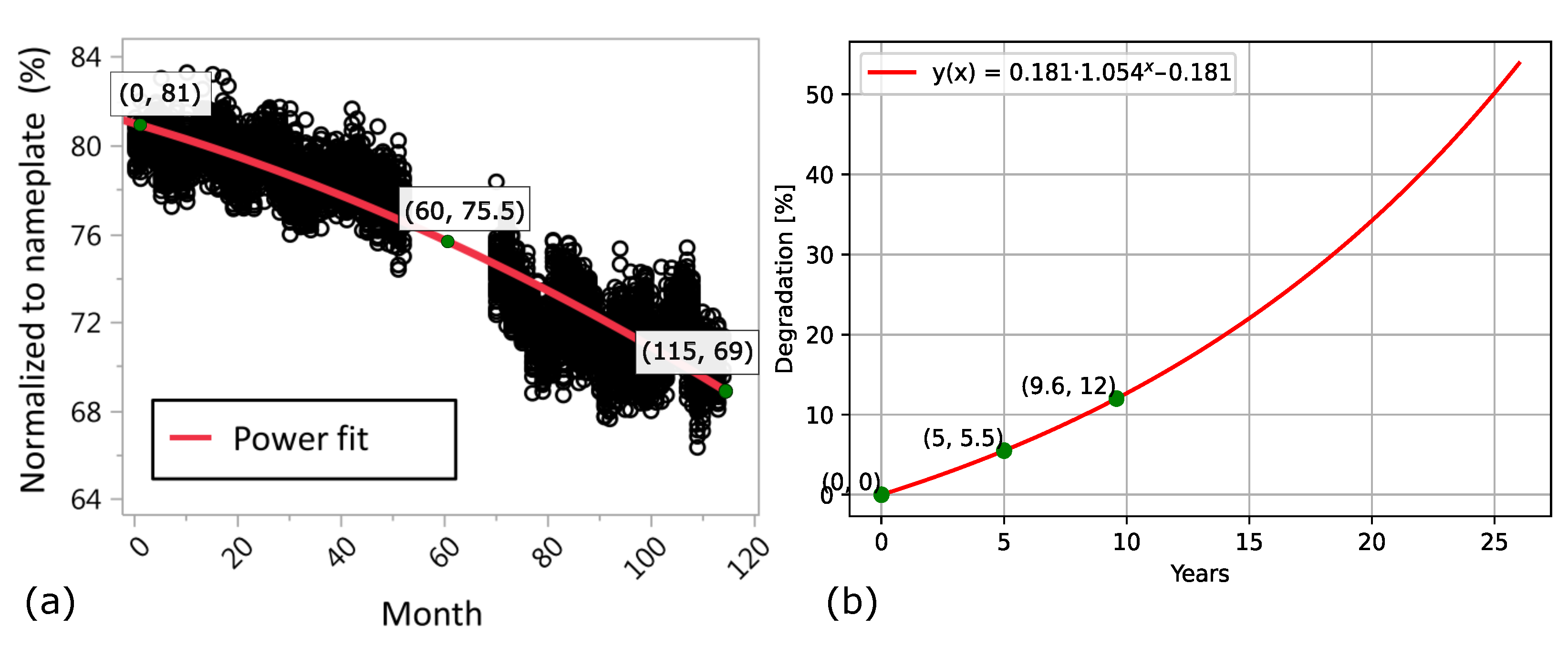
| Type of Degradation | Degradation Rate per Year | |
|---|---|---|
| Module degradation | Chile | 0.9% |
| Norway | 0.5% | |
| Defect degradation | [20] | 0% |
| [17] | 0.3% | |
| [18] | 0.8% | |
| [19] | Increasing: 0.181 · (1.055t − 1) where t is time in years |
| Module | Initial [W] | Post Damage [W] | ΔP [W] | Relative Change |
|---|---|---|---|---|
| Contr. defect 1 | 270.5 | 175.8 | −95 | −35% |
| Contr. defect 2 | 270.4 | 272.2 | 1.8 | 0.7% |
| Contr. defect 3 | 274.4 | 270.1 | −4.3 | −1.6% |
| Contr. defect 4 | 269.5 | 268.2 | −1.3 | −0.5% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lofstad-Lie, V.; Aarseth, B.L.; Roosloot, N.; Marstein, E.S.; Skauli, T. Modeling Cost-Effectiveness of Photovoltaic Module Replacement Based on Quantitative Assessment of Defect Power Loss. Solar 2024, 4, 728-743. https://doi.org/10.3390/solar4040034
Lofstad-Lie V, Aarseth BL, Roosloot N, Marstein ES, Skauli T. Modeling Cost-Effectiveness of Photovoltaic Module Replacement Based on Quantitative Assessment of Defect Power Loss. Solar. 2024; 4(4):728-743. https://doi.org/10.3390/solar4040034
Chicago/Turabian StyleLofstad-Lie, Victoria, Bjørn Lupton Aarseth, Nathan Roosloot, Erik Stensrud Marstein, and Torbjørn Skauli. 2024. "Modeling Cost-Effectiveness of Photovoltaic Module Replacement Based on Quantitative Assessment of Defect Power Loss" Solar 4, no. 4: 728-743. https://doi.org/10.3390/solar4040034
APA StyleLofstad-Lie, V., Aarseth, B. L., Roosloot, N., Marstein, E. S., & Skauli, T. (2024). Modeling Cost-Effectiveness of Photovoltaic Module Replacement Based on Quantitative Assessment of Defect Power Loss. Solar, 4(4), 728-743. https://doi.org/10.3390/solar4040034






