Modeling and Energy Management of a Microgrid Based on Predictive Control Strategies †
Abstract
1. Introduction
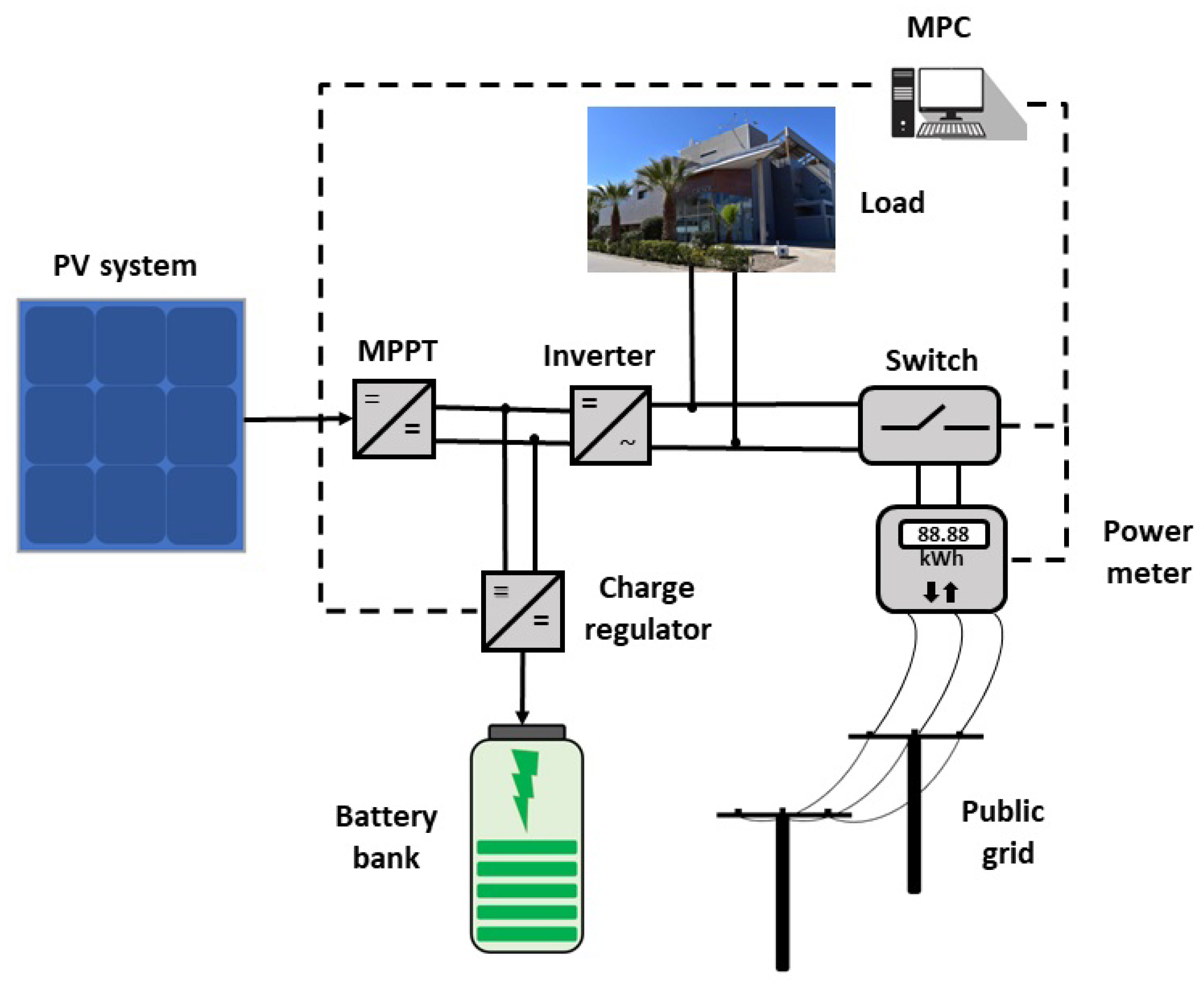
2. System Modeling
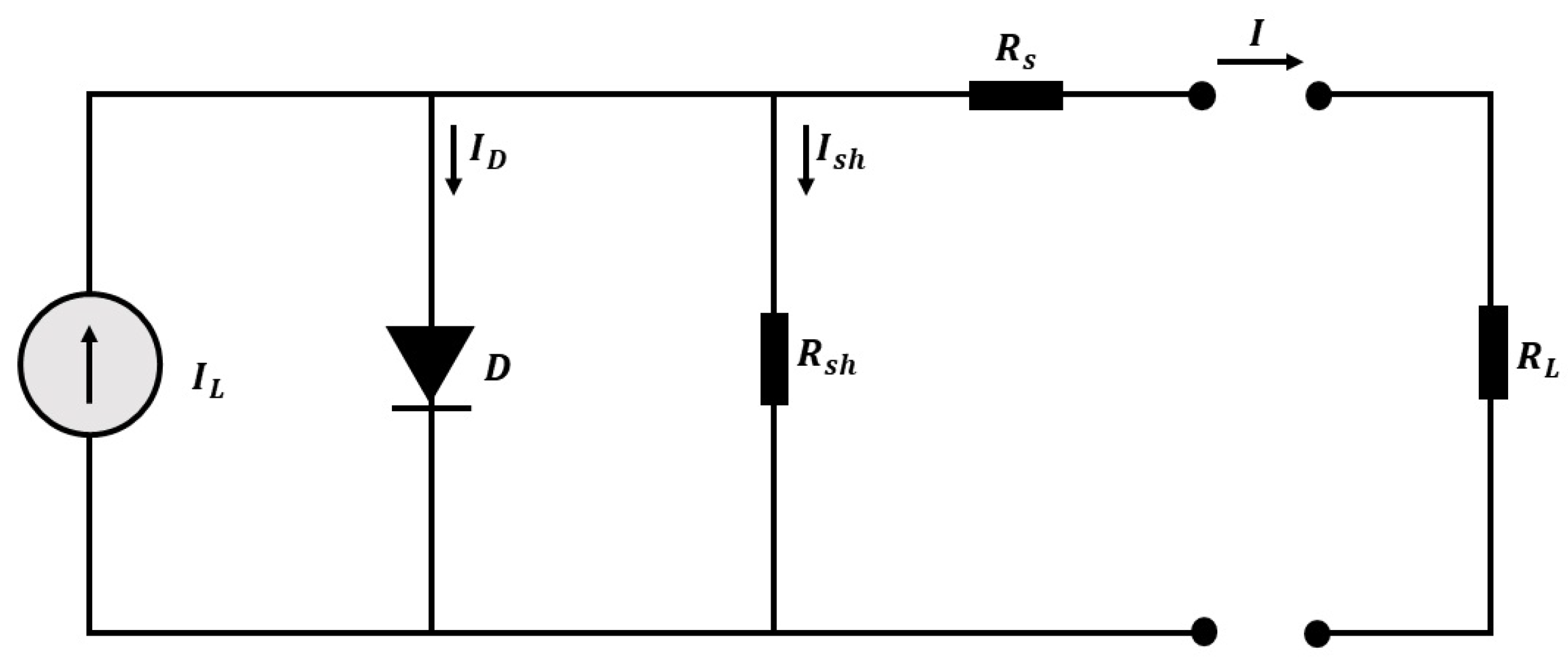
2.1. PV Panel Modeling
2.2. Battery Modeling
3. Controller Design
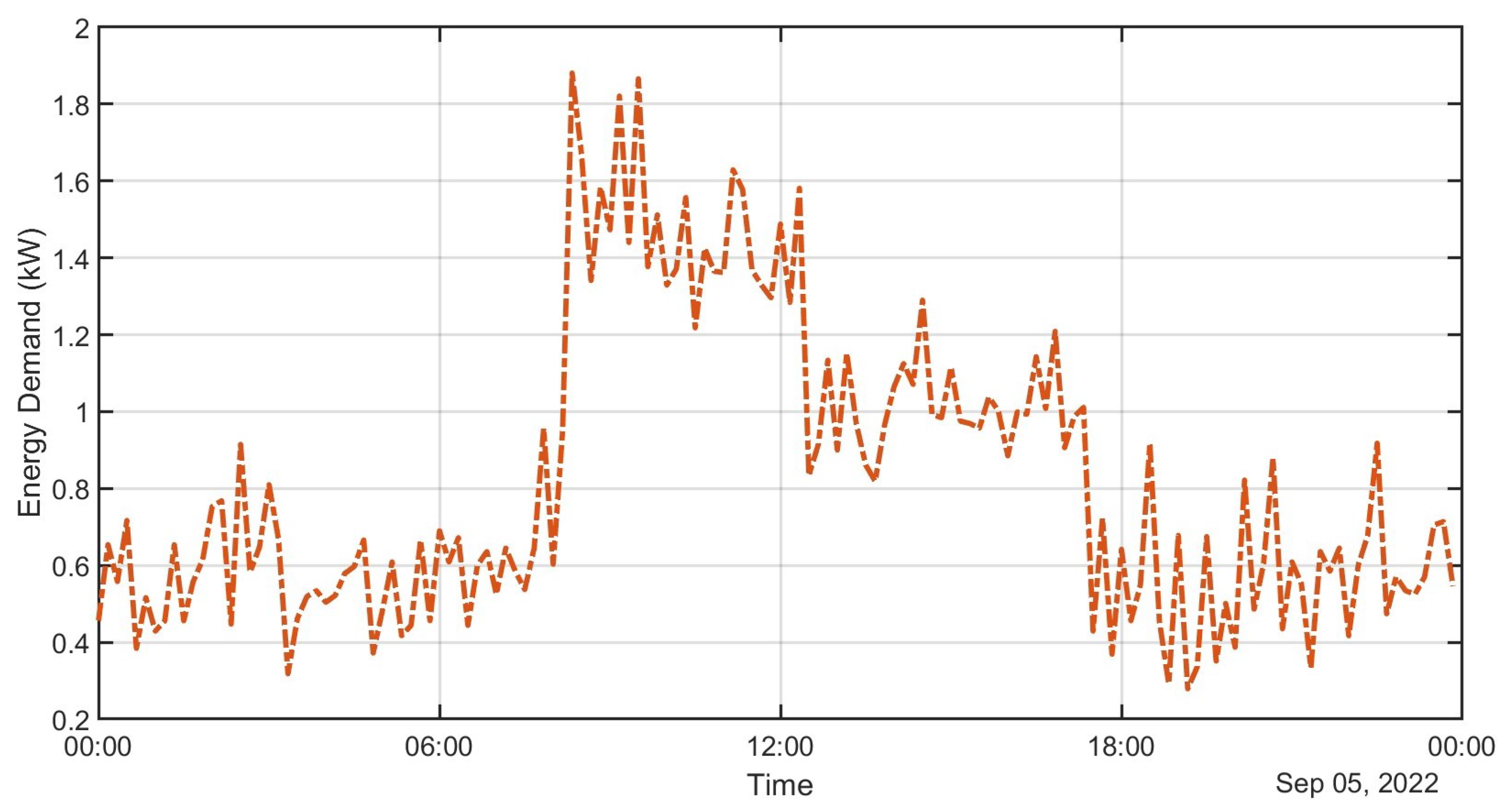
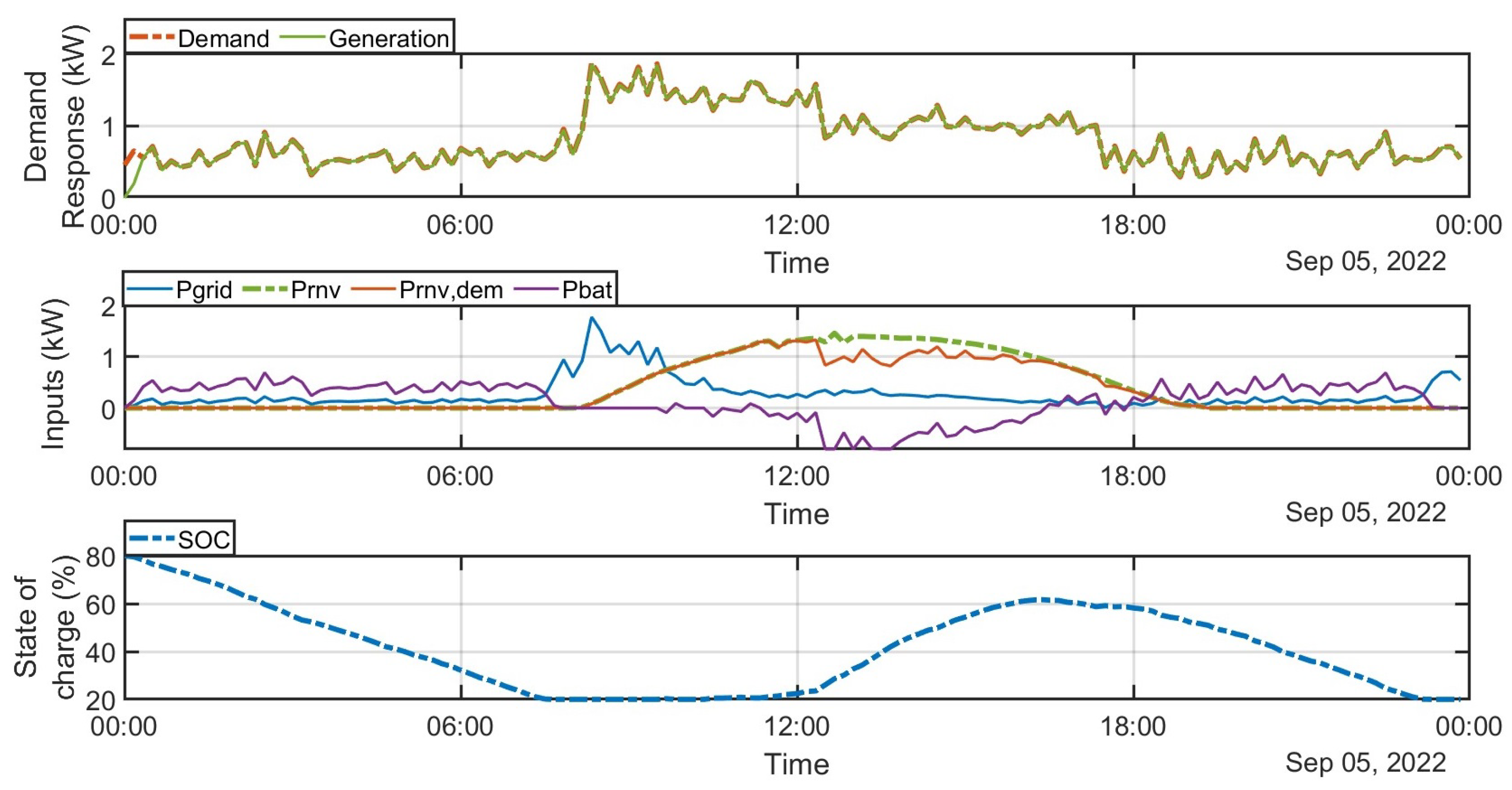
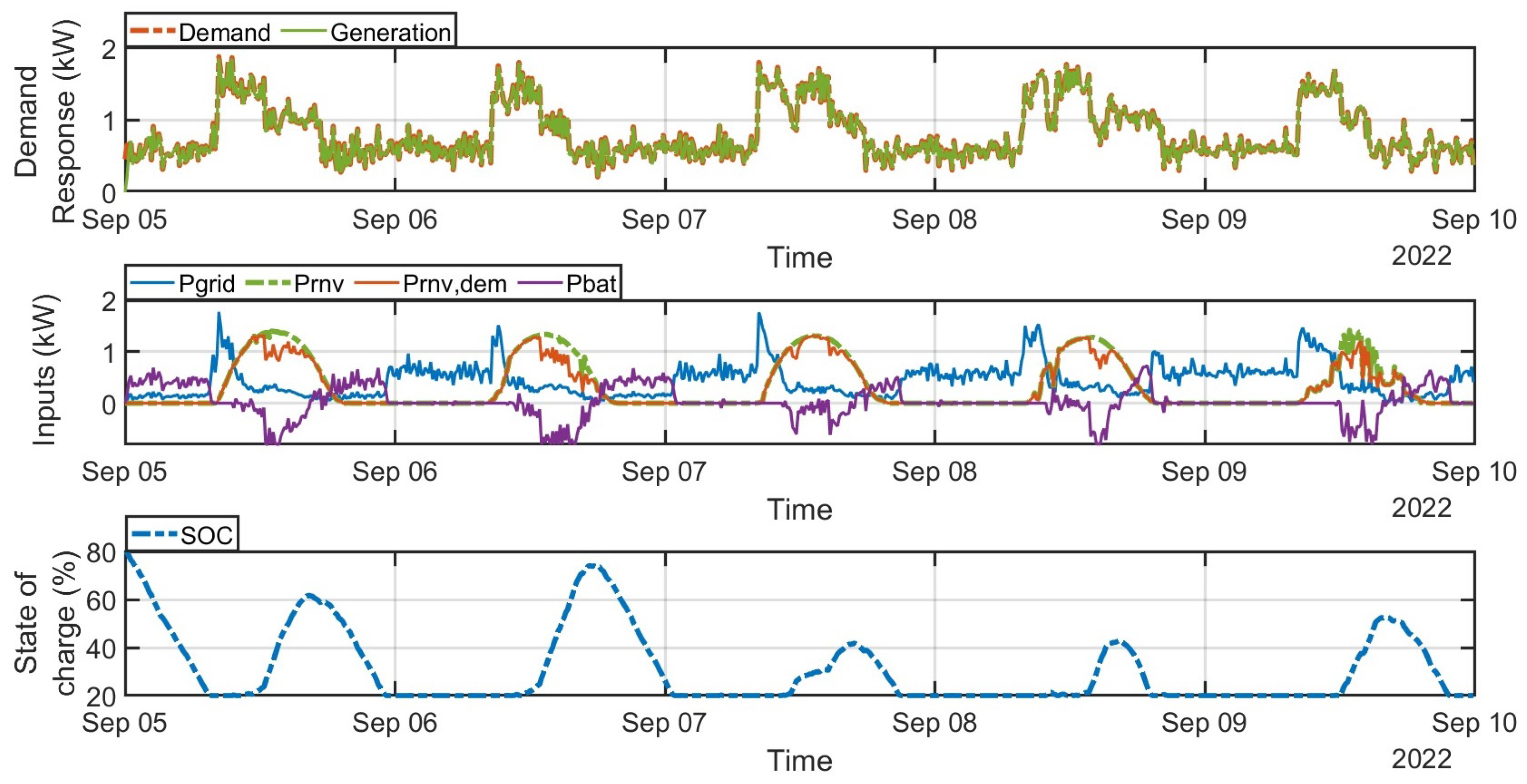
4. Analysis of Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| EMS | Energy management system |
| ESS | Energy storage system |
| EU | European Union |
| MG | Microgrid |
| MPC | Model predictive control |
| MPPT | Maximum power tracking |
| PV | Photovoltaic |
| RES | Renewable energy source |
| SOC | State of charge |
| STC | Standar tested conditions. |
References
- Moon, H.; Park, S.Y.; Jeong, C.; Lee, J. Forecasting electricity demand of electric vehicles by analyzing consumers’ charging patterns. Transp. Res. Part Transp. Environ. 2018, 62, 64–79. [Google Scholar] [CrossRef]
- Aune, F.R.; Golombek, R. Are Carbon Prices Redundant in the 2030 EU Climate and Energy Policy Package? Energy J. 2021, 42, 225–264. [Google Scholar] [CrossRef]
- Zhang, Y.; Meng, F.; Wang, R.; Zhu, W.; Zeng, X.J. A stochastic MPC based approach to integrated energy management in microgrids. Sustain. Cities Soc. 2018, 41, 349–362. [Google Scholar] [CrossRef]
- Gil, J.D.; Topa, A.O.; Álvarez, J.D.; Torres, J.L.; Pérez, M. A review from design to control of solar systems for supplying heat in industrial process applications. Renew. Sustain. Energy Rev. 2022, 163, 112461. [Google Scholar] [CrossRef]
- Topa Gavilema, Á.O.; Álvarez, J.D.; Torres Moreno, J.L.; García, M.P. Towards Optimal Management in Microgrids: An Overview. Energies 2021, 14, 5202. [Google Scholar] [CrossRef]
- Kroposki, B.; Lasseter, R.; Ise, T.; Morozumi, S.; Papathanassiou, S.; Hatziargyriou, N. Making microgrids work. IEEE Power Energy Mag. 2008, 6, 40–53. [Google Scholar] [CrossRef]
- Ali, S.; Zheng, Z.; Aillerie, M.; Sawicki, J.P.; Péra, M.C.; Hissel, D. A Review of DC Microgrid Energy Management Systems Dedicated to Residential Applications. Energies 2021, 14, 4308. [Google Scholar] [CrossRef]
- Jamal, S.; Tan, N.M.L.; Pasupuleti, J. A Review of Energy Management and Power Management Systems for Microgrid and Nanogrid Applications. Sustainability 2021, 13, 331. [Google Scholar] [CrossRef]
- Yan, Q.; Zhang, B.; Kezunovic, M. Optimized Operational Cost Reduction for an EV Charging Station Integrated With Battery Energy Storage and PV Generation. IEEE Trans. Smart Grid 2019, 10, 2096–2106. [Google Scholar] [CrossRef]
- Fontenot, H.; Dong, B. Modeling and control of building-integrated microgrids for optimal energy management—A review. Appl. Energy 2019, 254, 113689. [Google Scholar] [CrossRef]
- Farinis, G.K.; Kanellos, F.D. Integrated energy management system for Microgrids of building prosumers. Electr. Power Syst. Res. 2021, 198, 107357. [Google Scholar] [CrossRef]
- Boujoudar, Y.; Azeroual, M.; Moussaoui, H.E.; Lamhamdi, T. Intelligent controller based energy management for stand-alone power system using artificial neural network. Int. Trans. Electr. Energy Syst. 2020, 30, e12579. [Google Scholar] [CrossRef]
- Azeroual, M.; Boujoudar, Y.; Iysaouy, L.E.; Aljarbouh, A.; Fayaz, M.; Qureshi, M.S.; Rabbi, F.; Markhi, H.E. Energy management and control system for microgrid based wind-PV-battery using multi-agent systems. Wind Eng. 2022, 46, 1247–1263. [Google Scholar] [CrossRef]
- Córdova, S.; Cañizares, C.A.; Lorca, Á.; Olivares, D.E. Frequency-Constrained Energy Management System for Isolated Microgrids. IEEE Trans. Smart Grid 2022, 13, 3394–3407. [Google Scholar] [CrossRef]
- Roslan, M.; Hannan, M.; Ker, P.J.; Mannan, M.; Muttaqi, K.; Mahlia, T.I. Microgrid control methods toward achieving sustainable energy management: A bibliometric analysis for future directions. J. Clean. Prod. 2022, 348, 131340. [Google Scholar] [CrossRef]
- Bordons, C.; Garcia-Torres, F.; Ridao, M.A. Basic Energy Management Systems in Microgrids. In Model Predictive Control of Microgrids; Springer International Publishing: Cham, Switzerland, 2020; pp. 77–107. [Google Scholar] [CrossRef]
- Camacho, E.F.; Bordons, C. Model Predictive Controllers. In Model Predictive Control; Springer: London, UK, 2007; pp. 13–30. [Google Scholar] [CrossRef]
- Wang, L. Model Predictive Control System Design and Implementation Using MATLAB®; Springer: London, UK, 2009. [Google Scholar] [CrossRef]
- Negri, S.; Giani, F.; Massi Pavan, A.; Mellit, A.; Tironi, E. MPC-based control for a stand-alone LVDC microgrid for rural electrification. Sustain. Energy Grids Netw. 2022, 32, 100777. [Google Scholar] [CrossRef]
- Sen, S.; Kumar, M. MPC Based Energy Management System for Grid-Connected Smart Buildings with EVs. In Proceedings of the 2022 IEEE IAS Global Conference on Emerging Technologies (GlobConET), London, UK, 19–21 May 2022; pp. 146–151. [Google Scholar] [CrossRef]
- Ryu, K.S.; Kim, D.J.; Ko, H.; Boo, C.J.; Kim, J.; Jin, Y.G.; Kim, H.C. MPC Based Energy Management System for Hosting Capacity of PVs and Customer Load with EV in Stand-Alone Microgrids. Energies 2021, 14, 4041. [Google Scholar] [CrossRef]
- Freire, V.A.; De Arruda, L.V.R.; Bordons, C.; Márquez, J.J. Optimal Demand Response Management of a Residential Microgrid Using Model Predictive Control. IEEE Access 2020, 8, 228264–228276. [Google Scholar] [CrossRef]
- Dong, R.; Liu, S.; Liang, G.; An, X.; Xu, Y. Output Control Method of Microgrid VSI Control Network Based on Dynamic Matrix Control Algorithm. IEEE Access 2019, 7, 158459–158480. [Google Scholar] [CrossRef]
- Petrollese, M.; Valverde, L.; Cocco, D.; Cau, G.; Guerra, J. Real-time integration of optimal generation scheduling with MPC for the energy management of a renewable hydrogen-based microgrid. Appl. Energy 2016, 166, 96–106. [Google Scholar] [CrossRef]
- Parisio, A.; Wiezorek, C.; Kyntäjä, T.; Elo, J.; Johansson, K.H. An MPC-based Energy Management System for multiple residential microgrids. In Proceedings of the 2015 IEEE International Conference on Automation Science and Engineering (CASE), Gothenburg, Sweden, 24–28 August 2015; pp. 7–14. [Google Scholar] [CrossRef]
- Wang, X.; Atkin, J.; Bazmohammadi, N.; Bozhko, S.; Guerrero, J.M. Optimal Load and Energy Management of Aircraft Microgrids Using Multi-Objective Model Predictive Control. Sustainability 2021, 13, 13907. [Google Scholar] [CrossRef]
- Acevedo-Arenas, C.Y.; Correcher, A.; Sánchez-Díaz, C.; Ariza, E.; Alfonso-Solar, D.; Vargas-Salgado, C.; Petit-Suárez, J.F. MPC for optimal dispatch of an AC-linked hybrid PV/wind/biomass/H2 system incorporating demand response. Energy Convers. Manag. 2019, 186, 241–257. [Google Scholar] [CrossRef]
- Achour, Y.; Ouammi, A.; Zejli, D. Model Predictive Control Based Demand Response Scheme for Peak Demand Reduction in a Smart Campus Integrated Microgrid. IEEE Access 2021, 9, 162765–162778. [Google Scholar] [CrossRef]
- Maślak, G.; Orłowski, P. Microgrid Operation Optimization Using Hybrid System Modeling and Switched Model Predictive Control. Energies 2022, 15, 833. [Google Scholar] [CrossRef]
- Zhang, Y.; Meng, F.; Wang, R.; Kazemtabrizi, B.; Shi, J. Uncertainty-resistant stochastic MPC approach for optimal operation of CHP microgrid. Energy 2019, 179, 1265–1278. [Google Scholar] [CrossRef]
- Polimeni, S.; Meraldi, L.; Moretti, L.; Leva, S.; Manzolini, G. Development and experimental validation of hierarchical energy management system based on stochastic model predictive control for Off-grid Microgrids. Adv. Appl. Energy 2021, 2, 100028. [Google Scholar] [CrossRef]
- Zhang, J.; Li, J.; Wang, N.; Wu, B. An enhanced predictive hierarchical power management framework for islanded microgrids. IET Gener. Transm. Distrib. 2022, 16, 503–516. [Google Scholar] [CrossRef]
- Luo, Z.; Wu, Z.; Li, Z.; Cai, H.; Li, B.; Gu, W. A two-stage optimization and control for CCHP microgrid energy management. Appl. Therm. Eng. 2017, 125, 513–522. [Google Scholar] [CrossRef]
- Torres-Moreno, J.L.; Gimenez-Fernandez, A.; Perez-Garcia, M.; Rodriguez, F. Energy Management Strategy for Micro-Grids with PV-Battery Systems and Electric Vehicles. Energies 2018, 11, 522. [Google Scholar] [CrossRef]
- Velarde, P.; Valverde, L.; Maestre, J.; Ocampo-Martinez, C.; Bordons, C. On the comparison of stochastic model predictive control strategies applied to a hydrogen-based microgrid. J. Power Sources 2017, 343, 161–173. [Google Scholar] [CrossRef]
- Pereira, M.; Limon, D.; Muñoz de la Peña, D.; Valverde, L.; Alamo, T. Periodic Economic Control of a Nonisolated Microgrid. IEEE Trans. Ind. Electron. 2015, 62, 5247–5255. [Google Scholar] [CrossRef]
- Moya, F.D.; Torres-Moreno, J.L.; Álvarez, J.D. Optimal Model for Energy Management Strategy in Smart Building with Energy Storage Systems and Electric Vehicles. Energies 2020, 13, 3605. [Google Scholar] [CrossRef]
- Topa Gavilema, A.O.; Gil, J.D.; Álvarez Hervás, J.D.; Torres Moreno, J.L.; García, M.P. Modelado y gestión energética de una microrred basado en estrategias de control predictivo. In Proceedings of the XVIII Congreso Ibérico y XIV Congreso Iberoamericano de Energía Solar, Palma, Spain, 20–22 June 2022; pp. 355–361. [Google Scholar]
- Duffie, J.A.; Beckman, W.A.; Blair, N. Solar Engineering of Thermal Processes, Photovoltaics and Wind; John Wiley & Sons: Hoboken, NJ, USA, 2020. [Google Scholar]
- Ramos-Teodoro, J.; Rodriguez, F.; Berenguel, M. Modelado de Instalaciones Fotovoltaicas para la Gestión de un Energy hub con Recursos Heterogéneos. XVI Simposio CEA de Ingeniería de Control. 2018. Available online: http://hdl.handle.net/10835/5711 (accessed on 6 January 2023).
- Technosun. REC PE Peak Energy Series Solar Panels-Model REC 260PE. Technical Report, 2022.
- Alves, A.; Marinho, R.; Brigatto, G.; Garces, L. Multilayer Stratification Earth by Kernel Function and Quasi-Newton Method. IEEE Lat. Am. Trans. 2016, 14, 225–234. [Google Scholar] [CrossRef]

| Days | Horizons | FES (kWh) | RES (kWh) | ESS (kWh) | (s) | (s) |
|---|---|---|---|---|---|---|
| 1 | , | 6.4347 | 8.7414 | 4.5054 | 4.3540 | 0.3581 |
| , | 6.3684 | 8.7412 | 4.5719 | 4.0006 | 0.3235 | |
| , | 6.1528 | 8.7407 | 4.7880 | 4.2443 | 0.3521 | |
| 1 | , | 6.4224 | 8.7411 | 4.5180 | 3.5671 | 0.2963 |
| , | 6.3168 | 8.7412 | 4.6235 | 4.0783 | 0.3340 | |
| , | 5.8038 | 8.7406 | 5.1371 | 4.2133 | 0.3710 | |
| 1 | , | 6.4181 | 8.7411 | 4.5223 | 4.0393 | 0.3348 |
| , | 6.2764 | 8.7411 | 4.6640 | 3.9698 | 0.3281 | |
| , | 5.6037 | 8.7405 | 5.3373 | 4.1117 | 0.3435 | |
| 1 | , | 6.4089 | 8.7410 | 4.5316 | 3.8242 | 0.3086 |
| , | 6.2254 | 8.7408 | 4.7153 | 3.7905 | 0.3199 | |
| , | 5.5024 | 8.7403 | 5.4388 | 3.9997 | 0.3658 | |
| 5 | , | 51.2752 | 38.2301 | 9.4957 | 3.9969 | 0.2603 |
| , | 51.0022 | 38.2293 | 9.7695 | 3.6394 | 0.2714 | |
| , | 50.1760 | 38.2275 | 10.5975 | 4.3016 | 0.3152 | |
| 5 | , | 49.5084 | 38.2249 | 11.2677 | 4.0706 | 0.2800 |
| , | 49.1476 | 38.2244 | 11.6290 | 1.3030 | 0.0988 | |
| , | 45.5145 | 38.2180 | 15.2685 | 1.3726 | 0.1074 | |
| 5 | , | 48.4932 | 38.2191 | 12.2887 | 1.3061 | 0.0966 |
| , | 47.6247 | 38.2192 | 13.1571 | 1.2847 | 0.0975 | |
| , | 45.5145 | 38.2180 | 15.2685 | 1.3016 | 0.1048 | |
| 5 | , | 48.2799 | 38.2148 | 12.5063 | 1.2455 | 0.0997 |
| , | 46.9897 | 38.2167 | 13.7946 | 1.2292 | 0.1028 | |
| , | 44.2457 | 38.2162 | 16.5391 | 1.4956 | 0.1089 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Topa Gavilema, A.O.; Gil, J.D.; Álvarez Hervás, J.D.; Torres Moreno, J.L.; García, M.P. Modeling and Energy Management of a Microgrid Based on Predictive Control Strategies. Solar 2023, 3, 62-73. https://doi.org/10.3390/solar3010005
Topa Gavilema AO, Gil JD, Álvarez Hervás JD, Torres Moreno JL, García MP. Modeling and Energy Management of a Microgrid Based on Predictive Control Strategies. Solar. 2023; 3(1):62-73. https://doi.org/10.3390/solar3010005
Chicago/Turabian StyleTopa Gavilema, Alex Omar, Juan D. Gil, José Domingo Álvarez Hervás, José Luis Torres Moreno, and Manuel Pérez García. 2023. "Modeling and Energy Management of a Microgrid Based on Predictive Control Strategies" Solar 3, no. 1: 62-73. https://doi.org/10.3390/solar3010005
APA StyleTopa Gavilema, A. O., Gil, J. D., Álvarez Hervás, J. D., Torres Moreno, J. L., & García, M. P. (2023). Modeling and Energy Management of a Microgrid Based on Predictive Control Strategies. Solar, 3(1), 62-73. https://doi.org/10.3390/solar3010005










