A Practical Approach for Estimating the Optimum Tilt Angle of a Photovoltaic Panel for a Long Period—Experimental Recorded Data

Abstract

In this study, recorded empirical data were applied with a practical approach to investigate the optimal tilt angle of the flat plate collectors facing south for a long period in Tehran, Iran. The data included 20 years of recorded average total radiation on the horizontal plane in Tehran’s meteorological station. Based on the previous studies, the annual optimum tilt angle for Tehran was estimated at 33 degrees annually; however, this estimation does not focus on the energy absorption and effectiveness of changing the tilt angle monthly, seasonally, and bi-annually via measured data. This paper aims to explain this distinction between various radiation receptions with different tilt angle adjustments. This study shows that annual solar cumulative radiation energy gained via a monthly tilt angle can be approximately 7% higher than that achieved with an annual tilt angle setup. Additionally, the seasonal and bi-annual tilt angles have about 6% more annual cumulative radiation absorption than the annual tilt angle setup. Moreover, with consideration of similar monthly received radiation, the results illustrate that the radiation gained with a monthly tilt angle set up was 20% greater in the summer months than an annual tilt angle adjustment.

1. Introduction

1.1. Solar Energy

Most terrestrial forms of energy sources originate from the sun. Today, more than 99.9% of the total energy transmitted to the earth comes from the sun, which is 1.8 × 10¹⁵ TW, and the energy from the latter’s radiation that reaches the earth every day is 100,000 times the amount of the energy produced by all power plants in the world. Therefore, given the sun, there will be no potential energy shortage globally, and solar energy is equivalent to 20,000 times the current human consumption. This amount seems to be an excellent source to meet human needs, especially because its use does not cause any environmental damage or pollution [1,2,3].

The use of solar energy as a source of energy for sustenance is anticipated in the future. The major drawbacks in the application of solar energy are the lack of concentration, periodicity, and the instability of the amount of solar radiation. If a device is supposed to focus solar energy so that its fluctuations do not affect the received solar radiation much, the sun becomes a vast energy source that can meet century-old human energy needs. Given the state of power in the world and the growth of population and power consumption, if treated wisely, the sun is the only source of energy that is abundantly and freely available to humans in all eras. Assuming that the energy resource considers the efficiency of converting solar energy into human energy needs of only 1%, only 0.5% of the earth’s surface will be enough to fulfill the total energy requirement for humans. Therefore, by 2075, 50% to 75% of the fundamental human needs will be fulfilled by solar energy. According to the studies in the pertinent literature, the maximum average annual radiation density on a ground-level horizontal plane is about 300 watts per square meter. The Middle East has an abundance of solar energy. For example, the average annual radiation density in the central land of Iran is 250 watts per square meter [1,2]. The total amount of solar energy received in Iran, considering its area and the average number of sunny hours, which is 2800 hours, is about 10.6 MJ per year, equivalent to 1634 billion barrels of crude oil [3]. Solar power generation technologies are currently promising, and it can be expected that soon, with the development of various solar power generation technologies and the continuous reduction in electricity generation prices using these methods, the power plant solar panels account for a fair share of the world’s total electricity generation [1].

1.2. Literature Review of the Existing Studies

One of the most efficient methods for achieving clean and unlimited solar energy is to use solar collectors or photovoltaic panels, which are now widely used [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18]. Solar panels must be perpendicular to the solar panel to absorb as much radiation as possible, which is the basis of a solar photovoltaic detector. However, solar tracking systems have not always been possible, because the initial cost to purchase them has been very high. Furthermore, these systems need electricity to move, which, in turn, increases the cost. An alternative method is to use the optimal tilt and direction for receiving the maximum possible radiation in different periods. The optimal approach generally considers the geographical south, owing to the symmetry of the sun’s movement in the sky to the south, geographically. Previous studies have substantiated this argument with adequate evidence [6,7,8,9,10], while different techniques have been proposed to determine the optimal tilt angle. Extensive research has already been conducted to determine the optimal gradient in large parts of the world. The optimal tilt angle is usually reported as a function of latitude. El-Kassaby [2] reported the optimal slope for Cairo as ${\mathsf{\beta }}_{\mathrm{opt}}=\phi +3.5$. Here φ is the Northern or Southern latitude and β is the tilt angle of the modules with respect to the ground level. Gopinathan suggested the optimal tilt angle for South Africa as ${\mathsf{\beta }}_{\mathrm{opt}}=\phi$ [11]. Rusheng and Tong investigated the optimal gradient angle for different provinces in China, having varying climates [12]. Their results confirmed that the tilt angle varies with the weather and lies in the range ${\mathsf{\beta }}_{\mathrm{opt}}=\phi +\left(4~10\right)$. Ulgen suggested the optimal tilt angle for Izmir in Turkey is ${\mathsf{\beta }}_{\mathrm{opt}}=\phi -34$ during summer and ${\mathsf{\beta }}_{\mathrm{opt}}=\phi +19$ during winter [13]. The optimal slope for Amman in Jordan was studied by Tamimi [14]. He proposed an optimal tilt of ${\mathsf{\beta }}_{\mathrm{opt}}=31.3$, which is approximately the same as the optimal tilt reported by NASA for Amman. Talebzadeh et al. also studied the optimal tilt for various towns in Southeastern Iran [1]. Their results demonstrate that adjusting the tilt in a shorter time interval does not markedly change the radiation received.

1.3. Empirical Approach Background

Empirical models employed in most previous studies can be used to determine the amount of radiation on inclined plates. Liu and Jordan used a uniform sky model to estimate radiation on the ramp [15]. After a few years, researchers added certain correction factors to the uniform sky model to increase the accuracy of tilt estimation. These models are known as non-uniform sky models. Hay and Davies introduced a coefficient, known as the solar refractive index, into the uniform sky model [16]. Temp and Coualson added a horizontal brightness coefficient to the uniform sky model and noticeably increased its accuracy [17]. Klucher added a horizontal brightness correction factor to Temp and Coualson’s model and increased estimating radiation in partly cloudy conditions [18]. By combining the previous models, Reindel presented a model that eliminated most of the shortcomings of the previously proposed models [19]. To determine the radiation on an inclined plate, one required the amount of total and scattered radiation on a horizontal plane. However, no data are available to measure scattered radiation horizontally for the study area. The Erbs model can be used on the horizontal plane to determine the amount of scattered radiation [20]. This model is one of the most accurate and standard models of scattered radiation on a horizontal plane [21].

1.4. Aim of Current Study

Most studies in the solar panel optimum tilt angle specify the tilt angle based on the convenient adjustment and reducing the tilt angle set up per year. This work is considered the tilt angle by maximum energy production perspective with a convenient time to set up the inclined surface. This paper employed Liu and Jordan’s model, using empirical data to determine the amount of solar energy gained via different optimum tilt angle determinations, which is very important for efficient solar power production. The paper is organized as follows. Theory concepts used in this study and methods used to calculate solar energy characteristics are presented in Section 2. In Section 3, the main results are mentioned. Section 4 offers the discussion. Then, the conclusions are presented in Section 5.

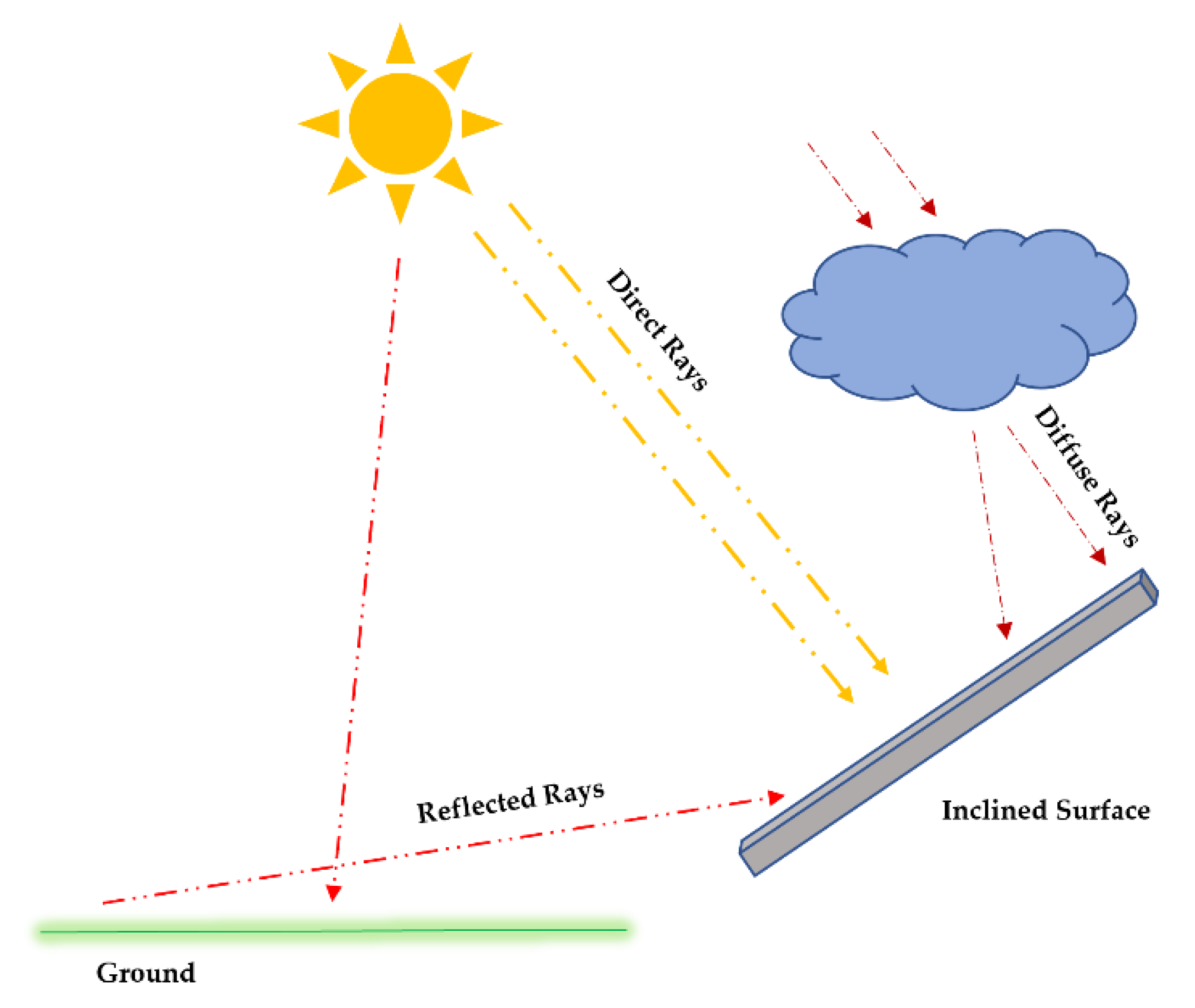
2. Methods

2.1. Theory

Using Liu and Jordan’s model, total radiation on the diagonal plate for tilt angles from −20 to 90 degrees was calculated in this study. According to this model, the total radiation on a diagonal surface includes direct radiation, diffuse radiation (diffusion), and reflective radiation from the surface. Figure 1 shows this model in a schematic view. It can be calculated using Equation (1) [21].

$${ \overline{\mathrm{H}}}_{\mathrm{t}}={ \overline{\mathrm{H}}}_{\mathrm{B}}+{ \overline{\mathrm{H}}}_{\mathrm{D}}+{ \overline{\mathrm{H}}}_{\mathrm{R}}$$

(1)

where ${ \overline{\mathrm{H}}}_{\mathrm{t}}$ is total radiation, ${ \overline{\mathrm{H}}}_{\mathrm{B}}$ is beam radiation, ${ \overline{\mathrm{H}}}_{\mathrm{D}}$ is diffuse solar radiation, and ${ \overline{\mathrm{H}}}_{\mathrm{R}}$ is reflective radiation.

These radiation values are described in the following terms:

Beam radiation ${ \overline{\mathrm{H}}}_{\mathrm{B}}$: This describes the part of the solar radiation that reaches the earth’s surface directly from the sun, without scattering or absorbing it through the atmosphere.

Diffuse solar radiation ${ \overline{\mathrm{H}}}_{\mathrm{D}}$: This is the sun’s radiation that is emitted or absorbed by the atmosphere. Scattered radiation reaches the earth in all directions from the sky.

Reflective radiation ${ \overline{\mathrm{H}}}_{\mathrm{R}}$: The amount of the solar radiation that is reflected from the earth’s surface.

Klein (1977) expanded Equation (1), as follows [21]:

$${ \overline{\mathrm{H}}}_{\mathrm{t}}=\left(\mathrm{H}-{ \overline{\mathrm{H}}}_{\mathrm{b}}\right)\overline{{\mathrm{R}}_{\mathrm{b}}}+{ \overline{\mathrm{H}}}_{\mathrm{d}}\left(\frac{1-\cos \mathsf{\beta }}{2}\right)+ \overline{\mathrm{H}} \mathsf{\rho }\left(\frac{1-\cos \mathsf{\beta }}{2}\right)$$

(2)

In this model, the diffuse and reflective radiation is assumed to be isotropic. $\mathrm{H}$ is the monthly average daily total radiation. $\overline{{\mathrm{R}}_{\mathrm{b}}}$ is a function of transmittance of the atmosphere; however, Liu and Jordan suggested that it can be estimated by assuming that it has the value which would be obtained if there were no atmosphere [20]. In this relation, $\overline{{\mathrm{R}}_{\mathrm{b}}}$ can be calculated as follows [20]:

$$\overline{{\mathrm{R}}_{\mathrm{b}}}=\frac{\cos \left(\phi -\mathsf{\beta }\right)\cos \mathsf{\delta }\cos {\acute{\mathsf{\omega }}}_{\mathrm{s}}+\left(\frac{\mathsf{\pi }}{180}\right){\acute{\mathsf{\omega }}}_{\mathrm{s}}\sin \left(\phi -\mathsf{\beta }\right)\sin \mathsf{\delta }}{\cos \phi \cos \mathsf{\delta }\cos {\mathsf{\omega }}_{\mathrm{s}}+\left(\frac{\mathsf{\pi }}{180}\right){\mathsf{\omega }}_{\mathrm{s}}\sin \phi \sin \mathsf{\delta }}$$

(3)

This model can only be used for panels where the ridge angle is zero.

The term ${\acute{\mathsf{\omega }}}_{\mathrm{s}}$ is the angle of the sunset clock for the average day of the month and is calculated from the following equation [20]:

$${\acute{\mathsf{\omega }}}_{\mathrm{s}}=\min \{\begin{array}{c}{\cos }^{-1}(-\tan \phi \tan \mathsf{\delta })\\ {\cos }^{-1}(-\tan \left(\phi -\mathsf{\beta }\right)\tan \mathsf{\delta })\end{array}$$

(4)

where $\mathsf{\rho }$ is the surface reflectance coefficient, which lies in the range 0.2–0.7 for different levels [16]. In this study, the reflectance coefficient of the surface around the photovoltaic panel was assumed to be 0.2. Thus, $\phi$ represents the latitude of the site, $\mathsf{\beta }$ is the module tilt angle with respect to the ground level, $\mathsf{\delta }$ is the angle of solar deflection, and ${\mathsf{\omega }}_{\mathrm{s}}$ is the sunset angle for the photovoltaic panel with a tilt angle $\mathsf{\beta }$, and it can be calculated by solar geometric relations for the monthly average.

2.2. Calculation of Daily Solar Radiation on Horizontal Surfaces Outside the Atmosphere

This section describes how the calculation of solar radiation incident on horizontal surfaces outside the atmosphere was performed. The total amount of radiation perpendicular to the surface daily was obtained using the following equation [21].

$${\mathrm{H}}_0=\frac{24\times 3600{\mathrm{G}}_{\mathrm{sc}}}{\mathsf{\pi }}\left(1+0.033\cos \frac{360\mathrm{n}}{365}\right)\times \left(\cos \phi \cos \mathsf{\delta }\sin {\mathsf{\omega }}_{\mathrm{s}}+\frac{{\mathsf{\pi }\mathsf{\omega }}_{\mathrm{s}}}{180}\sin \phi \sin \mathsf{\delta }\right)$$

(5)

where ${\mathrm{G}}_{\mathrm{sc}}$ is a solar constant, and its value is $1367\frac{\mathrm{W}}{{\mathrm{m}}^2}$ and n is nth day of the year.

Mean clearness index is the average filtration coefficient of the sky filtration index of the monthly average. ${ \overline{\mathrm{K}}}_{\mathrm{T}}$ is a function of the total radiation incident on the horizontal plane and the monthly extraterrestrial radiation ${\mathrm{H}}_0$, which is expressed using the following relation [21]:

$${ \overline{\mathrm{K}}}_{\mathrm{T}}= \overline{\mathrm{H}}/{\mathrm{H}}_0$$

(6)

In Equation (7), the value of $\overline{\mathrm{H}}$ is presented monthly by the measurements made using a pyranometer.

The value of ${ \overline{\mathrm{H}}}_{\mathrm{d}}$ also indicates the amount of scattered daily radiation of the monthly average on the horizontal plane, calculated using the following equations. It should be noted that the use of the following equation is possible only if the sky purity index lies in the range $0.3\le { \overline{\mathrm{K}}}_{\mathrm{T}}\le 0.8$ [20]:

$$\begin{array}{ll}{\mathrm{if} \mathsf{\omega }}_{\mathrm{s} }\le 81.4,& \\ & \frac{\overline{{\mathrm{H}}_{\mathrm{d}}}}{ \overline{\mathrm{H}}}=1.391-3.560{ \overline{\mathrm{K}}}_{\mathrm{T}}+4.189{ \overline{\mathrm{K}}}_{\mathrm{T}}{}^2-2.137{ \overline{\mathrm{K}}}_{\mathrm{T}}{}^3\\ {\mathrm{if} \mathsf{\omega }}_{\mathrm{s} }>81.4,& \\ & \frac{\overline{{\mathrm{H}}_{\mathrm{d}}}}{ \overline{\mathrm{H}}}=1.311-3.022{ \overline{\mathrm{K}}}_{\mathrm{T}}+3.427{ \overline{\mathrm{K}}}_{\mathrm{T}}{}^2-1.821{ \overline{\mathrm{K}}}_{\mathrm{T}}{}^3\end{array}$$

(7)

The following equation is used to determine the amount of beam radiation incident on the horizontal plane [20]:

$${ \overline{\mathrm{H}}}_{\mathrm{b}}= \overline{\mathrm{H}}-\overline{{\mathrm{H}}_{\mathrm{d}}}$$

(8)

Next, by obtaining the required values and substituting them in Equation (1), the value of ${ \overline{\mathrm{H}}}_{\mathrm{t}}$ can be calculated.

According to the flow diagram in Figure 2, the average monthly daily radiation is computed using Equations (2)–(7). After that, the obtained values are substituted in Equation (1). Hence, the total radiation of the daily input to the diagonal surface per month is gained for tilt angles varying from −20 to 90 degrees.

The tilt angle that corresponds to the maximum daily input radiation to the diagonal surface per month is selected as the optimal tilt angle for that month.

As well, the total radiation of the total entrance to the inclined surface for all days of each season, both biannually and annually, were calculated through the slopes’ average values from −20 to 90 degrees.

The tilt angle associated with the maximum total radiation of the entire input to the surface in that interval was selected and declared as the optimal tilt for that type of adjustment. It is worth mentioning that in this study, the surface side angle was calculated as zero degrees, and the ground reflection coefficient, assuming a normal ground without snow cover, was calculated as 0.2 [21].

3. Results

3.1. Monthly Tilt Angle

The optimal tilt changes were computed for different months of the year for angles between −20 and 90 degrees to adjust the panel with a fixed monthly tilt angle. Figure 3 and Figure 4 show the daily average radiation change in Tehran’s solar panel, facing south for different tilt angles during the year’s first and second halves. As the graphs show, the amount of input radiation is significantly dependent on the slope. In addition, every month, a tilt angle can be seen for which the total amount of radiation is the maximum. This angle is the monthly optimal tilt angle, which varies for each month. It is evidenced in these graphs that for April to August—i.e., the spring and summer months—the optimal tilt angles are close to each other with a minor difference, which is slightly more conspicuous for the other months. This acknowledges the fact that adjusting the inclination solar panel optimal tilt monthly is extremely useful for absorbing the maximum possible radiation. In

Table 1. Average diffusion and direct radiation values per day of the month.

Month	$\mathbf{n}$	$\overline{\mathbf{H}}$ $(\mathbf{M}\mathbf{j}/{\mathbf{m}}^2)$	${\overline{\mathbf{H}}}_{\mathbf{d}}$ $(\mathbf{M}\mathbf{j}/{\mathbf{m}}^2)$	${\overline{\mathbf{H}}}_{\mathbf{b}}$ $(\mathbf{M}\mathbf{j}/{\mathbf{m}}^2)$	${\mathbf{H}}_0$ $(\mathbf{M}\mathbf{j}/{\mathbf{m}}^2)$	${\overline{\mathbf{K}}}_{\mathbf{T}}$
January	17	11.92	2.92	8.99	17.85	0.66
February	47	14.85	3.89	10.95	22.93	0.64
March	75	16.82	6.07	10.74	29.30	0.57
April	105	17.98	7.64	10.33	35.67	0.50
May	135	18.47	8.61	9.85	39.94	0.46
June	162	18.65	8.96	9.68	41.60	0.44
July	198	18.07	8.77	9.29	40.72	0.44
August	228	18.51	8.01	10.49	37.31	0.49
September	258	18.34	6.53	11.80	31.65	0.57
October	288	15.81	4.85	10.95	24.86	0.63
November	318	12.60	3.17	4.42	19.09	0.66
December	344	10.77	2.76	8.00	16.45	0.65

, the amount of diffuse and direct radiation, the average filtration coefficient, and the amount of daily radiation outside the atmosphere for the middle day of the month are calculated using the average daily radiation information.

As Figure 3 depicts, the highest amount of radiation received in January is 22.52 MJ/m² and the lowest amount of radiation in July was 18.07 MJ/m². As evidenced in Figure 4, the highest amount of radiation was received in November.

By observing Figure 3 and Figure 4, the optimal monthly tilt can be easily determined. For example, the average daily amount of radiation in January for the angle −20 is about 6 MJ/m² and by increasing the tilt, the amount of radiation increases to 22.52 MJ/m² at an angle of 62 degrees—this tilt angle is optimal. For January and following months, by increasing the tilt, the amount of radiation on the photovoltaic panel decreases and reaches 21 MJ/m² for the vertical plate.

As Figure 5 illustrates, the optimal tilt changes occur throughout the year so that in winter, the solar panel is set at the highest tilt and in summer it is set at the lowest one. At times, the optimal daily tilt in summer has negative values, implying that the solar panel should face north. The absolute value of the tilt value was geographically installed.

Table 1 illustrates the average radiation and diffusion per specified day for every month. These results are obtained by applying Equations (1)–(8) in this study from recorded data.

Table 2. Daily average monthly radiation incident on an inclined surface under various settings $\frac{\mathrm{MJ}}{{\mathrm{m}}^2}.$

Monthly Period	${\mathsf{\beta }}_{\mathbf{o}\mathbf{p}\mathbf{t}}$ (Degree)	$\overline{{\mathbf{H}}_{\mathbf{t}}}$$(\mathbf{M}\mathbf{j}/{\mathbf{m}}^2)$	Seasonal Period	${\mathsf{\beta }}_{\mathbf{o}\mathbf{p}\mathbf{t}}$ (Degree)	$\overline{{\mathbf{H}}_{\mathbf{t}}}$$(\mathbf{M}\mathbf{j}/{\mathbf{m}}^2)$	Bi-Annual Period	${\mathsf{\beta }}_{\mathbf{o}\mathbf{p}\mathbf{t}}$ (Degree)	$\overline{{\mathbf{H}}_{\mathbf{t}}}$$(\mathbf{M}\mathbf{j}/{\mathbf{m}}^2)$	Annual Period	${\mathsf{\beta }}_{\mathbf{o}\mathbf{p}\mathbf{t}}$ (Degree)	$\overline{{\mathbf{H}}_{\mathbf{t}}}$$(\mathbf{M}\mathbf{j}/{\mathbf{m}}^2)$
January	62	22.52	Winter	51	22.14	Cold Months	54	23.13	Annually	40	21.04
February	53	22.29			22.28			22.29			21.83
March	36	19.71			19.22			19.00			19.68
April	18	18.56	Spring	6	18.30	Hot Months	11	18.48			17.60
May	3	18.48			18.47			18.38			16.26
June	−3	18.67			18.51			18.32			15.75
July	−1	18.07	Summer	15	17.67			17.85			15.54
August	11	18.74			18.71			18.74			17.24
September	33	20.25			19.79			19.50			19.98
October	47	21.40	Fall	57	21.16	Cold Months	54	21.28			21.26
November	60	22.23			22.21			22.13			21.08
December	64	21.56			21.40			21.25			19.87

mentions the received radiation on an inclined panel with various tilt settings from average daily monthly. Table 2 shows the different amounts of radiation with tilt angle set up monthly, seasonally, bi-annually, and annually. The majority of the radiation has a higher amount with monthly set up than annual adjustment.

The cumulative radiation received is presented in Figure 6 and Figure 7. Figure 6 shows monthly cumulative radiation for each month with various tilt angle adjustments. Apparently, the annual total radiation with annual optimal tilt angle has less value than other cases. A significant point could be figured out from this figure, which shows that summer months with monthly tilt angle will gain about 20% more radiation than an annual tilt angle. Figure 7 illustrates the annual cumulative radiation for specified tilt angle set up during a year. It shows that the summation of the radiation gained with the annual tilt angle in one year was around 6–7% less than other adjustments.

3.2. Seasonal Tilt Angle

Because of many technical and economic reasons [2,5,6,7,8,9,10,22], studies have been looking for a long time for an optimal tilt angle that could be seasonal, bi-annual, and annual. The optimal seasonal tilt determines that the most solar energy shines on the tilt angle in a particular season. The optimal seasonal tilt angle is shown in Figure 8. The average seasonal angle is obtained by averaging the optimal monthly grades in each season. Figure 8 illustrates the optimal monthly, biannual, and annual gradients in the form of three graphs during different months.

3.3. Six-Month Tilt Angle

From Figure 8, the difference between the optimal seasonal tilt angle during the year’s summer months is negligible. Furthermore, the optimal seasonal tilt during the winter months is slight, and the study of the optimal six month tilt angle could be considered.

Therefore, the optimal tilt angle is calculated for summer (second and third quarters of the year) and the optimal gradient for the winter season (first and fourth quarters). In other words, in this method, the optimal tilt angle is adjusted only twice a year. The fixed annual average angle can also be obtained from the moderate optimal angles in all months, and this angle is usually close to the latitude of the place in question.

Figure 9 shows the optimal tilt and maximum energy received during other months. This figure shows the trend of optimal tilt angle changes for different months. Moreover, the process of changing the maximum amount of input radiation to the panel surface can be examined through the ${\mathrm{H}}_{\mathrm{T}}$ curve, and in each ${\mathrm{H}}_{\mathrm{T}}$ value, the optimal slope value can be determined.

4. Discussion

The literature considers the solar gain energy by daily and monthly tilt angles to reach the inclined surface’s annual tilt angle. The studies specify the optimum tilt angle for cities in Iran and many places in the world to have a convenient setup per year [1,2,5,6,7,8,9,10,11,12,13,14,22], where there are many technical and economic reasons to prefer an annual tilt angle as an optimum selection [1,2,22]. From Table 2 and Figure 7 we can see that, on the monthly tilt angle adjustment, the amount of gained radiation is estimated to be 7% more than the annual tilt angle for Tehran, Iran. This amount of radiation has significant energy, and it is not easy to ignore it. Figure 3, Figure 4, Figure 6 illustrate this issue with more detail; every month, there is a specific tilt angle with maximum gained radiation. Nowadays, climate change, CO₂ emission, and sustainable energy are significant considerations; this paper shows it is necessary to focus on the optimum tilt angle, based on maximum sustainable energy absorption. Previous studies say that the annual tilt angle, or changing the angle bi-annually, is suitable, and it is without significant change to the monthly tilt angle set up [1,2,22]. It seems this statement was focused on minimizing inclined surface setup, but with the current experimental study in a specified city, there is about 6–7% distinction for changing the angle two or four times per year. This difference mentions how much energy will be lost during decades. Although, based on the capacity of the solar power plant, this 6–7% could be a significant amount of energy. With a consideration of the monthly tilt angle, for summer months, there is about 20% more energy received with a monthly tilt angle than an annual tilt angle. Usually, in places with high solar energy potential—the subject of this study—such as Middle Eastern countries, the summer months have warm weather, such that power consumption goes up because of air conditioning and cooling systems. Therefore, the base power grid will need more production to support the electricity demand. It is possible to have a monthly tilt angle that produces 20% more power than the annual tilt angle.

5. Conclusions

This paper aimed to consider long term, optimal tilt angles, based on the recorded data, to investigate the radiation amount gained with various tilt angle set ups. This empirical study shows that the annual optimal tilt angle, which have been usually preferred by previous studies that were focused on fewer adjustment-inclined surfaces, has less radiation absorption, particularly in the warm months (summer). The amount of radiation absorption with a monthly tilt angle in the summer is 20% more than that of the annual setup. On the other hand, from the authors’ experience and knowledge in the countries subject to this study, electricity demand in the summer increases. It is significant to have more base energy production via a monthly tilt angle setup.

Based on many reasons mentioned in the literature [1,2,6,22], it is challenging to have a monthly set up or a seasonal tilt angle adjustment, and often the annual and bi-annual tilt angle set up recommended. The results from this study suggest having the following set ups for inclined surfaces to achieve efficient solar energy absorption:

-

In the summer, the inclined surface is adjusted with a monthly tilt angle.

-

For the rest of the year, an annual tilt angle is set up.