Advanced Computational Insights into Coronary Artery Disease Drugs: A Machine Learning and Topological Analysis

Abstract

Machine learning (ML) is a powerful tool in drug design, enabling the rapid analysis of large and complex molecular graphs that represent the structural and chemical properties of medications. It enhances the precision and speed with which molecular interactions are predicted, drug candidates are refined, and potential therapeutic targets are identified. When combined with graph theory, ML allows for the prediction of structural properties, molecular behaviour, and the performance of chemical compounds. This integration promotes drug development, reduces costs, and increases the likelihood of producing effective medicines. In this study, we focus on the efficacy of medications used in the treatment of coronary artery disease (CAD) using graph-theoretical methodologies, such as topological indices. We computed several degree-based topological descriptors from chemical graphs, capturing essential connectivity and structural properties. These variables were incorporated into a machine learning framework to develop predictive models that identify structural factors influencing medication performance. Our study explores a dataset of known CAD drugs using supervised learning techniques to estimate their potential efficacy and support improved molecular design. The findings highlight the utility of graph-theoretical descriptors in enhancing prediction accuracy and providing insights into fundamental structural elements related to drug efficacy. Furthermore, this work emphasises the synergy between chemical graph theory and machine learning in accelerating drug development for CAD, offering a scalable and interpretable framework for future pharmaceutical applications.

1. Introduction

Chemical graph theory is a versatile and powerful field with numerous applications in materials science and chemistry. It provides a mathematical framework for understanding the behaviour and structure of chemical molecules. This framework is used in computational chemistry, cheminformatics, materials design, and drug discovery. Topological indices—mathematical values applied in studies such as QSPR/QSAR—are an essential component of this theory [1,2,3]. These indices are particularly valuable for estimating the potency of drug candidates and have attracted significant attention in the field [4,5,6].

A highly effective method for converting chemical structures into numerical values that correlate with physical properties is the use of topological indices. Among the various indices studied to date, many practical ones are based on distances or molecular configuration. In 1947, Wiener introduced the first distance-based index, now known as the Wiener index. His work demonstrated a strong relationship between the boiling point of alkanes and certain graph-theoretical parameters, which motivated the development of additional distance-type topological indices [7].

Topological indices play a central role in quantitative structure–property relationship (QSPR) and quantitative structure–activity relationship (QSAR) analyses, both of which support the development and optimisation of pharmaceutical compounds [8,9]. These analyses rely on molecular structure to predict physical, chemical, and biological characteristics. Degree-based indices such as the Atom–Bond Connectivity (ABC), Randić (RA), Geometric–Arithmetic (GA), Sum Connectivity (S), and Zagreb indices have been widely applied in modelling and characterising chemical compounds [10,11,12]. By comparing these indices with experimentally measured properties, researchers gain valuable insights into how molecular structure influences parameters such as molar volume, boiling point, and molecular complexity [13,14].

Recent developments have expanded the applicability of topological indices with the introduction of new graph degrees, such as the Ev-degree and Ve-degree. These graph invariants have enhanced the descriptive power of TIs, enabling the more accurate modelling of complex compounds. For example, antibiotic structures have been extensively investigated through indices based on reverse degrees. In drug development, topological indices are increasingly used to model and characterise drug molecules, aiding in the prediction of toxicity, side effects, and bioactivity [15,16,17]. By analysing the molecular graphs [18,19] of drug candidates, researchers can identify promising compounds, anticipate potential risks, and accelerate the discovery of new therapeutics—significantly reducing the need for time-consuming laboratory experiments.

Despite their demonstrated usefulness, a major challenge in applying topological indices in QSPR lies not in their numerical performance but in their qualitative nature [20,21]. Although both classical and advanced chemometric methods confirm that topological indices can effectively characterise various physicochemical, biological, environmental, and toxicological properties of organic compounds, they remain fundamentally qualitative. Unlike traditional chemical descriptors derived from geometric or quantum-mechanical principles, TIs rely on an ad hoc graph representation of molecules. Similar criticisms have been raised in the graph-based modelling of other systems, such as neural networks, social structures, and transportation networks [22,23]. While such systems can often be described topologically, molecular systems face additional scrutiny due to the availability of quantum-mechanical modelling approaches that appear more physically grounded.

Although several attempts have been made to clarify the theoretical nature of topological indices, none can yet be considered a true physical derivation. In this project, we explore two complementary approaches found in the literature: one employing chemometric techniques to analyse the behaviour of these descriptors, and the other relying on mathematical—particularly algebraic—methods to investigate the underlying invariants on which TIs are based. The structure of this paper is as follows: Section 2 presents the methodology used in this study. Section 3 introduces the molecular graphs of drugs for coronary artery disease (CAD) along with the corresponding topological indices. Section 4 describes the machine learning methods employed. Section 5 reports the numerical results and analysis. Finally, Section 6 concludes the study and highlights the key findings.

2. Methodology

Coronary artery disease (CAD) is a major cause of morbidity and mortality worldwide, affecting millions annually. It is caused by the buildup of atherosclerotic plaques in the coronary arteries, leading to reduced blood flow, myocardial ischaemia, heart attacks, heart failure, or sudden cardiac death. Key risk factors include hypertension, diabetes, hyperlipidaemia, smoking, and sedentary lifestyle. Research has extensively studied the cellular, molecular, and pathophysiological mechanisms underlying CAD, including endothelial dysfunction, inflammation, and plaque instability.

The management of CAD relies on drugs such as Isinopril, Amlodipine, Xarelto, Brilinta, Perindopril, Isoxsurprine, Azilsartan, and Metolazone. These medications act by lowering cholesterol, preventing platelet aggregation, and reducing myocardial oxygen demand. Their therapeutic efficacy and safety are influenced by dosage, selectivity, patient comorbidities, and molecular structure. Understanding the structural properties of these drugs is crucial to rational drug design, as it guides the development of molecules with improved potency, selectivity, and reduced side effects. Computational approaches can further leverage this structural information to predict drug behaviour, optimise efficacy, and accelerate the drug discovery process.

In this study, we integrate chemical graph theory with machine learning (ML) to analyse and predict the efficacy of CAD drugs. Machine learning has been successfully applied in diverse domains, including cybersecurity and IoT-based threat mitigation, demonstrating its versatility for predictive modelling [24]. Molecular structures are represented as chemical graphs, from which topological descriptors are extracted to capture connectivity and structural features. These descriptors serve as input to supervised ML models, enabling the identification of structural factors that influence drug performance. Our approach demonstrates that graph-theoretical descriptors can enhance prediction accuracy and provide mechanistic insights, offering a robust, interpretable, and scalable framework for CAD drug discovery. The main contributions of this study are depicted in Figure 1.

3. Molecular Graphs of Coronary Artery Disease Drugs and Graphical Indices

Coronary artery disease (CAD) is the most common type of heart disease, characterised by the narrowing or blockage of the coronary arteries due to the buildup of plaque (atherosclerosis). This condition reduces blood flow to the heart muscle, leading to chest pain (angina), shortness of breath, or even heart attacks. Risk factors include high cholesterol, hypertension, smoking, diabetes, obesity, and a sedentary lifestyle.

A variety of drugs are used to manage CAD by targeting different aspects of the disease. For example, Lisinopril and Perindopril are ACE inhibitors that lower blood pressure and reduce heart strain, while Amlodipine helps relax and widen blood vessels as a calcium channel blocker. Xarelto and Brilinta are antithrombotic agents that prevent blood clots, reducing the risk of stroke or heart attack. Azilsartan, an angiotensin receptor blocker (ARB), is effective in lowering blood pressure, and Metolazone, a diuretic, helps manage fluid retention. Additionally, Isoxsuprine improves blood flow by relaxing vascular smooth muscles. These drugs play a vital role in reducing CAD symptoms, improving heart function, and preventing complications. The molecular structures of drugs for coronary artery disease treatment are depicted in Figure 2.

In

Table 1. Physical and characteristic properties of the candidate drugs.

Drug Name	Molar Volume (cm3)	Boiling Point (°C)	Molecular Weight (g/mol)	Complexity	Flash Point (°C)
Lisinopril	323.9	666.4	405.495	550	356.9
Amlodipine	333	527.2	408.879	647	272.6
Xarelto	298.5	732.6	435.879	645	396.9
Brilinta	311.9	777.6	522.6	736	424
Perindopril	320.4	537.4	368.474	524	278.8
Isoxsurprine	251.16	484.51	301.4	299	246.6
Azilsartan	325.33	747.9	456.4	783	406.15
Metolazone	261.3	613.6	365.8	594	324.9

, we present the physical and characteristic properties of the drugs used in the treatment of coronary artery disease.

3.1. Graphical Indices

Molecular descriptors play a significant role in medicine, particularly in drug design and discovery. By applying degree-based topological indices to drugs used in disease therapy, researchers can analyse their structural features and establish connections to their biological activity. In this context, we will discuss some of these indices with respect to the previously mentioned drugs.

A molecular graph G is an ordered pair of $V\left(G\right)$, which denotes the vertices (atoms), and $E\left(G\right)$, which represents the edges (bonds between atoms). The degree of a vertex m is denoted by $d_m$ and defined as the number of edges connected to it. Molecular graphs can be analysed using topological indices, which serve as molecular descriptors to evaluate the physical and chemical properties of molecules and facilitate mathematical analyses.

Several graphical indices have been developed to study molecular structures. We discuss a few prominent indices as follows.

3.1.1. Atom–Bond Connectivity (ABC) Index

The Atom–Bond Connectivity index, $ABC\left(G\right)$, is utilised to evaluate the stability of alkanes and the strain energy of cycloalkanes. Proposed by Erciyes [25], the index is defined as

$$ABC\left(G\right)=\sum _{mn\in E\left(G\right)}\sqrt{{\displaystyle \frac{d_m+d_n-2}{d_m{d}_n}}}.$$

(1)

3.1.2. Zagreb Indices

The Zagreb indices are well-known molecular descriptors initially introduced by Gutman and Trinajstić [12]. These indices are used to explore the relationship between the total $\pi$-electron energy and molecular structure. The first and second Zagreb indices are defined as

$$M_1\left(G\right)=\sum _{mn\in E\left(G\right)}(d_m+d_n),$$

(2)

$$M_2\left(G\right)=\sum _{mn\in E\left(G\right)}\left(d_m{d}_n\right).$$

(3)

3.1.3. Randić Index

Proposed by Randić in 1975 [26], the Randić index, $RA\left(G\right)$, measures the branching complexity of molecular structures and is given by

$$RA\left(G\right)=\sum _{mn\in E\left(G\right)}{\displaystyle \frac{1}{\sqrt{d_m{d}_n}}}.$$

(4)

3.1.4. Sum Connectivity Index

The Sum Connectivity index, proposed by Zhou and Trinajstić [27], is expressed as

$$S\left(G\right)=\sum _{mn\in E\left(G\right)}\sqrt{{\displaystyle \frac{1}{d_m+d_n}}}.$$

(5)

3.2. Geometric–Arithmetic Index

Vujošević et al. [28] introduced the geometric–arithmetic index, $GA\left(G\right)$, which is defined as

$$GA\left(G\right)=\sum _{mn\in E\left(G\right)}{\displaystyle \frac{2\sqrt{d_m{d}_n}}{d_m+d_n}}.$$

(6)

3.3. Harmonic Index

Proposed by Fajtlowicz [5], the harmonic index, $H\left(G\right)$, is represented as

$$H\left(G\right)=\sum _{mn\in E\left(G\right)}{\displaystyle \frac{2}{d_m+d_n}}.$$

(7)

3.4. Hyper Zagreb Index

A modified version of the Zagreb index, the hyper Zagreb index, was introduced by Shirdel et al. [29] and is given by

$$HM\left(G\right)=\sum _{mn\in E\left(G\right)}{(d_m+d_n)}^2.$$

(8)

3.5. Forgotten Index

The forgotten index, $F\left(G\right)$, proposed by Furtula and Gutman [30], is widely used in QSAR/QSPR studies. It is defined as

$$F\left(G\right)=\sum _{mn\in E\left(G\right)}\left[{\left(d_m\right)}^2+{\left(d_n\right)}^2\right].$$

(9)

These indices provide valuable insights into molecular structure and behaviour, enabling researchers to correlate structural features with physical, chemical, and biological properties. The computed molecular descriptors for the candidate drugs are summarised in

Table 2. Molecular descriptors for the candidate drugs.

Index	Lisinopril	Amlodipine	Xarelto	Brilinta	Perindopril	Isoxsurprine	Azilsartan	Metolazone
$ABC$	45.9	46.4	36.8	50.44	43.63	32.94	42.42	30.6
$M_1$	342	287	277	382	332	222	306	221
$M_2$	448	346	359	504	436	249	385	277
$RA$	26.26	22.9	20.5	28.5	23.74	19.6	24.75	17.58
S	26.38	23.07	21.5	29.3	24.05	19.22	25.6	17.9
$GA$	55.07	47.7	46.3	62.3	50.5	38.58	54.47	37.68
H	23.18	20.26	18.69	25.64	20.54	17.39	22.85	15.8
$HM$	2038	1609	1589	2266	2034	1190	1672	1237
F	1142	917	871	1258	1162	692	902	683

.

4. Machine Learning Method

Machine learning provides a powerful framework for analysing complex chemical and biological data by detecting nonlinear patterns that traditional methods may not capture. It enhances prediction accuracy through models that learn directly from molecular descriptors, enabling the identification of key structural features that influence drug performance. By leveraging these capabilities, machine learning supports faster, more reliable, and data-driven approaches to drug discovery and development.

This study integrates graph-theoretical methods with machine learning techniques to support drug design for coronary artery disease (CAD). The overall workflow is structured as follows: Drug molecules and target proteins are first represented as molecular graphs, where atoms correspond to nodes and chemical bonds to edges. From these representations, a broad set of topological and structural descriptors is extracted to quantitatively characterise each molecule. Machine learning models, including linear regression model and Random Forest (RF), are subsequently trained on the extracted graph-based features.

Linear regression models: Regression techniques, particularly linear regression, are utilised to quantify the relationship between molecular descriptors and drug–target binding affinity. Linear regression provides a transparent and analytically tractable modelling framework, making it a widely used baseline in quantitative structure–activity relationship (QSAR) studies. Its closed-form solution via the normal equation enables efficient estimation of regression coefficients, while its interpretability allows researchers to identify key structural features that contribute to binding strength. Despite its simplicity, linear regression has demonstrated strong predictive utility in chemoinformatics, especially when molecular descriptors exhibit linear or near-linear associations with biological activity [31,32]. Furthermore, linear models serve as essential benchmarks for evaluating the performance of more complex machine learning algorithms. The linear regression model is a simple and widely used approach to predict a response variable y based on a set of input features. It assumes that the relationship between the response and the predictors is linear, which can be expressed as

$$\widehat{y}={\beta }_0+\sum _{j=1}^p{\beta }_j{x}_j$$

In this equation, $\widehat{y}$ represents the predicted value of the response, ${\beta }_0$ is the intercept which corresponds to the predicted value when all predictors are zero, $x_j$ denotes the j-th input feature, and ${\beta }_j$ is the coefficient that measures how much $\widehat{y}$ changes when $x_j$ increases by one unit while keeping other variables constant. Here, p is the total number of predictors included in the model. The coefficients ${\beta }_0,{\beta }_1,\dots ,{\beta }_p$ are estimated from the training dataset, which consists of observed pairs $(x_i,y_i)$, by minimising the sum of squared differences between the observed responses and the predicted values. This process ensures that the model captures the linear trends in the data as accurately as possible.

Random Forest (RF): The Random Forest algorithm is employed as a more flexible nonlinear model capable of capturing intricate interactions among structural descriptors. RF constructs an ensemble of decision trees, each trained on bootstrapped subsets of the data and descriptor space, thereby reducing variance and mitigating overfitting [33]. This ensemble strategy enables RF to model heterogeneous molecular patterns that may not be captured by linear methods. In drug discovery, RF has shown strong performance in both regression and classification settings, particularly in predicting bioactivity, physicochemical properties, and drug–target associations [34,35]. Its ability to quantify feature importance also provides valuable insights into which graph-theoretical descriptors most strongly influence predicted binding affinity. This makes RF an effective tool not only for prediction but also for mechanistic interpretation of molecular behaviour. The Random Forest prediction is given by

$${\widehat{f}}_{\mathrm{RF}}(X_0,\mathrm{\Theta })={\displaystyle \frac{1}{K}}\sum _{k=1}^K\widehat{f}(X_0,{\theta }_k)$$

where $X_0$ is the input feature vector for which the prediction is made, $\mathrm{\Theta }=\{{\theta }_1,{\theta }_2,\dots ,{\theta }_K\}$ is the set of random vectors defining the construction of each tree, K is the total number of trees in the forest, $\widehat{f}(X_0,{\theta }_k)$ is the prediction of the k-th decision tree, and ${\theta }_k$ represents the randomness in tree construction, including the bootstrap sample and the random subset of predictor variables used for splitting nodes.

In addition, a link prediction framework is implemented to identify novel drug candidates by estimating the likelihood of interactions between drug molecules and target proteins. Comparative analyses with existing drugs are conducted to evaluate predicted binding affinity and structural similarity. Finally, the contribution of each graph-theoretical descriptor is examined to identify the most influential features for accurate drug prediction.

5. Numerical Results

In this section, we present a comparison of our main results. We applied three approaches to predict key chemical properties of drug compounds, focusing on molar volume and molecular weight: (i) baseline linear model, (ii) linear regression with training data, and (iii) Random Forest regression. The dataset was preprocessed by handling missing values and normalising features to ensure reliable predictions. To prevent overfitting, the data were split into training and test sets for the machine learning models, while baseline linear regression was applied to the full dataset without training.

The baseline linear model provides a simple, interpretable reference for understanding linear relationships between molecular descriptors and target properties. Linear regression with training data improves predictive performance by fitting model parameters, whereas Random Forest, an ensemble learning method, captures complex and nonlinear dependencies. Model performance was evaluated using metrics such as the coefficient of determination ($r^2$), mean absolute error (MAE), and root mean square error (RMSE). Feature importance analysis was also conducted to assess the contribution of different molecular descriptors to the prediction of molar volume and molecular weight. Comparing the outputs of these models demonstrates the effectiveness of graph-theoretical descriptors and provides valuable insights for molecular modelling and CAD drug characterisation.

Based on the previous study, we have considered the two physicochemical properties named molar volume and molecular weight. These two properties have a high level of predictive accuracy for the degree-based topological indices, as shown in Table 3, Table 4, Table 5, Table 6, Table 7, Table 8, Table 9 and Table 10. It is important to highlight that the evaluation of these indices requires only two structural parameters: the number of vertices v and the number of edges e.

5.1. The Predicative Model of Considered Topological Indices and Molar Volume

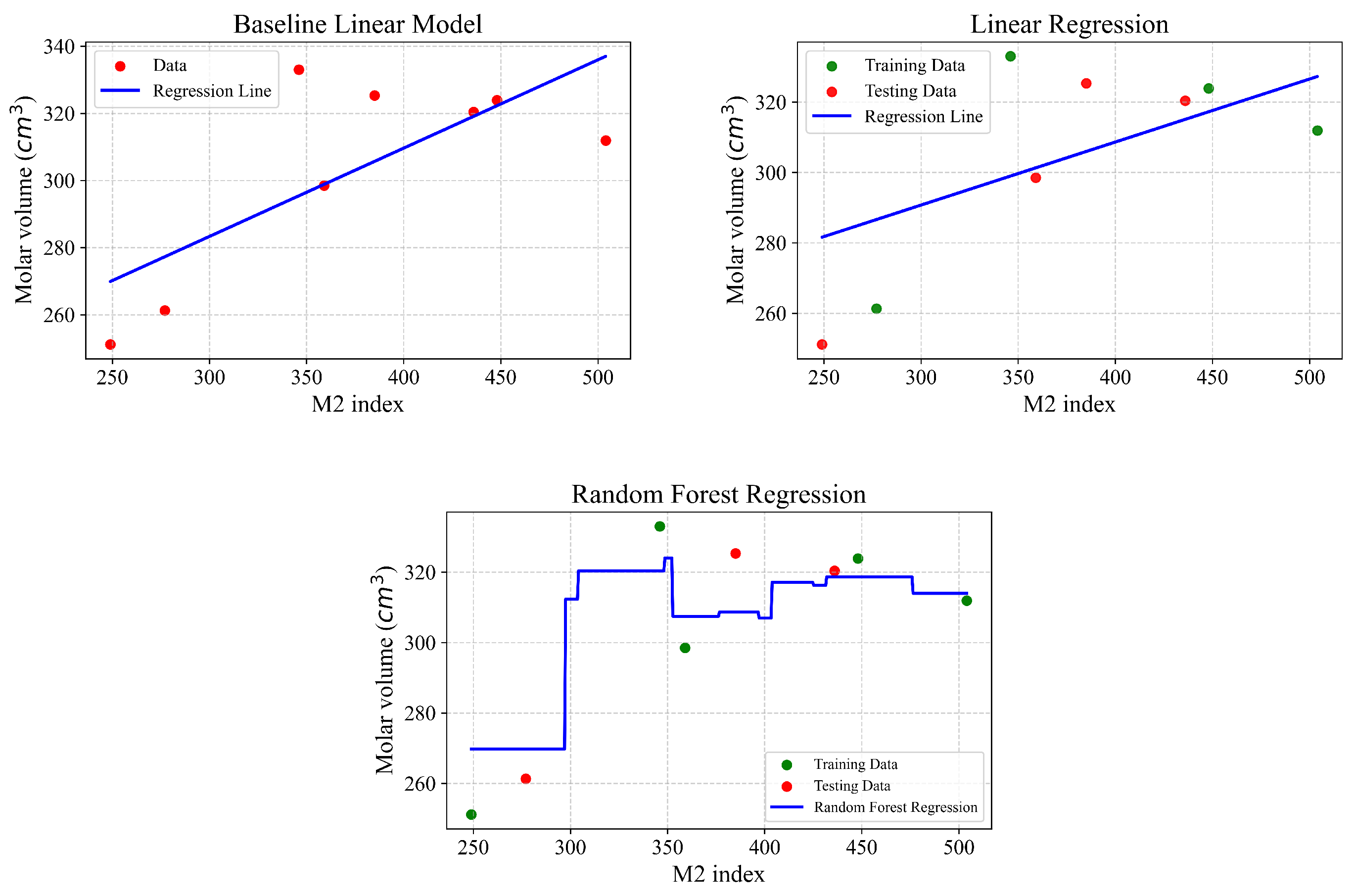
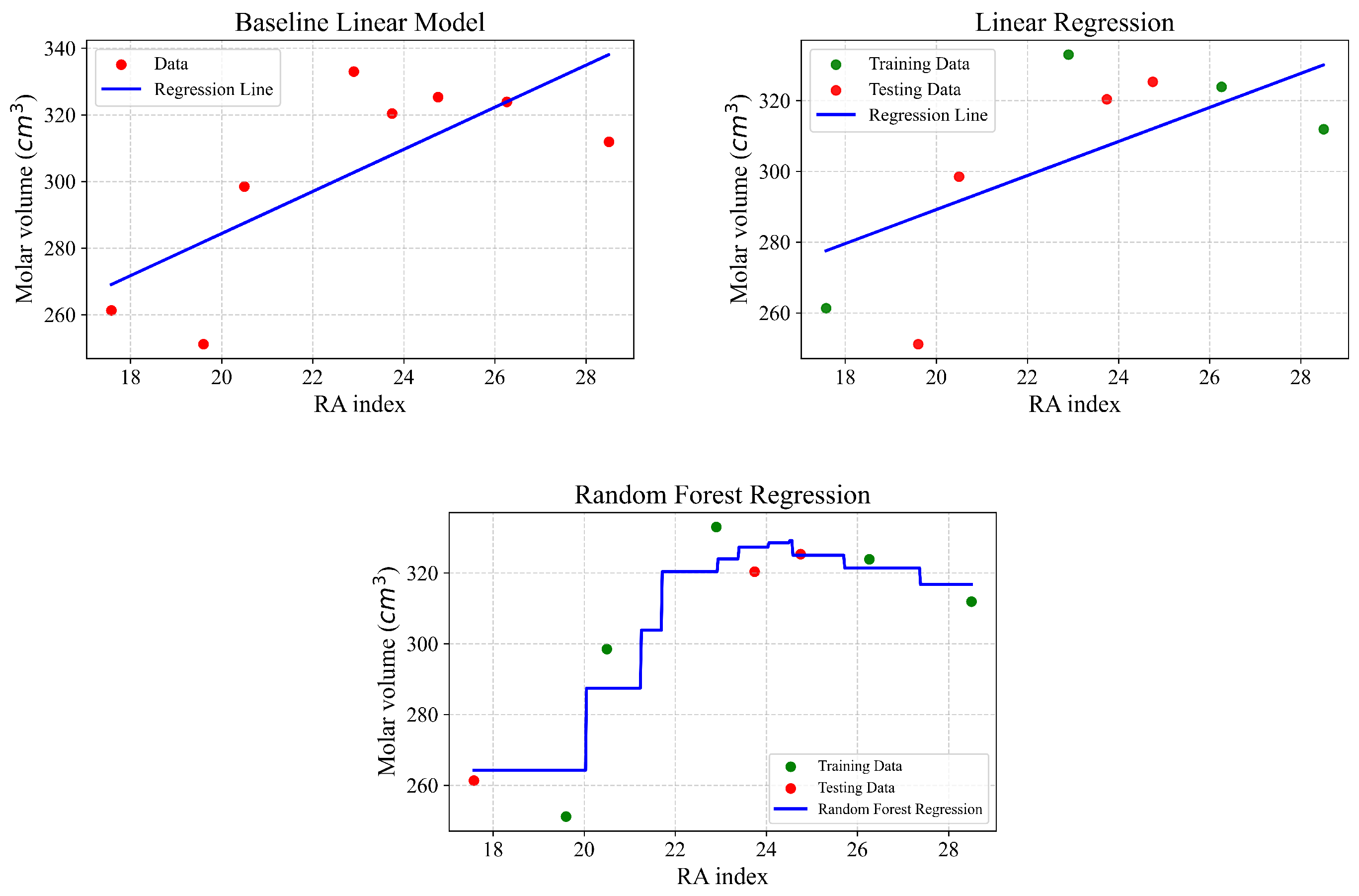
Table 3, Table 4, Table 5 and Table 6 summarise the performance of different classes of regression models and topological descriptors in predicting the molar volume of the drugs. It can be seen from Table 3 and Table 5 that the linear regression model has the highest predictive accuracy. Traditional degree-based and distance-based indices, such as the first general temperature index and the second general temperature index, exhibit strong correlations, with correlation values of 0.9204 and 0.9199, respectively. Our results attain the highest predictive accuracy with correlation values of 0.964 and 0.960. This highlights the superiority of the considered topological indices and demonstrates the advancement contributed by the present study. Similarly, Table 4 and Table 5 show that Random Forest attains the highest predictive accuracy with correlation values of 0.988 and 0.977. A graphical comparison of the predicted and actual molar volume values for each topological index is provided in Figure 3, Figure 4, Figure 5, Figure 6.

Table 3. The results of machine learning methods regarding ABC index and molar volume.

Type of Regression	r	${\mathit{r}}^2$	MSE	MAE
Baseline linear model	0.858	0.737	218.64	12.34
Linear regression	0.964	0.929	47.496	6.726
Random Forest	0.951	0.865	111.43	8.09

Table 3. The results of machine learning methods regarding ABC index and molar volume.

Type of Regression	r	${\mathit{r}}^2$	MSE	MAE
Baseline linear model	0.858	0.737	218.64	12.34
Linear regression	0.964	0.929	47.496	6.726
Random Forest	0.951	0.865	111.43	8.09

Table 4. The results of machine learning methods regarding M1 index and molar volume.

Type of Regression	r	${\mathit{r}}^2$	MSE	MAE
Baseline linear model	0.764	0.585	345.64	14.69
Linear regression	0.951	0.904	64.325	6.871
Random Forest	0.988	0.841	131.27	9.35

Table 4. The results of machine learning methods regarding M1 index and molar volume.

Type of Regression	r	${\mathit{r}}^2$	MSE	MAE
Baseline linear model	0.764	0.585	345.64	14.69
Linear regression	0.951	0.904	64.325	6.871
Random Forest	0.988	0.841	131.27	9.35

Table 5. The results of machine learning methods regarding M2 index and molar volume.

Type of Regression	r	${\mathit{r}}^2$	MSE	MAE
Baseline linear model	0.737	0.544	379.80	15.038
Linear regression	0.924	0.855	97.825	8.066
Random Forest	0.977	0.737	216.97	11.76

Table 5. The results of machine learning methods regarding M2 index and molar volume.

Type of Regression	r	${\mathit{r}}^2$	MSE	MAE
Baseline linear model	0.737	0.544	379.80	15.038
Linear regression	0.924	0.855	97.825	8.066
Random Forest	0.977	0.737	216.97	11.76

Table 6. The results of machine learning methods regarding RA index and molar volume.

Type of Regression	r	${\mathit{r}}^2$	MSE	MAE
Baseline linear model	0.74	0.549	374.9	16.16
Linear regression	0.960	0.922	52.433	7.101
Random Forest	0.956	0.883	96.52	8.82

Table 6. The results of machine learning methods regarding RA index and molar volume.

Type of Regression	r	${\mathit{r}}^2$	MSE	MAE
Baseline linear model	0.74	0.549	374.9	16.16
Linear regression	0.960	0.922	52.433	7.101
Random Forest	0.956	0.883	96.52	8.82

5.2. The Predicative Model of the Considered Topological Indices and Molecular Weight

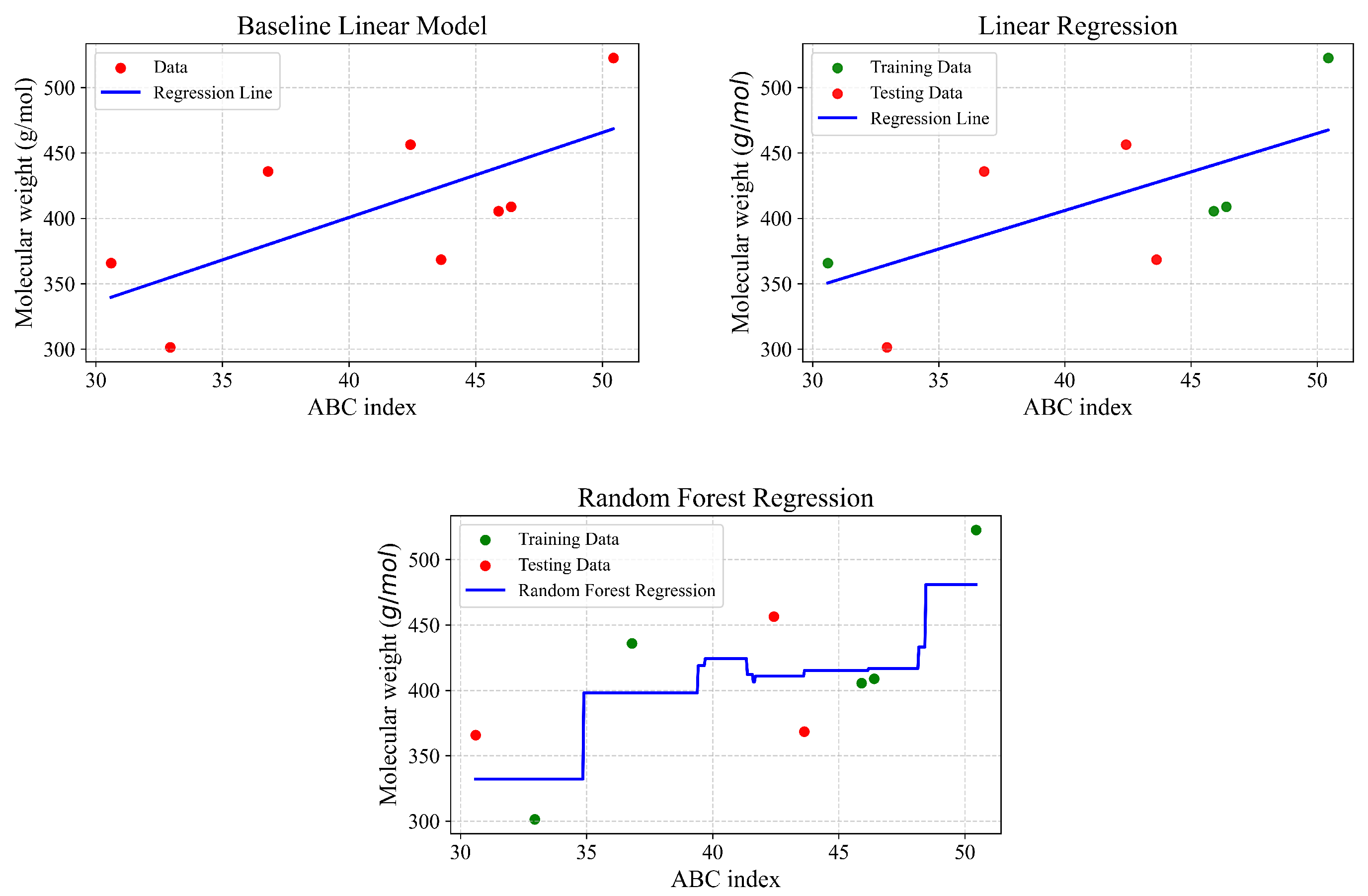
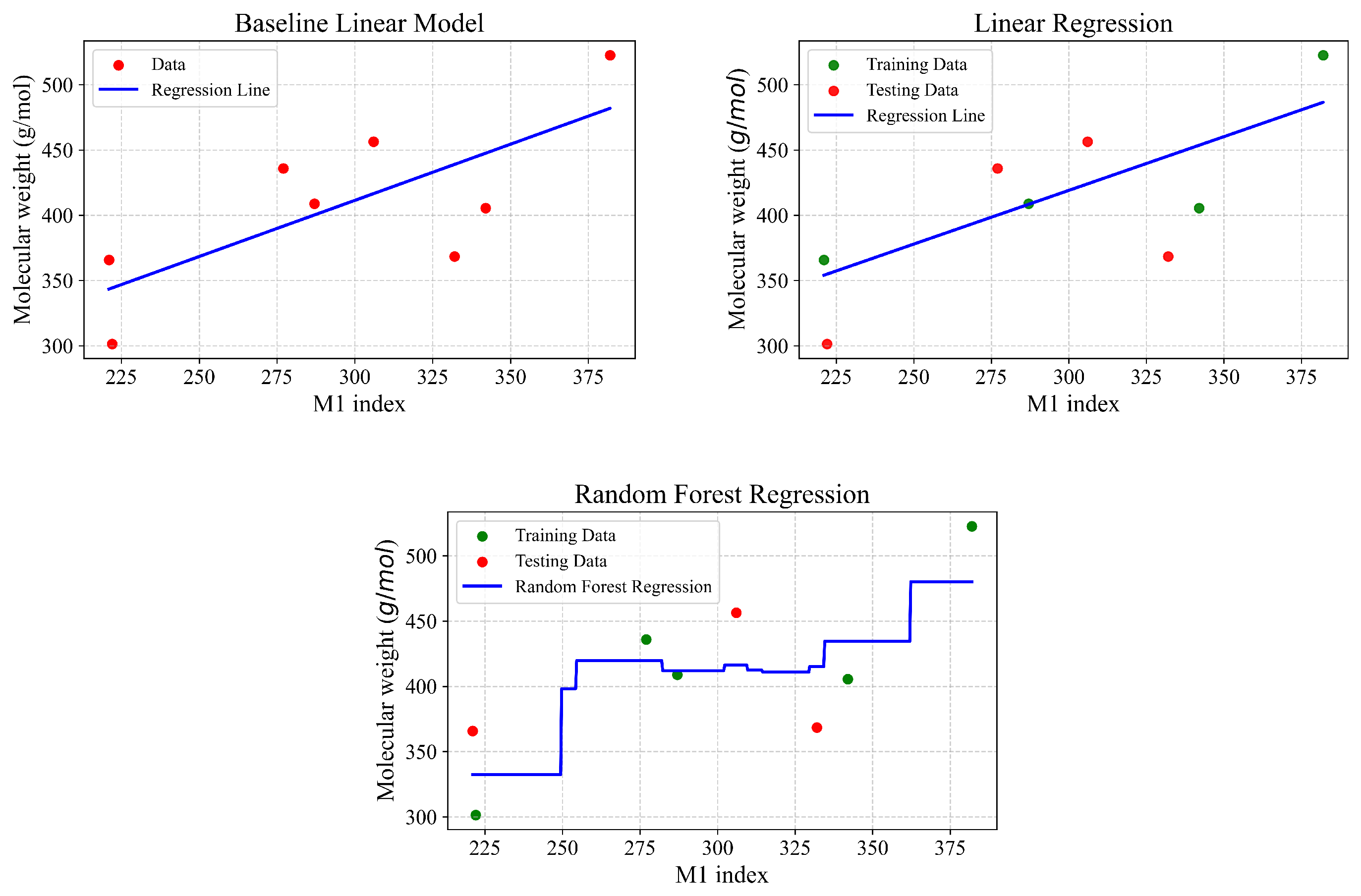
Table 7, Table 8, Table 9 and Table 10 summarise the performance of different classes of regression models and the topological descriptors in predicting the molecular weight of the drugs. It can be seen from these tables that the Random Forest model has the highest predictive accuracy. Traditional degree-based and distance-based indices, such as the first general temperature index and the second general temperature index, exhibit strong correlations, with correlation values of 0.910 and 0.912, respectively. Our results attain the highest predictive accuracy, with correlation values of 0.959, 0.963, 0.962, and 0.929. This highlights the superiority of the considered topological indices and demonstrates the advancement contributed by the present study. The graphical comparison of these indices for molecular weight are also given in Figure 7, Figure 8, Figure 9 and Figure 10.

Table 7. Results of machine learning methods regarding the ABC index and molecular weight.

Type of Regression	r	${\mathit{r}}^2$	MSE	MAE
Baseline linear model	0.682	0.465	2068.68	44.04
Linear regression	0.762	0.581	1430.5	35.102
Random Forest	0.959	0.830	853.95	25.57

Table 7. Results of machine learning methods regarding the ABC index and molecular weight.

Type of Regression	r	${\mathit{r}}^2$	MSE	MAE
Baseline linear model	0.682	0.465	2068.68	44.04
Linear regression	0.762	0.581	1430.5	35.102
Random Forest	0.959	0.830	853.95	25.57

Table 8. Results of machine learning methods regarding the M1 index and molecular weight.

Type of Regression	r	${\mathit{r}}^2$	MSE	MAE
Baseline linear model	0.732	0.536	1793.20	38.88
Linear regression	0.852	0.725	938.742	24.088
Random Forest	0.963	0.846	773.48	24.32

Table 8. Results of machine learning methods regarding the M1 index and molecular weight.

Type of Regression	r	${\mathit{r}}^2$	MSE	MAE
Baseline linear model	0.732	0.536	1793.20	38.88
Linear regression	0.852	0.725	938.742	24.088
Random Forest	0.963	0.846	773.48	24.32

Table 9. Results of machine learning methods regarding the M2 index and molecular weight.

Type of Regression	r	${\mathit{r}}^2$	MSE	MAE
Baseline linear model	0.739	0.546	1755.49	38.16
Linear regression	0.844	0.713	980.868	25.306
Random Forest	0.962	0.863	684.89	22.22

Table 9. Results of machine learning methods regarding the M2 index and molecular weight.

Type of Regression	r	${\mathit{r}}^2$	MSE	MAE
Baseline linear model	0.739	0.546	1755.49	38.16
Linear regression	0.844	0.713	980.868	25.306
Random Forest	0.962	0.863	684.89	22.22

Table 10. Results of machine learning methods regarding the RA index and molecular weight.

Type of Regression	r	${\mathit{r}}^2$	MSE	MAE
Baseline linear model	0.711	0.506	1910.80	39.41
Linear regression	0.825	0.681	1090.342	27.539
Random Forest	0.929	0.800	1003.87	28.43

Table 10. Results of machine learning methods regarding the RA index and molecular weight.

Type of Regression	r	${\mathit{r}}^2$	MSE	MAE
Baseline linear model	0.711	0.506	1910.80	39.41
Linear regression	0.825	0.681	1090.342	27.539
Random Forest	0.929	0.800	1003.87	28.43

6. Conclusions and Discussion

This study presents a computational framework integrating topological analysis with predictive modelling to investigate drugs for coronary artery disease (CAD) and atrial fibrillation (AF). Eight AF drugs, primarily beta-blockers, were analysed using topological indices (T-indices) to characterise their structural and physicochemical properties, including molar volume, molecular weight, complexity, boiling point, and flash point. Three predictive approaches were applied: (1) a baseline linear model, applied directly to the full dataset as a reference, providing interpretable correlations between T-indices and molecular properties; (2) a machine learning-based linear regression model, which improved predictive performance; and (3) Random Forest regression, which captured potential nonlinear relationships and enhanced accuracy for selected indices. The high predictability of molar volume reflects its direct representation of a molecule’s three-dimensional size and shape, which influence pharmaceutical properties such as solubility and membrane permeability. Topological indices effectively encode these structural features, explaining the strong performance of all models.

Despite these promising results, this study has several limitations. The dataset is small, comprising only eight beta-blocker drugs, which limits the generalisability of the predictions and increases the risk of overfitting, particularly for ensemble methods such as Random Forest. The absence of experimental or biological validation further restricts the applicability of the findings. Consequently, the results should be interpreted as preliminary insights rather than definitive conclusions. Future work should address these limitations by incorporating larger and more diverse drug datasets to improve model validation and statistical robustness. Advanced computational methods, such as Graph Neural Networks (GNNs), molecular docking, and molecular dynamics simulations, could provide more detailed structural and dynamic information. Finally, integrating experimental or clinical validation will be essential to confirming the practical relevance of these predictive models and support their application in AI-driven drug discovery and personalised medicine.