Mathematical Modeling of Canine and Human Rabies

Abstract

This article presents a deterministic model describing the joint dynamics of canine and human rabies in a cross-border context. This model explicitly integrates dog mobility between two neighboring countries and allows us to assess the impact of these movements on disease persistence. We analyze the basic reproduction number ${\mathcal{R}}_0$, study the local and global stability of equilibrium points, identify the most influential parameters through sensitivity analysis, and perform numerical simulations to test the effectiveness of different vaccination and movement control strategies.

1. Introduction

Rabies is a fatal viral zoonosis primarily affecting mammals, including humans. It is responsible for nearly 59,000 human deaths per year worldwide, with the majority occurring in Africa and Asia, with dogs accounting for over 99% of human transmissions [1,2]. Prevention mainly relies on vaccination of reservoir animals, particularly dogs, and post-exposure prophylaxis in humans. Numerous studies have confirmed that mass dog vaccination is the most effective tool for interrupting transmission, often more cost-effective than solely strengthening post-exposure prophylaxis [3,4].

However, cross-border dog mobility complicates control strategies, especially in border regions where inter-state coordination is often weak. For example, studies conducted at the border between Chad and Cameroon have shown the importance of considering canine migratory flows to understand the spatial dynamics of rabies [3,5]. In the Serengeti region, analyses have highlighted that regular reintroductions of the disease from neighboring areas can compromise local efforts, making large-scale vaccination necessary [6].

In several regions of the world, particularly in Africa and Asia, vaccination efforts are fragmented. Models applied to African urban contexts [7] or to China [8,9] have shown that vaccination coverage must exceed a critical threshold (often ≥70 %) to guarantee elimination, and that high turnover in the dog population leads to a rapid decline in coverage if campaigns are not repeated annually [10].

Mathematical models have improved our understanding of rabies transmission, particularly compartmental models of SIR [11] or SEIR type adapted to animal and human contexts [12]. These works also highlight the importance of integrating the dynamics of canine and human populations in a realistic spatial framework. However, few studies have explored the impact of cross-border dog exchanges in a multi-country framework, even though this approach is crucial for achieving the WHO’s “Zero human dog-mediated rabies deaths by 2030” strategy [1].

The aim of this study is to propose a multi-country mathematical model for canine rabies, taking into account dog movements between two neighboring countries to better understand the impact of cross-border mobility on disease dynamics and to evaluate the effectiveness of different control strategies.

Our specific objectives include:

Developing a country-structured compartmental model, integrating bidirectional dog movements between the two countries;

Calculating and analyzing the basic reproduction number ${\mathcal{R}}_0$ for this multi- country system;

Studying the stability of the rabies-free equilibrium and the conditions for endemic persistence in each country;

Performing sensitivity analysis to identify the most influential parameters on rabies spread;

Simulating the effect of different targeted vaccination and movement control strategies.

2. Model Formulation

To describe rabies dynamics in two interconnected countries, we construct a compartmental model structured into two subpopulations (human and canine) for each country denoted $i=1,2$ (country of origin) and $j=1,2$ (neighboring country) [13]. The model is inspired by previous work on canine rabies dynamics and interspecies transmission between dogs and humans [3,14,15], incorporating migration [16] as illustrated in Figure 1.

For each country i,

• The canine population $N_c^i$ is divided into compartments: susceptible ($S_c^i$), exposed ($E_c^i$), infectious ($I_c^i$), and vaccinated ($V_c^i$).
• The human population $N_h^i$ is divided into susceptible ($S_h^i$), exposed ($E_h^i$), and infected ($I_h^i$).
• Vaccination is applied only to dogs.
• The model is formulated for two interconnected countries $i=1,2$.
• Human movements and dog movements are considered equal.

The parameters ${\theta }^i$ and ${\alpha }^i$ are central to modeling post-exposure prophylaxis (PEP) in humans:

• ${\theta }^i$ represents the proportion of exposed humans who receive post-exposure prophylaxis after potential rabies exposure. This parameter captures the coverage and accessibility of healthcare services in country i.
• ${\alpha }^i$ represents the efficacy of post-exposure prophylaxis in preventing rabies development among treated individuals. This parameter accounts for the combined effectiveness of wound care, rabies vaccination, and rabies immunoglobulin administration.

In the model structure:

• The term ${\theta }^i{E}_h^i$ in Equation (1g) represents exposed individuals initiating PEP treatment
• The term ${\alpha }^i{\theta }^i{T}_h^i$ in Equation (1h) represents successfully treated individuals who recover and gain immunity
• The term $(1-{\theta }^i){\gamma }^i{E}_h^i$ in Equation (1i) represents exposed individuals who don’t receive treatment and progress to infectious rabies

Flow Diagram

The description of variables and parameters is given in

Table 1. Model variables for each country $i=1,2$.

Variable	Description
$S_c^i$	Number of susceptible dogs in country i
$E_c^i$	Number of exposed dogs in country i
$I_{d_i}$	Number of infected dogs in country i
$V_c^i$	Number of vaccinated dogs in country i
$S_h^i$	Number of susceptible humans in country i
$E_h^i$	Number of exposed humans in country i
$T_h^i$	Number of treated humans in country i
$I_h^i$	Number of infected humans in country i
$R_h^i$	Number of recovered humans in country i

and

Table 2. Model parameters.

Parameter	Description
${\mathrm{\Lambda }}_h^i$	Human recruitment rate in country i
${\mathrm{\Lambda }}_c^i$	Dog recruitment rate in country i
${\beta }_{ch}^i$	Dog-to-human transmission rate
${\beta }_{cc}^i$	Dog-to-dog transmission rate
${\mu }_c^i$	Natural mortality rate of dogs
${\alpha }^i$	Vaccine efficacy
${\nu }_c^i$	Canine vaccination rate
${\delta }_c^i$	Rabies-induced mortality rate in dogs
${\theta }^i$	Probability of receiving post-exposure treatment
${\mu }_h^i$	Natural mortality rate of humans
${\gamma }^i$	Progression rate to infection in humans
${\delta }_h^i$	Rabies-induced mortality rate in humans
mh, mc	Migration rates (humans, dogs) between countries

respectively.

The system of equations is given by:

• Dogs

$$\begin{array}{c}{\displaystyle \frac{d{S}_c^i}{dt}}={\mathrm{\Lambda }}_c^i-{\beta }_{cc}{S}_c^i{\displaystyle \frac{I_c^i}{N_c^i}}-{\nu }_c^i{S}_c^i-{\mu }_c^i{S}_c^i+m_c^S{S}_c^j-m_c^S{S}_c^i,\end{array}$$

(1a)

$$\begin{array}{c}{\displaystyle \frac{d{V}_c^i}{dt}}={\nu }_c^i{S}_c^i-{\mu }_c^i{V}_c^i+m_c^V{V}_{c_j}-m_c^V{V}_c^i\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} \end{array}$$

(1b)

$$\begin{array}{c}{\displaystyle \frac{d{I}_c^i}{dt}}={\beta }_{cc}{S}_c^i{\displaystyle \frac{I_c^i}{N_c^i}}-({\mu }_c^i+{\delta }_c^i)I_c^i+m_c^I{I}_c^j-m_c^I{I}_c^i,\hspace{1em}\hspace{1em} \end{array}$$

(1c)

where

$$N_c^i=S_c^i+V_c^i+I_c^i.$$

(1d)

• Humans

$$\begin{array}{c}{\displaystyle \frac{d{S}_h^i}{dt}}={\mathrm{\Lambda }}_h^i-{\beta }_{ch}^i{S}_h^i{\displaystyle \frac{I_c^i}{N_c^i}}-{\mu }_h^i{S}_h^i+m_h^S{S}_h^j-m_h^S{S}_h^i,\end{array}$$

(1e)

$$\begin{array}{c}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{\displaystyle \frac{d{E}_h^i}{dt}}={\beta }_{ch}^i{S}_h^i{\displaystyle \frac{I_c^i}{N_c^i}}-(1-{\theta }^i){\gamma }^i{E}_h^i-{\mu }_h^i{E}_h^i+m_h^E{E}_h^j-m_h^E{E}_h^i,\end{array}$$

(1f)

$$\begin{array}{c}{\displaystyle \frac{d{T}_h^i}{dt}}={\theta }^i{E}_h^i-{\alpha }^i{\theta }^i{T}_h^i-{\mu }_h^i{T}_h^i+m_h^T{T}_h^j-m_h^T{T}_h^i,\end{array}$$

(1g)

$$\begin{array}{c}\hspace{1em} {\displaystyle \frac{d{I}_h^i}{dt}}=(1-{\theta }^i){\gamma }^i{E}_h^i-({\delta }_h^i+{\mu }_h^i)I_h^i+m_h^I{I}_h^j-m_h^I{I}_h^i,\end{array}$$

(1h)

$$\begin{array}{c}{\displaystyle \frac{d{R}_h^i}{dt}}={\alpha }^i{\theta }^i{T}_h^i-{\mu }_h^i{R}_h^i+m_h^R{R}_h^j-m_h^R{R}_h^i.\end{array}$$

(1i)

with initial conditions

$$S_h^i\left(0\right),S_c^i\left(0\right)>0,\mathrm{and}{E}_h^i\left(0\right),I_h^i\left(0\right),I_c^i\left(0\right),V_c^i\left(0\right),T_h^{i}0\left(t\right),R_h^i\left(0\right)\ge 0.$$

(1j)

3. Model Analysis

3.1. Vector Form

Before proceeding further, let us specify some vector and matrix notations that will be used later.

Vectors are assumed to be column vectors but are written without particular orientation unless otherwise indicated [13]. If $\mathit{X}=(X_1,\dots ,X_n)\in {\mathbb{R}}^n$, then $\mathit{X}\ge \mathit{0}$ means that $X_i\ge 0$, $\mathit{X}>\mathit{0}$ means that $\mathit{X}\ge \mathit{0}$ and there exists at least one i such that $x_i>0$; finally, $\mathit{X}\gg \mathit{0}$ means that $X_i>0$ for all $i=1,\dots ,n$. For $\mathit{X},\mathit{Y}\in {\mathbb{R}}^n$, we have $\mathit{X}\ge \mathit{Y}$, $\mathit{X}>\mathit{Y}$ and $\mathit{X}\gg \mathit{Y}$ if, respectively, $\mathit{X}-\mathit{Y}\ge \mathit{0}$, $\mathit{X}-\mathit{Y}>\mathit{0}$ and $\mathit{X}-\mathit{Y}\gg \mathit{0}$. This same notation applies to matrices.

Writing system (1) in vector form is particularly useful for the subsequent work. We therefore introduce some notations here.

For any variable $X\in \{S_c,V_c,I_c,S_h,E_h,T_h,I_h,R_h\}$, we denote $\mathit{X}=(X_1,\dots ,X_n)$, and define:

$$\mathit{Z}={({\mathit{S}}_c,{\mathit{V}}_c,{\mathit{I}}_c,{\mathit{S}}_h,{\mathit{E}}_h,{\mathit{T}}_h,{\mathit{I}}_h,{\mathit{R}}_h)}^T$$

as the state variable vector of dimension $8n$.

Then the vector form of (1) is

$${\mathit{Z}}^{\prime }=\mathit{F}\left(\mathit{Z}\right)+\mathcal{M}\mathit{Z},$$

(2)

where $\mathit{F}\left(\mathit{Z}\right)$ represents the local infection and transition terms, and $\mathcal{M}$ is the global movement matrix defined by:

$$\mathcal{M}={\mathcal{M}}^{S_c}\oplus {\mathcal{M}}^{V_c}\oplus {\mathcal{M}}^{I_c}\oplus {\mathcal{M}}^{S_h}\oplus {\mathcal{M}}^{E_h}\oplus {\mathcal{M}}^{T_h}\oplus {\mathcal{M}}^{I_h}\oplus {\mathcal{M}}^{R_h}.$$

The local terms are given by:

$$\begin{array}{c}\hfill \mathit{F}\left(\mathit{Z}\right)=\left(\begin{array}{c}{\mathbf{\Lambda }}_c-{\mathit{\beta }}_{cc}{\mathit{S}}_c{\displaystyle \frac{{\mathit{I}}_c}{{\mathit{N}}_c}}-{\mathit{\nu }}_c{\mathit{S}}_c-{\mathit{\mu }}_c{\mathit{S}}_c\\ {\mathit{\nu }}_c{\mathit{S}}_c-{\mathit{\mu }}_c{\mathit{V}}_c\\ {\mathit{\beta }}_{cc}{\mathit{S}}_c{\displaystyle \frac{{\mathit{I}}_c}{{\mathit{N}}_c}}-({\mathit{\mu }}_c+{\mathit{\delta }}_c){\mathit{I}}_c\\ {\mathbf{\Lambda }}_h-{\mathit{\beta }}_{ch}{\displaystyle \frac{{\mathit{I}}_c}{{\mathit{N}}_c}}\circ {\mathit{S}}_h-\mathit{\mu }{\mathit{S}}_h\\ {\mathit{\beta }}_{ch}{\displaystyle \frac{{\mathit{I}}_c}{{\mathit{N}}_c}}\circ {\mathit{S}}_h-(1-\mathit{\theta })\mathit{\gamma }{\mathit{E}}_h-\mathit{\mu }{\mathit{E}}_h\\ \mathit{\theta }\mathit{\gamma }{\mathit{E}}_h-\mathit{\alpha }\mathit{\theta }{\mathit{T}}_h-\mathit{\mu }{\mathit{T}}_h\\ (1-\mathit{\theta })\mathit{\gamma }{\mathit{E}}_h-({\mathit{\delta }}_h+\mathit{\mu }){\mathit{I}}_h\\ \mathit{\alpha }\mathit{\theta }{\mathit{T}}_h-\mathit{\mu }{\mathit{R}}_h\end{array}\right).\end{array}$$

The diagonal matrices are defined by:

$${\mathbf{\Lambda }}_c={({\mathrm{\Lambda }}_{c1},\dots ,{\mathrm{\Lambda }}_{cn})}^T,{\mathbf{\Lambda }}_h={({\mathrm{\Lambda }}_{h1},\dots ,{\mathrm{\Lambda }}_{hn})}^T,{\mathit{\nu }}_c=\mathsf{diag}({\nu }_{c1},\dots ,{\nu }_{cn}),$$

$${\mathit{\mu }}_c=\mathsf{diag}({\mu }_{c1},\dots ,{\mu }_{cn}),{\mathit{\delta }}_c=\mathsf{diag}({\delta }_{c1},\dots ,{\delta }_{cn}),\mathit{\gamma }=\mathsf{diag}({\gamma }_1,\dots ,{\gamma }_n),$$

$$\mathit{\theta }=\mathsf{diag}({\theta }_1,\dots ,{\theta }_n),\mathit{\alpha }=\mathsf{diag}({\alpha }_1,\dots ,{\alpha }_n),\mathit{\mu }=\mathsf{diag}({\mu }_1,\dots ,{\mu }_n),{\mathit{\delta }}_h=\mathsf{diag}({\delta }_{h1},\dots ,{\delta }_{hn}),$$

$${\mathit{\beta }}_{cc}=\mathsf{diag}({\beta }_{cc}^1,\dots ,{\beta }_{cc}^n),{\mathit{\beta }}_{ch}=\mathsf{diag}({\beta }_{ch}^1,\dots ,{\beta }_{ch}^n).$$

For each compartment $X\in \{S_c,V_c,I_c,S_h,E_h,T_h,I_h,R_h\}$, the associated movement matrix is given by:

$${\mathcal{M}}^X=\left(\begin{array}{cccc}-{\displaystyle \sum _{k=1}^n}{m}_{k1}^X& m_{12}^X& \cdots & m_{1n}^X\\ m_{21}^X& -{\displaystyle \sum _{k=1}^n}{m}_{k2}^X& \cdots & m_{2n}^X\\ ⋮& ⋮& \ddots & ⋮\\ m_{n1}^X& m_{n2}^X& \cdots & -{\displaystyle \sum _{k=1}^n}{m}_{kn}^X\end{array}\right),$$

(3)

where ∘ denotes the Hadamard product (element-wise product).

Movement matrices of the form (3) possess many useful properties for the analysis of metapopulation systems [13,17], which we will use later in the analysis.

3.2. Positivity

Theorem 1.

The components $S_h^i\left(t\right),S_c^i\left(t\right),E_h^i\left(t\right),I_h^i\left(t\right),I_c^i\left(t\right),V_c^i\left(t\right),T_h^i\left(t\right),R_h^i\left(t\right)$ are positive at all times t.

Proof. 

Equation (1e) implies ${\displaystyle \frac{d{S}_h^i}{dt}}+({\beta }_{ch}^i{\displaystyle \frac{I_c^i}{N_c^i}}+{\mu }_h^i)S_h^i={\mathrm{\Lambda }}_h^i+m_h^S{S}_h^j-m_h^S{S}_h^i$. Its vector form gives ${\displaystyle \frac{d{\mathit{S}}_h}{dt}}+({\mathit{\beta }}_{ch}{\displaystyle \frac{{\mathit{I}}_c}{{\mathit{N}}_c}}+{\mathit{\mu }}_h-{\mathcal{M}}_c^S){\mathit{S}}_h={\mathbf{\Lambda }}_h$, where ${\mathcal{M}}_c^S$ denotes the movement matrix of susceptible canines. The solution of this differential equation is

$${\mathit{S}}_h\left(t\right)=e^{-{\int }_0^{t}f\left(\tau \right)d\tau }\left[{\mathit{S}}_h\left(0\right)+\mathrm{\Lambda }{\int }_0^t{e}^{-{\int }_0^{\tau }f\left(s\right)ds}\ge 0,\right]$$

with $g\left(t\right)={\mathit{\beta }}_{ch}{\displaystyle \frac{{\mathit{I}}_c\left(t\right)}{{\mathit{N}}_c\left(t\right)}}+{\mathit{\mu }}_h-{\mathcal{M}}_c^S$

Similarly, the solution of Equation (1a) is given by

$${\mathit{S}}_c\left(t\right)=e^{-{\int }_0^{t}g\left(\tau \right)d\tau }\left[{\mathit{S}}_c\left(0\right)+\mathbf{\Lambda }{\int }_0^t{e}^{-{\int }_0^{\tau }g\left(s\right)ds}\ge 0\right],$$

with $g\left(t\right)={\mathit{\beta }}_{cc}{\displaystyle \frac{{\mathit{I}}_c\left(t\right)}{{\mathit{N}}_c\left(t\right)}}+{\mathit{\nu }}_c+{\mathit{\mu }}_c-{\mathcal{M}}_c^S$. □

Theorem 2.

The total human $N_h^i$ and canine $N_c^i$ populations are bounded at all positive times t.

Proof. 

Define the total human population of country i: $N_h^i=S_h^i+E_h^i+T_h^i+I_h^i+R_h^i$.

Summing Equation (1e–i), we obtain:

$$\begin{array}{cc}\hfill N_h^{i^{\prime }}=& {\mathrm{\Lambda }}_h^i-({\mu }_h^i-m_h^i)N_h^i-{\delta }_h^i{I}_h^i\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} \hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill \le & {\mathrm{\Lambda }}_h^i-({\mu }_h^i-m_h^i)N_h^i,\sin \mathrm{ce}{\delta }_h^i{I}_h^i\ge 0,\mathit{and}{m}_h^{Si}=m_h^{Ei}=m_h^{Ii}=m_h^{Ri}=m_h^i.\hfill \end{array}$$

(5)

This differential inequality is linear, and its solution is

$$\begin{array}{cc}\hfill N_h^i\left(t\right)\le & e^{-({\mu }_h^i-m_h^i)t}\left[N_h\left(0\right)+{\mathrm{\Lambda }}^i{\int }_0^t{e}^{-({\mu }_h^i-m_h^i)\tau }d\tau \right]\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill =& e^{-({\mu }_h^i-m_h^i)t}\left[N_h\left(0\right)-{\displaystyle \frac{{\mathrm{\Lambda }}_h^i}{({\mu }_h^i-m_h^i)}}\right]+{\displaystyle \frac{{\mathrm{\Lambda }}_h^i}{({\mu }_h^i-m_h^i)}}.\hfill \end{array}$$

(7)

Thus:

− If $N_h^i\left(t\right)\le {\displaystyle \frac{{\mathrm{\Lambda }}_h^i}{({\mu }_h^i-m_h^i)}}$, then $0<N_h^i\left(t\right)\le {\displaystyle \frac{{\mathrm{\Lambda }}_h^i}{({\mu }_h^i-m_h^i)}}$.

− If $N_h^i\left(t\right)>{\displaystyle \frac{{\mathrm{\Lambda }}_h^i}{{\mu }_h^i-m_h^i}}$, then $N_h^i\left(t\right)\le N_h^i\left(0\right),\forall t\ge 0$.

We therefore obtain:

$$0\le N_h^i\left(t\right)\le max\left(N_h^i\left(0\right),{\displaystyle \frac{{\mathrm{\Lambda }}_h^i}{{\mu }_h^i-m_h^i}}\right).$$

(8)

The same reasoning applies to the total canine population:

$$0\le N_c^i\left(t\right)\le max\left(N_c^i\left(0\right),{\displaystyle \frac{{\mathrm{\Lambda }}_c^i}{{\mu }_c^i-m_c^i}}\right).$$

(9)

Thus, all human and canine populations are not only positive but also uniformly bounded in time. □

3.3. Isolated Case

In this section, we consider the initial model without movement.

3.3.1. Rabies-Free Equilibrium

The analysis of equilibrium points of a dynamical system allows identifying stationary states in which populations no longer vary over time.

Thus, by setting the differential equations to zero and assuming the absence of infected or exposed individuals $(E_h^i=I_h^i=I_c^i=T_h^i=R_h^i=0)$, we obtain:

$$S_c^{i\ast }={\displaystyle \frac{{\mathrm{\Lambda }}_c^i}{{\mu }_c^i+{\nu }_c^i}},V_c^{i\ast }={\displaystyle \frac{{\nu }_c^i{\mathrm{\Lambda }}_c^i}{{\mu }_c^i({\mu }_c^i+{\nu }_c^i)}},S_h^{i\ast }={\displaystyle \frac{{\mathrm{\Lambda }}_h^i}{{\mu }_h^i}},E_h^{i\ast }=I_h^{i\ast }=T_h^{i\ast }=R_h^{i\ast }=0$$

We thus have two rabies-free equilibrium points:

$$E_c^{*}=\left({\displaystyle \frac{{\mathrm{\Lambda }}_c^i}{{\mu }_c^i+{\nu }_c^i}},{\displaystyle \frac{{\nu }_c^i{\mathrm{\Lambda }}_c^i}{{\mu }_c^i({\mu }_c^i+{\nu }_c^i)}},0\right)\mathrm{and}{E}_h^{*}=\left({\displaystyle \frac{{\mathrm{\Lambda }}_h^i}{{\mu }_h^i}},0,0,0,0\right).$$

3.3.2. Basic Reproduction Number in an Isolated Location

To calculate the basic reproduction number,

We use the Next-Generation Matrix method of van den Driessche and Watmough [18].

We consider the following infectious variables for country i, $(I_c^i,E_h^i)$.

The dynamics of these variables is decomposed into two functions:

• ${\mathcal{F}}_c$: rate of appearance of new infections in each compartment and
• ${\mathcal{V}}_c$: rate of transition between compartments (exits and entries due to progression or recovery),

which are given by:

$${\mathcal{F}}_c={\beta }_{cc}^i{S}_c^i{\displaystyle \frac{I_c^i}{N_c^i}}\mathrm{and}{\mathcal{V}}_c=({\mu }_c^i+{\delta }_c^i)I_c^i.$$

We compute the Jacobian of F and V at the disease-free equilibrium (DFE), i.e., when $I_c^i=E_h^i=I_h^i=0$.

The Jacobian of $F_c$ and $V_c$ at DFE are:

$$F_c={\beta }_{cc}^i{\displaystyle \frac{S_c^{i\ast }}{N_c^{i\ast }}},\mathrm{and}{V}_c={\mu }_c^i+{\delta }_c^i\Rightarrow V_c^{-1}={\displaystyle \frac{1}{{\mu }_c^i+{\delta }_c^i}}$$

We define the next-generation matrix $F_c{V}_c^{-1}$:

$$F_c{V}_c^{-1}={\displaystyle \frac{{\beta }_{cc}^i{\mu }_c^i}{({\mu }_c^i+{\nu }_c^i)({\mu }_c^i+{\delta }_c^i)}}$$

The basic reproduction number ${\mathcal{R}}_0$ is the spectral radius (dominant eigenvalue) of $F_c{V}_c^{-1}$. Here, we have:

$${\mathcal{R}}_0^i={\mathcal{R}}_{0c}^i={\displaystyle \frac{{\beta }_{cc}^i{\mu }_c}{({\mu }_c^i+{\nu }_c^i)({\mu }_c^i+{\delta }_c^i)}}$$

(10)

Remark 1.

This model assumes that humans do not retransmit rabies, which is biologically correct (rabies is not transmissible between humans). This is why $I_h^i$ is not a source of new infections, and humans do not fuel the epidemic reproduction dynamics.

3.3.3. Local Stability Analysis

Theorem 3.

The disease-free equilibrium point is locally asymptotically stable when ${\mathcal{R}}_0^i<1$ and unstable otherwise.

Proof. 

The Jacobian matrix evaluated around the DFE is given by

$$J_{E_0}=\left[\begin{array}{ccc}-{\nu }_c^i-{\mu }_c^i& 0& -{\displaystyle \frac{{\beta }_{cc}^i{\mu }_c^i}{{\mu }_c^i+{\nu }_c^i}}\\ {\nu }_c^i& -{\mu }_c^i& 0\\ 0& 0& {\displaystyle \frac{{\beta }_{cc}^i{\mu }_c^i}{{\mu }_c^i+{\nu }_c^i}}-({\mu }_c^i+{\delta }_c^i)\end{array}\right]$$

The stability of the DFE depends on the sign of the eigenvalues of this matrix. We can see:

The 2 × 2 submatrix at the top left is triangular, so its eigenvalues are:

$${\lambda }_1=-{\nu }_c^i-{\mu }_c^i,{\lambda }_2=-{\nu }_c^i-{\mu }_c^i<0$$

The last eigenvalue (related to $I_c^i$ ) is:

$${\lambda }_3={\displaystyle \frac{{\beta }_{cc}^i{\mu }_c^i}{{\mu }_c^i+{\nu }_c^i}}-({\mu }_c^i+{\delta }_c^i)=({\mu }_c^i+{\delta }_c^i)\left[{\displaystyle \frac{{\beta }_{cc}^i{\mu }_c^i}{({\mu }_c^i+{\delta }_c^i)({\mu }_c^i+{\delta }_c^i)}}-1\right]=({\mu }_c^i+{\delta }_c^i)\left[{\mathcal{R}}_0^i-1\right].$$

Then, if ${\mathcal{R}}_0^i<1$, ${\lambda }_3<0$. So all eigenvalues have negative real parts. Therefore, the disease-free equilibrium $E_0$ is locally asymptotically stable.

But, if ${\mathcal{R}}_0^i>1$, ${\lambda }_3>0$. And since one of the eigenvalues is positive, then the disease-free equilibrium $E_0$ is unstable. □

3.3.4. Global Stability of the Disease-Free Equilibrium

Theorem 4.

The disease-free equilibrium $E_0$ is globally asymptotically stable if ${\mathcal{R}}_0^i<1$.

Proof. 

Let us verify the conditions of the Castillo-Chavez theorem.

• Let $z_1=(S_c^i,V_c^i)$ be the class of uninfected individuals, and $z_2=\left(I_c^i\right)$ the class of infected individuals.
  For $z_2=0$, the system becomes:

  $$\begin{array}{cc}\hfill {\displaystyle \frac{d{S}_c^i}{dt}}& ={\mathrm{\Lambda }}_c^i-{\beta }_{cc}{S}_c^i{\displaystyle \frac{I_c^i}{N_c^i}}-{\nu }_c^i{S}_c^i-{\mu }_c^i{S}_c^i,\hfill \end{array}$$

  (11)

  $$\begin{array}{cc}\hfill {\displaystyle \frac{d{V}_c^i}{dt}}& ={\nu }_c^i{S}_c^i-{\mu }_c^i{V}_c^i.\hfill \end{array}$$

  (12)
  Solving these equations:

  $$S_c\left(t\right)=e^{-({\nu }_c^i+{\mu }_c^i)t}\left(S_H\left(0\right)-{\displaystyle \frac{{\mathrm{\Lambda }}_H}{d}}+{\mathrm{\Lambda }}_c^i{\int }_0^t{e}^{({\nu }_c^i+{\mu }_c^i)\tau }d\tau \right)$$

  i.e.,

  $$S_c\left(t\right)=e^{-({\nu }_c^i+{\mu }_c^i)t}\left(S_c^i\left(0\right)-{\displaystyle \frac{{\mathrm{\Lambda }}_c^i}{{\nu }_c^i+{\mu }_c^i}}\right)+{\displaystyle \frac{{\mathrm{\Lambda }}_c^i}{{\nu }_c^i+{\mu }_c^i}}$$

  and

  $$V_c\left(t\right)=e^{-{\mu }_c^{i}t}\left(V_c^i\left(0\right)-{\displaystyle \frac{{\nu }_c^i{\mathrm{\Lambda }}_c^i}{{\mu }_c^i({\nu }_c^i+{\mu }_c^i)}}\right)+{\displaystyle \frac{{\nu }_c^i{\mathrm{\Lambda }}_c^i}{{\mu }_c^i({\nu }_c^i+{\mu }_c^i)}}.$$
  Taking the limit as $t\to \infty$, we obtain:

  $$\underset{t\to \infty }{lim}{z}_1=\left({\displaystyle \frac{{\mathrm{\Lambda }}_c^i}{{\nu }_c^i+{\mu }_c^i}},{\displaystyle \frac{{\nu }_c^i{\mathrm{\Lambda }}_c^i}{{\mu }_c^i({\nu }_c^i+{\mu }_c^i)}}\right)=z_1^{★}.$$

  (13)
  So $z_1^{★}$ is globally stable when $z_2=0$.
• Now consider the system for infected individuals:

  $$\begin{array}{cc}\hfill {\displaystyle \frac{d{I}_c^i}{dt}}& ={\beta }_{cc}{S}_c^i{\displaystyle \frac{I_c^i}{N_c^i}}-({\mu }_c^i+{\delta }_c^i)I_c^i=g_i.\hfill \end{array}$$

  (14)
  Let $A={\displaystyle \frac{\partial \left(g_i\right)}{\partial z_2}}\left(E_0\right)$, we have:

  $$A=\left(\begin{array}{c}{\beta }_{cc}^i{\displaystyle \frac{{\mu }_c^i}{{\mu }^i+{\nu }^i}}-{\delta }_c^i-{\mu }_c^i\end{array}\right).$$
  Then

  $$\begin{array}{cc}\hfill \widehat{G}& =A{z}_2-g_i\hfill \end{array}$$

  (15)

  $$\begin{array}{cc}\hfill & ={\beta }_{cc}^i{\displaystyle \frac{{\mu }_c^i}{{\mu }^i+{\nu }^i}}{I}_c^i-({\delta }_c^i+{\mu }_c^i)I_c^i-{\beta }_{cc}^i{\displaystyle \frac{S_c^i}{N_c^i}}+({\delta }_c^i+{\mu }_c^i)I_c^i\hfill \end{array}$$

  (16)

  $$\begin{array}{cc}\hfill & ={\beta }_{cc}^i{\displaystyle \frac{{\mu }_c^i}{{\mu }^i+{\nu }^i}}{I}_c^i-{\beta }_{cc}^i{\displaystyle \frac{S_c^i}{N_c^i}}{I}_c^i\hfill \end{array}$$

  (17)

  $$\begin{array}{cc}\hfill & ={\beta }_{cc}^i{I}_c^i\left({\displaystyle \frac{{\mu }_c^i}{{\mu }^i+{\nu }^i}}-{\displaystyle \frac{S_c^i}{N_c^i}}\right)\ge 0\hfill \end{array}$$

  (18)

  since from (13) and (9)

  $${\displaystyle \frac{S_c^i}{N_c^i}}\le {\displaystyle \frac{{\mu }_c^i}{{\mu }^i+{\nu }^i}}.$$

Thus, $E_0$ is globally asymptotically stable when ${\mathcal{R}}_0<1$. □

Theorem 5.

$E_0$ is globally asymptotically stable when ${\mathcal{R}}_0<1$.

Proof. 

Consider the Lyapunov function candidate:

$$L({\mathit{S}}_c,{\mathit{V}}_c,{\mathit{I}}_c)=a_1\left({\mathit{S}}_c-{\mathit{S}}_c^{★}-{\mathit{S}}_c^{★}ln{\displaystyle \frac{{\mathit{S}}_c}{{\mathit{S}}_c^{★}}}\right)+a_2\left({\mathit{V}}_c-{\mathit{V}}_c^{★}-{\mathit{V}}_c^{★}ln{\displaystyle \frac{{\mathit{V}}_c}{{\mathit{V}}_c^{★}}}\right)+a_1{\mathit{I}}_c$$

(19)

Its time derivative is expressed as:

$$\begin{array}{cc}\hfill {\displaystyle \frac{dL}{dt}}& =a_1\left(1-{\displaystyle \frac{{\mathit{S}}_c^{★}}{S_c}}\right)\left[{\mathbf{\Lambda }}_c-{\mathit{\beta }}_{cc}{S}_c{\displaystyle \frac{I_c}{N_c}}-({\mathit{\nu }}_c+{\mathit{\mu }}_c-{\mathcal{M}}^{{\mathit{S}}_c}){\mathit{S}}_c\right]\hfill \\ \hfill & +a_2\left(1-{\displaystyle \frac{{\mathit{V}}_c^{★}}{{\mathit{V}}_c}}\right)\left[{\mathit{\nu }}_c{\mathit{S}}_c-({\mathit{\mu }}_c-{\mathcal{M}}^{{\mathit{V}}_c}){\mathit{V}}_c\right]\hfill \\ \hfill & +a_3\left[{\mathit{\beta }}_{cc}{\mathit{S}}_c{\displaystyle \frac{{\mathit{I}}_c}{{\mathit{N}}_c}}-({\mathit{\mu }}_c+{\mathit{\delta }}_c-{\mathcal{M}}^{{\mathit{I}}_c}){\mathit{I}}_c\right]\hfill \end{array}$$

$${\displaystyle \frac{dL}{dt}}=-a_1({\mathit{\nu }}_c+{\mathit{\mu }}_c-{\mathcal{M}}^{{\mathit{V}}_c}){\displaystyle \frac{{({\mathit{S}}_c-{\mathit{S}}_c^{★})}^2}{{\mathit{S}}_c}}-a_2{\mu }_c{\displaystyle \frac{{({\mathit{V}}_c-{\mathit{V}}_c^{★})}^2}{{\mathit{V}}_c}}+a_1({\mathit{\mu }}_c+{\mathit{\delta }}_c-{\mathcal{M}}^{{\mathit{I}}_c})\left({\mathcal{R}}_0{\displaystyle \frac{{\mathit{S}}_c^{★}{\mathit{N}}_c}{{\mathit{S}}_c{\mathit{N}}_c^{★}}}-1\right){\mathit{I}}_c$$

(20)

where ${\mathcal{R}}_0={\displaystyle \frac{{\mathit{\beta }}_{cc}{\mathit{S}}_c^{★}}{{\mathit{N}}_c^{★}({\mathit{\mu }}_c+{\mathit{\delta }}_c-{\mathcal{M}}^{{\mathit{S}}_c})}}$ is the basic reproduction number.

• The first two terms are always negative or zero
• The third term satisfies:

  $${\mathcal{R}}_0{\displaystyle \frac{{\mathit{S}}_c^{★}{\mathit{N}}_c}{{\mathit{S}}_c{\mathit{N}}_c^{★}}}-1\le {\mathcal{R}}_0-1\sin \mathrm{ce}{\displaystyle \frac{{\mathit{S}}_c^{★}{\mathit{N}}_c}{{\mathit{S}}_c{\mathit{N}}_c^{★}}}\le 1$$

  (21)
• Therefore if ${\mathcal{R}}_0\le 1$, then ${\displaystyle \frac{dL}{dt}}\le 0$
• The equality ${\displaystyle \frac{dL}{dt}}=0$ is only achieved at the disease-free equilibrium

Conclusion: Under the condition ${\mathcal{R}}_0\le 1$, the derivative ${\displaystyle \frac{dL}{dt}}$ is negative semi-definite, guaranteeing the global asymptotic stability of the disease-free equilibrium $E_c^{★}$. □

3.4. Analytical Calculation of the Critical Vaccination Threshold

If

$${\mathcal{R}}_0={\displaystyle \frac{{\beta }_{cc}^i{\mu }_c^i}{({\mu }_c^i+{\nu }_c^i)({\mu }_c^i+{\delta }_c^i)}},$$

the condition ${\mathcal{R}}_0<1$ implies:

$$({\mu }_c^i+{\nu }_c^i)({\mu }_c^i+{\delta }_c^i)>{\beta }_{cc}^i{\mu }_c^i\Rightarrow {\nu }_c^i>{\mu }_c^i\left({\displaystyle \frac{{\beta }_{cc}^i}{{\mu }_c^i+{\delta }_c^i}}-1\right).$$

We define:

$${\nu }_c^{\mathrm{crit}}=max\left(0,{\mu }_c^i\left({\displaystyle \frac{{\beta }_{cc}^i}{{\mu }_c^i+{\delta }_c^i}}-1\right)\right).$$

• If ${\displaystyle \frac{{\beta }_{cc}^i}{{\mu }_c^i+{\delta }_c^i}}\le 1$, then ${\nu }_c^{\mathrm{crit}}\le 0$: no vaccination effort required to ensure ${\mathcal{R}}_0<1$ (theoretical viewpoint).
• If ${\displaystyle \frac{{\beta }_{cc}^i}{{\mu }_c^i+{\delta }_c^i}}>1$, then ${\nu }_c^{\mathrm{crit}}$ gives the minimum vaccination rate to achieve in steady state to obtain $R_0<1$.

Practical remark: this threshold is a theoretical guide; in reality, one must account for actual coverage, vaccine efficacies, parameter uncertainties, and logistics.

Corollary 1

(Critical canine vaccination threshold). From the expression

$${\mathcal{R}}_0={\displaystyle \frac{{\beta }_{cc}^i{\mu }_c^i}{({\mu }_c^i+{\nu }_c^i)({\mu }_c^i+{\delta }_c^i)}},$$

the condition ${\mathcal{R}}_0<1$ provides a minimum threshold for the vaccination rate ${\nu }_c^i$, denoted ${\nu }_c^{\mathrm{crit}}$, such that if ${\nu }_c^i>{\nu }_c^{\mathrm{crit}}$ then ${\mathcal{R}}_0<1$.

Explicit formula:

$${\nu }_c^{\mathrm{crit}}=max\left\{0,{\mu }_c^i\left({\displaystyle \frac{{\beta }_{cc}^i}{{\mu }_c^i+{\delta }_c^i}}-1\right)\right\}.$$

Proof. 

Condition on ${\nu }_c^i$ for ${\mathcal{R}}_0<1$. We start from

$${\mathcal{R}}_0={\displaystyle \frac{{\beta }_{cc}^i{\mu }_c^i}{({\mu }_c^i+{\nu }_c^i)({\mu }_c^i+{\delta }_c^i)}}<1.$$

–

Multiply by $({\mu }_c^i+{\nu }_c^i)({\mu }_c^i+{\delta }_c^i)>0$:

$${\beta }_{cc}^i{\mu }_c^i<({\mu }_c^i+{\nu }_c^i)({\mu }_c^i+{\delta }_c^i).$$

Divide by ${\mu }_c^i+{\delta }_c^i>0$:

$${\displaystyle \frac{{\beta }_{cc}^i{\mu }_c^i}{{\mu }_c^i+{\delta }_c^i}}<{\mu }_c^i+{\nu }_c^i.$$

Isolate ${\nu }_c^i$:

$${\nu }_c^i>{\displaystyle \frac{{\beta }_{cc}^i{\mu }_c^i}{{\mu }_c^i+{\delta }_c^i}}-{\mu }_c^i={\mu }_c^i\left({\displaystyle \frac{{\beta }_{cc}^i}{{\mu }_c^i+{\delta }_c^i}}-1\right).$$

–

Negative case: if ${\displaystyle \frac{{\beta }_{cc}^i}{{\mu }_c^i+{\delta }_c^i}}\le 1$, the right-hand side is $\le 0$, so a rate ${\nu }_c=0$ satisfies ${\mathcal{R}}_0<1$. Otherwise, a positive minimum vaccination effort is required.

–

Compact formulation:

$${\nu }_c^{\mathrm{crit}}=max\left\{0,{\mu }_c^i\left({\displaystyle \frac{{\beta }_{cc}^i}{{\mu }_c^i+{\delta }_c^i}}-1\right)\right\}.$$

□

3.4.1. Equivalent Expression of Vaccination Coverage p

We express p as the proportion of vaccinated dogs at equilibrium:

$$p={\displaystyle \frac{V_c^{i\ast }}{N_c^{i\ast }}}={\displaystyle \frac{{\nu }_c^i}{{\mu }_c^i+{\nu }_c^i}}.$$

Solving for ${\nu }_c^i$:

$${\nu }_c^i={\displaystyle \frac{p{\mu }_c^i}{1-p}}.$$

Substitute into ${\mathcal{R}}_0$:

$${\mathcal{R}}_0={\displaystyle \frac{{\beta }_{cc}^i}{{\mu }_c^i+{\delta }_c^i}}·{\displaystyle \frac{{\mu }_c^i}{1-p}}.$$

The condition ${\mathcal{R}}_0<1$ becomes:

$$1-p<{\displaystyle \frac{{\mu }_c^i+{\delta }_c^i}{{\beta }_{cc}^i}}\iff p>1-{\displaystyle \frac{{\mu }_c^i+{\delta }_c^i}{{\beta }_{cc}^i}}.$$

Critical coverage:

$$p^{\mathrm{crit}}=max\left\{0,1-{\displaystyle \frac{{\mu }_c^i+{\delta }_c^i}{{\beta }_{cc}^i}}\right\}.$$

We verify that this corresponds to ${\nu }_c^{\mathrm{crit}}$:

$${\nu }_c^{\mathrm{crit}}={\displaystyle \frac{p^{\mathrm{crit}}{\mu }_c^i}{1-p^{\mathrm{crit}}}}.$$

3.4.2. Generalization: Imperfect Vaccine

If the vaccine has an efficacy $0\le \epsilon \le 1$, the protected fraction is $\epsilon p$ and the remaining fraction is $1-\epsilon p$.

The condition becomes:

$$p^{\mathrm{crit}}=max\left\{0,1-{\displaystyle \frac{{\mu }_c^i+{\delta }_c^i}{{\epsilon }^i{\beta }_{cc}^i}}\right\}.$$

3.5. Disease-Free Equilibrium

Then, by setting the differential equations of system (2) to zero and assuming the absence of infected or exposed individuals $({\mathit{E}}_h={\mathit{I}}_h={\mathit{I}}_c={\mathit{T}}_h={\mathit{R}}_h=\mathit{0})$, and noting that the matrix $\mathit{\mu }-\mathcal{M}$ is non-singular and therefore invertible, we obtain:

$${\mathit{S}}_c^{*}={\mathbf{\Lambda }}_c{({\mathit{\mu }}_c+{\mathit{\nu }}_c-{\mathcal{M}}^{S_c})}^{-1},{\mathit{V}}_c^{*}={\mathit{\nu }}_c{\mathbf{\Lambda }}_c{\left({\mathit{\mu }}_c({\mathit{\mu }}_c+{\mathit{\nu }}_c)\right)}^{-1},{\mathit{S}}_h^{*}={\mathbf{\Lambda }}_h{\mathit{\mu }}_h^{-1},{\mathit{E}}_h^{*}={\mathit{I}}_h^{*}={\mathit{T}}_h^{*}={\mathit{R}}_h^{*}=0$$

We thus have two rabies-free equilibrium points:

$${\mathit{E}}_c^{*}=\left({\mathbf{\Lambda }}_c{({\mathit{\mu }}_c+{\mathit{\nu }}_c-{\mathcal{M}}^{S_c})}^{-1},{\mathit{\nu }}_c{\mathbf{\Lambda }}_c{\left({\mathit{\mu }}_c({\mathit{\mu }}_c+{\mathit{\nu }}_c)\right)}^{-1},\mathit{0}\right),{\mathit{E}}_h^{*}=\left({\mathbf{\Lambda }}_h{\mathit{\mu }}_h^{-1},\mathbf{0},\mathbf{0},\mathbf{0},\mathbf{0}\right).$$

(22)

3.6. Derivation of the Global Basic Reproduction Number

Considering the vector of infectious variables $\mathbf{x}={({\mathbf{I}}_{\mathbf{c}},{\mathbf{E}}_{\mathbf{h}})}^{\top }$, the vectorial transmission and transition functions are:

$$\mathcal{F}=\left(\begin{array}{c}{\mathit{\beta }}_{cc}{\mathbf{S}}_{\mathbf{c}}\circ {\displaystyle \frac{{\mathbf{I}}_{\mathbf{c}}}{{\mathbf{N}}_{\mathbf{c}}}}+{\mathbf{S}}_{\mathbf{c}}\circ {\mathcal{M}}^{I_c}{\displaystyle \frac{{\mathbf{I}}_{\mathbf{c}}}{{\mathbf{N}}_{\mathbf{c}}}}\\ {\mathit{\beta }}_{ch}{\mathbf{S}}_{\mathbf{h}}\circ {\displaystyle \frac{{\mathbf{I}}_{\mathbf{c}}}{{\mathbf{N}}_{\mathbf{c}}}}\end{array}\right),\mathcal{V}=\left(\begin{array}{c}({\mathit{\mu }}_c+{\mathit{\delta }}_c)\circ {\mathbf{I}}_{\mathbf{c}}-{\mathcal{M}}^{I_c}\left({\mathbf{S}}_{\mathbf{c}}\circ {\displaystyle \frac{{\mathbf{I}}_{\mathbf{c}}}{{\mathbf{N}}_{\mathbf{c}}}}\right)-{\mathcal{M}}^{I_c}\left({\mathbf{V}}_{\mathbf{c}}\circ {\displaystyle \frac{{\mathbf{I}}_{\mathbf{c}}}{{\mathbf{N}}_{\mathbf{c}}}}\right)\\ ({\mathit{\mu }}_h+{\mathit{\gamma }}_h)\circ {\mathbf{E}}_{\mathbf{h}}\end{array}\right)$$

The Jacobian matrices at the disease-free equilibrium ${\mathit{E}}^{★}$ are:

$$F=\left(\begin{array}{cc}{F}_{11}& \mathbf{0}\\ F_{21}& \mathbf{0}\end{array}\right),V=\left(\begin{array}{cc}{V}_{11}& \mathbf{0}\\ \mathbf{0}& V_{22}\end{array}\right)$$

with

$$F_{11}={\mathit{\beta }}_{cc}·\mathrm{diag}\left({\displaystyle \frac{{\mathbf{S}}_{\mathbf{c}}^{*}}{{\mathbf{N}}_{\mathbf{c}}^{*}}}\right)+\mathrm{diag}\left({\mathbf{S}}_{\mathbf{c}}^{*}\right){\mathcal{M}}^{I_c}\mathrm{diag}\left({\displaystyle \frac{1}{{\mathbf{N}}_{\mathbf{c}}^{*}}}\right),F_{21}={\mathit{\beta }}_{ch}·\mathrm{diag}\left({\displaystyle \frac{{\mathbf{S}}_{\mathbf{h}}^{*}}{{\mathbf{N}}_{\mathbf{c}}^{*}}}\right)$$

$$V_{11}={\mathit{\mu }}_c+{\mathit{\delta }}_c-{\mathcal{M}}^{I_c}·\mathrm{diag}\left({\displaystyle \frac{{\mathbf{S}}_{\mathbf{c}}^{*}}{{\mathbf{N}}_{\mathbf{c}}^{*}}}\right)-{\mathcal{M}}^{I_c}·\mathrm{diag}\left({\displaystyle \frac{{\mathbf{V}}_{\mathbf{c}}^{*}}{{\mathbf{N}}_{\mathbf{c}}^{*}}}\right),V_{22}={\mathit{\mu }}_h+{\mathit{\gamma }}_h$$

Using the approximations ${\displaystyle \frac{S_c^{i\ast }}{N_c^{i\ast }}}\approx {\displaystyle \frac{{\mu }_c^i}{{\mu }_c^i+{\nu }_c^i}}$ and ${\displaystyle \frac{V_c^{i\ast }}{N_c^{i\ast }}}\approx {\displaystyle \frac{{\nu }_c^i}{{\mu }_c^i+{\nu }_c^i}}$, and considering migration terms as second-order perturbations, we obtain:

$$F_{11}\approx {\mathit{\beta }}_{cc}{\mathit{\mu }}_c{({\mathit{\mu }}_c+{\mathit{\nu }}_c)}^{-1},V_{11}\approx {\mathit{\mu }}_c+{\mathit{\delta }}_c-{\mathcal{M}}^{I_c}$$

The next-generation matrix for the canine subsystem is therefore:

$$K_c=F_{11}{V}_{11}^{-1}={\mathit{\beta }}_{cc}{\mathit{\mu }}_c{({\mathit{\mu }}_c+{\mathit{\nu }}_c)}^{-1}{({\mathit{\mu }}_c+{\mathit{\delta }}_c-{\mathcal{M}}^{I_c})}^{-1}$$

Taking into account the influence of susceptible migration on the equilibrium distribution, we obtain the final form:

$$F{V}^{-1}={\mathit{\beta }}_{cc}{\mathit{\mu }}_c{({\mathit{\mu }}_c+{\mathit{\nu }}_c-{\mathcal{M}}^{S_c})}^{-1}{({\mathit{\mu }}_c+{\mathit{\delta }}_c-{\mathcal{M}}^{I_c})}^{-1}$$

The global basic reproduction number is the spectral radius of this matrix:

$${\mathcal{R}}_0^{global}=\rho \left({\mathit{\beta }}_{cc}{\mathit{\mu }}_c{({\mathit{\mu }}_c+{\mathit{\nu }}_c-{\mathcal{M}}^{S_c})}^{-1}{({\mathit{\mu }}_c+{\mathit{\delta }}_c-{\mathcal{M}}^{I_c})}^{-1}\right)$$

(23)

This expression generalizes the isolated case result and captures the effect of migration between patches on the global epidemic dynamics.

3.7. Local Stability

First, from [18] (Theorem 2), we have the following result.

Theorem 6.

$E_0^{★}$ is locally asymptotically stable if ${\mathcal{R}}_0<1$ and unstable if ${\mathcal{R}}_0>1$.

Proof. 

We need to verify that assumptions A1–A5 of [18] (Theorem 2) are satisfied. Assumptions A1–A4 follow from the procedure used above to derive F and V in the calculation of ${\mathcal{R}}_0$. Therefore, all we need to verify is that the disease-free system at DFE is locally asymptotically stable. In the absence of disease, (2) is a linear system

$$\begin{array}{cc}\hfill {\displaystyle \frac{d}{dt}}{\mathit{S}}_c& ={\mathbf{\Lambda }}_c+({\mathcal{M}}^{S_c}-{\mathit{\nu }}_c-{\mathit{\mu }}_c){\mathit{S}}_c+{\mathit{\epsilon }}_c{\mathit{R}}_c\hfill \\ \hfill {\displaystyle \frac{d}{dt}}{\mathit{V}}_c& ={\mathit{\nu }}_c{\mathit{S}}_c+({\mathcal{M}}^{V_c}-{\mathit{\mu }}_c){\mathit{V}}_c.\hfill \end{array}$$

This is exactly Section 3.5, so we know it has a unique equilibrium, the disease-free equilibrium (22). The Jacobian matrix of the system at any point takes the form

$$\left(\begin{array}{cc}{\mathcal{M}}^{S_c}-{\mathit{\nu }}_c-\mathit{\mu }& 0\\ {\mathit{\nu }}_c& {\mathcal{M}}^{V_c}-{\mathit{\mu }}_c\end{array}\right).$$

We saw in Section 3.1 that this matrix is invertible. From [17] (Lemma 2 and Proposition 3), the spectral abscissa of this matrix is negative, so the disease-free equilibrium is always (locally) asymptotically stable. The result then follows. □

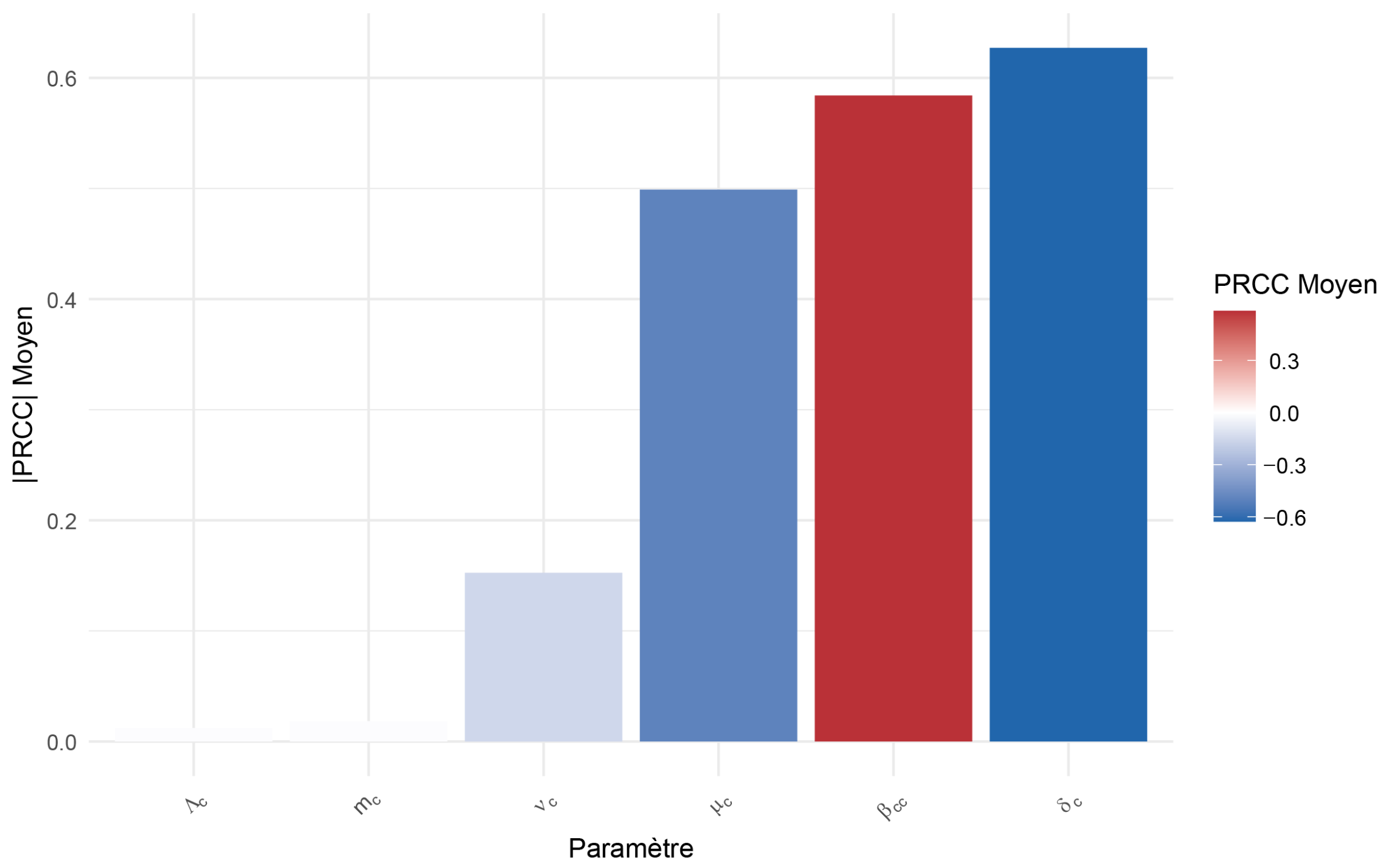
4. Sensitivity Analysis

We use the data from

Table 3. Model parameters.

Parameters	Intervals	Values	References
${\mathrm{\Lambda }}_h^i$	-	0.027	Assumed
${\mathrm{\Lambda }}_c^i$	-	0.5–1	[3]
${\beta }_{ch}^i$	0.000004–0.15	0.0001	[19]
${\beta }_{cc}^i$	0.1–0.5	0.3	[20]
${\mu }_c^i$	0.1–0.3	0.2	IRED Tchad (2024)
${\alpha }^i$	0.05–0.2	0.1	[3]
${\nu }_c^i$	0.01–0.1	0.05	[21]
${\delta }_c^i$	0.5–1	0.8	[19]
${\theta }^i$	0.001–0.01	0.005	[20]
${\mu }_h^i$	0.00003–0.00005	0.00004	INSEED Tchad (2020)
${\gamma }^i$	0.1–0.33	0.2	[22]
${\delta }_h^i$	0.9–1	0.99	[22]
mh, mc	0.001–0.01	0.005	[20]

for our numerical simulations. In this table, the parameter values are real data but are not yet available online. They are available from IRED (Institute of Livestock Research for Development) in Chad.

Interpretation: This analysis reveals which parameters to target for effective interventions:

Parameters with high positive PRCC (See Figure 2) represent priority targets for reduction measures (e.g., decreasing transmission rates). Parameters with high negative PRCC represent intervention opportunities (e.g., increasing vaccination or treatment rates).

5. Numerical Simulations

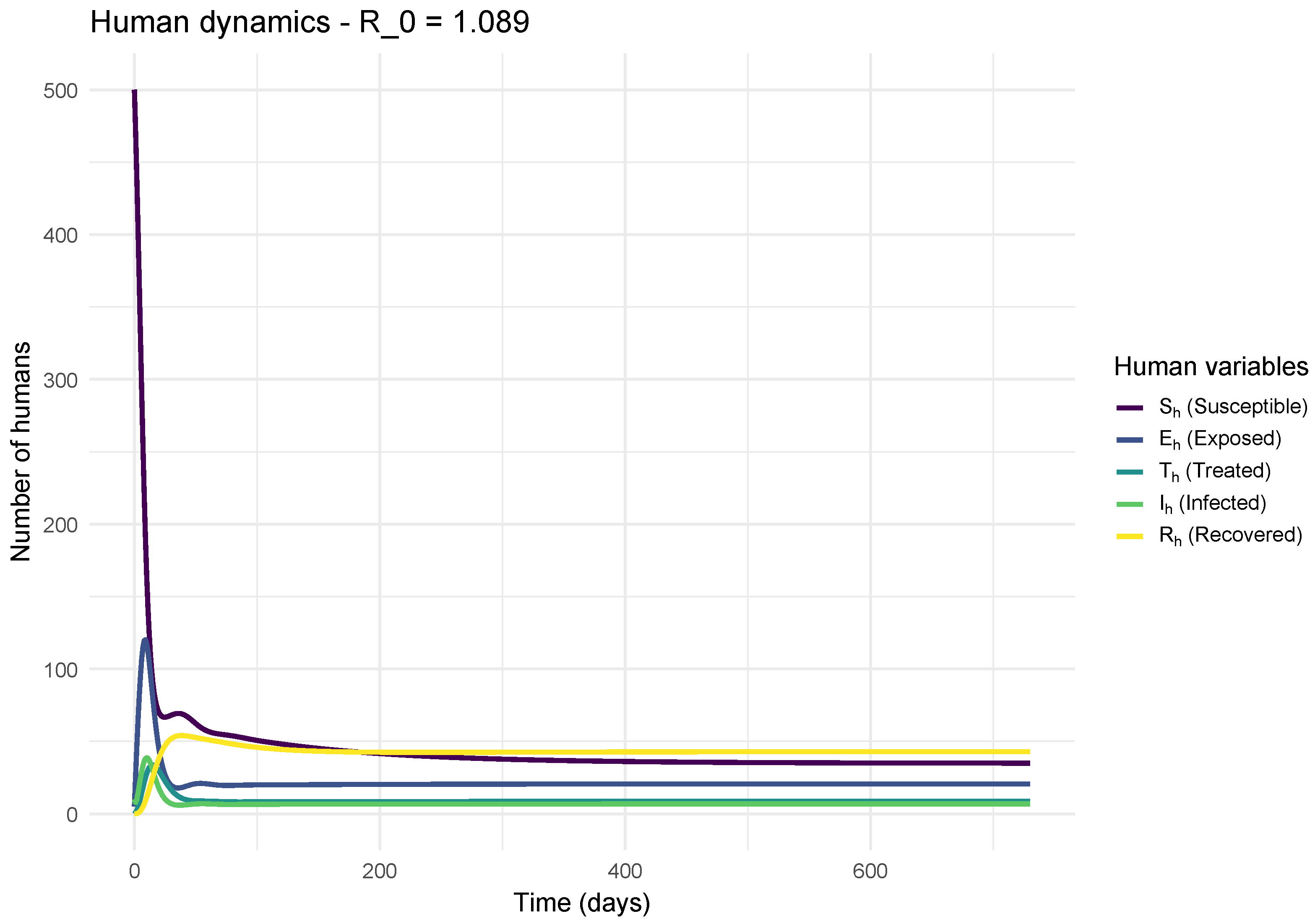
To visualize the temporal dynamics of the model and understand the impact of the basic reproduction number (${\mathcal{R}}_0$), we performed numerical simulations for canine and human populations. Two contrasting scenarios were studied: one where ${\mathcal{R}}_0<1$, indicating that the epidemic is theoretically controlled, and another where ${\mathcal{R}}_0>1$, a scenario in which the disease can spread within the population while accounting for canine mobility.

6. Discussion

Figure 3 shows the dynamics for ${\mathcal{R}}_0^c=1.827$. A fulminant epidemic is observed: the infected compartment ($I_c$) experiences rapid exponential growth, peaking at a high level where a large portion of the population is simultaneously infected; this is due to the high mobility of dogs between Patches. Subsequently, the number of infected decreases as the susceptible pool ($S_c$) is depleted, either by infection, vaccination, or the limited number of dog movements. This curve is characteristic of an uncontrolled epidemic.

In contrast, Figure 4 illustrates the scenario where ${\mathcal{R}}_0^c=0.818$. Here, the number of infected decreases monotonically from the start, without an epidemic peak. Each infected individual generates on average less than one new infection, leading to the natural and rapid extinction of the disease. The vaccinated population ($V_c$) remains significant, contributing to herd protection. This result validates the theoretical threshold: if ${\mathcal{R}}_0<1$, the disease cannot be maintained in the population.

The impact of the two canine scenarios on public health is striking. Figure 5 shows that an uncontrolled canine epidemic (${\mathcal{R}}_0^c>1$) leads to a significant risk for humans (${\mathcal{R}}_0^h=1.089>1$), resulting in an increase in exposed ($E_h$), infected ($I_h$), and treated ($T_h$) cases.

Conversely, Figure 6 demonstrates the beneficial effect of controlling rabies at its animal source. When ${\mathcal{R}}_0^c<1$, transmission from dog to human is interrupted, as evidenced by the value ${\mathcal{R}}_0^h=0.096\ll 1$. The curves of the exposed, infected, and treated compartments remain consistently at negligible, if not zero, levels. The human population remains mostly, if not entirely, in the susceptible ($S_h$) or immune ($R_h$) compartment, confirming that the best strategy to protect humans is to massively vaccinate dogs and reduce their mobility.

These results highlight the critical relationship between disease control in the animal reservoir (the dog) and the risk to human health. They emphasize the importance of maintaining sufficient canine vaccination coverage to ensure that ${\mathcal{R}}_0^c$ remains sustainably below 1, in order to prevent both canine epidemics and human rabies cases.

7. Conclusions

This study developed and analyzed a metapopulation-type mathematical model for canine and human rabies dynamics in a cross-border context. The theoretical analysis allowed determination of the basic reproduction number, ${\mathcal{R}}_0$, whose threshold value of 1 governs the stability of the disease-free equilibrium. The results rigorously demonstrate that this equilibrium is locally and globally asymptotically stable when ${\mathcal{R}}_0<1$, guaranteeing epidemic extinction, and unstable otherwise, leading to persistent endemicity. Sensitivity analysis identified the parameters most influential on ${\mathcal{R}}_0$, such as the inter-canine transmission rate (${\beta }_{cc}$) and the vaccination rate (${\nu }_c$), thus providing priority targets for intervention strategies.

Numerical simulations concretely illustrated the crucial impact of canine vaccination and canine mobility. Insufficient vaccination coverage, leading to ${\mathcal{R}}_0>1$, results in an explosive epidemic in the canine population, which immediately translates into an increased risk of transmission to humans. Conversely, vaccination coverage exceeding the critical threshold, ensuring ${\mathcal{R}}_0<1$, effectively extinguishes transmission in both dogs and humans. Our results emphasize that without coordinated management of canine mobility, even the highest local vaccination coverages cannot guarantee elimination. Mobility is not an accessory factor but the cornerstone of any sustainable eradication strategy to achieve the global goal of “Zero human dog-mediated rabies deaths by 2030”.