Optimal Strategies for Interval Economic Order Quantity (IEOQ) Model with Hybrid Price-Dependent Demand via C-U Optimization Technique
Abstract
1. Introduction
- It proposes an interval EOQ (IEOQ) framework in parametric form for perishable goods where demand rate is an interval-valued function which is the hybridization of linear and power pattern functions of selling price.
- The model uniquely combines advanced payment, preservation technology, and fixed discount facilities with interval uncertainty, an aspect not jointly addressed in earlier research.
- Unlike most existing works, the holding cost per unit is assumed to vary linearly with stock levels in an interval environment, capturing a more realistic cost structure.
- The work employs interval differential equations, interval parametric mathematics to obtain the interval-valued average profit and solves it using interval order relation-based optimization technique.
- The notable novel contribution of this work is the introduction of a new interval optimization technique named the C-U optimization technique to maximize interval-valued average profit.
2. Defining the Problem, Assumptions, and Notation
2.1. Problem Definition
2.2. Notation
2.3. Assumptions
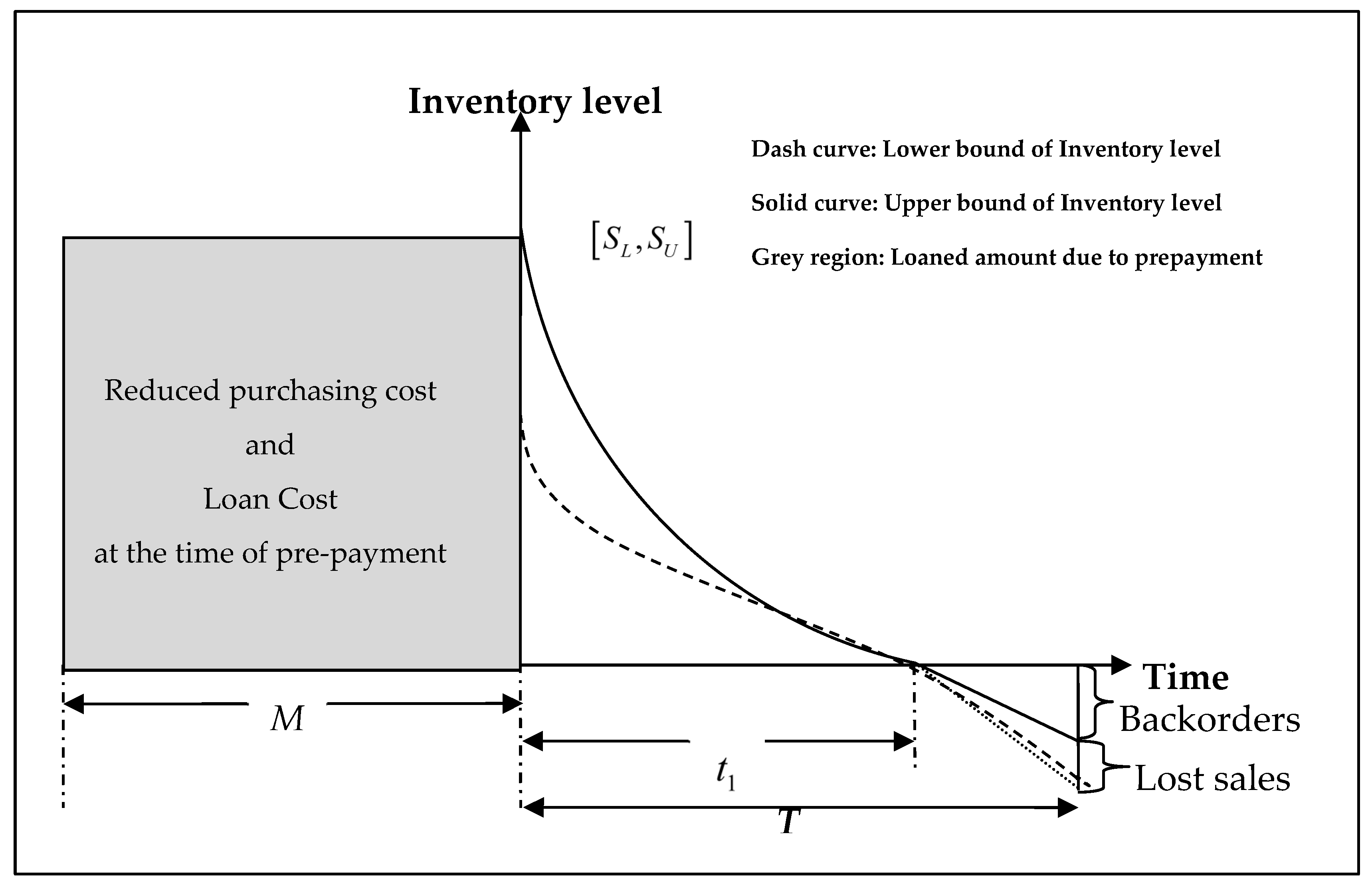
- The developed EOQ model pertains to a solitary deteriorating product with interval-valued demand rate, which is a convex combination of nonlinear and linear functions of price. The mathematical representation of the demand pattern is provided as follows: , be the parameter of convex combination.
- The bounds of the interval-valued deterioration rate, are constants and depend on the stock amount.
- Preservation technology is applied with an exponential interval-valued rate
- The replenishment rate is infinite, and the lead time remains constant.
- The inventory system’s total planning horizon extends infinitely.
- In this model, advanced payment with a discount facility is incorporated. Here, the buyer is required to settle the purchasing cost at time prior to product receipt. As a benefit, they are entitled to receive an imprecise percentage discount on the total purchasing cost. However, if the buyer prepays only a fraction of the total purchasing cost, the discount given upon receiving the goods will be less than the discount for full prepayment, and the remaining balance will be paid at that time.
- Shortages are permitted and have a constant backlogging rate
3. Model Formulation
- where
- respectively
- (a)
- Ordering cost:
- (b)
- Purchasing cost is given below:
- (c)
- Holding cost in parametric form is given by
- (d)
- Holding cost in parametric form is given by
- (e)
- Cost of loan:
- (f)
- Shortage cost in parametric form is
- (g)
- Opportunity cost in parametric form is given below:
- (h)
- Preservation technology cost is
- (i)
- Sales revenue is
4. Solution Methodology
4.1. Essential Definitions
- i
- ii
4.2. C-U Optimization Approach
- where
4.3. Computational Procedure
5. Numerical Examples
5.1. Materials and Data
- Interval-valued data (Example 1)—representing imprecise and uncertain real-world conditions.
- Degenerate interval data (Example 2)—representing fixed values that fall within the bounds of Example 1, serving as a benchmark deterministic case.
- Example 1.
- Initial customer’s demand ranges between 300 and 324 units for linear part of demand and ranges between 295 and 305 units for nonlinear part of demand. The other price sensitive parameters vary in the range of 0.1–0.3 for linear part and pricing power sensitivity is 0.5 for nonlinear part.
- The product deteriorates at about 14–16%, but preservation technology can reduce this by half with preservation cost $0.1–0.3.
- Each order costs about $348–352, and purchasing cost per unit is $14–16.
- Holding inventory costs $3–5 per unit per time, shortages cost $3.5 per unit per time, and deterioration costs $0.04–0.06 per unit per time.
- Bulk discounts from suppliers vary between 3 and 7%.
- Opportunity cost is $0.8–1.2 per unit per time, and loan cost is $0.3–0.5 per time unit.
- The selling price is $55 per unit.
- Solution.
- Example 2.
5.2. Discussions and Findings
5.3. Comparative Discussions with Previous Studies
- Khan et al. [13] analyzed advance payment with discount facility for deteriorating items, showing that advance payment provides liquidity benefits and positively affects ordering decisions. Our results align with this but go further by embedding advance payment into an interval framework, demonstrating through numerical evidence that concavity of profit still holds under uncertainty.
- Rahman et al. [6] proposed a hybrid price–stock-dependent model with advance payment and preservation. Their study highlighted that combining preservation technology with advance payment yields higher profitability in perishable goods. Our results strengthen this conclusion by showing, through Example 2, that even under degenerate intervals, preservation with prepayment policies secures optimal profit stability.
- Yadav et al. [40] considered interval number approaches for two warehouse-deteriorating items with preservation investment. Their results indicated that preservation effort reduces losses and enhances profit, but their framework did not integrate payment policies. Our results extend this by showing that preservation with payment flexibility in an interval environment further stabilizes profit outcomes, as evident from the concave optimal solutions in Examples 1 and 2.
- Time-based variables: and are measured in time units (months);
- Stock variables: and are measured in units of product (Quintal);
- Profit function: is measured in $/unit
6. Sensitivity Analysis
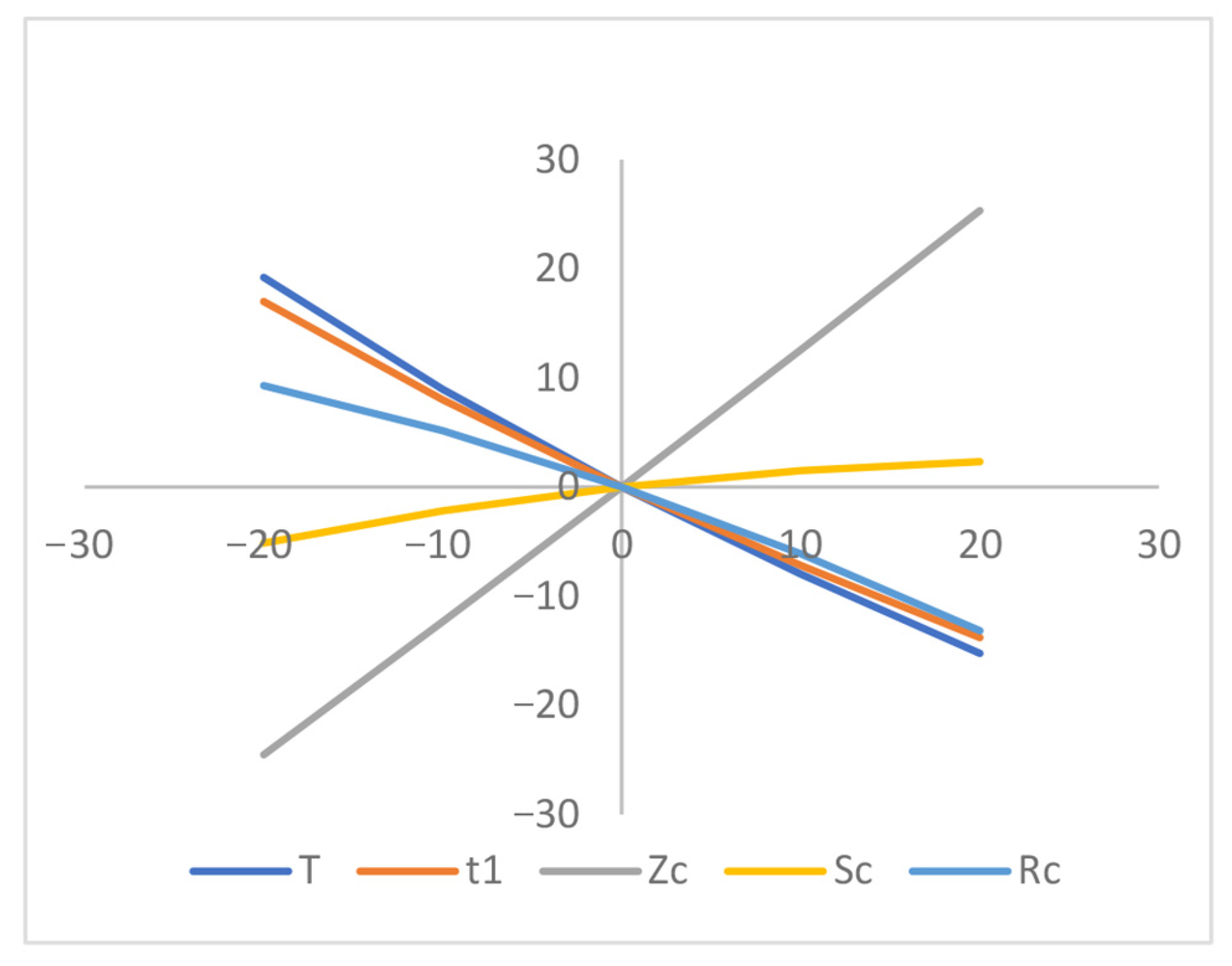
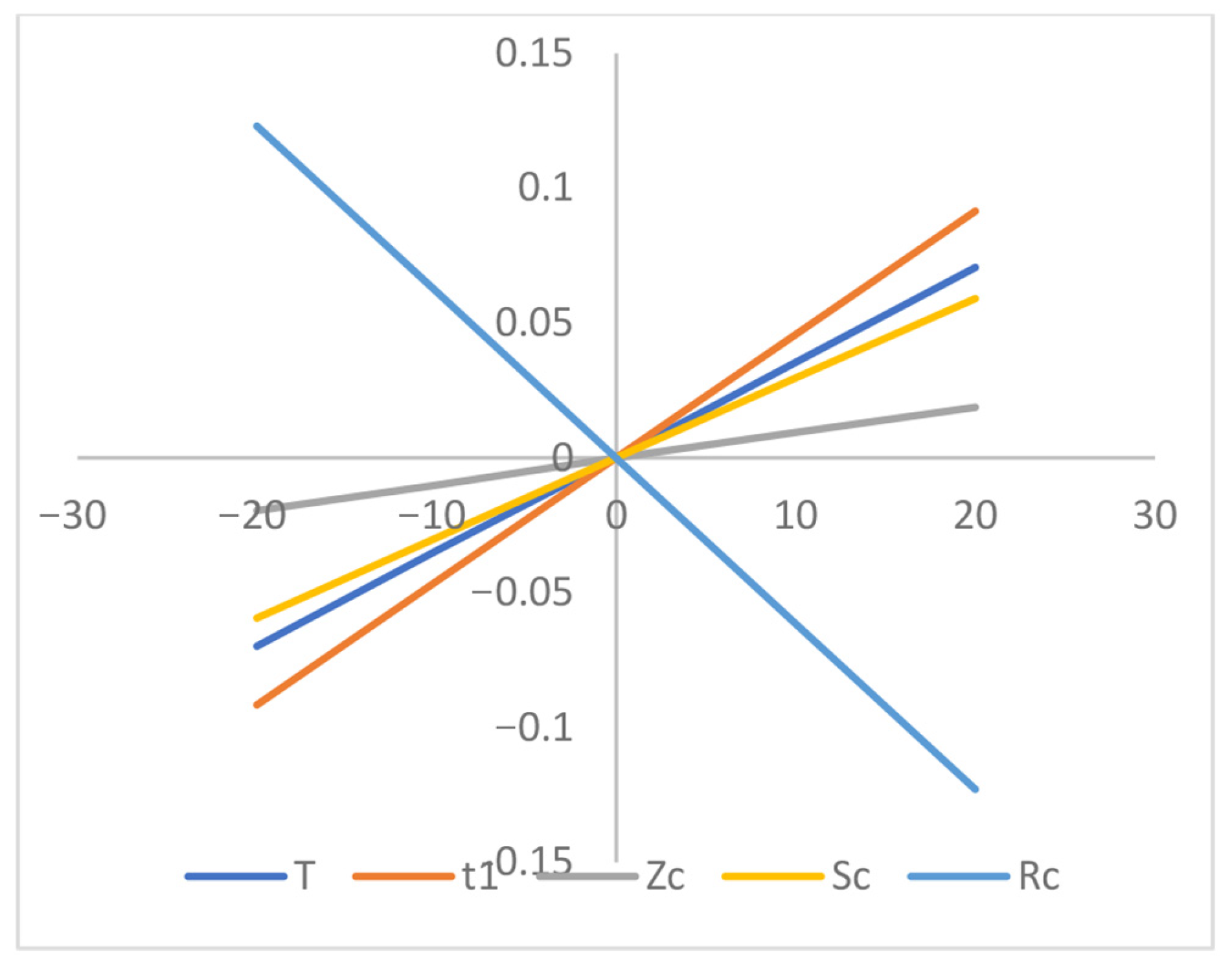
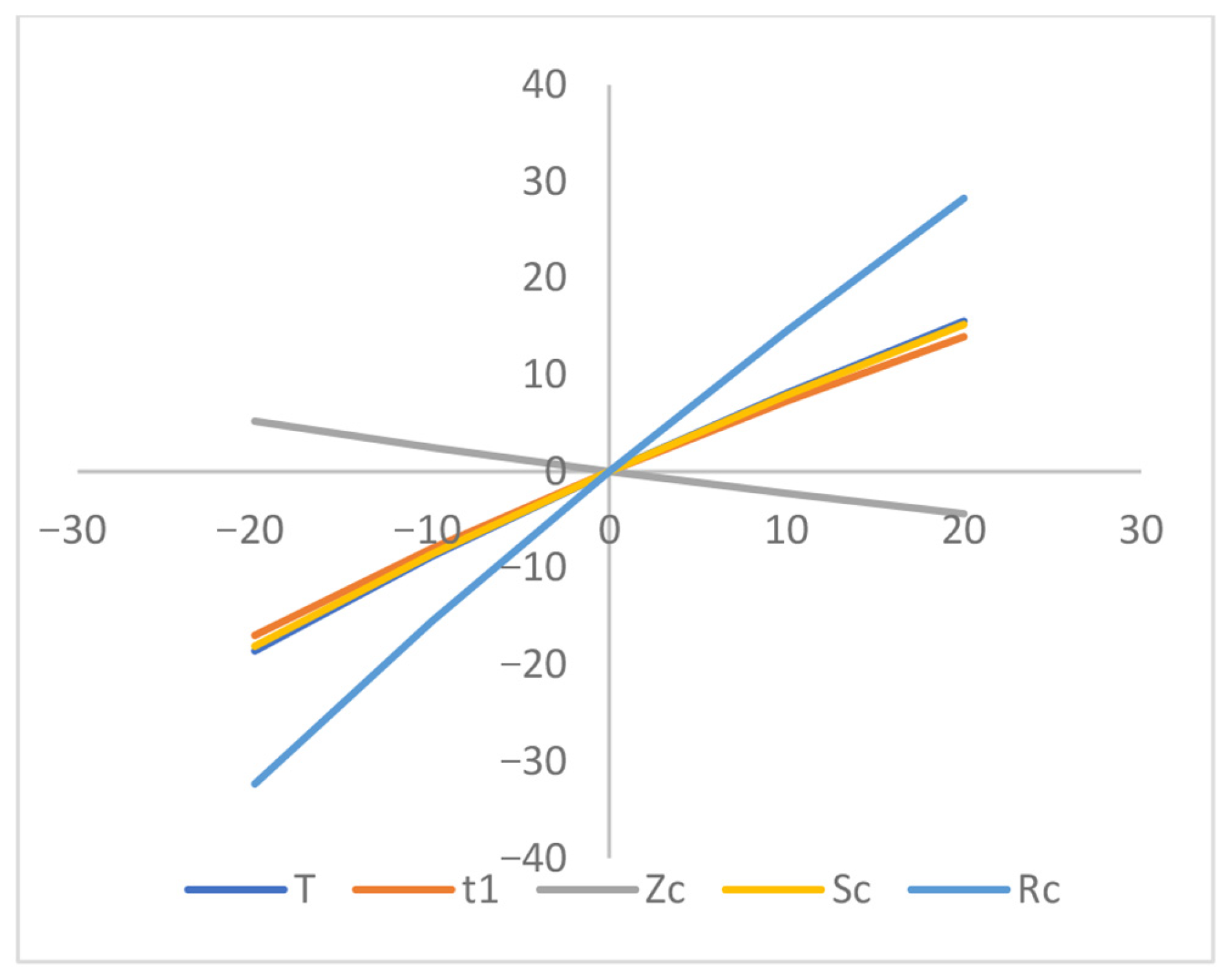
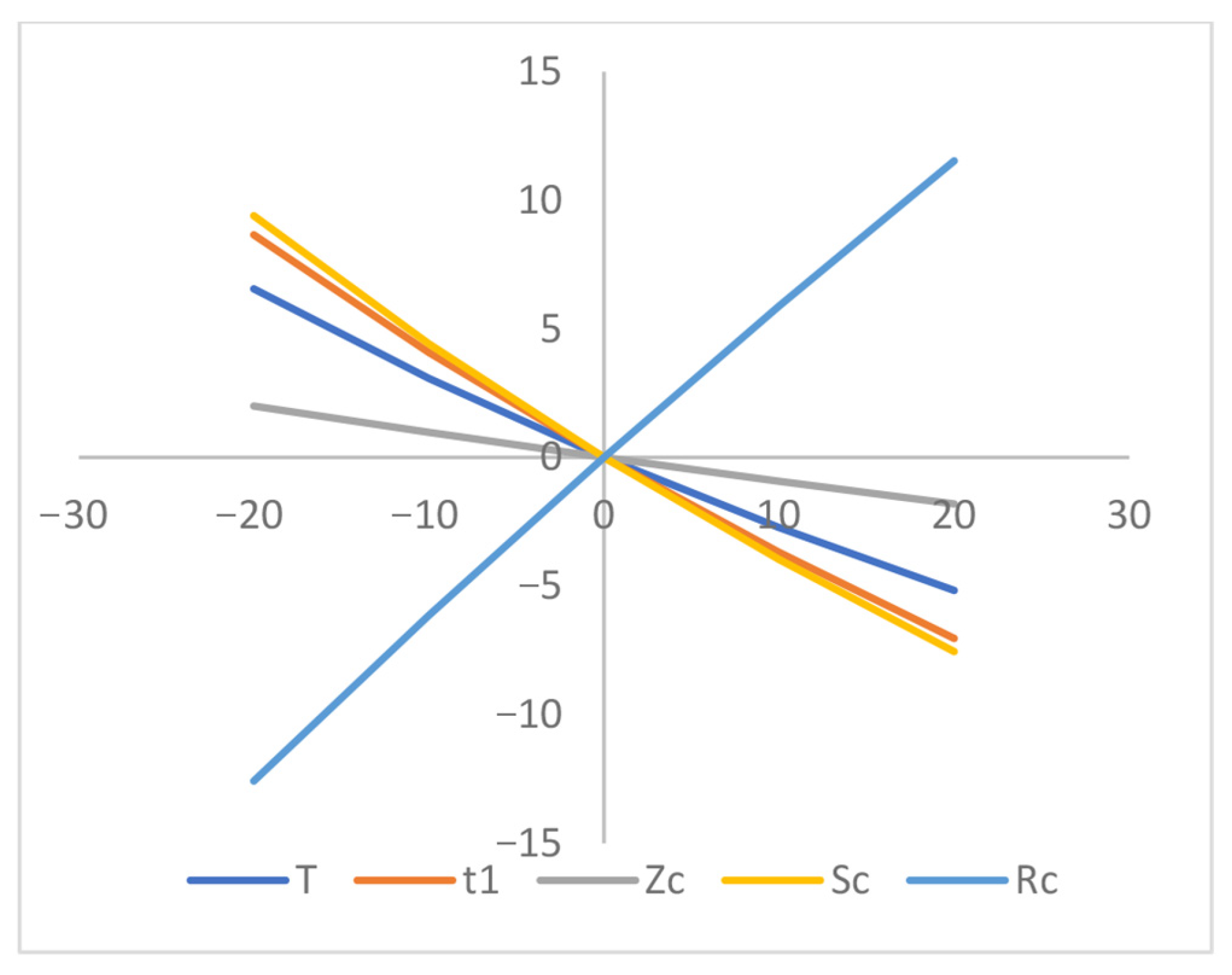
- Based on the sensitivity analyses depicted in Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12, the center of the average profit () exhibits high sensitivity with respect to p, , . However, the parameter demonstrates a reverse effect compared to parameter. Alternatively it shows less sensitivity to , , and , whereas it demonstrates insensitivity to changes in ‘’ and ‘’.
- Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12 illustrate that the business length () and the maximum shortage level, are highly sensitive . Both and demonstrate nearly equal sensitivity to and , respectively. Additionally, both and exhibit lower sensitivity to p, ) and , but parameters and show a reverse effect. Furthermore, both and are insensitive to positive or negative changes in ‘’, ‘’ and ‘, respectively.
- The maximum interval-valued shortage level () is heavily sensitive with the changes of ‘’, ‘’ and ‘p’ and it is slightly affected with respect to ‘’, ‘’ and ‘’, respectively. The shortage level () is much less sensitive with respect to ‘’, whereas ‘’ is insensitive with the changes in preservation rate parameter ‘’.
7. Managerial Insights
- Identify uncertain inputs (demand rate, deterioration rate, inventory cost, discount, etc.) and define their lower and upper bounds.
- Formulate the IEOQ model using interval differential equations and interval parametric approach.
- Apply the C–U optimization to obtain optimal order quantity, cycle time, and profit interval.
- Interpret the results—the center value gives expected profit, and the upper bound indicates the best outcome.
- Use sensitivity analysis to see how changes in key factors affect profit and policy decisions.
8. Concluding Remarks
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Arithmetic of Intervals
- (ii)
- (Increasing representation or IR),
- (ii)
- (Decreasing representation or DR).
Appendix A.2. Parametric Representation of Interval-Valued Function
- where
References
- Tayal, S.; Singh, S.R.; Sharma, R.; Chauhan, A. Two echelon supply chain model for deteriorating items with effective investment in preservation technology. Int. J. Math. Oper. Res. 2014, 6, 84–105. [Google Scholar] [CrossRef]
- Dye, C.Y.; Yang, C.T. Optimal dynamic pricing and preservation technology investment for deteriorating products with reference price effects. Omega 2016, 62, 52–67. [Google Scholar] [CrossRef]
- Panda, G.C.; Khan, M.A.A.; Shaikh, A.A. A credit policy approach in a two-warehouse inventory model for deteriorating items with price-and stock-dependent demand under partial backlogging. J. Ind. Eng. Int. 2019, 15, 147–170. [Google Scholar] [CrossRef]
- Adak, S.; Mahapatra, G.S. Effect of reliability on multi-item inventory system with shortages and partial backlog incorporating time dependent demand and deterioration. Ann. Oper. Res. 2020, 315, 1551–1571. [Google Scholar] [CrossRef]
- San-José, L.A.; Sicilia, J.; González-De-la-Rosa, M.; Febles-Acosta, J. Optimal inventory policy under power demand pattern and partial backlogging. Appl. Math. Model. 2017, 46, 618–630. [Google Scholar] [CrossRef]
- Rahman, M.S.; Khan, M.A.A.; Halim, M.A.; Nofal, T.A.; Shaikh, A.A.; Mahmoud, E.E. Hybrid price and stock dependent inventory model for perishable goods with advance payment related discount facilities under preservation technology. Alex. Eng. J. 2021, 60, 3455–3465. [Google Scholar] [CrossRef]
- Xu, C.; Zhao, D.; Min, J.; Hao, J. An inventory model for nonperishable items with warehouse mode selection and partial backlogging under trapezoidal-type demand. J. Oper. Res. Soc. 2020, 72, 744–763. [Google Scholar] [CrossRef]
- Karmakar, B. Inventory models with ramp-type demand for deteriorating items with partial backlogging and time-varing holding cost. Yugosl. J. Oper. Res. 2016, 24, 249–266. [Google Scholar] [CrossRef]
- Yadav, A.S.; Swami, A. A partial backlogging production-inventory lot-size model with time-varying holding cost and Weibull deterioration. Int. J. Procure. Manag. 2018, 11, 639–649. [Google Scholar]
- Soto, A.V.; Chowdhury, N.T.; Allahyari, M.Z.; Azab, A.; Baki, M.F. Mathematical modeling and hybridized evolutionary LP local search method for lot-sizing with supplier selection, inventory shortage, and quantity discounts. Comput. Ind. Eng. 2017, 109, 96–112. [Google Scholar] [CrossRef]
- Taleizadeh, A.A. Lot-sizing model with advance payment pricing and disruption in supply under planned partial backordering. Int. Trans. Oper. Res. 2017, 24, 783–800. [Google Scholar] [CrossRef]
- Shaikh, A.A.; Das, S.C.; Bhunia, A.K.; Panda, G.C.; Khan, M.A.A. A two-warehouse EOQ model with interval-valued inventory cost and advance payment for deteriorating item under particle swarm optimization. Soft Comput. 2019, 23, 13531–13546. [Google Scholar] [CrossRef]
- Khan, M.A.A.; Shaikh, A.A.; Panda, G.C.; Konstantaras, I.; Cárdenas-Barrón, L.E. The effect of advance payment with discount facility on supply decisions of deteriorating products whose demand is both price and stock dependent. Int. Trans. Oper. Res. 2020, 27, 1343–1367. [Google Scholar] [CrossRef]
- Taleizadeh, A.A.; Zarei, H.R.; Sarker, B.R. An optimal control of inventory under probablistic replenishment intervals and known price increase. Eur. J. Oper. Res. 2017, 257, 777–791. [Google Scholar] [CrossRef]
- Mondal, R.; Shaikh, A.A.; Bhunia, A.K. Crisp and interval inventory models for ameliorating item with Weibull distributed amelioration and deterioration via different variants of quantum behaved particle swarm optimization-based techniques. Math. Comput. Model. Dyn. Syst. 2019, 25, 602–626. [Google Scholar] [CrossRef]
- Rahaman, M.; Alam, S.; Alamin, A.; Mondal, S.P.; Singh, P. An application of intuitionistic fuzzy differential equation to the inventory model. In Fuzzy Optimization, Decision-Making and Operations Research: Theory and Applications; Springer International Publishing: Cham, Switzerland, 2023; pp. 679–702. [Google Scholar]
- Sadeghi, J.; Mousavi, S.M.; Niaki, S.T.A. Optimizing an inventory model with fuzzy demand, backordering, and discount using a hybrid imperialist competitive algorithm. Appl. Math. Model. 2016, 40, 7318–7335. [Google Scholar] [CrossRef]
- Ghorabaee, M.K.; Amiri, M.; Zavadskas, E.K.; Turskis, Z.; Antucheviciene, J. A new multi-criteria model based on interval type-2 fuzzy sets and EDAS method for supplier evaluation and order allocation with environmental considerations. Comput. Ind. Eng. 2017, 112, 156–174. [Google Scholar] [CrossRef]
- Mondal, S.P. Solution of Basic Inventory Model in Fuzzy and Interval Environments: Fuzzy and Interval Differential Equation Approach. In Handbook of Research on Fuzzy and Rough Set Theory in Organizational Decision Making; IGI Global: Hershey, PA, USA, 2017; pp. 65–95. [Google Scholar]
- Shaikh, A.A.; Bhunia, A.K.; Cárdenas-Barrón, L.E.; Sahoo, L.; Tiwari, S. A fuzzy inventory model for a deteriorating item with variable demand, permissible delay in payments and partial backlogging with shortage follows inventory (SFI) policy. Int. J. Fuzzy Syst. 2018, 20, 1606–1623. [Google Scholar] [CrossRef]
- Bhunia, A.K.; Shaikh, A.A. Investigation of two-warehouse inventory problems in interval environment under inflation via particle swarm optimization. Math. Comput. Model. Dyn. Syst. 2016, 22, 160–179. [Google Scholar] [CrossRef]
- Bhunia, A.K.; Shaikh, A.A.; Cárdenas-Barrón, L.E. A partially integrated production-inventory model with interval-valued inventory costs, variable demand and flexible reliability. Appl. Soft Comput. 2017, 55, 491–502. [Google Scholar] [CrossRef]
- Kumar, P.; Keerthika, P.S. An inventory model with variable holding cost and partial backlogging under interval uncertainty: Global criteria method. Int. J. Mech. Eng. Technol. 2018, 9, 1567–1578. [Google Scholar]
- Ruidas, S.; Seikh, M.R.; Nayak, P.K.; Sarkar, B. A single period production inventory model in interval environment with price revision. Int. J. Appl. Comput. Math. 2019, 5, 7. [Google Scholar] [CrossRef]
- Shaikh, A.A.; Cárdenas-Barrón, L.E.; Tiwari, S. A two-warehouse inventory model for non-instantaneous deteriorating items with interval-valued inventory costs and stock-dependent demand under inflationary conditions. Neural Comput. Appl. 2019, 31, 1931–1948. [Google Scholar] [CrossRef]
- Rahman, M.S.; Duary, A.; Shaikh, A.A.; Bhunia, A.K. An application of parametric approach for interval differential equation in inventory model for deteriorating items with selling-price-dependent demand. Neural Comput. Appl. 2020, 32, 14069–14085. [Google Scholar] [CrossRef]
- Rahman, M.S.; Manna, A.K.; Shaikh, A.A.; Bhunia, A.K. An application of interval differential equation on a production inventory model with interval-valued demand via center-radius optimization technique and particle swarm optimization. Int. J. Intell. Syst. 2020, 35, 1280–1326. [Google Scholar] [CrossRef]
- Rahman, M.S.; Duary, A.; Khan, M.A.A.; Shaikh, A.A.; Bhunia, A.K. Interval-valued demand related inventory model under all units discount facility and deterioration via parametric approach. Artif. Intell. Rev. 2022, 55, 2455–2494. [Google Scholar] [CrossRef]
- Cuevas, E.; Rodríguez, A.; Alejo-Reyes, A.; Del-Valle-Soto, C. Metaheuristic Algorithms Applied to the Inventory Problem. In Recent Metaheuristic Computation Schemes in Engineering; Springer International Publishing: Cham, Switzerland, 2021; pp. 237–277. [Google Scholar]
- Sajadi, S.J.; Ahmadi, A. An integrated optimization model and metaheuristics for assortment planning, shelf space allocation, and inventory management of perishable products: A real application. PLoS ONE 2022, 17, e0264186. [Google Scholar] [CrossRef]
- Huang, B. Metaheuristic-Based Supply Chain Network Optimization and Inventory Management Using Ant Colony Algorithm. Informatica 2025, 49, 17–32. [Google Scholar] [CrossRef]
- de Paula Vidal, G.H.; Caiado, R.G.G.; Scavarda, L.F.; Ivson, P.; Garza-Reyes, J.A. Decision support framework for inventory management combining fuzzy multicriteria methods, genetic algorithm, and artificial neural network. Comput. Ind. Eng. 2022, 174, 108777. [Google Scholar] [CrossRef]
- Saha, C.; Jana, D.K.; Duary, A. Enhancing production inventory management for imperfect items using fuzzy optimization strategies and Differential Evolution (DE) algorithms. Frankl. Open 2023, 5, 100051. [Google Scholar] [CrossRef]
- Manna, A.K.; Bhunia, A.K. Investigation of green production inventory problem with selling price and green level sensitive interval-valued demand via different metaheuristic algorithms. Soft Comput. 2022, 26, 10409–10421. [Google Scholar] [CrossRef]
- Duary, A.; Rahman, M.S.; Manna, A.K.; Shaikh, A.A. Optimal policy of an interval production problem with variable demand and warranty policy via 0 _ 1 parametrized optimization technique. Int. J. Syst. Assur. Eng. Manag. 2025, 16, 2967–2982. [Google Scholar] [CrossRef]
- Mashud, A.H.M.; Wee, H.M.; Sarkar, B.; Li, Y.H.C. A sustainable inventory system with the advanced payment policy and trade-credit strategy for a two-warehouse inventory system. Kybernetes 2020, 50, 1321–1348. [Google Scholar] [CrossRef]
- Saren, S.; Sarkar, B.; Bachar, R.K. Application of various price-discount policy for deteriorated products and delay-in-payments in an advanced inventory model. Inventions 2020, 5, 50. [Google Scholar] [CrossRef]
- Mondal, R.; Das, S.; Das, S.C.; Shaikh, A.A.; Bhunia, A.K. Pricing strategies and advance payment-based inventory model with partially backlogged shortages under interval uncertainty. Int. J. Syst. Sci. Oper. Logist. 2023, 10, 2070296. [Google Scholar] [CrossRef]
- Akhtar, F.; Khan, M.A.A.; Shaikh, A.A.; Alrasheedi, A.F. Interval-valued inventory model for deterioration, carbon emissions and selling price dependent demand considering buy now and pay later facility. Ain Shams Eng. J. 2024, 15, 102563. [Google Scholar] [CrossRef]
- Yadav, K.K.; Yadav, A.S.; Bansal, S. Interval number approach for two-warehouse inventory management of deteriorating items with preservation technology investment using analytical optimization methods. Int. J. Interact. Des. Manuf. (IJIDeM) 2024, 1–17. [Google Scholar] [CrossRef]
- Ramezanadeh, M.; Heidari, M.; Fard, O.S.; Borzabadi, A.H. On the interval differential equation: Novel solution methodology. Adv. Differ. Equ. 2015, 2015, 338. [Google Scholar] [CrossRef]







| Related Works | Demand | Discount Policy | Advanced Payment | Preservation Technology | Backlogging | Governing Differential Equations | Solution Procedure |
|---|---|---|---|---|---|---|---|
| Dye and Yang [1] | variable | No | No | Yes | No | Crisp | Analytically |
| Shaikh et al. [20] | variable | No | No | No | Yes | Fuzzy | Analytically |
| Shaikh et al. [25] | variable | No | Yes | No | No | Interval | PSO |
| Mashud et al. [36] | variable | No | Yes | No | No | Crisp | Analytically/Numerically |
| Saren et al. [37] | variable | Yes | No | No | No | Crisp | Analytically |
| Rahman et al. [26] | Interval-valued and price-dependent | No | No | No | No | Interval | QPSO |
| Mondal et al. [38] | Interval-valued and price-dependent | No | Yes | No | Yes | Interval | Soft-computing |
| Akhtar et al. [39] | Interval-valued and price | No | No | No | Yes | Interval | Soft-computing |
| Yadav et al. [40] | time | No | No | Yes | Yes | Interval | Analytical |
| Symbols | Units | Descriptions |
|---|---|---|
| Units | Interval-valued inventory level where | |
| Units | Interval-valued inventory level t where | |
| Per units | Interval-valued demand rate | |
| Units | Interval-valued order size per cycle | |
| Units | Interval-valued highest stock level | |
| Units | Interval-valued maximum shortages level | |
| Constant | Interval-valued deterioration rate | |
| Constant | Interval-valued backlogging rate | |
| Time unit | Prepayment period | |
| Units | Interval-valued parameters in linear part of demand | |
| Units | Interval-valued parameters in nonlinear part of demand | |
| Units | Preservation technology scaling parameter | |
| % | Interval-valued percentage discount applied to the total purchasing cost | |
| $/order | Interval-valued restocking cost | |
| $/unit | Interval-valued purchasing cost | |
| $/unit/time unit | Parameters of interval-valued holding cost | |
| $/unit/time unit | Interval-valued shortages cost | |
| $/unit | Interval-valued deterioration cost | |
| $/unit | Interval-valued opportunity cost | |
| $/time unit | Interval-valued cost of loan rate | |
| $/time unit | Interval-valued the total cost | |
| $/unit | Interval-valued preservation cost | |
| $/unit | Selling price | |
| Decision variables | ||
| Time unit | Stock-in time | |
| T | Time unit | Business cycle |
| Variables | C-U Optimal Values |
|---|---|
| 1.12016 | |
| 0.895745 | |
| [459.324, 1827.99] | |
| [32.4868, 46.1317] | |
| [5.75245, 11.2361] |
| Variables | C-U Optimal Values |
|---|---|
| 1.15994 | |
| 1.04871 | |
| [1278.96, 1278.96] | |
| [45.8497, 45.8497] | |
| [4.22362, 4.22362] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rahman, M.S. Optimal Strategies for Interval Economic Order Quantity (IEOQ) Model with Hybrid Price-Dependent Demand via C-U Optimization Technique. AppliedMath 2025, 5, 151. https://doi.org/10.3390/appliedmath5040151
Rahman MS. Optimal Strategies for Interval Economic Order Quantity (IEOQ) Model with Hybrid Price-Dependent Demand via C-U Optimization Technique. AppliedMath. 2025; 5(4):151. https://doi.org/10.3390/appliedmath5040151
Chicago/Turabian StyleRahman, Md Sadikur. 2025. "Optimal Strategies for Interval Economic Order Quantity (IEOQ) Model with Hybrid Price-Dependent Demand via C-U Optimization Technique" AppliedMath 5, no. 4: 151. https://doi.org/10.3390/appliedmath5040151
APA StyleRahman, M. S. (2025). Optimal Strategies for Interval Economic Order Quantity (IEOQ) Model with Hybrid Price-Dependent Demand via C-U Optimization Technique. AppliedMath, 5(4), 151. https://doi.org/10.3390/appliedmath5040151





