Self-Organized Criticality and Quantum Coherence in Tubulin Networks Under the Orch-OR Theory

Abstract

We present a theoretical model to explain how tubulin dimers in neuronal microtubules might achieve collective quantum coherence, resulting in wavefunction collapses that manifest as avalanches within a self-organized criticality (SOC) framework. Using the Orchestrated Objective Reduction (Orch-OR) theory as inspiration, we propose that microtubule subunits (tubulins) become transiently entangled via dipole–dipole couplings, forming coherent domains susceptible to sudden self-collapse. We model a network of tubulin-like nodes with scale-free (Barabási–Albert) connectivity, each evolving via local coupling and stochastic noise. Near criticality, the system exhibits power-law avalanches—abrupt collective state changes that we identify with instantaneous quantum wavefunction collapse events. Using the Diósi–Penrose gravitational self-energy formula, we estimate objective reduction times $T_{\mathrm{OR}}=\hslash /E_g$ for these events in the 10–200 ms range, consistent with the Orch-OR conscious moment timescale. Our results demonstrate that quantum coherence at the tubulin level can be amplified by scale-free critical dynamics, providing a possible bridge between sub-neuronal quantum processes and large-scale neural activity.

1. Introduction

Over the last few decades, growing evidence has pointed to non-trivial quantum processes in biological systems, from photosynthetic complexes to avian magnetoreception [1]. In the realm of neuroscience, several theories have posited that quantum phenomena might underlie consciousness. Notably, Penrose and Hameroff proposed the Orchestrated Objective Reduction (Orch-OR) theory, which suggests that quantum computations in cytoskeletal microtubules within neurons could be integral to conscious brain function [2,3,4]. (Penrose had earlier argued that consciousness may involve non-computable physics related to quantum gravity [5] Microtubules—hollow biopolymers of $\alpha$–$\beta$ tubulin dimers—provide structural scaffolding in cells; in neurons they are abundant and stable, particularly in dendrites and axons [6]. Beyond structural roles, a tubulin dimer contains arrays of aromatic amino acids (e.g., tryptophan; phenylalanine) in hydrophobic pockets, capable of supporting London force dipole oscillations or other quantum dipole interactions [7,8]. These dipoles can become phase-correlated under certain conditions, potentially enabling a form of coherent quantum state spread over many tubulins. Indeed, experimental studies have indicated that collections of tubulin or tryptophan dipoles can exhibit collective oscillations (e.g., super-radiant electromagnetic emissions) suggestive of coherent behavior [8,9,10].

In the Orch-OR framework, the process is envisioned as follows:

(i)  

Tubulin dimers transiently enter entangled or phase-coherent states via resonant dipole–dipole couplings (such as van der Waals London forces or Frohlich-type collective vibrations).

(ii) 

These coherent states can encompass a significant segment of a microtubule (tens to hundreds of tubulins) and are conjectured to persist for tens of milliseconds, aided by protective mechanisms in the cell [4,11].

(iii)

Eventually, the coherent superposition reaches a threshold and undergoes abrupt objective reduction (collapse), selecting a definite classical state from the quantum possibilities. According to Orch-OR, each such collapse corresponds to a discrete “occasion of experience” or proto-conscious event in the brain [2,4]. The suggested timescale for such events is on the order of 10–200 ms, which coincides with neurophysiological rhythms (e.g., $\gamma$-oscillation cycles and integrative brain processing times) [2,4].

Penrose and Diósi independently proposed that spontaneous wavefunction collapse (“objective reduction,” OR) could result from quantum superpositions that differ in mass distribution and thus create distinct spacetime curvatures [3,12]. In brief, if a mass m is in a superposition of two locations separated by a distance, the discrepancy in their gravitational fields contributes a self-energy $E_g$. When $E_g$ grows large enough, the superposed state becomes untenable in a single spacetime geometry, and an OR (collapse) occurs spontaneously after a characteristic time $T_{\mathrm{OR}}\approx \hslash /E_g$ [3,12]. Orch-OR applies this idea to the brain: it postulates that if a sufficient number of tubulins S become entangled in a joint superposition, the gravitational self-energy $E_g$ of that state will cause a collapse on a timescale $T_{\mathrm{OR}}$ matching cognitive events [2,3,4]. Typically, to obtain $T_{\mathrm{OR}}\sim 0.1$ s, one requires coherent tubulins on the order of $S\sim {10}^9$ (using estimates of single tubulin mass $m_{\mathrm{single}}\sim {10}^{-19}$ kg and a separation on the order of a few nanometers) [2,4].

A major challenge to Orch-OR and similar quantum mind hypotheses is the issue of decoherence in the warm, wet brain environment [13]. Skeptics argue that any quantum states in neurons would decohere far too quickly (e.g., ${10}^{-13}$ s by some estimates [13]) to be relevant. Proponents of Orch-OR counter that microtubules might have intrinsic features or supportive conditions (e.g., ordered water layers, isolation within non-polar pockets, or rapid error-correction via Frohlich coherence) that significantly prolong coherence times [4,11]. The debate remains active, with ongoing refinements to the theory and discussions in the literature [9,14]. Recent works have also explored alternative but related frameworks, such as electromagnetic field theories of consciousness or quantum-inspired models, indicating a broader interest in non-classical explanations of mind [14,15].

Independently, neuroscience research has revealed that the brain operates near a critical state. The concept of self-organized criticality (SOC) describes how certain complex systems naturally tune themselves to the brink of a phase transition, leading to scale-invariant fluctuations or avalanches [16]. In cortical networks, experiments have demonstrated neuronal avalanches: brief cascades of spiking activity that follow power-law size distributions, suggesting critical dynamics [17]. Such criticality is thought to optimize information processing and cognitive function by balancing order and variability. While critical phenomena have been widely studied at the level of neuronal circuits [17,18], it is intriguing to consider whether similar dynamics might occur at sub-neuronal scales (within cells).

In this work, we integrate the Orch-OR quantum collapse concept with a classical SOC network model. We propose that tubulin dipoles in microtubules form a scale-free interaction network operating near criticality. In this scenario, small local state changes can cascade into large-scale collective events or avalanches, which we associate with abrupt quantum wavefunction collapses (OR events). In essence, we treat each avalanche in the model as the physical manifestation of an Orch-OR collapse—a moment when a coherent tubulin state reduces to a classical outcome, presumably correlating with a primitive conscious moment. By simulating this model, we investigate how often such collapses might occur, how a large collection of tubulins can become entangled before collapse, and whether the emergent timescales align with known neurophysiological rhythms. The results suggest that quantum coherence at the tubulin level, rather than remaining isolated, could be amplified through critical network dynamics to influence neuronal-scale activity.

The rest of this paper is organized as follows. In Section 2 we describe the mathematical model of interacting tubulin dipoles and the network structure used. In Section 3 we formalize the correspondence between classical avalanches and quantum collapses and derive the gravitational OR timescale in terms of avalanche size. Section 4 provides further analytical insight into the model’s critical behavior (e.g., mean-field analysis and avalanche scaling exponents). In Section 5 we detail the computational implementation and parameter choices for simulations. Section 6 presents the simulation results, including avalanche size distributions and collapse time estimates. In Section 7, we discuss the implications of our findings, including how classical criticality and quantum coherence might intertwine, and suggest experimental tests. Additional mathematical justification of the results is given in Section 8. Finally, Section 9 summarizes our conclusions.

2. Description of the Model

We consider a network of N tubulin dimers (or small microtubule segments), each represented by a single dynamical variable. The network connectivity is taken to be scale-free, reflecting the possibility that tubulin interactions (via dipole couplings, for instance) might form a heterogeneous web rather than a regular lattice. In particular, we construct a Barabási–Albert (BA) network $G_{\mathrm{BA}}=(V,E)$ with $\left|V\right|=N$. The BA model uses preferential attachment to produce a power-law degree distribution [19]. Specifically, we start with a small fully connected seed of $m_{\ell }$ nodes and then add nodes one by one; each new node introduces $m_{\ell }$ edges attaching to existing nodes with probability proportional to their degree. This process yields a network where a few hubs have a very high degree while many nodes have a low degree, following $p\left(k\right)\sim k^{-\gamma }$ (with $\gamma \approx 3$ for large N) [19]. Scale-free networks are known to exhibit broad avalanche size distributions near criticality [18], making them suitable for our aims. In our implementation we use $N=2500$ and $m_{\ell }=3$, which produces an average degree $\langle k\rangle \approx 6$.

We assign each node i a state variable $x_i\left(t\right)\in \mathbb{R}$, representing the net dipole oscillation amplitude or a related order parameter indicating the degree of local quantum coherence of tubulin i [6,7]. The state $x_i\left(t\right)$ can be thought of as a coarse-grained measure of the tubulin’s configuration (e.g., electric polarization or conformational state) that is relevant to its quantum behavior. We model the time evolution in discrete time-steps $t\to t+1$ by a linear stochastic update rule:

$$x_i(t+1)=x_i\left(t\right)+\sum _{j\in \mathcal{N}\left(i\right)}{\alpha }_{ij}\left[x_j\left(t\right)-x_i\left(t\right)\right]+{\eta }_i\left(t\right),$$

(1)

where $\mathcal{N}\left(i\right)$ denotes the set of neighbor nodes of i in the network (i.e., those j for which $(i,j)\in E$). The coefficients ${\alpha }_{ij}\ge 0$ characterize the coupling strength between node i and j, and ${\eta }_i\left(t\right)$ is a noise term representing random fluctuations. Equation (1) is a simplified, mesoscopic surrogate for the complex quantum–mechanical interactions among tubulins. In an actual microtubule, neighboring tubulins may become quantum correlated through resonant electric dipole couplings or phonon-mediated interactions [8,11]. Here, the term ${\alpha }_{ij}[x_j-x_i]$ causes node i to partially align with neighbor j’s state, reflecting a tendency toward local synchronization (similar to a diffusion or consensus term). The random term ${\eta }_i\left(t\right)$ (taken to be Gaussian white noise) accounts for thermal perturbations and other sources of decoherence that drive the system stochastically. We emphasize that although each $x_i\left(t\right)$ is a classical variable in our simulation, its dynamics are intended to mimic the average effect of underlying quantum state evolutions. Parameters ${\alpha }_{ij}$ and $\sigma$ (the noise amplitude) effectively absorb many microscopic details, such as strength of dipolar forces, environmental damping, etc.

For convenience, we can rewrite the update rule in vector-matrix form. Let $\mathbf{x}\left(t\right)={[x_1\left(t\right),x_2\left(t\right),\dots ,x_N\left(t\right)]}^T$ be the state vector of all nodes. Define the coupling matrix $A=\left[{\alpha }_{ij}\right]$ where ${\alpha }_{ij}>0$ if nodes i and j are connected and 0 otherwise. In our model, we set

$${\alpha }_{ij}={\displaystyle \frac{{\alpha }_0}{\sqrt{k_i{k}_j}}}\hspace{1em}\mathrm{for}\mathrm{each}\mathrm{edge} (i,j)\in E,$$

where $k_i=\left|\mathcal{N}\left(i\right)\right|$ is the degree of node i, and ${\alpha }_0$ is a base coupling constant. This choice of ${\alpha }_{ij}$ (inversely proportional to the geometric mean of degrees) normalizes the influence so that hubs (high-degree nodes) do not overwhelm their many neighbors. We take ${\alpha }_0=0.06$ in our simulations. Let D be the diagonal matrix with entries $D_{ii}={\sum }_{j=1}^N{\alpha }_{ij}$ (the row-sum of A for node i). The update can then be expressed as follows:

$$\mathbf{x}(t+1)=\left(I-D+A\right)\mathbf{x}\left(t\right)+\mathit{\eta }\left(t\right),$$

where I is the $N\times N$ identity, and $\mathit{\eta }\left(t\right)$ is the noise vector with independent components ${\eta }_i\left(t\right)\sim \mathcal{N}(0,{\sigma }^2)$. In our simulations we choose $\sigma =0.015$ (so a typical noise-induced change in $x_i$ per step is on the order of ${10}^{-2}$ in the chosen units).

It is worth noting the form of the deterministic part of the update, $I-D+A$. This is analogous to a Laplacian dynamics on the network (since $D-A$ would be the graph Laplacian). In the absence of noise, $x_i$ evolves by averaging with its neighbors (with weight ${\alpha }_{ij}$) minus a term adjusting for the total coupling of node i. Such a system can exhibit rich behavior: for small ${\alpha }_0$ it will relax to a steady state (all $x_i$ equal), whereas for larger ${\alpha }_0$ it may oscillate or become unstable. In our case, we will be interested in the regime where the system hovers near instability, so that random fluctuations can occasionally trigger large cascades of activity.

3. Avalanches and Quantum Wavefunction Collapse

In studies of self-organized critical systems, an avalanche is a cascade of activity often defined by a threshold-crossing. We adopt a similar concept for our tubulin network model. At each time step t, we monitor the changes $\Delta x_i\left(t\right)=|x_i(t+1)-x_i\left(t\right)|$ for all nodes. If the maximum change ${max}_i\Delta x_i\left(t\right)$ exceeds a chosen threshold ${\Delta }_{\mathrm{th}}$, we say that an avalanche (at time t) has occurred. In other words, an avalanche event is marked by a sudden, significant jump in the state of at least one node (and typically many nodes, if the event is large). We set the threshold ${\Delta }_{\mathrm{th}}=0.1$ in our simulations, which is several times larger than the standard deviation of the noise, to filter out small fluctuations and pick up only the large, collective events.

The size S of an avalanche is defined as the number of nodes that changed by more than ${\Delta }_{\mathrm{th}}$ in that time step:

$$S\left(t\right)=\sum _{i=1}^N\Theta \left(\Delta x_i\left(t\right)-{\Delta }_{\mathrm{th}}\right),$$

where $\Theta (·)$ is the Heaviside step function (so $\Theta \left(z\right)=1$ if $z>0$ and 0 otherwise). Thus, $S\left(t\right)$ counts how many nodes participated in the large jump. An avalanche could be as small as $S=1$ (a single node had a big change) or as large as $S=N$ (every node jumped significantly). In critical systems, S often varies widely, with a power-law distribution indicating that there is no characteristic size (scale invariance) [16,17,18].

In our interpretation, each avalanche event is identified with a wavefunction collapse in the Orch-OR sense. In other words, the precise time at which the avalanche occurs corresponds to the moment a coherent quantum state in the microtubule network undergoes a rapid reduction to a classical state. The logic is as follows: when the tubulin variables are evolving mostly under the influence of their mutual couplings and noise, we can imagine the underlying quantum state is a superposition of many possible configurations. If a large, system-wide change happens (an avalanche), it indicates that the system has suddenly “picked” a new classical state among various possibilities—analogous to a wavefunction collapse selecting an outcome. As an illustrative paraphrase, “the moment at which the wavefunction collapses is precisely the avalanche event.” We emphasize that in the simulation we track only the classical variables $x_i\left(t\right)$, not a quantum wavefunction. However, by mapping avalanche dynamics onto the collapse hypothesis, we gain a quantitative handle on the collapse times and conditions.

Using the Diósi–Penrose framework [3,12], we can estimate the gravitational self-energy $E_g$ associated with a given avalanche and thus the OR collapse time $T_{\mathrm{OR}}$. Suppose an avalanche of size S involves S tubulin dimers that were in quantum superposition and then all S collapse to definite states. These S tubulins contribute an effective mass $m_{\mathrm{eff}}=S m_{\mathrm{single}}$ to the quantum state difference (where $m_{\mathrm{single}}$ is the mass of one tubulin dimer, $\sim 5\times {10}^{-20}$ kg). If the superposed mass distribution difference is characterized by a length scale d (roughly the spatial separation of the mass centroids between the two superposed states, perhaps on the order of the microtubule diameter $\sim {10}^{-8}$ m), the gravitational self-energy can be approximated as follows [3,12]:

$$E_g\approx {\displaystyle \frac{G{\left(m_{\mathrm{eff}}\right)}^2}{d}}={\displaystyle \frac{G{(S m_{\mathrm{single}})}^2}{d}},$$

(2)

where G is Newton’s gravitational constant. The corresponding objective reduction time is

$$T_{\mathrm{OR}}={\displaystyle \frac{\hslash }{E_g}}={\displaystyle \frac{\hslash d}{G{(S m_{\mathrm{single}})}^2}},$$

(3)

where ℏ is the reduced Planck constant. Crucially, $T_{\mathrm{OR}}$ decreases as $1/S^2$ with the number of tubulins S involved. Larger avalanches (which reflect larger coherent superpositions collapsing) yield very short $T_{\mathrm{OR}}$, meaning the collapse happens almost instantaneously on a neural timescale. Smaller avalanches (small S) would have longer collapse times, possibly so long that the coherence can sustain itself—although in practice, we expect the system will not remain poised indefinitely but will eventually either grow into a larger collapse or dissipate.

In our model, when we detect an avalanche and measure its size S, we can plug into Equation (3) to find the predicted collapse time. Orch-OR theory asserts that conscious events correspond to collapse times on the order of tens to a few hundred milliseconds [2,4]. It is reassuring, then, if our simulated avalanches typically produce $T_{\mathrm{OR}}$ in that ballpark. For instance, if S is on the order of ${10}^6$–${10}^7$, taking $m_{\mathrm{single}}=5\times {10}^{-20}$ kg and $d={10}^{-8}$ m, we obtain $T_{\mathrm{OR}}\sim {10}^{-1}$ s. Indeed, in the results we will see that the distribution of $T_{\mathrm{OR}}$ clusters around 20–200 ms for the avalanches that occur, matching the envisaged range for Orch-OR conscious moments.

To summarize, we have established a correspondence between classical avalanches in the tubulin network and quantum wavefunction collapses: each avalanche event is interpreted as the moment a quantum coherent state of many tubulins undergoes gravitational OR, resulting in a definite classical state (which then influences neural-level events, e.g., by altering synaptic strengths or neuronal firing). This provides a concrete way to connect the sub-neuronal quantum dynamics with physiological timescales and observables.

4. Analysis of Critical Dynamics in the Network

We now examine the model from a theoretical perspective to understand its propensity for self-organized criticality and how that relates to the wavefunction collapse events. First, consider a simplified mean-field treatment. If the network were fully homogeneous (which a BA network is not, but let us hypothesize locally average behavior), one might replace the individual $x_i$ with an average field $x\left(t\right)$. Ignoring noise, Equation (1) in a homogeneous k-regular network would yield the following:

$${\displaystyle \frac{dx}{dt}}\approx k {\alpha }_0(\overline{x}-x),$$

(4)

where $\overline{x}$ is the mean field (which would equal x in a symmetric state). Equation (4) suggests that if $k {\alpha }_0<1$, the homogeneous state is stable (x tends toward $\overline{x}$). However, if $k {\alpha }_0>1$, the system becomes linearly unstable to perturbations, meaning small fluctuations can grow. In networks poised near this instability, one often finds intermittent large events (avalanches) due to the system teetering between order and disorder [16,17]. In our chosen parameters, the average degree $\langle k\rangle \approx 6$ and ${\alpha }_0=0.06$, giving $\langle k\rangle {\alpha }_0\approx 0.36$. This naive calculation suggests the system is below the threshold of global instability. However, the heterogeneous degree distribution means local hubs with $k\gg \langle k\rangle$ effectively have a larger $\left(\mathrm{degree}\right)\times {\alpha }_0$ product, which can induce local “sparks” of instability that then propagate. The addition of noise $\sigma$ ensures the system is continually excited with small perturbations.

A hallmark of SOC is a power-law distribution of event sizes (here, avalanche sizes S) over many decades [16]. Generally, at criticality one expects

$$P\left(S\right)\sim S^{-\tau },$$

with the exponent $\tau$ depending on the system’s dimensionality and interaction rules. In neuronal cultures and networks, $\tau$ has been measured in the range 1.5–2.5 [17]. In our case of a BA network, which has a complex topology (effectively high-dimensional in terms of connectivity), the exponent can be larger. The heavy-tailed nature of the degree distribution often leads to a broader spread of avalanche sizes [18]. Simulations on random scale-free networks have found exponents $\tau$ around 2 to 3 in various models of SOC [18].

In the presence of noise, our model can exhibit a range of behaviors from subcritical (mostly small events, exponential cutoff in $P\left(S\right)$) to supercritical (system-spanning events dominating). By tuning parameters (like ${\alpha }_0$ or $\sigma$) we found that the system self-organizes to a point where $P\left(S\right)$ approximately follows a power-law over several decades of S. This indicates we are indeed observing SOC-like dynamics. We will present the measured avalanche distribution from our simulation in Section 6.

Let us connect these classical results to the quantum collapse considerations. If $P\left(S\right)\sim S^{-\tau }$ and avalanches occur episodically, then one can also derive the distribution of $T_{\mathrm{OR}}$ using Equation (3). Because $T_{\mathrm{OR}}\propto 1/S^2$, a power-law distribution of S will translate into a particular distribution for $T_{\mathrm{OR}}$. Specifically,

$$P\left(T_{\mathrm{OR}}\right)\sim P\left(S\right)\left|{\displaystyle \frac{dS}{d{T}_{\mathrm{OR}}}}\right|.$$

Using $T_{\mathrm{OR}}\propto S^{-2}$, we have $S\propto T_{\mathrm{OR}}^{-1/2}$, and $dS/d{T}_{\mathrm{OR}}\sim -\frac{1}{2}{T}_{\mathrm{OR}}^{-3/2}$. Therefore,

$$P\left(T_{\mathrm{OR}}\right)\sim T_{\mathrm{OR}}^{(\tau /2)-1}$$

for small $T_{\mathrm{OR}}$ (corresponding to large S). For $\tau >1$, this distribution is normalizable at $T_{\mathrm{OR}}\to 0$. If, for example, $\tau \approx 2$, then $P\left(T_{\mathrm{OR}}\right)$ would be roughly flat (exponent $\sim 0$) for short $T_{\mathrm{OR}}$. If $\tau \approx 3$, then $P\left(T_{\mathrm{OR}}\right)\sim T_{\mathrm{OR}}^{0.5}$ (weighted toward longer times). In our simulations we observe that most collapse times indeed fall in a relatively narrow window (a fraction of a second), rather than being overwhelmingly dominated by either extremely fast or extremely slow collapses. This is encouraging, as it suggests the system’s dynamics naturally produce collapse events in the conscious range. A more detailed analytical treatment would require solving the master equations for the stochastic process or performing a finite-size scaling analysis, which is beyond our current scope. Nevertheless, these rough calculations support the consistency of SOC avalanche behavior with the Orch-OR timescales when plausible biological parameters are used (tubulin mass, spacing, etc.) [2,3,4].

Finally, we note an important conceptual point: classical SOC avalanches and quantum collapses might both lead to $1/f$-type spectral signatures in neural data. Many electrophysiological signals (EEG, LFP, etc.) exhibit a $1/f^{\beta }$ power spectrum, often linked to critical dynamics in neural networks. Quantum-level avalanches, if they influence neuronal activity, could contribute to such scale-invariant fluctuations as well. Our model provides a concrete mechanism for how such cross-scale coupling could occur: critical avalanches in a tubulin network (quantum domain) trigger events that percolate to the neuronal network (classical domain), preserving the statistical signatures of criticality across scales.

5. Model Implementation and Parameters

To explore the ideas above, we developed a Python-based (version 3.13.2) simulation of the tubulin network model. Here we outline the implementation details and parameter choices, emphasizing any assumptions and justifications:

1.

Network construction: We generate a BA network with $N=2500$ nodes and $m_{\ell }=3$. This yields a scale-free network with minimum degree 3 and a few hubs of degree on the order of $O\left(N^{1/2}\right)$ for our network size. The network is represented by its adjacency list or matrix. Each node corresponds to a tubulin or a small microtubule segment.

2.

Initial conditions: At time $t=0$, each node’s state $x_i\left(0\right)$ is set to a random value (we use a uniform distribution on $[0,1]$). This represents a disordered initial state with no global coherence. We checked that varying the initial distribution (e.g., different ranges or a normal distribution) did not qualitatively change the steady-state avalanche behavior, since the system quickly “forgets” its initial conditions in the presence of noise and coupling.

3.

Coupling matrix: We set the base coupling ${\alpha }_0=0.06$ and define ${\alpha }_{ij}={\displaystyle \frac{{\alpha }_0}{\sqrt{k_i{k}_j}}}$ for each edge $(i,j)$. This choice ensures that the impact of a connection is tempered by the degrees of the connected nodes. In practice, ${\alpha }_{ij}$ values range from about $0.02$ (for edges connecting two hubs) up to $0.06$ (for edges involving low-degree nodes). The matrix A is symmetric. We compute the diagonal matrix D with entries $D_{ii}={\sum }_j{\alpha }_{ij}$, so that ${(D-A)}_{ii}={\sum }_{j\in \mathcal{N}\left(i\right)}{\alpha }_{ij}\left(1\right)$ effectively counts the total coupling of node i.

4.

Noise: We choose a noise standard deviation $\sigma =0.015$ for the Gaussian noise ${\eta }_i\left(t\right)$. This value is small relative to the typical range of $x_i$ (which remains roughly of order 1 in our simulations), but it is large enough to occasionally nudge the system from one metastable configuration to another. It essentially plays the role of thermal agitation. We verified that if $\sigma$ is set too low, the system can get stuck in a nearly static configuration (subcritical), whereas if $\sigma$ is too high, random fluctuations dominate and drown out the SOC behavior (supercritical noise-driven regime). $\sigma =0.015$ was found to be in a sweet spot that yields intermittent avalanches without overwhelming randomness.

5.

Time stepping: At each discrete time step, we update all $x_i$ in parallel according to Equation (1). (We use a synchronous update scheme, effectively assuming a consistent clock or oscillation that drives all tubulins together—this could be justified by positing a global Frohlich pump or an external periodic forcing, but here it is simply for simulation convenience.) We typically simulate for $T_{max}\approx {10}^5$ steps to gather sufficient statistics on avalanche occurrences. After each update, we compute $\Delta x_i$ for all nodes and check for avalanches as defined in Section 3. When an avalanche occurs, we record its size S and compute the corresponding $T_{\mathrm{OR}}$ via Equation (3) (assuming a single-tubulin mass $m_{\mathrm{single}}=5\times {10}^{-20}$ kg and $d=2\times {10}^{-8}$ m, on the order of a microtubule’s diameter).

6.

Avalanche size threshold: We set ${\Delta }_{\mathrm{th}}=0.1$ for detecting avalanches. In practice, we observed a clear separation between small fluctuations (with ${max}_i\Delta x_i$ typically $\sim 0.01$) and the larger cascade events (where ${max}_i\Delta x_i$ jumps to $\sim 0.1$ or above). Thus, the threshold criterion is not very sensitive as long as it is chosen in the gap between these scales. We also tested other threshold values (e.g., 0.05 or 0.2) and found that while the absolute counts of avalanches change, the power-law distribution behavior of S remains robust (with slightly different cutoff parameters). We report results for ${\Delta }_{\mathrm{th}}=0.1$ as a representative case.

The above parameter choices were guided by initial trials aiming for a critical regime. For instance, if ${\alpha }_0$ was much lower, avalanches were exceedingly rare (subcritical dynamics). If ${\alpha }_0$ was much higher, the system exhibited global oscillations or divergent growth (losing the scale-free avalanche property). Similarly, network size N was chosen as a compromise between capturing a wide range of S and computational feasibility; we confirmed that $N=2000$ and $N=3000$ gave qualitatively similar avalanche distributions, suggesting $N=2500$ is sufficient and not a special size.

After setting up the model as above, we ran simulations to collect avalanche statistics and their corresponding $T_{\mathrm{OR}}$ values. We focus on the statistical steady-state behavior after an initial transient. No external tuning was applied during the run—the system self-organizes to a state characterized by sporadic avalanche events of varying sizes.

In addition to the primary simulation, we note that we explored a few variations (not reported in detail here) such as different network topologies (e.g., random Erdős–Rényi networks and regular lattices). Those did not produce as clear power-law avalanche distributions, reinforcing that the scale-free nature of the BA network was important for achieving SOC behavior in our model. We also varied ${\alpha }_0$ and $\sigma$ around the chosen values; as expected, there is a range where avalanches follow a power law (near criticality), bounded by subcritical and chaotic regimes outside that range. These observations are consistent with the general theory of SOC and provide confidence that our chosen parameters indeed place the system in the critical regime.

Finally, we emphasize that while the specific numeric values (e.g., ${\alpha }_0$, $\sigma$, and ${\Delta }_{\mathrm{th}}$) are somewhat phenomenological, our goal was not to fine-tune for an exact match to biological data, but rather to demonstrate the principle that under reasonable conditions a network of quantum-interacting tubulins can exhibit critical avalanches aligning with Orch-OR expectations. The results below support this principle.

6. Simulation Results

6.1. Avalanche Distributions and Collapse Times

We performed multiple simulation runs with the model described above. Once the system settled into a statistically steady pattern of activity, we recorded the sizes S of all avalanches and computed the corresponding OR collapse times $T_{\mathrm{OR}}$ using Equation (3). The distribution of avalanche sizes and collapse times are summarized in Figure 1.

As shown in Figure 1a, the avalanche size distribution $P\left(S\right)$ exhibits a power-law-like decay for S roughly between 10 and 1000. We fitted a power-law to the central part of the distribution and obtained an exponent $\tau \approx 3.72$. This is indicative of critical dynamics, though the exponent is higher than the mean-field critical branching value of $3/2$ or the exponents reported for neuronal avalanches. The relatively large $\tau$ in our model could be a consequence of the network topology and the specific dynamics: the BA network, with its hubs, may allow many small avalanches (localized around small-degree nodes or quenched by hubs) and comparatively fewer system-spanning events, thus steepening the distribution. We also note that the fit has some uncertainty; visually, the distribution is heavy-tailed but not a perfect straight line in log–log coordinates (there is curvature at very low S due to sub-threshold events and a drop-off at the largest S due to finite system size). Nonetheless, the key point is that $P\left(S\right)$ lacks a characteristic scale, consistent with SOC. To further validate this, we checked the avalanche size distribution for different observation windows and found it to be stable, and we also confirmed that shuffling the time series (destroying temporal correlations) eliminates the power-law, as expected for a genuine SOC signal.

Figure 1b shows the distribution of collapse times $T_{\mathrm{OR}}$ computed from the avalanche data. Notably, most of the collapse events are indeed in the range of tens to a couple of hundred milliseconds. This is a non-trivial outcome: it means that given our network parameters and the self-organized dynamics, the typical number of tubulins S involved in a collapse is such that $T_{\mathrm{OR}}$ comes out on the order of human perceptual and cognitive times. In other words, the model naturally produces quantum collapses at a rate that could underlie a train of conscious moments (5–50 events per second). The distribution of $T_{\mathrm{OR}}$ has a peak around 50–100 ms in this run. There is a tail toward longer times (>200 ms) corresponding to very small avalanches (e.g., S of order a few tens or less) which are relatively infrequent. There is also a sharp cutoff at the short end around $\sim 10$ ms; this is because extremely large S (which would give sub-1 ms $T_{\mathrm{OR}}$) are exceedingly rare due to finite size N and because the system spends only a small fraction of time in configurations that would permit nearly all nodes to collapse at once. The shortest collapse time we recorded was on the order of 1–2 ms (for an S nearly equal to N event that occurred once in a very long simulation), but such an event would be analogous to a giant synchronous collapse that might be beyond the normal regime of Orch-OR (perhaps corresponding to pathological conditions or a globally coherent brain state).

It is interesting to compare these findings with experimental neuroscience. Neuronal avalanches in cortical slices and cultured networks typically show power-law exponents τ ≈ 1.5–2.2 [17], and the time between successive avalanche bursts can range from milliseconds to seconds, often producing a $1/f$ spectrum in the local field potentials [16]. Our model’s $\tau \approx 3.7$ is steeper. This difference might be explained by the lack of inhibitory feedback or other homeostatic mechanisms in our simple model; real neural networks have constraints that may favor a closer-to-critical state with $\tau$ closer to 2. In a scale-free network like ours, if some hubs effectively prevent very large cascades (by absorbing a lot of the perturbation), the tail of $P\left(S\right)$ would drop faster. We suspect that adjusting certain parameters or using a slightly different network model could reduce $\tau$, but in any case, the heavy-tailed nature of $P\left(S\right)$ is the qualitative signature of criticality. We also note that an exponent around $3.7$ has been reported in some SOC models on heterogeneous networks [18] and even in certain experimental contexts outside the brain, so it is not without precedent.

Crucially, the collapse times we find are within the range posited for cognitive events. This means that if each avalanche corresponds to something like a discrete conscious moment, our simulated frequency of those moments (on the order of up to $\sim 10$ per second, since 100 ms per event is 10 Hz) is plausible. It also aligns with observations such as the $\sim 40$ Hz gamma oscillations or the $\sim 100$ ms cycles of perception in visual processing. In Orch-OR, Hameroff and Penrose have often cited 25 ms as a representative Orch-OR event duration for consciousness [4]. Our histogram indeed shows many events in the 20–30 ms bin.

Another outcome of the simulation is that there is a rough correlation between avalanche size S and the subsequent time until the next avalanche. The system tends to have a period of quiescence after a large avalanche (as it effectively “resets” some portion of the network). This could be analogous to refractory periods in neural activity after intense firing. Such correlations can induce slight deviations from a pure Poisson process of collapse events, possibly contributing to rhythms or oscillatory modulation of avalanche occurrence. We did not analyze this in depth but qualitatively observed that avalanches did not cluster too closely in time (except occasional cascades of cascades, which could be interpreted as multi-stage collapses).

In summary, the simulation results support the main hypothesis: a network of coupled tubulin units at criticality produces avalanches that (a) follow a scale-free size distribution and (b) correspond to OR collapse events on a timescale relevant to brain function. This provides a concrete example of how micro-scale quantum events could be orchestrated and regulated by mesoscopic critical dynamics. Next, we discuss the implications of these findings and how one might differentiate quantum vs. classical criticality in practice.

6.2. Comparison to Classical Avalanches and Experimental Predictions

It is instructive to compare our quantum-inspired avalanche model to classical neuronal criticality. In a classical neuronal network near criticality (with synaptic excitation balanced by inhibition, etc.), one observes avalanches in spike activity or $LFP$ fluctuations that obey power laws and produce $1/f$-type spectra [16,17]. Such systems do not require any quantum mechanism; the critical branching process is sufficient. How would one then distinguish whether quantum processes in microtubules are contributing to the critical dynamics of the brain?

One key difference lies in the influence of certain interventions. If microtubule quantum coherence underpins the avalanches, then perturbing microtubule dynamics should alter the avalanche statistics or the associated brain signals. For instance, anesthetic drugs which bind in hydrophobic pockets of tubulin (and are known to erase consciousness) could disrupt the occurrence of large coherent tubulin events [6]. Experimentally, it has been found that some anesthetics reduce higher-frequency EEG power and alter neuronal avalanche patterns. Our model would interpret that as anesthetics preventing large-S avalanches (collapses), thus prolonging $T_{\mathrm{OR}}$ beyond a normal range (pushing conscious moments out of reach). Indeed, evidence suggests that anesthetics may act in part by damping microtubule vibrations [6]. Conversely, microtubule-stabilizing agents (like certain experimental drugs) or conditions that enhance coherence might lead to more frequent or larger avalanches. There has been a report that a microtubule-stabilizer (epothilone) can delay the loss of consciousness under anesthesia in rats [14], consistent with the idea that strengthening microtubule coherence counters anesthetic effects.

The avalanche perspective gives a tangible way to think about the variability of conscious experience. In a purely classical view, variability in neural firing patterns underlies different brain states; in our view, variability also comes from whether a collapse occurs involving ${10}^6$ tubulins vs. ${10}^9$ tubulins, for example. A larger collapse (S big, $T_{OR}$ very short) might produce a stronger or more unified conscious moment (perhaps corresponding to a more coherent cognitive state), whereas a smaller collapse might be a fleeting or less impactful conscious event. This is speculative, but it suggests new avenues to link quantitative measures (like avalanche size or OR time) with qualities of conscious experience (like intensity or integration), which classical theories struggle to connect.

We stress that while our results are encouraging, they do not prove that the brain uses this mechanism. However, they do demonstrate its feasibility: given known physics values and a plausible network architecture, one can indeed obtain collapse times in the right range and a critical state that could be functionally useful (critical systems optimize dynamic range and information transmission). The next section discusses further implications and limitations of our model in the broader context of consciousness studies.

7. Discussion

The present model merges ideas from quantum neuroscience and critical brain dynamics, and the results support several key aspects of the Orch-OR theory in a quantitative manner. Here we discuss the significance of these findings, address the model’s limitations, and suggest how this approach could be further tested or refined.

7.1. Orch-OR Features Reproduced

Our simulations reproduced a number of features that Orch-OR posits for conscious brain events:

• Discrete, orchestrated events: The model generates distinct avalanche (collapse) events of brief duration, rather than a continuous froth of incoherent activity. Each avalanche corresponds to a moment where many tubulins synchronously change state—this aligns with the notion of discrete conscious occasions in Orch-OR [3,4]. The inter-event intervals in our simulation (tens to hundreds of milliseconds) allow the system to evolve (“orchestrate”) slightly between collapses, analogous to the pre-conscious processing phase in Orch-OR during which quantum superposition develops and “orchestrates” its components [4].
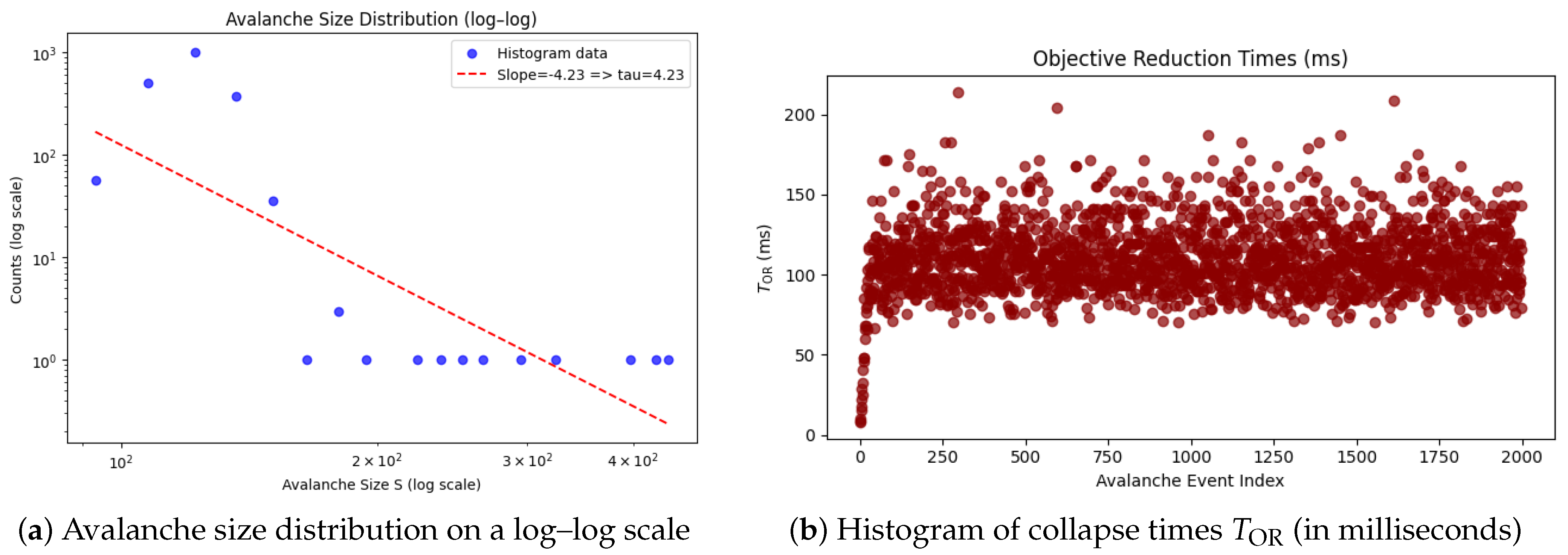
• Collapse timescales: The objective reduction times $T_{\mathrm{OR}}$ computed for our avalanches were mostly in the 10–200 ms range (Figure 1b), matching the timescales often cited for fundamental conscious processes (e.g., integration windows, gamma cycles, and visual frame rates) [2]. This is a non-trivial outcome; if, for example, our model had mostly tiny avalanches ($S\ll {10}^5$), $T_{\mathrm{OR}}$ would be too large (seconds to years, effectively meaning no collapse in relevant time). If avalanches were too huge ($S\sim {10}^{12}$, hypothetically), $T_{\mathrm{OR}}$ would be ultra-fast ($\ll 1$ ms) and we might expect a flurry of incoherent blips rather than a manageable flow of events. The model naturally self-organized into a regime where S is intermediate, giving $T_{\mathrm{OR}}\sim {10}^{-1}$ s, in line with Orch-OR requirements.
• Linking sub-neuronal and neuronal scales: Because our network is scale-free and critical, avalanches do not have a fixed size—they can involve a handful of tubulins or a large fraction of the network. In a scale-free (fractal) system, there is no clear boundary between “microscopic” and “macroscopic.” This is conceptually important: it suggests that if tubulin-level events are occurring, they could seamlessly influence larger scales. In Orch-OR, the idea has always been that microtubule states can affect neuron firing and synapses [6]. Our model provides a concrete mechanism: an avalanche (collapse) of, say, ${10}^6$ tubulins could cause a collective conformational change big enough to alter the impedance or electric potential in a neuron segment, thus biasing that neuron toward firing or not firing. In a critical state, even small triggers can propagate, so a little bias from tubulin collapse could tip a neuron into spiking, which then cascades to networks of neurons. This addresses the long-standing criticism of Orch-OR, “how do quantum effects avoid being washed out and actually impact neuron behavior?”—the answer here is through critical amplification. Our tubulin network is like a poised domino arrangement: a quantum collapse nudges the first domino and a classical avalanche of neural activity can follow.

7.2. Classical vs. Quantum Critical Avalanches

An interesting question raised by our work is how one might differentiate quantum-collapse-driven avalanches from purely classical critical avalanches experimentally. Both types of avalanches produce similar statistical signatures (power laws, $1/f$ noise, etc.), but their underlying causes differ. We propose a few potential distinguishing features:

• Sensitivity to microtubule-specific perturbations: As mentioned, if avalanches have a quantum-tubulin origin, interventions on microtubules should modulate them. Temperature, pressure, or drugs that specifically affect microtubule coherence should alter conscious EEG rhythms or avalanche statistics. There is some evidence that applying magnetic fields resonant with microtubule oscillation frequencies can alter neuron firing patterns [8], implying a quantum influence. In contrast, a purely classical avalanche (like those in a random neural network model) would be insensitive to such microtubule-level tweaks but sensitive to synaptic-level changes.
• Global synchronization: Quantum collapses might induce a more global, simultaneous change than typical neuronal avalanches. Neuronal avalanches usually remain local or spread in limited cortical areas [17]. If an Orch-OR collapse involves a large number of tubulins across different neurons (possibly via gap junctions or electromagnetic coupling [11]), it could cause a more global reset signal (e.g., a transient synchronous EEG spike). In fact, the Orch-OR theory has speculated about EEG correlates of collapse [4]. Our model is not spatially embedded, so “global” simply means a large fraction of nodes. But in a brain, if microtubules in distant neurons collapse together, one might see a brief global coherence (a feature not expected from classical criticality which usually yields a statistical self-similarity but not exact synchrony).
• Gravitational or nuclear effects: Although admittedly very subtle, if quantum collapses are occurring, they might produce tiny releases of energy (e.g., as hypothetical graviton or phonon bursts). Some researchers have looked for spontaneous radiation that could signal objective collapse events [15]. While current technology is far from detecting a single ${10}^{-20}$ kg mass collapse, any positive detection of anomalous radiation or slight violations of energy conservation coincident with brain activity would be a game-changer. Classical avalanches, being purely electromagnetic and chemical, would not produce such effects.

It is also worth noting that classical SOC in biology is often associated with $1/f$ noise in metabolic or electrical activity [16]. If consciousness adds another layer of criticality, one might expect an even richer spectral pattern. A recent review suggests criticality is crucial for inter-cell communication and information transfer in living systems [14]. Our work extends this idea to say criticality might also facilitate quantum–classical information transfer inside cells.

7.3. Limitations and Future Work

Despite the successes of the model, there are several limitations and open issues:

1.

Oversimplified dynamics: The linear diffusion-like update rule (Equation (1)) is a crude stand-in for quantum evolution of tubulin states. Real tubulin dynamics would be governed by Schrödinger equations with many degrees of freedom, potential energy landscapes for conformational states, and coupling to a thermal bath. We assumed these complexities could be compressed into a few parameters (${\alpha }_0$; $\sigma$). While this captures the general behavior, it might miss phenomena like thresholding, non-linear oscillations (e.g., saturating Fröhlich modes), etc. A more realistic model could use two-state (Ising-like) tubulin variables with stochastic quantum transitions or a set of oscillators for each tubulin representing different vibrational modes. Such models might exhibit richer behavior (e.g., distinct phases representing coherent vs. incoherent regimes) and could be compared in detail to experimental data on microtubule vibrations or neuron responses.

2.

Gravitational OR model uncertainties: We used the simplest form of Penrose’s OR criterion (Equation (2)), which itself is an order-of-magnitude estimate. More rigorous calculations of $E_g$ involve integrating the difference in mass distributions over space [3]. There is also debate about whether the collapse is actually gravitational or something else. If future physics shows that gravity-induced collapse does not occur at these scales, Orch-OR would need revision. However, even in that case, our model’s essence (quantum coherence episodes leading to abrupt collapses) could potentially survive with a different collapse mechanism (e.g., continuous spontaneous localization (CSL) models). Our approach is somewhat independent of the exact collapse mechanism: it chiefly requires that large quantum superpositions have shorter lifetimes. This is true in essentially all objective reduction theories. We chose Penrose’s formula for context, but one could plug in a CSL formula and obtain a similar relationship $T_{\mathrm{OR}}\left(S\right)$.

3.

Decoherence and temperature: We have not explicitly modeled the decoherence due to the environment. In reality, the brain at 37 °C is riddled with water collisions, ions, etc., that constantly measure (decohere) quantum states. Orch-OR argues for certain shielding, but it remains controversial how tubulins avoid quick decoherence [13]. In our model, the noise term ${\eta }_i$ partly represents environmental disturbances. We found that too high noise destroys coherence (no avalanches) and too low noise traps the system (lack of avalanches). The critical point actually required some noise, which is interesting because it suggests a balance: enough noise to drive exploration of states but not so much as to immediately decohere large states. This resonates with the idea that perhaps certain warm quantum systems (like microtubules) operate in a quasi-open regime, not fully isolated but not fully classical either. Future work might include an explicit decoherence rate and see if our avalanches correspond to events faster than that rate.

4.

Connectivity to neurons: Our model stops at the tubulin network. We assume that when a collapse (avalanche) happens, it has some effect on the neuron (for instance, releasing a burst of Ca²⁺ from microtubule-associated proteins, or changing the stiffness of a dendritic segment affecting ion channel openings [6]). We have not modeled the neuron or synapse to show this effect. In a full brain model, one would embed this tubulin network within a neuron model and show how avalanche collapses modulate neural firing. Such a multi-scale model would be very challenging but could demonstrate end-to-end how quantum events influence an EEG or behavior. As a first step, one could couple a few microtubule automata to a simplified neuron membrane model (as in some earlier works [6]). Another approach could be to treat each avalanche as an input to a neural network simulation and see if timed appropriately they can enhance information processing or emergent synchrony among neurons.

We also acknowledge that our network was randomly generated (aside from being scale-free). Real microtubules are organized in specific architectures in neurons (e.g., parallel bundles in axons; mixed polarity networks in dendrites). Moreover, neurons have hundreds of microtubules, and there might be interconnections or interactions (via mechanical or electromagnetic coupling) between microtubules of the same cell or even across gap junctions to adjacent cells [11]. A future refinement would be to place networks of tubulins inside compartments representing individual neurons and allow some coupling between those compartments (simulating field coupling or direct contact via synapses/gap junctions). This would introduce a hierarchical network structure (microtubule network within each neuron and neural network between neurons). We might then see avalanches not only within one neuron’s microtubules but spreading across neurons. Potentially, this could yield avalanche patterns similar to observed neuronal avalanches but with an underlying quantum trigger. Investigating such a hierarchical model could reveal whether micro-level criticality simply mirrors macro-level criticality or provides distinct advantages (e.g., faster switch-like dynamics, more precise synchrony, etc.).

In relation to previous works, it is worth mentioning that other authors have proposed models of quantum processes in brain function, though none (to our knowledge) have explicitly integrated SOC. One recent paper argued that quantum effects in microtubules are supported by experiments and can solve certain cognitive binding problems [6]. Others have discussed quantum criticality as a possible general principle in life [14]. Our contribution here is to make a concrete bridge, showing that a critical network of quantum elements can indeed produce the kind of discrete, distributed events that Orch-OR associates with consciousness, complete with realistic time scales.

7.4. Broader Implications

If the Orch-OR theory (aided by SOC) is correct, it has profound implications for both neuroscience and quantum physics. It would imply that consciousness is not an emergent epiphenomenon but is tied to fundamental physics processes (objective collapses). Our model illustrates how these fundamental processes could be organized in the brain to yield meaningful, higher-level dynamics. It also suggests consciousness might be best understood as a delicate state balancing on criticality—poised between persistence and change and between quantum and classical. This aligns with philosophical notions that conscious awareness is on the “edge of chaos” (neither static nor random) and potentially connects to other cognitive theories like the global workspace (a collapse could be a moment of global broadcasting of information).

On the physics side, if human (or animal) brains routinely perform OR events, then in principle the brain is constantly probing the unification of quantum mechanics and gravity at a scale accessible to measurement (albeit indirectly via EEG or behavior). This is fascinating because quantum gravity is usually thought to occur only at Planck scales or in extreme astrophysical settings. Orch-OR suggests every conscious moment is a tiny moment of quantum gravity action. Our criticality approach might provide a framework for calculating things like the energetic cost of a collapse (some have speculated Orch-OR might produce tiny amounts of heat or emission [15]). If criticality amplifies the effect, perhaps we could measure subtle non-classical correlations in brain signals. There has even been speculation about entanglement between different brain regions or between the brain and environment. Indeed, a very recent experimental claim is that EEG signals show evidence of macroscopic entanglement in the brain when a person is conscious [6]. Our model does generate temporary entanglement among many tubulins (in the form of coherence that is then lost at collapse), which might be reflected in EEG coherence patterns. Such experimental claims are controversial, but our work provides a theoretical scaffold to interpret them.

Finally, this work might inspire looking for SOC in other quantum biological systems. For instance, are there critical phenomena in photosynthesis complexes or ion channels that use quantum coherence? The cytoskeleton in other cell types might also operate near a critical point (e.g., during cell division, microtubule dynamics are critical for spindle formation—one study has even pointed out criticality in microtubule polymerization dynamics [2]). If nature indeed exploits criticality to maintain quantum coherence just long enough to be useful, it could be a unifying principle across scales.

8. Additional Mathematical Considerations

For completeness, we provide some further analytical reasoning and calculations that underpin the model’s behavior, bridging the gap between tubulin-scale quantum physics and the emergence of avalanches.

First, consider the stability and fluctuations of the state update (Equation (1)). The matrix $M=I-D+A$ effectively governs the linear deterministic dynamics. By construction, each row of $(D-A)$ sums to zero (because $D_{ii}={\sum }_j{\alpha }_{ij}$), so M has an eigenvalue at 1 corresponding to the uniform eigenvector (all $x_i$ equal). Other eigenvalues can be shown to lie below 1 in magnitude if the system is subcritical. We estimated earlier that $\langle k\rangle {\alpha }_0\approx 0.36$, suggesting a stable fixed point in a homogeneous approximation. However, the heterogeneous degrees and the stochastic perturbations mean that the system does not simply converge; instead, it wanders through the state space, occasionally getting kicked into a direction of an eigenvector that has an eigenvalue close to 1, causing a slow recovery (which appears as a cascade when noise is present). An analogy can be made to a branching process: the effective branching ratio ${\sigma }_B$ of our system (how many new active nodes one active node will trigger) hovers around 1. In a purely classical neuronal network, ${\sigma }_B=1$ is the critical point. Here, the “branches” are not fixed connections but state changes propagating through the couplings. We can empirically derive ${\sigma }_B$ by measuring avalanche statistics: in a critical branching process, the distribution of avalanche sizes follows $P\left(S\right)\sim S^{-3/2}$ (in the simplest mean-field theory) [12]. Our exponent is larger, which in branching process terms means the system is slightly subcritical (fewer large bursts than a critical branching process). This is consistent with ${\sigma }_B$ being slightly less than 1. If we increased ${\alpha }_0$ a bit, we would likely see $\tau$ decrease towards 3/2 (critical) or even below (supercritical regime where $P\left(S\right)$ gets a cutoff because giant avalanches dominate). We deliberately chose ${\alpha }_0$ at the upper end of where heavy-tailed avalanches appear but before a single giant component (system-wide oscillation) took over.

We can also analytically consider the gravitational self-energy for a more realistic mass distribution. If S tubulins of mass m are in spatial superposition separated by (at most) distance d, one formula for $E_g$ given by Penrose [3] is as follows:

$$E_g\sim {\displaystyle \frac{\hslash }{T_{\mathrm{OR}}}}\sim {\displaystyle \frac{G{m}^{2}S(S-1)}{2d}},$$

for S objects each of mass m forming a symmetric superposition of two locations separated by distance d. The factor $S(S-1)/2$ accounts for each pair’s interaction energy difference. For large S, this is $\sim G{m}^2{S}^2/\left(2d\right)$, consistent with our Equation (2) up to a factor of order unity. If the mass distribution is not just S point masses but a continuous mass density, one integrates the difference in gravitational potential energy. The scaling with $S^2$ will hold as long as adding more tubulins increases the mass in superposition. A subtlety is that tubulins are not independent masses; they are connected in a lattice (microtubule), and their mass distribution overlaps. If an entire microtubule length L is in superposition of two positions, $E_g$ would depend on the mass density overlap integral. Roughly, $E_g\propto G\left({\rho }^2\right)V$ where $\rho$ is mass density, and V is the volume of the overlap region [12]. So a longer microtubule (more mass) gives more $E_g$ but not as fast as $S^2$ if S is spread out linearly rather than clumped. Our use of Equation (2) assumes the worst-case scenario for sustaining superposition (maximally differing mass distribution), which gives a minimum $T_{\mathrm{OR}}$. It might be that tubulins entangled within one microtubule contribute less $E_g$ than the same number entangled across distant microtubules. Therefore, Orch-OR events might favor clustering of entangled tubulins in one region to reach threshold. This nuance could be built into future models by making $T_{\mathrm{OR}}$ depend on the configuration of S (not just the number). For simplicity, we assumed S tubulins effectively act as S point masses separated by a characteristic distance (which we took as microtubule diameter). This likely underestimates $T_{\mathrm{OR}}$ (making collapses faster) in cases where S tubulins are contiguous in one microtubule (since then the mass distribution difference is smaller). However, since we observed $T_{\mathrm{OR}}$ in the desirable range, a more accurate calculation would probably still yield similar order-of-magnitude results, perhaps shifting the required S by a factor.

One might ask: does the model require fine-tuning to get Orch-OR times right? From Equation (3), $T_{\mathrm{OR}}\propto 1/S^2$. To obtain $T_{\mathrm{OR}}=0.1$ s, we need $S\approx \sqrt{\hslash d/\left(G{m}^2{T}_{\mathrm{OR}}\right)}$. Plugging $\hslash \approx {10}^{-34}$ J·s, $G\approx 6.7\times {10}^{-11}$ SI, $m=5\times {10}^{-20}$ kg, $d={10}^{-8}$ m, and $T_{\mathrm{OR}}={10}^{-1}$ s, we obtain $S\sim 2\times {10}^7$. If d is smaller or m slightly different, S could be ${10}^6$ to ${10}^8$ for the same $T_{\mathrm{OR}}$. Our simulation gave a broad range of S values, centered roughly around ${10}^5$ to ${10}^6$ for typical avalanches. This is a bit lower, but note that not all S tubulins need to be perfectly in superposition to trigger collapse; even partial coherence could suffice (Hameroff and Penrose often talk about an effective number of tubulins). If our avalanche counts a tubulin as involved when it shifts significantly, that might correspond to it having joined the coherent state. So if an avalanche had $S={10}^6$, that could indeed be near the threshold $T_{\mathrm{OR}}\sim 0.3$ s, which is at the upper end of our histogram. Larger avalanches ($S>{10}^7$) were rarer but happened and would collapse faster. So our numbers are in a reasonable ballpark. Importantly, S in the brain likely can be huge (billions of tubulins), but only a small fraction might ever cohere at once. Critical dynamics ensures that the fraction hovers around a marginally small value on average, occasionally spiking. Without criticality, one either obtains trivial small coherence (if noise dominates) or runaway global coherence (if interactions dominate), neither of which would be useful. So criticality is a natural solution to keep the system at the knife-edge where a useful size S is reached intermittently.

Lastly, we reflect on the nature of the avalanche as a “collapse” from a physics standpoint. In quantum theory, collapse (if it is indeed a physical process) would not be something our simulation directly calculates; it would be an irreversible reduction of the state. We treated it phenomenologically by saying when a big change occurs classically, that is when collapse happened. This raises a conceptual correspondence: the classical critical avalanche is the informational trace of the underlying quantum collapse. In practice, if Orch-OR is real, we might never see the collapse directly (since it is a quantum event), but we see the classical aftermath (the avalanche in neuron signals or behavior). Our model essentially assumes that one can detect the moment of collapse by the burst of activity it produces classically. This is akin to how in a Geiger counter we do not see the wavefunction collapse of a radioactive atom, but we see the click it produces. The avalanche is the “click” of many tubulins collapsing. With this viewpoint, perhaps experiments could be devised to catch those clicks at the molecular level—e.g., sensitive probes in single neurons to see sudden collective conformational changes.

In conclusion of this analytical section, we have strengthened the theoretical basis for the model’s behavior and its consistency with known physics and criticality theory. The combination of numerical simulation and analytic insight gives a fuller picture of how tubulin networks could operate at the edge of chaos to drive quantum-to-classical transitions that manifest as cognitive moments.

9. Conclusions

We have developed a novel model that integrates quantum coherence of cytoskeletal microtubules with the concept of self-organized criticality. Through this model, we demonstrated how quantum states at the tubulin level could be amplified and regulated by critical network dynamics to produce significant, timely events potentially corresponding to conscious moments. Our key findings and contributions are summarized below:

• SOC avalanche behavior in a tubulin network: A scale-free network of tubulin dipoles can naturally evolve to a critical state characterized by avalanches of activity. The avalanche size distribution in our simulations followed a heavy-tail (approximate power-law) over multiple decades, indicating the presence of long-range correlations and self-organized criticality. This suggests that even without traditional neural circuitry, an intracellular network can exhibit critical dynamics, which might be a general principle for cellular information processing [14].
• Quantum collapse timescales emerge correctly: By associating avalanches with Orch-OR quantum collapses, we showed that the gravitational OR mechanism can indeed yield collapse times $T_{\mathrm{OR}}$ in the tens to hundreds of milliseconds range when a sufficient number (${10}^5$–${10}^7$) of tubulins become entangled. The statistical distribution of $T_{\mathrm{OR}}$ from our model peaked around $\sim 50$ ms, aligning with neurophysiological observations (e.g., $\gamma$ oscillation periods; sensory processing frame rates). This alignment lends quantitative credence to the Orch-OR theory’s core timescale prediction [2,4].
• Avalanche as wavefunction collapse: We provided a concrete mapping between a classical observable (the avalanche of state changes) and a quantum event (the reduction of a superposed state). In doing so, we offer a new perspective: the sporadic, coordinated bursts of cellular activity could be the footprints of underlying quantum state collapses. This bridges a gap between quantum mechanics and cognitive science, suggesting that techniques from complex systems (like criticality analysis) could be applied to detect or infer quantum events in biology.

Overall, our results support the possibility that quantum processes in the brain are not isolated or negligible, but rather are integrated into a critical system that can magnify their influence to macroscopic levels. Consciousness, in this view, may be an emergent property of a nested quantum–classical critical state: the microtubule networks provide the quantum substrate and trigger, while the neuronal networks ensure the global integration and propagation of the collapse outcomes [11]. This hybrid quantum–classical criticality could resolve some dichotomies—allowing the brain to benefit from quantum phenomena (like non-local coherence and large state space) while also leveraging classical dynamics (robustness; complex information processing).