Analytic Solutions and Conservation Laws of a 2D Generalized Fifth-Order KdV Equation with Power Law Nonlinearity Describing Motions in Shallow Water Under a Gravity Field of Long Waves
Abstract
1. Introduction
2. Point Symmetries of (3)
3. Conservation Laws for (3)
3.1. Conserved Vectors via the Multiplier Approach
3.1.1. Conserved Vectors for (3)
3.1.2. Conserved Vectors of (3) When and
3.2. Conserved Vectors via Ibragimov’s Method
3.2.1. Conserved Vectors of (3)
3.2.2. Conserved Vectors of (3) When
4. Analytic Solutions of Equation (3)
4.1. Symmetry Reductions and Solutions Using , ,
4.2. Symmetry Reductions and Solutions Using
4.3. Symmetry Solutions Using and
4.4. Symmetry Reductions and Solutions Using
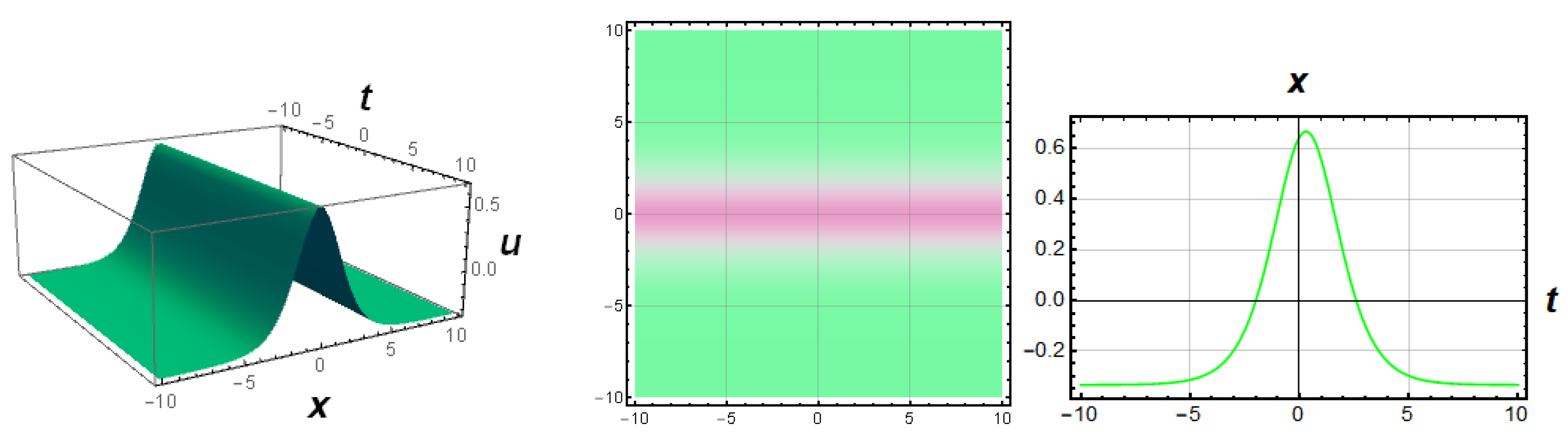
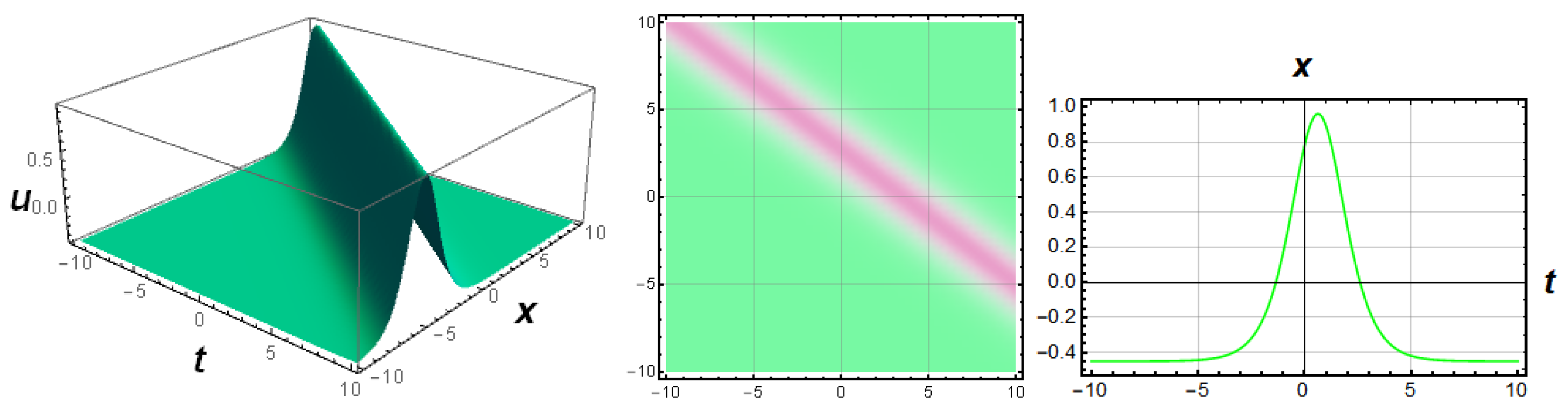
4.5. Results and Discussion
5. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, X.; Jüngel, A.; Wang, L. The Shigesada-Kawasaki-Teramoto cross-diffusion system beyond detailed balance. J. Differ. Equ. 2023, 360, 260–286. [Google Scholar] [CrossRef]
- Khalique, C.M.; Plaatjie, K. Exact solutions and conserved vectors of the two-dimensional generalized shallow water wave equation. Mathematics 2021, 9, 1439. [Google Scholar] [CrossRef]
- Wazwaz, A.M. Multiple soliton solutions and other scientific solutions for a new Painlevé integrable fifth-order equation. Chaos. Solitons Fractals 2025, 196, 116307. [Google Scholar] [CrossRef]
- Li, S.; Li, L. Painlevé integrability, auto-Bäcklund transformation and exact solutions of an extended (3+1)-dimensional Boussinesq equation. Qual. Theory Dyn. Syst. 2025, 24, 110. [Google Scholar] [CrossRef]
- Ovsiannikov, L.V. Group Analysis of Differential Equations; Academic Press: New York, NY, USA, 1982. [Google Scholar]
- Olver, P.J. Applications of Lie Groups to Differential Equations, 2nd ed.; Springer: Berlin, Germany, 1993. [Google Scholar]
- Hirota, R. The Direct Method in Soliton Theory; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Salas, A.H.; Gomez, C.A. Application of the Cole-Hopf transformation for finding exact solutions to several forms of the seventh-order KdV equation. Math. Probl. Eng. 2010, 2010, 194329. [Google Scholar] [CrossRef]
- Kudryashov, N.A.; Loguinova, N.B. Extended simplest equation method for nonlinear differential equations. Appl. Math. Comput. 2008, 205, 396–402. [Google Scholar] [CrossRef]
- Saheli, A.E.; Zogheib, B. Symmetry Analysis of the 3D Boundary-Layer Flow of a Non-Newtonian Fluid. AppliedMath 2024, 4, 1588–1599. [Google Scholar] [CrossRef]
- Yadav, S. QPDE: Quantum Neural Network Based Stabilization Parameter Prediction for Numerical Solvers for Partial Differential Equations. AppliedMath 2023, 3, 552–562. [Google Scholar] [CrossRef]
- Monyayi, V.T.; Goufo, E.F.D.; Toudjeu, I.T. Mathematical Analysis of a Navier–Stokes Model with a Mittag–Leffler Kernel. AppliedMath 2024, 4, 1230–1244. [Google Scholar] [CrossRef]
- Sekhesa, T.M.; Nchejane, N.J.; Poka, W.D.; Kalebe, K.M. Exact solutions of the (1+1)-dissipative Westervelt equation using an optimal system of Lie sub-algebras and modified simple equation method. Partial Differ. Equ. Appl. Math. 2025, 14, 101178. [Google Scholar] [CrossRef]
- Chatziafratis, A.; Fokas, A.S.; Kalimeris, K. The Fokas method for evolution partial differential equations. Partial Differ. Equ. Appl. Math. 2025, 14, 101144. [Google Scholar] [CrossRef]
- Ahmed, D.M.; Mahmood, B.A.; Alalyani, A. On the solution of the coupled Whitham–Broer–Kaup problem using a hybrid technique for improved accuracy. Partial Differ. Equ. Appl. Math. 2025, 14, 101184. [Google Scholar] [CrossRef]
- Darvishi, M.T.; Najafi, M. A modification of extended homoclinic test approach to solve the (3+1)-dimensional potential-YTSF equation. Chin. Phys. Lett. 2011, 28, 040202. [Google Scholar] [CrossRef]
- Chen, Y.; Yan, Z. New exact solutions of (2+1)-dimensional Gardner equation via the new sine-Gordon equation expansion method. Chaos Solitons Fract. 2005, 26, 399–406. [Google Scholar] [CrossRef]
- Wang, M.; Li, X.; Zhang, J. The (G′/G)-Expansion method and travelling wave solutions for linear evolution equations in mathematical physics. Phys. Lett. A 2005, 24, 1257–1268. [Google Scholar]
- Feng, L.; Tian, S.; Zhang, T.; Zhou, J. Lie symmetries, conservation laws and analytical solutions for two-component integrable equations. Chin. J. Phys. 2017, 55, 996–1010. [Google Scholar] [CrossRef]
- Weiss, J.; Tabor, M.; Carnevale, G. The Painlevé property and a partial differential equations with an essential singularity. Phys. Lett. A 1985, 109, 205–208. [Google Scholar] [CrossRef]
- Wazwaz, A.M. Traveling wave solution to (2+1)-dimensional nonlinear evolution equations. J. Nat. Sci. Math. 2007, 1, 1–13. [Google Scholar]
- Zheng, C.L.; Fang, J.P. New exact solutions and fractional patterns of generalized Broer-Kaup system via a mapping approach. Chaos Solitons Fractals 2006, 27, 1321–1327. [Google Scholar] [CrossRef]
- Chun, C.; Sakthivel, R. Homotopy perturbation technique for solving two point boundary value problems-comparison with other methods. Comput. Phys. Commun. 2010, 181, 1021–1024. [Google Scholar] [CrossRef]
- Zeng, X.; Wang, D.S. A generalized extended rational expansion method and its application to (1+1)-dimensional dispersive long wave equation. Appl. Math. Comput. 2009, 212, 296–304. [Google Scholar] [CrossRef]
- Kudryashov, N.A. One method for finding exact solutions of nonlinear differential equations, Commun. Nonlinear Sci. Numer. Simulat. 2012, 17, 2248–2253. [Google Scholar] [CrossRef]
- Gu, C.H. Soliton Theory and Its Application; Zhejiang Science and Technology Press: Hangzhou, China, 1990. [Google Scholar]
- Lü, J.; Bilige, S.; Chaolu, T. The study of lump solution and interaction phenomenon to (2+1)-dimensional generalized fifth-order KdV equation. Nonlinear Dyn. 2018, 91, 1669–1676. [Google Scholar] [CrossRef]
- Liu, J.G. Lump-type solutions and interaction solutions for the (2+1)-dimensional generalized fifth-order KdV equation. Appl. Math. Lett. 2018, 86, 36–41. [Google Scholar] [CrossRef]
- Guo, B.; Fang, Y.; Dong, H. On soliton solutions, periodic wave solutions and asymptotic analysis to the nonlinear evolution equations in (2+1) and (3+1) dimensions. Heliyon 2023, 9, e15929. [Google Scholar] [CrossRef]
- Ibragimov, N.H. Elementary Lie Group Analysis and Ordinary Differential Equations; John Wiley & Sons: Chichester, NY, USA, 1999. [Google Scholar]
- Ibragimov, N.H. A new conservation theorem. J. Math. Anal. Appl. 2007, 333, 311–328. [Google Scholar] [CrossRef]
- Wang, M.; Zhou, Y.; Li, Z. Application of a homogeneous balance method to exact solutions of nonlinear equations in mathematical physics. Phys. Lett. A 1996, 216, 67–75. [Google Scholar] [CrossRef]
- Simbanefayi, I.; Khalique, C.M. An optimal system of group-invariant solutions and conserved quantities of a nonlinear fifth-order integrable equation. Open Phys. 2020, 18, 829–841. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khalique, C.M.; Sebogodi, B.P. Analytic Solutions and Conservation Laws of a 2D Generalized Fifth-Order KdV Equation with Power Law Nonlinearity Describing Motions in Shallow Water Under a Gravity Field of Long Waves. AppliedMath 2025, 5, 96. https://doi.org/10.3390/appliedmath5030096
Khalique CM, Sebogodi BP. Analytic Solutions and Conservation Laws of a 2D Generalized Fifth-Order KdV Equation with Power Law Nonlinearity Describing Motions in Shallow Water Under a Gravity Field of Long Waves. AppliedMath. 2025; 5(3):96. https://doi.org/10.3390/appliedmath5030096
Chicago/Turabian StyleKhalique, Chaudry Masood, and Boikanyo Pretty Sebogodi. 2025. "Analytic Solutions and Conservation Laws of a 2D Generalized Fifth-Order KdV Equation with Power Law Nonlinearity Describing Motions in Shallow Water Under a Gravity Field of Long Waves" AppliedMath 5, no. 3: 96. https://doi.org/10.3390/appliedmath5030096
APA StyleKhalique, C. M., & Sebogodi, B. P. (2025). Analytic Solutions and Conservation Laws of a 2D Generalized Fifth-Order KdV Equation with Power Law Nonlinearity Describing Motions in Shallow Water Under a Gravity Field of Long Waves. AppliedMath, 5(3), 96. https://doi.org/10.3390/appliedmath5030096






