Neural Networks and Markov Categories
Abstract
1. Introduction
2. Neural Networks as Markov Categories
 and satisfying the commutative comonoid equations,
and satisfying the commutative comonoid equations, as well as compatibility with the monoidal structure,
as well as compatibility with the monoidal structure,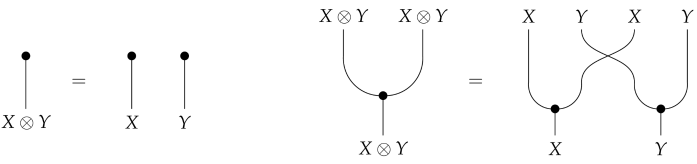 and naturality of, which means that
and naturality of, which means that for every morphism f.
for every morphism f.A Neural Network Markov Category
- (i)
- The empty set ⌀ and X belong to τ.
- (ii)
- The intersection of a finite number of sets in τ is also in τ.
- (iii)
- The union of an arbitrary number of sets in τ is also in τ.
- (i)
- For every , the map is -measurable.
- (ii)
- For every , the map defines a probability measure on .
3. Modeling the Neural Network Markov Category
Interacting Particle System Approach
4. Emergence in Neural Networks Dynamics
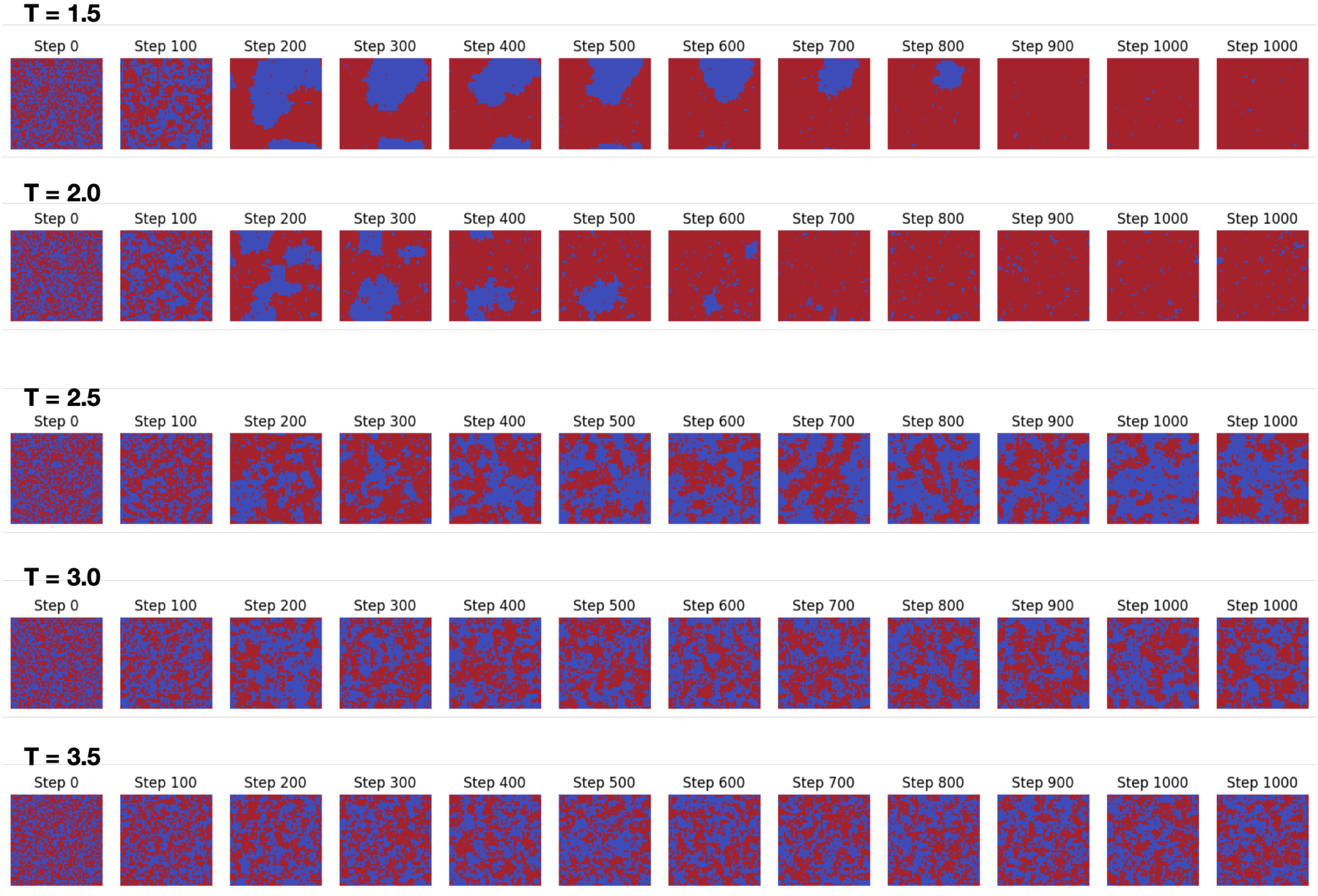
Numerical Computations
- 1.
- Deep sub-critical (). The density is sharply local: the system either stays in the same state () or makes a near-neighbor move (). Long-range jumps are practically forbidden, reflecting a single-basin energy landscape.
- 2.
- Near-critical (). The distribution broadens and develops broad shoulders at . As the curve in the figure is averaged over 50 runs, this spread quantifies genuine dynamical diversity as follows: different realizations explore macroscopically distinct pathways with comparable weight. The increased width signals a higher degree of emergence, as the system spends non-negligible probability mass in multiple, topologically distant regions of state space.
- 3.
- Super-critical regime (). In contrast to the broad, multi-modal curve observed at criticality, the transition-probability density collapses into a sharp peak centered at . At high temperature each spin flips almost independently; the energy increments of the trial moves add up to a sum of weakly correlated random variables. By the central limit theorem the distribution of these sums (and therefore of the sweep–level transition probabilities) becomes Gaussian with variance , i.e. vanishingly small for macroscopic lattices. Physically, the system no longer supports large, coherent domains, so any individual flip typically changes the energy by only a single-bond amount and the net change over a sweep is close to zero with overwhelming probability. The disappearance of side lobes therefore signals the loss of emergent structure in the high-temperature phase.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bossy, M.; Fontbona, J.; Olivero, H. Synchronization of stochastic mean field networks of Hodgkin–Huxley neurons with noisy channels. J. Math. Biol. 2019, 78, 1771–1820. [Google Scholar] [CrossRef] [PubMed]
- Fasoli, D. Attacking the Brain with Neuroscience: Mean-Field Theory, Finite Size Effects and Encoding Capability of Stochastic Neural Networks. Ph.D. Thesis, Université Nice Sophia Antipolis, Nice, France, 2013. [Google Scholar]
- Philippe, R.; Vignoud, G. Stochastic models of neural synaptic plasticity. SIAM J. Appl. Math. 2021, 81, 1821–1846. [Google Scholar] [CrossRef] [PubMed]
- Sacerdote, L.; Giraudo, M.T. Stochastic Integrate and Fire Models: A review on mathematical methods and their applications. In Stochastic Biomathematical Models: With Applications to Neuronal Modeling; Springer: Berlin/Heidelberg, Germany, 2013; pp. 99–148. [Google Scholar]
- Faugeras, O.; Touboul, J.; Cessac, B. A constructive mean-field analysis of multi-population neural networks with random synaptic weights and stochastic inputs. Front. Comput. Neurosci. 2009, 3. [Google Scholar] [CrossRef] [PubMed]
- Parr, T.; Sajid, N.; Friston, K.J. Modules or Mean-Fields? Entropy 2020, 22, 552. [Google Scholar] [CrossRef] [PubMed]
- Fong, B.; Spivak, D.; Tuyéras, R. Backprop as Functor: A compositional perspective on supervised learning. In Proceedings of the 34th Annual ACM/IEEE Symposium on Logic in Computer Science (LICS), Vancouver, BC, Canada, 24–27 June 2019; pp. 1–13. [Google Scholar] [CrossRef]
- Li, J.J.; Prado-Guerra, S.; Basu, K.; Silva, G. A Categorical Framework for Quantifying Emergent Effects in Network Topology. arXiv 2024, arXiv:2311.17403. [Google Scholar]
- Haruna, T. Theory of interface: Category theory, directed networks and evolution of biological networks. Biosystems 2013, 114, 125–148. [Google Scholar] [CrossRef] [PubMed]
- Otter, N.; Porter, M.A. A unified framework for equivalences in social networks. arXiv 2020, arXiv:2006.10733. [Google Scholar]
- Northoff, G.; Tsuchiya, N.; Saigo, H. Mathematics and the Brain: A Category Theoretical Approach to Go Beyond the Neural Correlates of Consciousness. Entropy 2019, 21, 1234. [Google Scholar] [CrossRef]
- Pardo-Guerra, S.; Silva, G. Preradical, entropy and the flow of information. Int. J. Gen. Syst. 2024, 53, 1121–1145. [Google Scholar] [CrossRef]
- Parzygnat, A.J. Inverses, disintegrations, and Bayesian inversion in quantum Markov categories. arXiv 2020, arXiv:2001.08375. [Google Scholar]
- Golubtsov, P.V. Monoidal Kleisli category as a background for information transformers theory. Inf. Theory Inf. Process. 2002, 2, 62–84. [Google Scholar]
- Fong, B. Causal Theories: A Categorical Perspective on Bayesian Networks. arXiv 2013, arXiv:1301.6201. [Google Scholar]
- Jacobs, B.; Zanasi, F. A Predicate/State Transformer Semantics for Bayesian Learning. Electron. Theor. Comput. Sci. 2016, 325, 185–200. [Google Scholar] [CrossRef]
- Cho, K.; Jacobs, B. Disintegration and Bayesian inversion via string diagrams. Math. Struct. Comput. Sci. 2019, 29, 938–971. [Google Scholar] [CrossRef]
- Fritz, T. A synthetic approach to Markov kernels, conditional independence and theorems on sufficient statistics. Adv. Math. 2020, 370, 107239. [Google Scholar] [CrossRef]
- Bogolyubov, N.N. On model dynamical systems in statistical mechanics. Physica 1966, 32, 933–994. [Google Scholar] [CrossRef]
- Sakthivadivel, D. Magnetisation and mean field theory in the Ising model. SciPost Phys. Lect. Notes 2022, 35. [Google Scholar] [CrossRef]
- Rosas, F.E.; Geiger, B.C.; Luppi, A.I.; Seth, A.K.; Polani, D.; Gastpar, M.; Mediano, P.A. Software in the natural world: A computational approach to hierarchical emergence. arXiv 2024, arXiv:2402.09090. [Google Scholar]
- Glauber, R.J. Time-Dependent Statistics of the Ising Model. J. Math. Phys. 1963, 4, 294–307. [Google Scholar] [CrossRef]
- Adam, E.M. Systems, Generativity and Interactional Effects. Ph.D. Thesis, Department of Electrical Engineering and Computer Science, Massachusetts Institute of Technology, Cambridge, MA, USA, 2017. [Google Scholar]
- Morales, I.; Landa, E.; Angeles, C.; Toledo, J.; Rivera, A.; Temis, J.; Frank, A. Behavior of early warnings near the critical temperature in the two-dimensional Ising model. PLoS ONE 2015, 10, e0130751. [Google Scholar] [CrossRef] [PubMed]
- Morningstar, A.; Melko, R. Deep learning the ising model near criticality. J. Mach. Learn. Res. 2018, 18, 1–17. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pardo-Guerra, S.; Li, J.J.; Basu, K.; Silva, G.A. Neural Networks and Markov Categories. AppliedMath 2025, 5, 93. https://doi.org/10.3390/appliedmath5030093
Pardo-Guerra S, Li JJ, Basu K, Silva GA. Neural Networks and Markov Categories. AppliedMath. 2025; 5(3):93. https://doi.org/10.3390/appliedmath5030093
Chicago/Turabian StylePardo-Guerra, Sebastian, Johnny Jingze Li, Kalyan Basu, and Gabriel A. Silva. 2025. "Neural Networks and Markov Categories" AppliedMath 5, no. 3: 93. https://doi.org/10.3390/appliedmath5030093
APA StylePardo-Guerra, S., Li, J. J., Basu, K., & Silva, G. A. (2025). Neural Networks and Markov Categories. AppliedMath, 5(3), 93. https://doi.org/10.3390/appliedmath5030093





