The Sequential Hotelling Game with One Parameterized Location
Abstract
1. Introduction
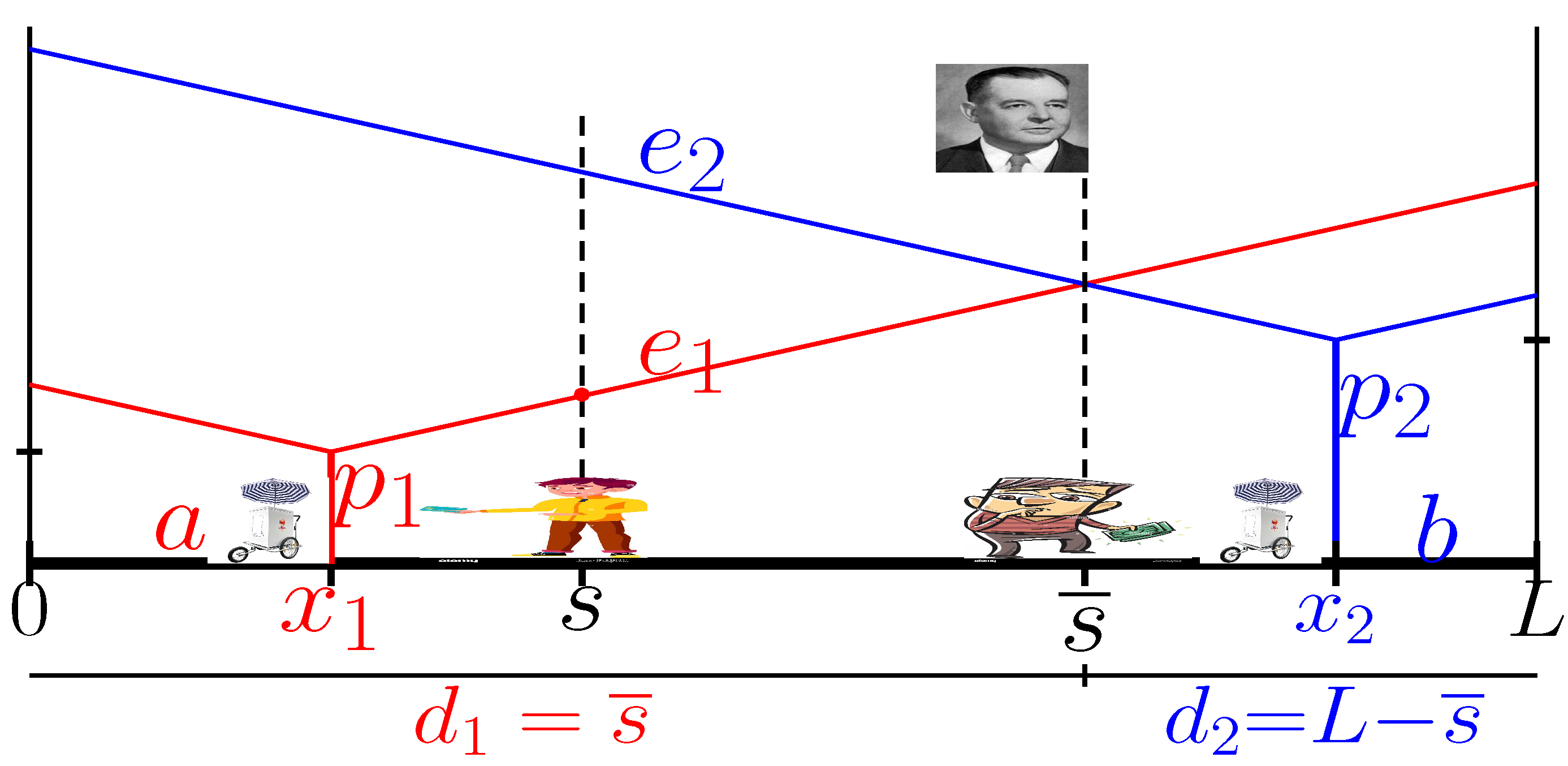
2. The Hotelling Game
The Sequential Hotelling Game
3. Numerical Simulation
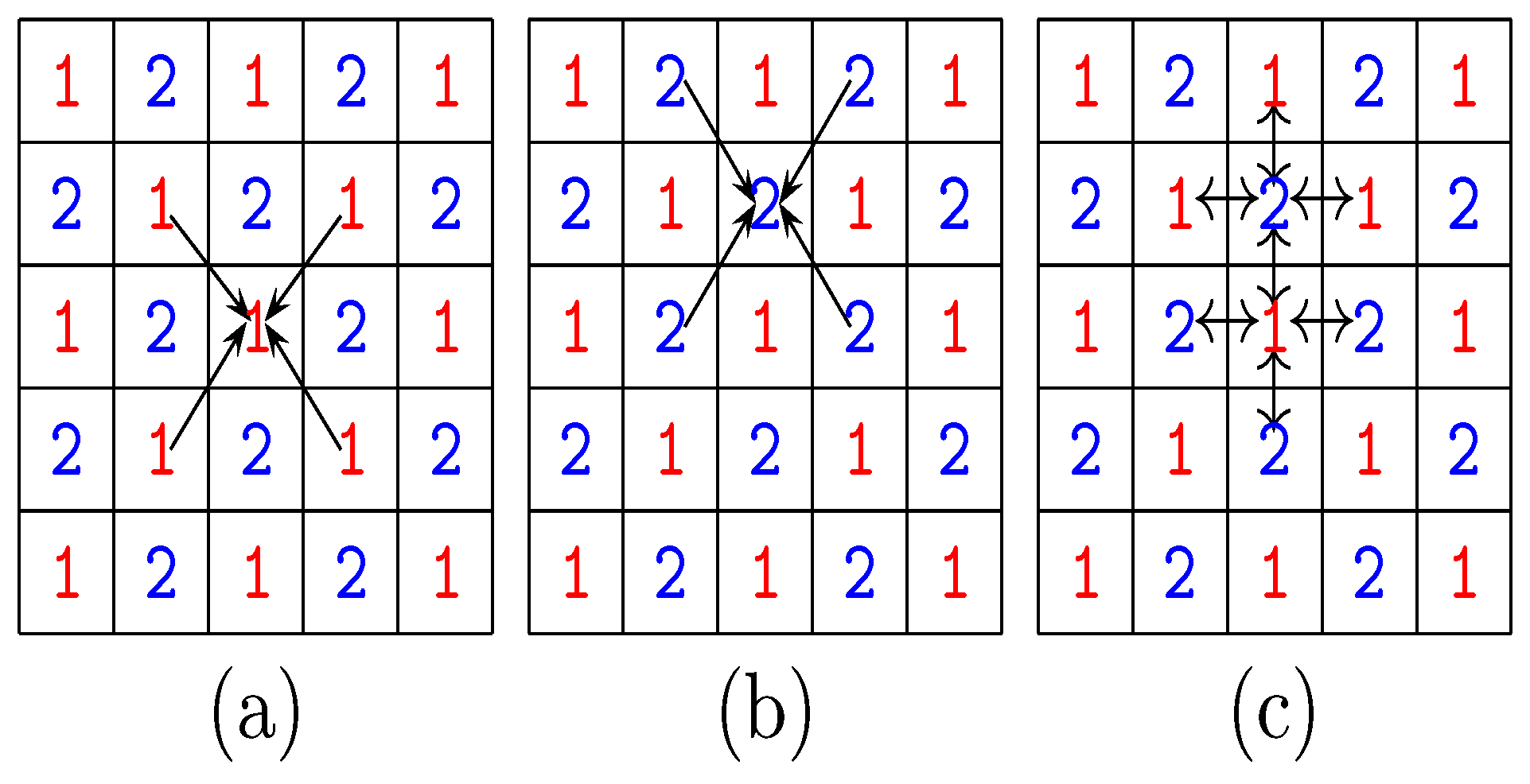
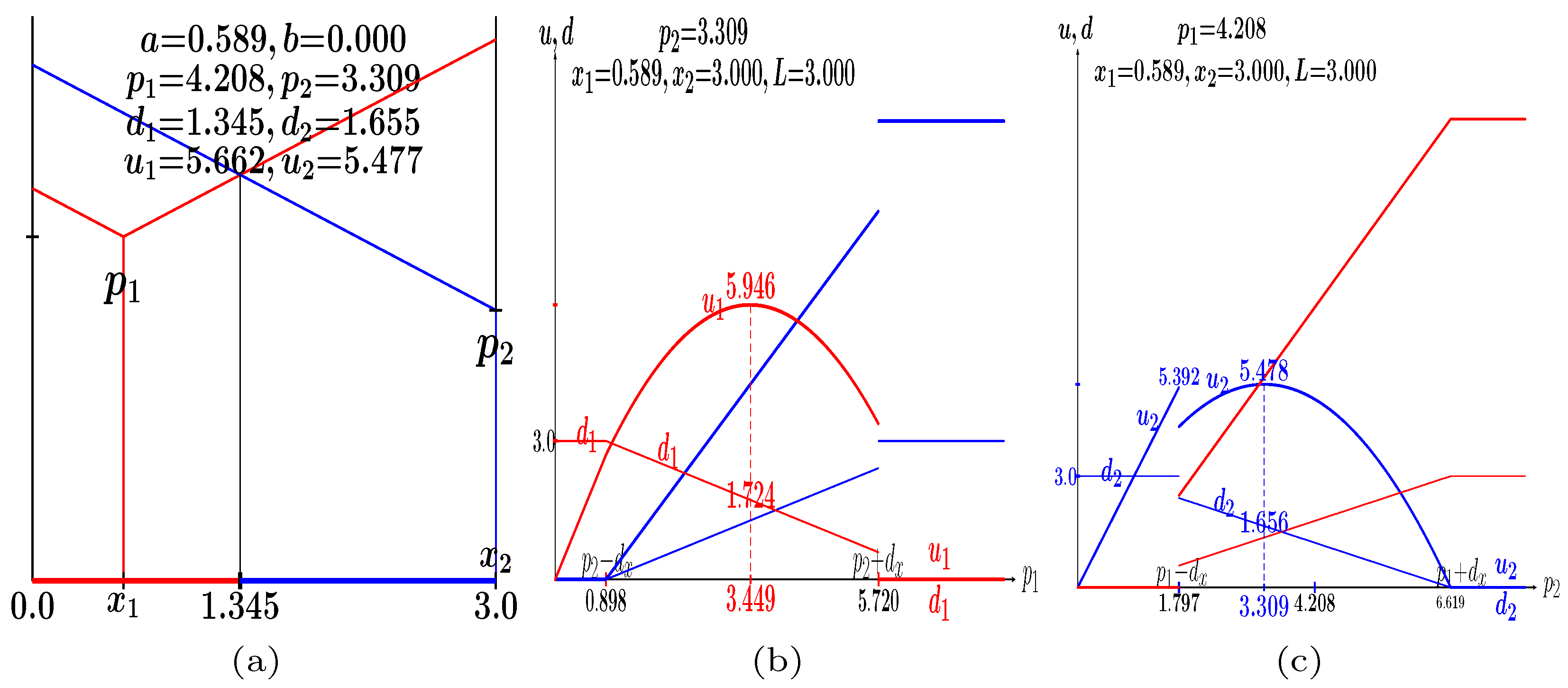
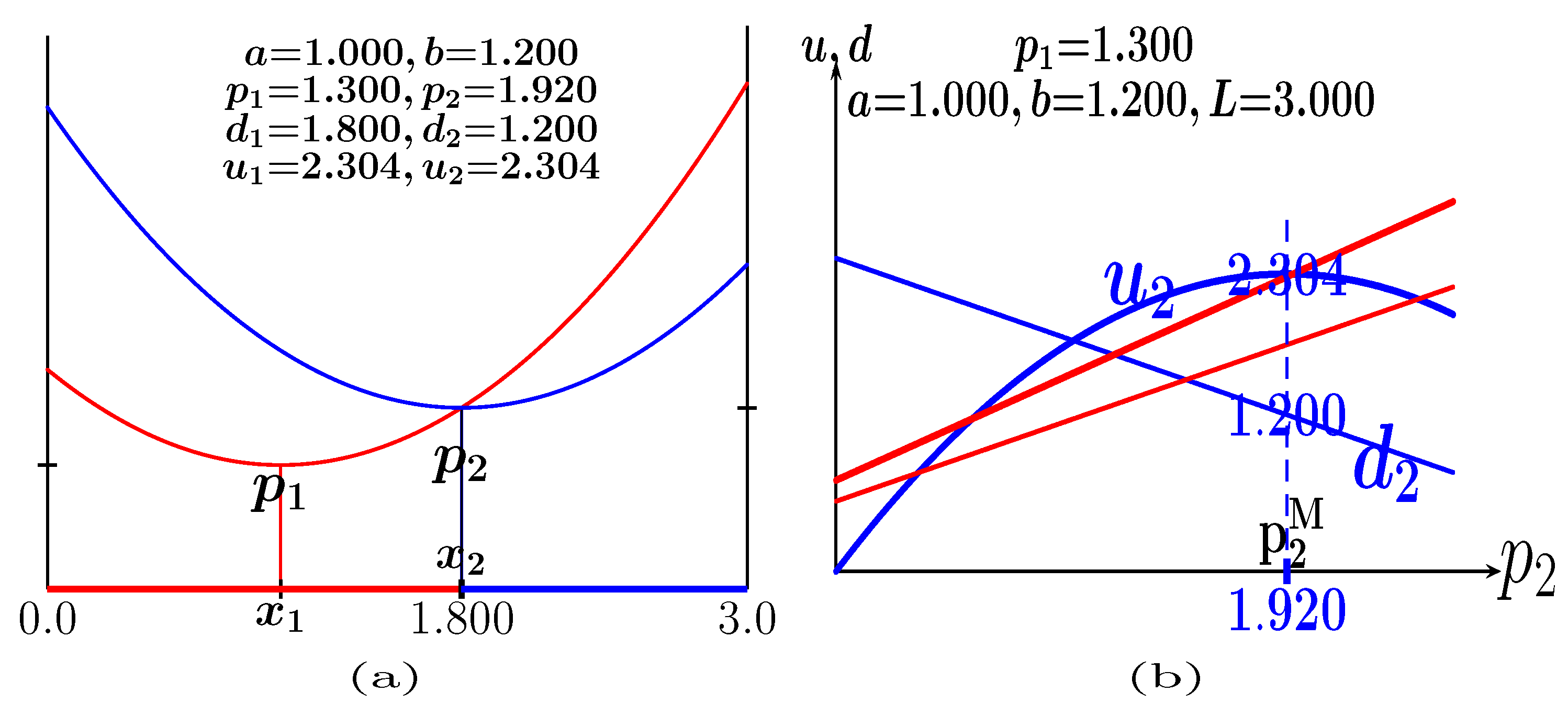
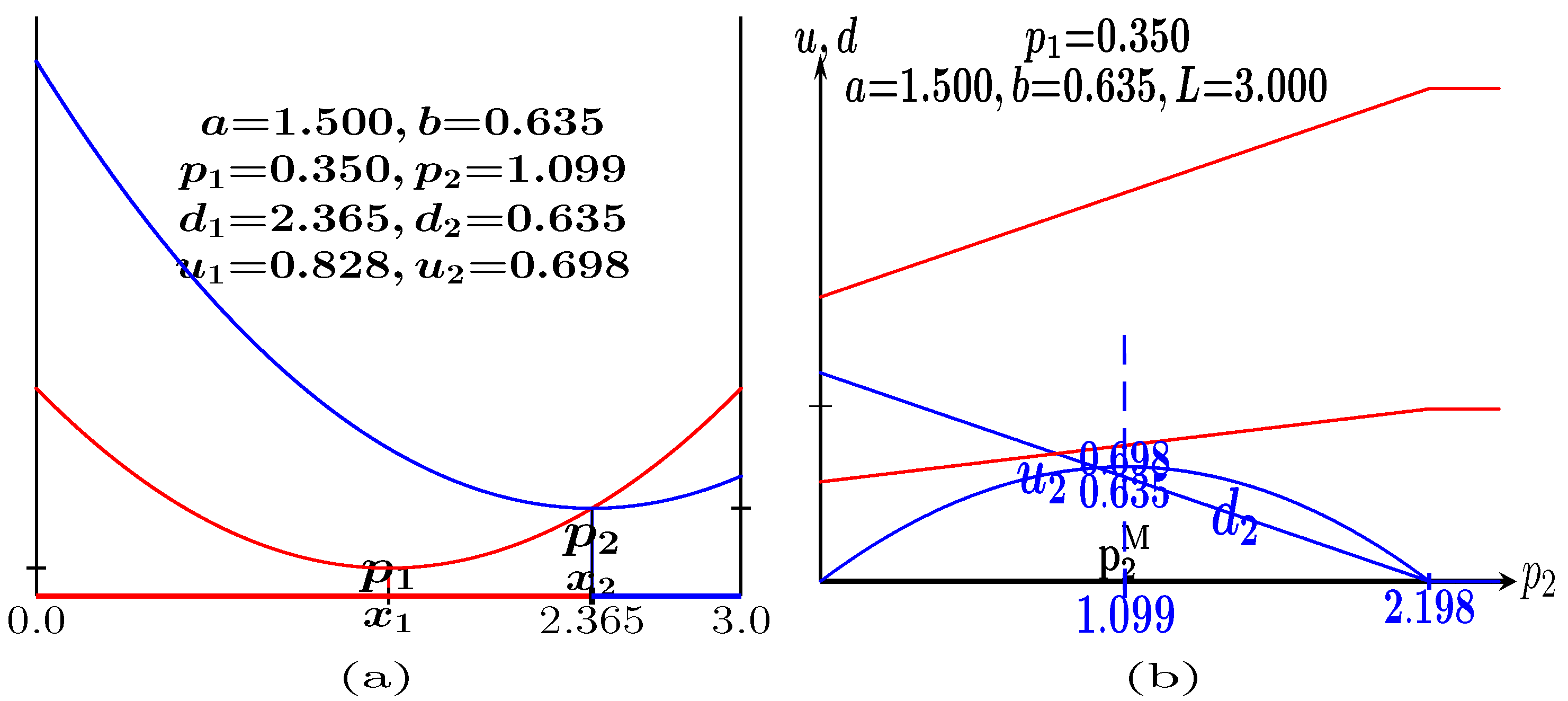
- Every leader player 1 in the lattice will act first and will locate which state variables among that of himself and those of his mate neighbors would provide him the highest payoff applying the backwards induction principle. Such a generic leader will adopt the best local state variables (Figure 3a).
- After updating the state variables of every player 1 in the lattice, each follower player 2 will locate among that of himself and those of his mate neighbors the state variables that provide the best payoff when playing with his partner neighbors: The generic follower will adopt the best values of the state variables (Figure 3b).
- Once the moves are made, every player plays with his four adjacent partners such that the payoff of a given individual at time-step is the average over these four games (Figure 3c).
4. Simulation of the Sequential Hotelling Game
4.1. The SHOT-b Game
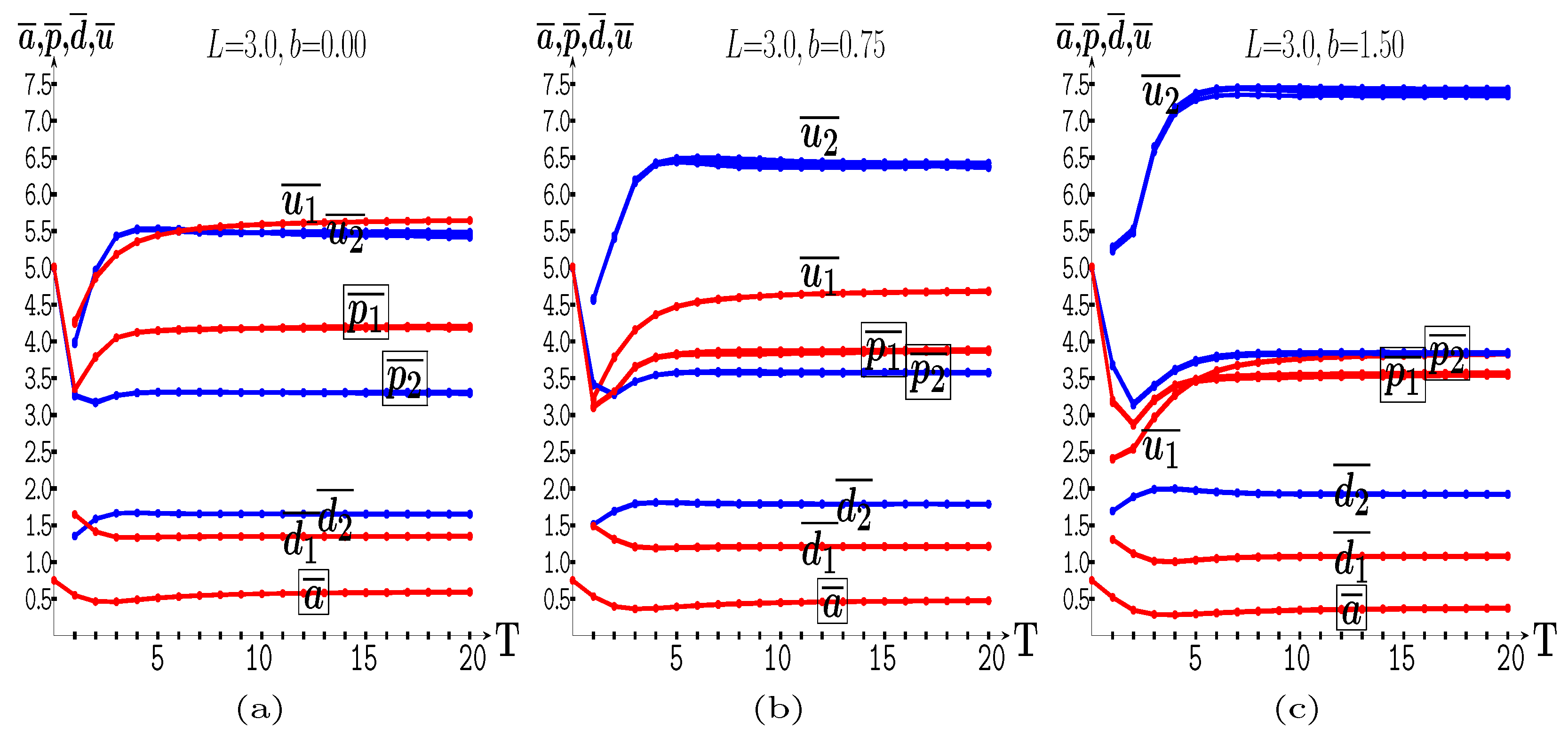
4.1.1. Simulation Dynamics
4.1.2. -Response Given and Prices
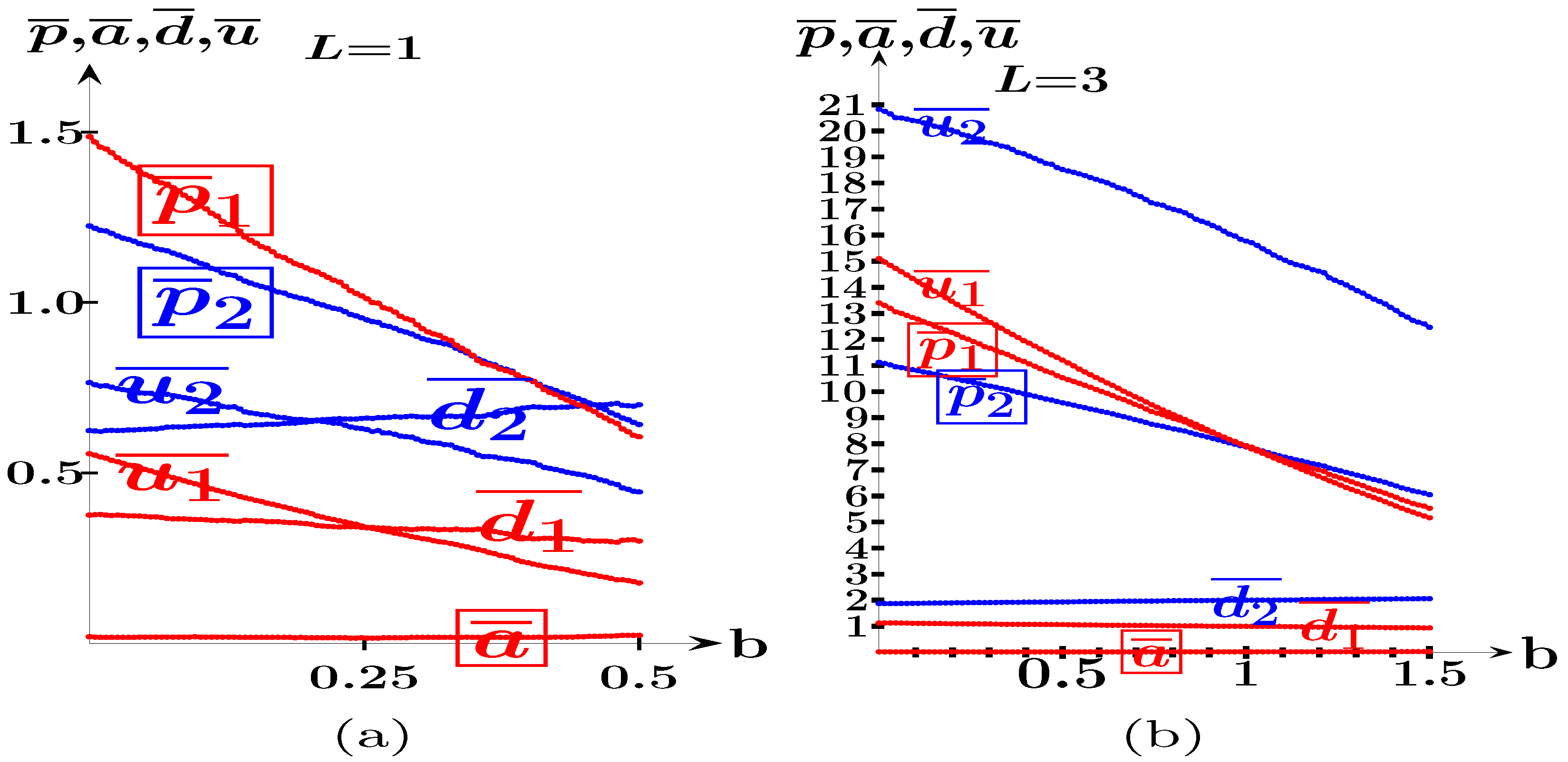
4.1.3. Parameterized b
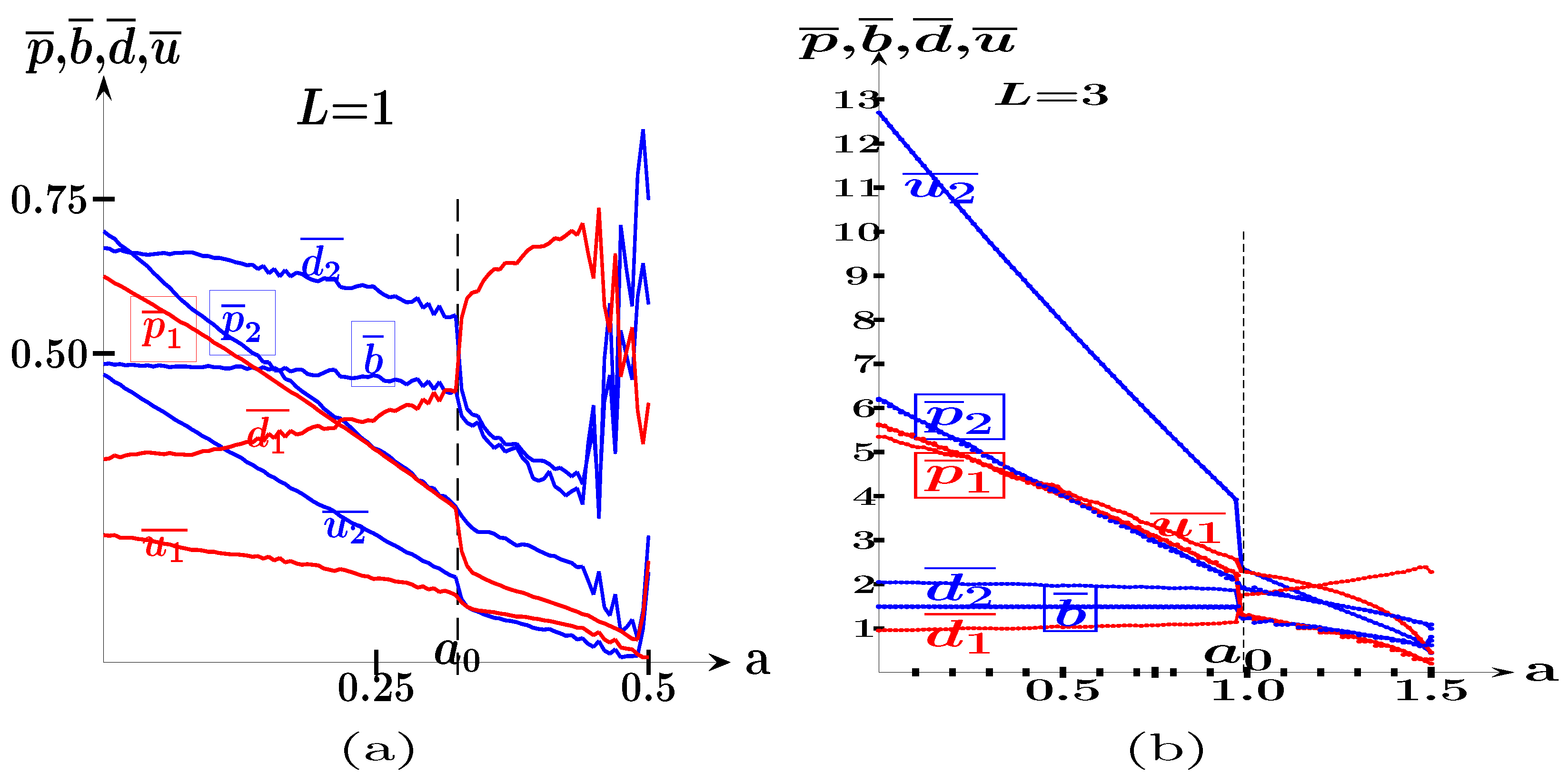
4.2. The SHOT-a Game
5. Quadratic Transportation Cost
5.1. The SHOT2-b Game
5.2. The SHOT2-a Game
6. Conclusions
- The subgame perfect equilibrium (SPE) solution exists in both scenarios regardless of the proximity of players in a finite market of length .
- The follower overrates the leader as a general rule. The only exception applies to the SHOT-b game with very low , that is, in which case the leader overrates the follower to a low extent.
- In the SHOT-b game, the advantage of the follower increases with in a linear-like way, reaching its maximum when the follower is located in the market center.
- In the SHOT-a game, the effect of the variation in is quite sophisticated, so the maximum payoff of the leader is reached at , which defines the SPE solution in the location–price SHOT game.
- In the SHOT game with quadratic transportation cost, the follower advantage notably increases compared to that found with linear transportation cost, and in the SPE solution in the location–price SHOT game, the leader shifts to his market end.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Initial Simulation Iteration

Appendix A.2. Patterns

Appendix A.3. Fortran Codes
| SUBROUTINE SHOTALEAD(BC,WPP,p1p,i,j,n) |
| double precision WPP(n,n);integer BC(0:n+1) |
| COMMON /HOT/ rL,rL2,r2L,xx1 |
| ux=0.d0;p1p=WPP(i,j);fx2=rL2/1000.d0 |
| DO jj=j-1,j+1;DO ii=i-1,i+1;ik=BC(ii);jh=BC(jj) |
| if(mod(ik+jh,2)==1)cycle;pp1=WPP(ik,jh) |
| p2x=0.d0;x2x=0.d0;u2x=0.d0 |
| DO ix2=1,1001 |
| x2=rL2+(ix2-1)*fx2;diffx=x2-xx1;sumx=x2+xx1 |
| p2=pp1-diffx-0.001d0;if(p2x<0.d0) goto 1 !U |
| u2=p2*rL |
| if(u2>u2x)then;p2x=p2;x2x=x2;u2x=u2;endif |
| 1 p2=(pp1+r2L-sumx)/2.d0 !M |
| call HOT(rL,pp1,p2,xx1,x2,u1,u2) |
| if(u2>u2x)then;p2x=p2;x2x=x2;u2x=u2;endif |
| p2=pp1+diffx-0.001d0 !N |
| call HOT(rL,pp1,p2,xx1,x2,u1,u2) |
| if(u2>u2x)then;p2x=p2;x2x=x2;u2x=u2;endif |
| ENDDO |
| call HOT(rL,pp1,p2x,xx1,x2x,u1,u2) |
| if(u1>ux)then;ux=u1;p1p=pp1;endif |
| ENDDO;ENDDO |
| END |
| SUBROUTINE SHOTAFOLLOW(BC,WPP,WXX,p2p,x2x,i,j,n) |
| double precision WPP(n,n),WXX(n,n) |
| integer BC(0:n+1);COMMON /HOT/ rll,xx1 |
| ux=0.d0;p2p=0.d0;x2x=0.d0 |
| DO jj=j-1,j+1;DO ii=i-1,i+1;ik=BC(ii);jh=BC(jj) |
| if(mod(ik+jh,2)==0)cycle |
| p2=WPP(ik,jh);x2=WXX(ik,jh);uux=0.d0 |
| DO jjj=j-1,j+1;DO iii=i-1,i+1;ik=BC(iii);jh=BC(jjj) |
| if(mod(ik+jh,2)==1)cycle |
| p1p=WPP(ik,jh) |
| call HOT(rll,p1p,p2,xx1,x2,u1,u2) |
| uux=uux+u2 |
| ENDDO;ENDO |
| if(uux>ux)then;ux=uux;p2p=p2;x2x=x2;endif |
| ENDDO;ENDDO |
| END |
| SUBROUTINE SHOTA-SCRATCH integer, parameter::nsx=1000; double precision SHOTA(nsx+1,8) commom/HOT/ rL,rL2; rix=rL2/nsx plim=2.d0;if(rL==3.d0)plim=10.d0;pip=plim/nsx DO ia=1,nsx+1;xa=(ia-1)*rix uli=0.d0;pa=0.d0;xb=0.d0;pb=0.d0 DO ipi=1,nsx+1;plix=(ipi-1)*pip xbx=0.d0;fop=0.d0;pli=0.d0;ufo=0.d0 DO ixb=1,nsx+1;bx=(ixb-1)*rix x2=rll-bx;diffx=x2-xa fopx=plix-diffx-0.001d0 !————-U————— if(fopx<0.d0)goto 1 u2=fopx*rll if(u2>ufo)then; xbx=bx;fop=fopx;pli=plix;ufo=u2; endif 1 fopx=(plix+rll-xa+bx)/2.d0 !——–M—————- call XHOT(rll,plix,fopx,xa,x2,u1,u2) if(u2>ufo)then; xbx=bx;fop=fopx;pli=plix;ufo=u2; endif fopx=plix+diffx-0.001d0 !————-N—————- call XHOT(rll,plix,fopx,xa,x2,u1,u2) if(u2>ufo)then; xbx=bx;fop=fopx;pli=plix;ufo=u2; endif ENDDO call HOT(rL,pli,fop,xa,rL-xbx,u1,u2) if(u1>uli)then; uli=u1;pa=pli;xb=xbx;pb=fop; endif ENDDO SHOTA(ia,1)=xa;SHOTA(ia,2)=pa;SHOTA(ia,3)=xb;SHOTA(ia,4)=pb ENDDO DO ia=1,nsx+1 xa=SHOTA(ia,1);pa=SHOTA(ia,2);xb=SHOTA(ia,3);pb=SHOTA(ia,4) call XHOT(rL,pa,pb,xa,rL-xb,d1,d2,u1,u2) SHOTA(ia,5)=d1;SHOTA(ia,6)=d2;SHOTA(ia,7)=u1;SHOTA(ia,8)=u2 ENDDO c————– print SHOTA———— END |
| subroutine RAWBLEAD(bc,WPP,WXX,p1p,x1x,i,j,n) |
| double precision WPP(n,n),WXX(n,n) |
| integer bc(0:n+1);common/hot/rll,xx2 |
| ux=0.d0;p1p=WPP(i,j) |
| DO jj=j-1,j+1;DO ii=i-1,i+1;ik=bc(ii);jh=bc(jj) |
| if(mod(ik+jh,2)==1)cycle;pp1=WPP(ik,jh);xx1=WXX(ik,jh) |
| diffx=xx2-xx1 |
| p2x=0.d0;u2x=0.d0;fp2=(pp1+diffx)/1000.d0 |
| DO ipo=1,1001 |
| p2=(ipo-1)*fp2 |
| call HOT2(rll,pp1,p2,xx1,xx2,u1,u2) |
| if(u2>u2x)then;u2x=u2;p2x=p2;endif |
| ENDDO |
| call HOT2(rll,pp1,p2x,xx1,xx2,u1,u2) |
| if(u1>ux)then;ux=u1;p1p=pp1;x1x=xx1;endif |
| ENDDO;ENDDO |
| end |
References
- Hotelling, H. Stability in competition. Econ. J. 1929, 39, 41–57. [Google Scholar] [CrossRef]
- Hinloopen, J.; Martin, S. The Hotelling Line at 95: Introduction to the Special Issue. Rev. Ind. Organ. 2024, 65, 627–648. [Google Scholar] [CrossRef]
- d’Aspremont, C.; Gabszewicz, J.J.; Thisse, J.F. On Hotelling’s “Stability in competition”. Econometrica 1979, 47, 1145–1150. [Google Scholar] [CrossRef]
- Puu, T. Hotelling’s “Ice cream dealers” with elastic demand. Ann. Reg. Sci. 2002, 36, 1–17. [Google Scholar] [CrossRef]
- Graitson, D. On Hotelling’s ’stability in competition’ again. Econ. Lett. 1980, 6, 1–6. [Google Scholar] [CrossRef]
- Iskakov, M.; Iskakov, A. Solution of the Hotelling’s game in secure strategies. Econ. Lett. 2012, 117, 115–118. [Google Scholar] [CrossRef]
- Shy, O. Hotelling’s Model with Firms Located Close to Each Other. Rev. Ind. Organ. 2024, 65, 649–668. [Google Scholar] [CrossRef]
- Puu, T.; Sushko, I. Oligopoly Dynamics: Models and Tools; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Gabszewicz, J.J.; Schweizer, U.; Thisse, J.F.; Fujita, M. Location Theory; Routledge: London, UK, 2001. [Google Scholar]
- Anderson, S. Spatial competition and price leadership. Int. J. Ind. Organ. 1987, 5, 69–398. [Google Scholar] [CrossRef]
- Neven, D. Two stage (perfect) equilibrium in Hotelling’s game. J. Ind. Econ. 1985, 23, 317–325. [Google Scholar] [CrossRef]
- Garcia-Perez, L.; Grau-Climent, J.; Losada, J.C.; Alonso-Sanz, R. Simulation of the Stackelberg-Hotelling game. Games 2024, 15, 34. [Google Scholar] [CrossRef]
- Wolfram, S. A New Kind of Science; Wolfram Media: Champaign, IL, USA, 2002. [Google Scholar]
- Fleckinger, P.; Lafay, T. Product flexibility and price competition in Hotelling’s duopoly. Math. Soc. Sci. 2010, 60, 61–68. [Google Scholar] [CrossRef][Green Version]
- Grau-Climent, J.; Garcia-Perez, L.; Losada, J.C.; Alonso-Sanz, R. Simulation of the Hotelling-Smithies game: Hotelling was not so wrong. Commun. Nonlinear Sci. Numer. Simul. 2022, 110, 106513. [Google Scholar] [CrossRef]
- Lerner, A.P.; Singer, H.W. Some notes on duopoly and spatial competition. J. Political Econ. 1937, 45, 145–186. [Google Scholar] [CrossRef]
- Smithies, A. Optimum location in spatial competition. J. Political Econ. 1941, 49, 423–439. [Google Scholar] [CrossRef]
| 1 | The NE obtained in [1] is achieved at the intersection of the optimized reaction functions of the two players obtained via derivatives. Namely, at the intersection of , i.e., , and , i.e., . |
| 2 | . . In the location-symmetric game it is , in which case supports . |
| 3 | , and . Both constraints reduce in the location-symmetric game to . |
| 4 | . Thus, in Figure 8a, , so that , .In Figure 8b, , so that , . In Figure 8c, , so that . In Figure 8c, becomes , so that with it is . |
| 5 | |
| 6 | From a generic , it is . Thus, . |
| 7 | . |
| 8 | This value arises from with , that is, from . |
| 9 | Note that there is no value discontinuity in the prices at . Thus, for example, in the case of at it is as follows: and |
| 10 | This may be proven by maximizing the given in Equation (10b) or just referring to footnote 7 in the particular case of |
| 11 | . = |
| 12 | =. It is |
| 13 | . Note that at it is, , and Therefore, there is no discontinuity in the values of the variables at . Moreover, if it is according to Equation (12a). That is why it is when . |
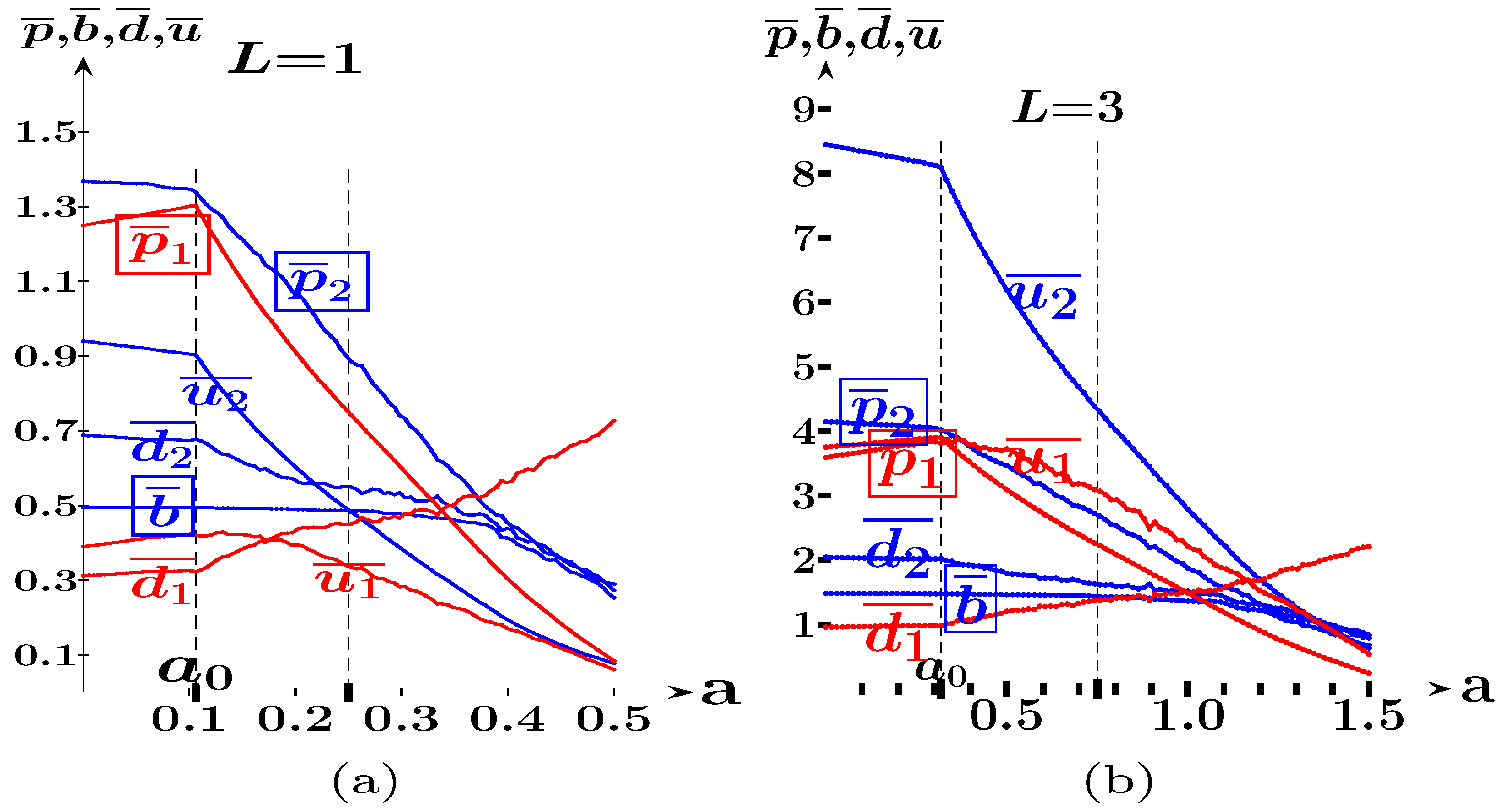
| 14 | In Figure 13 at , with it is , , , , and with it is , , , . |
| 15 | ; |
| 16 | . |
| 17 | . It is ; therefore, undercuts player 2 when in Figure 16c, far beyond the scope of in this figure. |
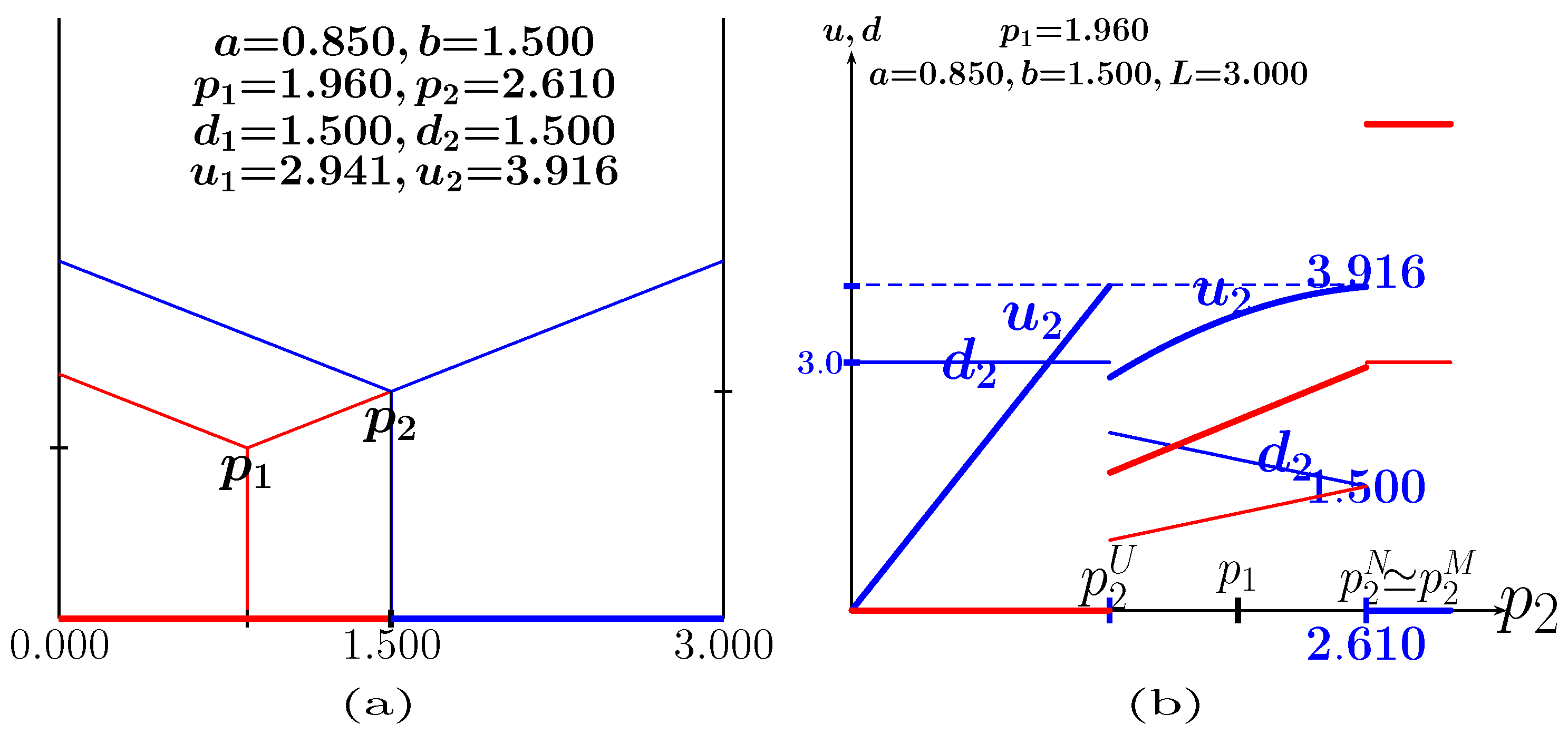
| 18 | With it is , , ; and with it is , , . |
| 19 | . Additionally, . Therefore, . |
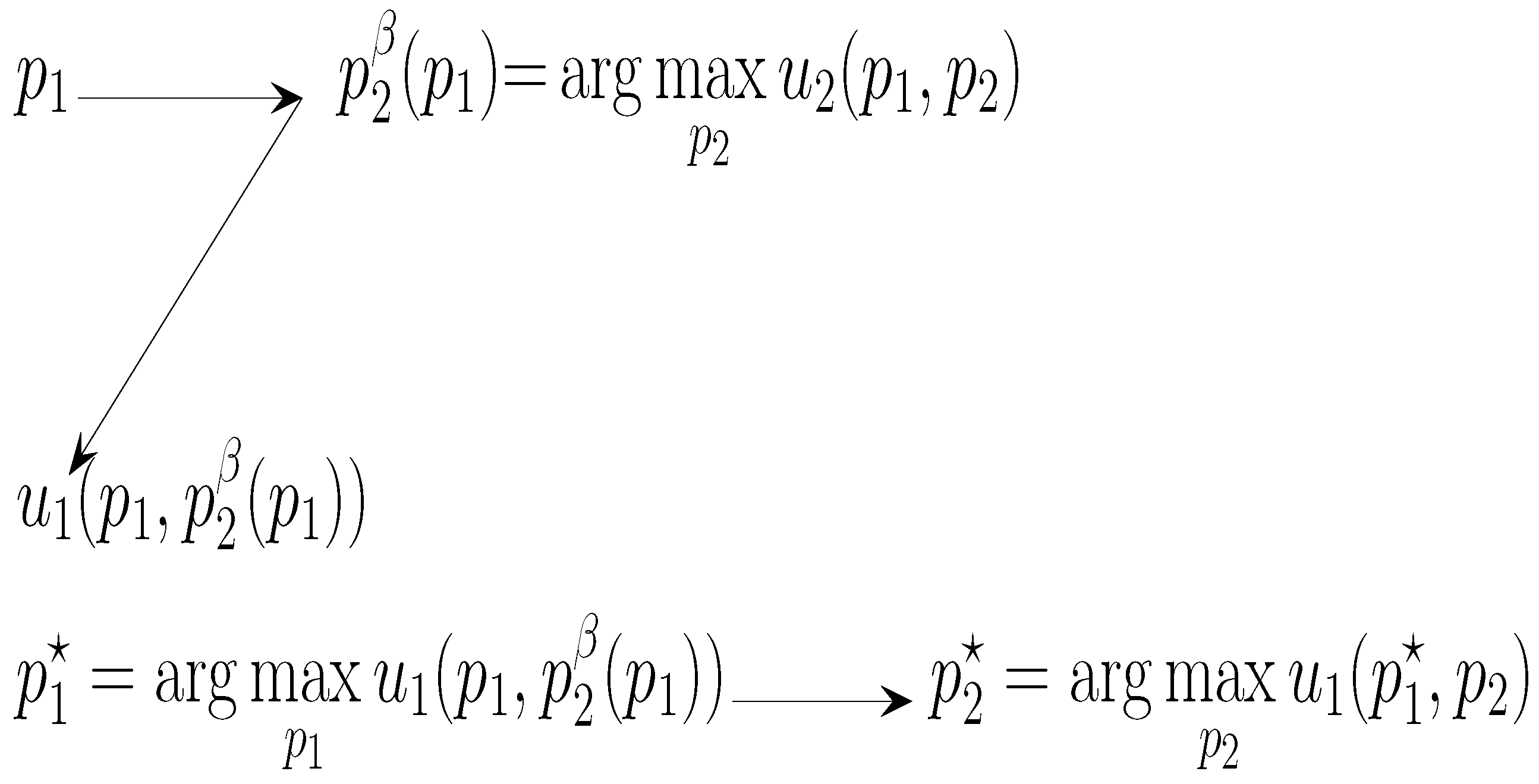








| subroutine SHOTBLEAD(bc,WPP,WXX,p1p,x1x,i,j,n) |
| double precision WPP(n,n),WXX(n,n);integer bc(0:n+1) |
| common /hot/rL,r2L,xx2 |
| ux=0.d0;p1p=WPP(i,j);x1x=WXX(i,j) |
| DO jj=j-1,j+1;DO ii=i-1,i+1;ik=bc(ii);jh=bc(jj) |
| if(mod(ik+jh,2)==1)cycle |
| pp1=WPP(ik,jh);xx1=WXX(ik,jh) |
| p2x=0.d0;u2x=0.d0 |
| diffx=xx2-xx1;sumx=xx2+xx1 |
| p2=pp1-diffx-0.001d0;if(p2x<0.d0) goto 1 !U |
| u2=p2*rL |
| if(u2>u2x)then;p2x=p2;u2x=u2;endif |
| 1 p2=(pp1+r2L-sumx)/2.d0 !M |
| call HOT(rL,pp1,p2,xx1,xx2,u1,u2) |
| if(u2>u2x)then;p2x=p2;u2x=u2;endif |
| p2=pp1+diffx-0.001d0 !N |
| call HOT(rL,pp1,p2,xx1,xx2,u1,u2) |
| if(u2>u2x)then;p2x=p2;u2x=u2;endif |
| call HOT(rL,pp1,p2x,xx1,xx2,u1,u2) |
| if(u1>ux)then;ux=u1;p1p=pp1;x1x=xx1;endif |
| ENDDO;ENDDO |
| end |
| suboutine SHOTBFOLLOW(BC,WPP,WXX,p2p,i,j,n) |
| double precision WPP(n,n),WXX(n,n) |
| integer BC(0:n+1); common/hot/rL,xx2 |
| ux=0.d0;p2p=0.d0 |
| DO jj=j-1,j+1;DO ii=i-1,i+1;ik=BC(ii);jh=BC(jj) |
| if(mod(ik+jh,2)==0)cycle |
| p2=WPP(ik,jh);uux=0.d0 |
| DO jjj=j-1,j+1;DO iii=i-1,i+1;ik=BC(iii);jh=BC(jjj) |
| if(mod(ik+jh,2)==1)cycle |
| p1p=WPP(ik,jh);x1x=WXX(ik,jh) |
| call HOT(rL,p1p,p2,x1x,xx2,u1,u2) |
| uux=uux+u2 |
| ENDDO;ENDDO |
| if(uux>ux)then;ux=uux;p2p=p2;endif |
| ENDDO;ENDDO |
| end |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Garcia-Perez, L.; Grau-Climent, J.; Losada, J.C.; Alonso-Sanz, R. The Sequential Hotelling Game with One Parameterized Location. AppliedMath 2025, 5, 69. https://doi.org/10.3390/appliedmath5020069
Garcia-Perez L, Grau-Climent J, Losada JC, Alonso-Sanz R. The Sequential Hotelling Game with One Parameterized Location. AppliedMath. 2025; 5(2):69. https://doi.org/10.3390/appliedmath5020069
Chicago/Turabian StyleGarcia-Perez, Luis, Juan Grau-Climent, Juan C. Losada, and Ramon Alonso-Sanz. 2025. "The Sequential Hotelling Game with One Parameterized Location" AppliedMath 5, no. 2: 69. https://doi.org/10.3390/appliedmath5020069
APA StyleGarcia-Perez, L., Grau-Climent, J., Losada, J. C., & Alonso-Sanz, R. (2025). The Sequential Hotelling Game with One Parameterized Location. AppliedMath, 5(2), 69. https://doi.org/10.3390/appliedmath5020069






