New Exploration of Phase Portrait Classification of Quadratic Polynomial Differential Systems Based on Invariant Theory
Abstract
1. Introduction and Statement of the Main Results
2. Preliminary Efinitions
2.1. Equilibrium Points
- If the , we say that the equilibrium q is non-degenerate;
- If the real part of the two eigenvalues of the matrix are non-zero, we say that the equilibrium q is hyperbolic;
- If only one of the eigenvalues of the matrix is zero, we say that the equilibrium q is semi-hyperbolic.
- If the two eigenvalues of the matrix are non-zero, we say that the equilibrium q is elemental;
- If only one of the eigenvalues of the matrix is zero, we say that the equilibrium q is semi-elemental;
- If the two eigenvalues are zero but the matrix is not the zero matrix, we say that the equilibrium q is nilpotent;
- If the matrix is the zero matrix, we say that the equilibrium q is intricate;
- If , we say that the equilibrium q is an elemental saddle;
- If and any neighborhood of q is filled with periodic orbits (otherwise, the equilibrium q is a center), we say that the equilibrium q is an elemental anti-saddle, i.e., it is either a node or a focus.
2.2. Reducing the Number of Parameters of Systems VII and VIII
2.3. Invariants
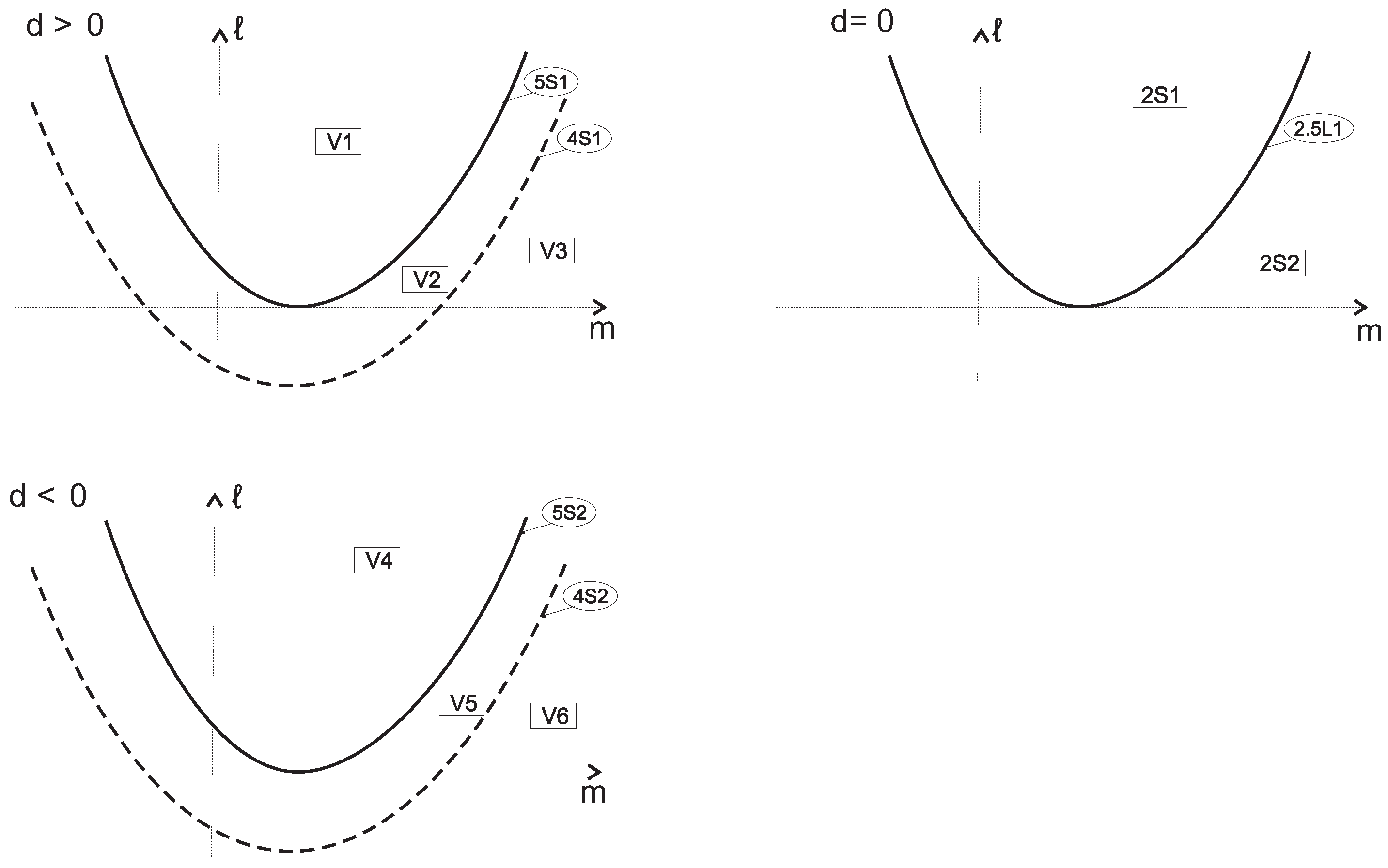
2.3.1. Algebraic Bifurcation Surfaces
2.3.2. Non-Algebraic Bifurcation Hypersurfaces
2.3.3. Differences from Previous Works Using the Same Technique
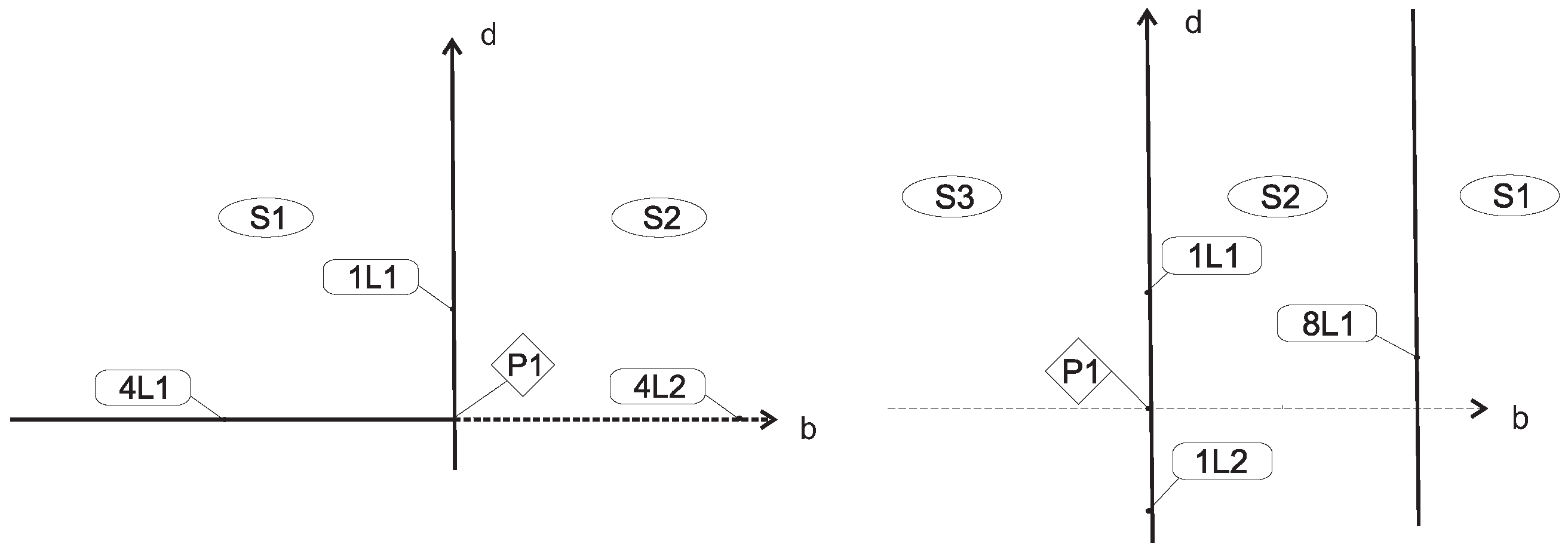
3. Phase Portraits
3.1. Phase Portraits of Systems VII(A)
3.2. Phase Portraits of Systems VII(B)
3.3. Phase Portraits of Systems VII(C) and VII(D)
3.4. Phase Portraits of Systems VIII(A)
3.5. Phase Portraits of Systems VIII(B)
3.6. Phase Portraits of Systems VIII(C)
4. Global Geometrical Properties of Family VII
- (12) ;
- (13) ;
- (14) ;
- (23) ;
- (44) ;
- (45) ;
- (46) ;
- (47) ;
- (50) ;
- (51) ;
- (52) ;
- (71) ;
- (72) ;
- (84) ;
- (124) ;
- (134) ;
- (135) ;
- (137) ;
- (138) ;
- (141) .
- (142) ;
- (144) ;
- (145) ;
- (146) ;
- (147) ;
- (149) .
- (152) ;
- (153) ;
- (160) ;
- (161) ;
- (162) ;
- (163) ;
- (164) ;
- (166) ;
- (167) ;
- (168) ;
- (170) ;
- (186) ;
- (188) ;
- (190) ;
- (195) ;
- (196) ;
- (198) ;
- (202) ,
- (203) ;
- (208) .
5. Global Geometrical Properties of Family VIII
6. Conclusions and Comments
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
- ,
- ,
- ,
- ,
- ,
- ,
- ,
- ,
- ,
- ,
- ,
- ,
- ,
- ,
- ,
- ,
- ,
- ,
- .
- ,
- ,
- ,
- ,
- ,
- ,
- ,
- ,
- ,
- ,
- ,
- ,
- ,
- ,
- ,
- ,
- ,
- ,
- .
References
- Coppel, W.A. A Survey of Quadratic Systems. Differ. Equ. 1966, 2, 293–304. [Google Scholar] [CrossRef]
- Büchel, W. Zur Topologie der Durch Eine Gewöhnliche Differentialgleichung Erster Ordnung und Ersten Grades Definierten Kurvenschar; Druck von BG Teubner: Leipzig, Germany, 1904; pp. 33–68. [Google Scholar]
- Chicone, C.; Tian, J. On general properties of quadratic systems. Am. Math. Mon. 1982, 89, 167–178. [Google Scholar] [CrossRef]
- Artés, J.C.; Llibre, J.; Schlomiuk, D.; Vulpe, N. Geometric Configurations of Singularities of Planar Polynomial Differential Systems. In A Global Classification in the Quadratic Case; Birkhäuser: Basel, Switzerland, 2021. [Google Scholar]
- Ye, Y. Theory of limit cycles. In Translations of Mathematical Monographs; American Mathematical Society: Providence, RI, USA, 1986; Volume 66. [Google Scholar]
- Gasull, A.; Li-Ren, S.; Llibre, J. Chordal quadratic systems. Rocky Mt. Math. 1986, 16, 751–782. [Google Scholar] [CrossRef]
- Artés, J.C.; Cairó, L.; Llibre, J. Phase portraits of the family IV of the quadratic polynomial differential systems. Qual. Theory Dyn. Syst. 2025, 24, 66. [Google Scholar] [CrossRef]
- Cairó, L.; Llibre, J. Phase portraits of the families VII and VIII of the Quadratic Systems. Axioms 2025, 12, 756. [Google Scholar] [CrossRef]
- Artés, J.C.; Llibre, J.; Schlomiuk, D.; Vulpe, N. Global analysis of Riccati quadratic differential systems. Int. J. Bifurc. Chaos 2024, 34, 2450004. [Google Scholar] [CrossRef]
- Artés, J.C.; Llibre, J.; Schlomiuk, D. The geometry of quadratic differential systems with a weak focus of second order. Int. Bifur. Chaos Appl. Sci. Eng. 2006, 16, 3127–3194. [Google Scholar] [CrossRef]
- Schlomiuk, D.; Vulpe, N. Planar quadratic differential systems with invariant straight lines of at least five total multiplicity. Qual. Theory Dyn. Syst. 2004, 5, 135–194. [Google Scholar] [CrossRef]
- Schlomiuk, D.; Vulpe, N. Integrals and phase portraits of planar quadratic differential systems with invariant lines of at least five total multiplicity. Rocky Mt. Math. 2008, 38, 2015–2075. [Google Scholar] [CrossRef]
- Schlomiuk, D.; Vulpe, N. Integrals and phase portraits of planar quadratic differential systems with invariant lines of total multiplicity four. Bul. Acad. Ştiinţe Repub. Mold. Mat. 2008, 56, 27–83. [Google Scholar]
- Schlomiuk, D.; Vulpe, N. Planar quadratic differential systems with invariant straight lines of total multiplicity four. Nonlinear Anal. 2008, 68, 681–715. [Google Scholar] [CrossRef]
- Schlomiuk, D.; Vulpe, N. Global classification of the planar Lotka–Volterra differential systems according to their configurations of invariant straight lines. J. Fixed Point Theory Appl. 2010, 8, 177–245. [Google Scholar] [CrossRef]
- Schlomiuk, D.; Vulpe, N. Global topological classification of Lotka–Volterra quadratic differential systems. Electron. J. Differ. Equ. 2012, 2012, 69. [Google Scholar]
- Artés, J.C.; Llibre, J.; Schlomiuk, D.; Vulpe, N. Global topological configurations of singularities for the whole family of quadratic differential systems. Qual. Theory Dyn. Syst. 2020, 19, 51. [Google Scholar] [CrossRef]
- Reyn, J.W. Phase portraits of planar quadratic systems. In Mathematics and Its Applications; Springer: New York, NY, USA, 2007; Volume 583, xvi+334p. [Google Scholar]

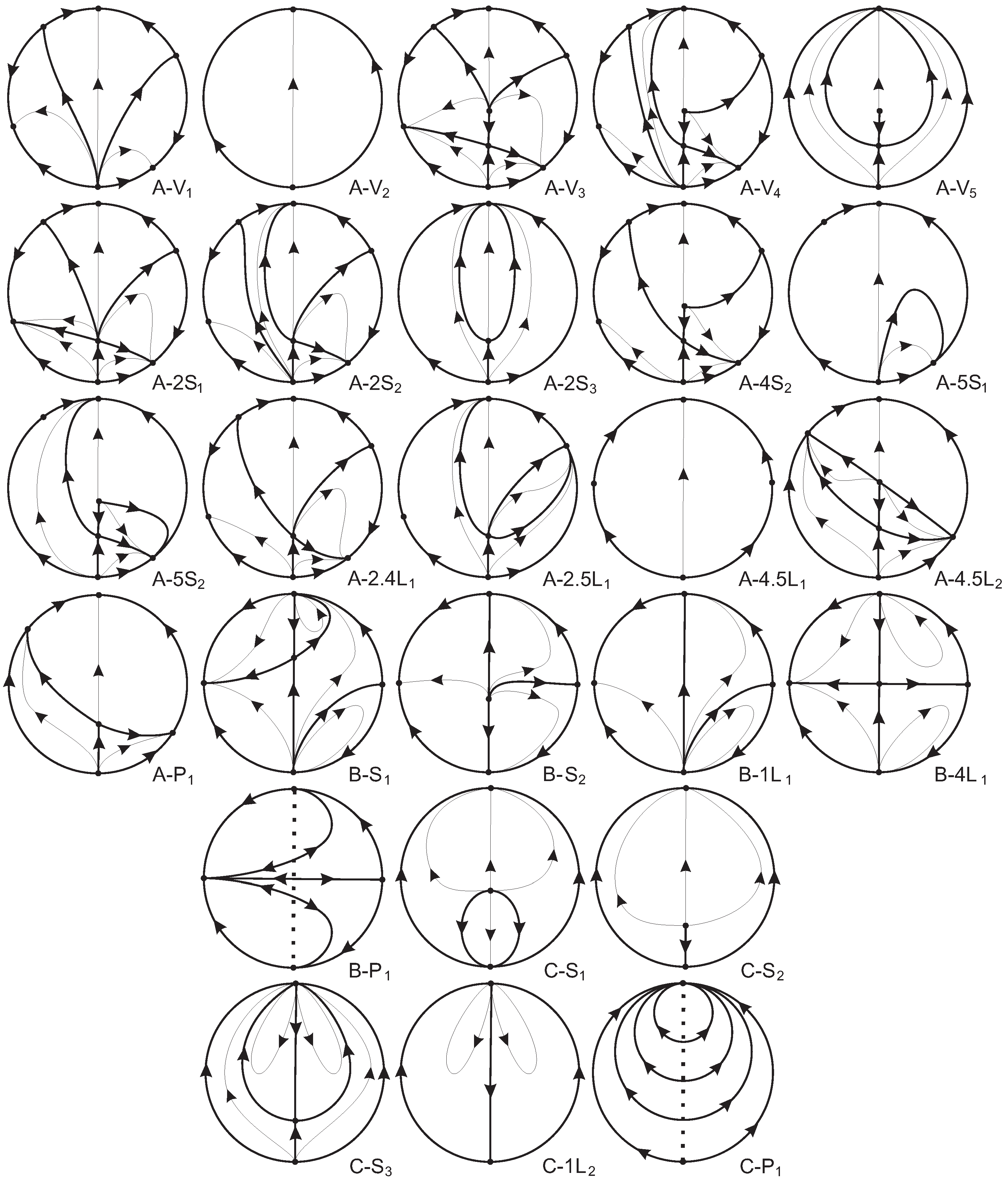


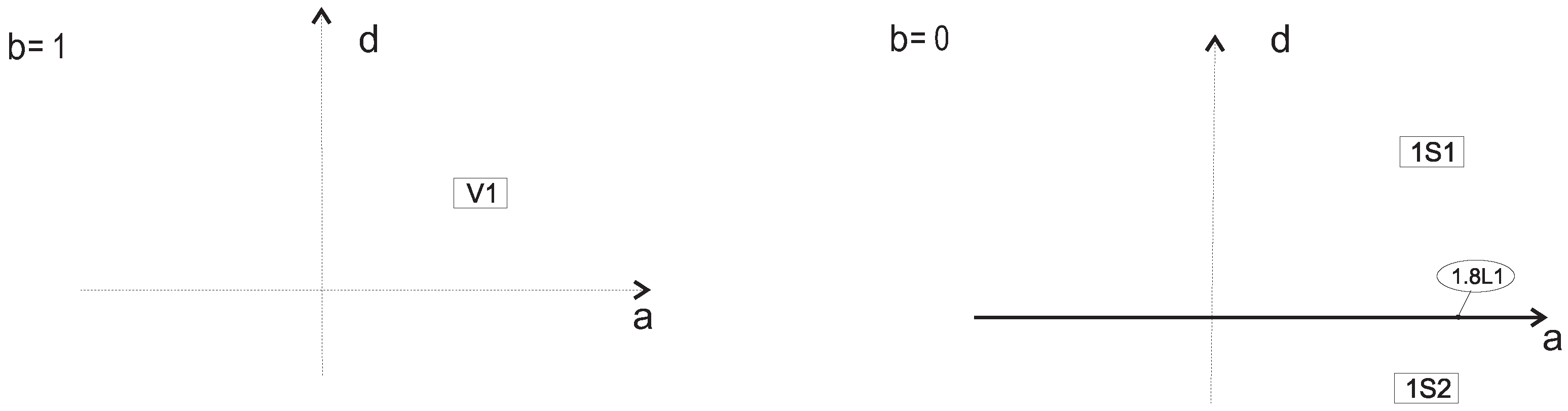
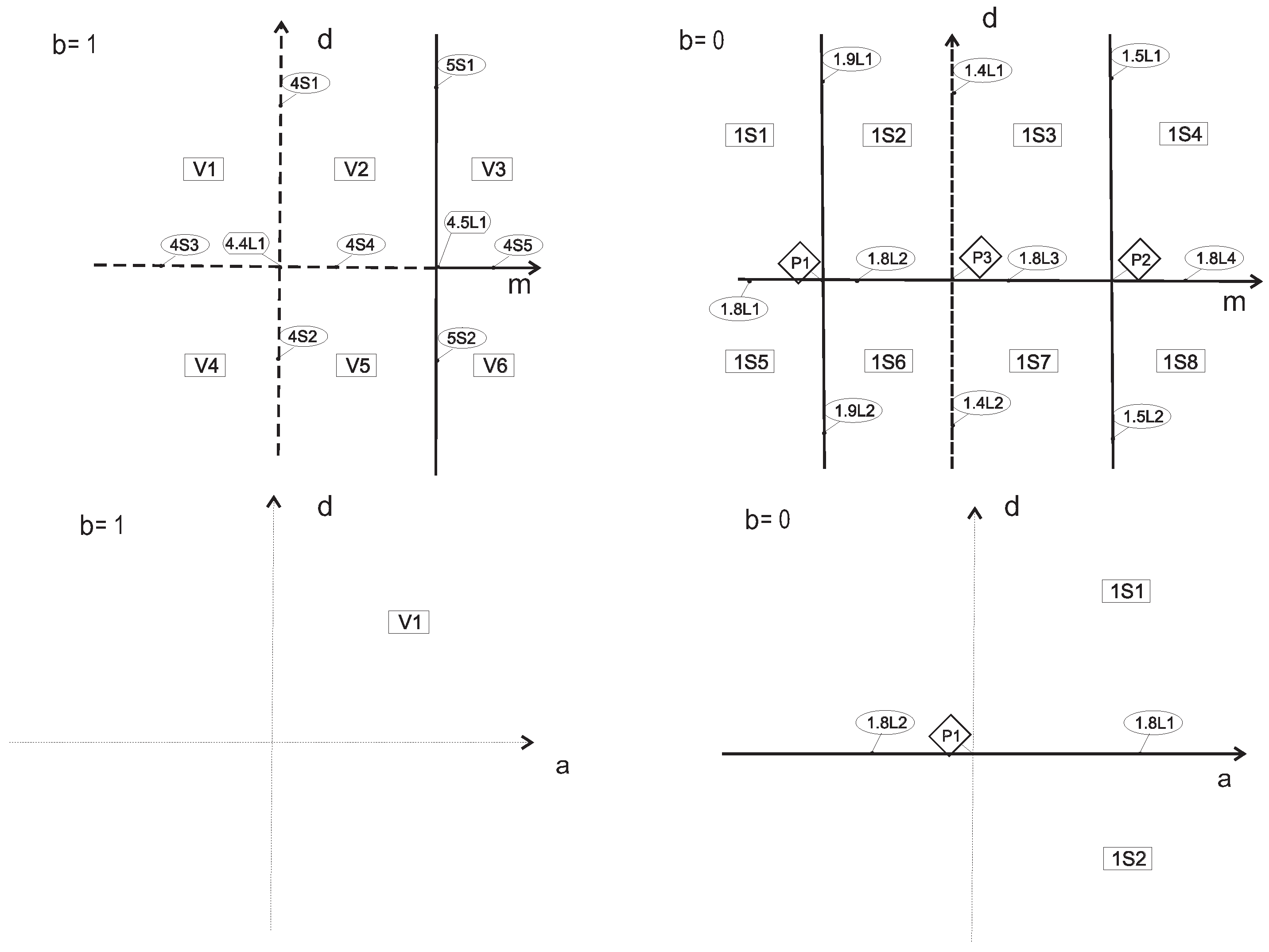

| Presented Phase Portrait | Multiple Equilibrium | Invariant Straight Line | Other Reasons |
|---|---|---|---|
| , , , | |||
| , , | , , , | ||
| , | |||
| , , | |||
| , , | |||
| , | , | , , | |
| , , | |||
| , | ,, | , , | |
| , | |||
| , , | |||
| , | |||
| , | |||
| , | |||
| , | |||
| Presented Phase Portrait | Multiple Equilibrium | Invariant Straight Line | Other Reasons |
|---|---|---|---|
| , , | , , | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Artés, J.C.; Cairó, L.; Llibre, J. New Exploration of Phase Portrait Classification of Quadratic Polynomial Differential Systems Based on Invariant Theory. AppliedMath 2025, 5, 68. https://doi.org/10.3390/appliedmath5020068
Artés JC, Cairó L, Llibre J. New Exploration of Phase Portrait Classification of Quadratic Polynomial Differential Systems Based on Invariant Theory. AppliedMath. 2025; 5(2):68. https://doi.org/10.3390/appliedmath5020068
Chicago/Turabian StyleArtés, Joan Carles, Laurent Cairó, and Jaume Llibre. 2025. "New Exploration of Phase Portrait Classification of Quadratic Polynomial Differential Systems Based on Invariant Theory" AppliedMath 5, no. 2: 68. https://doi.org/10.3390/appliedmath5020068
APA StyleArtés, J. C., Cairó, L., & Llibre, J. (2025). New Exploration of Phase Portrait Classification of Quadratic Polynomial Differential Systems Based on Invariant Theory. AppliedMath, 5(2), 68. https://doi.org/10.3390/appliedmath5020068






