Novel Hybrid Function Operational Matrices of Fractional Integration: An Application for Solving Multi-Order Fractional Differential Equations
Abstract
1. Introduction
Motivation and Contributions
- This work introduces a novel application of orthogonal HFs for solving multi-order FDEs formulated in the Caputo fractional derivative sense.
- A generalized one-shot operational matrix was derived to approximate the fractional-order integral of HFs, expressing the integral explicitly in terms of HFs themselves.
- The derived operational matrix was applied to transform the original multi-order FDEs into a system of algebraic equations, significantly simplifying the computational process. The resulting algebraic equations were solved using a nonlinear algebraic solver.
- The developed numerical algorithm was applied to a set of linear and nonlinear multi-order FDEs to demonstrate the applicability of the proposed algorithm to a wide variety of multi-order FDEs.
- A comparative study was conducted to highlight the superior performance of the proposed algorithm over the existing methods.
2. Orthogonal Hybrid Functions
3. Generalized One-Shot Operational Matrices for Fractional Integration
- Example 3.1
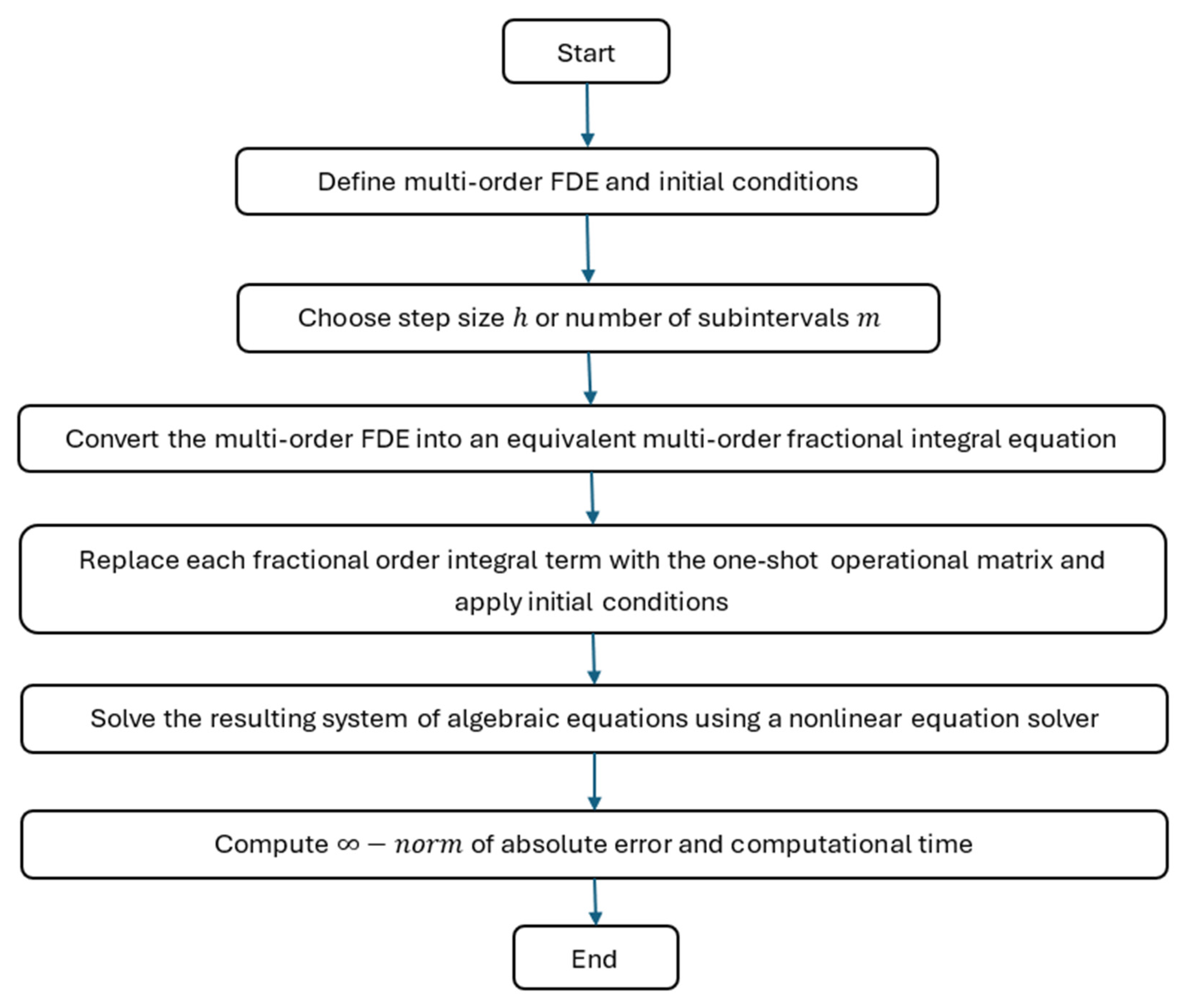
4. Algorithm for Solving Multi-Order FDEs (HFM)
5. Application of the Proposed Numerical Algorithm to Benchmark Examples
5.1. Numerical Examples
- Example 5.1
- Case 1
- Case 2
- Example 5.2
- Case 1
- Case 2
- Example 5.3
- Case 1
- Case 2
- Example 5.4
- Case 1
- Case 3
- Case 4
- Example 5.5
- Case 1
- Example 5.6
- Case 1
5.2. Effect of Step Size on Accuracy and Computational Complexity
6. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Basic Properties of HFs
Appendix A.2. Proof of Theorem 1
Appendix A.3. Proof of Theorem 2
References
- Oldham, K.B.; Spanier, J. The Fractional Calculus: Theory and Applications of Differentiation and Integration to Arbitrary Order; Dover Publications: New York, NY, USA, 1974. [Google Scholar]
- Damarla, S.K.; Kundu, M. Fractional Order Processes: Simulation, Identification, and Control; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar] [CrossRef]
- Gaul, L.; Klein, P.; Kempfle, S. Impulse response function of an oscillator with fractional derivative in damping description. Mech. Res. Comm. 1989, 16, 4447–4472. [Google Scholar] [CrossRef]
- Gaul, L.; Klein, P.; Kempfle, S. Damping description involving fractional operators. Mech. Syst. Signal Process. 1991, 5, 8–88. [Google Scholar] [CrossRef]
- Suarez, L.E.; Shokooh, A. An eigenvector expansion method for the solution of motion containing fractional derivatives. ASME J. Appl. Mech. 1997, 64, 629–635. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Diethelm, K.; Ford, N.J.; Freed, A.D. A predictor-corrector approach for the numerical solution of fractional differential equations. Nonlinear Dyn. 2002, 29, 3–22. [Google Scholar] [CrossRef]
- Odibat, Z.M.; Momani, S. An algorithm for the numerical solution of differential equations of fractional order. J. Appl. Math. Inform. 2008, 26, 15–27. [Google Scholar]
- Adomian, G. Solving Frontier Problems of Physics: The Decomposition Method; Kluwer Academic Publishers: Boston, MA, USA, 1994. [Google Scholar]
- He, J.H. Variational iteration method—A kind of non-linear analytical technique: Some examples. Int. J. Non Linear Mech. 1999, 34, 699–708. [Google Scholar] [CrossRef]
- He, J.H. Homotopy perturbation technique. Comput. Method Appl. Mech. Eng. 1999, 178, 257–262. [Google Scholar] [CrossRef]
- Arigoklu, A.; Ozkol, I. Solution of fractional differential equations by using differential transform method. Chaos Soliton. Fract. 2007, 34, 1473–1481. [Google Scholar]
- Zurigat, M.; Momani, S.; Odibat, Z.; Alawneh, A. The homotopy analysis method for handling systems of fractional differential equations. Appl. Math. Modell. 2010, 34, 24–35. [Google Scholar] [CrossRef]
- Varsha, D.-G.; Hossein, J. An iterative method for solving nonlinear functional equations. J. Math. Anal. Appl. 2006, 316, 753–763. [Google Scholar]
- Li, Y.; Sun, N. Numerical solution of fractional differential equations using the generalized block pulse operational matrix. Comput. Math. Appl. 2011, 62, 1046–1054. [Google Scholar] [CrossRef]
- Tripathi, M.P.; Baranwal, V.K.; Pandey, R.K.; Singh, O.P. A new numerical algorithm to solve fractional differential equations based on operational matrix of generalized hat functions. Commun. Nonlinear Sci. Numer. Simulat. 2013, 18, 1327–1340. [Google Scholar] [CrossRef]
- Doha, E.H.; Bhrawy, A.H.; Ezz-Eldien, S.S. Efficient Chebyshev spectral methods for solving multi-term fractional orders differential equations. Appl. Math. Model. 2011, 35, 5662–5672. [Google Scholar] [CrossRef]
- Doha, E.H.; Bhrawy, A.H.; Ezz-Eldien, S.S. A new Jacobi operational matrix: An application for solving fractional differential equations. Appl. Math. Model. 2012, 36, 4931–4943. [Google Scholar] [CrossRef]
- Saadatmandi, A.; Dehghan, M. A new operational matrix for solving fractional-order differential equations. Comput. Math. Appl. 2010, 59, 1326–1336. [Google Scholar] [CrossRef]
- Saadatmandi, A. Bernstein operational matrix of fractional derivatives and its applications. Appl. Math. Model. 2014, 38, 1365–1372. [Google Scholar] [CrossRef]
- Esmaeili, S.; Shamsi, M.; Luchko, Y. Numerical solution of fractional differential equations with a collocation method based on Muntz polynomials. Comput. Math. Appl. 2011, 62, 918–929. [Google Scholar] [CrossRef]
- Bhrawy, A.H.; Taha, T.M. An operational matrix of fractional integration of the Laguerre polynomials and its application on a semi-infinite interval. Math. Sci. 2012, 6, 41. [Google Scholar] [CrossRef]
- Khader, M.M. An efficient approximate method for solving linear fractional Klein–Gordon equation based on the generalized Laguerre polynomials. Int. J. Comput. Math. 2013, 90, 1853–1864. [Google Scholar] [CrossRef]
- Li, X. Operational method for solving fractional differential equations using cubic B-spline approximation. Int. J. Comput. Math. 2014, 91, 2584–2602. [Google Scholar] [CrossRef]
- Muthukumar, P.; Priya, B.G. Numerical solution of fractional delay differential equation by shifted Jacobi polynomials. Int. J. Comput. Math. 2017, 94, 471–492. [Google Scholar] [CrossRef]
- Xu, X.; Xu, D. Legendre wavelets method for approximate solution of fractional-order differential equations under multi-point boundary conditions. Int. J. Comput. Math. 2018, 95, 998–1014. [Google Scholar] [CrossRef]
- Talib, I.; Tunc, C.; Noor, Z.A. New operational matrices of orthogonal Legendre polynomials and their operational. J. Taibah Univ. Sci. 2019, 13, 377–389. [Google Scholar] [CrossRef]
- Wang, J.; Xu, T.-Z.; Wei, Y.-Q.; Xie, J.-Q. Numerical solutions for systems of fractional order differential equations with Bernoulli wavelets. Int. J. Comput. Math. 2019, 96, 317–336. [Google Scholar] [CrossRef]
- Mall, S.; Chakraverty, S. A novel Chebyshev neural network approach for solving singular arbitrary order Lane-Emden equation arising in astrophysics. Netw. Comput. Neural Syst. 2020, 31, 142–165. [Google Scholar] [CrossRef] [PubMed]
- Hosseininia, M.; Heydari, M.H.; Avazzadeh, Z.; Maalek Ghaini, F.M. A hybrid method based on the orthogonal Bernoulli polynomials and radial basis functions for variable order fractional reaction-advection-diffusion equation. Eng. Anal. Bound. Elem. 2021, 127, 18–28. [Google Scholar] [CrossRef]
- Ahmed, H.M. Enhanced shifted Jacobi operational matrices of derivatives: Spectral algorithm for solving multiterm variable-order fractional differential equations. Bound. Value Probl. 2023, 2023, 108. [Google Scholar] [CrossRef]
- Matoog, R.T.; Ramadan, M.A.; Arafa, H.M. A hybrid numerical technique for solving fractional Fredholm–Volterra integro-differential equations using Ramadan group integral transform and Hermite polynomials. Alex. Eng. J. 2024, 108, 889–896. [Google Scholar] [CrossRef]
- Azarnavid, B.; Emamjomeh, M.; Nabati, M.; Dinmohammadi, A. An efficient iterative method for multi-order nonlinear fractional differential equations based on the integrated Bernoulli polynomials. Comput. Appl. Math. 2024, 43, 68. [Google Scholar] [CrossRef]
- Chaudhary, R.; Aeri, S.; Bala, A.; Kumar, R.; Baleanu, D. Solving system of fractional differential equations via Vieta-Lucas operational matrix method. International. J. Appl. Comput. Math. 2024, 10, 14. [Google Scholar] [CrossRef]
- Manohara, G.; Kumbinarasaiah, S. An innovative operational matrix approach for the numerical solution of fractional order diabetes mellitus model using the Genocchi wavelets. Nonlinear Sci. 2025, 3, 100019. [Google Scholar] [CrossRef]
- Deb, A.; Ganguly, A.; Sarkar, G.; Biswas, A. Numerical solution of third order linear differential equations using generalized one-shot operational matrices in orthogonal hybrid function domain. Appl. Math. Comput. 2012, 219, 1485–1514. [Google Scholar] [CrossRef]
- Deb, A.; Roychoudhury, S.; Sarkar, G. Analysis and Identification of Time-Invariant Systems, Time-Varying Systems, and Multi-Delay Systems Using Orthogonal Hybrid Functions; Theory and Algorithms with MATLAB; Springer International Publishing AG: Cham, Switzerland, 2016. [Google Scholar]
- Caputo, M. Linear models of dissipation whose Q is almost frequency. Part II. J. Roy Austral. Soc. 1967, 13, 529–539. [Google Scholar] [CrossRef]
- Ford, N.J.; Connolly, J.A. Systems-based decomposition schemes for the approximate solution of multi-term fractional differential equations. J. Comput. Appl. Math. 2009, 229, 382–391. [Google Scholar] [CrossRef]
- Shiralashetti, S.C.; Deshi, A.B. An efficient Haar wavelet collocation method for the numerical solution of multi-term fractional differential equations. Nonlinear Dyn. 2016, 83, 293–303. [Google Scholar] [CrossRef]
- Hesameddini, E.; Rahimi, A.; Asadollahifard, E. On the convergence of a new reliable algorithm for solving multi-order fractional differential equations. Commun. Nonlinear Sci. Numer. Simulat. 2016, 34, 154–164. [Google Scholar] [CrossRef]
- Bhrawy, A.H.; Baleanu, D.; Assas, L.M. Efficient generalized Laguerre-spectral methods for solving multi-term fractional differential equations on the half line. J. Vib. Control. 2013, 20, 973–985. [Google Scholar] [CrossRef]
- El-Mesiry, A.E.M.; El-Sayed, A.M.A.; El-Saka, H.A.A. Numerical methods for multi-term fractional (arbitrary) orders differential equations. Appl. Math. Comput. 2005, 160, 683–699. [Google Scholar] [CrossRef]
- EL-Sayed, M.A.; EL-Mesiry, A.E.M.; EL-Saka, H.A.A. Numerical solution for multi-term fractional (arbitrary) orders differential equations. Comput. Appl. Math. 2004, 23, 33–54. [Google Scholar] [CrossRef]
- El-Sayed, A.M.A.; El-Kalla, I.L.; Ziada, E.A.A. Analytical and numerical solutions of multi-term nonlinear fractional orders differential equations. Appl. Numer. Math. 2010, 60, 788–797. [Google Scholar] [CrossRef]
- Javidi, M.; Nyamoradi, N. A numerical scheme for solving multi-term fractional differential equations. Commun. Frac. Calc. 2013, 4, 38–49. [Google Scholar]






| CPU Time (s) | ||
|---|---|---|
| 0.5 | 1.11022302462516 × 10−16 | 0.021720 |
| 1 | 0 | 0.020514 |
| 1.5 | 5.551115123125783 × 10−17 | 0.022866 |
| 2 | 2.775557561562891 × 10−17 | 0.021033 |
| 2.5 | 1.387778780781446 × 10−17 | 0.023839 |
| 3 | 6.938893903907228 × 10−18 | 0.021494 |
| 3.5 | 8.673617379884035 × 10−19 | 0.021404 |
| 4 | 0 | 0.022049 |
| 4.5 | 1.084202172485504 × 10−19 | 0.021662 |
| 5 | 2.168404344971009 × 10−19 | 0.021855 |
| Method | Step Size, | Maximal Absolute Error |
|---|---|---|
| HFM | 1/10 | 1.73 × 10−13 |
| HWCM [40] | 1/512 | 1.86 × 10−9 |
| Method 1a [39] | 1/512 | 2.96 × 10−4 |
| Method 1b [39] | 1/512 | 2.71 × 10−4 |
| Method 2 [39] | 1/512 | 1.79 × 10−5 |
| Method 3 [39] | 1/512 | 2.96 × 10−4 |
| Method 1a (2) [39] | 1/512 | 8.14 × 10−7 |
| Method 3 (2) [39] | 1/512 | 8.14 × 10−7 |
| RVIM * [41] | - | 8.55 × 10−10 |
| Example | Step Size | CPU Time (in Seconds) | |
|---|---|---|---|
| Case 1 | Case 2 | ||
| 5.1 | 1/10 | 1.89 × 10−1 | 1.96 × 10−1 |
| 5.2 | 1/500 | 19.621 | 20.527 |
| 5.3 | 1/500 | 19.278 | 15.573 |
| Method | Maximal Absolute Error | Method | Maximal Absolute Error | ||
|---|---|---|---|---|---|
| HFM HWCM [40] Method 1a [39] Method 1b [39] Method 2 [39] Method 3 [39] Method 1a (2) [39] Method 3 (2) [39] | 1/10 1/512 1/512 1/512 1/512 1/512 1/512 1/512 | 5.91 × 10−12 1.86 × 10−9 3.54 × 10−3 6.93 × 10−5 1.18 × 10−4 5.43 × 10−4 3.10 × 10−6 5.07 × 10−6 | GLT (GQ) a [42] (N = 64) GLT (GRQ) b [42] (N = 64) | 0 1 2 3 0 1 2 3 | 2.16 × 10−7 2.51 × 10−6 7.29 × 10−6 1.43 × 10−5 3.08 × 10−7 4.95 × 10−6 1.80 × 10−5 4.29 × 10−5 |
| Method | Step Size | Maximal Absolute Error | |
|---|---|---|---|
| Case 1 | Case 2 | ||
| HFM | 1/500 | 2.66 × 10−5 | 7.006 × 10−6 |
| ET | 1/1000 | 9.98 × 10−4 | 9.95 × 10−4 |
| ER | 1/1000 | 9.53 × 10−4 | 9.80 × 10−4 |
| Method | Step Size | Maximal Absolute Error | |
|---|---|---|---|
| Case 1 | Case 2 | ||
| HFM | 1/500 | 1.84 × 10−7 | 1.96 × 10−7 |
| PECE | 1/1000 | 4.09 × 10−4 | 4.37 × 10−4 |
| Method | Step Size | Maximal Absolute Error | |
|---|---|---|---|
| Case 1 | Case 2 | ||
| HFM | 1/10 | 7.20 × 10−14 | 5.26 × 10−14 |
| ET | 1/1000 | 8.92 × 10−4 | 9.71 × 10−4 |
| ER | 1/1000 | 7.89 × 10−4 | 9.43 × 10−4 |
| PNM | 1/2000 | 3.99 × 10−4 | 3.88 × 10−4 |
| ADM * | - | 1.50 × 10−4 | 5.74 × 10−6 |
| NM | 1/2000 | 9.39 × 10−5 | 2.6866 × 10−4 |
| Method | CPU Time (in Seconds) | |
|---|---|---|
| Case 1 | Case 2 | |
| HFM | 1.95 × 10−4 | 1.99 × 10−1 |
| PNM | 894.99 | 952.90 |
| ADM | 478.57 | 506.95 |
| NM | 5.938 | 5.906 |
| Method | Step Size | Maximal Absolute Error | |
|---|---|---|---|
| Case 3 | Case 4 | ||
| HFM | 1/500 | 2.80 × 10−5 | 8.55 × 10−5 |
| 2E | 1/1000 | 1.34 × 10−3 | 1.50 × 10−3 |
| 3E | 1/1000 | 1.20 × 10−3 | 1.49 × 10−3 |
| Method | Step Size | Maximal Absolute Error | |
|---|---|---|---|
| Case 1 | Case 2 | ||
| HFM | 1/300 | 4.96 × 10−6 | 1.62 × 10−7 |
| PECE | 1/1000 | 6.32 × 10−6 | 5.76 × 10−4 |
| Example | Step Size | CPU Time (in Seconds) | |
|---|---|---|---|
| Case 1 | Case 2 | ||
| 5.5 | 1/300 | 6.81 | 5.07 |
| 5.6 | 1/500 | 36.83 | 48.63 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Damarla, S.K.; Kundu, M. Novel Hybrid Function Operational Matrices of Fractional Integration: An Application for Solving Multi-Order Fractional Differential Equations. AppliedMath 2025, 5, 55. https://doi.org/10.3390/appliedmath5020055
Damarla SK, Kundu M. Novel Hybrid Function Operational Matrices of Fractional Integration: An Application for Solving Multi-Order Fractional Differential Equations. AppliedMath. 2025; 5(2):55. https://doi.org/10.3390/appliedmath5020055
Chicago/Turabian StyleDamarla, Seshu Kumar, and Madhusree Kundu. 2025. "Novel Hybrid Function Operational Matrices of Fractional Integration: An Application for Solving Multi-Order Fractional Differential Equations" AppliedMath 5, no. 2: 55. https://doi.org/10.3390/appliedmath5020055
APA StyleDamarla, S. K., & Kundu, M. (2025). Novel Hybrid Function Operational Matrices of Fractional Integration: An Application for Solving Multi-Order Fractional Differential Equations. AppliedMath, 5(2), 55. https://doi.org/10.3390/appliedmath5020055






