A Nonlinear Ordinary Differential Equation Model for a Society Strongly Dependent on Non-Renewable Resources

Abstract

In this work, we investigate an ODE system designed to describe the interplay between human society and the environment, with a strong focus on the role of non-renewable resources. Specifically, our model captures how the depletion and replenishment of non-renewable resources (along with renewable ones) and dependence on wealth drive population and resource dynamics in a society. We prove that the solutions of the system remain in the non-negative cone and are bounded, implying that indefinite unbounded growth in wealth or population cannot occur within this model. Next, we compute and classify all equilibrium points, exploring which equilibria can be stable and physically relevant. In particular, we show that, depending on parameter regimes, the system may admit a stable equilibrium with positive levels of population, renewable resources, non-renewable resources, and wealth, suggesting a possible sustainable long-term outcome for a heavily resource-dependent society.

1. Introduction

In this paper, we continue a line of research begun in our two previous works [1,2], aiming to develop and analyze simple yet insightful nonlinear ODE models that capture different aspects of the interactions between society and natural resources. Understanding these interactions is increasingly crucial, especially as contemporary industrialized economies rely heavily on non-renewable resources such as oil, coal, and natural gas. This dependence profoundly affects wealth creation, population change, and the sustainability of both renewable and non-renewable resources. Although technological advances can sometimes partially replenish or substitute for non-renewable resources, complete replacements are never fully guaranteed and often lead to new risks of resource exhaustion. In this paper, we propose and study a system of nonlinear ordinary differential equations (ODEs) tailored to capture these interactions, focusing on how strong dependence on non-renewable resources may determine the dynamics of both human population and wealth. Our research started, in [1], from the HANDY model, which has been introduced in [3] (see also [4]) and then studied by several authors (see [5,6,7,8,9,10]). Our work was linked in particular with [10], who simplified and clarified the original HANDY model, and [9], who introduced non-renewable resources. In the paper [2], we introduced a different model that can no longer be considered a HANDY model. The present work builds on and extends [2], offering a new perspective on how resource depletion processes might primarily be driven by non-renewable resources.

The main motivation for our current approach stems from observing contemporary industrialized societies: while technological progress can uncover new deposits or extraction methods, the finite nature of non-renewable resources fundamentally constrains economic expansion. Consequently, the depletion of non-renewables has profound impacts on wealth and population. Our model captures this by letting the depletion and consumption rates depend strongly on the quantity of non-renewable resources, denoted by z.

The model that we will study in the present paper is the following:

$$\left\{\begin{array}{cc}\hfill x^{\prime }& =-cx+d{\displaystyle \frac{\mu xw}{w^2+{\mu }^2{x}^2}}x,\hfill \\ \hfill y^{\prime }& =\gamma y(\lambda -y)-{\delta }_{1}yz,\hfill \\ \hfill z^{\prime }& =k{\displaystyle \frac{w{z}^2}{wz+1}}-\delta z^2,\hfill \\ \hfill w^{\prime }& ={\delta }_{1}yz+\delta z^2-\sigma zw.\hfill \end{array}\right.$$

(1)

Here, $x\left(t\right)$ represents the population size, $y\left(t\right)$ the amount of renewable resources, $z\left(t\right)$ the non-renewable resources, and $w\left(t\right)$ the accumulated wealth in the society. The parameters $c, d, \mu , \gamma , \lambda , {\delta }_1, k, \delta , \sigma$ are strictly positive. In detail, the population equation $x^{\prime }$ in (1) states that, in a very poor society (wealth per capita $w/\left(\mu x\right)$ close to zero) or in a society so wealthy as to have low birth rates, the population tends to decline, which reflects the observed demographic transitions in modern developed countries. The equation for $y^{\prime }$ is a standard logistic one with a term ${\delta }_{1}yz$, which represents the depletion of renewable resources driven by the presence of z (i.e., resource usage intensively aided by the non-renewable resource). The equation for $z^{\prime }$ includes a non-renewable resource “replenishment” term of the form $f\left(zw\right)z$, where the replenishment rate is driven by w and z and the function $f\left(t\right)=k{\displaystyle \frac{t}{t+1}}$ is a saturation function of standard use in population dynamics. This term is intended to capture moderate optimism in human ingenuity to find new non-renewable reserves, though with a saturating upper bound. In the equation, we also have a depletion term with rate of depletion $\delta z$, giving rise to the term $\delta z^2$. Finally, $w^{\prime }$ describes the rate of change in wealth: it increases by extracting and using resources y and z (captured by ${\delta }_{1}yz$ and $\delta z^2$) but decreases due to consumption at a rate proportional to $\sigma zw$. In this way, the model highlights how the consumption (both in resource usage and wealth depletion) is sustained by non-renewable resources z. Our formulation emphasizes that the burn rate of non-renewables drives the consumption of all resources and the dynamics of wealth, reflecting the structure of industrialized economies, and this is the main difference with respect to previous models, like HANDY-type models or our previous one expounded in [2].

Using this simple model, we try to give an answer to some questions central to sustainability:

• Are unbounded increases in population or wealth possible under heavy reliance on non-renewable resources?
• Can a society reach a stable equilibrium in which population, renewable resources, non-renewable resources, and wealth coexist at positive levels?
• How sensitive are these outcomes to parameters such as $\delta$ or ${\delta }_1$, which measure depletion rates of resources?

The following are some of the results that we obtain about system (1) that give partial answers to these questions.

• We first show that all trajectories relevant for the model (those starting with non-negative population, resources, and wealth) remain non-negative and bounded for all time. This implies that an uncontrolled increase in wealth or population cannot occur in our model.
• We compute all the possible equilibrium points, explaining which equilibria correspond to zero or positive values of the variables (i.e., extinction scenarios or sustainable states) and which might appear only for specific parameter regimes.
• We analyze local stability and asymptotic stability of the equilibria. Physically, stability means that, if the system starts near a particular equilibrium, it tends to remain close to it, while asymptotical stability implies also a convergence to the equilibrium of nearby trajectories. As a consequence, an asymptotically stable equilibrium gives relevant information on the long-term behavior of the system, at least for trajectories starting in a neighborhood of the equilibrium. If an equilibrium with zero population is asymptotically stable, nearby trajectories describe a collapse path. On the other hand, the existence of an asymptotically stable equilibrium with positive values for all variables suggests that the society can attain a sustainable steady state.
• Our analysis unveils that many equilibria involving zero resources or zero population are unstable, so they are not physically relevant. However, for certain ranges of parameters (e.g., small depletion rates ${\delta }_1,\delta$), there exist stable equilibria with strictly positive $x,y,z,w$.
• We provide numerical simulations illustrating these phenomena, corroborating that small resource extraction rates can favor stable equilibria with positive population.

This paper is organized as follows: in Section 2, we prove that solutions remain defined and non-negative for all $t\ge 0$ and that the variables stay bounded. Section 3 provides a complete classification of the equilibrium points for (1). In Section 4, Section 5, Section 6 and Section 7, we analyze their stability properties, paying special attention to small $\delta$ and ${\delta }_1$. Numerical simulations illustrating the main dynamical behaviors are presented in Section 8, alongside a discussion of how parameter changes might reflect different real-world scenarios. Finally, Section 9 summarizes our main findings and suggests potential directions for future refinements of the model.

2. General Results

We work in the positive cone

$$\mathcal{C}=\left\{(x,y,z,w)\in {\mathbb{R}}^4|x>0,y>0,z>0,w>0\right\}$$

or in its closure

$$\overline{\mathcal{C}}=\left\{(x,y,z,w)\in {\mathbb{R}}^4|x\ge 0,y\ge 0,z\ge 0,w\ge 0\right\}$$

or in

$${\mathcal{C}}_0=\left\{(x,y,z,w)\in {\mathbb{R}}^4|x>0,y>0,z>0,w\ge 0\right\}.$$

Let us write $X=(x,y,z,w)\in {\mathbb{R}}^4$ and let $F\left(X\right)$ be the vector field of the ODE system (1). Let us define the open sets

$$\begin{array}{ccc}\hfill A_1& =\{X\in {\mathbb{R}}^4|x\ne 0\},\hfill & \hfill A_2=\{X\in {\mathbb{R}}^4|w\ne 0\},\\ \hfill A_3& =\{X\in {\mathbb{R}}^4|zw\ne -1\},\hfill & \hfill A=(A_1\cup A_2)\cap A_3.\end{array}$$

We have $F\in C^{\infty }(A,{\mathbb{R}}^4)$ and ${\mathcal{C}}_0\subseteq A$. Hence, by standard ODE theory, we obtain a result of local existence and uniqueness.

Proposition 1.

For any $t_0\in \mathbb{R},X_0\in {\mathcal{C}}_0$, the problem

$$\left\{\begin{array}{c}{X}^{\prime }\left(t\right)=F\left(X\right)\hfill \\ X^{\prime }\left(t_0\right)=X_0\hfill \end{array}\right.$$

(2)

has a unique solution defined in a maximal interval $J=(a,b)$.

We will study the solutions of (2) with $t_0=0$.

Proposition 2.

Let $t_0=0,X_0\in {\mathcal{C}}_0$ and $X\left(t\right)$ be the solution of (2) defined in $(a,b)$ with $-\infty \le a<0<b\le +\infty$. Then, $X\left(t\right)\in \mathcal{C}$ for all $t\in (0,b)$.

Proof. 

It is obvious that $x\left(t\right)>0$, $y\left(t\right)>0$, $z\left(t\right)>0$ for all $t\in (a,b)$ because $x_0>0$, $y_0>0$, $z_0>0$, and the constant zero function ($g\left(t\right)=0$ for all t) is a solution for the equations relating to x, y, and z; hence, it cannot be crossed. As for w, we notice that there exists $\beta \in (0,b)$ such that $w\left(t\right)>0$ in $(0,\beta )$. Indeed, this is obvious if $w_0>0$, while, if $w_0=0$, we just have to remark that $w^{\prime }\left(0\right)={\delta }_1{y}_0{z}_0+\delta z_0^2>0$. We then define

$${\tau }_0=sup\left\{\tau >0\left|w\right(s)>0,\forall s\in (0,\tau )\right\}.$$

If ${\tau }_0=b$, then $w\left(s\right)>0$ in $(0,b)$ and the claim is proved. If ${\tau }_0<b$, then it is easy to see that $w\left(s\right)>0$ for all $s\in (0,{\tau }_0)$ and $w\left({\tau }_0\right)=0$; hence, $w^{\prime }\left({\tau }_0\right)\le 0$. But, from (1), we obtain $w^{\prime }\left({\tau }_0\right)={\delta }_{1}y\left({\tau }_0\right)z\left({\tau }_0\right)+{\delta }_2{z}^2\left({\tau }_0\right)>0$, that is, a contradiction. Hence, ${\tau }_0=b$ and the proposition is proved.  □

We now prove that $X\left(t\right)$ is bounded in $[0,b)$. The proof is divided into four steps, one for each variable.

Proposition 3.

$y\left(t\right)$ is bounded in $[0,b)$.

Proof. 

The proof is the same as in our previous work [1], so we skip it.  □

Proposition 4.

$z\left(t\right)$ is bounded in $[0,b)$.

Proof. 

We have

$$z^{\prime }=z^2\left(k{\displaystyle \frac{w}{wz+1}}-\delta \right)\le z^2\left({\displaystyle \frac{k}{z}}-\delta \right).$$

If ${\displaystyle z\left(t\right)\ge \frac{2k}{\delta }}$ for all $t\in [0,b)$, then $z^{\prime }<0$, so z is decreasing; hence, $0<z\left(t\right)\le z_0$ for all $t\in [0,b)$ and z is bounded. Now, we assume that ${\displaystyle z\left({\tau }_0\right)<\frac{2k}{\delta }}$ for some ${\tau }_0\in [0,b)$. If ${\displaystyle z\left(t\right)<\frac{2k}{\delta }}$ for all $t\in ({\tau }_0,b)$, then, obviously, z is bounded in $[0,b)$. Hence, assume that ${\tau }_1>{\tau }_0$ exists such that ${\displaystyle z\left({\tau }_1\right)\ge \frac{2k}{\delta }}$. Define

$${\tau }_2=sup\left\{\tau \in ({\tau }_0,{\tau }_1)|z\left(s\right)<{\displaystyle \frac{2k}{\delta }},\forall s\in ({\tau }_0,\tau )\right\}.$$

By continuity of z, it is easy to deduce that ${\displaystyle {\tau }_2\in ({\tau }_0,{\tau }_1],z\left(s\right)<\frac{2k}{\delta }}$ for all ${\displaystyle s\in [{\tau }_0,{\tau }_2),z\left({\tau }_2\right)=\frac{2k}{\delta }}$; hence, $z^{\prime }\left({\tau }_2\right)\ge 0$. On the other hand,

$$z^{\prime }\left({\tau }_2\right)\le z^2\left({\tau }_2\right)\left({\displaystyle \frac{k}{z\left({\tau }_2\right)}}-\delta \right)={\left({\displaystyle \frac{2k}{\delta }}\right)}^2\left({\displaystyle \frac{\delta }{2}}-\delta \right)=-{\displaystyle \frac{\delta }{2}}{\left({\displaystyle \frac{2k}{\delta }}\right)}^2<0,$$

which is a contradiction. So, this last case is ruled out, and we are left with the previous ones, which imply that z is bounded in $[0,b)$.  □

Proposition 5.

$w\left(t\right)$ is bounded in $[0,b)$.

Proof. 

From Propositions 3 and 4, we see that there exists $M>0$ such that ${\delta }_{1}y\left(t\right)+\delta z\left(t\right)<M\sigma$ for all $t\in [0,b)$. Hence,

$$w^{\prime }\left(t\right)=z({\delta }_{1}y+\delta z-\sigma w)\le \sigma z(M-w)$$

for all $t\in [0,b)$. If $w\left(t\right)\ge M$ for all $t\in [0,b)$, then w is decreasing, and hence is bounded. So, we assume that ${\tau }_0\in [0,b)$ exists such that $w\left({\tau }_0\right)<M$. If $w\left(t\right)<M$ for all $t>{\tau }_0$, then $w\left(t\right)$ is bounded in $[0,b)$. So, let us assume that $\exists {\tau }_1>{\tau }_0$ such that $w\left({\tau }_1\right)\ge M$. Define

$${\tau }_2=sup\left\{\tau \in ({\tau }_0,{\tau }_1)|w\left(s\right)<M,\forall s\in ({\tau }_0,\tau )\right\}.$$

By continuity, we have ${\tau }_2\in ({\tau }_0,{\tau }_1],w\left(s\right)<M$ for all $s\in ({\tau }_0,{\tau }_2),w\left({\tau }_2\right)=M$; hence, $w^{\prime }\left({\tau }_2\right)\ge 0$. But,

$$w^{\prime }\left({\tau }_2\right)=z({\delta }_{1}y\left({\tau }_2\right)+\delta z\left({\tau }_2\right)-\sigma w\left({\tau }_2\right))=z({\delta }_{1}y\left({\tau }_2\right)+\delta z\left({\tau }_2\right)-\sigma M)<0$$

and the contradiction rules out this case, so we are left with the previous ones, which imply that w is bounded in $[0,b)$.  □

Proposition 6.

$x\left(t\right)$ is bounded in $[0,b)$.

Proof. 

We have

$$x^{\prime }=\left(-c+d{\displaystyle \frac{\mu xw}{w^2+{\mu }^2{x}^2}}\right)x=\left(-c+d{\displaystyle \frac{{\displaystyle \frac{w}{\mu x}}}{{\displaystyle \frac{w^2}{{\mu }^2{x}^2}+1}}}\right)x.$$

Consider the function

$${\displaystyle h\to -c+d\frac{h}{h^2+1}=\frac{-c{h}^2+dh-c}{h^2+1}=g\left(h\right).}$$

It is obvious that $g\left(h\right)=0$ if and only if ${\displaystyle h=h_{1,2}=\frac{d\pm \sqrt{d^2-4c^2}}{2c}}$ and $g\left(h\right)>0$ if and only if

$$0<h_1={\displaystyle \frac{d-\sqrt{d^2-4c^2}}{2c}}<h<h_2={\displaystyle \frac{d+\sqrt{d^2-4c^2}}{2c}}.$$

Hence, $x^{\prime }<0$ when ${\displaystyle \frac{w}{\mu x}<h_1}$, that is, when ${\displaystyle x>\frac{w}{\mu h_1}}$. We know that w is bounded, so let us write $w\le M_0$. We have that $x>{\displaystyle \frac{M_0}{\mu h_1}}=M_1$ implies that $x^{\prime }<0$, and, setting $M_2=2M_1$, we have that $x\ge M_2$ implies that $x^{\prime }<0$.

Now, if $x\left(t\right)\ge M_2$ for all $t\in [0,b)$, then $x^{\prime }\left(t\right)<0$ in $[0,b)$, so $x\left(t\right)$ is decreasing and obviously it is bounded. So, let us assume that $x\left({\tau }_0\right)<M_2$ for some ${\tau }_0\in [0,b).$ If $x\left(t\right)<M_2$ for all $t\in [{\tau }_0,b)$, then $x\left(t\right)$ is obviously bounded. So, we assume that $x\left({\tau }_1\right)\ge M_2$ for some ${\tau }_1\in ({\tau }_0,b).$ Define

$${\tau }_2=sup\left\{\tau \in ({\tau }_0,{\tau }_1)|x\left(s\right)<M_2,\forall s\in ({\tau }_0,\tau )\right\}.$$

By continuity, we have ${\tau }_2\in ({\tau }_0,{\tau }_1],x\left({\tau }_2\right)=M_2,x\left(s\right)<M_2$ for all $s\in ({\tau }_0,{\tau }_2)$; hence, $x^{\prime }\left({\tau }_2\right)\ge 0$. But, $x\left({\tau }_2\right)=M_2$ implies that $x^{\prime }\left({\tau }_2\right)<0$. We have obtained a contradiction, so this last case cannot hold, and we are left with the previous two ones, which imply that x is bounded in $[0,b)$.  □

An easy consequence of the previous propositions is the following.

Corollary 1.

$b=+\infty$.

Proof. 

We have proved that $X\left(t\right)$ is bounded in $[0,b)$. The result derives from standard ODE theory.  □

3. Equilibrium Points

Equilibrium points are the solutions of the system

$$\begin{array}{cc}\hfill & x\left(-c+d{\displaystyle \frac{{\displaystyle \frac{w}{\mu x}}}{{\displaystyle \frac{w^2}{{\mu }^2{x}^2}+1}}}\right)=0\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill & y(\gamma \lambda -\gamma y-{\delta }_{1}z)=0\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill & z^2\left(k{\displaystyle \frac{w}{wz+1}}-\delta \right)=0\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill & z\left({\delta }_{1}y+\delta z-\sigma w\right)=0\hfill \end{array}$$

(6)

We notice that the first Equation (3) is independent from the other three, so it can be solved independently and gives either $x=0$ or ${\displaystyle x=\frac{w}{\mu t_i},i=1,2}$, where $t_1, t_2$ are the solutions of ${\displaystyle -c+\frac{dt}{t^2+1}=0}$ and satisfy

$$t_1={\displaystyle \frac{d-\sqrt{d^2-4c^2}}{2c}}<t_2={\displaystyle \frac{d+\sqrt{d^2-4c^2}}{2c}}d\ge 2c\Rightarrow t_2>1,t_1\in (0,1].$$

(7)

Let us now study the system given by the last three equations. We distinguish several cases.

(1)

$y=z=0$. In this case, Equation (5) is satisfied for all w, and we have the following three families of equilibria:

$$\begin{array}{cc}\hfill & \left\{(0,0,0,W)\mid W\ge 0\right\}\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill & \left\{\left({\displaystyle \frac{W}{\mu t_1}},0,0,W\right)\mid W\ge 0\right\}\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill & \left\{\left({\displaystyle \frac{W}{\mu t_2}},0,0,W\right)\mid W\ge 0\right\}\hfill \end{array}$$

(10)

with $W\ge 0$. Notice that $W=0$ gives the origin, where F is not defined, so this point is not, properly speaking, an equilibrium. In any case, we will see what happens to the trajectories starting nearby the origin.

(2)

$y=0,z\ne 0$. In this case, from (5) and (6), we obtain the system

$$\left\{\begin{array}{c}{\displaystyle \frac{kw}{wz+1}}=\delta \hfill \\ \sigma w=\delta z\Rightarrow w={\displaystyle \frac{\delta z}{\sigma }}\hfill \end{array}\right.$$

so that

$$z_1={\displaystyle \frac{k-\sqrt{k^2-4\sigma \delta }}{2\delta }},z_2={\displaystyle \frac{k+\sqrt{k^2-4\sigma \delta }}{2\delta }},k\ge 2\sqrt{\sigma \delta }.$$

In this case, the equilibrium points are

$$\begin{array}{cc}\hfill & P_i=\left(0,0,z_i,{\displaystyle \frac{\delta z_i}{\sigma }}\right),i=1,2\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill & Q_{i,j}=\left({\displaystyle \frac{\delta z_j}{\mu \sigma t_i}},0,z_j,{\displaystyle \frac{\delta z_j}{\sigma }}\right),i,j=1,2\hfill \end{array}$$

(12)

(3)

Assuming that $y\ne 0$ and $z=0$, we obtain $y=\lambda$. There is no condition on w, so we have three families of points, similar to case (1). Specifically, we have the following:

$$\begin{array}{cc}\hfill & \left\{(0,\lambda ,0,W)\mid W\ge 0\right\},\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill & \left\{\left({\displaystyle \frac{W}{\mu t_i}},\lambda ,0,W\right)\mid W\ge 0\right\},i=1,2\hfill \end{array}$$

(14)

with $W\ge 0$. As above, when $W=0$, we obtain a point where F is not defined, so it is not, properly speaking, an equilibrium. However, we will study the behavior of the trajectories starting nearby this point.

(4)

$y\ne 0,z\ne 0$. Then, ${\displaystyle y=\lambda -\frac{{\delta }_1}{\gamma }z}$. From (5) and (6), we obtain

$$\left\{\begin{array}{c}w={\displaystyle \frac{\delta }{k-\delta z}}\hfill \\ w={\displaystyle \frac{1}{\sigma }}\left(\delta -{\displaystyle \frac{{\delta }_1^2}{\gamma }}\right)z+{\displaystyle \frac{{\delta }_1\lambda }{\sigma }}\hfill \end{array}\right.$$

and, from these, we obtain the following equation for z:

$$\delta \left(\delta \gamma -{\delta }_1^2\right)z^2+\left({\delta }_1\delta \lambda \gamma +k{\delta }_1^2-k\gamma \delta \right)z+\sigma \gamma \delta -k{\delta }_1\lambda \gamma =0$$

(15)

For suitable values of the parameters, this equation has two real solutions $z_1, z_2$, which yield six equilibrium points:

$$\begin{array}{cc}\hfill & P_i=\left({\displaystyle 0,\lambda -\frac{{\delta }_1}{\gamma }{z}_i,z_i,\frac{\delta }{k-\delta z_i}}\right),i=1,2\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill & Q_{i,j}=\left({\displaystyle \frac{\delta }{\mu t_i(k-\delta z_j)},\lambda -\frac{{\delta }_1}{\gamma }{z}_j,z_j,\frac{\delta }{k-\delta z_j}}\right),i,j=1,2.\hfill \end{array}$$

(17)

In the next sections, we will study the stability and instability of these equilibria. In many cases, we will be able to obtain asymptotic results as $\delta \to 0^{+}$. As for ${\delta }_1$, we will consider two cases: $\left(i\right)$ ${\delta }_1$ is small but fixed; $\left(ii\right)$ ${\delta }_1\sim \delta$, which means that both ${\delta }_1,\delta \to 0^{+}$ and ${\delta }_1/\delta \to 1$.

4. Stability and Instability: Case 1

We begin by studying case 1. These equilibria correspond to scenarios where both types of resources are zero $(y=z=0)$ but potentially a certain wealth $W\ge 0$ might remain (as the product of previous history). Such “resource-free” equilibria typically indicate a collapse state for the environment.

Let P be any of the points that we have found. Fix ${\displaystyle ϵ\in \left(0,\frac{\gamma \lambda }{2(\gamma +{\delta }_1)}\right)}$ and let $B_{ϵ}\left(P\right)$ be the ball with center P and radius $ϵ$. Let us pick any $Q\in B_{ϵ}\left(P\right)\cap {\mathcal{C}}_0$ and let $u\left(t\right)=u(t,Q)$ be the trajectory starting at Q for $t=0$. Assume that $u\left(t\right)\in B_{ϵ}\left(P\right)$ for all $t\in [0,+\infty )$. We then have $\left|y\right|<ϵ$, $\left|z\right|<ϵ$, for all $t\ge 0$; hence,

$$\gamma y+{\delta }_{1}z<\gamma ϵ+{\delta }_1ϵ=(\gamma +{\delta }_1)ϵ<(\gamma +{\delta }_1){\displaystyle \frac{\gamma \lambda }{2(\gamma +{\delta }_1)}}={\displaystyle \frac{\gamma \lambda }{2}}.$$

As a consequence, we have

$$\gamma \lambda -\gamma y-{\delta }_{1}z>\gamma \lambda -{\displaystyle \frac{\gamma \lambda }{2}}={\displaystyle \frac{\gamma \lambda }{2}}.$$

Hence,

$$y^{\prime }=y(\gamma \lambda -\gamma y-{\delta }_{1}z)>y{\displaystyle \frac{\gamma \lambda }{2}},\forall t\ge 0$$

which implies that $y\left(t\right)\ge y_0$ exp$\left({\displaystyle \frac{\gamma \lambda t}{2}}\right)$ for all $t\ge 0$. Then, $y\left(t\right)\to +\infty$ as $t\to +\infty$, a contradiction with the hypothesis $u\left(t\right)\in B_{ϵ}\left(P\right)$. The contradiction proves that, for any $Q\in B_{ϵ}\left(P\right)\cap {\mathcal{C}}_0$, the trajectory $u(t,Q)$ leaves the ball $B_{ϵ}\left(P\right)$. This clearly implies the instability of the equilibria that we are studying. This holds for any choice of the parameters, in particular, for any $\delta ,{\delta }_1>0$. Notice that the argument works also in the case of the origin, which is not, properly speaking, an equilibrium. We have then proved the following proposition:

Proposition 7.

The points of case 1 are all unstable equilibria for any value of the parameters.

In other words, if y and z are near zero, the system tends to deviate from such resource-free states, reflecting the fact that renewable resources recover thanks to the logistic dynamic that they are driven by.

5. Stability and Instability: Case 3

We now treat case 3, which is similar to case 1. Physically, $z=0$ means that no non-renewable resources remain, while y is at its carrying capacity $\lambda$. Such a society has exhausted non-renewables and is left with only a fully amount of renewable resources. We investigate whether such a scenario can be stable. Let P be any of the equilibria of case 3. As above, let us fix $ϵ>0$ and $Q\in B_{ϵ}\left(P\right)\cap {\mathcal{C}}_0$. Define $u\left(t\right)=u(t,Q)$ as the trajectory starting at Q for $t=0$. Assume that $u\left(t\right)\in B_{ϵ}\left(P\right)$ for all $t\ge 0$. We study the stability of P distinguishing several cases.

(i)

We first assume that ${\delta }_1\lambda >\sigma W$ and take $0<ϵ<{\displaystyle \frac{{\delta }_1\lambda -\sigma W}{{\delta }_1+\sigma +\frac{1}{2}}}$, which implies that

$${\delta }_1\left(\lambda -ϵ\right)-\sigma \left(W+ϵ\right)>{\displaystyle \frac{ϵ}{2}}.$$

Hence, the trajectory $u(t,Q)=\left(x\right(t),y(t),z(t),w(t\left)\right)$ satisfies

$$w^{\prime }\left(t\right)=z\left(t\right)\left({\delta }_{1}y\left(t\right)+\delta z\left(t\right)-\sigma w\left(t\right)\right)>z\left(t\right)\left({\delta }_1\left(\lambda -ϵ\right)-\sigma \left(W+ϵ\right)\right)>z\left(t\right){\displaystyle \frac{ϵ}{2}}.$$

On the other hand, we have $z^{\prime }\left(t\right)>-\delta z^2\left(t\right)$. By a simple integration, this implies that $z\left(t\right)>{\displaystyle \frac{1}{z_1+\delta t}}$, where $z_1=1/z_0$ and $Q=\left(x_0,y_0,z_0,w_0\right)$ with $z_0>0$. Hence, we obtain $w^{\prime }\left(t\right)>{\displaystyle \frac{1}{z_1+\delta t}}{\displaystyle \frac{ϵ}{2}}$, which implies, by another simple integration, that

$$w\left(t\right)\ge w_0+{\displaystyle \frac{ϵ}{2\delta }}log\left(z_1+\delta t\right),$$

for all $t\ge 0$; hence, ${lim}_{t\to +\infty }w\left(t\right)=+\infty$, a contradiction with $u(t,Q)\in B_{ϵ}\left(P\right)$ for all $t\ge 0$. The contradiction proves that, for any point $Q\in B_{ϵ}\left(P\right)\cap {\mathcal{C}}_0$, the trajectory $u(t,Q)$ must exit $B_{ϵ}\left(P\right)$, and this proves the instability of P. Notice that this includes the case $W=0$.

(ii)

We now assume that ${\delta }_1\lambda <\sigma W$. Let us take $ϵ<{\displaystyle \frac{\sigma W-{\delta }_1\lambda }{{\delta }_1+\delta +\sigma +\frac{1}{2}}}$, which implies that

$${\delta }_1\left(\lambda +ϵ\right)+\delta ϵ-\sigma \left(W-ϵ\right)<-{\displaystyle \frac{ϵ}{2}}.$$

Hence, we obtain

$$w^{\prime }\left(t\right)<z\left(t\right)\left({\delta }_1\left(\lambda +ϵ\right)+\delta ϵ-\sigma \left(W-ϵ\right)\right)<-z\left(t\right){\displaystyle \frac{ϵ}{2}}.$$

As above, we have $z\left(t\right)>{\displaystyle \frac{1}{z_1+\delta t}}$, which implies that $w^{\prime }\left(t\right)<-{\displaystyle \frac{1}{z_1+\delta t}}{\displaystyle \frac{ϵ}{2}}$; hence, by integration,

$$w\left(t\right)\le w_0-{\displaystyle \frac{ϵ}{2\delta }}log\left(z_1+\delta t\right).$$

This holds for all $t\ge 0$; hence, ${lim}_{t\to +\infty }w\left(t\right)=-\infty$, a contradiction. As above, this proves the instability of P.

We conclude that, if ${\delta }_1\lambda -\sigma W\ne 0$, these equilibria are unstable.

(iii)

Let us now assume that $kW>\delta$. By continuity, we can take $ϵ>0$ such that

$${\displaystyle \frac{k\left(W-ϵ\right)}{ϵ\left(W+ϵ\right)+1}}>\delta +ϵ.$$

Consider as above the ball $B_{ϵ}\left(P\right)$, a point $Q\in B_{ϵ}\left(P\right)\cap {\mathcal{C}}_0$, and the trajectory $u(t,Q)$. If $u(t,Q)\in B_{ϵ}\left(P\right)$ for any $t\ge 0$, then

$${\displaystyle \frac{kw\left(t\right)}{z\left(t\right)w\left(t\right)+1}}>{\displaystyle \frac{k\left(W-ϵ\right)}{ϵ\left(W+ϵ\right)+1}}>\delta +ϵ,$$

so that

$$z^{\prime }\left(t\right)\ge ϵz^2.$$

A simple integration then gives that $z\left(t\right)$ blows in finite time, a contradiction. Hence, the trajectory $u(t,Q)$ must leave the ball $B_{ϵ}\left(P\right)$, and this holds for any $Q\in B_{ϵ}\left(P\right)\cap {\mathcal{C}}_0$, proving the instability of P.

The cases not covered by the previous results are those when ${\delta }_1\lambda =\sigma W$ and $kW\le \delta$, which implies that $k{\displaystyle \frac{{\delta }_1\lambda }{\sigma }}\le \delta$. Hence, we can state the following proposition:

Proposition 8.

If one of the following conditions is satisfied, the equilibrium points P of case 3 are unstable:

(i)

${\delta }_1\lambda \ne \sigma W$.

(ii)

$kW>\delta$.

(iii)

$k{\displaystyle \frac{{\delta }_1\lambda }{\sigma }}>\delta$.

As a consequence of $\left(iii\right)$, we obtain the following corollary.

Corollary 2.

(i)

If ${\delta }_1>0$ is fixed, then all the equilibria of case 3 are unstable for $\delta <k{\displaystyle \frac{{\delta }_1\lambda }{\sigma }}$.

(ii)

If $k\lambda >\sigma$ and $\delta \sim {\delta }_1$, then there exists ${\delta }^{*}>0$ such that, for all $\delta \in (0,{\delta }^{*})$, it holds that ${\displaystyle \frac{k\lambda }{\sigma }}>{\displaystyle \frac{\delta }{{\delta }_1}}$; hence, all the equilibria of case 3 are unstable.

Hence, a stable equilibrium of this kind could only arise if ${\delta }_1\lambda =\sigma W$ and $kW\le \delta$ and $k{\displaystyle \frac{{\delta }_1\lambda }{\sigma }}\le \delta$. The latter implies that $k\lambda \le {\displaystyle \frac{\delta }{{\delta }_1}}$ if ${\delta }_1>0$. In practice, for large $k\lambda$ or small $\delta ,{\delta }_1$, these equilibria become unstable or non-physical. Thus, a scenario with zero non-renewables but carrying-capacity-level renewables is generally unstable unless very special conditions are met, indicating that small perturbations would drive the system away.

6. Stability and Instability: Case 2

To analyze the other cases, we introduce the Jacobian matrix of F at X:

$$JF\left(X\right)=\left(\begin{array}{cccc}{\displaystyle -c+2d\mu \frac{x{w}^3}{{(w^2+{\mu }^2{x}^2)}^2}}& 0& 0& {\displaystyle \frac{d\mu x^2({\mu }^2{x}^2-w^2)}{{(w^2+{\mu }^2{x}^2)}^2}}\\ \\ 0& \gamma \lambda -2\gamma y-{\delta }_{1}z& -{\delta }_{1}y& 0\\ \\ 0& 0& {\displaystyle \frac{kwz(wz+2)}{{(wz+1)}^2}-2\delta z}& {\displaystyle \frac{k{z}^2}{{(wz+1)}^2}}\\ \\ 0& {\delta }_{1}z& {\delta }_{1}y+2\delta z-\sigma w& -\sigma z\end{array}\right).$$

(18)

We will denote by $J_{jk}$ the entry of this matrix located in position $j,k=1,\cdots ,4$. Let us see how to simplify these entries. Recall that, for the equilibria of case 2, it holds that ${\displaystyle \delta =\frac{kw}{wz+1}}$ and ${\displaystyle z=\frac{w\sigma }{\delta }}$; hence,

$${\displaystyle \frac{kwz}{{(wz+1)}^2}}={\displaystyle \frac{\sigma }{k\delta }}{\displaystyle \frac{k^2{w}^2}{{(wz+1)}^2}}={\displaystyle \frac{\sigma }{k}}\delta ,$$

so that

$${\displaystyle J_{33}=\frac{kwz(wz+2)}{{(wz+1)}^2}-2\delta z=\frac{\sigma }{k}\delta \left(\frac{\delta z^2}{\sigma }+2\right)-2\delta z=\frac{{\delta }^2}{k}{z}^2+\frac{2\sigma \delta }{k}-2\delta z.}$$

Also, we have

$$J_{34}={\displaystyle \frac{k{z}^2}{{(wz+1)}^2}}={\displaystyle \frac{{\sigma }^2}{k{\delta }^2}}{\displaystyle \frac{k^2{w}^2}{{(wz+1)}^2}}={\displaystyle \frac{{\sigma }^2}{k}}.$$

Given that $y=0$ and $\delta z=\sigma w$, the Jacobian (18) in case 2 becomes

$$J\left(X\right)=\left(\begin{array}{cccc}{\displaystyle -c+2d\mu \frac{x{w}^3}{{(w^2+{\mu }^2{x}^2)}^2}}& 0& 0& {\displaystyle \frac{d\mu x^2({\mu }^2{x}^2-w^2)}{{(w^2+{\mu }^2{x}^2)}^2}}\\ \\ 0& \gamma \lambda -{\delta }_{1}z& 0& 0\\ \\ 0& 0& {\displaystyle -2\delta z+\frac{{\delta }^2{z}^2}{k}+\frac{2\sigma \delta }{k}}& {\displaystyle \frac{{\sigma }^2}{k}}\\ \\ 0& {\delta }_{1}z& \delta z& -\sigma z\end{array}\right).$$

In this case, we have to deal with the values

$$z_1={\displaystyle \frac{k-\sqrt{k^2-4\sigma \delta }}{2\delta }},z_2={\displaystyle \frac{k+\sqrt{k^2-4\sigma \delta }}{2\delta }},k\ge 2\sqrt{\sigma \delta }.$$

Recalling that

$$\sqrt{k^2-4\sigma \delta }=k\sqrt{1+{\displaystyle \frac{-4\sigma \delta }{k^2}}}=k\left(1-{\displaystyle \frac{2\sigma \delta }{k^2}}+\mathcal{O}\left({\delta }^2\right)\right)=k-{\displaystyle \frac{2\sigma }{k}}\delta +\mathcal{O}\left({\delta }^2\right),$$

the asymptotic developments of z and w as $\delta \to 0^{+}$ are given by

$$\begin{array}{ccc}\hfill & z_1={\displaystyle \frac{\sigma }{k}}+\mathcal{O}\left(\delta \right)\hfill & \hfill w_1={\displaystyle \frac{\delta }{k}}+\mathcal{O}\left({\delta }^2\right)\\ \hfill & z_2={\displaystyle \frac{k}{\delta }}-{\displaystyle \frac{\sigma }{k}}+\mathcal{O}\left(\delta \right)\hfill & \hfill w_2={\displaystyle \frac{k}{\sigma }}-{\displaystyle \frac{\delta }{k}}+\mathcal{O}\left({\delta }^2\right).\end{array}$$

Note that $\gamma \lambda -{\delta }_{1}z$ is always an eigenvalue. We have, for $z=z_1$,

$$\begin{array}{cc}\hfill {\delta }_1{z}_1& ={\displaystyle \frac{\sigma {\delta }_1}{k}}+\mathcal{O}\left(\delta \right)\to 0,{\delta }_1\mathrm{fixed},\delta \to 0\hfill \\ \hfill {\delta }_1{z}_1& =\mathcal{O}\left(\delta \right),{\delta }_1\sim \delta \to 0^{+},\hfill \end{array}$$

(19)

while, for $z=z_2$, we obtain

$$\begin{array}{cc}\hfill {\delta }_1{z}_2& ={\displaystyle \frac{k{\delta }_1}{\delta }}-{\displaystyle \frac{\sigma {\delta }_1}{k}}+\mathcal{O}\left(\delta \right),{\delta }_1\mathrm{fixed},\delta \to 0\hfill \\ \hfill {\delta }_1{z}_2& =k+\mathcal{O}\left(\delta \right),{\delta }_1\sim \delta \to 0^{+}.\hfill \end{array}$$

6.1. Equilibria ${\displaystyle P_i=\left(0,0,z_i,\frac{\delta z_i}{\sigma }\right),i=1,2}$

Now, let us study the equilibria ${\displaystyle P_i=\left(0,0,z_i,\frac{\delta z_i}{\sigma }\right),i=1,2}$. We obtain

$$J\left(P_i\right)=\left(\begin{array}{cccc}{\displaystyle -c}& 0& 0& 0\\ \\ 0& \gamma \lambda -{\delta }_1{z}_i& 0& 0\\ \\ 0& 0& {\displaystyle -2\delta z_i+\frac{{\delta }^2}{k}{z}_i^2+\frac{2\sigma \delta }{k}}& {\displaystyle \frac{{\sigma }^2}{k}}\\ \\ 0& {\delta }_1{z}_i& \delta z_i& -\sigma z_i\end{array}\right).$$

6.1.1. Case $\delta \sim {\delta }_1$

We first assume that $\delta \sim {\delta }_1$, and we start studying $P_1$. From (19), we derive the following statement for the Jacobian calculated at $P_1$

$$\underset{{\delta }_1,\delta \to 0^{+}}{lim}J\left(P_1\right)=\left(\begin{array}{cccc}{\displaystyle -c}& 0& 0& 0\\ \\ 0& \gamma \lambda & 0& 0\\ \\ 0& 0& 0& {\displaystyle \frac{{\sigma }^2}{k}}\\ \\ 0& 0& 0& {\displaystyle -\frac{{\sigma }^2}{k}}\end{array}\right).$$

This is an upper triangular matrix, and its eigenvalues are ${\displaystyle {\rho }_1=-c,{\rho }_2=\gamma \lambda ,{\rho }_3=0,{\rho }_4=-\frac{{\sigma }^2}{k}}$. As $\gamma \lambda >0$, by continuity of the eigenvalues of a matrix with respect to the entries, we obtain that there exists ${\delta }^{*}>0$ such that, for all $\delta ,{\delta }_1\in (0,{\delta }^{*})$, $J\left(P_1\right)$ has a positive eigenvalue, so $P_1$ is unstable for $\delta ,{\delta }_1\in (0,{\delta }^{*})$.

Let us now look for $P_2$, again in the case ${\delta }_1\sim \delta$. In this case, we have an eigenvalue given by

$${\rho }_2=\gamma \lambda -\left({\displaystyle \frac{k{\delta }_1}{\delta }}-{\displaystyle \frac{\sigma {\delta }_1}{k}}+\mathcal{O}\left({\delta }_1\delta \right)\right)=(\gamma \lambda -k)+o\left(1\right).$$

(20)

If $\gamma \lambda -k>0$, then ${\rho }_2>0$ when $\delta \to 0^{+}$, and $P_2$ is unstable. If $\gamma \lambda -k<0$, then we obtain that, for $\delta \to 0^{+}$, the first two eigenvalues ${\rho }_1, {\rho }_2$ are negative, while the last two ${\rho }_3, {\rho }_4$ are obtained as the eigenvalues of the following $2\times 2$ matrix $J_1$:

$$J_1=\left(\begin{array}{cc}{\displaystyle J_{3,3}}& J_{3,4}\\ \\ J_{4,3}& J_{4,4}\end{array}\right).$$

Using the formulas for $z_2$, we obtain the following asymptotic developments:

$$J_{3,3}=-k+\mathcal{O}\left(\delta \right),J_{3,4}={\displaystyle \frac{{\sigma }^2}{k}},J_{4,3}=k+\mathcal{O}\left(\delta \right),J_{4,4}=-{\displaystyle \frac{\sigma k}{\delta }}+\mathcal{O}\left(1\right).$$

Hence, we have Trace $\left(J_1\right)=-{\displaystyle \frac{\sigma k}{\delta }}+\mathcal{O}\left(1\right)<0$ as $\delta \to 0^{+}$, and Det $\left(J_1\right)={\displaystyle \frac{\sigma k^2}{\delta }}+\mathcal{O}\left(1\right)>0$ as $\delta \to 0^{+}$, so it is easy to conclude that $J_1$ has two real strictly negative eigenvalues, as $\delta \to 0^{+}$.

Let us summarize the results now obtained in the following proposition:

Proposition 9.

In the case where ${\delta }_1\sim \delta$ and $\delta \to 0^{+}$, the equilibrium $P_1$ in case 2 is unstable while the equilibrium $P_2$ is unstable if $\gamma \lambda -k>0$ and is asymptotically stable if $\gamma \lambda -k<0$.

Interpretation: $\gamma \lambda <k$ means that the carrying capacity of renewable resources is relatively small compared to the factor k capturing the potential for discovering new non-renewable reserves. In that regime, a positive z can remain, and $(x=0,y=0)$ can be stable. Physically, if a trajectory starts with low values for population and renewable resources, the population goes extinct, even if some non-renewable resource remains stable.

6.1.2. Case ${\delta }_1$ Fixed

Here, we study the stability of equilibria $P_i$ keeping ${\delta }_1$ fixed (but small) and letting $\delta \to 0^{+}$. We obtain

$$\underset{\delta \to 0^{+}}{lim}J\left(P_1\right)=\left(\begin{array}{cccc}{\displaystyle -c}& 0& 0& 0\\ \\ 0& {\displaystyle \gamma \lambda -\frac{\sigma {\delta }_1}{k}}& 0& 0\\ \\ 0& 0& 0& {\displaystyle \frac{{\sigma }^2}{k}}\\ \\ 0& {\delta }_1{z}_i& 0& -\sigma z_i\end{array}\right).$$

In this case, for ${\delta }_1<{\displaystyle \frac{\gamma \lambda k}{\sigma }}$, we have the eigenvalue ${\rho }_2=\gamma \lambda -{\displaystyle \frac{\sigma {\delta }_1}{k}}>0$, which implies that the equilibrium $P_1$ is unstable as $\delta \to 0^{+}$. As for $P_2$, we obtain

$$J\left(P_2\right)=\left(\begin{array}{cccc}{\displaystyle -c}& 0& 0& 0\\ \\ 0& {\displaystyle -\frac{k{\delta }_1}{\delta }+\mathcal{O}\left(1\right)}& 0& 0\\ \\ 0& 0& -k+\mathcal{O}\left(\delta \right)& {\displaystyle \frac{{\sigma }^2}{k}}\\ \\ 0& {\displaystyle \frac{k{\delta }_1}{\delta }+\mathcal{O}\left(1\right)}& k+\mathcal{O}\left(\delta \right)& {\displaystyle -\frac{\sigma k}{\delta }+\mathcal{O}\left(1\right)}\end{array}\right).$$

In this case, the eigenvalue ${\rho }_2=\gamma \lambda -{\delta }_1{z}_2=-{\displaystyle \frac{k{\delta }_1}{\delta }}+\mathcal{O}\left(1\right)$ is negative as $\delta \to 0^{+}$. The behavior of the point $P_2$ thus depends on the remaining two eigenvalues, which do not depend on ${\delta }_1$ and are the same as those of the matrix $J_1$ that we have seen above, so, in this case, they are both strictly negative as $\delta \to 0^{+}$. We can therefore summarize our results in the following proposition:

Proposition 10.

For any ${\delta }_1\in \left(0,{\displaystyle \frac{\gamma \lambda k}{\sigma }}\right)$, there is ${\delta }^{*}>0$ such that, for all $\delta \in \left(0,{\delta }^{*}\right)$, the equilibrium $P_1$ is unstable. For any ${\delta }_1>0$, there is ${\delta }^{**}>0$ such that, for all $\delta \in \left(0,{\delta }^{**}\right)$, the equilibrium $P_2$ is asymptotically stable.

In both settings, the stability of equilibrium $P_2$ physically corresponds to a possible extinction trajectory, at least for trajectories starting nearby.

6.2. Equilibria $Q_{i,j}$

Let us now treat the equilibria ${\displaystyle Q_{i,j}=\left(\frac{\delta z_j}{\mu \sigma t_i},0,z_j,\frac{\delta z_j}{\sigma }\right),i,j=1,2}$. The Jacobian matrix $J\left(Q_{ij}\right)$ is given by

$$J\left(Q_{ij}\right)=\left(\begin{array}{cccc}{\displaystyle \frac{c}{1+t_i^2}(t_i^2-1)}& 0& 0& {\displaystyle \frac{d\mu x^2({\mu }^2{x}^2-w^2)}{{(w^2+{\mu }^2{x}^2)}^2}}\\ \\ 0& \gamma \lambda -{\delta }_1{z}_j& 0& 0\\ \\ 0& 0& {\displaystyle -2\delta z_j+\frac{{\delta }^2}{k}{z}_j^2+\frac{2\sigma \delta }{k}}& {\displaystyle \frac{{\sigma }^2}{k}}\\ \\ 0& {\delta }_1{z}_j& 2\delta z_j-\sigma w& -\sigma z_j\end{array}\right).$$

We have that $J_{11}$ is an eigenvalue of the matrix, and, by simplifying its expression, we obtain

$$\begin{array}{cc}\hfill {\displaystyle J_{11}}& =-c+2d\mu {\displaystyle \frac{x{w}^3}{{(w^2+{\mu }^2{x}^2)}^2}}=-c+2\underset{c}{\underbrace{d{\displaystyle \frac{\mu xw}{w^2+{\mu }^2{x}^2}}}}{\displaystyle \frac{w^2}{w^2+{\mu }^2{x}^2}}=c\left[-1+2{\displaystyle \frac{w^2}{w^2+{\mu }^2{x}^2}}\right]\hfill \\ \hfill & =c\left[-1+2{\displaystyle \frac{t_i^2}{1+t_i^2}}\right]={\displaystyle \frac{c}{1+t_i^2}}(t_i^2-1).\hfill \end{array}$$

(21)

Hence, ${\rho }_1=J_{11}>0$ if $(t_i^2-1)>0$, i.e., if $t_i>1$. From the definition of $t_i$ in (7), we have that $t_1\in (0,1)$ while $t_2>1$. Therefore, the Jacobian matrices $J\left(Q_{2,j}\right)$, corresponding to the case $t=t_2$, have a positive eigenvalue, so we can conclude that the points $Q_{2,j}$ are unstable equilibria for any $\delta ,{\delta }_1$. We only need to analyze the points $Q_{1j},j=1,2$ related to the case $t=t_1$. We first study the case ${\delta }_1\sim \delta$.

6.2.1. Case ${\delta }_1\sim \delta$

We notice that an eigenvalue is given by ${\rho }_2=J_{22}$. With the same argument as above, we have that ${\rho }_2$ is positive, as $\delta \to 0^{+}$ and ${\delta }_1\sim \delta$, in the case where $z=z_1$ and in the case where $z=z_2$ with $\gamma \lambda -k>0$. Therefore, we can state that, in the hypotheses $\delta \to 0^{+}$ and ${\delta }_1\sim \delta$, $Q_{1,1}$ is an unstable equilibrium while $Q_{1,2}$ is unstable for $\gamma \lambda -k>0$. We are left with the analysis of $Q_{1,2}$ when $\gamma \lambda -k<0$. Taking into account that, in the present case, we have $\sigma w=\delta z$, we can easily obtain that the two remaining eigenvalues of the matrix $J\left(Q_{1,2}\right)$ have the same sign as those of the matrix $J_1$ above; hence, they are both negative, as $\delta \to 0^{+}$. We summarize the results obtained in the following two propositions:

Proposition 11.

The equilibria $Q_{2,1},Q_{2,2}$ are unstable for any ${\delta }_1,\delta$.

Proposition 12.

As $\delta \to 0^{+}$ and ${\delta }_1\sim \delta$, the equilibrium $Q_{1,1}$ is unstable, while the equilibrium $Q_{1,2}$ is unstable if $\gamma \lambda -k>0$ and asymptotically stable if $\gamma \lambda -k<0$.

We now study the stability of equilibria $Q_{1,j}$ in the case in which ${\delta }_1$ is fixed (but small) and $\delta \to 0^{+}$.

6.2.2. Case of Fixed ${\delta }_1$

As we said above, we only need to analyze the points $Q_{1,j},j=1,2$. If $z=z_1$, we have, as in the case of equilibrium $P_1$, an eigenvalue ${\displaystyle {\rho }_2=\gamma \lambda -\frac{\sigma {\delta }_1}{k}+\mathcal{O}\left(1\right)}$, which is positive for ${\delta }_1<{\displaystyle \frac{\gamma \lambda k}{\sigma }}$ and $\delta \to 0^{+}$, so we can conclude that $Q_{11}$ is an unstable equilibrium. If $z=z_2$, the second eigenvalue is given by ${\displaystyle {\rho }_2=-\frac{k{\delta }_1}{\delta }+\mathcal{O}\left(1\right)}$, and this is negative as $\delta \to 0^{+}$. The remaining two eigenvalues have the same sign as those seen for the point $P_2$ and are therefore negative. Thus, the point $Q_{12}$ is an asymptotically stable equilibrium for $\delta \to 0^{+}$. We summarize our results as follows:

Proposition 13.

When ${\delta }_1<{\displaystyle \frac{\gamma \lambda k}{\sigma }}$ and $\delta \to 0^{+}$, the equilibrium $Q_{11}$ is unstable. For any ${\delta }_1>0$, the equilibrium $Q_{12}$ is asymptotically stable as $\delta \to 0^{+}$.

In sum, $Q_{1,2}$ is the only potentially stable equilibrium with positive population in this case.

7. Stability and Instability: Case 4

We recall that the equilibria in this case are given by

$$P_j=\left({\displaystyle 0,\lambda -\frac{{\delta }_1}{\gamma }{z}_j,z_j,\frac{\delta }{k-\delta z_j}}\right)$$

(22)

$(j=1,2)$ and

$$Q_{i,j}=\left({\displaystyle \frac{\delta }{\mu t_i(k-\delta z_j)},\lambda -\frac{{\delta }_1}{\gamma }{z}_j,z_j,\frac{\delta }{k-\delta z_j}}\right)$$

(23)

$(i,j=1,2)$.

We refer to (18) and, recalling that ${\displaystyle \delta =\frac{kw}{wz+1}}$ and ${\displaystyle w=\frac{\delta }{k-\delta z}=\frac{1}{\sigma }\left[\left(\delta -\frac{{\delta }_1^2}{\gamma }\right)z+{\delta }_1\lambda \right]}$, we have

$$\begin{array}{cc}\hfill J_{22}& =\gamma \lambda -2\gamma y-{\delta }_{1}z=\gamma \lambda -2\gamma \left(\lambda -{\displaystyle \frac{{\delta }_1}{\gamma }}z\right)-{\delta }_{1}z=-\gamma \lambda +{\delta }_{1}z\hfill \\ \hfill J_{33}& ={\displaystyle \frac{kwz(wz+2)}{{(wz+1)}^2}}-2\delta z=\underset{{\delta }^2}{\underbrace{{\displaystyle \frac{k^2{w}^2}{{(wz+1)}^2}}}}{\displaystyle \frac{z^2}{k}}+\underset{{\delta }^2}{\underbrace{{\displaystyle \frac{k^2{w}^2}{{(wz+1)}^2}}}}{\displaystyle \frac{2z}{kw}}-2\delta z={\displaystyle \frac{z^2}{k}}{\delta }^2+{\displaystyle \frac{2z}{kw}}{\delta }^2-2\delta z\hfill \\ & ={\displaystyle \frac{z^2}{k}}{\delta }^2+{\displaystyle \frac{2z}{k}}{\displaystyle \frac{k-\delta z}{\delta }}{\delta }^2-2\delta z={\displaystyle \frac{z^2}{k}}{\delta }^2+2z\delta -2{\displaystyle \frac{z^2}{k}}{\delta }^2-2\delta z=-{\displaystyle \frac{z^2}{k}}{\delta }^2\hfill \\ \hfill J_{34}& ={\displaystyle \frac{k{z}^2}{{(wz+1)}^2}}{\displaystyle \frac{w^{2}k}{w^{2}k}}={\displaystyle \frac{z^2}{w^{2}k}}\underset{{\delta }^2}{\underbrace{{\displaystyle \frac{w^2{k}^2}{{(wz+1)}^2}}}}={\displaystyle \frac{z^2}{k}}{\displaystyle \frac{{\delta }^2}{w^2}}={\displaystyle \frac{z^2}{k}}{\displaystyle \frac{{(k-\delta z)}^2}{{\delta }^2}}{\delta }^2={\displaystyle \frac{z^2}{k}}{(k-\delta z)}^2\hfill \\ \hfill J_{43}& ={\delta }_{1}y+2\delta z-\sigma w={\delta }_1\left(\lambda -{\displaystyle \frac{{\delta }_1}{\gamma }}z\right)+2\delta z-\sigma \underset{w}{\underbrace{\left[{\displaystyle \frac{1}{\sigma }\left(\delta -\frac{{\delta }_1^2}{\gamma }\right)z+\frac{{\delta }_1\lambda }{\sigma }}\right]}}=\delta z.\hfill \end{array}$$

Thus, the Jacobian matrix (18) in case 4 becomes

$$J\left(X\right)=\left(\begin{array}{cccc}{\displaystyle -c+2d\mu \frac{x{w}^3}{{(w^2+{\mu }^2{x}^2)}^2}}& 0& 0& {\displaystyle \frac{d\mu x^2({\mu }^2{x}^2-w^2)}{{(w^2+{\mu }^2{x}^2)}^2}}\\ \\ 0& -\gamma \lambda +{\delta }_{1}z& {\displaystyle -{\delta }_1\lambda +\frac{{\delta }_1^2}{\gamma }{z}_i}& 0\\ \\ 0& 0& {\displaystyle -\frac{z^2}{k}{\delta }^2}& {\displaystyle \frac{z^2}{k}{(k-\delta z)}^2}\\ \\ 0& {\delta }_{1}z& \delta z& -\sigma z\end{array}\right).$$

(24)

To study stability, we first note that, for all the equilibria that we are now dealing with, we have the eigenvalue ${\rho }_1=J_{11}$. This eigenvalue is always negative for the points $P_1,P_2$, whereas, in the case of the points $Q_{ik},k,i=1,2$, the sign of this eigenvalue is the same as that obtained in (21). So, we have a positive eigenvalue in the case $t=t_2$ and a negative eigenvalue in the case $t=t_1$. We can therefore already state the following.

Proposition 14.

The points $Q_{2,j},j=1,2$ are unstable equilibria for any $\delta ,{\delta }_1>0$.

We now have to study the stability of the equilibria $P_j,Q_{1,j},j=1,2$. For this, we will study the eigenvalues of the $3\times 3$ submatrix given by

$$J_3\left(X\right)=\left(\begin{array}{ccc}-\gamma \lambda +{\delta }_{1}z& {\displaystyle -{\delta }_1\lambda +\frac{{\delta }_1^2}{\gamma }z}& 0\\ \\ 0& {\displaystyle -\frac{z^2}{k}{\delta }^2}& {\displaystyle \frac{z^2}{k}{(k-\delta z)}^2}\\ \\ {\delta }_{1}z& \delta z& -\sigma z\end{array}\right).$$

(25)

Its characteristic polynomial will be denoted by $p_3\left(\rho \right)={\rho }^3+a_1{\rho }^2+a_2\rho +a_3$.

Analyzing further, we also note that $J_3\left(P_j\right)=J_3\left(Q_{1,j}\right),j=1,2$; indeed, the equilibria $P_j$ differ from the $Q_{1,j}$ ones only for the x-component, which does not appear in the matrix $J_3$. As a consequence, the stability behavior of $P_j$ will be the same as that of $Q_{1,j},j=1,2$.

We first study the case in which ${\delta }_1\sim \delta \to 0^{+}$. Given the greater complexity of case 4, in this scenario, we restrict our study to the particular case ${\delta }_1=\delta$. We will then keep ${\delta }_1$ fixed at a small value and study the behavior as $\delta \to 0^{+}$.

7.1. Equilibria $P_i,Q_{1,i}$, Case ${\delta }_1=\delta$

We need to obtain the asymptotic development of the values $z_i$ ( $i=1,2$), which are solutions of Equation (15). We set ${\delta }_1=\delta$, and Equation (15), dividing by $\delta$, becomes

$$\delta \left(\gamma -\delta \right)z^2+[-k\gamma +(\lambda \gamma +k)\delta ]z+\gamma (\sigma -k\lambda )=0.$$

(26)

We now give some asymptotic developments for the roots of this equation. First, the discriminant is given by

$${\gamma }^2{k}^2+(2{\gamma }^{2}k\lambda -4{\gamma }^2\sigma -2\gamma k^2)\delta +\mathcal{O}\left({\delta }^2\right)$$

and that of the reciprocal of the first coefficient multiplied by two is given by

$${\displaystyle \frac{1}{2(\gamma \delta -{\delta }^2)}}={\displaystyle \frac{1}{2\gamma \delta }}+{\displaystyle \frac{1}{2{\gamma }^2}}+\mathcal{O}\left(\delta \right).$$

We then obtain

$$\begin{array}{cc}\hfill z_i=& \left[k\gamma -(\lambda \gamma +k)\delta \pm \left(k\gamma +{\displaystyle \frac{\gamma k\lambda -2\gamma \sigma -k^2}{k}}\delta +\mathcal{O}\left({\delta }^2\right)\right)\right]\hfill \\ & \left\{{\displaystyle \frac{1}{2\gamma \delta }}+{\displaystyle \frac{1}{2{\gamma }^2}}+\mathcal{O}\left(\delta \right)\right\},i=1,2\hfill \end{array}$$

We then obtain the following developments for the z-coordinates of the equilibria.

$$\begin{array}{cc}\hfill & z_1=z\left(P_1\right)=z\left(Q_{1,1}\right)=-{\displaystyle \frac{k\lambda -\sigma }{k}}+\mathcal{O}\left(\delta \right)\hfill \\ \hfill & z_2=z\left(P_2\right)=z\left(Q_{1,2}\right)={\displaystyle \frac{k}{\delta }}-{\displaystyle \frac{\sigma }{k}}+\mathcal{O}\left(\delta \right).\hfill \end{array}$$

Let us start to study $P_1,Q_{1,1}$. If $k\lambda >\sigma$, then $z_1<0$ as $\delta \to 0^{+}$; hence, the equilibria are not in $\overline{\mathcal{C}}$. So, we assume that $k\lambda <\sigma$, and the previous formula for $z_1$, together with (22) and (23), proves that all the coordinates of $P_1,Q_{1,1}$ are non-negative, as $\delta \to 0^{+}$. Analyzing $J_3\left(P_1\right)\equiv J_3\left(Q_{1,1}\right)$, the Jacobian (25) evaluated at these points becomes

$$\left(\begin{array}{ccc}{\displaystyle -\gamma \lambda +\mathcal{O}\left(\delta \right)}& -\lambda \delta +\mathcal{O}\left({\delta }^2\right)& 0\\ 0& \mathcal{O}\left({\delta }^2\right)& {\displaystyle \frac{{(k\lambda -\sigma )}^2}{k}+\mathcal{O}\left(\delta \right)}\\ {\displaystyle -\frac{(k\lambda -\sigma )}{k}\delta +\mathcal{O}\left({\delta }^2\right)}& {\displaystyle -\frac{(k\lambda -\sigma )}{k}\delta +\mathcal{O}\left({\delta }^2\right)}& {\displaystyle \frac{\sigma (k\lambda -\sigma )}{k}+\mathcal{O}\left(\delta \right)}\end{array}\right)$$

(27)

If we call $J_3$ this matrix, it is easy to obtain

$$det\left(J_3\right)=-{\displaystyle \frac{\gamma {(k\lambda -\sigma )}^3\lambda }{k^2}}\delta +\mathcal{O}\left({\delta }^2\right).$$

But, the characteristic polynomial $p_3\left(\rho \right)$ of this matrix is given by det $\left(\rho I-J_3\right)$; hence,

$$p_3\left(0\right)=det\left(-J_3\right)=-det\left(J_3\right)={\displaystyle \frac{\gamma {(k\lambda -\sigma )}^3\lambda }{k^2}}\delta +\mathcal{O}\left({\delta }^2\right).$$

As we are assuming that $k\lambda <\sigma$, we obtain $p_3\left(0\right)<0$ as $\delta \to 0^{+}$; hence, the equation $p_3\left(\rho \right)=0$ has at least a real positive solution and the equilibria $P_1$ and $Q_{1,1}$ are unstable.

Let us now study the equilibria $P_2,Q_{1,2}$. Recall that we are still in the hypothesis $\delta ={\delta }_1$. Combining the formula above for $z_2$ with (22) and (23), we obtain that the y-coordinate of these equilibria satisfies

$$y\left(P_2\right)=y\left(Q_{1,2}\right)=\lambda -{\displaystyle \frac{k}{\gamma }}+\mathcal{O}\left(\delta \right).$$

If $\lambda \gamma -k<0$, we have $y\left(P_2\right)=y\left(Q_{1,2}\right)<0$ as $\delta \to 0^{+}$, and the equilibria are not in $\overline{\mathcal{C}}$. Hence, we assume that $\lambda \gamma -k>0$, and it is easy to verify that all the coordinates of the equilibria are non-negative, as $\delta \to 0^{+}$. The Jacobian matrix evaluated at these equilibria becomes

$$J_3\left(P_2\right)\equiv J_3\left(Q_{1,2}\right)=\left(\begin{array}{ccc}-\gamma \lambda +k+\mathcal{O}\left(\delta \right)& \mathcal{O}\left(\delta \right)& 0\\ 0& -k+\mathcal{O}\left(\delta \right)& {\displaystyle \frac{{\sigma }^2}{k}+\mathcal{O}\left(\delta \right)}\\ k+\mathcal{O}\left(\delta \right)& k+\mathcal{O}\left(\delta \right)& {\displaystyle -\frac{\sigma k}{\delta }+\frac{{\sigma }^2}{k}+\mathcal{O}\left(\delta \right)}\end{array}\right)$$

(28)

and the coefficients of the characteristic polynomial are the following:

$$\begin{array}{cc}\hfill & a_1={\displaystyle \frac{k\sigma }{\delta }}+\mathcal{O}\left(1\right)\hfill \\ \hfill & a_2={\displaystyle \frac{\gamma \lambda \sigma k}{\delta }}+\mathcal{O}\left(1\right)\hfill \\ \hfill & a_3={\displaystyle \frac{k^2(\gamma \lambda -k)\sigma }{\delta }}+\mathcal{O}\left(1\right)\hfill \\ \hfill & a_1{a}_2-a_3={\displaystyle \frac{k^2{\sigma }^2\gamma \lambda }{{\delta }^2}}+\mathcal{O}\left({\delta }^{-1}\right).\hfill \end{array}$$

According to the Routh–Hurwitz criterion, therefore, the equilibria $P_2,Q_{1,2}$ are asymtpotically stable if $\gamma \lambda -k>0$. Let us summarize the results now obtained in the following proposition:

Proposition 15.

In the case where ${\delta }_1=\delta \to 0^{+}$, the points $P_1,Q_{1,1}$ are in the positive cone for $k\lambda -\sigma <0$ and are unstable equilibrium points, while the points $P_2$ and $Q_{1,2}$ are in the positive cone for $\gamma \lambda -k>0$ and are asymptotically stable equilibrium points.

Now, we study the case with ${\delta }_1$ fixed and arbitrarily small.

7.2. Equilibria $P_i,Q_{1,i}$, Case ${\delta }_1$ Fixed

We rewrite (15) as

$$(-{\delta }_1^2\delta +\gamma {\delta }^2)z^2+(k{\delta }_1^2+\gamma ({\delta }_1\lambda -k)\delta )z-k{\delta }_1\lambda \gamma +\sigma \gamma \delta =0,$$

(29)

and we look for asymptotic expansions of the roots $z_1,z_2$.

This is a quadratic equation in z whose asymptotic expansion of the discriminant is given by

$$k^2{\delta }_1^4-2{\delta }_1^2\gamma k({\delta }_1\lambda +k)\delta +({\delta }_1^2{\gamma }^2{\lambda }^2+2{\delta }_1{\gamma }^{2}k\lambda +4{\delta }_1^2\gamma \sigma +{\gamma }^2{k}^2){\delta }^2+\mathcal{O}\left({\delta }^3\right),$$

and the reciprocal of the first coefficient multiplied by two is given by

$${\displaystyle \frac{1}{2(-{\delta }_1^2\delta +\gamma {\delta }^2)}}=-{\displaystyle \frac{1}{2{\delta }_1^2\delta }}-{\displaystyle \frac{\gamma }{2{\delta }_1^4}}-{\displaystyle \frac{{\gamma }^2}{2{\delta }_1^6}}\delta +\mathcal{O}\left({\delta }^2\right).$$

From here, we obtain

$$\begin{array}{cc}\hfill z_i=& \left\{-k{\delta }_1^2+\gamma (k-{\delta }_1\lambda )\delta \pm \left[k{\delta }_1^2-\gamma ({\delta }_1\lambda +k)\delta +{\displaystyle \frac{2\gamma \sigma }{k}}{\delta }^2+\mathcal{O}\left({\delta }^3\right)\right]\right\}\hfill \\ & \left\{-{\displaystyle \frac{1}{2{\delta }_1^2\delta }}-{\displaystyle \frac{\gamma }{2{\delta }_1^4}}-{\displaystyle \frac{{\gamma }^2}{2{\delta }_1^6}}\delta +\mathcal{O}\left({\delta }^2\right)\right\},i=1,2\hfill \end{array}$$

so

$$\begin{array}{cc}& z_1=z\left(P_1\right)=z\left(Q_{1,1}\right)={\displaystyle \frac{k}{\delta }}+{\displaystyle \frac{\sigma \gamma }{k{\delta }_1^2}}\delta +\mathcal{O}\left({\delta }^2\right)\hfill \\ & z_2=z\left(P_2\right)=z\left(Q_{1,2}\right)={\displaystyle \frac{\lambda \gamma }{{\delta }_1}}+{\displaystyle \frac{(\gamma k\lambda -{\delta }_1\sigma )}{k{\delta }_1^3}}\gamma \delta +\mathcal{O}\left({\delta }^2\right).\hfill \end{array}$$

(30)

From these expansions, together with (22) and (23), it is easy to obtain the corresponding expansions for $y_i$ ($i=1,2$).

$$\begin{array}{cc}\hfill & y_1=-{\displaystyle \frac{{\delta }_{1}k}{\gamma \delta }}+\lambda -{\displaystyle \frac{\sigma }{{\delta }_{1}k}}\delta +\mathcal{O}\left({\delta }^2\right)\hfill \\ \hfill & y_2=-{\displaystyle \frac{\gamma k\lambda -{\delta }_1\sigma }{{\delta }_1^{2}k}}\delta +\mathcal{O}\left({\delta }^2\right)\hfill \end{array}$$

(31)

If ${\delta }_1$ is fixed and $\delta \to 0$, we have $y_1<0$; hence, the points $P_1,Q_{1,1}$ are not in $\overline{\mathcal{C}}$ and we can avoid studying them. In a similar way, we are interested in fixed but small ${\delta }_1$s; hence, we can assume that ${\delta }_1<{\displaystyle \frac{\gamma \lambda k}{\sigma }}$, so $y_2<0$ for $\delta \to 0$ and also $P_2$ and $Q_{1,2}$ do not belong to $\overline{\mathcal{C}}$.

Let us summarize these results in the following proposition:

Proposition 16.

The equilibrium points $P_1,Q_{1,1}$ are not in $\overline{\mathcal{C}}$ as $\delta \to 0^{+}$. Assuming that ${\delta }_1<{\displaystyle \frac{\gamma \lambda k}{\sigma }}$, the equilibria $P_2,Q_{1,2}$ are not in $\overline{\mathcal{C}}$ as $\delta \to 0^{+}$.

Hence, we summarize as follows: in case 4, a stable equilibrium with $x,y,z,w>0$ is given by Proposition 15, and it emerges if $\delta \sim {\delta }_1\to 0$ and $\gamma \lambda >k$, exactly matching the scenario that non-renewables are exploited slowly ($\delta ,{\delta }_1$ small), but the environment can still sustain a positive population.

8. Simulations

We now present the results obtained from simulations using Matlab’s ode45 solver, which employs an explicit adaptive Runge–Kutta method. In these simulations, we aimed to validate our theoretical analyses. We show our results both in the form of Cartesian graphs, particularly in cases of instability where the figure appeared more significant, and in the form of phase graphs in cases of stability. Additionally, we simply report the data obtained in other cases to have the broadest possible range of cases.

In the displayed Cartesian graphs, the evolution of variables is obtained by uniformly perturbing the initial value around the equilibrium point, and it is shown in different colors: population in magenta, renewable resources in green, non-renewable resources in black, and accumulated wealth in blue. Dashed lines represent the coordinates of the equilibrium point being considered, with matching colors for the corresponding components (e.g., magenta for population). On the x-axis, we use a generic time unit that does not correspond to specific periods such as days, months, or years. It is a generic unit that does not necessarily cover long intervals. We suspend our simulation when the behavior becomes apparent.

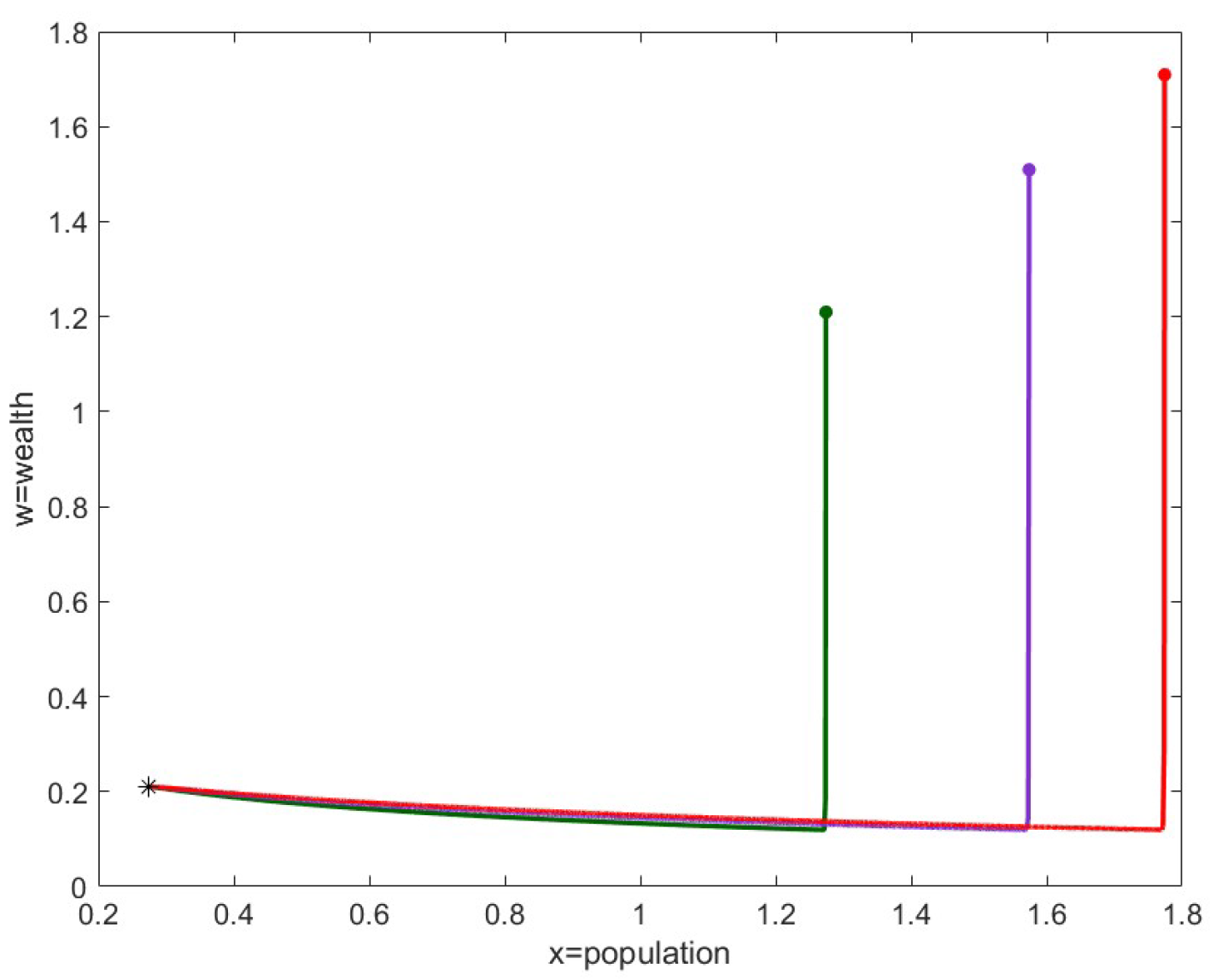
The phase graphs illustrate the evolution of population and wealth near steady points discussed in our study. These graphs focus on two key variables, population and wealth, plotting three different trajectories (described with dark green, purple, and red colors) obtained with three different perturbations on the critical point, in a two-dimensional space. The graphs depict stable points, where the dynamics gradually guide the system toward the equilibrium. The starting points are marked by small circles while the steady states are indicated by a small star.

The simulations were performed by varying the parameters $\delta$ and ${\delta }_1$. In these experiments, we kept some parameter values constant based on what is generally found in the literature; see [2,9,10]. Specifically, we set the regeneration factor of nature $\gamma =0.01$, the factor regulating the potential increase in non-renewable resources $k=1$, and the factors governing the population dynamics $c=1$, $d=3$, $\mu =2$. For stability tests, ensuring that the solutions remain within the cone or graphical requirements, we considered different values for the nature’s carrying capacity $\lambda$ and the wealth consumption $\sigma$, indicating their values in each specific case.

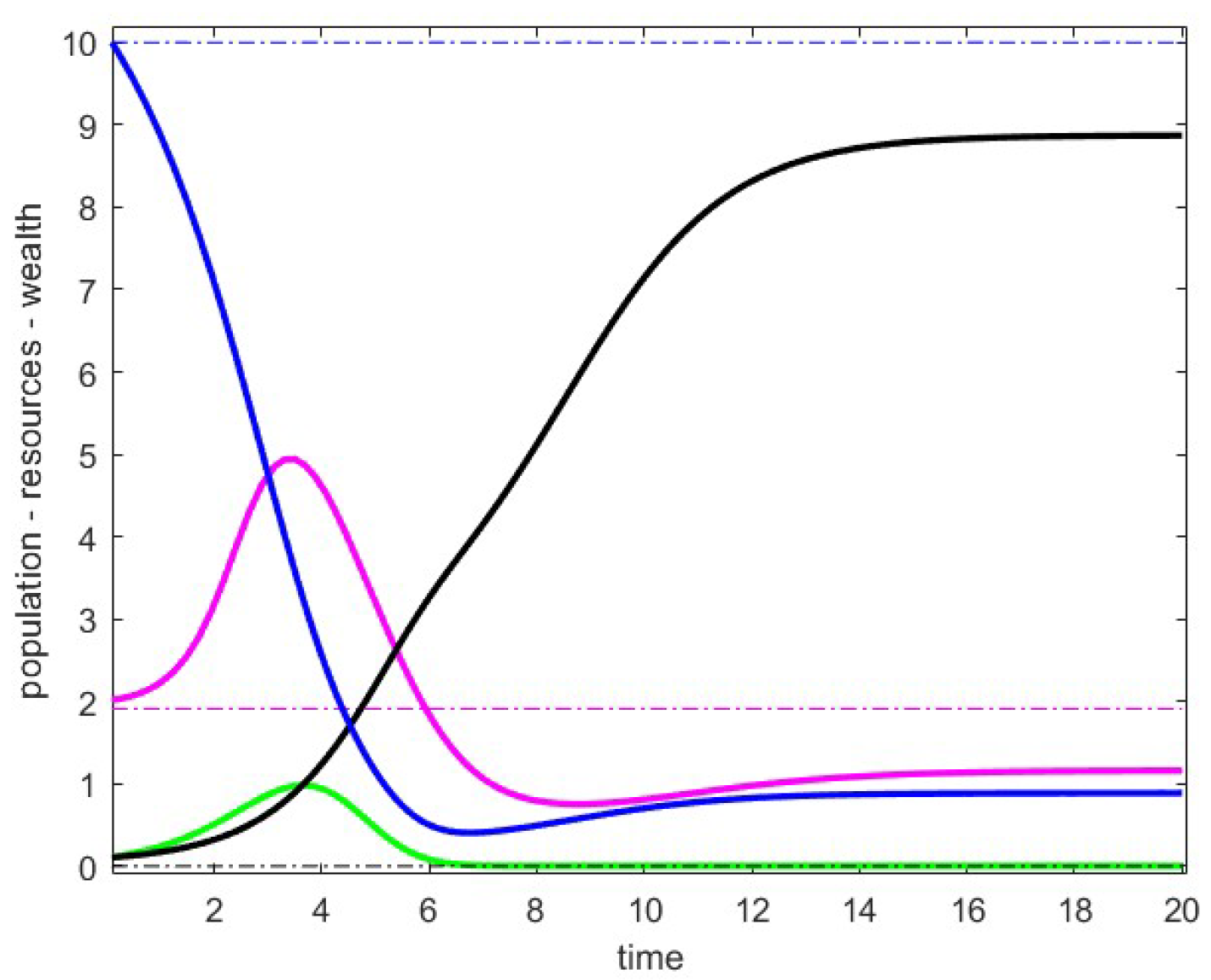
8.1. Case 1

In Figure 1, we visualize the behavior of the trajectories obtained by perturbing a point belonging to the family (10), which we now denote as point Q. We have chosen the parameters $\sigma =1, \lambda =100, W=10$ and have depicted the data related to $Q=(1.9098,0,0,10.0000)$, with the eigenvalues of the Jacobian at the point being ${\rho }_1=0.7454, {\rho }_2=1.0000, {\rho }_3={\rho }_4=0$ in the case with ${\delta }_1=1$ fixed while $\delta =0.1$.

In this scenario, the behavior of the trajectories seems to stabilize outside the critical point. We have verified that the trajectories converge to the point $Q_{12}=(1.1615, 0, 8.8730, 0.8873)$ of case 2, with eigenvalues $(-0.7454, -8.9813, -0.6790, -7.8730)$. We recall that the points $Q_{12}$ of case 2 are stable for fixed ${\delta }_1$ and $\delta \to 0^{+}$.

8.2. Case 2

Regarding case 2, we first analyze the point $Q_{12}$. This point is a stable equilibrium with a positive population when ${\delta }_1$ is fixed and $\delta \to 0^{+}$, regardless of the choice of other parameters, or when $\gamma \lambda -k<0$ in the case $\delta ={\delta }_1\to 0^{+}$.

The graph in Figure 2 illustrates the evolution of population and wealth near the point $Q_{12}=(1.1615, 0, 8.8730, 0.8873)$, obtained by setting $\lambda =150$, $\sigma =1$, so $\gamma \lambda -k=0.5>0$ and $\delta ={\delta }_1=0.1$. These values give instability, and we verify this fact for three different perturbations. We recall that the starting points are marked by small circles while the steady state is indicated by a small star. Notice that, if we set $\delta =0.1$ and ${\delta }_1=1$, we obtain stability, with eigenvalues ${\rho }_1=-0.7454, {\rho }_2=-8.9813, {\rho }_3=-0.6790, {\rho }_4=-7.3730$, which differ from the eigenvalues obtained for the case in Figure 2 only in the value of ${\rho }_4=0.6127$.

We also report the data concerning the unstable equilibrium $Q_{11}=(0.1475, 0, 1.1270, 0.1127)$. This point is unstable both when $\delta ={\delta }_1\to 0^{+}$ and when ${\delta }_1$ is fixed with ${\delta }_1<{\displaystyle \frac{\gamma \lambda k}{\sigma }}$. The eigenvalues obtained for the case $\delta ={\delta }_1=0.1$ are ${\rho }_1=-0.7454$, ${\rho }_2=-1.2203$, ${\rho }_3=0.0806$, and ${\rho }_4=0.8873$. In contrast, when $\delta =0.1$ and ${\delta }_1=1$, the last eigenvalue changes to ${\rho }_4=-0.1270$. In these computations, we used the parameters $\sigma =1$ and $\lambda =100$.

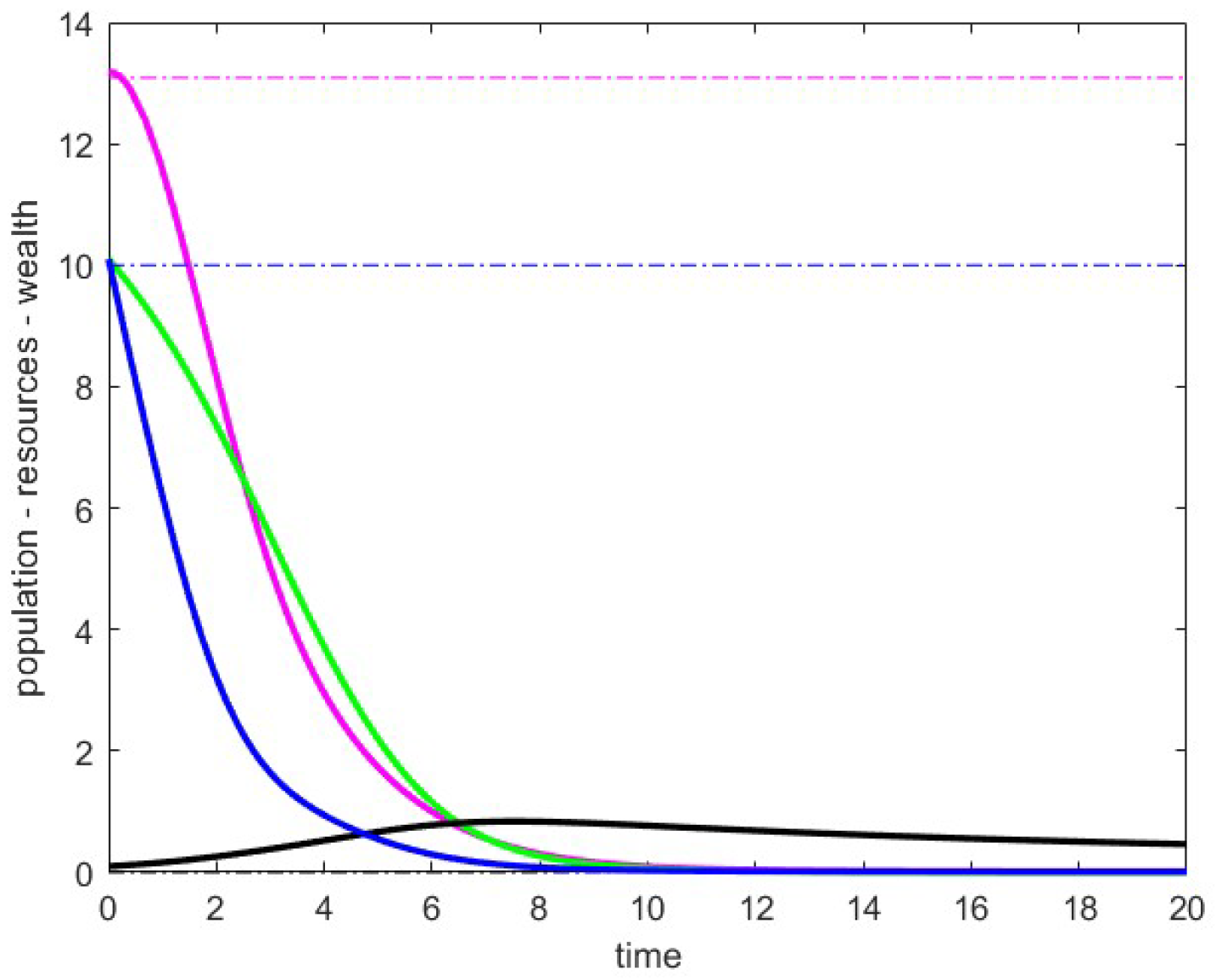
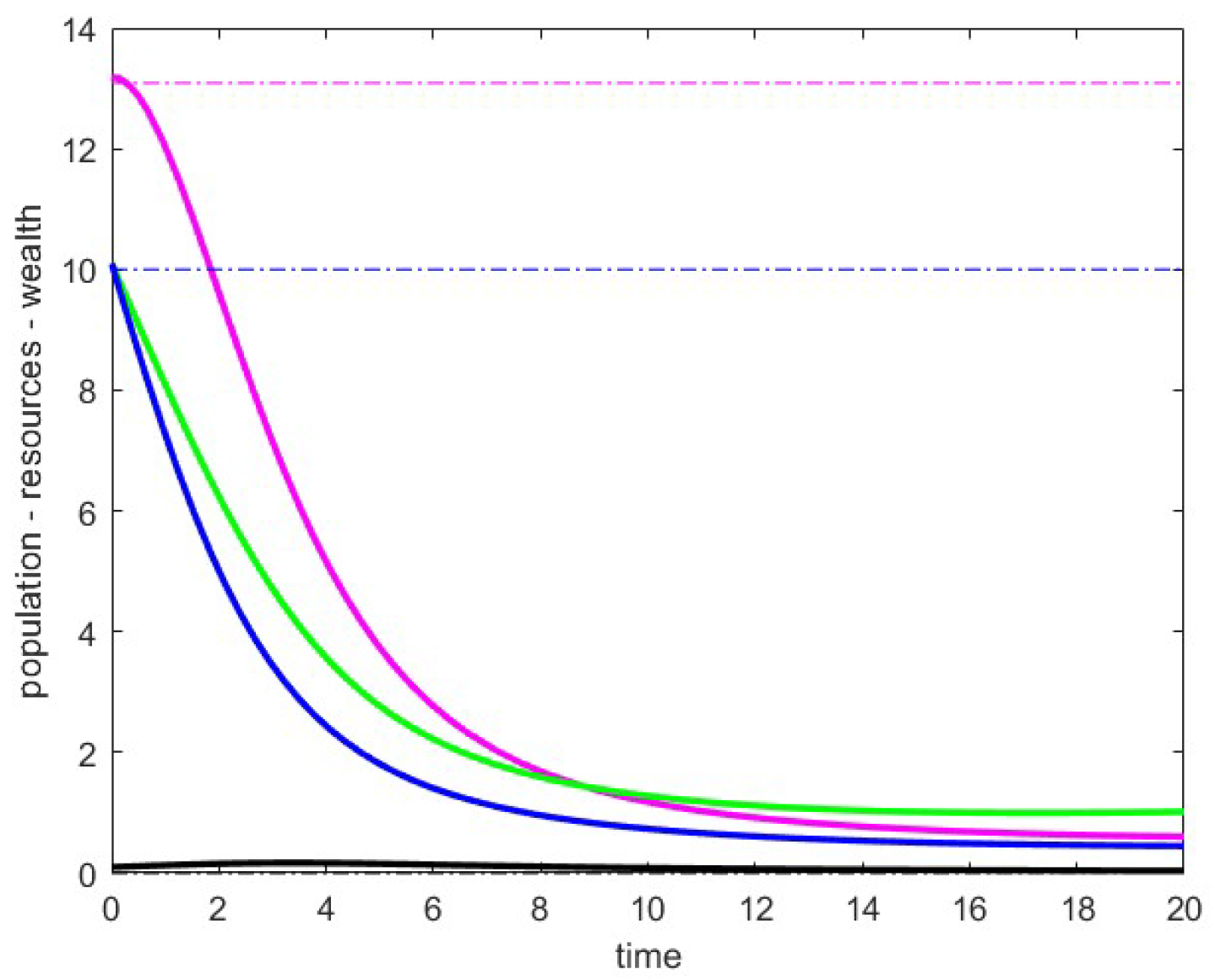
8.3. Case 3

In these simulations, we considered the following parameter values: $\sigma =5, \lambda =10$. In Figure 3 and Figure 4, we present the data related to the unstable critical point P of the family (14), referred to as $t_1$. In particular, we obtain the point $P=(13.0902, 10, 0, 10)$ with the eigenvalues of the Jacobian matrix at the point given by ${\rho }_1=-0.7454, {\rho }_2=-0.1000, {\rho }_3={\rho }_4=0$. In Figure 3, we report the trajectories obtained with fixed ${\delta }_1$ and small $\delta$, namely $\delta =0.1,{\delta }_1=1$. In Figure 4, we report the trajectories for large values of $\delta$, specifically $\delta ={\delta }_1=2$. We aimed to simulate these scenarios over large time intervals. In the situation of Figure 3, we verified that the trajectories do not stabilize and sometimes exhibit gradually damped oscillations. Meanwhile, in the situation of Figure 4, the curves appear to stabilize at a point with a positive population. We exclude the possibility that this point could be the point $Q_{12}$ from case 2 because, with the chosen parameters, this point does not belong to the positive cone. Therefore, we suppose that it might be the point $Q_{12}$ from case 4, for which we have theoretical results only for very small values of $\delta$.

8.4. Case 4

Regarding case 4, we analyze the scenarios given by $Q_{12}$. This point take positive values in its components, meaning that it is within the cone, and the established asymptotic behavior is obtained only for small values of $\delta$, i.e., $\delta \le {10}^{-3}$. Therefore, as can be seen from the developments, the variable z takes very large values and the equilibrium is reached immediately.

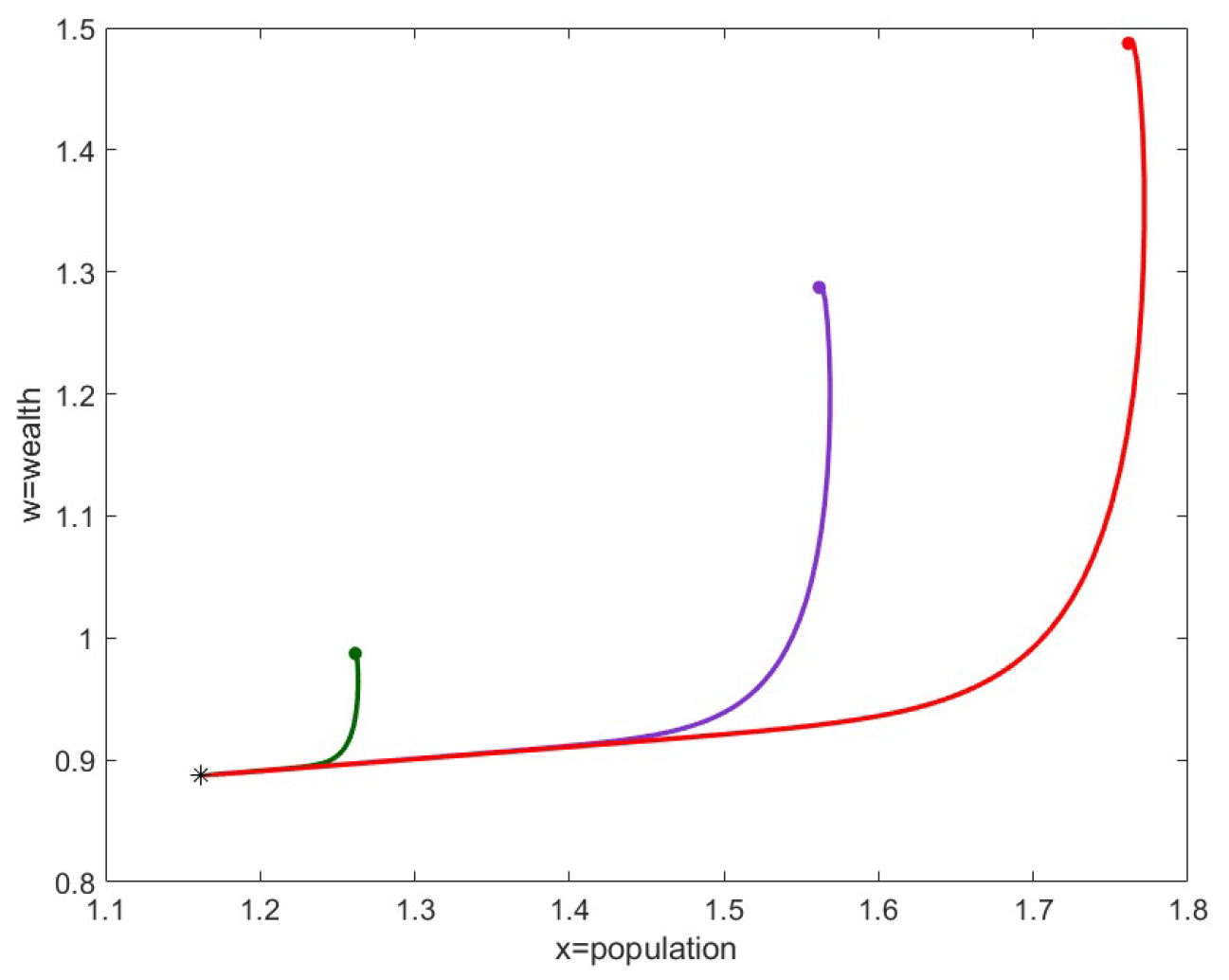
In Figure 5 and Figure 6, we show the analysis of the point $Q_{12}$. The coordinates of $Q_{12}$ are $(0.2741, 50.4775, 995.2250, 0.2094)$, and it is obtained using the parameters $\sigma =5$, $\lambda =150$, and $\delta ={\delta }_1={10}^{-3}$. Under these conditions, we have $\gamma \lambda -k=0.5>0$. The eigenvalues of the Jacobian calculated at this point are ${\rho }_1=-0.7454, {\rho }_2=-4976.1295, {\rho }_3=-0.5052, {\rho }_4=-0.9855$, giving a stable critical equilibrium with positive population. The graph in Figure 5 illustrates the evolution of population and wealth near $Q_{12}$. The three different starting points are marked by small circles while the steady state is indicated by a small star. The graph in Figure 6 shows the trajectory of the curves obtained with a non-uniform perturbation of the components of $Q_{12}$. Specifically, for the variable z, a negative perturbation of −500 was chosen to visualize the initial point without further increasing the already large difference between the component values.

For completeness, we also provide additional data, particularly for the point $P_1=(0, 9.9950, 5.0057, 1.0000·{10}^{-5})$, along with the eigenvalues of the Jacobian matrix calculated at this point, which are ${\rho }_1=-75.0863$, ${\rho }_2=1.6684·{10}^{-5}$, ${\rho }_3=-9.9950·{10}^{-2}$, ${\rho }_4=-1.0000$. To ensure that the point lies within the cone, we set $\sigma =15$ and $\lambda =10$. An analogous case is obtained for the point $Q_{11}=(1.3090·{10}^{-5}, 9.9950, 5.0057, 1.0000·{10}^{-5})$, where the eigenvalues of the Jacobian matrix are the same except for ${\rho }_4=-0.7454$.

We also report the simulation data for the unstable point $Q_{21}=(0.0002, 9.4425, 5.5750,$ $0.0010)$, where we set $\sigma =15,\lambda =10$ to obtain $k\lambda -\sigma =-5<0$; the eigenvalues are ${\rho }_1=0.7454, {\rho }_2=-83.6270, {\rho }_3=-0.0942, {\rho }_4=0.0018$. In this last case, we had to further reduce the value of $\delta ={\delta }_1=0.001$ so that the point remains in the cone.

9. Conclusions

Let us summarize the main results of this paper. First, we have obtained that all the relevant trajectories (that is, the trajectories starting in ${\mathcal{C}}_0$) are bounded. So, in our model, an indefinite growth in the variables is ruled out, and this is true in particular for population and wealth. Secondly, we have obtained that most of the equilibria of the system are unstable (or are outside $\overline{\mathcal{C}}$) but there are, at least for some range of the parameters, stable equilibria with positive values for all the variables (see Proposition 15 and Figure 5 and Figure 6). Hence, a general indication that can be drawn from our study is the following: on one hand, it seems pointless, or even dangerous, to pursue the idea of an indefinite growth in wealth and/or population, even assuming, as we do here, a moderate optimism in the replenishment of non-renewable resources; on the other hand, it is possible to drive the society toward a safe stationary state. Our results also show that this safe state is attainable when ${\delta }_1=\delta \to 0^{+}$, that is, for small rates of exploitation of resources.

We notice that the numerical simulations related to Figure 3 and Figure 4 also seem interesting: indeed, they suggest that, for a trajectory starting near an equilibrium with zero non-renewable resources, the values of population and wealth collapse and remain very small (at least, along all our simulations). This fits very well with the idea that our model describes a society strongly dependent on non-renewable resources; indeed, it means that, in such a society, a crisis in non-renewable resources leads to a general collapse.

We remark that we have obtained similar results in our previous papers [1,2]. These three papers work with different hypotheses, and the fact that similar results are obtained seems to us relevant because it proves that these results are robust and do not depend on some particular characteristic of a model. We will try to pursue these kinds of results in a forthcoming paper, where a new variation of the model will be introduced.

Limitations and future work.

We highlight that the present model, while offering some interesting insights, does not incorporate the following:

• Potential societal inequalities or multiple social classes, as in the original HANDY approach;
• More realistic functional forms for consumption, e.g., logistic or saturating resource usage by the population, or wealth-based changes in x beyond the ratio $w/x$;
• Seasonal or stochastic fluctuations in resource discovery and usage;
• Policy interventions, technological breakthroughs, or externalities beyond the simple form $k{\displaystyle \frac{w{z}^2}{wz+1}}$.

We also do not consider large-time-scale feedback such as climate change. These omissions are limitations that could be addressed in future extensions. These extensions could further clarify the conditions needed for stable, prosperous, and sustainable societies.

In future work, we also aim to test the robustness of these results by introducing further versions of our models. In addition, we would like to expand the study of the dynamics. In this paper, we have a picture of the long-term behavior of the trajectories only when they start near stable equilibria. It is well known that mapping the equilibria and their stability is a necessary but initial step in the study of a dynamical system. Further steps are the research of a pattern of the long-term behavior of generic trajectories and, in particular, the search for possible periodic solutions and chaotic dynamics. We will face some of these problems in a forthcoming paper.