Modified Lagrange Interpolating Polynomial (MLIP) Method: A Straightforward Procedure to Improve Function Approximation
Abstract
1. Introduction
2. Description of the Proposed Modified Lagrange Interpolating Polynomial (MLIP) Method
3. Applications of Modified Lagrange Interpolating Polynomial (MLIP) Method
3.1. Case Study 1
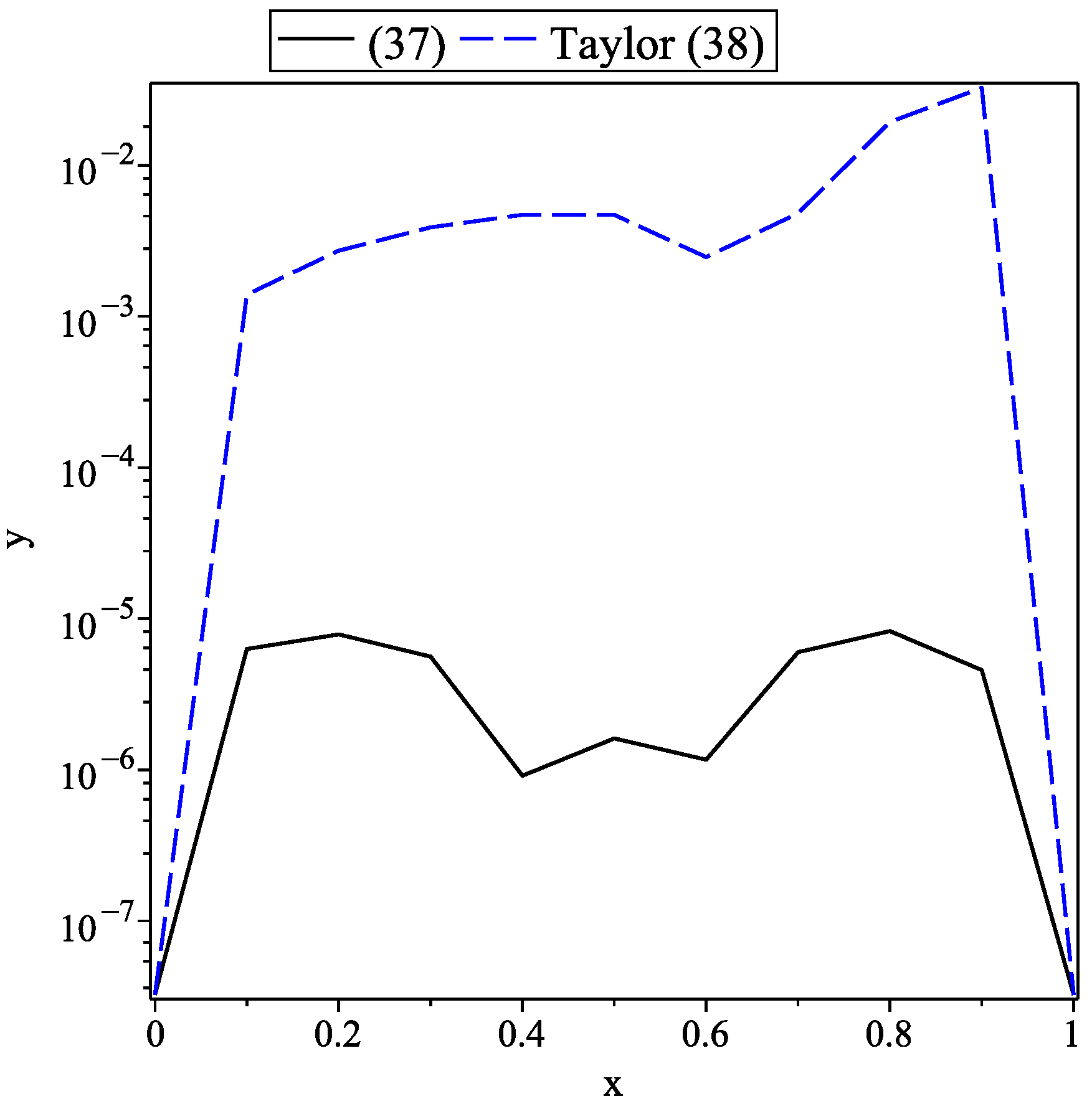
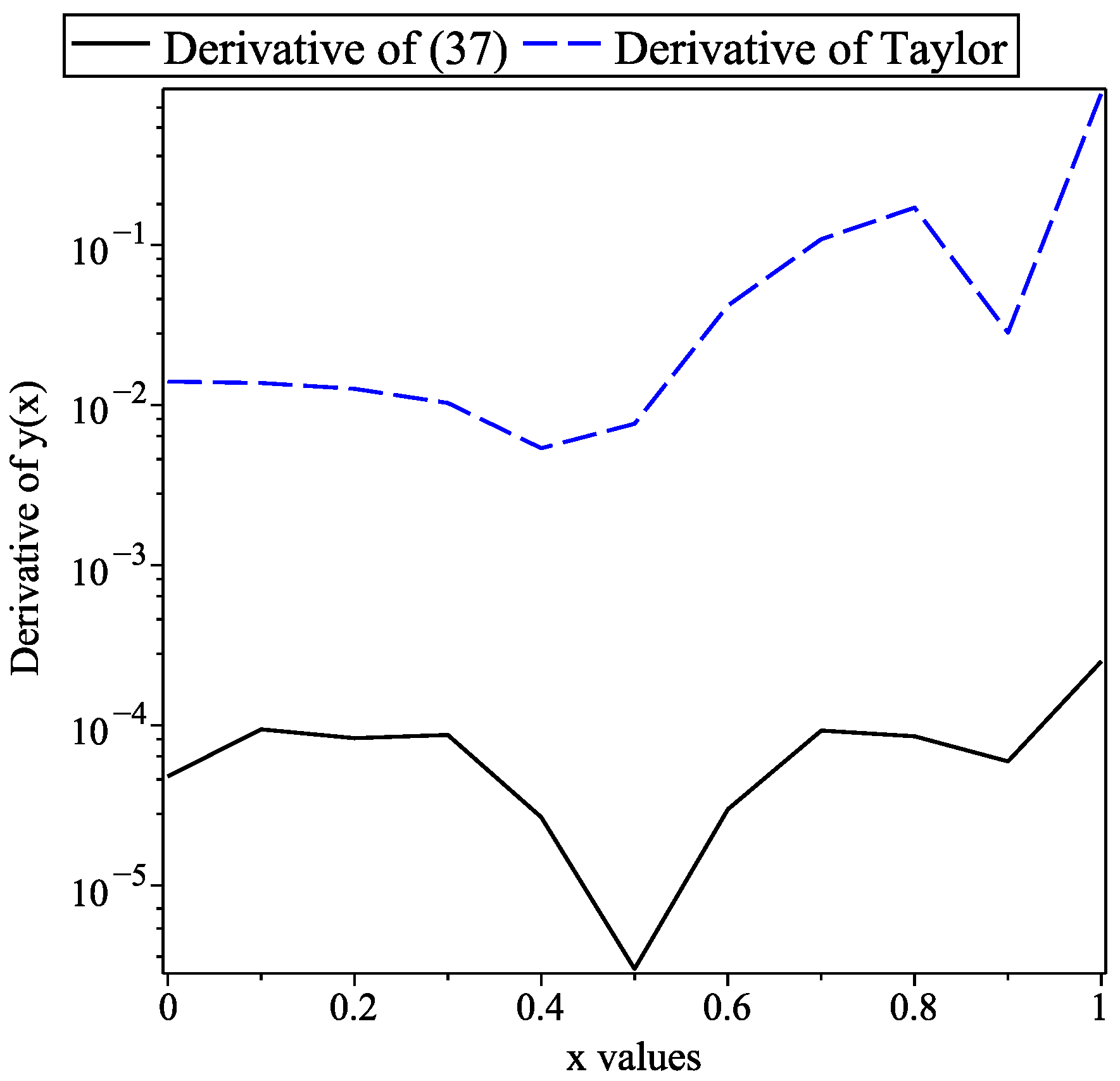
3.2. Case Study 2
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Faires, J.D.; Burden, R.L. Numerical Methods, 3rd ed.; Brooks Cole: Pacific Grove, CA, USA, 2002. [Google Scholar]
- Liu, Y.P.; He, J.H. A fast and accurate estimation of amperometric current response in reaction kinetics. J. Electroanal. Chem. 2025, 978, 118884. [Google Scholar] [CrossRef]
- Hurtado, A.N.; Sánchez, F.C.D. Métodos Numéricos: Aplicados a la Ingeniería; Grupo Editorial Patria: Puebla, Mexico, 2014. [Google Scholar]
- Chapra, S.C.; Canale, R.P. Numerical Methods For Engineers, 5th ed.; McGraw-Hill: New York, NY, USA, 2006. [Google Scholar]
- Hamming, R. Numerical Methods for Scientists and Engineers, 2nd ed.; Courier Corporation: North Chelmsford, MA, USA, 2012. [Google Scholar]
- Epperson, J. An Introduction to Numerical Methods and Analysis; John Wiley and Sons: Hoboken, NJ, USA, 2021. [Google Scholar]
- Griffiths, D.; Higham, D. Numerical Methods for Ordinary Differential Equations: Initial Value Problems; Springer: Berlin/Heidelberg, Germany, 2010; Volume 5. [Google Scholar] [CrossRef]
- Zhao, H.; Sun, J.Z.; Wang, F.; Zhao, L. A finite equivalence of multisecret sharing based on Lagrange interpolating polynomial. In Security and Communication Networks; Wiley Online Library: Hoboken, NJ, USA, 2013. [Google Scholar] [CrossRef]
- Roy, S.K. Lagrange’s Interpolating Polynomial Approach to solve multi-choice transportation problem. Int. J. Appl. Comput. Math. 2015, 1, 639–649. [Google Scholar] [CrossRef][Green Version]
- Adams, W.P. Use of Lagrange Interpolating Polynomials in the RLT. In Wiley Encyclopedia of Operations Research and Management Science; Cochran, J.J., Ed.; John Wiley and Sons, Inc.: Hoboken, NJ, USA, 2010. [Google Scholar]
- Errrachid, M.; Essanhaji, A.; Messaondi, A. RMVPIA: A new algorithm for computing the Lagrange multivariate polynomial interpolation. Numer. Algorithms 2020, 84, 1507–1534. [Google Scholar] [CrossRef]
- Wilson, L.; Vaughn, N.; Krasny, R. A GPU-accelerated fast multipole method based on barycentric Lagrange interpolation and dual tree traversal. Comput. Phys. Commun. 2021, 265, 108017. [Google Scholar] [CrossRef]
- Ide, N.A.D. Using Lagrange interpolation for solving nonlinear algebraic equations. Eng. Math. 2016, 1, 39–43. [Google Scholar]
- Yadav, O.P.; Sahu, A.K. Electrocardiogram estimation using Lagrange interpolation. Electron. Lett. 2021, 57, 169–172. [Google Scholar] [CrossRef]
- Zhou, S.P. Simultaneous Lagrange Interpolating Approximation Need Not Always Be Convergent. Constr. Approx. 1994, 10, 87–93. [Google Scholar] [CrossRef]
- Ibrahim, S. Application of Lagrange Interpolation Method to Solve First-Order Differential Equation Using Newton Interpolation Approach. Eurasian J. Sci. Eng. 2023, 9, 89–98. [Google Scholar] [CrossRef]
- Wang, M.F.; Au, F. Precise integrations methods based on Lagrange Piecewise Interpolation Polynomials. Int. J. Numer. Methods Eng. 2009, 77, 998–1014. [Google Scholar] [CrossRef]
- Marzaban, H.; Hoseini, S.; Razzaghi, M. Solution of Volterra’s populations model via block-pulse functions and Lagrange interpolating polynomials. Math. Methods Appl. Sci. 2009, 32, 127–134. [Google Scholar] [CrossRef]
- Chen, G.; Liu, J.; Wang, L. Color Image Sharing Method Based on Lagrange’s Interpolating Polynomial. In Health Information Science; He, J., Liu, X., Krupinski, E.A., Xu, G., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2012; Volume 7231, pp. 63–75. [Google Scholar] [CrossRef]
- Senapati, M.K.; Pradhan, C.; Nayak, P.K.; Samantaray, S.R. Lagrange Interpolating Polynomial based deloading control scheme for variable speed wind turbines. Int. Trans. Electr. Energy Syst. 2019, 29, e2824. [Google Scholar] [CrossRef]
- Vazquez-Leal, H.; Sandoval-Hernandez, M.A.; Filobello-Nino, U. The novel family of transcendental Leal-functions with applications to science and engineering. Heliyon 2020, 6, e05418. [Google Scholar] [CrossRef] [PubMed]
- Mohsen, A. A simple solution of the Bratu problem. Comput. Math. Appl. 2014, 67, 26–33. [Google Scholar] [CrossRef]
- Ascher, U.M.; Mattheij, R.M.M.; Russell, R.D. Numerical Solution of Boundary Value Problems for Ordinary Differential Equations; Classics in Applied Mathematics; SIAM: Philadelphia, PA, USA, 1995; p. xxv×593. [Google Scholar] [CrossRef]
- Ascher, U.M.; Petzold, L.R. Computer Methods for Ordinary Differential Equations and Differential-Algebraic Equations; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1998. [Google Scholar] [CrossRef]
- Vazquez-Leal, H.; Sandoval-Hernandez, M.; Castaneda-Sheissa, R.; Filobello-Nino, U.; Sarmiento-Reyes, A. Modified Taylor solution of equation of oxygen diffusion in a spherical cell with Michaelis-Menten uptake kinetics. Int. J. Appl. Math. Res. 2015, 4, 253–258. [Google Scholar] [CrossRef]
- He, J.H. Variational iteration method—A kind of non-linear analytical technique: Some examples. Int. J.-Non-Linear Mech. 1999, 34, 699–708. [Google Scholar] [CrossRef]
- He, J.H. An Old Babylonian Algorithm and Its Modern Applications. Symmetry 2024, 16, 1467. [Google Scholar] [CrossRef]
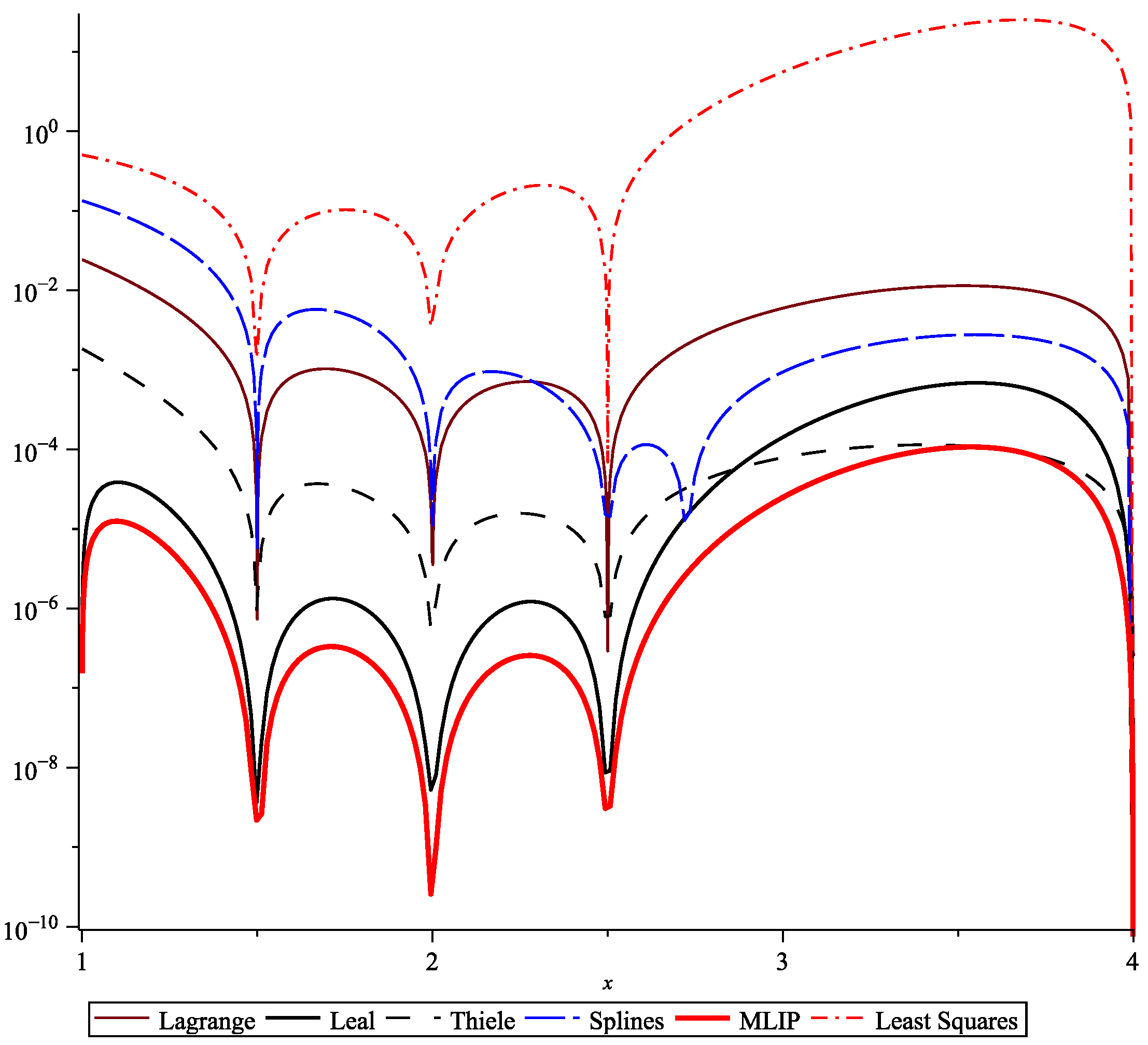

| x | Ln(x) | (20) | (23) | LIP Passing Through Five Nodes | Thiele Interpolation | Least Squares Method | Splines | (26) | Leal Polynomial [21] |
|---|---|---|---|---|---|---|---|---|---|
| 1.2 | 0.182321556 | 0.157113360 | 0.181465970 | 0.180683490 | 0.182224332 | 0.128851000 | 0.171459184 | 0.182323063 | 0.182326443 |
| 1.7 | 0.530628251 | 0.509463177 | 0.530871113 | 0.531175597 | 0.530647608 | 0.582791313 | 0.53361834 | 0.530628426 | 0.530628954 |
| 2.2 | 0.788457360 | 0.804050729 | 0.788256876 | 0.787939614 | 0.788445392 | 0.659409851 | 0.787723445 | 0.788457525 | 0.788458127 |
| 2.7 | 0.993251773 | 1.040876016 | 0.993866911 | 0.995029632 | 0.993280323 | 2.034778342 | 0.993296370 | 0.993253767 | 0.993262355 |
| 3.0 | 1.098612288 | 1.155245300 | 1.100754996 | 1.105164383 | 1.098698751 | 7.224870552 | 1.097578265 | 1.098639716 | 1.098768749 |
| 3.5 | 1.252762968 | 1.299650963 | 1.257094249 | 1.267060235 | 1.252902950 | 28.544006237 | 1.249322210 | 1.252896335 | 1.253608595 |
| x | (37) | (38) | |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0.1 | 0.29858379 | 0.298590087 | 0.297190666 |
| 0.2 | 0.55122088 | 0.551213018 | 0.548501319 |
| 0.3 | 0.74489845 | 0.74489284 | 0.741018925 |
| 0.4 | 0.86723883 | 0.867239748 | 0.862540412 |
| 0.5 | 0.90914265 | 0.909144265 | 0.904447458 |
| 0.6 | 0.86723883 | 0.867240001 | 0.864771632 |
| 0.7 | 0.74489845 | 0.744892447 | 0.749705070 |
| 0.8 | 0.55122088 | 0.55121261 | 0.570507225 |
| 0.9 | 0.29858378 | 0.298588354 | 0.331136834 |
| 1.0 | 0 | 0 | 0 |
| x | Derivative (37) | Derivative of (38) | |
|---|---|---|---|
| 0 | 3.174730842 | 3.174682878 | 3.160707044 |
| 0.1 | 2.777204768 | 2.777110353 | 2.763472447 |
| 0.2 | 2.253529923 | 2.253446744 | 2.240896836 |
| 0.3 | 1.598927344 | 1.599014466 | 1.588620933 |
| 0.4 | 0.832272053 | 0.832298764 | 0.826893790 |
| 0.5 | 0 | 0.000030120 | 0.007643290 |
| 0.6 | −0.832272053 | −0.832301972 | −0.790433990 |
| 0.7 | −1.598927344 | −1.599020127 | −1.490226272 |
| 0.8 | −2.253529923 | −2.253444516 | −2.082633859 |
| 0.9 | −2.777204768 | −2.777145209 | −2.748868191 |
| 1.0 | −3.174730842 | −3.174479705 | −4.059588223 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Filobello-Nino, U.A.; Vazquez-Leal, H.; Sandoval-Hernandez, M.A.; Dominguez-Chavez, J.A.; Salinas-Castro, A.; Jimenez-Fernandez, V.M.; Huerta-Chua, J.; Hoyos-Reyes, C.; Carrillo-Ramon, N.; Flores-Mendez, J. Modified Lagrange Interpolating Polynomial (MLIP) Method: A Straightforward Procedure to Improve Function Approximation. AppliedMath 2025, 5, 34. https://doi.org/10.3390/appliedmath5020034
Filobello-Nino UA, Vazquez-Leal H, Sandoval-Hernandez MA, Dominguez-Chavez JA, Salinas-Castro A, Jimenez-Fernandez VM, Huerta-Chua J, Hoyos-Reyes C, Carrillo-Ramon N, Flores-Mendez J. Modified Lagrange Interpolating Polynomial (MLIP) Method: A Straightforward Procedure to Improve Function Approximation. AppliedMath. 2025; 5(2):34. https://doi.org/10.3390/appliedmath5020034
Chicago/Turabian StyleFilobello-Nino, Uriel A., Hector Vazquez-Leal, Mario A. Sandoval-Hernandez, Jose A. Dominguez-Chavez, Alejandro Salinas-Castro, Victor M. Jimenez-Fernandez, Jesus Huerta-Chua, Claudio Hoyos-Reyes, Norberto Carrillo-Ramon, and Javier Flores-Mendez. 2025. "Modified Lagrange Interpolating Polynomial (MLIP) Method: A Straightforward Procedure to Improve Function Approximation" AppliedMath 5, no. 2: 34. https://doi.org/10.3390/appliedmath5020034
APA StyleFilobello-Nino, U. A., Vazquez-Leal, H., Sandoval-Hernandez, M. A., Dominguez-Chavez, J. A., Salinas-Castro, A., Jimenez-Fernandez, V. M., Huerta-Chua, J., Hoyos-Reyes, C., Carrillo-Ramon, N., & Flores-Mendez, J. (2025). Modified Lagrange Interpolating Polynomial (MLIP) Method: A Straightforward Procedure to Improve Function Approximation. AppliedMath, 5(2), 34. https://doi.org/10.3390/appliedmath5020034








