Exploring Price Patterns of Vegetables with Recurrence Quantification Analysis
Abstract
1. Introduction
2. Methodology
2.1. Recurrence Plots
2.2. Recurrence Quantification Analysis
- %Recurrence or RR: the ratio of the number of recurrence points to the total number of points in the plot
- %Determinism or DET: The percentage of recurrence points which form diagonal lines:
- Average Diagonal Line Length, L: The average length of the diagonal line segments in the plot, excluding the main diagonal.
- Laminarity LAM: The percentage of recurrence points which form vertical lines:
- Trapping Time, TT: It shows the average length of the vertical lines. Trapping Time represents the average time that the system has been trapped in the same state.
2.3. Data
3. Results
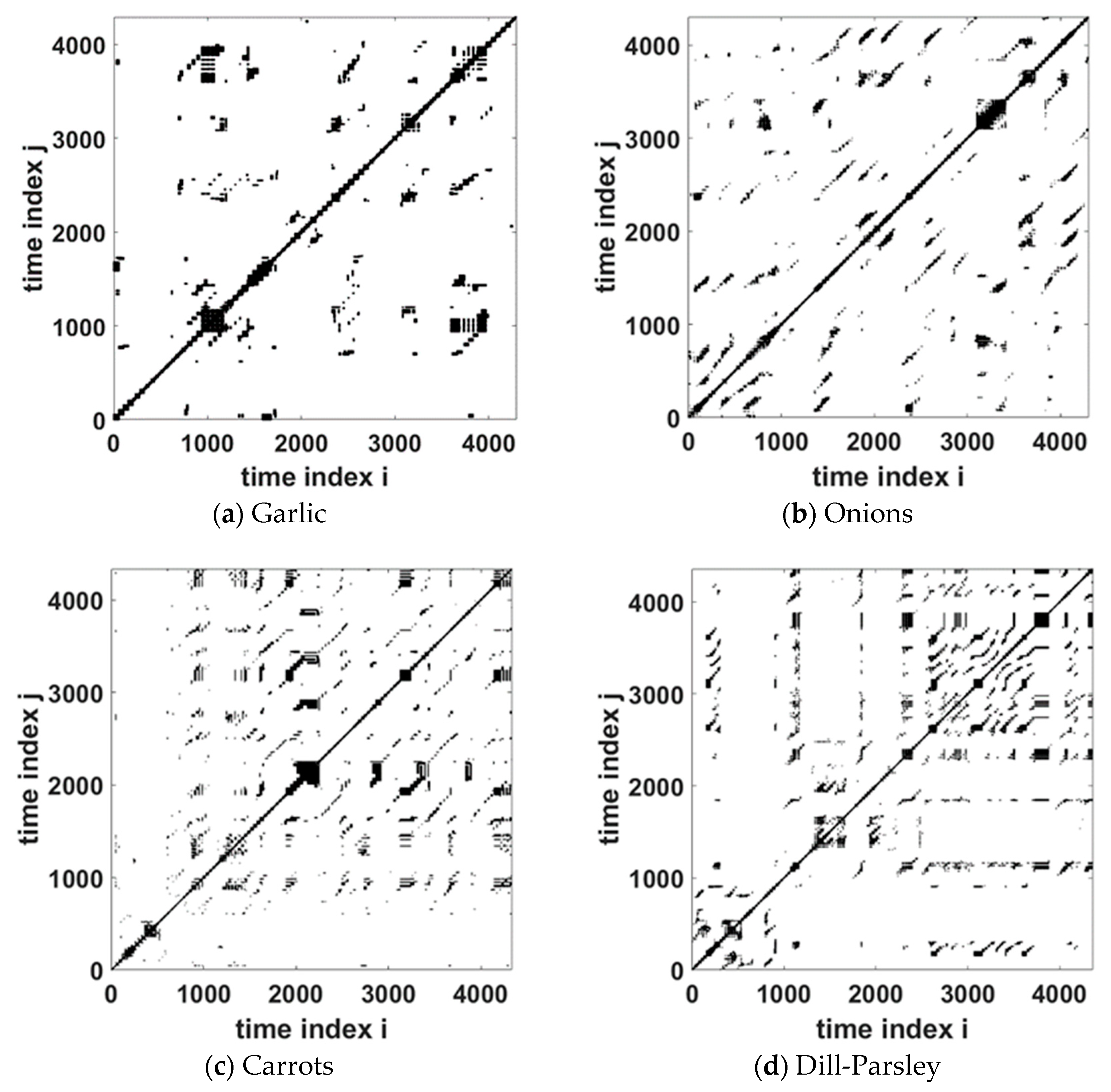
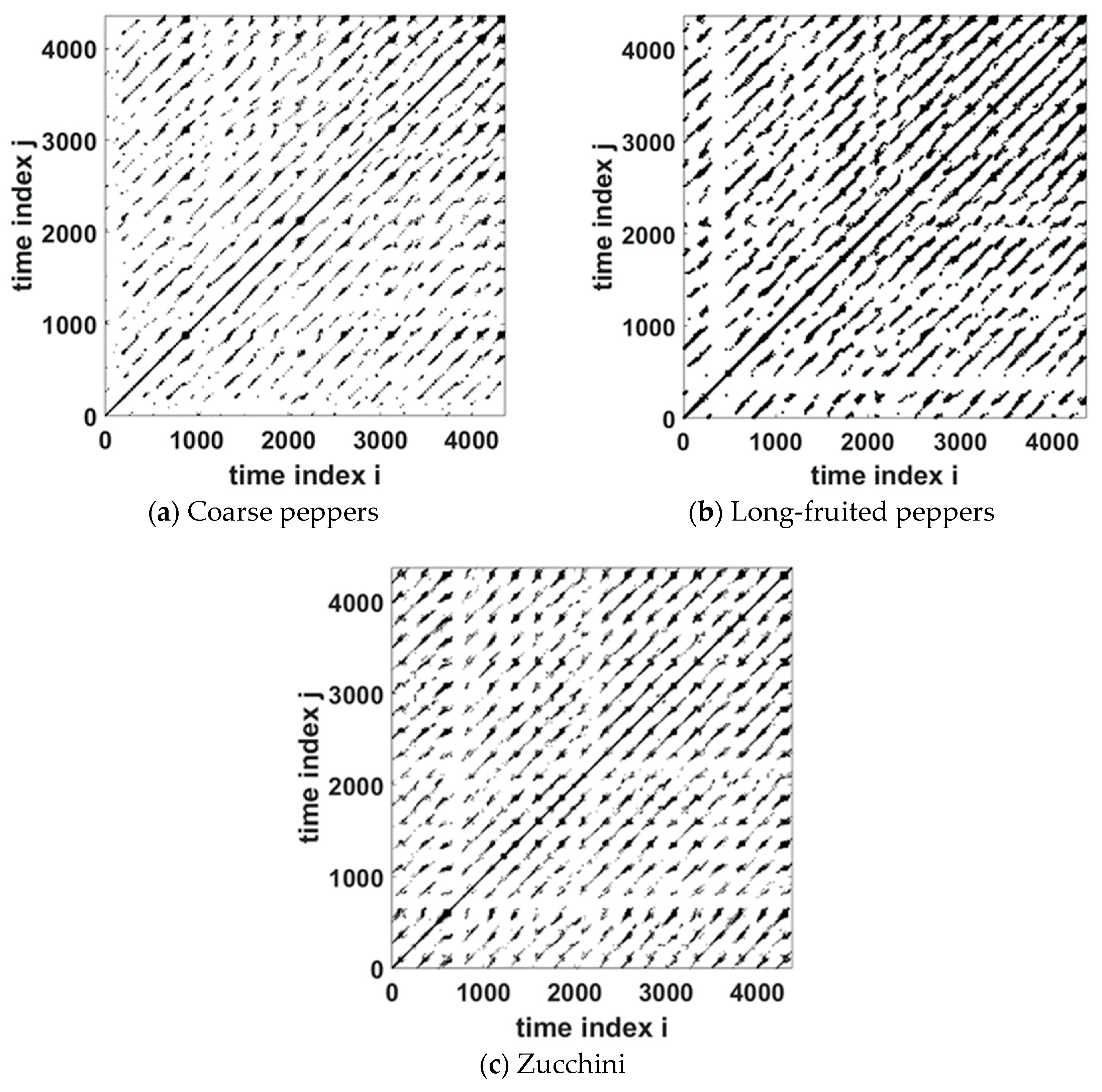
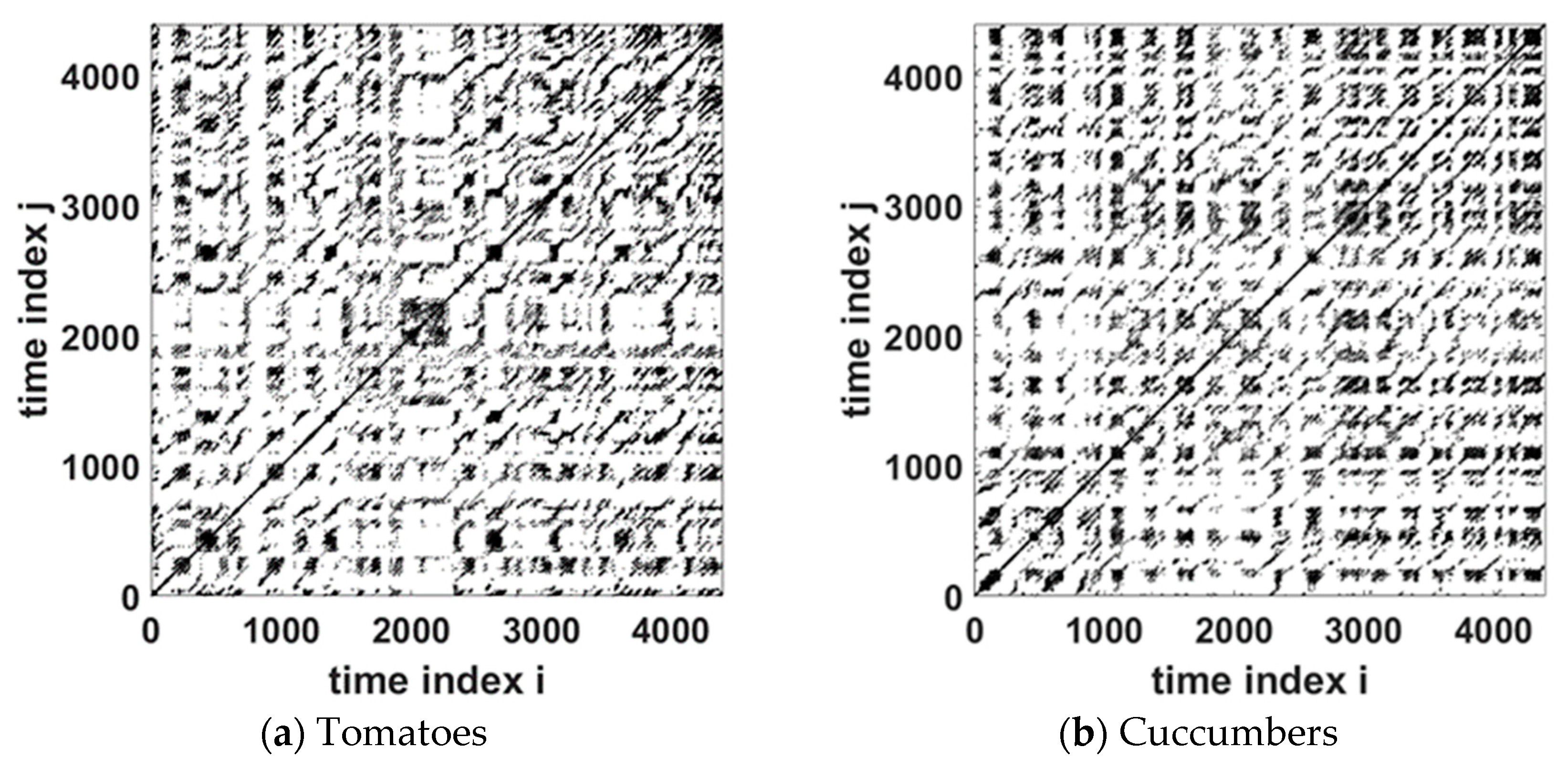
3.1. Recurrence Plots
- Diagonal lines parallel to the main diagonal, which vary in length and quantity depending on the case.
- White regions, which in some cases constitute a significant part of the plot.
- Small dark regions with a large density of diagonal and horizontal lines.
- G1(vis): {Garlic, Onions, Carrots, Dill—Parsley}
- G2(vis) {Celery, Spring onions, Knossos cucumbers, Beetroots}
- G3(vis) {Coarse peppers. Long-fruited peppers. Zucchini}.
- G4(vis) = {Spinach, Salads, Endives, Lettuce}
- G5(vis): {Tomatoes. cucumbers}
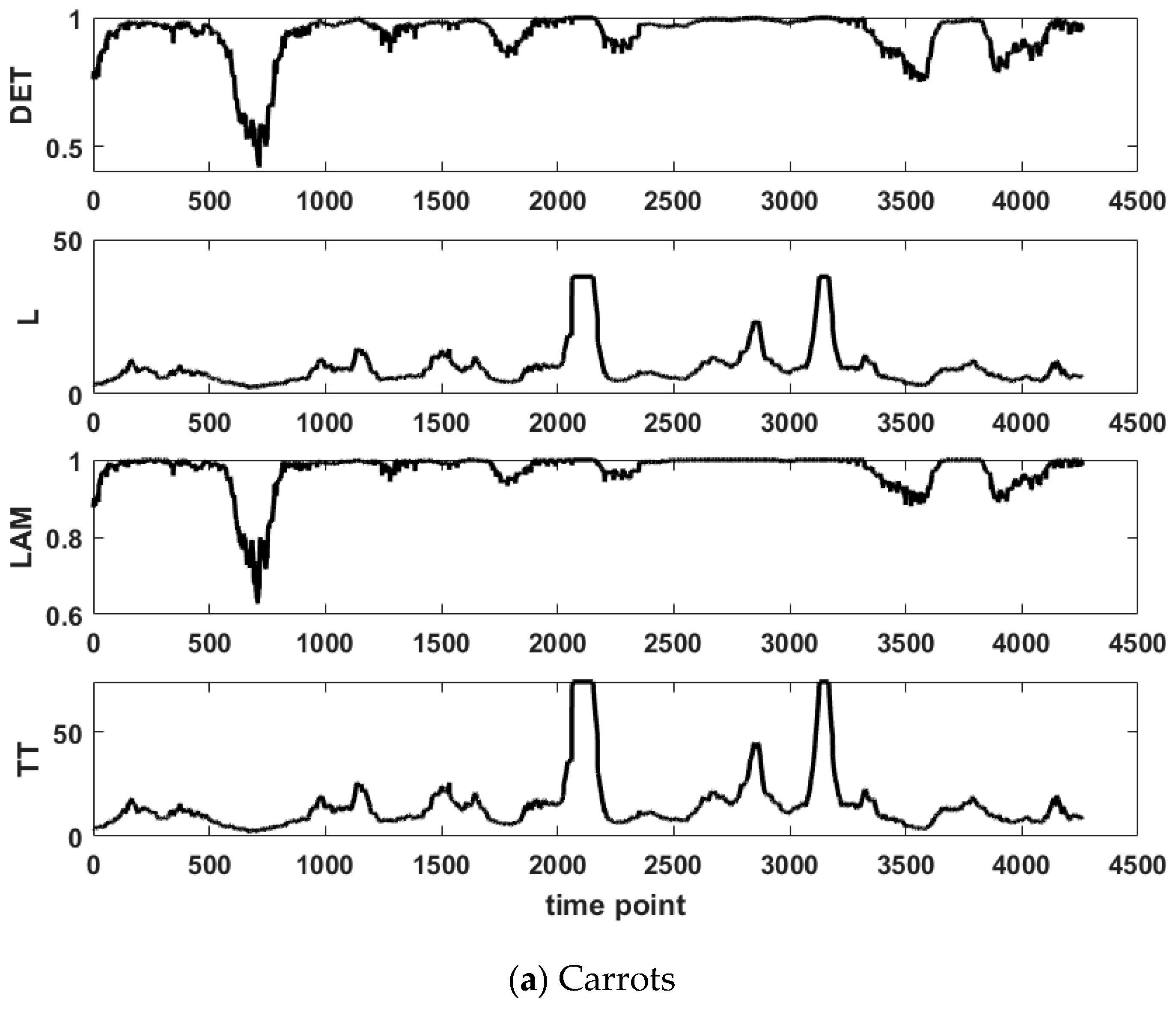
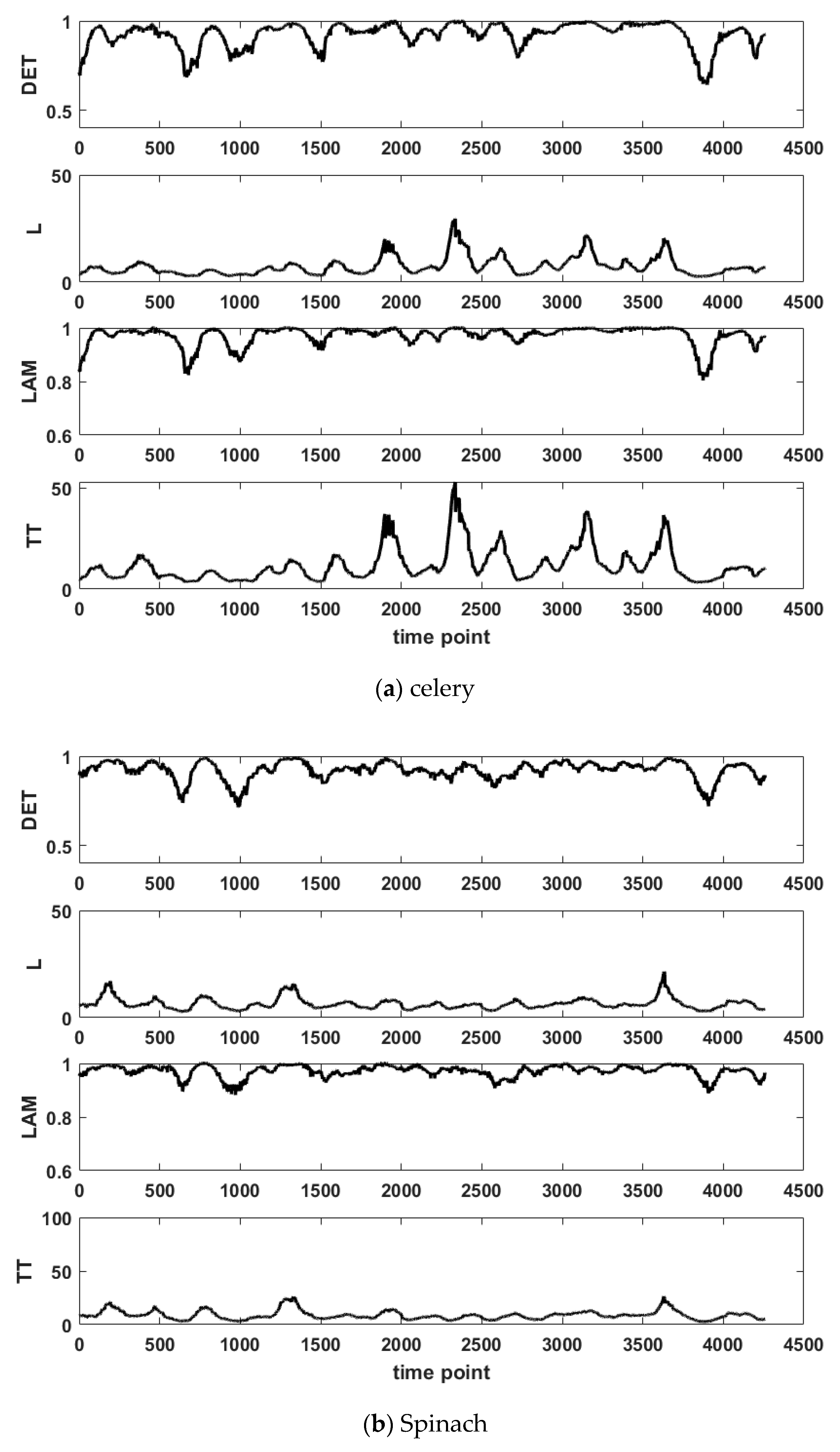
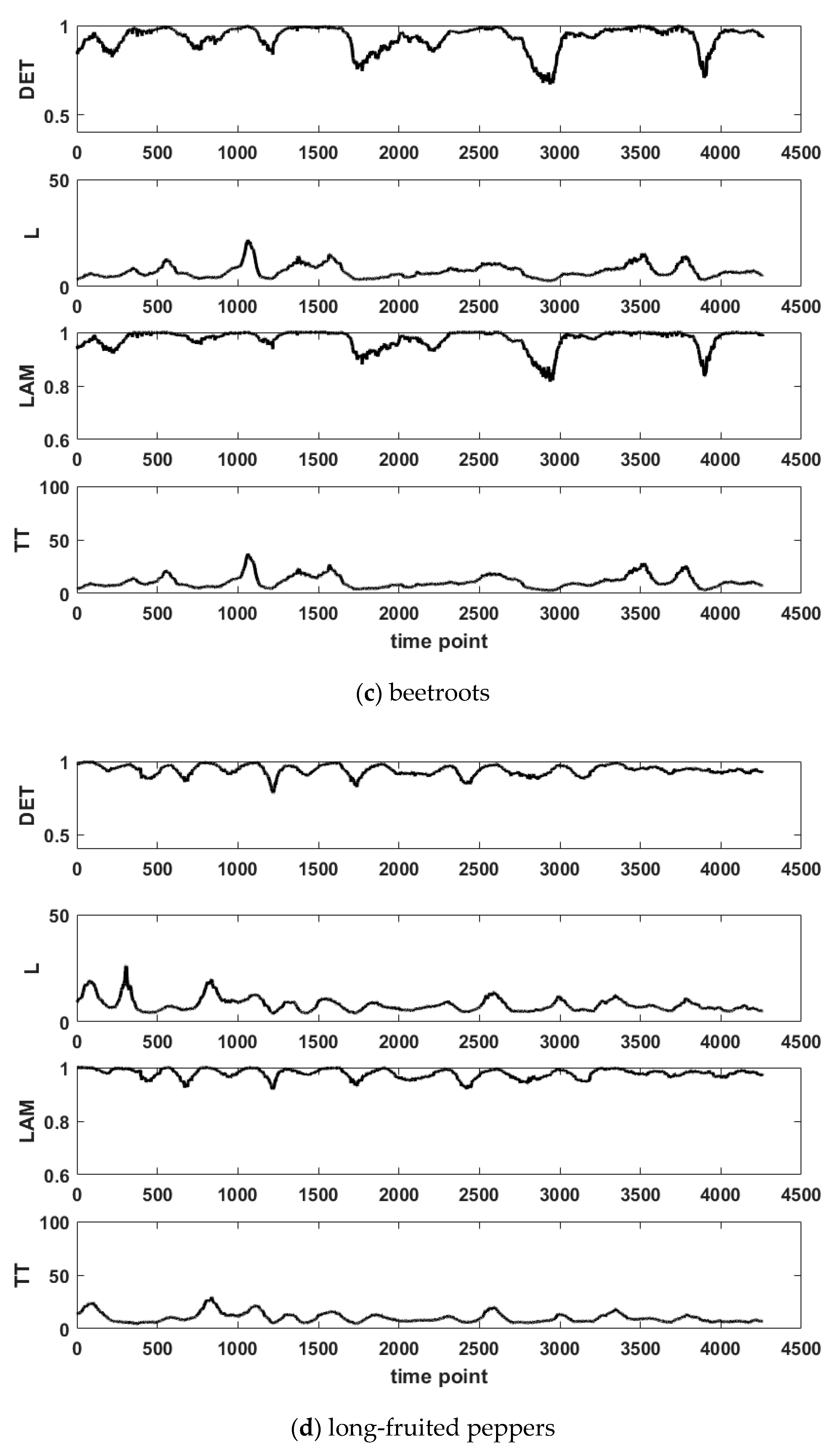
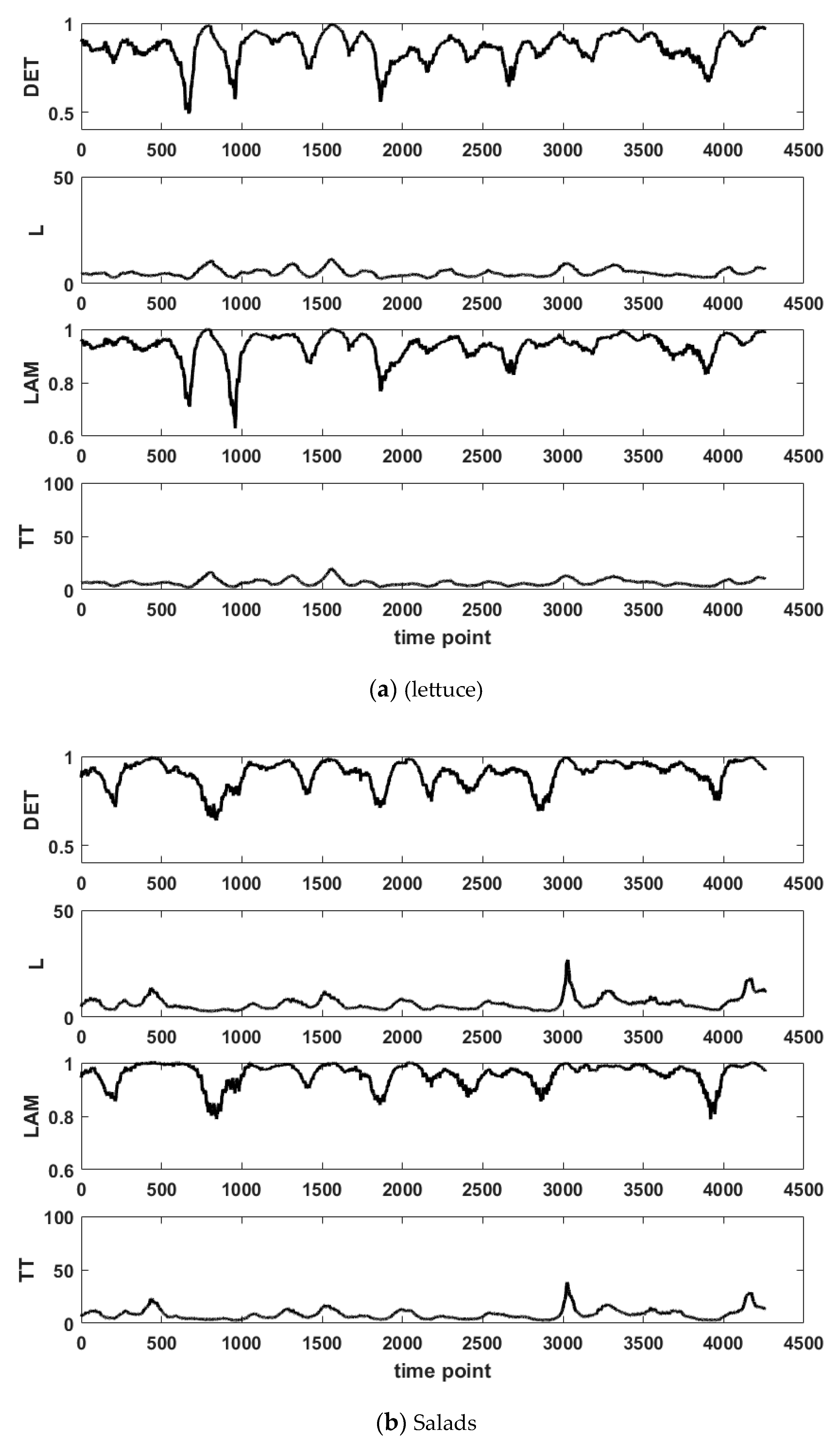
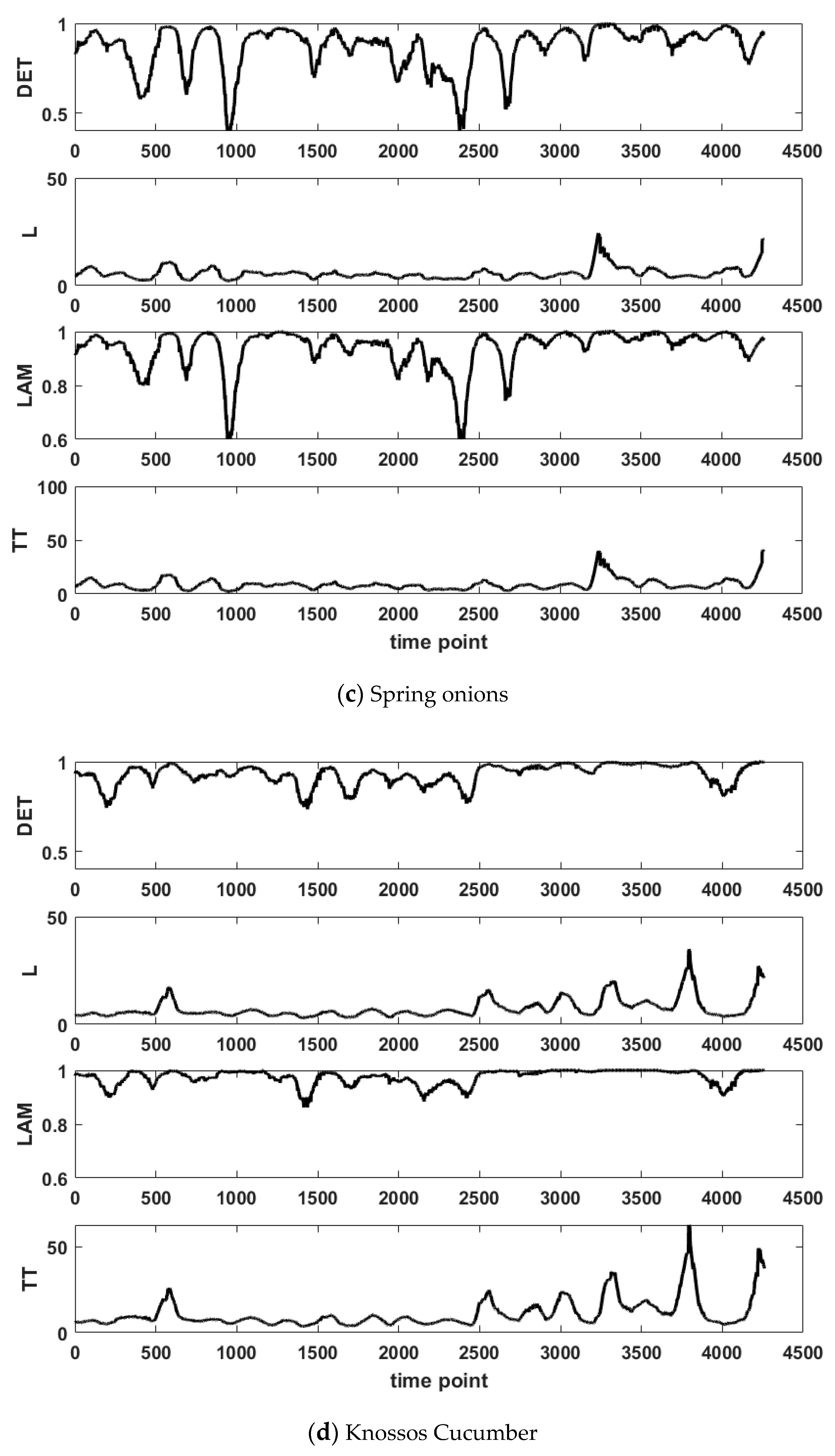
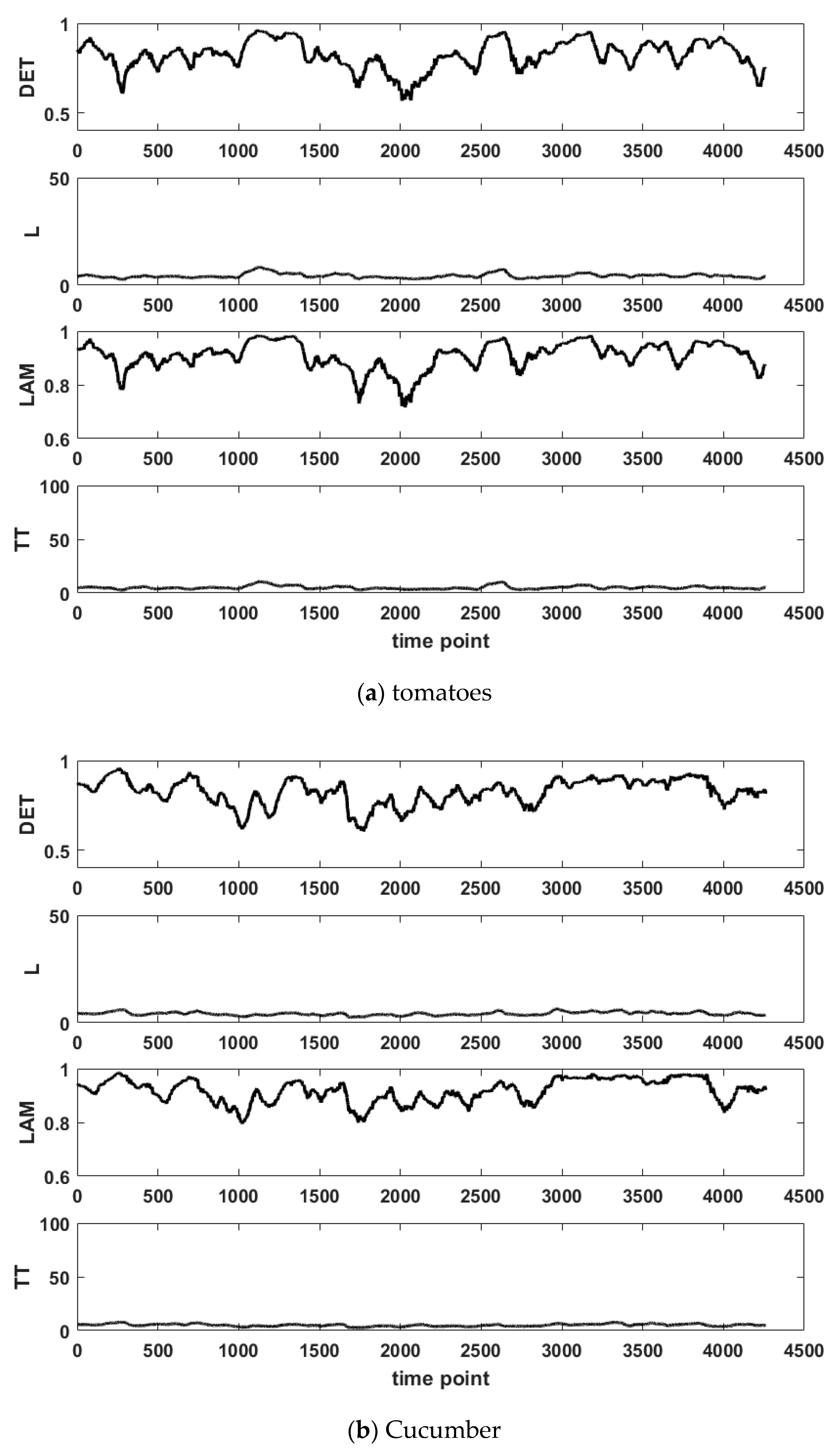
3.2. RQA Results
- G1(clust) = {Garlic-id1}
- G2(clust) = {Onion-id2, Carrots-id3, Dill-Parsley-id4}
- G3(clust) = {Celery-id5, Knossos cucumbers-id6, beetroots-id7, spring onions-id8, coarse peppers-id9}
- G4(clust) = {long-fruited peppers-id10, spinach-id12, zucchini-id11, salads-id12, endives-id14}
- G5(clust) = {tomatoes-id16, cucumbers-id17, lettuce-id15}
- G1(clust)
- G2(clust)
- G3(clust)
- G4(clust)
- G5(clust)
3.3. Recurrence Analysis with Epochs
- G1 (epochs) = {onions, garlic}
- G2(epochs) = {Carrots, Dill-Parsley)
- G3(epochs) = {celery, spinach, beetroots, Long-fruited peppers, Coarse-grained peppers}
- G4(epochs) = {Lettuce, Salads, Spring onions, Knossos Cucumber, Endives}
- G5(epochs) = {Tomatoes, Cucumber, zucchini}
4. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Claro, R.M.; Carmo, H.C.E.d.; Machado, F.M.S.; Monteiro, C.A. Income, Food Prices, and Participation of Fruit and Vegetables in the Diet. Rev. Saúde Pública 2007, 41, 557–564. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Miller, V.; Yusuf, S.; Chow, C.K.; Dehghan, M.; Corsi, D.J.; Lock, K.; Popkin, B.; Rangarajan, S.; Khatib, R.; Lear, S.A.; et al. Availability, Affordability, and Consumption of Fruits and Vegetables in 18 Countries across Income Levels: Findings from the Prospective Urban Rural Epidemiology (PURE) Study. Lancet Glob. Health 2016, 4, e695–e703. [Google Scholar] [CrossRef]
- French, S.A. Pricing Effects on Food Choices. J. Nutr. 2003, 133, 841S–843S. [Google Scholar] [CrossRef]
- Cassady, D.; Jetter, K.M.; Culp, J. Is Price a Barrier to Eating More Fruits and Vegetables for Low-Income Families? J. Am. Diet. Assoc. 2007, 107, 1909–1915. [Google Scholar] [CrossRef]
- Li, Y.; Liu, J.; Yang, H.; Chen, J.; Xiong, J. A Bibliometric Analysis of Literature on Vegetable Prices at Domestic and International Markets—A Knowledge Graph Approach. Agriculture 2021, 11, 951. [Google Scholar] [CrossRef]
- Hameed, A.A.A. The Impact of Petroleum Prices on Vegetable Oils Prices: Evidence from Cointegration Tests. In Proceedings of the 3rd International Borneo Business Conference (IBBC), Kota Kinabalu, Malaysia, 15–17 December 2008. [Google Scholar]
- Bozma, G.; İmamoğlu, İ.K. The Effects of Gasoline Price, Real Exchange Rate and Food Price on Vegetable and Fruit Export. Uluslar. İktisadi Ve İdari İncelemeler Derg. 2023, 182–198. [Google Scholar] [CrossRef]
- Pal, D.; Mitra, S.K. Interdependence between Crude Oil and World Food Prices: A Detrended Cross Correlation Analysis. Phys. Stat. Mech. Its Appl. 2018, 492, 1032–1044. [Google Scholar] [CrossRef]
- Moradi, M.; Salehi, M.; Keivanfar, M. A Study of the Effect of Oil Price Fluctuation on Industrial and Agricultural Products in Iran. Asian J. Qual. 2010, 11, 303–316. [Google Scholar] [CrossRef]
- Du, W.; Wu, Y.; Zhang, Y.; Gao, Y. The Impact Effect of Coal Price Fluctuations on China’s Agricultural Product Price. Sustainability 2022, 14, 8971. [Google Scholar] [CrossRef]
- Yang, H.; Cao, Y.; Shi, Y.; Wu, Y.; Guo, W.; Fu, H.; Li, Y. The Dynamic Impacts of Weather Changes on Vegetable Price Fluctuations in Shandong Province, China: An Analysis Based on VAR and TVP-VAR Models. Agronomy 2022, 12, 2680. [Google Scholar] [CrossRef]
- Qiao, Y.; Kang, M.; Ahn, B. Analysis of Factors Affecting Vegetable Price Fluctuation: A Case Study of South Korea. Agriculture 2023, 13, 577. [Google Scholar] [CrossRef]
- Beniwal, A.; Poolsingh, D.; Shastry, S.S. Trends and Price Behaviour Analysis of Onion in India. Indian J. Agric. Econ. 2022, 77, 632–642. [Google Scholar] [CrossRef]
- Birthal, P.; Negi, A.; Joshi, P.K. Understanding Causes of Volatility in Onion Prices in India. J. Agribus. Dev. Emerg. Econ. 2019, 9, 255–275. [Google Scholar] [CrossRef]
- Shengwei, W.; Yanni, L.; Jiayu, Z.; Jiajia, L. Agricultural Price Fluctuation Model Based on SVR. In Proceedings of the 2017 9th International Conference on Modelling, Identification and Control (ICMIC), Kunming, China, 10–12 July 2017; pp. 545–550. [Google Scholar]
- Jin, D.; Yin, H.; Gu, Y.; Yoo, S.J. Forecasting of Vegetable Prices Using STL-LSTM Method. In Proceedings of the 2019 6th International Conference on Systems and Informatics (ICSAI), Shanghai, China, 2–4 November 2019; pp. 866–871. [Google Scholar]
- Charakopoulos, A.; Karakasidis, T.; Sarris, L. Pattern Identification for Wind Power Forecasting via Complex Network and Recurrence Plot Time Series Analysis. Energy Policy 2019, 133, 110934. [Google Scholar] [CrossRef]
- Sankararaman, S. Recurrence Network and Recurrence Plot: A Novel Data Analytic Approach to Molecular Dynamics in Thermal Lensing. J. Mol. Liq. 2022, 366, 120353. [Google Scholar] [CrossRef]
- Pitsik, E.; Frolov, N.; Hauke Kraemer, K.; Grubov, V.; Maksimenko, V.; Kurths, J.; Hramov, A. Motor Execution Reduces EEG Signals Complexity: Recurrence Quantification Analysis Study. Chaos Interdiscip. J. Nonlinear Sci. 2020, 30, 023111. [Google Scholar] [CrossRef] [PubMed]
- Andreadis, I.; Fragkou, A.D.; Karakasidis, T.E.; Serletis, A. Nonlinear Dynamics in Divisia Monetary Aggregates: An Application of Recurrence Quantification Analysis. Financ. Innov. 2023, 9, 16. [Google Scholar] [CrossRef]
- Fragkou, A.D.; Karakasidis, T.E.; Sarris, I.E. Recurrence Quantification Analysis of MHD Turbulent Channel Flow. Phys. Stat. Mech. Its Appl. 2019, 531, 121741. [Google Scholar] [CrossRef]
- Charakopoulos, A.Κ.; Karakasidis, T.E.; Papanicolaou, P.N.; Liakopoulos, A. The Application of Complex Network Time Series Analysis in Turbulent Heated Jets. Chaos Interdiscip. J. Nonlinear Sci. 2014, 24, 024408. [Google Scholar] [CrossRef]
- Eckmann, J.-P.; Kamphorst, S.O.; Ruelle, D. Recurrence Plots of Dynamical Systems. Europhys. Lett. 1987, 4, 973. [Google Scholar] [CrossRef]
- Takens, F. Detecting Strange Attractors in Turbulence. In Dynamical Systems and Turbulence, Warwick 1980: Proceedings of the Symposium Held at the University of Warwick 1979/80; Rand, D., Young, L.-S., Eds.; Springer: Berlin/Heidelberg, Germany, 1981; pp. 366–381. [Google Scholar]
- Packard, N.H.; Crutchfield, J.P.; Farmer, J.D.; Shaw, R.S. Geometry from a Time Series. Phys. Rev. Lett. 1980, 45, 712–716. [Google Scholar] [CrossRef]
- Fraser, A.M.; Swinney, H.L. Independent Coordinates for Strange Attractors from Mutual Information. Phys. Rev. A 1986, 33, 1134–1140. [Google Scholar] [CrossRef] [PubMed]
- Abarbanel, H.D.I.; Kennel, M.B. Local False Nearest Neighbors and Dynamical Dimensions from Observed Chaotic Data. Phys. Rev. E 1993, 47, 3057–3068. [Google Scholar] [CrossRef]
- Zbilut, J.P.; Webber, C.L. Embeddings and Delays as Derived from Quantification of Recurrence Plots. Phys. Lett. A 1992, 171, 199–203. [Google Scholar] [CrossRef]
- Marwan, N.; Carmen Romano, M.; Thiel, M.; Kurths, J. Recurrence Plots for the Analysis of Complex Systems. Phys. Rep. 2007, 438, 237–329. [Google Scholar] [CrossRef]
- Marwan, N. TOCSY Toolbox. Available online: https://tocsy.pik-potsdam.de/ (accessed on 13 August 2024).
- Hegger, R.; Kantz, H.; Schreiber, T. Practical Implementation of Nonlinear Time Series Methods: The TISEAN Package. Chaos Interdiscip. J. Nonlinear Sci. 1999, 9, 413–435. [Google Scholar] [CrossRef]
- TISEAN: Nonlinear Time Series Analysis. Available online: https://www.pks.mpg.de/tisean/ (accessed on 13 August 2024).
- Sarantopoulos, A.; Korovesis, S. Effects of Climate Change in Agricultural Areas of Greece, Vulnerability Assessment, Economic-Technical Analysis, and Adaptation Strategies. Environ. Sci. Proc. 2023, 26, 173. [Google Scholar] [CrossRef]
- Georgopoulou, E.; Mirasgedis, S.; Sarafidis, Y.; Vitaliotou, M.; Lalas, D.P.; Theloudis, I.; Giannoulaki, K.-D.; Dimopoulos, D.; Zavras, V. Climate Change Impacts and Adaptation Options for the Greek Agriculture in 2021–2050: A Monetary Assessment. Clim. Risk Manag. 2017, 16, 164–182. [Google Scholar] [CrossRef]
- Barros, L.R.; Soares, G.G.P.; Correia, S.; Duarte, G.; Costa, S.C. Classification of Recurrence Plots of Voice Signals Using Convolutional Neural Networks. In Proceedings of the XXXVIII Simpósio Brasileiro de Telecomunicações e Processamento de SINAIS—SBrT 2020, Florianópolis, Brazil, 22–25 November 2020. [Google Scholar]
- Lansford, J.L.; Vlachos, D.G. Infrared Spectroscopy Data- and Physics-Driven Machine Learning for Characterizing Surface Microstructure of Complex Materials. Nat. Commun. 2020, 11, 1513. [Google Scholar] [CrossRef]













| Description |
|---|
| Cucumbers |
| Knossos Cucumbers |
| Dill, Parsley bales |
| Endives |
| Carrots |
| Zucchini |
| Spring onions, fresh bale |
| Onions |
| Lettuce |
| Beetroot |
| Long-fruited peppers |
| Coarse peppers |
| Salads |
| Celery |
| Garlic |
| Spinach |
| Tomatoes |
| Product | Delay | Embedding | Threshold |
|---|---|---|---|
| Cucumber | 15 | 4 | 0.147 |
| Knossos cucumbers | 23 | 4 | 0.176 |
| Dill—Parsley | 27 | 4 | 0.0435 |
| Endives | 22 | 4 | 0.105 |
| Carrots | 35 | 4 | 0.046 |
| Zucchini | 21 | 4 | 0.25 |
| Spring onions | 25 | 3 | 0.029 |
| Onions | 35 | 5 | 0.075 |
| Lettuce | 25 | 4 | 0.185 |
| Beetroot | 29 | 4 | 0.105 |
| Long-fruited peppers | 25 | 4 | 0.33 |
| Coarse peppers | 27 | 4 | 0.41 |
| Salads | 26 | 5 | 0.34 |
| Celery | 25 | 4 | 0.18 |
| Garlic | 50 | 4 | 0.2235 |
| Spinach | 25 | 5 | 0.28 |
| Tomatoes | 16 | 4 | 0.2291 |
| ID | Vegetable | DET | LAM | L | TT |
|---|---|---|---|---|---|
| 1 | Garlic | 0.991 | 0.997 | 14.886 | 26.723 |
| 2 | Onions | 0.965 | 0.987 | 9.234 | 15.267 |
| 3 | Carrots | 0.959 | 0.984 | 8.867 | 15.315 |
| 4 | Dill-Parsley | 0.958 | 0.983 | 8.104 | 13.960 |
| 5 | Celery | 0.932 | 0.975 | 6.318 | 10.295 |
| 6 | Knossos Cucumbers | 0.932 | 0.975 | 5.977 | 9.322 |
| 7 | Beetroots | 0.928 | 0.975 | 5.612 | 9.003 |
| 8 | Spring onions | 0.897 | 0.957 | 5.624 | 9.203 |
| 9 | Coarse Peppers | 0.915 | 0.962 | 6.036 | 8.494 |
| 10 | Long-fruited peppers | 0.893 | 0.954 | 5.015 | 7.118 |
| 11 | Zucchini | 0.836 | 0.920 | 4.351 | 6.057 |
| 12 | Spinach | 0.884 | 0.950 | 4.796 | 7.059 |
| 13 | Salads | 0.857 | 0.933 | 4.471 | 6.286 |
| 14 | Endives | 0.851 | 0.939 | 4.305 | 6.466 |
| 15 | Lettuce | 0.800 | 0.906 | 3.838 | 5.405 |
| 16 | Tomatoes | 0.716 | 0.850 | 3.209 | 4.194 |
| 17 | Cucumbers | 0.713 | 0.858 | 3.130 | 4.167 |
| RQA Measures | Onions | Garlic |
|---|---|---|
| DET | 0.869–1 | 0.876–1 |
| L | 4.701–21.727 | 3.365–17.050 |
| LAM | 0.937–1 | 0.952–1 |
| TT | 7.180–39 | 4.507–29 |
| RQA Measures | Dill-Parsley | Carrots |
|---|---|---|
| DET | 0.408–0.999 | 0.418–0.999 |
| L | 2.080–50 | 2.214–38 |
| LAM | 0.556–1 | 0.627–1 |
| TT | 2.229–98 | 2.485–74 |
| RQA Measures | Celery | Spinach | Beetroots | Long-Fruited Peppers | Coarse Peppers |
|---|---|---|---|---|---|
| DET | 0.642–0.998 | 0.714–0.992 | 0.669–0.997 | 0.784–0.996 | 0.777–0.998 |
| L | 2.666–29.576 | 2.775–21.480 | 2.685–21.878 | 3.796–26.083 | 2.940–25.652 |
| LAM | 0.804–1 | 0.882–1 | 0.815–1 | 0.918–1 | 0.885–1 |
| TT | 3.341–53.114 | 2.870–26.440 | 2.794–37.154 | 4.606–29.543 | 3.510–29.085 |
| RQA Measure | Lettuce | Salads | Spring Onions | Knossos Cucumber | Endives |
|---|---|---|---|---|---|
| DET | 0.491–0.992 | 0.640–0.995 | 0.307–0.997 | 0.735–0.999 | 0.523–0.998 |
| L | 2.214–11.585 | 2.666–26.875 | 2.181–24.333 | 2.95–34.923 | 2.371–26.895 |
| LAM | 0.629–1 | 0.788–1 | 0.515–1 | 0.862–1 | 0.710–1 |
| TT | 2.342–19.870 | 2.745–38.459 | 2.264–40 | 3.551–62.745 | 2.718–51 |
| RQA Measure | Tomatoes | Cucumber Pair | Zucchini |
|---|---|---|---|
| DET | 0.567–0.962 | 0.603–0.958 | 0.471–0.986 |
| L | 2.626–8.627 | 2.566–6.523 | 2.757–12.363 |
| LAM | 0.716–0.984 | 0.794–0.986 | 0.673–0.999 |
| TT | 2.735–10.668 | 2.759–8.041 | 2.870–17.175 |
| Vegetables | DET | LAM | L | TT | G1 (Vis) | G2 (Vis) | G3 (Vis) | G4 (Vis) | G5 (Vis) | G1 (Clust) | G2 (Clust) | G3 (Clust) | G4 (Clust) | G5 (Clust) | G1 (Epoch) | G2 (Epoch) | G3 (Epoch) | G4 (Epoch) | G5 (Epoch) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Garlic | 0.991 | 0.997 | 14.886 | 26.723 | |||||||||||||||
| Onions | 0.965 | 0.987 | 9.234 | 15.267 | |||||||||||||||
| Carrots | 0.959 | 0.984 | 8.867 | 15.315 | |||||||||||||||
| Dill-Parsley | 0.958 | 0.983 | 8.104 | 13.960 | |||||||||||||||
| Celery | 0.932 | 0.975 | 6.318 | 10.295 | |||||||||||||||
| Knossos Cucumbers | 0.932 | 0.975 | 5.977 | 9.322 | |||||||||||||||
| Beetroots | 0.928 | 0.975 | 5.612 | 9.003 | |||||||||||||||
| Spring Onions | 0.897 | 0.957 | 5.624 | 9.203 | |||||||||||||||
| Coarse Peppers | 0.915 | 0.962 | 6.036 | 8.494 | |||||||||||||||
| Long-fruited Peppers | 0.893 | 0.954 | 5.015 | 7.118 | |||||||||||||||
| Zucchini | 0.836 | 0.920 | 4.351 | 6.057 | |||||||||||||||
| Spinach | 0.884 | 0.950 | 4.796 | 7.059 | |||||||||||||||
| Salads | 0.857 | 0.933 | 4.471 | 6.286 | |||||||||||||||
| Endives | 0.851 | 0.939 | 4.305 | 6.466 | |||||||||||||||
| Lettuce | 0.800 | 0.906 | 3.838 | 5.405 | |||||||||||||||
| Tomatoes | 0.716 | 0.850 | 3.209 | 4.194 | |||||||||||||||
| Cucumbers | 0.713 | 0.858 | 3.130 | 4.167 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karakasidou, S.; Fragkou, A.; Zachilas, L.; Karakasidis, T. Exploring Price Patterns of Vegetables with Recurrence Quantification Analysis. AppliedMath 2024, 4, 1012-1046. https://doi.org/10.3390/appliedmath4030055
Karakasidou S, Fragkou A, Zachilas L, Karakasidis T. Exploring Price Patterns of Vegetables with Recurrence Quantification Analysis. AppliedMath. 2024; 4(3):1012-1046. https://doi.org/10.3390/appliedmath4030055
Chicago/Turabian StyleKarakasidou, Sofia, Athanasios Fragkou, Loukas Zachilas, and Theodoros Karakasidis. 2024. "Exploring Price Patterns of Vegetables with Recurrence Quantification Analysis" AppliedMath 4, no. 3: 1012-1046. https://doi.org/10.3390/appliedmath4030055
APA StyleKarakasidou, S., Fragkou, A., Zachilas, L., & Karakasidis, T. (2024). Exploring Price Patterns of Vegetables with Recurrence Quantification Analysis. AppliedMath, 4(3), 1012-1046. https://doi.org/10.3390/appliedmath4030055







