Innovative Ways of Developing and Using Specific Purpose Alternatives for Solving Hard Combinatorial Network Routing and Ordered Optimisation Problems

Abstract

This paper reviews some recent contributions by the authors and their associates and highlights a few innovative ideas, which led them to address some hard combinatorial network routing and ordered optimisation problems. The travelling salesman, which is in the NP hard category, has been reviewed and solved as an index-restricted shortest connected graph, and therefore, it opens a question about its ‘NP Hard’ category. The routing problem through ‘K’ specified nodes and ordered optimum solutions are computationally demanding but have been made computationally feasible. All these approaches are based on the strategic creation and use of an alternative solution in that situation. The efficiency of these methods requires further investigation.

1. Introduction

Mathematics of OR has provided support in many real-life industrial, business, and government decision-making processes. Changing technology has always been a source of new challenges, and accordingly, new mathematical methods and tools have been developed for providing necessary decision-making support for better and informed decisions. Routing problems and their variants in graph theory have attracted a lot of attention from researchers due to various industrial applications. Shortest route, shortest connected graph, and the travelling salesman are just a few of them. Variants of these problems have been identified from time to time. Ordered optimisation is another field where obtaining an ordered optimum, i.e., the $k^{th }best, k\ge 2$ solution, can be a highly challenging task. In this paper, we review a few specific innovative ideas for developing an alternative in a given situation, and use that alternative solution to solve some difficult combinatorial hard optimisation situations; for example, we find the following:

(1)

The minimum travelling salesman tour, which is in the ‘NP Hard’ category, is solved as an index-restricted minimum connected graph;

(2)

The path passing through a set of specified nodes, which is computationally demanding due to the path being constrained to pass through a set of specified nodes, is also solved as an index-restricted minimum connected graph;

(3)

The second-best optimal solution for the shortest route and the assignment problem.

All these approaches develop an alternative solution and use that solution in a strategic way to solve the problem under consideration. These new approaches need further investigation to establish their efficiency, if any. That work is currently being conducted. Among the above problems, the minimum travelling salesman tour (MTST) has been classified as ‘NP Hard’; see [1]. Similarly, determination of the shortest route through ‘K’ specified nodes and finding an ordered optimum solution have been classified as computationally demanding; see [2,3]. approach based on the index-restricted shortest connected graph for the travelling salesman problem raises a question—“Is the TSP really an ‘NP-Hard’ problem?” A similar question arises again for the path through K specified nodes. The question is, “Is the path through specified nodes computationally demanding?” The development of the restricted minimum spanning tree is based on the idea of developing an alternative and making use of that alternative to find the index-restricted minimum spanning tree.

We extend the idea of developing an alternative solution for the shortest route and an assignment problem and find the second-best optimal solution for these problems, without excessively increasing computations. This approach is in its initial stage, and more computational work is necessary to establish its computational efficiency for different problems.

Many real-life situations can be represented in the form of a network, which is made of nodes and links. These links are formed by joining the nodes, and weights associated with these links provide a kind of measure of the relationship between the nodes. The network representing a physical situation can be a directed or a non-directed network. Analysis of a non-directed network is usually more demanding compared to a directed graph, simply because directions in a directed graph provide additional information, which is missing in a non-directed network. Many industrial situations have been modelled as directed networks and were analysed by using dynamic programming techniques; see [4,5,6]. These problems, once transformed into a network model, were analysed by using the network-related theory and tools. The outcome of the analysis can be interpreted in terms of the real-life situation that was modelled as a network. For recent developments, see [7,8].

In general, a network can be represented by $G(N,L)$, where $N$ represents a set of some entities represented by the nodes $N=\{1, 2, \dots , n\}$ and $L$ is the set of links joining various nodes representing properties associated with pairs of these nodes. These links are denoted by $\left(i,j\right), \mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e} i \mathrm{a}\mathrm{n}\mathrm{d} j \mathrm{a}\mathrm{r}\mathrm{e} \mathrm{t}\mathrm{h}\mathrm{e} \mathrm{n}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{s} 1, 2, \dots , n \mathrm{a}\mathrm{n}\mathrm{d} i\ne j.$ In weighted networks, we associate a number with each link, providing a quantitative measure of the relationship between those two nodes. For example, it may just be the distance between the two nodes, or it may represent the time of travel between the pair of nodes, $i \mathrm{a}\mathrm{n}\mathrm{d} j.$ This weight associated with the link $\left(i,j\right)$ is denoted by $c_{ij},$ which can be a positive or a negative quantity, depending on the situation.

Some ideas used in this paper have been reviewed in Section 2, and their applications, in the form of the travelling salesman and routing problems, have been presented in Section 3. The ordered optimum problem has been discussed in Section 4. Finally, concluding remarks are presented in Section 5.

2. Modification of a Classical Shortest Connected Network Problem and Its Applications

The shortest connected network (SCN) of any given undirected connected network $G\left(N,L\right)$ is a classical network problem. It comprises $\left(n-1\right)$ links, where $n$ represents the number of nodes in the given network $G\left(N,L\right)$. Since the given network is connected, there must be a unique path from every node to every other node, and that path will be free of loops. In such a connected graph, if any link is removed, it will make the graph disconnected. This SCN can be obtained by a greedy approach according to [9,10,11]. A modification of the shortest connected graph problem was discussed in [12], which is briefly presented below.

2.1. Modification of the Shortest Connect Network (SCN)

2.1.1. Statement of the Modified Shortest Connected Network

For a network $G\left(N,L\right),$the SCN can be obtained by any known method. From the SCN, one can find a node index for each node. The node index is the number of links emanating from that node in the SCN. Let $n_i$ represent the index of the node $i$, where $1\le n_i\le (n-1).$ In the modification discussed in [12] in which the SCN is restricted, the node index $n_i$ satisfies $1\le n_i$ $\le 2$for each node. This means that if the original SCN does not satisfy the restriction on the index value on any node, the SCN obtained by using the classical approach must be modified to satisfy the condition $1\le n_i\le 2, \forall i.$ In the given index-restricted network, two nodes will have an index value of 1 and the other nodes will have an index value of 2; thus, they will form a path joining two nodes and passing through all other remaining nodes of the network. We may assume that in the given connected network, all nodes are such that at least two links emanate from each node.

2.1.2. Some Essential Terms and a Theorem to Modify the SCN Obtained by the Greedy Approach to an Index-Restricted SCN (IRSCN)

The necessary terms are the following:

T1. Index of a node: Since each selected link generates two indices, the total number of indices of the selected $(n-1)$ links forming the SCN will be 2$(n-1).$ For a path passing through all nodes, two of these nodes will have only one index value (from where the path starts to where it ends), and the remaining $(n-2)$ nodes will have an index of 2. The index-restricted SCN or IRSCN will form a path joining two nodes, which passes through all other remaining nodes of the network.

T2. Basic and non-basic links: A link joining two nodes $i and j$ is said to be basic if $x_{ij}=1,$i.e., that link belongs to the SCN and, if $x_{ij}\ne 1$, then it is a non-basic link.

T3. High- and low-index nodes: Once an SCN has been identified using any known method, we know the values of node indices for all nodes. These values are given by $1\le n_i\le (n-1)$. They must be changed to satisfy the condition $1\le n_i\le 2 \forall i,$i.e., for the origin and the destination nodes, the $index n_i=1,$ and for all other remaining $(n-2)$ nodes, $n_i=2.$ The high- and low-index nodes can be easily identified by their current value against the desired node index value for that node.

T4. Neighbouring nodes and links: A node $i$ is said to be a neighbouring node to node $j,$ if the nodes $i$ and $j$ are connected by a single link. In a completely connected network, all nodes are neighbouring nodes as all nodes are connected by a direct link. A neighbouring link is defined as a link that emanates from a neighbouring node.

Theorem 1. 

Index-balancing theorem: Adding the same constant to all links emanating from the same node does not change the relative merit of any given selected link in the SCN obtained by the greedy approach. However, the index-balancing theorem can create alternatives. From the SCN obtained by the greedy approach, we know the index for each node; therefore, low- and high-index nodes can be easily identified. The index-balancing theorem commences its work by adding constants to all links that emanate from the same node, which has been classified as a high-index node. The idea is to create alternatives for the selection of a link, and thus, it reduces the index at a high-index node and increases the index of a low-index node; when a link from a high-index node is removed and placed on a node with a low index value, the imbalance is reduced This process is repeated until all nodes attain the required index and satisfy all index restrictions.

Theorem 2. 

For any given SCN solution, a basic link can be altered by adding a constant to all emanating links from that node, i.e., changing the status of a link from basic to non-basic and that of some other link from non-basic to basic. Repeated applications can generate an SCN path joining two nodes passing through all other nodes in a network, i.e., it will satisfy the index condition on each node.

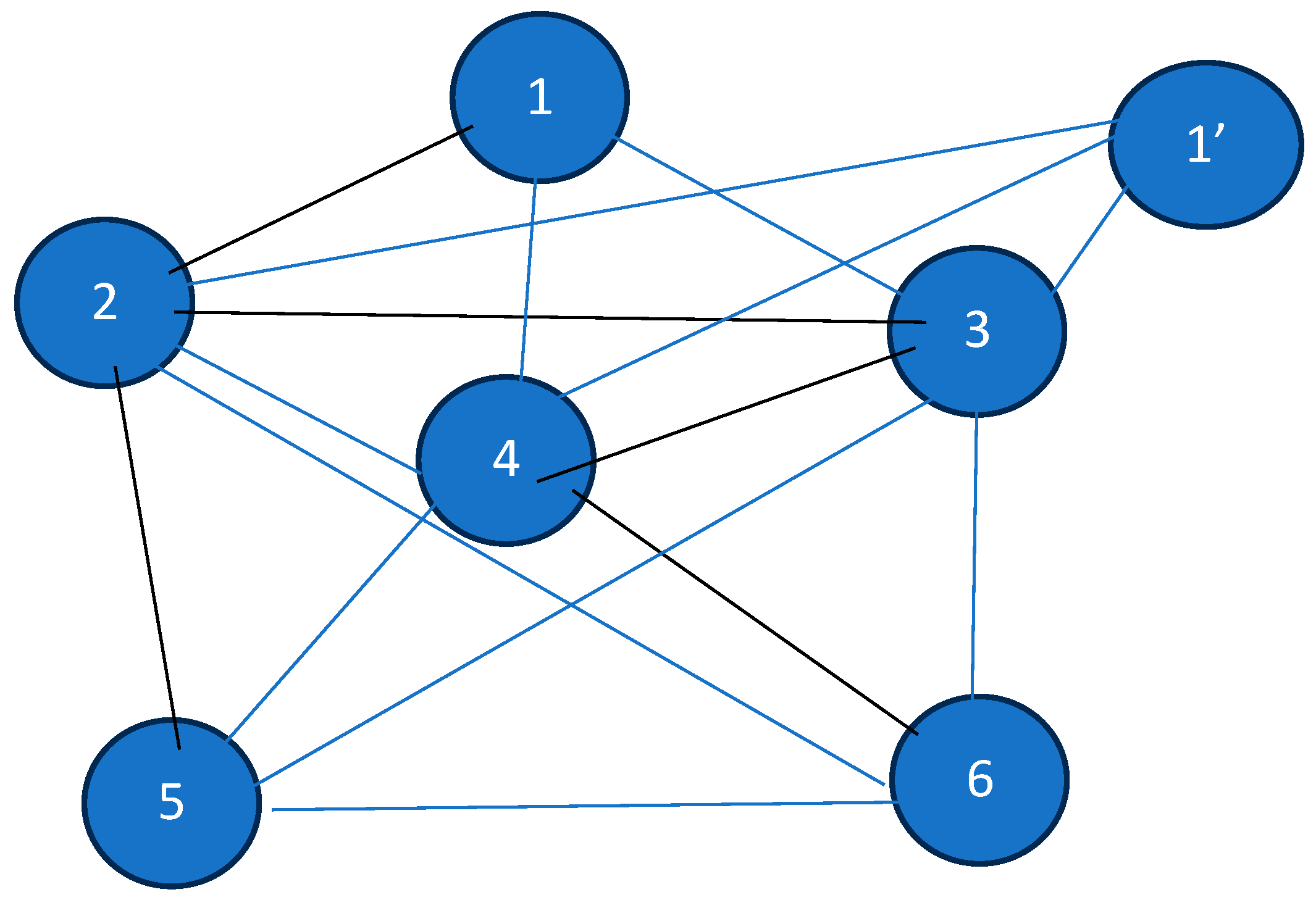
2.1.3. Numerical Illustration

Consider a simple but interesting trivial example: the $c_{ij}$ values given in

Table 1. A 6-node completely connected network with weighted links.

i\j	1	2	3	4	5	6
1	-	1	1	1	1	1
2	1	-	2	2	2	2
3	1	2	-	3	3	3
4	1	2	3	-	4	4
5	1	2	3	4	-	5
6	1	2	3	4	5	-

.

The SCN can be obtained by using the greedy approach, which is shown in Figure 1. One can start from any node, say node 6, and select the link (6,1) as the first link; the next selected links can be (1,2), (1,3), and so on. The SCN will be as given in Figure 1.

The incidence matrix for the SCN in Figure 1 is shown in

Table 2. Incidence matrix of the SCN in Figure 1.

Nodes	1	2	3	4	5	6
Incidence	5	1	1	1	1	1

.

This means that if we want a path, say, between nodes 5 and 6, nodes 5 and 6 are balanced with a node index value of 1, and all other nodes are imbalanced. Node 1 is a high-index node, and nodes 2, 3, and 4 are low-index nodes. As an application of the index-balancing theorem, add a constant value of 1 to all links emanating from the high-index node, which is node 1; the relative merits of the links (1,2), (1,3), (1,4), (1,5), and (1,6) will remain unchanged. However, an alternative has been developed by adding 1 to all links emanating from node 1. The alternative is a link starting from node 2, instead of a link starting from node 1. Therefore, the link (1,4) can be removed and replaced by the link (2,4). This change is possible as an alternative has been created to start from node 2. Note that it will lower the index of the high-index node 1 by 1, and it will increase the index value of the low-index node 2 by 1. This is shown in Figure 2. Similarly, again, if 1 is added to all links emanating from nodes 1 and 2, the link (1,5) can be removed and replaced by the link (3,5). One more application of the index-balancing theorem will result in the SCN as shown in Figure 3.

However, nodes 3 and 4 are still low-index nodes and node 1 is a high-index node. Another application gives the index-restricted SCN as shown in Figure 3.

Suppose our interest was to find the shortest connected graph with an index restriction of 2 on all nodes except the starting and finishing nodes, where the index is restricted to 1. The total incidence of the selected SCN will be 2$\left(n-1\right)$ = 10, as in this example, $n$ = 6. In other words, the IRSCN will be a path between two nodes, and it will pass through $\left(n-2\right)$ number of nodes. The connected network in Figure 3 is a required IRSCN, and it may not be unique.

3. The Index-Restricted SCN and Its Applications

3.1. The Travelling Salesman Problem

The minimum travelling salesman tour is a well-known problem in graph theory. It deals with the determination of a minimum-cost tour passing through all nodes and returning to the home city. This classical travelling salesman problem has a lot of industrial applications, and it has been classified as an NP Hard problem; see [1,13,14,15]. Another problem dealing will all nodes in graph theory is the shortest connected graph, which has been obtained by the greedy approach; see [11]. In an earlier paper [12], the authors developed an approach to convert the shortest connected network (SCN) to an index-restricted shortest connected graph, as discussed in Section 2. The index-restricted SCN can be used to find the minimum travelling salesman tour. The index-restricted SCN is developed by using the index-balancing theorem [12]. It, therefore, raises a question: is the travelling salesman problem really NP Hard? The SCN in a modified form has been used to find the travelling salesman tour in different ways, [16,17], and finally, the minimum spanning tree under the index restriction has been established as equal to the travelling salesman tour [18]. We briefly explain these approaches in Section 3.1.1, Section 3.1.2 and Section 3.1.3.

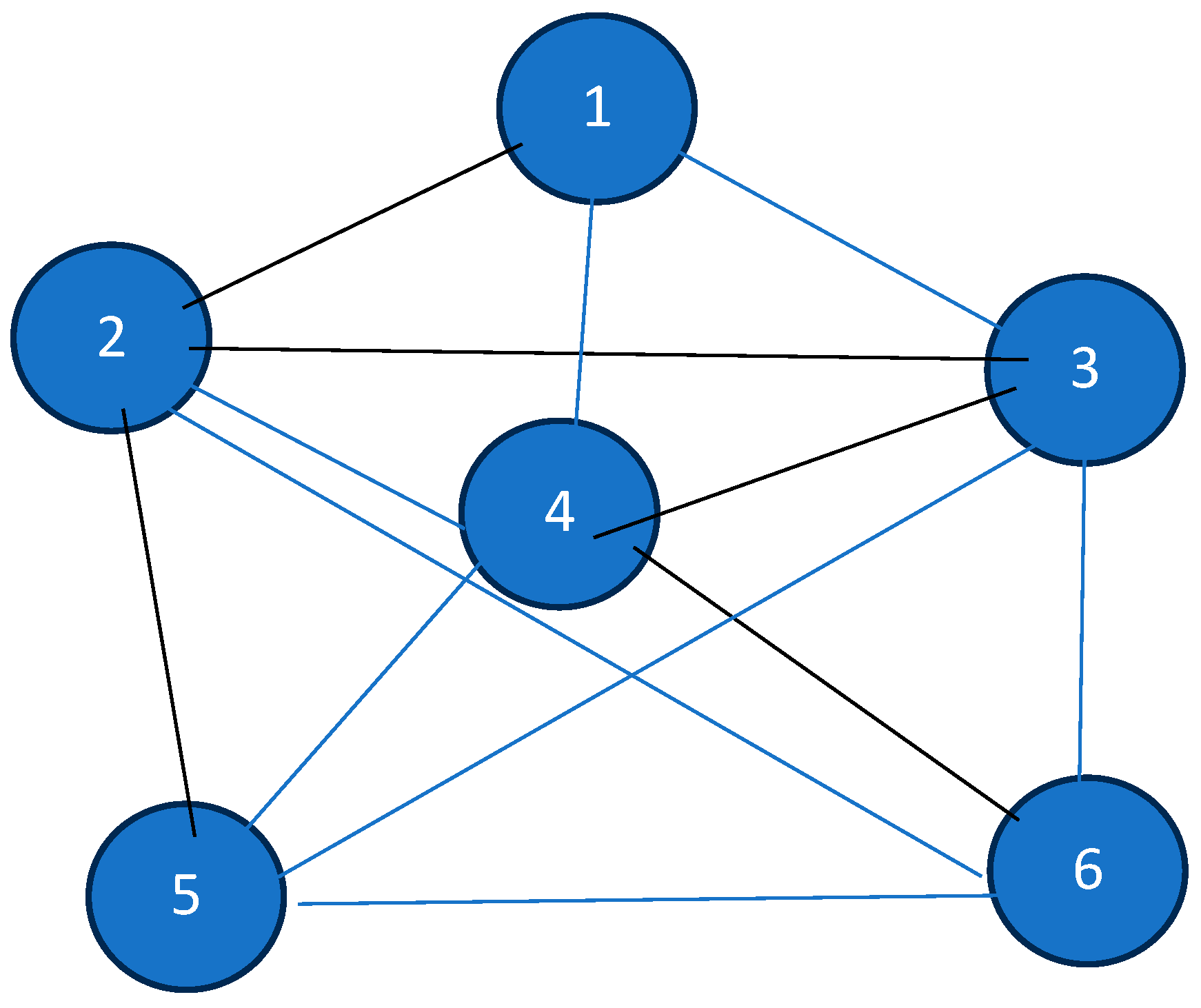
3.1.1. A Minimum Spanning Tree-Based Approach to Find the Minimum Travelling Salesman Tour (MTST) of the Network $G\left(N,L\right)$: Approach 1 (Complexity $r_{C_2}$)

We propose starting the minimum travelling salesman tour from the node with a minimum node index value, i.e., the node from where a minimum number of links are emanating. It is also true that every node will have two links, which will form a part of the minimum travelling salesman tour. If the minimum-index node is denoted by the node $p$ and its index value is r, i.e., r links are emanating from the $p$, two of these links will form a part of the minimum salesman tour. We examine all such possibilities. $\mathrm{L}\mathrm{e}\mathrm{t} \mathrm{u}\mathrm{s} \mathrm{d}\mathrm{e}\mathrm{n}\mathrm{o}\mathrm{t}\mathrm{e} \mathrm{t}\mathrm{h}\mathrm{e}\mathrm{s}\mathrm{e} r \mathrm{l}\mathrm{i}\mathrm{n}\mathrm{k}\mathrm{s} \mathrm{e}\mathrm{m}\mathrm{a}\mathrm{n}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{n}\mathrm{g} \mathrm{f}\mathrm{r}\mathrm{o}\mathrm{m} \mathrm{t}\mathrm{h}\mathrm{e} \mathrm{n}\mathrm{o}\mathrm{d}\mathrm{e} p \mathrm{b}\mathrm{y} p_r.$ The minimum travelling salesman tour can be identified by evaluating an $r_{C_2}$ number of index-restricted shortest connected trees from the modified network $G\left((N-1),(L-p_r\right))$. This symbol indicates that the modified network is obtained after removing the node $p$ and all links that are emanating from the node $p$. Hence, the modified network will have $\left(N-1\right)$ nodes and the number of links will be given by $(L-p_r)$. Every index-restricted tree becomes a travelling salesman tour when the initial two arbitrarily selected edges are joined to that path or that IRSCN. The required minimum salesman tour becomes the one with the minimum value of these $r_{C_2}$ travelling salesman tours.

In the above, we suggested starting the travelling salesman tour from a node with a minimum node index value. To explain this point, one may refer to the network in Figure 4 and note that the index value of node 1 is 3; nodes 2, 3, and 4 have an index value of 5; and anodes 5 and 6 have an index value of 4. These index values are the number of emanating links from that node. To minimise the computational work, we may prefer to start the salesman tour from node 1, where only $3_{c_2}$ number of evaluations will be required; more would be required if we started from any other node.

This approach was discussed in [17].

3.1.2. A Minimum Spanning Tree-Based Approach to Find the Minimum Travelling Salesman Tour (MTST) of $G\left(N,L\right)$: Approach 2 (Complexity $p_r)$

As discussed above, we can once again use the index-restricted shortest connected graph to find the minimum travelling salesman tour. Consider a slightly different modification of the given network. This time, we consider a modification and denote this modified network by $G\left(N,(L-1\right))$. It means there is no change in the number of nodes, and only one link connecting node p to some other node, say to node q, has been removed. Let these r links be denoted by {(p, $q_1$), (p, $q_2$), …, (p, $q_r$)}. In this approach, it is proposed to find r number of shortest connected trees joining the nodes ${(p,q}_1$), ${(p,q}_2$), …, ${(p,q}_r$), after removing only one link at a time. For example, let us remove the link ${(p,q}_1)$and find the IRSCN joining the nodes $p$ and $q_1.$ After joining the link ${(p,q}_1),$the index-restricted path will become a travelling salesman tour. Similarly, we find the index-restricted shortest connected networks joining the nodes $p$ and $q_r$, $r$ = 1, 2, …, $r$. After joining the link ($p$, $q_r$) and the minimum shortest connected graph, it will form a salesman tour and the minimum of these $r$ tours will be the required minimum travelling salesman tour. Therefore, the complexity is reduced to $r$ index-restricted shortest connected trees compared to the complexity $r_{C_2},$as was the case in the previous approach.

This approach was discussed in [16].

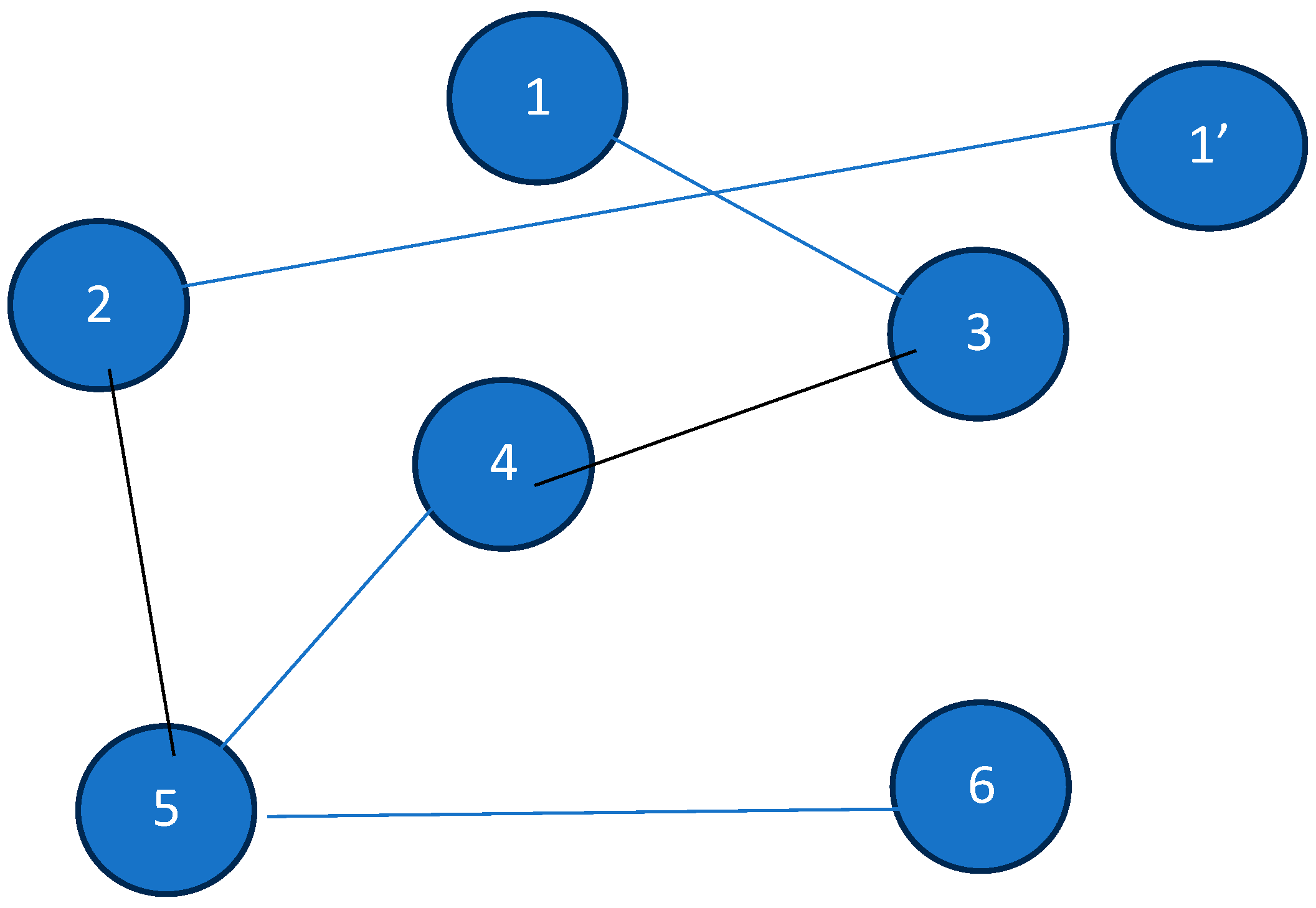
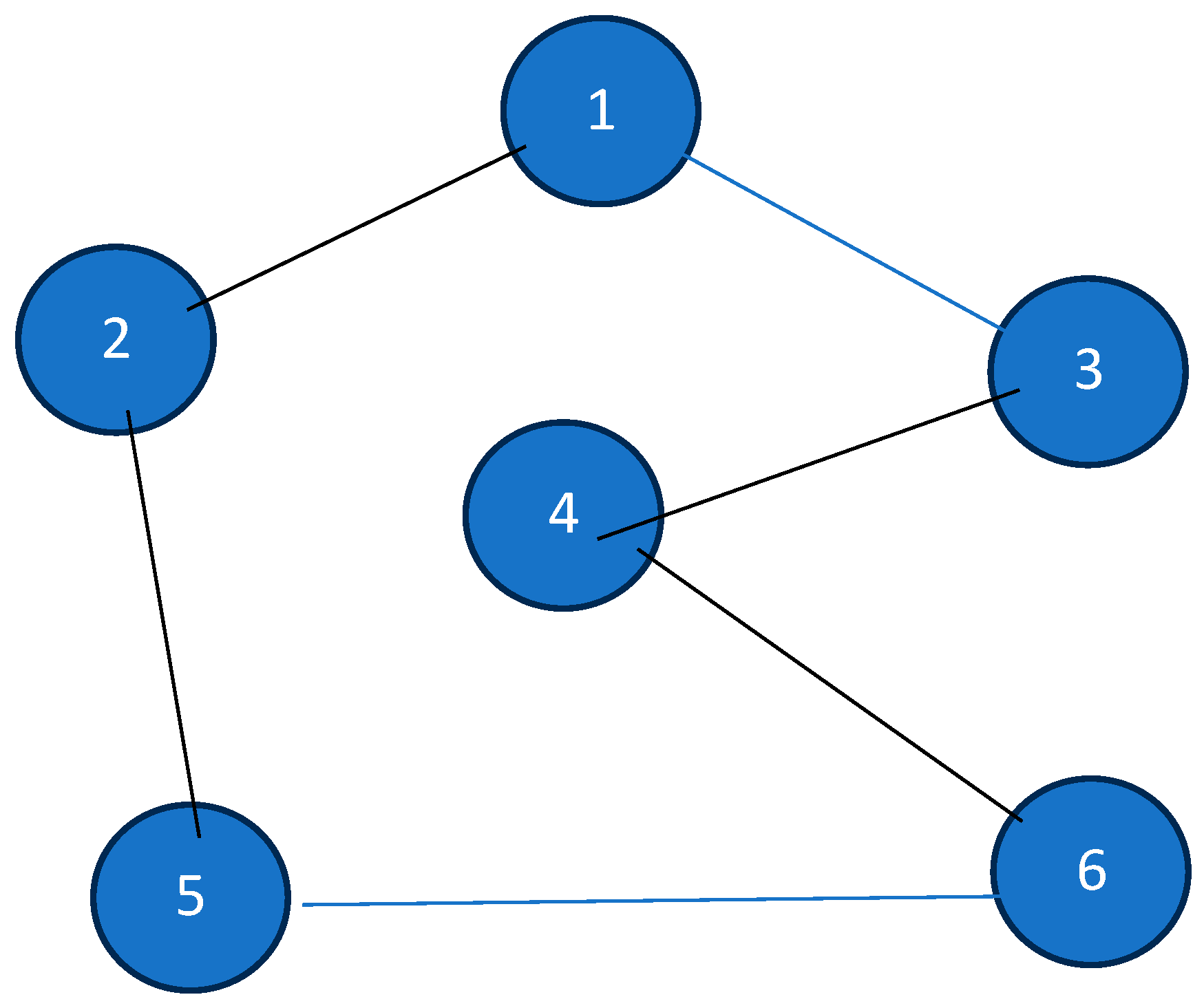
3.1.3. A Minimum Spanning Tree-Based Approach to Establish That the Minimum Salesman Tour Is Equivalent to Index-Restricted Minimum Spanning Tree: Approach 3 (Complexity 1)

Once again, let the selected node be $p$. The given network $G\left(N,L\right)$ can be modified by adding node $p^{\prime }$, and the links emanating from node $p$ are also added as links emanating from node $p^{\prime }$; the given network is transformed to $G\left\{\left(N+1),(L+p_r\right)\right\}$. It should be noted that this time, instead of removing some nodes or links, we are adding node $p$ and all links emanating from this node to the modified network. To maintain a difference in the selected node, its duplicate, and, similarly, the links that are emanating from the duplicate node, we have used the notation $p$ and $p^{\prime }$. Since node $p$ and all links emanating from this have been duplicated, their use is possible only once as the existence of the duplicate links is virtual. Node $p^{\prime }$ is also virtual; however, when we overlap $p^{\prime }$ on $p$, we are talking about one node $p$, which is real. In the following, we explain how to take care of these virtual entities, i.e., node $p^{\prime }$ and the associated virtual links from node $p^{\prime }$.

Since nodes $p$ and $p^{\prime }$ are essentially the same, the index-restricted path from node $p$ to node $p^{\prime }$ will form a salesman tour. Thus, in this case, with the help of some creative thinking, we find the index-restricted shortest connected tree joining nodes $p$ and $p^{\prime }$, and it gives us the required minimum salesman tour.

In the above modification of the given network, the usual greedy approach is not directly applicable to finding the minimum spanning tree. The $p_r$ number of extra links added to the node $p^{\prime }$ is not real; only one of them exists when selected to be part of the minimum spanning tree, and the other link must vanish. This means that as soon as one of these links becomes basic, the other must disappear. In other words, if the link $\left(p,q_j\right)$is basic, the link $\left(p^{\prime },q_j\right)$ will have an infinite length. Similarly, if the duplicate link is basic, the original link is changed to infinite value. However, if these links are non-basic, they can co-exist as non-basic links, as they have no meaningful existence in the travelling salesman tour.

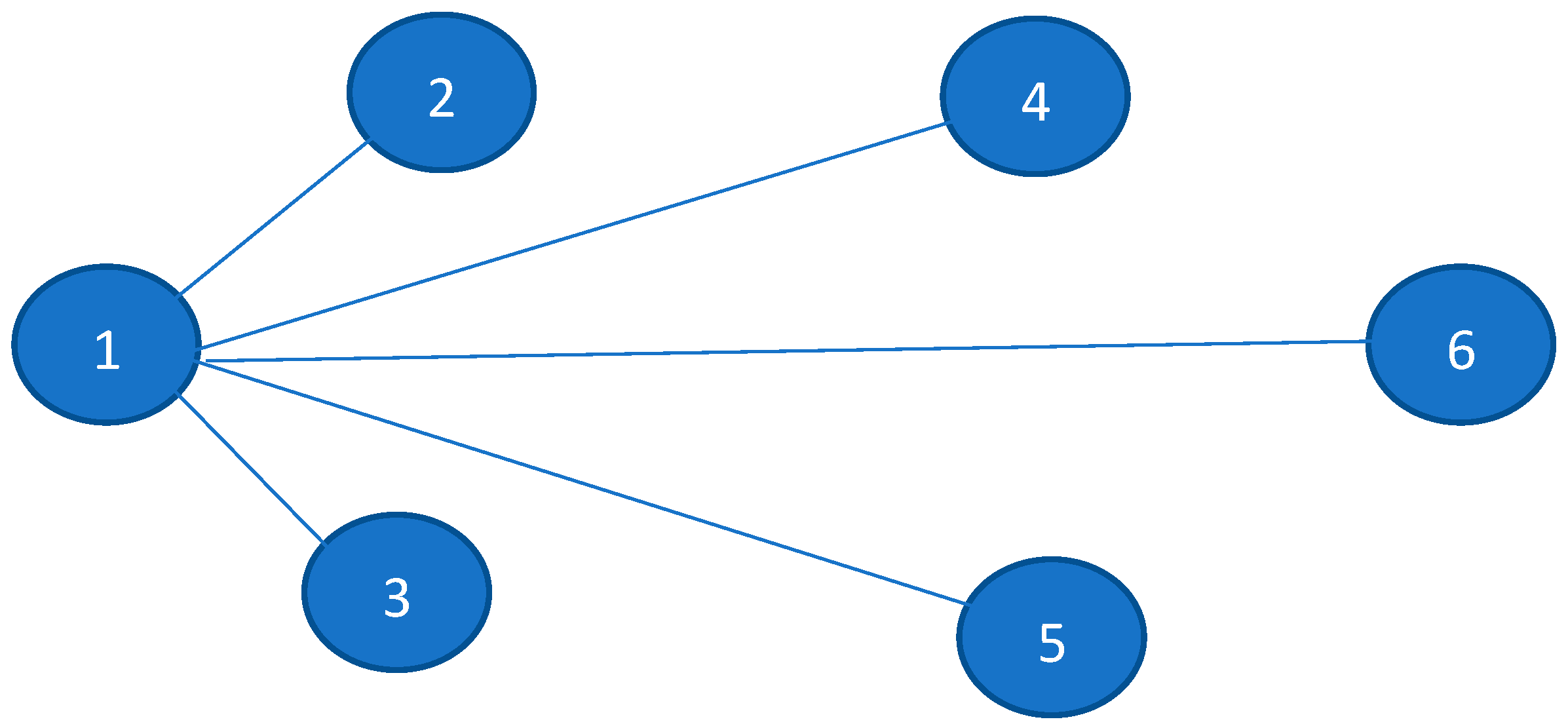
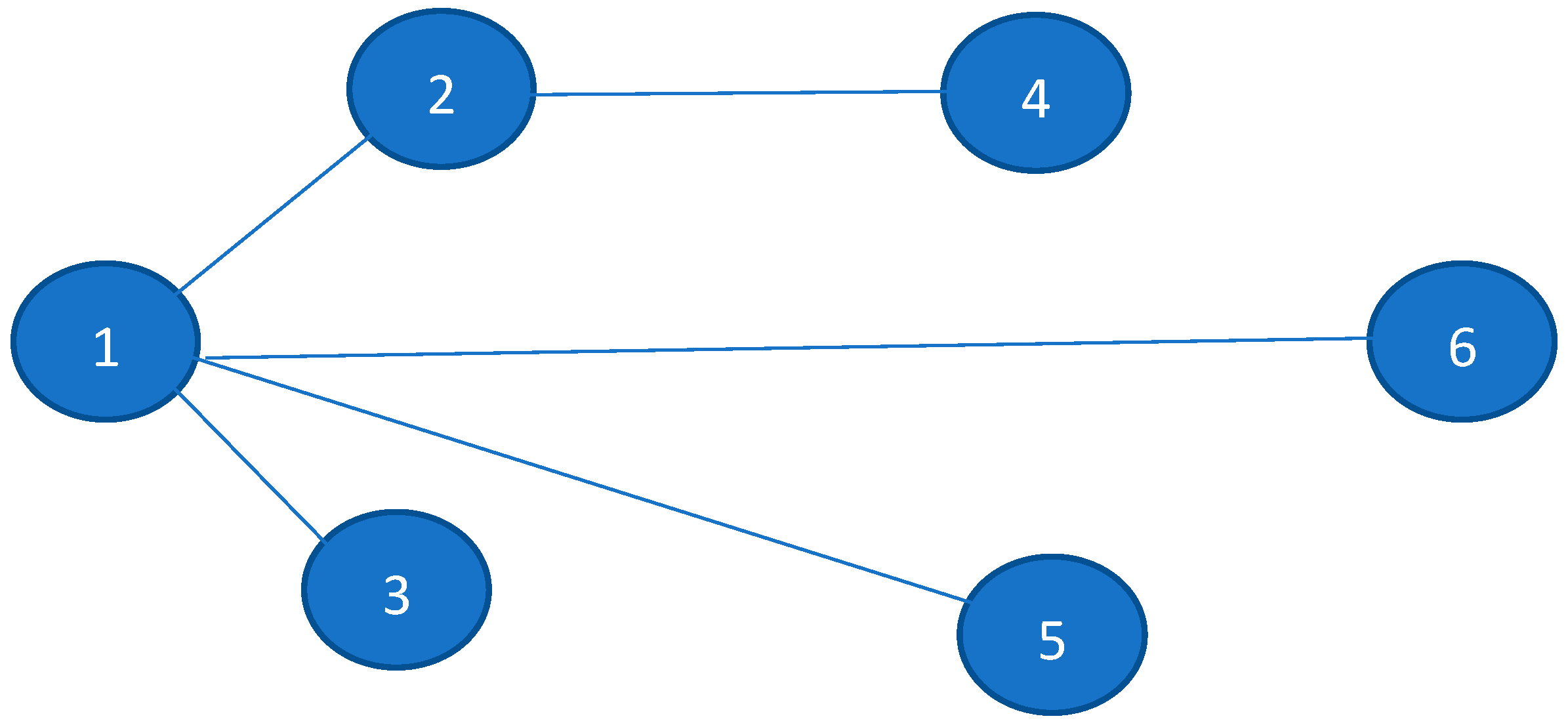
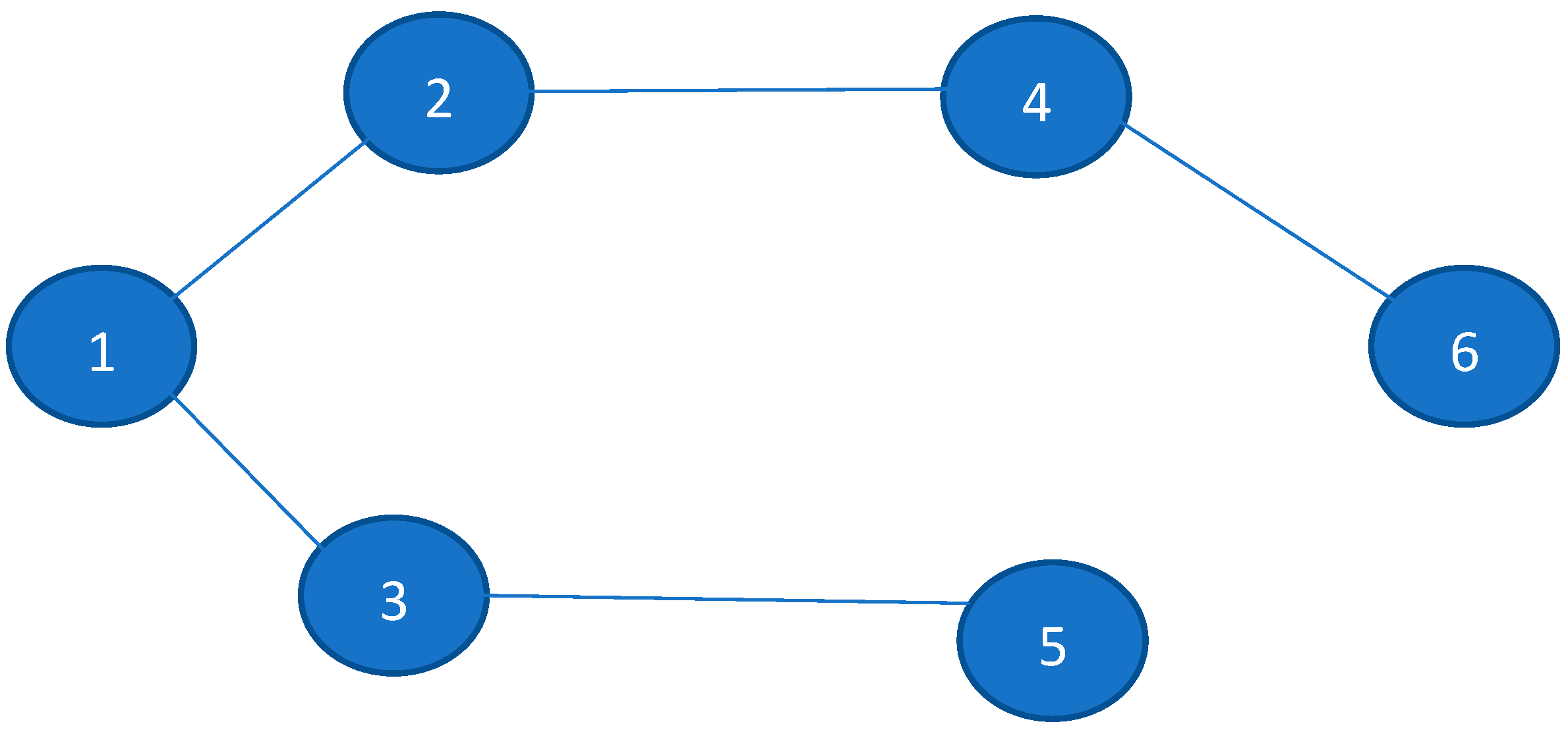
Modified Network and Steps for Obtaining the Minimum Spanning Tree of $G\left\{\left(N+1),(L+p_r\right)\right\}$

• Step 1: For the given network $G\left(N,L\right)$, develop the network $G\left\{\left(N+1),(L+p_r\right)\right\}$ and arrange links in increasing order. Initially, all links are non-basic, so all duplicate links will be the same as in $G\left(N,L\right)$. Links that have been duplicated are called Type 2 links and those which have not been duplicated are called Type 1 links. The number of Type 1 links is $\left(L-p_r\right)$ and that of Type 2 is 2 $p_r$. Type 2 links are such that at least two links have the same length value, initially.
• Step 2: Set a counter K = 1. Select the link of minimum length, include it in the minimum spanning tree, and go to Step 3.
• Step 3: If the selected link is Type 1 and K < n, set K = K + 1, and select the next minimum length. If K = n, go to Step 7.
• Step 4: If the selected edge was Type 2 and K < n, first, set the length of the duplicate link equal to $\infty$ and then rearrange lengths in increasing order. Set K = K + 1 and select the next minimum. If K = n, go to Step 7.
• Step 5: If the selected link forms a cycle with the spanning tree formed so far, discard it, or else include it. If this last link was Type 1, return to Step 3. If the selected link was Type 2, go to Step 6.
• Step 6: For the selected edge, check the following:
  • 6.1: If the inclusion of the edge does not lead to an isolated node in the network, discard it.
  • 6.2: If alternatives exist, go in favour of the edge that develops better balance among the index of nodes forming the minimum spanning tree.

Return to Step 4 as the selected link is of Type 2.

• Step 7: Stop as the minimum spanning tree has been obtained.

Numerical Illustration

Consider the following network $G\left(6,13\right)$ shown in Figure 4 the link weights are given in

Table 3. Link distances for the network in Figure 4.

F\T	1	2	3	4	5	6
1	-	12	10	10	-	-
2	12	-	15	11	11	16
3	10	15	-	7	14	12
4	10	11	7	-	10	11
5	-	11	14	10	-	9
6	-	16	12	11	9	-

.

Now, consider the modified network that will be $G\left((6+1),(13+3)\right)$ or $G\left(7,16\right)$ as shown in Figure 5, where the node 1 has been duplicated as 1’.

Type 1 links are (2,3), (2,4), (2,5), (2,6), (3,4), (3,5), (3,6), (4,5), (4,6), and (5,6).

Type 2 links are (1,2), (1,3), (1,4), (1’,2), (1’,3), and (1’,4).

Arranging links in increasing order, we have 7 (3,4)T1, 9(5,6)T1, 10(4,5)T1, 10(1,3)T2, 10(1,4)T2, 10(1’,3)T2, 10(1’,4)T2, 11(2,4)T1, 11(2,5)T1, 11(4,6)T1, 11(4,6)T1, 12 (3,6)T1, 12(1,2)T2, 12(1’,2)T2, 15 (2,3)T1, and 16(2,6)T1.

Determination of MST: Link 7(3,4) T1 included, link 9(5,6) T1 included, 10(4,5) T1 included, 10(1,3) T2 included; however, now the link (1’,3) is changed to infinity, so the list of increasing order is changed as given below:

10(1,4) T2, 10(1’,4) T2, 11(2,4) T1, 11(2,5) T1, 11(4,6) T1, 11(4,6) T1, 12 (3,6) T1, 12(1,2) T2, 12(1’,2) T2, 15 (2,3) T1, and 16(2,6) T1, $\infty$(1’,3) T2.

Note that the greedy approach will identify the next link (1,4) of length 10, but it makes a circuit, and if we go in favour of (1’,4), it also makes a circuit 1-3-4-1’, as nodes 1 and 1’ are the same. It is also excluded. The next link (2,4) is excluded, and the link (2,5) is included. The link (4,6) is excluded. Finally, we have Figure 6.

Looking at Figure 6, we find that nodes 5 and 6 are imbalanced as the node index at node 5 is 3 and the node index at node 6 is 1. If 1 is added to all nodes emanating from node 5, the weight associated with the link (4,5) will become equal to the weight of the link (4,6); therefore, it will result in an alternative. It creates a possibility of removing the link (4,5) and replacing it by the link (4,6). This is shown in Figure 7.

This path in the network $G\left(7,16\right)$ has an interpretation of an index-restricted minimum spanning tree joining nodes 1 and 1’ under the node index restriction and a salesman tour interpretation for the network $G\left(\mathrm{6,13}\right).$ It is given in Figure 8. The cost for this tour will be 12(1,2) + 11(2,5) +9(5,6) + 11(6,4) + 7(4,3) + 10((3,1) = 60 (1-> 2 -> 5 -> 6 -> 4 -> 3 -> 1).

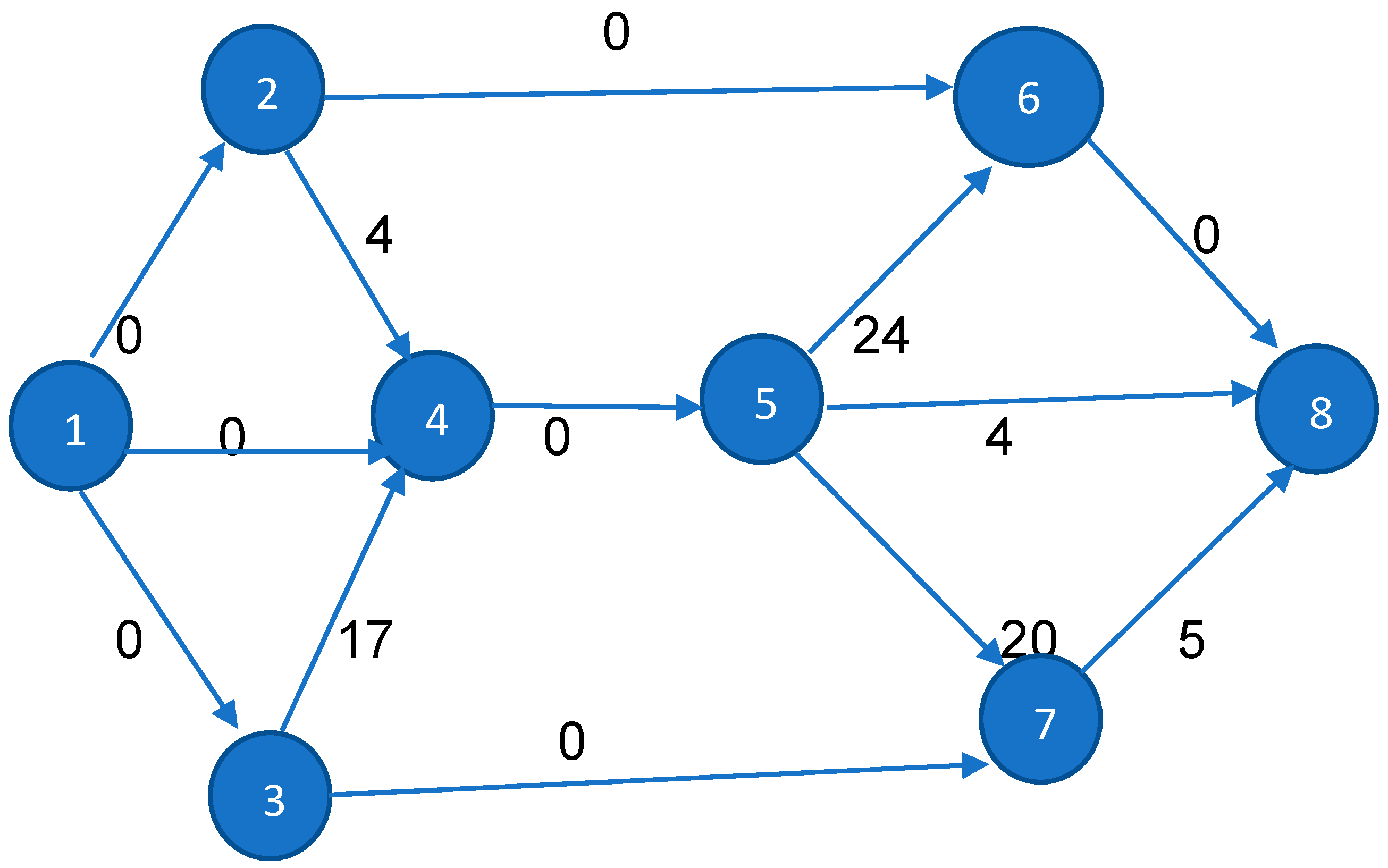
3.2. Shortest Path in a Non-Directed Network under the Condition of Passing through K Specified Nodes

Kalaba [19] suggested a constrained routing problem that finds a path from the origin node to the destination node, passing through K number of specified nodes. Using the dynamic programming technique, this problem was attempted in [20]. When the specified set is empty, the problem is reduced to an ordinary routing problem, and when the set of specified nodes contains all nodes and returns to the node we started from, it becomes the salesman tour problem. Due to the combinatorial nature of the problem, it is difficult to solve this problem by the dynamic programming technique; however, when this problem is attempted by using the shortest spanning tree under the node index restriction, the computational load becomes manageable. All nodes are included in the SCN, and the combinatorial aspect, which makes the problem computationally demanding for the dynamic programming approach, is changed. For the specified nodes, we simply apply an index restriction by making sure that the specified node is visited on route. It is achieved by imposing an index restriction of 2 or more and making sure that the restriction is satisfied. See, for example [21], where authors considered an industrial application of service calls, and the problem was developed in mathematical form as a path through K specified links. All these routing problems, where the path is restricted to pass through a set of specified nodes or links, are computationally demanding, but when these problems are attempted as an index-restricted SCN, the computational complexity is reduced. In fact, it is easy to find the index-restricted SCN under any condition, such as

$$1\le n_i\le k_i, where k_i is a given number between 1\le k_i\le \left(n-1\right).$$

4. Ordered Optimum

The best solution of $K^{th} (K\ge 2)$in general is an ordered optimisation problem. The $K^{th} \mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}, \left(K\ge 2\right),$ is defined as the best solution after excluding ($K$ − 1) ordered optimal solutions. There is no well-defined theory for the determination of ordered optimal solutions to optimisation problems, except for [22], where the authors developed a characteristic equation that identifies ordered optimum solutions for a pure linear integer programming problem. Here, we will consider the mathematics of OR problems to find the second-best solution, using the concept of an alternative optimal solution. Many suggestions have been proposed in the past, but they can be computationally demanding. These problems arise in various real-life situations, and in general, the best or optimal solution can be identified as all existing methods have defined conditions for the optimality of the solution, and when those conditions are satisfied, one can easily conclude that the optimal solution has been obtained. However, the existence of the optimality conditions for the $K^{th}$ best solution, $K\ge 2$, has not been defined; rather, the $K^{th}$ optimal is defined as the best, excluding a ($K$ − 1) number of best solutions. A need for the $K^{th}$ best solution arises in many different situations (see [2] for an example), where the $K^{th}$ best is required for a linear program to analyse the extreme point mathematical programming problem.

The $K^{th}$ best solution is required for different reasons in different situations. In this section, we approach the problem of ordered optimum, which can be computationally demanding, again, by developing an alternative solution and using that solution to identify the 2nd-best solution. Two problems have been used to illustrate the determination of the 2nd-best solution: (1) the 2nd-shortest route for a shortest route problem, and (2) the assignment problem. For the assignment problem, Murthy [3] proposed a method for ranking all the assignments in order of increasing costs. In an $nXn$assignment problem, Murthy [3] obtained the second-best solution by solving $n$ assignment problems by assigning high cost to one of the optimal assignments at a time, and the best of all these $n$ solutions was the second-best solution for that problem. His idea is that the second best will differ from the best in at least one assignment, and he evaluates all such possibilities.

In this paper, the idea is to increase the length of the current optimal solution by a certain amount to establish two or more alternative optimal solutions. One of these alternative solutions is the existing optimal solution and the other is a newly created alternative optimal solution. Since the value of the optimal solution is increased in a controlled way, these two alternative optimal solutions have an interesting interpretation of the best and the 2nd-best solutions with respect to the original cost information. We illustrate the idea by taking the shortest route problem in a network and an assignment problem to find the best and 2nd-best solutions.

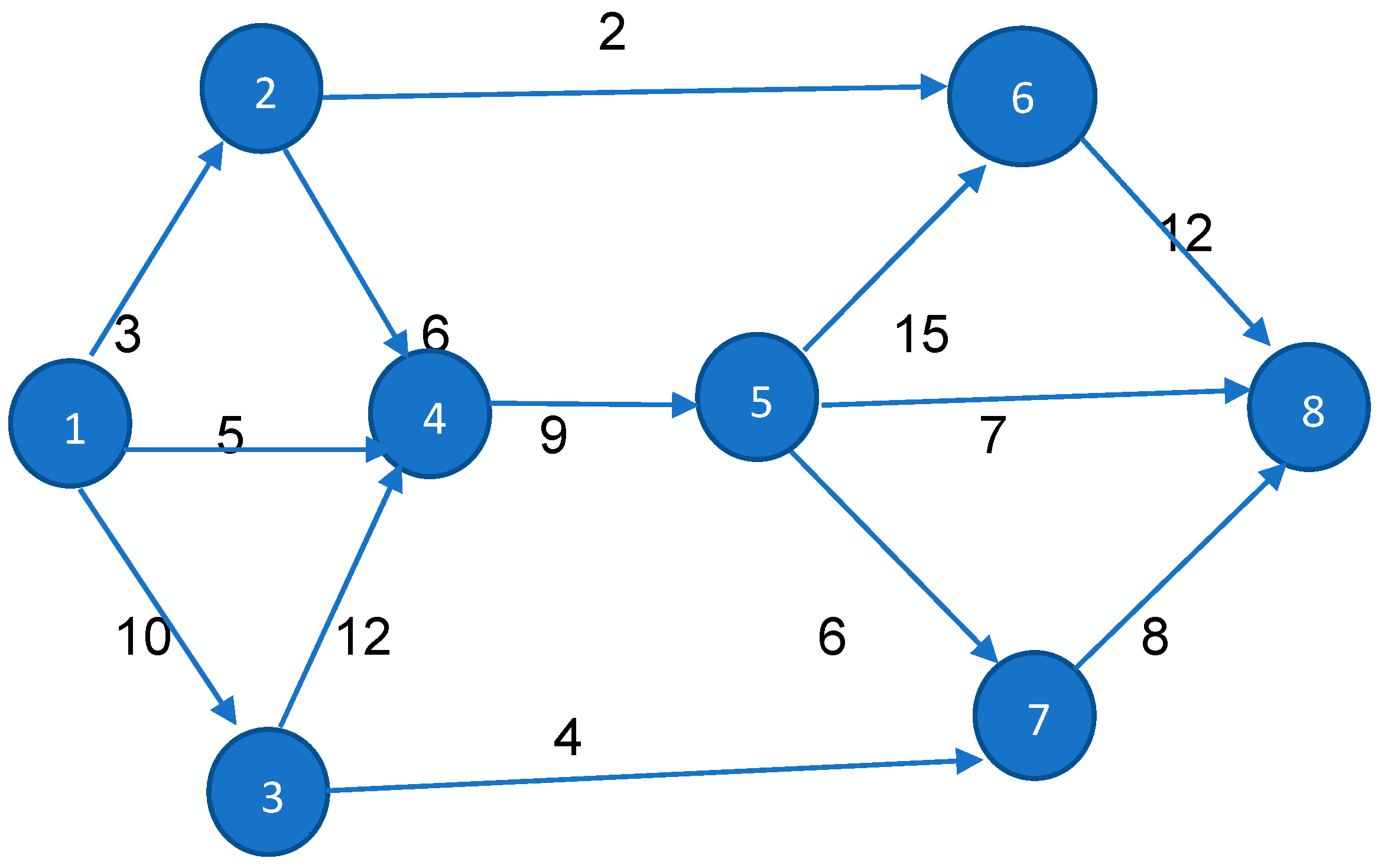
4.1. The 2nd-Best Route for the Conventional Routing Problem in a Directed Network

Numerical Illustration to Find the 2nd-Best Shortest Route

Let us apply the idea of developing alternative solutions to the network routing problem considered in Figure 9, which was transformed into Figure 10 to find the optimal solution.

The optimal solution for the network in Figure 9 was identified as 17 units, and the path was 1 -> 2 -> 6 -> 8.

We use the minimum-weight labelling approach developed in [23]. The transformed network after seven iterations of the minimum-weight label approach is shown in Figure 10.

The labels generated while applying the minimum-weight labelling approach are summarised in

Table 4. Labels obtained by the minimum-weight label method.

Node	1	2	3	4	5	6	7	8
Label	(1,0)	(1,3)	(1,10)	(1,5)	(4,14)	(2,5)	(3,14)	(6,17)

.

We arrive at node 8 from node 6, arrive at node 6 from node 2, and arrive at node 2 from node 1, resulting in the optimal path being 1 -> 2 -> 6 -> 8 and the minimum cost being 17.

The minimum non-zero cost is 4 in Figure 10, for two links. Changing the weight associated with the link (2,4) does not generate a second path, but changing the weight associated with the link (5,8) will generate a second path. We can generate two alternative paths when the link (6,8) is increased by 4 units. When the problem is solved again, we have two paths, which give the best and the 2nd best.

The best path is, as was given above, a cost of 17, and the route is 1 to 2 to 6 to 8.

The second-best path will be a cost of 21, and the route will be 1 to 4 to 5 to 8.

Increasing the link weight of (2,6) or (6,8) by 4 units will give rise to two alternative solutions.

The main idea is to increase the length of the current optimal solution by 4 units, and if we can establish two alternative optimal paths with a total length of 21 units after increasing the length of the current optimal path by 4 units, the previous path is optimal and the other is a new path that has a length equal to 21. The previous path will be the best solution and the other path will be the 2nd-best solution. Therefore, from these two alternative paths, we establish the optimal and 2nd-best solutions to the shortest route problem.

This idea can be easily extended to the non-directed network by using the labelling approach discussed in [24].

4.2. Numerical Illustration for the 2nd-Best Solution to an Assignment Problem

We reconsider the assignment problem considered by Murthy [3]. The assignment problem is given in

Table 5. Assignment cost values for Murthy’s Illustration.

R\C	1	2	3	4	5	6	7	8	$9 \mathbf{V}\downarrow$1	10
$1\to$	7	51	52	87	38	60	74	66	0	20
2	50	12	0	64	8	53	0	46	76	42
3	27	77	0	18	22	48	44	13	0	57
4	62	0	3	8	5	6	14	0	26	39
5	0	97	0	5	13	0	41	31	62	48
6	79	68	0	0	15	12	17	47	35	43
7	76	99	48	27	34	0	0	0	28	0
8	0	20	9	27	46	15	84	19	3	24
9	56	10	45	39	0	93	67	79	19	24
10	27	0	39	53	46	24	69	46	23	1

→ and ↓ indicate one horizontal and one vertical line.

.

The optimal solution with a total cost of 0 is given by the following assignments, which is denoted by A (1), given below:

A (1) = {(1,9), (2,7), (3,3), (4,8), (5,6), (6,4), (7,10), (8,1), (9,5), (10,2)}.

These allocations in Table 5 are shown in red. Vertical lines are drawn to cover zero entries in columns 9, 3, 4, 1, 5, 2, and 7. Rows are covered by three horizontal lines 4, 5, and 7. For the second-best assignment, Murthy solved 9 problems by setting one assignment from the optimal solution at a time equal to $\infty$. For example, if we set the link (1,9) =$\infty$, the problem can be solved again. Similarly, Murthy solved 9 assignment problems, which were summarised by Murthy in [3] as follows:

$$\begin{gathered} M_1=\left\{\overline{(1,9)}\right\}=10, \\ {M}_2=\left\{\right(1,9), \overline{(2,7)}\}=14 \\ {M}_3=\left\{\right(1,9), (2,7), \overline{(3,3)}\}=Cost 14 \\ {M}_4=\left\{\right(1,9), (2,7), (3,3), \overline{(4,8)}\}=Cost 1 \\ {M}_5=\left\{\right(1,9), (2,7), (3,3), (4,8), \overline{(5,6)}\}=Cost 12 \\ {M}_6=\left\{\right(1,9), (2,7), (3,3), (4,8), (5,6), \overline{(6,4)}\}=Cost 53 \\ {M}_7=\left\{\right(1,9), (2,7), (3,3), (4,8), (5,6), (6,4), \overline{(7,10)}\}=Cost 45 \\ {M}_8=\left\{\right(1,9), (2,7), (3,3), (4,8), (5,6), (6,4), (7,10), \overline{(8,1)}\}=Cost 47 \\ {M}_9=\left\{\right(1,9), (2,7), (3,3), (4,8), (5,6), (6,4), (7,10), (8,1) \overline{(9,5)}\}=Cost 56 \end{gathered}$$

From the above, he concluded that the second-best solution corresponds to the string $M_4$. This string of assignments is given by

A (2) = {(1,9), (2,7), (3,3), (4,2), (5,6), (6,4), (7,8), (8,1), (9,5), (10,10)} with total cost 1.

Now, we apply the concept of creating an alternative. From Table 5, the minimum non-zero element is 1 in the cell (10,10). In column 10 and row 10, we have an allocation in the optimal solution denoted by the string A (1). These allocations are in the cells (7,10) and (10,2). To create an alternative, the cost associated with the element (7,10) is increased by one unit or the cost associated with the element (10,2) is increased by one unit. Therefore, either column 10 or row 10 will be without a zero number, and by subtracting the minimum, we will create two zero elements in the cells (10,2) and (10,10) in row 10, which will lead to two alternative solutions. A similar case will arise with an increase in cost in the cell (7,10). The two alternative optimal solutions will lead to the best and 2nd-best solutions.

First solution: {(1,9), (2,7), (3,3), (4,2), (5,6), (6,4), (7,8), (8,1), (9.5), (10,10)}.

Second solution: {(1,9), (2,7), (3,3), (4,8), (5,6), (6,4), (7,10), (8,1), (9,5), (10,2)}.

With respect to the data in Table 5, the first solution is the second best with a total cost of 1. The second solution is the optimal solution with a total cost of 0, as obtained in [3].

The challenge remains to find the $K^{th}$ best when $K>2.$

5. Concluding Remarks

In this paper, we have considered a few combinatorial network optimisation problems, which were transformed into a form that became computationally manageable. The central idea behind these transformations is the development of an alternative, and by using that alternative, we obtained the desired solution. The problems addressed in this paper are the following:

(1) The travelling salesman problem;

(2) The path through K specified nodes;

(3) The ordered optimal solution, i.e., the second-best solution for the shortest route and assignment problem.

All approaches use the alternative solution, which has been created in each situation differently and used to reduce the computational load. The combinatorial aspect of the travelling salesman and the path through specified nodes was reduced to a manageable form by the development of the index-restricted minimum spanning tree.

The second-best solution for the shortest route and the assignment problem was obtained by increasing the optimal solution to a controlled and strategic position to obtain two optimal solutions, one of which was the optimal and the other was the second-best solution.

Our approach also raised a few questions that deserve further investigation.

• Is the minimum travelling salesman tour problem really NP Hard?
• Is the constrained routing problem computationally demanding?
• Ordered optimisations require further investigation to find the $K^{th}$ best when $K\ge 3$ for the two cases discussed in this paper, and for other situations.

This paper has been confined to some classical problems due to the authors’ long association with them; however, it would be desirable to investigate the application of these ideas to routing problems considered by [25,26,27].

The approaches reviewed in this paper need further investigation to establish the computational efficiency of various situations discussed in this paper. This is under investigation and will be reported when ready.