Appendix A
As indicated in the Introduction, a substantial knowledge of geometrical theory is required in order to appreciate exactly how de Rham’s theorem links holes in the topology of smooth manifolds with the chaotic behavior of integral flow fields on a manifold. A full understanding of the link depends on familiarity with (i) simplicial complexes, (ii) singular homology groups, (iii) singular chain complexes, (iv) chain maps, (v) computing singular homology groups, (vi) the Mayer–Vietoris theorem, (vii) homotopy invariance, (viii) singular cohomology and the coboundary operator, (ix) skew-symmetric tensors, (x) Grassmann algebra and (xi) de Rham cohomology groups and the Hodge star operator, as well as knowledge of the Laplacian operator and harmonic flow fields. Some of these have been touched on in the text. In this
Appendix A, we provide a more detailed overview of the differential geometry involved. Proofs are available in a variety of texts [
7,
11,
12,
25,
26,
27,
28,
29,
30].
Appendix A.1. Simplicial Complexes
In 3D Euclidean spaces, , where the are points in , are the simplicial building blocks that can be glued together along their boundary faces to form 0-, 1-, 2- and 3-dimensional oriented connected compact subspaces in . These glued structures are called simplicial complexes, on which 0, 1, 2 and 3rd degree differential forms, respectively, can be integrated. A standard 3-simplex in is defined such that , , and . This standard 3-simplex defines a Cartesian coordinate system on where defines the origin and define unit-length vectors along mutually orthogonal Cartesian coordinates , respectively. A 2-simplex in defines a triangle in 3D space that includes all the points along its oriented boundary faces as well as all the internal points. Given vectors from the origin to each of the points , respectively, if the vectors and are linearly independent, we say that the points are affinely independent (unlike a vector space, an affine space does not span the origin). As the vector is moved about in , the affinely independent 2-simplex can be moved to any place in . By gluing together a collection of 2-simplices along common boundary faces, a 2-dimensional compact oriented surface known as a simplicial complex can be constructed in . Such a surface is referred to as a 2-chain, denoted by . Many different 2-chains can be constructed in . Many different 0-chains (discrete points), 1-chains (wire-frame models), 2-chains (2-dimensional surfaces) and 3-chains (3-dimensional subspaces) can be constructed in . In general, simplicial complexes are closed and bounded polyhedrons.
Given a 3D smooth manifold , a 2-simplex in can be mapped by a smooth map into . Such a smooth map is a nonlinear map giving rise to a singular 2-simplex in . Because of the nonlinear mapping, such a singular 2-simplex may no longer look like a triangle. It can lose rank and may even appear as a single point. For this reason, it is referred to as a singular simplex. The same applies for one, two and three singular simplices in 3D manifolds.
Of all the possible 2-chains that can be constructed in , there are some 2-chains that close on themselves (like 2-spheres) and have empty boundaries (i.e., . Such 2-chains with empty boundaries are called 2-cycles, represented by the notation . A similar property applies to 0-, 1-, 2- and 3-chains in , giving 0-, 1-, 2- and 3-cycles with zero boundaries.
Appendix A.2. Singular Homology Groups
Singular 2-cycles in the underlying topology of can be used to detect the existence of 2-dimensional holes in . The singular 2-homology group on the underlying topology of is defined to be all of the 2-cycles (represented by the free Abelian group ) on the underlying topology of that are not boundaries of 3-chains . Such 2-cycles enclose 2-dimensional holes in the underlying topology. Define to be all of the 2-cycles in that are boundaries of 3-chains . The singular 2-homology group is then defined by the quotient (i.e., the group of all 2-cycles that are not boundaries of 3-chains). The dimension of the free Abelian group equals the number of 2-dimensional holes in the underlying topology of . This can be generalized to -th degree homology groups with in the underlying topology of an -dimensional smooth manifold . This intuitive description of singular homology groups can be formalized by defining a sequence of singular homology groups attached to the underlying topology of smooth manifolds.
Appendix A.3. Singular Chain Complexes
A long sequence of Abelian groups connected by homomorphisms
is said to be exact if
for all
.
The first isomorphism theorem for groups implies that a short 5-term sequence
is exact if and only if the homomorphism
is injective and the homomorphism
is surjective. This implies that for a short 4-term sequence
to be exact, the homomorphism
has to be both injective and surjective. This fact is useful when computing singular homology groups of higher-dimensional topological spaces (e.g., high-dimensional spheres described below).
A long sequence of free Abelian groups (chains) together with homomorphisms
is called a singular chain complex, denoted by
, if the composition of any two consecutive homomorphisms
is zero. This is the same as requiring
.
The
-th singular homology group of the singular chain complex
is
where
is the space of all
-cycles in
, and
is the space of all
-cycles in
that are boundaries of
-chains
in
. It follows that the singular chain complex
is exact if and only if
is zero for all values of
. In other words, the singular homology groups
provide a precise measure of the failure of the chain complex
to be exact. This occurs when there is an
-dimensional hole(s) in any of the
-chains.
Appendix A.4. Chain Maps
A chain map
between singular chain complexes associated with topological spaces
and
, respectively, is a collection of homomorphisms
for all
such that
, as illustrated below:
A continuous map
between topological spaces
and
induces a singular chain map
between the singular chain complex
and the singular chain complex
. This map is defined by the homomorphisms
for all values of
, as illustrated. Since
maps
to
and
to
, it follows that the continuous map
between topological spaces
and
induces a singular homology group homomorphism
for all values of
.
Because the image of any one singular simplex is connected, it has to lie entirely in one path-connected component of the topological space . So it follows that the -th singular homology group for equals the direct sum of the -th singular homology groups for each of the path-connected components (i.e., ).
Appendix A.5. Computing Singular Homology Groups
The definition given above of singular homology groups involves the notion of -chain complexes consisting of every possible -chain that can be constructed in a topological space. This is a very large number of -chains, so it does not help much in telling us how we can actually compute singular homology groups. However, powerful tools based on the so-called Mayer–Vietoris exact sequence and the zigzag lemma have been developed for computing the homology groups for most if not all topological spaces. Some singular homology groups can be deduced directly from the definition, in particular (i) degree zero singular homology groups for any topological space and (ii) all singular homology groups for all values of on a discrete topological space .
Appendix A.5.1. Degree Zero Singular Homology Groups
For every topological space
, the boundary
of the zero-dimensional chain complex
is zero because there is no
chain. It follows that every singular 0-chain is a 0-cycle (i.e.,
). On the other hand, a singular 0-chain is a formal linear combination of points
in
with integer coefficients (i.e.,
). Assuming that
is path-connected, we can define a surjective map
by
, where
is the group of all integers. The kernel of this map corresponds to all points
in
that are boundary points of a 1-chain, and consequently, from the first isomorphism theorem for groups,
Thus, for any topological space , the zero singular homology space is isomorphic to the group of integers , and the dimension of is equal to the number of path-connected components in . This dimension is the Betti number.
Appendix A.5.2. Homology Groups for Discrete Topological Spaces
For a discrete space
, each isolated point corresponds to a connected component of
, so
is a free Abelian group isomorphic to the group of integers
with dimension
equal to the number of discrete points in
. Although each connected component of
is a single isolated point, the boundary
for a singular
-simplex
is given by the alternating sum
, where
represents the singular
-th boundary face. For single point spaces, the singular faces
are all equal to
. Thus,
is an isomorphism when
is even and zero when
is odd. Consequently, we obtain a singular chain complex
where the boundary maps
are 0-maps for odd values of
and are isomorphisms for even values of
. It follows that the sequence is exact at each Abelian group
except
. But we have already dealt with
for
. Since the singular homology groups
provide a measure of the deviation from exactness, it follows that the singular homology group
for each isolated point of a discrete topological space
is equal to zero for all
.
Appendix A.6. Mayer–Vietoris Theorem
The Mayer–Vietoris theorem is an important tool for computing singular homology groups for topological spaces. If
is a topological space and
are open subsets of
whose union is
, then for each
there is a homomorphism called the
connection homomorphism , such that the following long sequence of homology groups is exact:
where
:
with
and
with
where
and
represent singular homology classes [
8].
To illustrate how the Mayer–Vietoris theorem can be combined with other properties of topological spaces to compute singular homology groups, consider computing the singular homology groups for all values of
and for all dimensions
of a unit sphere. Consider a unit
-sphere
with open subset
equal to
with the south pole removed and open subset
equal to
with the north pole removed. A part of the Mayer–Vietoris exact sequence is
where the connecting homomorphism is
. All points in
can be contracted to the north pole and all points in
can be contracted to the south pole. This means that both
and
are contractible and therefore simply connected (i.e., contain no holes). It follows that
Consequently, when
and
, the exact sequence can be rewritten as
This is an exact 4-term sequence as described above and, consequently, the connecting homomorphism
is a bijective map (i.e., an isomorphism). Just as the equator of a unit 2-sphere
is topologically equivalent to a unit circle
, the equatorial sphere
of a unit
-sphere
is topologically equivalent to a unit
-sphere
. This means
for
and
and
if
. We already know that
and
if
, so we have all the singular homology groups for higher-dimensional spheres.
Appendix A.7. Homotopy Invariance
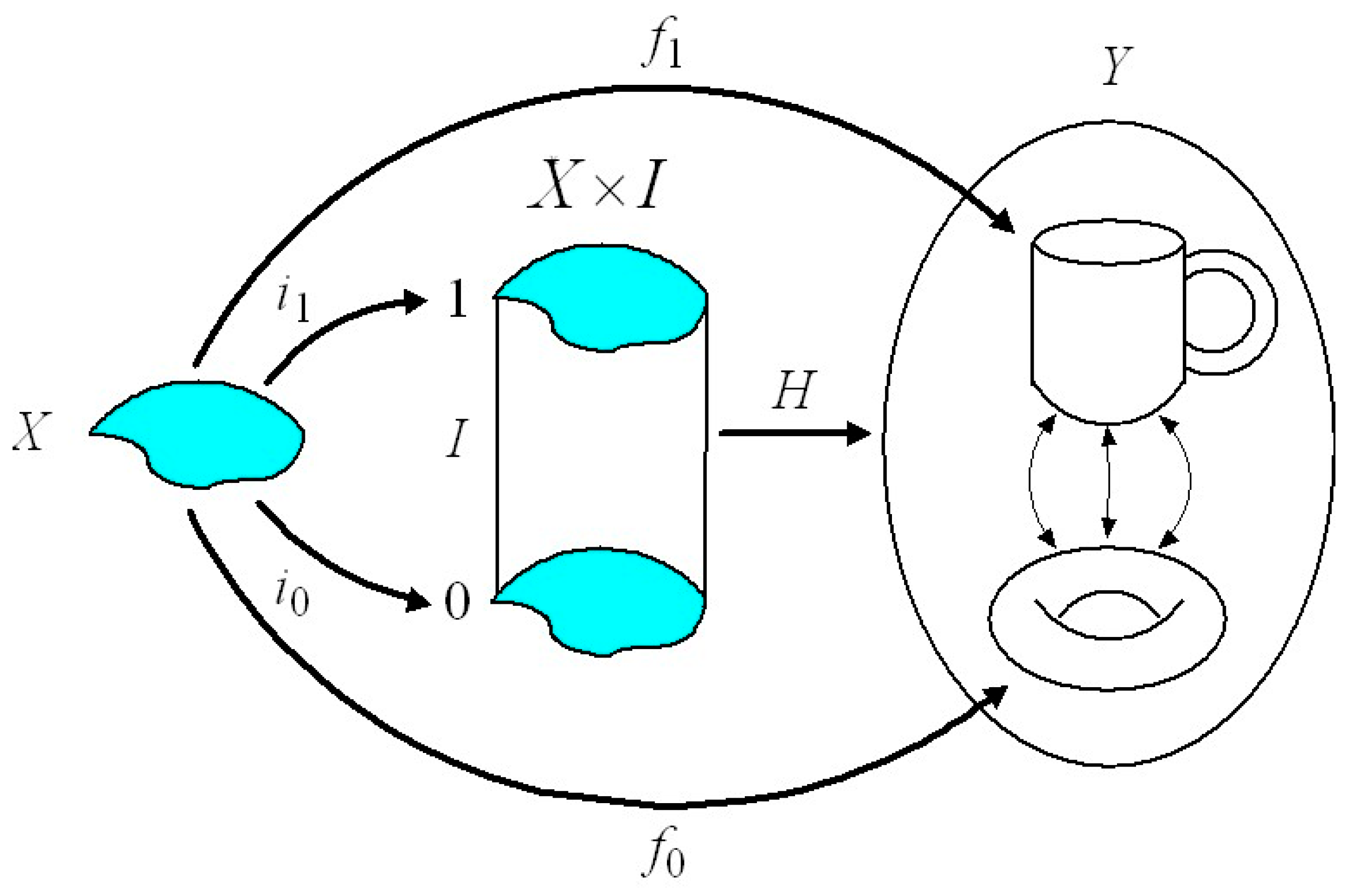
A 2-torus has two one-dimensional holes and one two-dimensional hole. In other words, it has a two-dimensional degree-one singular homology group and a one-dimensional degree-two singular homology group . The rubber sheet geometry of the 2-torus allows it to be deformed into many different sizes and shapes. As long as it is not cut, torn, punctured or glued, all the different sizes and shapes of can be mapped homeomorphically onto each other and the topological structure remains unchanged (i.e., the number of holes and hence the singular homology groups and remain unchanged). A similar property holds for all topological spaces. The number of holes of various dimensions, and hence their singular homology groups, are homotopically and topologically invariant. Let be continuous homotopic maps (i.e., in and in can be morphed into each other without changing their topological structure), then and (together with all the intermediate shapes along the homotopy transformation pathway between and ) have the same singular homology groups. In other words, continuous homotopy maps induce singular homology group homomorphisms for all values of . A continuous map : between topological spaces and is said to be a homotopy equivalence if there is a continuous pull-back map : such that the composition is homotopic to the identity map on Y and the composition is homotopic to the identity map on . If : is a homotopy equivalence between topological spaces and , then for each , the map is an isomorphism.
Appendix A.8. Singular Cohomology
Singular homology groups are covariant functors from the category of topological spaces to the category of free Abelian groups. For many applications, including de Rham’s theory of differential forms, it is more useful to have contravariant functors. Singular cohomology is a pull-back version of singular homology. It does not give any new information but simply presents the same information in a different way.
The transformation from covariant functor to contravariant functor is based on the following fact. If A and B are Abelian groups under pointwise addition, then the set of group homomorphisms from A to B is itself an Abelian group under pointwise addition. For any fixed Abelian group G, each homomorphism gives an induced pull-back homomorphism . If and , then . This pull-back map can be used to relate the free Abelian group of all singular -chains on a topological space to the free Abelian group of all singular -cochains on the same topological space . For free Abelian groups, the group equals the group of integers . A continuous map : between topological spaces and induces a homomorphism between the free Abelian groups of all possible -chains on and (i.e., = where we use the notation to represent a single -chain in ). It also induces a pull-back homomorphism , or equivalently, (i.e., where ).
Coboundary Operator
The boundary operator
between free Abelian groups of all possible
-chains and all possible
-chains on
induces a pull-back coboundary operator
between all possible
-cochains and all possible
-cochains on
(notice increasing values of
). For the coboundary of a single
-chain
on
, we obtain
, where
. More simply, this shows that
. It also follows that
, because
and
. Because
, there exists an exact long cochain complex and cochain map
between topological spaces
and
(notice decreasing
).
An -cochain is an -cocycle if (i.e., it has an empty coboundary), and it is a bounding cocycle if there exists a cocycle such that (i.e., it is a coboundary of an -cochain). Both the -cocycles and the -bounding cocycles are preserved by cochain maps , so we can define the -th singular cohomology group of with coefficients in to be the quotient .
It can be concluded that a continuous map : between topological spaces and induces a pull-back homomorphism between -th singular cochains on and -th singular cochains on This in turn induces a pull-back homomorphism between the -th singular cohomology group on and the -th singular cohomology group on . Just as singular homology groups are homotopically and topologically invariant, so are singular cohomology groups. In other words, singular cohomology groups are isomorphic to their corresponding singular homology groups.
Appendix A.9. Skew-Symmetric Tensors on a Smooth -Manifold M
At every point
on a smooth
-manifold
, there exists an
-dimensional tangent space
and an
-dimensional cotangent space
. A covector or 1-form
in
acts on a vector
in
and transforms it into a real number (i.e.,
). A type
skew-symmetric tensor
operating on two vectors
and
in
to give a real number changes sign if the order of the two vectors is reversed (i.e.,
). If
are unit basis vectors spanning the tangent vector space
at
and
are unit basis covectors dual to
spanning the cotangent vector space
, then we can write the type
skew-symmetric tensor
in the form
, where
This defines the wedge product
to be a basis for the type
skew-symmetric tensor space
at
, and
is the component of the type
skew-symmetric tensor (vector) projected onto the basis vector
. This can be generalized to a skew-symmetrization (or alternating) operator
A for a type
,
skew-symmetric tensor
by the formula
where
is the number of permutations
of
objects taken
at a time when order matters and with
and
in this case,
is the sum over all
permutations of the
vectors
, and
is the parity of each permutation (i.e.,
if the number of interchanges of two vectors is even and
if the number of interchanges is odd).
If is an -form and is an -form, then is an -form.
The wedge product is
- (i)
associative ,
- (ii)
(anti)-commutative (), and
- (iii)
distributive where and are both -forms here.
Basis vectors (skew-symmetric tensors) spanning the -th skew-symmetric tensor space are .
Appendix A.10. Grassmann Algebra
At each
on a smooth
-manifold
, there exists a family of skew-symmetric tensor spaces
. The skew-symmetric tensors in these skew-symmetric tensor spaces are called differential forms. An
-form in
acts on
vectors
in
and transforms them into a real number for all values of
. The dimension of each skew-symmetric tensor space
is given by
. From this formula, the skew-symmetric tensor spaces
and
are both one-dimensional. The dimension increases linearly with
from
to
and then decreases linearly to
. This implies that the dimension of
is equal to the dimension of
. Indeed, the skew-symmetric tensor space
is isomorphic to the skew-symmetric tensor space
. An isomorphic operator
known as the Hodge star operator transforms
-forms in
into
-forms in
for all values of
. For
and
, the skew-symmetric tensor spaces
are empty spaces and the differential forms are set to zero. An operator
, known as the exterior derivative, transforms an
-form into an
-form. Importantly, the composition
is always zero. It follows that there exists a sequence of skew-symmetric tensor spaces connected by the exterior differential operator
where each arrow corresponds to an exterior differential
. An operator
transforms an
-form into an
-form. More generally,
, where
is the Hodge star operator, that is, an isomorphism between
and
. The operators
and
are not inverses of each other, they are adjoints. The direct sum of skew-symmetric tensor spaces forms a graded algebra
, known as an exterior algebra or Grassmann algebra. Any
-form
for which
is said to be a closed
-form, while any
-form
equal to
where
is an
-form is said to be an exact
-form.
Appendix A.11. De Rham Cohomology Groups
From Grassmann algebra and the fact that
, it follows that every exact differential form is closed. It does not follow, however, that every closed differential form is exact. De Rham’s theory of differential forms makes it clear that whether or not a closed differential form is exact depends uniquely on the underlying topological structure of the manifold. Specifically, it depends on the presence or absence of holes of various dimensions in the underlying topology. As illustrated by the amount of theory summarized in this appendix, a significant amount of differential geometry is needed to appreciate this remarkable fact. Because the exterior differential
is linear, its kernel
closed
-forms and its image
exact
-forms are linear vector spaces. Since every exact form is closed, it follows that the exact
-forms are a subspace of the closed
-forms (
). Thus, the
-th de Rham cohomology group can be defined to be the quotient vector space
(i.e., the space of all closed forms that are not exact).
While is a real vector space, it is also a Lie group under addition. Since for and , it follows that equals zero for these values of . It also follows that for if and only if every globally closed -form on is globally exact.
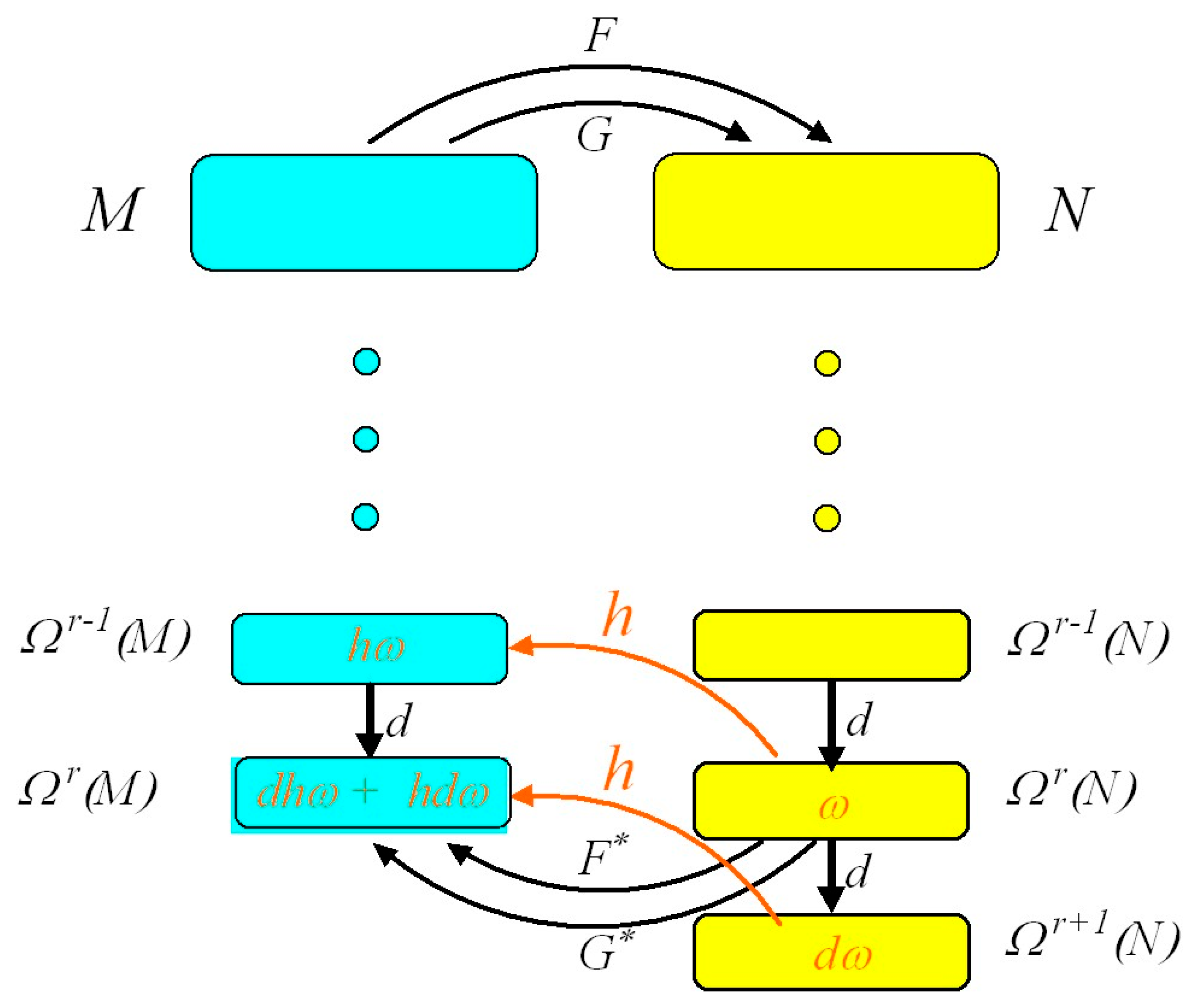
The vector quotient space partitions the space of closed -forms into equivalence classes. For any closed -form on that is not exact, we let denote the equivalence class of . If and then they differ by an exact -form (i.e., ), and we say that and are cohomologous. This is easy to visualize in terms of homology groups, where it simply means that there can exist multiple -cycles that contain the same -dimensional hole. Just as a continuous map : between topological spaces and induces a pull-back homomorphism between the -th singular cohomology group on and the -th singular cohomology group on , a smooth map between smooth manifolds and induces a pull-back between the -th de Rham cohomology groups of and , respectively. This corresponds to a contravariant functor between the category of smooth maps between smooth manifolds and the category of de Rham cohomology groups.
We can form an interesting picture of a relation between degree-one de Rham cohomology groups on a connected smooth manifold and the underlying topology of the manifold as measured by the fundamental group All the 1-cycles in all the possible 2-chains in the underlying topology of the smooth manifold that contain a 1-dimensional hole correspond not only to but also to the fundamental group . The fundamental group consists of all the loops associated with the point in the underlying topology of that cannot be contracted to a point. The set of group homomorphisms from the fundamental group to the additive group of real numbers is a vector space under addition and multiplication by constants. We can define a linear map as follows: Given a cohomology class , define by a real number, where is any path homotopy class in and is any piecewise smooth curve representing the same loop path class . The map is a well-defined homomorphism between groups. It follows that when the topology underlying the smooth manifold is simply connected (i.e., has no 1-dimensional holes and no loops that cannot be contracted to a point).
Appendix A.12. De Rham’s Theorem
De Rham’s theorem hinges on the fact that, just like singular homology and singular cohomology groups, de Rham’s cohomology groups for all values of are homotopically and topologically invariant. Assume that smooth maps and between smooth manifolds and are homotopic (i.e., in can be morphed into in and vice versa). Define a homotopy operator for all values of . Suppose and so that , where and are smooth pull-back maps from to for all values of . If we let be a closed -form on (i.e., ), we find . Consequently, and differ by an exact form in , so it follows that and are cohomologous, and the induced pull-back maps for all values of are isomorphic. De Rham cohomology groups for all values of are homotopically and topologically invariant. It can be concluded that if and are homotopy-equivalent smooth manifolds with or without boundary, then for each value of . Smooth homotopy equivalence between smooth manifolds induces isomorphisms between de Rham cohomology groups.
From Stokes’ theorem and the definition of a period
where
is an
-cycle and
is an
-form, we can define a bracket
:
, where
is the free Abelian group of all possible
-chains
in
and
is the free Abelian group of all possible
-cochains (i.e.,
-forms)
in
, by setting
. For every
-form
, the map
is linear on
, and for every
, the map
is linear on
. This induces a bracket on the singular
-homology group
and the
-th de Rham cohomology group
by setting
where
is an
-homology class,
is an
-th de Rham cohomology class,
is any representative of
and
is any representative of
. The period
only equals zero if the closed
-form
is exact, otherwise it is a real non-zero number. For any fixed de Rham
-th cohomology class
, the map
given by
is a well-defined linear functional on
. De Rham’s theorem asserts that this correspondence between linear functionals on
and de Rham cohomology classes
is bijective. The bilinear map
:
is non-degenerate in both arguments [
27]. Essentially, de Rham’s theorem says that the
-th de Rham cohomology group is isomorphic with the dual space of the
-th homology group (i.e., with the space of the singular cohomology group). This implies that an
-form
is globally exact if and only if all of its periods vanish. This can only happen if there are no
-dimensional holes in the underlying topology of the smooth manifold.