Abstract
The transition zone (TZ) of hydrocarbon reservoirs is an integral part of the hydrocarbon pool which contains a substantial fraction of the deposit, particularly in carbonate petroleum systems. Consequently, knowledge of its thickness and petrophysical properties, viz. its pore size distribution and wettability characteristic, is critical to optimizing hydrocarbon production in this zone. Using classical formation evaluation techniques, the thickness of the transition zone has been estimated, using well logging methods including resistivity and Nuclear Magnetic Resonance, among others. While hydrocarbon fluids’ accumulation in petroleum reservoirs occurs due to the migration and displacement of originally water-filled potential structural and stratigraphic traps, the development of their TZ integrates petrophysical processes that combine spontaneous capillary imbibition and wettability phenomena. In the literature, wettability phenomena have been shown to also be governed by electrostatic phenomena. Therefore, given that reservoir rocks are aggregates of minerals with ionizable surface groups that facilitate the development of an electric double layer, a definite theoretical relationship between the TZ and electrostatic theory must be feasible. Accordingly, a theoretical approach to estimating the TZ thickness, using the electrostatic theory and based on the electric double layer theory, is attractive, but this is lacking in the literature. Herein, we fill the knowledge gap by using the interfacial electrostatic theory based on the fundamental tenets of the solution to the Poisson–Boltzmann mean field theory. Accordingly, we have used an existing model of capillary rise based on free energy concepts to derive a capillary rise equation that can be used to theoretically predict observations based on the TZ thickness of different reservoir rocks, using well-established formation evaluation methods. The novelty of our work stems from the ability of the model to theoretically and accurately predict the TZ thickness of the different lithostratigraphic units of hydrocarbon reservoirs, because of the experimental accessibility of its model parameters.
1. Introduction
In addition to solid minerals, such as sedimentary sources of uranium deposits [1], detrital auriferous deposits [2], and evaporate deposits [3], sediments host energy resources in the form of oil and gas deposits [4,5,6]. In these energy resources hosted geologic systems, several process occur in concert that eventually leads to the accumulation of oil or gas in hydrocarbon reservoirs that have the ability to hold and transmit fluids, thanks to the inherent porosity and permeability respectively [7]. Consequently, in light of the biogenic origin of hydrocarbon fluids [8], organic deposits in the form shale-lithostratigraphic [9,10] units underwent diagenetic transformation with progressive burial through the sedimentary column, eventually forming kerogen as the principal source of oil and gas through thermogenic cracking [11].
Following the generation of oil and gas, subsequent geologic processes that integrate migration through porous rocks result in their accumulation in potential hydrocarbon traps of varying tectonic and stratigraphic characters [12,13], where they are eventually undergo hydrodynamic trapping by low permeability shale-cap stratigraphic units overlying the deposits [14,15]. Within the hydrocarbon column, two distinct zones exist starting from the oil-water contact where a zone of 100% water saturation exists below the deposit. Thus, above the oil-water column, capillary phenomena, mediated by wettability effects cause capillary induced water spontaneous imbibition from the zone of full water saturation to into the hydrocarbon bearing zone. Such a two phase flow process involving a hydrocarbon fluid (oil or gas) cause a height dependent water saturation that decreases to a height where it equals the irreducible water saturation created by hydrocarbon migration in the reservoir [16,17,18,19]. This zone of varying water saturation is the transition zone (TZ) [20,21,22].
The TZ can be extensive, having thicknesses that can reach several hundreds of feet [23,24], depending on the pore size distribution and wettability state of the reservoir rock [25,26]. Within the TZ, the existence of oil and water phases coupled with the possibility of an extensive zone means some petroleum reservoirs can have significant portions of their hydrocarbon accumulations in it. For instance, carbon reservoirs having thick TZ have been known to hots substantial hydrocarbon deposits in the TZ [22]. Consequently, accurate determination of this the thickness of this this zone constitutes a systematic approach to determining producible hydrocarbon in place. Consequently several approaches have been used for the TZ determination involving mathematical modeling (Bera et al., 2016) [21], well logging [27] and numerical simulators [28]. However, petroleum reservoirs are sediments derived from originally existing rocks with aggregarde of minerals that have ionisable surface group when in contact with aqueous phase due to hydrolysis reactions [29]. Consequently, the formation of the lelectric double layer within hydrocarbon reservoirss is possible via dissociation reactions surface ionsable groups of minerals and the pH, zeta potential, free energy, and its thickness affects wettability [30] and capillary imbibition within the TZ.
Within the thermodynamic literature, the analytical solutions to the Poisson Boltzmann Equation (PBE) and its modified forms [31,32] provide fundamental approaches for contimuum electristatics, and permit calculation of the ion distribution, potential distribution and the free energy of the electric doble layer [33]. Also, the derivation of this equation based on Helmholtz free energy is possible [34,35] and the development of a wettability evaluation criterion based on the change in Helmholtz free energy during the spontaneous imbibition process has been demonstrated [36]. Moreover, a first-principle electrostatic based model has been developed and coupled with a multi-fluid computational fluid dynamic (CFD) model to understand the effect of electrostatics on the bulk polymer, polymer fines, and catalyst particles. The model was then successfully applied to a pilot-plant-scale polymerization fluidized-bed reactor [37]. In geologic systems, electrostatics have been coupled to electrokinetic phenomena to develop a model for understanding transport in double-porosity media [38] In the field of tribology, triboelectrification and its underlying mechanisms have been studied over several decades to provide deterministic tools which can aid prediction of their occurrences [39]. Herein, we exploit the analytical solution to the PBE and the concept of free energy of spontaneous imbibition to modify and existing theoretical model that links the thickness of the TZ of hydrocarbon reservoirs to the electrokinetic properties of reservoir rocks, and relevant petrophysical parameters of porosity, permeability and a specific wettability state defined by the contact angle at the point of zero charge of the reservoir rock surface. In addition, we discussed the validity of our model based on the experimental accessibility of model parameters. Our theoretical derivation enables the theoretical interpretation of the prediction of the TZ thickness in a manner that agrees with generalized observations based on well-established formation evaluation methods in the petroleum industry which supports its novelty.
2. Study Background: The Transition Zone in Hydrocarbon Reservoirs
The term transition zone refers to that lower part of a hydrocarbon reservoir column above the free water level (FWL) which containing water saturations above irreducible water saturation with respect to a specific rock type (See Figure 1). Combined capillary action mediated by pore structure and wettability control the development of the TZ by spontaneous imbibition from the zone of 100% water saturation.
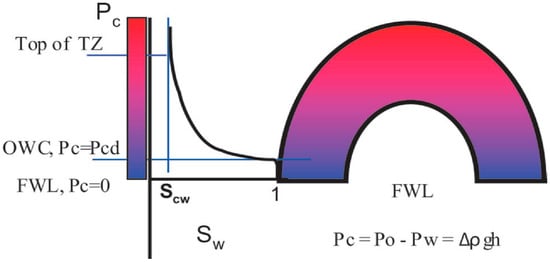
Figure 1.
Schematics of the transition zone of hydrocarbon reservoirs [40].
Capillary forces are mainly controlled by surface tension, contact angle/wettability, and pore size distribution characteristics. Consequently, spontaneous imbibition in reservoirs is mainly affected by the pore structure, wetting phenomena, fluid properties, and the boundary condition [41,42]. The TZs of oil reservoirs typically produce only water or varying proportions of oil and water [23].
Interest in the TZ stems from its hydrocarbon content, and the potential for its production. In carbonate reservoirs, significant reserves are held in the TZ of an Abu Dhabi carbonate reservoir [22]. Consequently, modeling and simulation of TZ in tight carbonate reservoirs by incorporation of improved rock typing and hysteresis models has been conducted to explore the potential for additional hydrocarbon recovery [22], using petrophysical rock typing method based on pore size distribution decoding techniques where Mercury Intrusion Capillary Pressure Data were critical. Christiansen et al. [43] has experimentally examined the variation of oil saturation with height within the TZ and the link between trapped oil with the help of water-wet glass beads and proppants, where there demonstrated the possibility for oil recover. They demonstrated a considerable possibility for oil recovery from the TZs. They also mentioned that the centrifuge method can be used to establish trapped hydrocarbon relationships and their respective relative permeabilities. Moreover, according to Christiansen et al. (2000) [43], permeability variations and hydrocarbon migration history can provide insight into the saturation distribution and hydrocarbon relative mobility in the zone. Jackson et al. [44], used a 3D pore-scale network model, in addition to conventional reservoir-scale simulation, to demonstrate variation of wettability within an oil/water TZ and its impact on production. Buiting (2011) [45] has proposed an upscaling saturation-height technique to improve TZ characterization for Arab carbonates reservoirs. The review work of Masalmeh et al. (2007) [40] contains a description of the methodology based on extensive experimental measurements and numerical simulation, for modeling both static and dynamic properties in capillary TZs. They (Masalmeh et al. (2007)) [40] also addressed how to calculate initial-oil-saturation distribution in the carbonate fields by reconciling log and core data and taking into account the effect of reservoir wettability and its impact on petrophysical interpretations. Therefore, while significant research work has been devoted to several aspects of TZ, no research work has so far been devoted to modeling the thickness with specific attention to electrostatics albeit the electrostatic phenomena related to the imminent evolution of the electric double layer in such systems control wettability via double layer repulsion [46,47,48]. In what follows, we will endeavor to fill this knowledge gap.
3. Theoretical Foundations
Model Derivation from Free Energy Concepts
The extreme state of non-wetting is characterized by maximum contact angle at the point of zero charge pH [49,50]. Therefore, equilibrium theory of capillary rise related to ionizable surfaces can be conveniently derived based on two distinct steps [51]. Accordingly, the first step uses measurement at the point of zero charge (pzc) for the parameterization of capillary force due to un-ionized groups associated with the negative of gravity forces. The second step combines this empirical force term with the forces predicted by electrical double layer and chemical reaction theory in light of the possibility of free energy quantification in terms of Helmholtz free [34,52]. The extent of electric double layer formation and the associated distribution of ions and potential depend on the degree of ionization of surface groups, which is pH dependent [53]. As the liquid imbibes spontaneously, there is interaction with ionized and unionized surface groups and the total free energy depends on this interaction. Accordingly, the total free energy of imbibition for the case of non-ionized surface groups consist of a gravitation component and an addition term related to the point of zero charge pH. Due to the pH dependent ionization degree, additional free energies accounting for electrostatic and chemical effects are required to define the total free energy of spontaneous imbibition.
Assuming a homogeneous surface with acidic groups, the site dissociation model is applicable [54]:
The dissociation constant is calculated as:
In Equations (1) and (2) is the surface ionisable acidic group, is the deprotonated surface acidic group, is the hydrogen ion, is then acidic surface group dissociation constant [M], the surface concentration of deprotonated group [Mm−2], is the hydrogen ion concentration [M], and is the surface concentration of ionisable acidic group [Mm2].
Based on a sound mathematical approach formulation based on free energy concepts, the following equation gives the equilibrium capillary rise height [55]:
In which, is the equilibrium rise as a function of pH [m], is the equilibrium rise at the point of zero charge pH, s is the characteristic dimension of the capillary in which imbibition occurs [m], is the density of fluid [kgm3], g is gravitational acceleration [ms−1] is the surface charge density on the surface of the solid in which imbibition occurs [Cm−2], is then surface potential [V], is the permittivity of space [Fm−1], is the relative permittivity [-], K is the reciprocal of the Debye length [m−1], is Boltzmann constant [JK−1], T is absolute temperature, NS is the number density of ionisable groups on the surface of the solid [m−2], α is the degree of ionization of surface ionisable groups [-], is dissociation constant for acidic group on the surface of the solid [M], and e is the electronic charge [C].
The degree of ionization is given as:
For a cylindrical surface, the solution to the PBE in cylindrical geometry [56,57] permits calculation of the surface charge density as [58]:
where:
where zi and ni,∞ are the valence number and bulk density of ion species i.
In Equation (5), K is the reciprocal of the Debye length scale ( [m−1] and R is the radius of the capillary [m]
The surface potential is the potential across the electric double layer that can be obtained by using the Nernst equation as [58]:
In Equation (6), is the valence of cation [-], is the concentration of cation [M], and is the concentration of cation at the point of zero charge pH.
However, since hydrogen and hydroxide ions are the potential determining ions, Equation (6) can be modified as [59]:
Consequently, following Amadu and Miadonye [60,61], the surface potential can be derived from Equation (7) to give the following Equation:
From Equation (4), the model of surface charge density requires knowledge of the cylindrical parallel pores that forms petroleum reservoirs [62]. Assuming mean values for porosity and permeability, the effective mean value can be calculated based on the definition of Leverette radius as [63]:
In which is the effective radius of the porous system [µm], K is the permeability [m2] and is the porosity [-].
Combining Equation (5) with Equation (9) gives the surface charge density equation as:
The equilibrium capillary rise for a given wettability state defined by a definite contact angle, pore/capillary radius and interfacial tension is calculated as [64,65]:
In Equation (11), is the equilibrium height [m], is the interfacial tension [Nm−], θ is the thermodynamic contact angle [0], ρ is the density of imbibing liquid [kgm−3], and r is the radius of the capillary radius [m].
From Equation (11), the equilibrium height corresponding to the point of zero charge gives:
For a porous system, r in Equation (12) can be substituted for its equivalent in the case of a porous medium (Equation (8)). Therefore, the second term of Equation (3) can be written based on Equation (9) as:
From Equation (8), and Equation (9) the surface charge density Equation (10) can be written as:
Summarily, Equation (3) can be written as
Equation (15) is the modified version of the original equation [3] that integrates the macroscopic parameters of the porous system (hydrocarbon reservoirs in addition to electrostatic parameters of the fluid-solid interface. Therefore, the analytical solution to the PBE, that yields analytical expressions for the surface charge density in cylindrical coordinate permits the application of auxiliary equations specified by Equation (2) through Equation (10), for the calculation of the equilibrium capillary rise in the TZ of the hydrocarbon reservoir and this task will be undertaken for model natural gas reservoir system with a transition zone.
4. Discussions
The applicability of the model equation, Equation (12) depends on the experimental accessibility of its parameters. In classical petroleum reservoir engineering, two distinct types of flow are available in the literature, namely Forces Imbibition (FI) and Spontaneous Imbibition (SI). In the former, a non-wetting phase fluid invades a porous system originally containing a wetting fluid [66] while in the latter; a wetting fluid invades a porous system originally containing a non-wetting phase fluid [67]. As a typical two-phase flow process, the spontaneous imbibition process plays a critical role in numerous practical problems such as oil production from fractured reservoirs [68,69], while the forced imbibition process plays a significant role in environmental remediation strategies related to geological carbon storage in deep saline aquifers [70,71,72]. The formation of the TZ is inherently capillary process driven [66]. Therefore, a model that meaningfully calculates the TZ thickness must contain parameters that reflect two phase flow in porous media related to SI. Accordingly, Equation (12) contains contact angle, interfacial tension and the macroscopic parameters of the porous system, namely porosity and permeability in addition to electrostatic and dielectric properties of the imbibing fluid. Therefore, its applicability will be discussed in the context of its parameters.
4.1. Experimental Accessibility of Model Parameters
Several methods exist for the determination of the point of zero charge pH. For instance, electrokinetic methods involving zeta potential measurements have been used to determine its value for sandstones and sandstone [73] (Jaafar, Nasir, & Hamid, Measurement of Isoelectric Point of Sandstone and Carbonate Rock for Monitoring Water Encroachment, 2014). Samples of rocks can also be used for point of zero charge pH determination, using the pH drift method [74]. In the field of sensors, atomic force microscopy has been used for the determination of the point of zero charge pH [75] as has titrimetric methods [76]. In cases where natural gas systems are hosted by sands with a very high percentage of silica and low clay content similar to that of Fontainebleau sandstone [77], the surface of reservoir rock can be approximated by glass, following which the approach of Amadu and Miadonye (2017) [78], based on spontaneous imbibition can be employed for the determination of the point of zero of charge pH. Surface charge density has been determined using Second Harmonic Generation [79] where signal from nanoparticles is measured as a function of added salt concentration. Experimental results are then fitted to the Gouy-Chapman model and to the numerical solution of the PBE in spherical geometry which accommodates the curvature effect. Also, the surface charge density determination on magnetic colloids has been achieved using Single Potentiometric Method (SPM) and Potentiometric-Conductometric Method (PCM) [80]. Elsewhere, the application of X-ray photoelectron microscopy for the determination of the surface charge density dispersions consisting of SiO2 colloids in 20 mM NaCl and 100 mM KCl electrolyte solutions with a pH between 9 and 2 has also been demonstrated [81]. Accordingly, the determination of surface potential based on this method is also proven [82,83] (Brown, et al., Determination of Surface Potential and Electrical Double-Layer Structure at the Aqueous Electrolyte-Nanoparticle, 2016). In petroleum reservoir engineering, characterization of reservoir rock samples based on Special Core Analysis is a routine procedure which also integrates porosity and permeability Measurement on core plugs using well established procedures in the petroleum industry [84]. Digital pH meters are available for pH measurements with excellent precision across a broad range of industries. The number density of surface ionisable groups has been determined using. The number density of surface ionisable groups, such as silanol has been quantified using deuterium exchange and pH measurement [85,86] (Schrader, et al., Surface chemical heterogeneity modulates silica surface hydration, 2018). Based on proven surface charge density measurement, the degree of ionization can be calculated, using Equation (4). Therefore, the applicability of Equation (12) for the determination of the TZ thickness in hydrocarbon reservoirs is technically feasible.
4.2. Applicability
In Equation (15), the second term on the right-hand contains rock and fluid properties, namely contact angle, porosity, permeability and interfacial tension, and it derivation relates to spontaneous imbibition flow. The TZ develops in both oil [87], and natural gas systems [21], and in a hydrologic system where it is called the vadose zone [88]. In hydrocarbon systems, hydrocarbon columns formed by oil migration into hydrocarbon traps are water wetting, and spontaneous imbibition into these zones by bottom aquifers [89] and adjacent aquifers [90] is feasible. Consequently, Equation (15) applies to all hydrocarbon reservoirs. Moreover, in both water and hydrocarbon zones, the surfaces of rock minerals with ionisable surface groups were originally covered and wetted by formation brine and the spontaneous development of the electric double was feasible. Therefor the application of an electrostatic based approach for the theoretical calculation of the TZ in this paper is scientifically meaningful, given the universal validity of the mean field continuum electrostatic theory and its application to wettability problems in geologic systems [60] and to a broad spectrum of scientific problems [91,92].
4.3. Implication of Model for Different Lithology
The thickness of the TZ depends on several properties including the hydrocarbon density, the reservoir pore sizes distribution etc., and can range from a few meters to several hundreds of meters [21,93]. Equation (15) can be arranged to give the following Equation (16):
Chalk has been known to be one of the major lithologies for North Sea petroleum reservoirs. Chalk reservoirs have on average thicker TZs compared to other reservoirs, and the free water level (FWL) in chalk reservoirs in the North Sea may be hard to establish owing to strong influence from capillary forces [94]. Also, argillaceous chalk intervals within North Sea petroleum systems are characterized by matrix permeabilities as low as 0.2 mD and therefore they are defined as tight chalks [95]. From Equation (15), hydrocarbon reservoirs with small effective pore throat radii characteristic of North Sea systems described above will have averagely thicker TZ, and such thicknesses will be controlled by pore size distribution as acknowledged [90].
5. Summary and Conclusions
The TZ is an integral part of the hydrocarbon reservoir that can contain significant proportions of oil in place, particularly for carbonate systems. In the past, production from the TZ was not a motivation for operators because of excessive produced water that increased production cost [44]. With the exponential trends in the demand for hydrocarbon fluids both for energy and for other industrial processes of economic and technological importance, optimization of production output is becoming the major concern for the petroleum industry. In the past, well logging methods have been used to determine the TZ thickness by noting resistivity variation with depth in the hydrocarbon column [24]. Recently, Abiola et al. [20] carried out a systematic analysis of the TZ, using capillary pressure data. Also, Abdulkarim et al. [93] have used high temperature susceptibility measurement to determine the thickness of the TZ. Given the intimate relationship between continuum electrostatic theory that has its foundation on the analytical solution to the PBE and the thermodynamic free energy related to spontaneous imbibition, we have modified an existing model to show how electrostatic theory can be applied for the determination of the TZ thickness. Given the lack of research work related to coupling of electrostatic phenomena in geologic systems to the TZ of hydrocarbon reservoirs, our research work fills the knowledge gap. Ocean tides have been known to affect the thickness of the TZ. In the derivation of our model, we exclude tidal effect. The following sum up the conclusion of this research work:
- Electrostatic theory based on the analytical solution to the Poisson Boltzmann equation provide a sound theoretical foundation for exploiting the spontaneous imbibition mechanism for determination of the oil-water transition zone,
- The model Equation obtained in this research work contains parameters that are experimentally accessible,
- The research work fills the knowledge gap related to the application of electrostatic theory to the thickness of the oil-water transition zone,
- Our model provides a solid foundation for the experimental determination of the transition zone thickness in an integrated manner like how the fundamental Darcy equation has laid down the foundation for permeability determination using Hassler core holder,
- Our model provides a generalized theoretical approach to predicting the transition zone thickness in line with observations using well established formation evaluation methods in the petroleum industry.
6. Future Work
Our theoretical model provokes interest in electrostatic based models of the transition zone of hydrocarbon reservoir. We intend to advance our course in our next research work. The electrostatics of geologic systems falls within surface complexation in geochemistry [95]. Ionisation of surface ionisable groups of minerals and the formation of the electric double layer constitute geochemical reactions. Moreover, geochemical reaction codes are divided into two general categories: namely, speciation-solubility codes and reaction codes [94]. Reaction codes include the capabilities to calculate aqueous speciation in addition to calculating surface concentrations of ionisable groups which permits calculation of the equilibrium constant defined by Equation (2). We intend to advance our research in the context of these well-established geochemical models, which will afford us the opportunity to numerically determine the transition zone thickness of hydrocarbon reservoirs, given the experimental accessibility of its model parameters.
Author Contributions
M.A. and A.M. conceptualized the research work; M.A. and A.M. worked together to plan different sections of the manuscript; M.A. wrote the manuscript and A.M. read through for confirmation of the text’s suitability. All authors have read and agreed to the published version of the manuscript.
Funding
This research work did not receive direct funding apart from that of Adango Miadonye’s payments for research materials that were subscribed to.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Acknowledgments
We wish to acknowledge the support of the Research Office and Faculty of Graduate Studies of Cape Breton University for encouraging research among their faculty members and postdoctoral fellows.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Rose, A.W.; Wright, R.J. Geochemical exploration models for sedimentary uranium deposits. J. Geochem. Explor. 1980, 13, 153–179. [Google Scholar] [CrossRef]
- Yeend, W.; Shawe, D.R. Gold in Placer Deposits; Department of the Interior, U.S. Geological Survey Bulletin 1857-G: Dallas, TX, USA, 1989. [Google Scholar]
- Moore, G.W. Origin and Chemical Composition of Evaporite Deposits; United States Geological Survey: Washington, DC, USA, 1960. [Google Scholar]
- Civan, F. Chapter 2—Description and characterization of oil and gas reservoirs for formation damage potential. In Reservoir Formation Damage (Fourth Edition): Fundamentals, Modeling, Assessment, and Mitigation; GPP: Valbonne, France, 2023; pp. 15–36. [Google Scholar]
- Aminzadeh, F.; Dasgupta, S.N. Chapter 2—Fundamentals of Petroleum Geology. In Developments in Petroleum Science: Chapter 2—Fundamentals of Petroleum Geology; Elsevier: Amsterdam, The Netherlands, 2013; Volume 60, pp. 15–36. [Google Scholar]
- Ziemelis, K. Hydrocarbon reservoirs. Nat. Insight 2003, 426, 317. [Google Scholar] [CrossRef]
- Lim, J.-S.; Kim, J. Reservoir Porosity and Permeability Estimation from Well Logs Using Fuzzy Logic and Neural Networks. In Proceedings of the SPE Asia Pacific Oil and Gas Conference and Exhibition, Perth, Australia, 18–20 October 2004; SPE: Perth, Australia, 2004; pp. 1–9. [Google Scholar]
- Volkova, I.; Gura, D.; Aksenov, I. Abiogenic and Biogenic Petroleum Origin: A Common Theory for Geological Surveys. Asian J. Water Environ. Pollut. 2021, 18, 59–65. [Google Scholar] [CrossRef]
- Alafnan, S. Petrophysics of Kerogens Based on Realistic Structures. ACS Omega 2021, 6, 9549–9558. [Google Scholar] [CrossRef]
- Alafnan, S.; Alafnan, S.; Solling, T.; Alafnan, S.; Solling, T.; Mahmoud, M. Effect of Kerogen Thermal Maturity on Methane Adsorption Capacity: A Molecular Modeling Approach. Molecules 2020, 25, 3764. [Google Scholar] [CrossRef]
- Mahlstedt, N. Thermogenic Formation of Hydrocarbons in Sedimentary Basins. In Hydrocarbons, Oils and Lipids: Diversity, Origin, Chemistry and Fate; Springer: Berlin/Heidelberg, Germany, 2018; pp. 1–30. [Google Scholar]
- Biddle, K.T.; Wielchowsky, C.C. Hydrocarbon Traps: The Petroleum System—From Source to Trap; American Association of Petroleum Geologists: Tulsa, OK, USA, 1994; Volume 60. [Google Scholar]
- Biddle, K.T.; Wielchowsky, C.C. Hydrocarbon Trap: Chapter 13: Part III. Proocesse. AAPG Special Volume. 1994; pp. 219–235. Available online: https://archives.datapages.com/data/specpubs/methodo2/data/a077/a077/0001/0200/0219.htm (accessed on 2 February 2024).
- Wendebourg, J.; Biteau, J.-J.; Grosjean, Y. Hydrodynamics and hydrocarbon trapping: Concepts, pitfalls and insights from case studies. Mar. Pet. Geol. 2018, 96, 190–201. [Google Scholar] [CrossRef]
- Thara, Y.Y. Development of a Physical Hydrodynamic Hydrocarbon-Trap Model. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 24–26 September 2018; SPE: Dallas, TX, USA, 2018; pp. 1–10. [Google Scholar]
- Su, Y.-L.; Fu, J.-G.; Li, L.; Wang, W.-D.; Zafar, A.; Zhang, M.; Ouyang, W.-P. A new model for predicting irreducible water saturation in tight gas reservoirs. Pet. Sci. 2020, 17, 1087–1100. [Google Scholar] [CrossRef]
- Wheaton, R. Chapter 2—Basic Rock and Fluid Properties. In Fundamentals of Applied Reservoir Engineering: Appraisal; GPP: Sophia-Antipolis, France, 2016. [Google Scholar]
- Baker, R.O.; Yarranton, H.W.; Jensen, J.L. 8—Special Core Analysis—Rock–Fluid Interactions. In Practical Reservoir Engineering and Characterization; Elsevier: Amsterdam, The Netherlands, 2015; pp. 239–295. [Google Scholar]
- Widarsono, B. Irreducible water saturation and its governing factors: Characteristics of some sandstones in western indonesia. Limitgas Sci. Publ. 2011, 34, 19–34. [Google Scholar] [CrossRef]
- Abiola, O.; Obasuyi, F.O. Transition zones analysis using empirical capillary pressure model from well logs and 3D seismic data on ‘Stephs’ field, onshore, Niger Delta, Nigeria. J. Pet. Explor. Prod. Technol. 2020, 10, 1227–1242. [Google Scholar] [CrossRef]
- Bera, A.; Belhaj, H. A comprehensive review on characterization and modeling of thick capillary transition zones in carbonate reservoirs. J. Unconv. Oil Gas Resour. 2016, 16, 76–89. [Google Scholar] [CrossRef]
- Fu, D.; Belhaj, H.; Bera, A. Modeling and simulation of transition zones in tight carbonate reservoirs by incorporation of improved rock typing and hysteresis models. J. Pet. Explor. Prod. Technol. 2018, 8, 1051–1068. [Google Scholar] [CrossRef]
- Kirkham, A.; Juma, M.B. Fluid Saturation Predictions in a “Transition Zone” Carbonate Reservoir, Abu Dhabi. GeoArabia 1996, 1, 551–556. [Google Scholar] [CrossRef]
- Akba, M.N.; Permadi, P. Estimation of Fluid-Fluid Contact and the Transition Zone: A Case Study of Low Contrast Resistivity Zone. In Proceedings of the International Petroleum Technology Conference, Bangkok, Thailand, 14–16 November 2016. [Google Scholar]
- Shen, R.; Zhang, X.; Ke, Y.; Xiong, W.; Guo, H.; Liu, G.; Zhou, H.; Yang, H. An integrated pore size distribution measurement method of small angle neutron scattering and mercury intrusion capillary pressure. Sci. Rep. 2021, 11, 17458. [Google Scholar] [CrossRef] [PubMed]
- Knight, R.J. Effects of pore structure and wettability on the electrical resistivity of partially saturated rocks—A network study. Geophysics 1997, 62, 1045–1346. [Google Scholar]
- Guo, J.; Ling, Z.; Xu, X.; Zhao, Y.; Yang, C.; Wei, B.; Zhang, Z.; Zhang, C.; Tang, X.; Chen, T.; et al. Saturation Determination and Fluid Identification in Carbonate Rocks Based on Well Logging Data: A Middle Eastern Case Study. Processe 2023, 11, 1282. [Google Scholar] [CrossRef]
- Fanchi, J.; Christiansen, R.; Heymans, M. Estimating Oil Reserves of Fields with Oil/Water Transition Zones. SPE Res. Eval. Eng. 2002, 5, 311–316. [Google Scholar] [CrossRef]
- Rahman, I.A.; Padavettan, V. Synthesis of Silica Nanoparticles by Sol-Gel: Size-Dependent Properties, Surface Modification, and Applications in Silica-Polymer Nanocomposites—A Review. J. Nanomater. 2012, 2012, 132424. [Google Scholar] [CrossRef]
- Ikpeka, P.M.; Ugwu, J.O.; Pillai, G.G.; Russell, P. Efectiveness of electrokinetic enhanced oil recovery (EK EOR): A systematic review. J. Eng. Appl. Sci. 2022, 69, 60. [Google Scholar] [CrossRef]
- Ringe, S.; Oberhofer, H.; Hille, C.; Matera, S.; Reuter, K. Function-Space-Based Solution Scheme for the Size-Modified Poisson–Boltzmann Equation in Full-Potential DFT. Chem. Theory Comput. 2016, 12, 4052–4066. [Google Scholar] [CrossRef]
- Borukhov, I.; Andelman, D.; Orland, H. Steric Effects in Electrolytes: A Modified Poisson-Boltzmann Equation. Phys. Rev. Lett. 1997, 79, 435–438. [Google Scholar] [CrossRef]
- Bossa, G.V.; May, S. Debye-Hückel Free Energy of an Electric Double Layer with Discrete Charges Located at a Dielectric Interface. Membranes 2021, 11, 129. [Google Scholar] [CrossRef]
- Kleijn, W.; Bruner, L. Derivation of the Poisson—Boltzmann equation by minimization of the helmholtz free energy using a variational principle. J. Colloid Interface Sci. 1983, 96, 20–27. [Google Scholar] [CrossRef]
- Bohinc, K.; Shrestha, A.; May, S. The Poisson-Helmholtz-Boltzmann model. Eur. Phys. J. E Soft Matter 2011, 34, 108. [Google Scholar] [CrossRef]
- Alinejad, A.; Dehghanpour, H. Evaluating porous media wettability from changes in Helmholtz free energy using spontaneous imbibition profiles. Adv. Water Resour. 2021, 157, 104038. [Google Scholar] [CrossRef]
- Rokkam, R.G.; Fox, R.O.; Muhle, M.E. Computational fluid dynamics and electrostatic modeling of polymerization fluidized-bed reactors. Powder Technol. 2010, 203, 109–124. [Google Scholar] [CrossRef]
- López-Vizcaíno, R.; Cabrera, V.; Sprocati, R.; Muniruzzaman, M.; Rolle, M.; Navarro, V.; Yustres, Á. A modeling approach for electrokinetic transport in double-porosity media. Electrochim. Acta 2022, 431, 141139. [Google Scholar] [CrossRef]
- Chowdhury, F.; Ray, M.; Sowinski, A.; Mehrani, P.; Passalacqua, A. A review on modeling approaches for the electrostatic charging of particles. Powder Technol. 2021, 2021, 104–118. [Google Scholar] [CrossRef]
- Masalmeh, S.K.; Shiekah, I.A.; Jing, X.D. Improved Characterization and Modeling of Capillary Transition Zones in Carbonate Reservoirs. SPE Res. Eval. Eng. 2007, 10, 191–204. [Google Scholar] [CrossRef]
- Schmid, K.; Alyafei, N.; Geiger, S.; Blunt, M. Analytical solutions for spontaneous imbibition: Fractional-flow theory and experimental analysis. SPE J. 2016, 21, 2308–2316. [Google Scholar] [CrossRef]
- Meng, Q.; Liu, H.; Wang, J. A critical review on fundamental mechanisms of spontaneous imbibition and the impact of boundary condition, fluid viscosity and wettability. Adv. Geo-Energy Res. 2017, 1, 1–17. [Google Scholar] [CrossRef]
- Jackson, M.D.; Valvatne, P.H.; Blunt, M.J. Prediction of Wettability Variation within an Oil/Water Transition Zone and Its Impact on Production. SPE J. 2005, 10, 185–195. [Google Scholar] [CrossRef]
- Buiting, J. Upscaling Saturation-Height Technology for Arab Carbonates for Improved Transition-Zone Characterization. SPE Res. Eval. Eng. 2011, 14, 11–24. [Google Scholar] [CrossRef]
- Buckley, J.S.; Takamura, K.; Morrow, N.R. Influence of Electrical Surface Charges on the Wetting Properties of Crude Oils. SPE Res. Eng. 1989, 4, 332–340. [Google Scholar] [CrossRef]
- Nasralla, R.A.; Nasr-El-Din, H.A. Double-Layer Expansion: Is It a Primary Mechanism of Improved Oil Recovery by Low-Salinity Waterflooding? SPE Res. Eval. Eng. 2014, 17, 49–59. [Google Scholar] [CrossRef]
- Anthony Quinn, R.S. Influence of the Electrical Double Layer in Electrowetting. Phys. Chem. B 2003, 107, 1163–1169. [Google Scholar] [CrossRef]
- Horiuchi, H.; Nikolov, A.; Wasan, D. Calculation of the surface potential and surface charge density by measurement of the three-phase contact angle. J. Colloid Interface Sci. 2012, 385, 218–224. [Google Scholar] [CrossRef]
- Ismail, M.F.; Islam, M.A.; Khorshidi, B.; Sadrzadeh, M. Prediction of surface charge properties on the basis of contact angle titration models. Mater. Chem. Phys. 2021, 258, 123933. [Google Scholar] [CrossRef]
- Chatelier, R.C.; Hodges, A.M.; Drummond, C.J.; Chan, D.Y.; Griesser, H.J. Determination of the Intrinsic Acid-Base DissociationConstant and Site Density of Ionizable Surface Groups by Capillary Rise Measurements. Langmuir 1997, 13, 3043–3046. [Google Scholar] [CrossRef]
- Zhu, X.; Tang, F.; Suzuki, T.S.; Sakka, Y. Role of the Initial Degree of Ionization of Polyethylenimine in the Dispersion of Silicon Carbide Nanoparticles. J. Am. Ceram. Soc. 2003, 86, 189–191. [Google Scholar] [CrossRef]
- Onizhuk, M.O.; Panteleimonov, A.V.; Kholin, Y.V.; Ivanov, V.V. Dissociation constants of silanol groups of silic acids: Quantum chemical estimations. J. Struct. Chem. 2018, 59, 261–271. [Google Scholar] [CrossRef]
- Rice, C.L.; Whitehead, R. Electrokinetic Flow in a Narrow Cylindrical Capillary. J. Phys. Chem. Am. Chem. 1965, 69, 4017–4024. [Google Scholar] [CrossRef]
- Keh, H.J.; Tseng, H.C. Transient Electrokinetic Flow in Fine Capillaries. J. Colloid Interface Sci. 2001, 242, 450–459. [Google Scholar] [CrossRef]
- Kesler, V.; Murmann, B.; Soh, H.T. Going beyond the Debye Length: Overcoming Charge Screening Limitations in Next-Generation Bioelectronic Sensors. ACS Nano 2020, 14, 16194–16201. [Google Scholar] [CrossRef]
- Kim, D.-S. Mesurement of point of zero charge of bentonite by solubilization technique and its dependence of surface potential on pH. Environ. Eng. Res. 2003, 4, 222–227. [Google Scholar] [CrossRef]
- Amadu, M.; Miadonye, A. Applicability of the linearized Poisson–Boltzmann theory to contact angle problems and application to the carbon dioxide–brine–solid systems. Sci. Rep. 2022, 12, 5710. [Google Scholar] [CrossRef]
- Bowden, J.; Posner, A.; Quirk, J. Ionic adsorption on variable charge mineral surfaces. Teoretical-charge development and, titration curves. Aust. J. Soil. Res. 1997, 15, 21–136. [Google Scholar]
- Luo, H.; Jougnot, D.; Jost, A.; Teng, J.; Thanh, L.D. A Capillary Bundle Model for the Electrical Conductivity of Saturated Frozen Porous Media. J. Geophys. Res. Sokid Earth 2023, 128, e2022JB025254. [Google Scholar] [CrossRef]
- Garrouch, A.A. A Modified Leverett J-Function for the Dune and Yates Carbonate Fields: A Case Study Carbonate Fields. Energy Fuels 1999, 13, 1021–1029. [Google Scholar] [CrossRef]
- Wijnhorst, R.; de Goede, T.; Bonn, D.; Shchidzadeh, N. Surfactant effects on the dynamics of capillary rise and finger formation in square capillaries. Langmuir 2020, 36, 13784–13792. [Google Scholar] [CrossRef]
- Extrand, C.; Moon, S. Experimental measurement of forces and energies associated with capillary rise in a vertical tube. J. Colloid. Interface Sci. 2013, 407, 488–492. [Google Scholar] [CrossRef]
- Andersen, P.Ø.; Salomonsen, L.; Sleveland, D.S. Characteristic Forced and Spontaneous Imbibition Behavior in Strongly Water-Wet Sandstones Based on Experiments and Simulation. Energies 2022, 15, 3531. [Google Scholar] [CrossRef]
- Qin, C.-Z.; Wang, X.; Hefny, M.; Zhao, J.; Chen, S.; Guo, B. Wetting Dynamics of Spontaneous Imbibition in Porous Media: From Pore Scale to Darcy Scale. Geophys. Res. Lett. 2022, 49, e2021GL097269. [Google Scholar] [CrossRef]
- Mattax, C.C.; Kyte, J.R. Imbibition oil recovery from fractured, water-drive reservoir. Soc. Pet. Eng. J. 1962, 2, 177–184. [Google Scholar] [CrossRef]
- Mason, G.; Morrow, N.R. Developments in spontaneous imbibition and possibilities for future work. J. Pet. Sci. Eng. 2013, 110, 268–293. [Google Scholar] [CrossRef]
- Fawad, M.; Mondol, N.H. Monitoring geological storage of CO2: A new approach. Sci. Rep. 2022, 11, 5942. [Google Scholar] [CrossRef]
- Zhang, Y.; Jackson, C.; Krevor, S. An Estimate of the Amount of Geological CO2 Storage over the Period of 1996–2020. Environ. Sci. Technol. Lett. 2022, 9, 693–698. [Google Scholar] [CrossRef]
- Diao, Y.; Zhu, G.; Cao, H.; Zhang, C.; Li, X.; Jin, X. Mesoscale Assessment of CO2 Storage Potential and Geological Suitability for Target Area Selection in the Sichuan Basin. Geofluids 2017, 2017, 9587872. [Google Scholar] [CrossRef]
- Jaafar, M.; Nasir, A.M.; Hamid, M. Measurement of Isoelectric Point of Sandstone and Carbonate Rock for Monitoring Water Encroachment. J. Appl. Sci. 2014, 14, 3349–3353. [Google Scholar] [CrossRef][Green Version]
- Dang, Y.T.; Dang, M.-H.D.; Mai, N.X.; Nguyen, L.H. Room temperature synthesis of biocompatible nano Zn-MOF for the rapid and selective adsorption of curcumin. J. Sci. Adv. Mater. Devices 2020, 5, 560–565. [Google Scholar] [CrossRef]
- Raiteri, R.; Margesin, B.; Grattarola, M. An atomic force microscope estimation of the point of zero charge of silicon insulators. Sens. Actuators B Chem. 1998, 46, 126–132. [Google Scholar] [CrossRef]
- Zuyi, T.; Taiwei, C. Points of Zero Charge and Potentiometric Titrations. Adsorpt. Sci. Technol. 2003, 21, 607–616. [Google Scholar] [CrossRef]
- Revil, A.; Kessouri, P.; Torres-Verdín, C. Electrical conductivity, induced polarization, and permeability of the Fontainebleau sandstone. Geophysics 2014, 79, 303–318. [Google Scholar] [CrossRef]
- Amadu, M.; Miadonye, A. Determination of the Point of Zero Charge pH of Borosilicate Glass Surface Using Capillary Imbibition Metho. Int. J. Chem. 2017, 9, 67–84. [Google Scholar] [CrossRef]
- Kumal, R.R.; Karam, T.E.; Haber, L.H. Determination of the Surface Charge Density of Colloidal Gold Nanoparticles Using Second Harmonic Generation. J. Phys. Chem. C 2015, 119, 16200–16207. [Google Scholar] [CrossRef]
- Camposa, A.F.; Medeirosa, W.C.; Aquinoa, R.; Depeyrotb, J. Surface Charge Density Determination in Water Based Magnetic Colloids: A Comparative Study. Mater. Res. 2017, 20, 1729–1734. [Google Scholar] [CrossRef]
- Cardenas, J.F. Surface charge of silica determined using X-ray photoelectron spectroscopy. Colloids Surf. A Physicochem. Eng. Asp. 2005, 252, 213–219. [Google Scholar] [CrossRef]
- Brown, M.A.; Abbas, Z.; Kleibert, A.; Green, R.G.; Goel, A.; May, S.; Squires, T.M. Determination of Surface Potential and Electrical Double-Layer Structure at the Aqueous Electrolyte-Nanoparticle. Phys. Rev. 2016, 6, 011007–011012. [Google Scholar] [CrossRef]
- Brown, M.A.; Jordan, I.; Redondo, A.B.; Kleibert, A.; Wörner, H.J.; van Bokhoven, J.A. In Situ Photoelectron Spectroscopy at the Liquid/Nanoparticle Interface. Surf. Sci. 2013, 610, 1–6. [Google Scholar] [CrossRef]
- SCAL. Special Core Analysis. 2021. Available online: http://www.scalinc.com/specialcoreanalysis.html (accessed on 10 October 2023).
- Schrader, A.M.; Monroe, J.I.; Sheil, R.; Dobbs, H.A.; Keller, T.J.; Li, Y.; Jain, S.; Shell, M.S.; Israelachvili, J.N.; Han, S. Surface chemical heterogeneity modulates silica surface hydration. Proc. Natl. Acad. Sci. USA 2018, 115, 2890–2895. [Google Scholar] [CrossRef]
- Zhuravlev, L. Catalysis in Institutes of Higher Education; Balandin, A.A., Kobozev, N.I., Eds.; Part II; Moscow State University Press: Moscow, Russia, 1962; Volume 1, p. 52. [Google Scholar]
- Spearing, M.C.; Abdou, M.; Azagbaesuweli, G.; Kalam, M.Z. Transition Zone Behaviour: The Measurement of Bounding and Scanning Relative Permeability and Capillary Pressure Curves at Reservoir Conditions for a Giant Carbonate Reservoir. In Proceedings of the Abu Dhabi International Petroleum Exhibition and Conference, Abu Dhabi, United Arab Emirates, 10–13 November 2014; SPE: Abu Dhabi, United Arab Emirates, 2014. [Google Scholar]
- Man, J.; Wang, G.; Chen, Q.; Yao, Y. Investigating the role of vadose zone breathing in vapor intrusion from contaminated groundwater. J. Hazard. Mater. 2021, 416, 126272. [Google Scholar] [CrossRef]
- Pinilla, A.; Asuaje, M.; Pantoja, C.; Ramirez, L.; Gomez, J.; Ratkovich, N. CFD study of the water production in mature heavy oil fields with horizontal wells. PLoS ONE 2021, 16, e0258870. [Google Scholar] [CrossRef] [PubMed]
- Gillespie, J.M.; Stephens, M.J.; Chang, W.; Warden, J.G. Mapping aquifer salinity gradients and effects of oil field produced water disposal using geophysical logs: Elk Hills, Buena Vista and Coles Levee Oil Fields, San Joaquin Valley, California. PLoS ONE 2022, 17, e0263477. [Google Scholar] [CrossRef] [PubMed]
- Grünberg, M.D.; von Grünberg, H.-H. Osmotic pressure of charged colloidal suspensions: A unified approach to linearized Poisson-Boltzmann theory. Phys. Rev. E 2002, 66, 011401. [Google Scholar]
- Hallez, Y.; Diatta, J.; Meireles, M. Quantitative Assessment of the Accuracy of the Poisson-Boltzmann Cell Model for Salty Suspensions. Langmuir 2014, 30, 6721–6729. [Google Scholar] [CrossRef] [PubMed]
- Abdulkarim, M.A.; Muxworthy, A.R.; Fraser, A. High temperature susceptibility measurements: A potential tool for the identification of oil-water transition zone in petroleum reservoirs. Front. Erath Sci. 2022, 10, 973385. [Google Scholar] [CrossRef]
- Larsen, J.K.; Fabricius, I.L. Interpretation of Water Saturation above the Transitional Zone in Chalk Reservoirs. SPE Res. Eval. Eng. 2004, 2, 155–163. [Google Scholar] [CrossRef]
- Faÿ-Gomord, O.; Verbiest, M.; Lasseur, E.; Caline, B.; Allanic, C.; Descamps, F.; Vandycke, S.; Swennen, R. Geological and mechanical study of argillaceous North Sea chalk: Implications for the characterisation of fractured reservoirs. Mar. Pet. Geol. 2018, 92, 962–978. [Google Scholar] [CrossRef]
- Iglauer, S.; Muggeridge, A. The Impact of Tides on the Capillary Transition Zone. Transp. Porous Media 2013, 97, 87–103. [Google Scholar] [CrossRef][Green Version]
- Serne, R.J.; Arthur, R.C.; Krupka, K.M. Review of Geochemical Processes and Codes for Assessment of Radionuclide Migration Potential at Commercial LLW Sites; Pacific Northwest Laboratory: College Park, MA, USA, 1990. [Google Scholar]
- Davis, J.A.; Kent, D. Surface Complexation Modeling in Aqueous Geochemistry. Rev. Mineral. Geochem. 1990, 23, 177–244. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).