The Role of the Volatility in the Option Market
Abstract
:1. Introduction
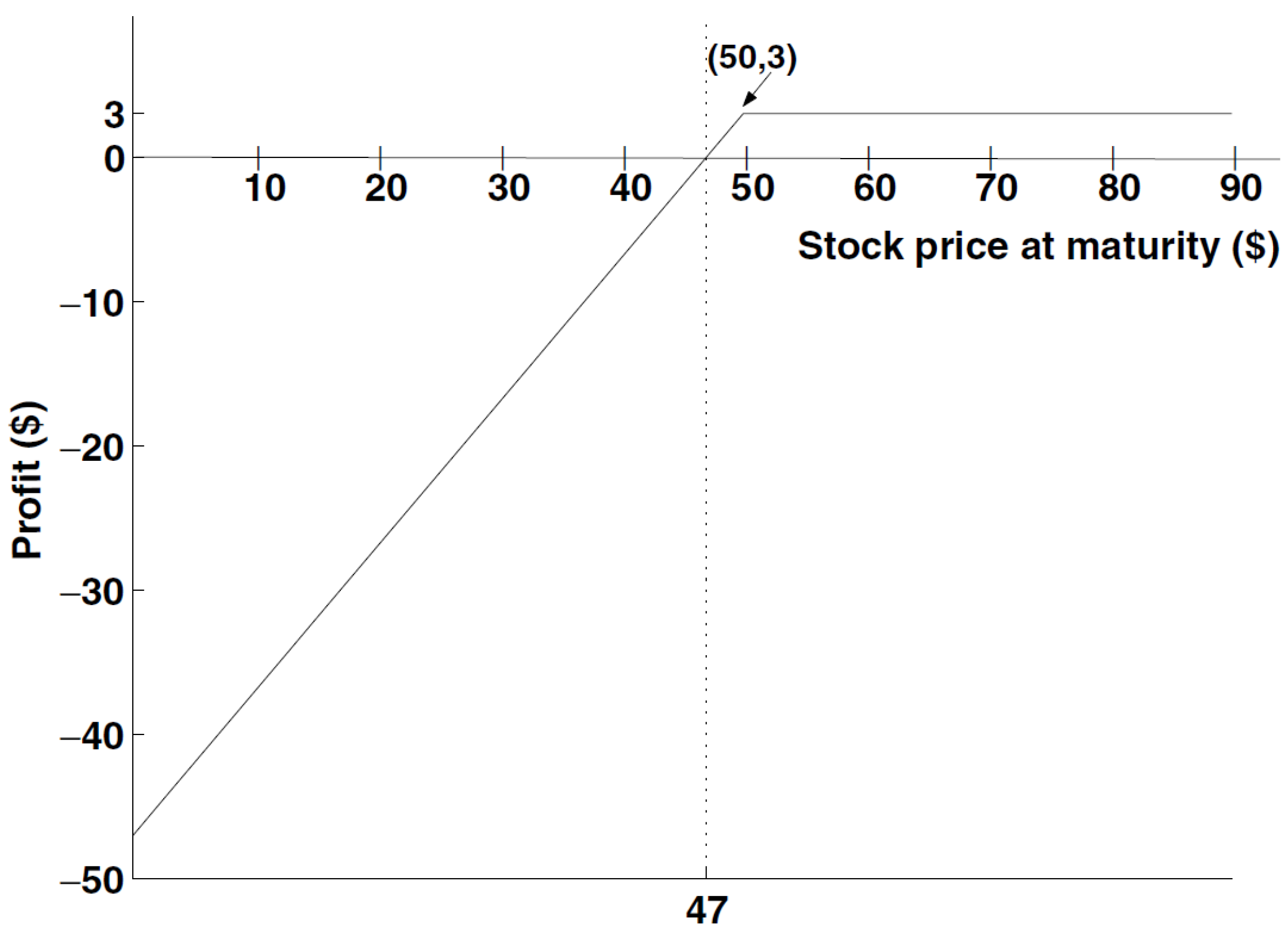
2. The Option Market
3. The Black–Scholes Equation
3.1. Black–Scholes Hamiltonian Formulation
3.2. The Evolution of Probability in the Black–Scholes Equation
3.3. Black–Scholes Pricing Kernel
3.4. The Influence of the Non-Conservation of the Probability in the Prices of the Stocks under the Black–Scholes Formulation
4. The Merton–Garman Equation
4.1. Derivation of the Merton–Garman Equation
4.2. Hamiltonian Form of the Merton–Garman Equation
4.3. The Merton–Garman Kernel
4.4. The Flow of Probability in the MG Case
5. Spontaneous Symmetry Breaking from the Black–Scholes Hamiltonian
5.1. The Martingale Condition as a Vacuum State
5.2. Broken Symmetries in the Financial Equations
5.3. Spontaneous Symmetry Breaking: Symmetries under Changes of Prices
6. Local Equivalence between the Black–Scholes and the Merton–Garman Equation
The Merton–Garman Equation Emerging from the Black–Scholes Equation
7. The Higgs Mechanism in Quantum Finance: The Dynamical Origin of the Volatility
The Dynamical Origin of the Volatility
8. Solutions for the Black-Scholes Equation
Implied Volatility and Making Decisions Based on the Volatility Estimation
9. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sundaresan, S. Fixed Income Markets and Their Derivatives; South-Western College Publishing: Cincinnati, OH, USA, 1997. [Google Scholar]
- de Weert, F. An Introduction to Options Trading; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2006; ISBN-13 978-0-470-02970-1 (PB)/ISBN-10 0-470-02970-6 (PB). [Google Scholar]
- Black, F.; Scholes, M. The Pricing of Options and Corporate Liabilities. J. Political Econ. 1973, 81, 637. [Google Scholar] [CrossRef]
- Baaquie, B.E. Quantum Finance: Path Integrals and Hamiltonians for Options and Interestrates; Cambridge University Press: Cambridge, UK, 2004; pp. 52–75. [Google Scholar]
- Yavuz, M. European option pricing models described by fractional operators with classical and generalized Mittag-Leffler kernels. Numer. Methods Partial. Differ. Equ. 2022, 38, 434–456. [Google Scholar]
- Yavuz, M.; Özdemir, N. European vanilla option pricing model of fractional order without singular kernel. Fractal Fract. 2018, 2, 3. [Google Scholar] [CrossRef]
- Chesney, M.; Scott, L. Pricing European currency options: A comparison of the modified Black-Scholes model and a random variance model. J. Financ. Quant. Anal. 1989, 24, 267–284. [Google Scholar] [CrossRef]
- Griffiths, D.J. Introduction to Quantum Mechanics; Prentice Hall: Saddle River, NJ, USA, 1995. [Google Scholar]
- Arraut, I.; Au, A.; Ching-biu Tse, A. Spontaneous symmetry breaking in quantum finance. EPL 2020, 131, 68003. [Google Scholar] [CrossRef]
- Arraut, I.; Lobo Marques, J.A.; Gomes, S. The probability flow in the Stock market and Spontaneous symmetry breaking in Quantum Finance. Math. EPL 2021, 9, 2777. [Google Scholar] [CrossRef]
- Arraut, I. Gauge symmetries and the Higgs mechanism in Quantum Finance. arXiv 2023, arXiv:2306.03237. [Google Scholar] [CrossRef]
- Merton, R.C. The theory of rational Option Pricing. Bell J. Econ. Manag. Sci. 1973, 4, 141–183. [Google Scholar] [CrossRef]
- Merton, R.C. Option pricing when underlying stock returns are discontinous. J. Financ. Econ. 1976, 3, 125. [Google Scholar] [CrossRef]
- Linetsky, V. The Path Integral Approach to Financial Modeling and Options Pricing. Comput. Econ. 1998, 11, 129. [Google Scholar] [CrossRef]
- Baaquie, B.E.; Coriano, C.; Srikant, M. Hamiltonian and Potentials in Derivative Pricing Models: Exact Results and Lattice Simulations. Phys. A 2004, 334, 531–557. Available online: http://xxx.lanl.gov/cond-mat/0211489 (accessed on 4 December 2003). [CrossRef]
- Baaquie, B.E. A Path Integral Approach to Option Pricing with Stochastic Volatility: Some Exact Results. J. Phys. I 1997, 7, 1733. [Google Scholar] [CrossRef]
- Arraut, I.; Au, A.; Ching-Biu Tse, A.; Lobo Marques, J.A. On the probability flow in the Stock market I: The Black-Scholes case. arXiv 2001, arXiv:2001.00516. [Google Scholar]
- Alexandre, J.; Ellis, J.; Millington, P.; Seynaeve, D. Gauge invariance and the Englert-Brout-Higgs mechanism in non-Hermitian field theories. Phys. Rev. D 2019, 99, 075024. [Google Scholar] [CrossRef]
- Alexandre, J.; Ellis, J.; Millington, P.; Seynaeve, D. Spontaneous symmetry breaking and the Goldstone theorem in non-Hermitian field theories. Phys. Rev. D 2018, 98, 045001. [Google Scholar] [CrossRef]
- Alexandre, J.; Millington, P.; Seynaeve, D. Symmetries and conservation laws in non-Hermitian field theories. Phys. Rev. D 2017, 96, 065027. [Google Scholar] [CrossRef]
- Eleuch, H.; Rotter, I. Nearby states in non-Hermitian quantum systems. Eur. Phys. J. D 2015, 69, 229–230. [Google Scholar] [CrossRef]
- Krejcirik, D.; Siegl, P.; Tater, M.; Viola, J. Pseudospectra in non-Hermitian quantum mechanics. J. Math. Phys. 2015, 56, 103513. [Google Scholar] [CrossRef]
- Alexandre, J.; Millington, P.; Seynaeve, D. Consistent description of field theories with non-Hermitian mass terms. J. Phys. Conf. Ser. 2018, 952, 012012. [Google Scholar] [CrossRef]
- Bender, C.M. Making Sense of Non-Hermitian Hamiltonians. Rept. Prog. Phys. 2007, 70, 947. [Google Scholar] [CrossRef]
- Yahoo Finance Can Be Found in the Link. Available online: https://finance.yahoo.com/ (accessed on 20 September 2023).
- Hull, J.C. Options, Futures and Other Derivatives, 5th ed.; Prentice-Hall International: Saddle River, NJ, USA, 2003. [Google Scholar]
- Jones, E.P. Option arbitrage and strategy with large price changes. J. Financ. Econ. 1984, 13, 91. [Google Scholar] [CrossRef]
- Arraut, I.; Au, A.; Ching-Biu Tse, A.; Segovia, C. The connection between multiple prices of an Option at a given time with single prices defined at different times: The concept of weak-value in quantum finance. Phys. A 2019, 526, 121028. [Google Scholar] [CrossRef]
- Tobin, J.; Golub, S.S. Money, Credit and Capital; McGraw-Hill/Irwin: Irvine, CA, USA, 1998; 17p. [Google Scholar]
- Heston, S.L. A Closed-Form Solution for Options with Stochastic Volatility with Application to Bond and Currency Options. Rev. Financ. Stud. 1993, 6, 327. [Google Scholar] [CrossRef]
- Hull, J.C.; White, A. An Analysis of the Bias in Option Pricing Caused by a Stochastic Volatility. Adv. Futur. Options Res. 1988, 3, 27. [Google Scholar]
- Hull, J.C.; White, A. The Pricing of Options on Assets with Stochastic Volatilities. J. Financ. 1987, 42, 281. [Google Scholar] [CrossRef]
- Johnson, H.; Shanno, D. Option Pricing when the Variance is Changing. J. Financ. Quant. Anal. 1987, 22, 143. [Google Scholar] [CrossRef]
- Mervill, L.H.; Pieptea, D.R. Stock Price Volatility: Mean-Reverting Diffusion and Noise. J. Financ. Econ. 1989, 24, 193. [Google Scholar] [CrossRef]
- Poterba, J.M.; Summers, L.H. The Persistence of Volatility and Stock Market Fluctuations. Am. Econ. Rev. 1986, 76, 1142. [Google Scholar]
- Scott, L.O. Option Pricing When the Variance Changes Randomly: Theory, Estimation and an Application. J. Financ. Quant. Anal. 1987, 22, 419. [Google Scholar] [CrossRef]
- Lamoureux, C.G.; Lastrapes, W.D. Forecasting Stock-Return Variance: Toward an Understanding of Stochastic Implied Volatilities. Rev. Financ. Stud. 1993, 6, 293. [Google Scholar] [CrossRef]
- Marakani, S. Option Pricing with Stochastic Volatility. Honours Thesis, National University of Singapore, Singapore, 1998. [Google Scholar]
- Goldstone, J.; Salam, A.; Weinberg, S. Broken Symmetries. Phys. Rev. 1962, 127, 965. [Google Scholar] [CrossRef]
- Ising, E. Beitrag zur Theorie des Ferromagnetismus. Z. Phys. 1925, 31, 253–258. [Google Scholar] [CrossRef]
- Peskin, M.E.; Schroeder, D.V. An Introduction to Quantum Field Theory; CRC Press; Taylor and Francis Group: Boca Raton, FL, USA, 2018; pp. 347–351. [Google Scholar]
- Bludman, S.A.; Klein, A. Broken Symmetries and Massless Particles. Phys. Rev. 1963, 131, 2364. [Google Scholar] [CrossRef]
- Goldstone, J. Field Theories with Superconductor Solutions. Nuovo Cim. 1961, 9, 154. [Google Scholar] [CrossRef]
- Nambu, Y.; Jona-Lasinio, G. Dynamical Model of Elementary Particles Based on an Analogy with Superconductivity. Phys. Rev. 1961, 122, 345. [Google Scholar] [CrossRef]
- Yang, C.N. The spontaneous magnetization of a two-dimensional Ising model. Phys. Rev. Ser. II 1952, 85, 808–816. [Google Scholar] [CrossRef]
- Onsager, L. Crystal statistics. I. A two-dimensional model with an order-disorder transition. Phys. Rev. Ser. II 1944, 65, 117–149. [Google Scholar] [CrossRef]
- Montroll, E.W.; Potts, R.B.; Ward, J.C. Correlations and spontaneous magnetization of the two-dimensional Ising model. J. Math. Phys. 1963, 4, 308–322. [Google Scholar] [CrossRef]
- Campbell, J.Y.; Low, A.S.; Mackinlay, A.C. The Econometrics of Financial Markets; Princeton University Press: Princeton, NJ, USA, 1997. [Google Scholar]
- Harrison, J.M.; Pliska, S. Martingales and Stochastic Integrals in the Theory of Continuous Trading. Stoch. Process. Their Appl. 1981, 11, 215. [Google Scholar] [CrossRef]
- Hughston, L.P. Vasicek And Beyond Approaches to Building and Applying Interest Rate Models; Risk Books: London, UK, 1997. [Google Scholar]
- Misner, C.W.; Thorne, K.S.; Wheeler, J.A. Gravitation; Princeton University Press: Princeton, NJ, USA, 2017. [Google Scholar]
- Wolfgang, P. Relativistic Field Theories of Elementary Particles. Rev. Mod. Phys. 1941, 13, 203–232. [Google Scholar]
- Arraut, I. The graviton Higgs Mechanism. Europhys. Lett. 2015, 111, 61001. [Google Scholar] [CrossRef]
- Higgs, P.W. Broken Symmetries and the Masses of Gauge Bosons. Phys. Rev. Lett. 1964, 13, 508509. [Google Scholar] [CrossRef]
- Englert, F.; Brout, R. Broken Symmetry and the Mass of Gauge Vector Mesons. Phys. Rev. Lett. 1964, 13, 321323. [Google Scholar] [CrossRef]
- Nielsen, L.T. Understanding N(d1) and N(d2): Risk-Adjusted Probabilities in the Black-Scholes Model; INSEAD: Fontainebleau, France, 1993; Volume 14, pp. 95–106. [Google Scholar]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arraut, I.; Lei, K.-I. The Role of the Volatility in the Option Market. AppliedMath 2023, 3, 882-908. https://doi.org/10.3390/appliedmath3040047
Arraut I, Lei K-I. The Role of the Volatility in the Option Market. AppliedMath. 2023; 3(4):882-908. https://doi.org/10.3390/appliedmath3040047
Chicago/Turabian StyleArraut, Ivan, and Ka-I Lei. 2023. "The Role of the Volatility in the Option Market" AppliedMath 3, no. 4: 882-908. https://doi.org/10.3390/appliedmath3040047
APA StyleArraut, I., & Lei, K.-I. (2023). The Role of the Volatility in the Option Market. AppliedMath, 3(4), 882-908. https://doi.org/10.3390/appliedmath3040047






