A Hybrid Approach to Representing Shared Conceptualization in Decentralized AI Systems: Integrating Epistemology, Ontology, and Epistemic Logic

Abstract

Artificial Intelligence (AI) systems are increasingly being deployed in decentralized environments where they interact with other AI systems and humans. In these environments, each participant may have different ways of expressing the same semantics, leading to challenges in communication and collaboration. To address these challenges, this paper presents a novel hybrid model for shared conceptualization in decentralized AI systems. This model integrates ontology, epistemology, and epistemic logic, providing a formal framework for representing and reasoning about shared conceptualization. It captures both the intensional and extensional components of the conceptualization structure and incorporates epistemic logic to capture knowledge and belief relationships between agents. The model’s unique contribution lies in its ability to handle different perspectives and beliefs, making it particularly suitable for decentralized environments. To demonstrate the model’s practical application and effectiveness, it is applied to a scenario in the healthcare sector. The results show that the model has the potential to improve AI system performance in a decentralized context by enabling efficient communication and collaboration among agents. This study fills a gap in the literature concerning the representation of shared conceptualization in decentralized environments and provides a foundation for future research in this area.

1. Introduction

The field of AI systems has experienced a significant increase in the use of decentralized environments, where multiple agents and systems operate independently while needing to share knowledge and information [1]. A prime example of such decentralized AI systems is multi-agent systems. These systems necessitate a shared understanding of the environment and its entities, referred to as shared conceptualization. Representing shared conceptualization in such environments, however, is a challenging task, as it demands a balance between the flexibility of decentralized environments and the stability of closed environments [2].

In multi-agent systems, each agent may have its own perspective and beliefs about the world, leading to different ways of expressing the same semantics. A key challenge in AI is representing knowledge and beliefs in such a decentralized context [3].

Previous studies have suggested various conceptualization models, such as extensional and intensional models [4]. These models, however, have limitations when applied to decentralized environments. To address these limitations and improve AI system performance in decentralized settings, we propose a formal model for representing shared conceptualization that combines elements from ontology, epistemology, and epistemic logic.

Epistemology, particularly in the context of computer science and AI systems, is closely related to intensional representation. It involves the formal specification of shared conceptualization without necessarily making the specification explicit [5]. In essence, epistemology concentrates on the meanings of terms and expressions, capturing the diverse perspectives and interpretations of different agents.

Our proposed model integrates epistemology, ontology (which is more extensional), and modal logic to tackle the challenges of representing shared conceptualization in decentralized environments. This approach combines the strengths of both extensional and intensional representations to offer a more comprehensive and adaptable framework for representing knowledge and beliefs in AI systems operating in decentralized contexts.

A key aspect of our proposed model is the incorporation of possible worlds, which enables a more comprehensive representation of diverse perspectives and beliefs in decentralized environments. This overcomes the limitations of existing models based on extensional representations. Possible worlds, rooted in modal logic, facilitate modeling alternative states of affairs and provide a formal structure for reasoning about knowledge, beliefs, and uncertainties [6]. In this context, each AI or information system can be considered a possible world, representing its unique perspective and understanding of the environment.

Incorporating possible worlds into our hybrid model aims to address the limitations of existing extension-based models and enhance the representation of shared conceptualization in decentralized environments. This approach enables AI systems to better understand and reason about the diverse perspectives and beliefs of agents and entities within these environments, ultimately resulting in improved performance and more effective collaboration.

The proposed model builds upon the work of [2], who proposed a hybrid model for representing shared conceptualization in dynamic closed environments. The model consists of three levels: the domain level, the possible worlds level, and the extension level. The domain level defines the entities and concepts in the universe of discourse, the possible worlds level defines the possible states of affairs, and the extension level defines the relations between entities in different possible worlds.

By employing this model, we aim to enhance AI systems’ performance in decentralized environments by ensuring that the knowledge and information shared among agents and systems remain consistent and accurate. The proposed model can also be utilized to formally specify and represent shared conceptualization, which may be beneficial in developing and maintaining AI systems in decentralized environments.

1.1. Research Question and Key Contributions of the Paper

This paper seeks to answer the following research question: How can shared conceptualization be formally modeled in a decentralized environment to enhance the performance of AI systems? To address this, we put forth a hybrid model for the formal modeling of conceptualization in AI systems and assess its efficacy using a scenario in the healthcare sector.

The primary contributions of this study encompass:

• Elucidation and definition of the core concepts pertinent to the research question, including ontology, epistemology, and epistemic logic within a decentralized environment.
• Identification and analysis of existing gaps in the literature regarding the representation of shared conceptualization in a decentralized context.
• Introduction of an innovative formal model for conceptualization in decentralized AI systems that amalgamates ontology, epistemology, and epistemic logic.
• Demonstration of the proposed model’s potential to enhance AI system performance in a decentralized setting, as evidenced by a healthcare sector scenario.
• Emphasis on the significance of comprehending the philosophical foundations of science and AI for the accurate and meaningful interpretation of research findings in interdisciplinary research.

1.2. Research Methodology

Our research methodology is a blend of literature review, model development, and an exploratory scenario that showcases the application of our hybrid model in the context of decentralized AI systems.

The literature review involves identifying key concepts, theories, and studies pertinent to the research question, analyzing gaps in the existing literature, and discussing previous studies and models relevant to the topic. This review lays the theoretical groundwork for our hybrid approach, which integrates epistemology, ontology, and epistemic logic.

In contrast to previous models that utilize First-Order Logic (FOL) and Description Logic (DL), both of which are extensional in nature, our model employs Modal Logic, which is intensional. This allows our model to capture different perspectives and beliefs, providing a more comprehensive representation of shared conceptualization in decentralized AI systems. FOL and DL are powerful tools for representing knowledge, but their extensional nature can limit their ability to capture the diversity of perspectives and beliefs in decentralized environments. In contrast, the intensional nature of Modal Logic allows our model to represent not only the entities and relationships in a domain but also the different ways these entities and relationships can be understood by different agents.

In the model development phase, we create a formal framework for representing and reasoning about shared conceptualization in decentralized AI systems. This process involves defining the intensional and extensional components of the conceptualization structure. We detail how we defined the intensional and extensional components of the conceptualization structure and discuss how we incorporated epistemic logic to capture knowledge and belief relationships between agents. This includes the use of modal operators and the definition of extensional structures for different perspectives in a given scenario.

The exploratory scenario phase is designed to demonstrate the practical application and effectiveness of the proposed model. By applying the model to a real-world scenario in the healthcare sector, we can evaluate its potential to improve AI system performance in a decentralized context and gain insights into its broader applicability. We provide a detailed account of the exploratory scenario phase, including how we applied the model to a real-world scenario and evaluated its effectiveness. We also discuss the insights gained about the model’s broader applicability and potential areas for improvement. This phase also helps identify any limitations or areas for improvement in the model, which can inform future research and development efforts.

2. Theoretical Foundations and Approaches

2.1. Related Work

The study of ontology, epistemology, and epistemic logic plays a crucial role in this research, as it helps to understand the nature of knowledge and how it can be acquired, represented, and shared [7,8,9].

The literature on ontology in AI systems is extensive and encompasses a diverse array of topics. The term “ontology” is borrowed from philosophical ontology, which is concerned with the study of being and the nature of existence in the world that humans can acquire knowledge about. It assists researchers in understanding the certainty they can have regarding the nature and existence of the objects they investigate and the ‘truth claims’ they can make about reality [10].

In the context of AI and computer science, ontology has been adapted and reinterpreted, distinguishing it from its philosophical roots. Gruber characterizes ontology in this context as “an explicit specification of a conceptualization” [11]. Here, “conceptualization” is defined as “the objects, concepts, and other entities that are assumed to exist in some area of interest and the relationships that hold among them” [12]. Consequently, ontology does not seek to objectively capture the entirety of reality but focuses on specific aspects. Ontology corresponds to a representation in a particular language, with its meaning made as explicit as possible within the ontology itself.

Gruber also presents an alternative view of conceptualization as “a simplified, abstract view of the world for some purpose that we wish to represent” [11]. This interpretation highlights the intensional structure of conceptualization. Other definitions propose that ontology is associated with a formal specification of shared conceptualizations agreed upon by a community of individuals or artificial agents [13]. This formal representation facilitates interoperability between software systems.

Studer provides a hybrid definition, describing ontology as “a formal, explicit specification of a shared conceptualization” [14]. Guarino refines Gruber’s definition, distinguishing between ontology and conceptualization by defining ontology as “a logical theory accounting for the intended meaning of a conceptualization” [7]. Guarino critiques Gruber’s definition, stating that the term “conceptualization” in this context pertains to ordinary mathematical relations or extensional relationships within the domain. Guarino argues that these relations mirror specific states of affairs, such as a particular arrangement of blocks on a table in the blocks world scenario [7].

Epistemology, which pertains to the study of knowledge, delves into the aspects of validity, scope, and methodologies involved in acquiring knowledge. This includes inquiries into the constituents of knowledge claims, the methods for acquiring or generating knowledge, and the assessment of its transferability. Epistemology holds significant importance as it profoundly influences how researchers structure their investigations and endeavors to uncover knowledge [15].

There are several different types of epistemologies, each with their own unique perspective on how knowledge is acquired and how it should be used. Objectivist epistemology assumes that reality exists outside, or independently, of the individual mind. Objectivist research is useful in providing reliability (consistency of results obtained) and external validity (applicability of the results to other contexts) [15].

Constructionist epistemology, on the other hand, rejects the idea that objective ‘truth’ exists and is waiting to be discovered. Instead, it argues that ‘truth’ or meaning arises from our engagement with the realities in our world [16]. In other words, a ‘real world’ does not preexist independently of human activity or symbolic language. Constructionist epistemology is particularly relevant in the field of AI, as it highlights the importance of understanding the role of human cognition and interpretation in the creation of knowledge [17].

Constructionist epistemology emphasizes the importance of context and the role of human interpretation in shaping knowledge. In AI systems, this perspective can inform the design of systems that can adapt to different contexts and thereby understand the nuances of human communication. For example, a constructionist approach to natural language processing would focus on understanding the ways in which language is used in different contexts and how it is shaped by cultural and social factors [17].

Subjectivist epistemology, on the other hand, relates to the idea that reality can be expressed in a range of symbols and language systems and is stretched and shaped to fit the purposes of individuals. This perspective emphasizes the role of the individual in shaping their own understanding of reality [17]. In AI systems, subjectivist epistemology can inform the design of systems that are able to adapt to the unique needs and perspectives of individual users.

Different types of epistemologies can have a significant influence on the design and development of AI systems. Realist epistemology emphasizes the importance of objective truth and the ability to understand the world independently of human experience. Constructionist epistemology highlights the importance of context and human interpretation in shaping knowledge, while subjectivist epistemology emphasizes the role of the individual in shaping their own understanding of reality [18,19]. Understanding the different types of epistemologies and their implications for AI systems can help to inform the design and development of more effective and efficient AI systems.

Brachman distinguishes between the epistemological and conceptual levels in knowledge representation. He posits that knowledge representation should focus on epistemological links instead of conceptual links, emphasizing the minimal formal structure of a concept required to ensure formal inferences about the relationship (subsumption) between one concept and another [20]. This approach relates to the intensional level of representation, which occurs after the conceptualization phase and concerns the formal structure of concepts and their relationships.

Brachman proposes a classification of knowledge representation formalisms, which includes the logical and epistemological levels. The logical level deals with representing concepts and relationships in a domain using predicates and logical operators. It emphasizes the logical form of statements and the rules for deducing new statements from existing ones. Logical languages, based on formal logic such as predicate calculus, provide precise semantics for representing concepts and relationships. However, the predicates used in logical languages can have multiple interpretations, leading to ontological neutrality. This means that the real-world meaning of the predicates is arbitrary, making it challenging to construct meaningful and consistent ontologies. The logical level offers a foundation for knowledge representation with its precise semantics and logical form, but it should be used with caution when building ontologies.

Epistemic logic is a branch of logic that deals with knowledge and belief. It is used to formally specify and represent shared conceptualization in AI systems. This is particularly important in decentralized environments, where the sharing of knowledge is crucial for the effective functioning of the system [21,22].

The gap between epistemology and epistemic logic arises from the different levels of abstraction they operate on. While epistemology is concerned with the nature of knowledge itself, epistemic logic is more focused on the formal representation and reasoning of knowledge. Bridging this gap is crucial for developing a comprehensive model of shared conceptualization in decentralized AI systems.

In our model, we integrate ontology and epistemology using a modal logic approach. This approach allows us to connect the extensional level of modal logic to ontology and the intensional level to epistemology, thereby bridging the gap between these two concepts. The extensional level, associated with ontology, instantiates concepts and relationships based on specific instances or examples in the real world, facilitating a concrete representation of knowledge. On the other hand, the intensional level of representation, linked to epistemology, defines general concepts and their relationships, offering a framework for understanding and representing abstract knowledge.

By accommodating multiple extensional levels, our model can incorporate various perspectives and beliefs, enabling more effective communication, collaboration, and reasoning among agents in a multi-agent system. In this context, we redefine epistemology in artificial intelligence as the systematic examination of the intrinsic nature, structural foundations, and justificatory principles related to knowledge representation and reasoning processes within intelligent systems.

Previous studies and models related to the topic of providing shared conceptualization structures for various settings include the work of [2,4,7,11]. For closed systems, Ref. [11] proposed an extensional structure, while [4,10] proposed an intensional structure. A hybrid model has been proposed by [2] that combines elements of extensional and intensional structures and which is particularly suitable for decentralized environments.

In summary, previous studies and models, such as those proposed by the work cited above, have significantly contributed to understanding ontology in AI systems. However, a gap in the literature remains concerning the representation of shared conceptualization in decentralized environments, specifically regarding the integration of ontology and epistemology. Brachman acknowledges this gap and emphasizes the importance of addressing it in the development of AI systems [20].

Furthering this discourse, recent research has explored various aspects of integrating ontology with epistemology and epistemic logic in multi-agent systems. For instance, Miedema and Gattinger (2023) have made significant strides in the field of knowledge and information dynamics in multi-agent systems, exploring the use of Zero-suppressed Decision Diagrams (ZDDs) for symbolically encoding Kripke models in Dynamic Epistemic Logic [23]. However, their research does not explicitly focus on integrating ontology with epistemology and epistemic logic, leaving a gap for a more comprehensive and nuanced representation of the knowledge and beliefs of the agents in the system.

In the context of practical applications, Bouarfa, Aydoğan, and Sharpanskykh (2021) propose a new airline disruption management strategy using multi-agent system modeling, simulation, and verification [24]. While this work provides valuable insights into the integration of ontology with epistemology and epistemic logic in multi-agent systems, it does not delve deeply into the aspect of shared conceptualization, particularly in the context of multi-agent systems where agents have diverse perspectives and beliefs.

Belardinelli, Lomuscio, and Yu (2020) explore the verification of multi-agent systems under the assumption of bounded recall [25]. While their research offers a unique perspective on the intensional aspects of shared conceptualization, it does not fully address the diversity of these perspectives and beliefs. This leaves a gap for research focusing on how to adequately represent the diverse perspectives and beliefs of the agents, which are crucial for effective collaboration and decision making in multi-agent systems.

The work of Malinowski, Pietrowicz, and Szalacha-Jarmużek (2020) provides a unique perspective on the representation of diverse perspectives and beliefs of the agents [26]. However, the concept of possible worlds, where each agent can be considered a possible world representing its unique perspective and understanding of the environment, is not explicitly addressed in their work, leaving a gap for research employing the concept of possible worlds in the context of multi-agent systems.

In addition to the above, the work by Borri, Camarda, and Stufano (2014) titled “Spatial primitives and knowledge organization in planning and architecture: some experimental notes” provides a unique perspective on the role of space perception and representation in the common environmental ontology of cities and territories [27]. While their work provides valuable insights, it does not discuss the application of these concepts in the healthcare sector, leaving a gap for research presenting a scenario in the healthcare sector to illustrate the application of a comprehensive model integrating ontology with epistemology and epistemic logic.

Collectively, these studies provide a comprehensive overview of the current state of research on the integration of ontology with epistemology and epistemic logic in multi-agent systems. However, they also highlight several gaps in the literature, including the need for a more comprehensive integration of ontology with epistemology and epistemic logic, a deeper exploration of shared conceptualization, a more adequate representation of diverse perspectives and beliefs, the employment of the concept of possible worlds, and the application of these concepts in the healthcare sector. These gaps provide valuable directions for further research in this field.

This study aims to fill these gaps by proposing a model that integrates ontology with epistemology and epistemic logic to provide a comprehensive and nuanced representation of shared conceptualization in decentralized environments.

2.2. Types of Environments

In the literature [2,28], environments are categorized based on the level of agreement and coordination among observers, leading to the identification of three main categories:

• Closed environments are characterized by strong agreement and coordination among observers. In these environments, observations are consistent with a shared understanding of the environment, enabling effective collaboration among participating entities. Closed environments are typically found in controlled settings, such as laboratory experiments and controlled studies, where variables are limited and conditions can be easily manipulated.
• Decentralized environments, on the other hand, are prevalent in autonomous and multi-agent systems where there is a lack of consensus and coordination among observers. While observers in decentralized environments may be autonomous and independent, they generally share a common understanding of the observed domain. In healthcare, for example, different healthcare providers may have different views on a patient’s condition, but they generally share a common understanding of medical terminology and best practices. Decentralized environments require the development of methods and models that enable efficient communication and collaboration of agents in the face of inconsistent information.
• Open environments represent complex and dynamic situations, such as natural disasters and intricate social systems, characterized by significant diversity and uncertainty among observers. In these environments, observers may have different or even conflicting concepts about the observed domain. For example, if the same individual is observed by different domains, such as agriculture, healthcare, and law, each domain may have a unique perspective on the individual, with different goals, values, and methods of evaluation. These environments are both decentralized and open, and they pose significant challenges due to conflicting or inconsistent observations, necessitating a shared understanding or shared conceptualization of the environment and its entities.

2.3. Conceptualization

Conceptualization is a crucial aspect in the field of artificial intelligence (AI), as it provides an abstract representation of an observed domain, allowing computers to comprehend and reason about the world in a manner akin to human cognition [10,11]. Conceptualization can be categorized into two primary types: extensional and intensional [2,4,7].

Extensional conceptualization involves constructing an abstract representation of the observed domain by pinpointing key concepts and relationships and organizing them meaningfully and usefully. This process entails recognizing the internal structure of the domain, and the resulting representation is assessed based on its truth value, aiming to accurately reflect the observed domain in line with reality. Extensional conceptualization is crucial for knowledge representation and reasoning systems, enabling computers to understand and reason about the world consistent with objective, verifiable facts.

Conversely, intensional conceptualization focuses on creating an abstract representation of the observed domain by taking into account multiple viewpoints or perspectives. This approach may include subjectivity and interpretation, as it involves generating a representation that embodies the observer’s subjective experiences and beliefs. The resulting representation might not accurately capture the full spectrum of factors and relationships within the observed domain and could be comparable to a false belief if not grounded in objective, verifiable facts. Intensional conceptualization is an essential component of AI systems, as it enables computers to understand and reason about the world, considering various perspectives and accommodating subjectivity and interpretation.

A significant advantage of employing conceptualization in AI systems, compared to alternative methods of knowledge representation, lies in its potential to provide a more accurate and comprehensive depiction of domain-specific knowledge. Identifying and defining entities, relationships, and concepts within a domain enables AI systems to more accurately represent the knowledge present in that domain. Moreover, determining the possible states of affairs and their interrelations allows AI systems to more accurately represent the various ways knowledge can be organized and understood [4].

2.4. Limitations of Ontology-Based Representation in Decentralized Environments

In decentralized environments, ontology-based representation faces two main challenges: interpretation and reasoning.

• Interpretation: Achieving a common understanding of concepts and relationships is crucial but difficult in decentralized environments due to the varying interpretations of concepts and relationships among different observer domains. While ontology offers an extensional representation by focusing on the extension of concepts and their relationships, the diverse interpretations necessitate an intensional representation that emphasizes the concepts themselves and the meanings attributed to them by different observer domains.
• Consequently, ontology-based representation methods, which rely on a shared understanding and a common ontology, are limited in these contexts [29].

To address the interpretation challenge, it is essential to explore alternative semantic approaches capable of overcoming the limitations of ontology-based representation methods [30]. Such semantic approaches should establish a structured framework to comprehend the diverse perspectives and interpretations of different observer domains while also accommodating varying ontological views and beliefs present in these environments.

3.

Reasoning: Decentralized environments introduce unique challenges regarding the representation and reasoning of complex and heterogeneous knowledge [31]. Although ontology-based representation can categorize information, it is limited by the constraints of classical logics, such as first-order logic and description logic. These logics are ill-suited to represent and reason about multiple perspectives on a subject, and their incapacity to express modality and possibility hinders the representation and reasoning of relationships between various perspectives.

To address the reasoning challenge, a more expressive logical framework is needed to represent and reason about the relationships between various perspectives in decentralized environments. This will involve supplementing ontology with methods that account for differing interpretations and perspectives of observer domains, as well as exploring new logical frameworks capable of handling modality and possibility.

In summary, the limitations of ontology-based representation in decentralized environments stem from challenges in both interpretation and reasoning. Addressing these challenges requires the development of alternative semantic approaches and more expressive logical frameworks to better represent and reason about the diverse perspectives and interpretations found in decentralized environments.

2.5. Representing Conceptualization Structure: Challenges and Limitations of Classic Logics

First-order logic (FOL) and description logic (DL) are popular representation languages in the field of artificial intelligence and knowledge representation. However, they have limitations in representing the complex and multi-faceted nature of the conceptualization structure in a decentralized environment.

Consider a patient journey in the healthcare domain. The same patient may be seen by multiple healthcare professionals, each with their own perspectives on the patient’s medical history, treatment plan, and prognosis. FOL and DL would struggle to represent and reason about these different perspectives in a formal and rigorous way. In decentralized environments, these perspectives can be viewed as distinct possible worlds, where a possible world is a complete, self-consistent description of a specific scenario or state of affairs. Each possible world represents a unique understanding of the domain held by different actors, such as individuals, organizations, or AI systems. Modal logic, particularly epistemic logic, provides a natural framework for representing and reasoning about these possible worlds, as it can express relationships between them and handle the uncertainty and variability inherent in decentralized environments.

In FOL, we would need to represent each perspective or viewpoint as a separate formula and use the rules of FOL to reason about the relationships between these formulas. For example, we might represent the perspective or viewpoint of the pharmacist using the following FOL formula:

$$\forall x\left(Patient\right(x)\wedge TakesMedicationA(x)\wedge HasAllergies(x\left)\right)$$

This formula expresses the fact that all patients must take medication A and have allergies. However, this formula does not capture the fact that the perspective or viewpoint of the pharmacist is distinct from the perspective of the doctor or physiotherapist, and it does not allow us to reason about the relationships between these different perspectives in a formal and rigorous way.

In DL, we would need to represent each perspective as a separate concept or class, which would not capture the fact that these perspectives are related to the same subject. For example, we might represent the perspective of the pharmacist using the following DL axioms:

$$\begin{array}{c}PatientandTakesMedicationAsubclassOfPharmacistPatient\\ PatientandHasAllergiessubclassOfPharmacistPatient\end{array}$$

This representation expresses the fact that the class of patients who take medication A and the class of patients who have allergies are both subclasses of the class of patients seen by the pharmacist. However, this representation does not capture the fact that the same patient may be seen by multiple healthcare professionals with different perspectives, and it does not allow us to reason about the relationships between these different perspectives in a formal and rigorous way.

Therefore, while FOL and DL are suitable for representing certain types of information and relationships, they are limited in their ability to represent the complex and multi-faceted nature of the conceptualization structure in a decentralized environment. A more suitable representation language will be needed to fully capture the possible worlds and the relationships between them.

The conceptualization structure for the decentralized environment requires a representation that captures the intensional properties and relations of entities across different possible worlds. However, DL and FOL, as well as frame-based representation systems, are limited in their ability to handle intensional properties and relations due to their extensional nature. They are based on symbols and axioms that define the relationships between entities in a single, actual world and do not provide a way to reason about different possible states or worlds in which entities can exist. As a result, they cannot be used to fully represent the complex and dynamic nature of the decentralized environment and its underlying ontology.

When observing decentralized environments, it is clear that individual perspectives and information systems or ontologies are represented independently. These individual perspectives have two key aspects when it comes to the representation of conceptualization:

• The individual interpretation of the conceptualization
• The intensional representation required to handle the diversity of these interpretations.

The importance of accurately capturing the diverse perspectives of individuals in a decentralized environment requires a precise representation language. The explicit specification of the representation language must align with each individual’s extensional interpretation, ensuring that their unique perspectives are accurately represented. However, the diversity of individual interpretations can pose a challenge in creating a coherent representation. To address this, a layer of specification that adheres to epistemic views is necessary. This layer provides a means to abstract the individual interpretations into a common intensional representation, thereby preserving the diversity of perspectives in a consistent manner.

Gottlob Frege, a seminal philosopher of language, has greatly influenced our understanding of the distinction between the extensional and intensional aspects of language [32]. He argued that expressions can have both an extension and an intension, where the extension refers to the object an expression refers to, and the intension refers to the way it refers to the object. In the following section, we will delve into Frege’s arguments on this topic and explore the significance of considering both extensions and intensions in representation languages.

2.6. The Importance of Understanding Extensions and Intensions in Representation

The distinction between extensions and intensions is a traditional linguistic concept related to expressions and their semantics. An expression can possess both an extension and an intension. For instance, consider the example provided by Frege: the expressions “morning star” and “evening star” both refer to the same entity, the planet Venus; hence they share the same extension. However, each expression carries a different meaning or perspective; “evening star” refers to the first star to appear in the evening and “morning star” refers to the last luminous body to disappear in the morning. Hence, these expressions have distinct intensions.

The distinction between extensions and intensions, as introduced by Frege, has had a significant impact on contemporary discussions in logic and the philosophy of language, as well as influencing fields such as artificial intelligence and computer science. Frege’s insights have helped to clarify the differences between the reference of an expression and the way in which it refers to the object, leading to new avenues of research in semantics and providing a framework for understanding how expressions with the same referent can convey different meanings or perspectives.

There are certain classes of statements that fail extensionality, meaning that two expressions can refer to the same object but convey different meanings [33]. One such class is identity statements, as illustrated by Frege’s Puzzle. The statement “evening star is evening star” does not add any new information, whereas the statement “evening star is morning star” has more cognitive significance as it tells us that the two senses refer to the same object.

Another class of statements that fail extensionality is substitutivity in referentially opaque contexts. In these contexts, the reference of an expression is not determined by its normal denotation but rather by its sense. For example, the statement “John believes that the ‘evening star’ is beautiful” does not imply that “John believes that the ‘morning star’ is beautiful”, even though they refer to the same object. This is due to the referential opacity in constructs such as quotations, indirect speech, and propositional attitudes (beliefs, knowledge, etc.). The replacement of an expression with another that refers to the same object often results in a change in meaning. For instance, “Lex Luthor discovered that Clark Kent was Superman”; using Clark Kent to replace Superman in “Lex Luthor discovered that Clark Kent was Clark Kent”, produces a change in the meaning of the sentence, although the two expressions have the same referent.

In AI and computer science, the view that the extension pertains to the reference of an expression, while the intension refers to its meaning, has been influential, despite alternative perspectives such as Fodor’s. This process can be divided into extensional and intensional representation of conceptualization, with extensional representation conceptualization striving for greater accuracy and intensional representation conceptualization, allowing for subjectivity and interpretation. This perspective has had a significant impact on the development of computational models.

2.7. Ontology and Epistemology in Conceptualization: A Modal Logic Approach

The integration of ontology and epistemology in knowledge representation is a vital aspect of creating resilient, adaptive, and context-aware AI systems. We embrace Brachman’s concept, which involves the integration of ontology and epistemology in knowledge representation, an essential aspect of developing robust, adaptive, and context-sensitive AI systems. This approach provides a unique contribution to the understanding and representation of knowledge.

Ontology focuses on depicting concepts and relationships in a specific domain using predicates and logical operators. Despite its clear semantics and logical structure, ontology is neutral in terms of real-world meaning, which can lead to challenges when creating meaningful and consistent ontologies.

Incorporating an epistemological level between ontology and conceptual levels is essential, as demonstrated in the literature. This level offers a structured and meaningful knowledge representation, considering the truth and necessity of propositions and providing a framework for reasoning about belief and truth in various contexts.

Consider the statement “All apples are red”. At the ontology level, this statement consists of predicates, “apple” and “red”, connected by the logical operator “are”. The statement’s truth is assessed based on the truth of the predicates and the operator connecting them. In this scenario, the statement is deemed true if all entities in the domain considered apples also possess the property of being red.

However, at the epistemological level, this statement might not be regarded as true or necessary. For instance, not all apples are inherently red since various apple varieties come in different colors. In this situation, the statement would be viewed as false or uncertain. The epistemological level offers a more refined perspective on knowledge, considering not only the statement’s logical form but also the context and domain knowledge affecting its truth.

Another example is the statement “Snow is white”. At the logical level, this statement consists of predicates “snow” and “white” connected by the operator “is”. The statement’s truth would be assessed based on the truth of the predicates and the operator connecting them. At the epistemological level, this statement is considered true or necessary in many domains, as snow is typically white. However, there might be situations or domains where the statement is not necessarily true, such as in areas where snow is contaminated and appears black or gray. The epistemological level considers the context and domain knowledge that influence the statement’s truth, offering a more accurate understanding of what is necessary and true.

Both examples demonstrate the differences between ontology and epistemological levels in knowledge representation. The first example underscores the limitations of the logical level in capturing real-world complexities, while the second example highlights the importance of context and domain knowledge at the epistemological level.

In this paper, we examine the integration of ontology and epistemology using a modal logic approach, connecting the extensional level of modal logic to ontology and the intensional level to epistemology. This linkage allows for a more comprehensive understanding of shared conceptualization in multi-agent systems.

The intensional level of representation, linked to epistemology, defines general concepts and their relationships, offering a framework for understanding and representing abstract knowledge. The extensional level, associated with ontology, instantiates these concepts and relationships based on specific instances or examples in the real world, facilitating a concrete representation of knowledge.

By accommodating multiple extensional levels, the knowledge representation system incorporates various perspectives and beliefs, enabling more effective communication, collaboration, and reasoning among agents in a multi-agent system. In this context, epistemology in artificial intelligence is redefined as the systematic examination of the intrinsic nature, structural foundations, and justificatory principles related to knowledge representation and reasoning processes within intelligent systems.

2.8. Modal Logic for Representing and Reasoning in Decentralized Environments

Modal logic is a powerful and versatile formalism employed in various fields such as philosophy, computer science, and linguistics. It has been used to reason about necessity, possibility, knowledge, belief, and temporal relations, among other things. Typically, modal logic extends classical propositional or predicate logic with modal operators that express notions of necessity and possibility, enabling more expressive representations of statements and accounting for different modalities.

In our research, we adapt modal logic to represent and reason about different perspectives in decentralized environments. Although modal logic has been applied in a range of contexts, including some similar to ours, we believe our approach offers valuable benefits that merit further exploration. By using modal logic, we can explicitly model individual agents’ or observers’ beliefs and knowledge within the system, effectively capturing their diverse perspectives more effectively than classical logic alone. This approach facilitates the representation of shared conceptualization in decentralized environments, where agents may have conflicting or incompatible views on relationships between entities.

Given the definitions provided by [7,14], the term “formal” in the context of ontology and shared conceptualization refers to a logical, structured, and explicit representation of a shared understanding of concepts and their relationships. In this sense, a formal model should be grounded in a well-defined logical framework, providing a clear and unambiguous specification of the concepts, their properties, and the relationships between them.

In the proposed model, the “formal” aspect is achieved through the utilization of modal logic as a structured and logically rigorous formalism for representing and reasoning about abstract concepts, their properties, and the relationships between them. By building on the expressiveness of modal logic and its ability to capture the intensional and extensional aspects of meaning, the model aims to provide a formal, explicit specification of the shared understanding among agents in a decentralized environment.

Modal logic features two levels of semantics: the extensional level and the intensional level. These levels help differentiate aspects of meaning in each statement or expression.

• Extensional level (ontology): At the extensional level, the focus is on the relationships between specific objects, instances, or entities in the world. It deals with actual instances or examples of concepts and their relationships, aligning with ontology. By representing actual relationships among objects, the extensional level allows for more precise and accurate models of entities and their interactions in each domain.
• Intensional level (epistemology): At the intensional level, the focus is on abstract concepts, their properties, and the inherent relationships between them. This level deals with the general aspects of meaning, corresponding to epistemology. By capturing the essence of a concept or relationship, the intensional level provides a structured and meaningful representation of knowledge suitable for the development of ontologies and other knowledge representation systems.

By utilizing both levels, the proposed model effectively represents shared conceptualization in decentralized environments, accommodating diverse perspectives and beliefs while enabling more effective communication, collaboration, and reasoning among agents in a multi-agent system.

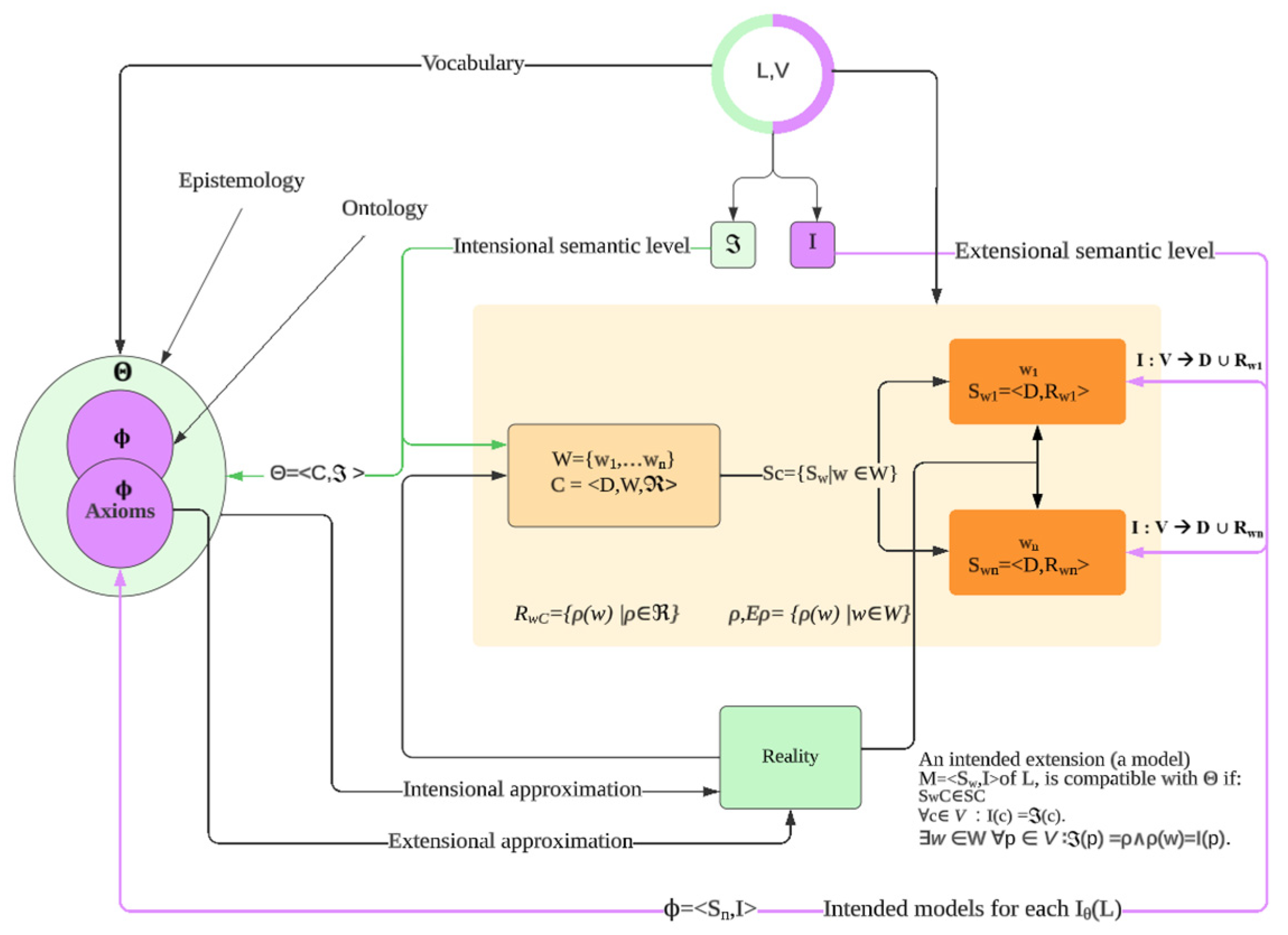
3. Formal Modeling of Conceptualization in Decentralized Environments

3.1. Formal Modeling

The conceptualization in our model is represented through a series of formal structures operating at different levels. At the highest level, we define the intensional structure $C=⟨D,W,\mathfrak{R}⟩$, encompassing all possible worlds within the decentralized environment. Moving to the lower level, we interpret it as a function mapping possible worlds to extensional structure sets, represented $asS{w}_1=⟨D,R_{w1}⟩,\dots ,S{w}_n=⟨D,R_{wn}⟩$.

For better clarity, please refer to Figure 1, illustrating the conceptualization structure with its two distinct levels.

To precisely define the structure, we employ the $notation{\rho }^n:W\to 2^{D^n}$. Here, ${\rho }^n$ denotes intensional relations defined on the environment $<D,W>,$ where $D$ represents the set domains in the environment, and $W$ is a set encompassing maximal extensional structures within those domains.

For any generic extensional relation $\rho$, we define $E\rho =\left\{\rho \left(w\right)∣w\in W\right\}$, signifying the admissible extensions of $\rho$.

Moreover, we introduce $S_{w}C=<D,R_{w}C>$ as the intended extensional structure for $w$ under C. Furthermore, $R_{w}C=\rho \left(w\right)\mid \rho \in R$ represents the set of extensions (relative to $w$) for the elements in $R$.

By considering all the intended world structures of $C$, we define $SC$ as the set $\left\{S_{w}C∣w\in W\right\}$, incorporating the complete set of intended world structures within the decentralized environment.

Finally,$C=<D,R>=S_{w}C$ serves as the extensional structure of the environment, taking on the form of an extensional model for the conceptualization structure in decentralized environments.

3.2. Epistemology: A Proposed Formulation

To align with the conceptualization, we introduce a formal treatment of epistemology and ontology based on two distinct semantic levels: intensional $\left(\mathsf{\Theta }\right)$ and extensional $\left(\mathsf{\Phi }\right)$. Intensional semantics generally encompass broader meanings compared to extensional semantics. If we have knowledge of the intensional aspect of an expression, we can deduce its extension concerning a specific world [34].

To maintain coherence with the conceptualization, a deliberate specification necessitates the precise definition of the intensional meaning of the vocabulary and the establishment of constraints on its models. This imperative arises from the fundamental association of models with an extensional account of meaning [7].

In this regard, considering an intensional structure $<D,W,\mathfrak{R}>$, an intensional language L, and an intensional interpretation employing a vocabulary $V$, we formally define the intensional semantic level of epistemology. This semantic level aligns with the concept of ontological commitment [7] and is expressed as follows:

$$\mathsf{\Theta }=<C,\mathfrak{I}>$$

where:

• $C$ denotes the conceptualization.
• $\mathfrak{I}$ stands for an intensional interpretation function, which maps entity elements of $D$ to constant symbols of $V$ and relation elements of $\mathfrak{R}$ to predicate symbols of $V$.

  $$\mathfrak{I}:V\to D\cup \mathfrak{R}$$

To restrict the utilization of the semantic level $\mathsf{\Theta }$, which pertains to intensional aspects, by the intensional interpretation function $I$ to a well-defined domain, an extensional interpretation $I$, along with a set of axioms, becomes necessary.

3.3. Ontology: A Proposed Formulation

Now, considering the intensional semantic level $\mathsf{\Theta }$ and an extensional interpretation I, we can identify an intended extension (a model) $M=<S_w,I>$ of language L is deemed compatible with $\mathsf{\Theta }$ if the following conditions are satisfied:

• $S_{w}C\in SC$.
• For all constant symbols $c\in V:I\left(c\right)=I\left(c\right).$
• There exists a world $w\in W$ such that for all predicate symbols $p\in V:I\left(p\right)=\rho and\rho \left(w\right)=I\left(p\right).$

Consequently, for a language $L$ and conceptualization $C$, the collection of all extensions (models) of $L$ that are consistent with the intensional semantic level $\mathsf{\Theta }$ denotes the set of intended extensions I_Θ(L) in accordance with $\mathsf{\Theta }$.

The extensional semantic level $\Phi$ of $\mathsf{\Theta }$ is formulated by a language $L$, an extensional interpretation $I,$ and a set of axioms aimed at approximating the intensional interpretation to the intended extensions (models) I_Θ(L) within the conceptualization $C$.

In summary, we can state the following:

• $\mathsf{\Theta }$ is deemed committed to $C$ when it is structured to characterize $C$ and effectively approximates reality $D$ through its extensions.
• A language $L$ exhibits commitment to $\mathsf{\Theta }$ if it adheres to the conceptualization $C$ in such a manner that $\mathsf{\Phi }$ aligns harmoniously with $C$.
• $L$ demonstrates commitment to $\mathsf{\Phi }$, given $\mathsf{\Theta }$, by ensuring that the models for $\Phi$ comprehensively encompass the intended extensions I_Θ(L)

Please refer to Figure 2 below for an illustration depicting the derivation of the intensional semantic level from an intensional interpretation and the extensional semantic level from an extensional interpretation to form an ontological perspective.

3.4. Modal Logic Examples in the Healthcare Sector

In the healthcare sector, let us consider conceptualization C, where the universe of discourse D is defined as the set of all possible entities in the domain, including patients, physicians, nurses, and medical facilities. Set W represents the possible worlds in the conceptualization, representing different states of affairs in the healthcare sector. The set R represents the conceptual relations that hold within each possible world, including relations such as Patient1 (representing the set of patients), Physician1 (representing the set of physicians), Nurse1 (representing the set of nurses), and Facility1 (representing the set of medical facilities).

We can define a function ${\rho }^n:W\to 2^{D^n}$ that maps each possible world w in W to a set of extensional structures ρ(w) representing the entities and relationships that hold within that world. Formally, ${\forall }_w\in W$, we have:

• $Patien{t}_{\left(w\right)}^1\subseteq D$ represents the set of patients in world w.
• $Physicia{n}_{\left(w\right)}^1\subseteq D$ represents the set of physicians in world w.
• $Nurs{e}_{\left(w\right)}^1\subseteq D$ represents the set of nurses in world w.
• $Facilit{y}_{\left(w\right)}^1\subseteq D$ represents the set of medical facilities in world w.
• $Diagnosi{s}_{\left(w\right)}^2\subseteq D\times D$ represents the set of diagnoses made by physicians in world w.
• $Assis{t}_{\left(w\right)}^2\subseteq D\times D\mathrm{ }$ represents the set of assistance provided by nurses in $worldw$.

3.4.1. Example 1: Representing Relations between Patients, Physicians, and Nurses

In the healthcare sector, let us consider two possible worlds, w₁ and w₂. In world w₁, there is a patient p₁ who is diagnosed with a disease d₁ by physician ph₁. Nurse n₁ provides assistance to p₁. The relations in this world can be represented using the function ρ as follows:

• $Patien{t}_{\left(w1\right)}^1=p_1$
• $Physicia{n}_{\left(w1\right)}^1=p{h}_1$
• $Nurs{e}_{\left(w1\right)}^1=n_1$
• $Diagnosi{s}_{\left(w1\right)}^2=\left(p_1,d_1\right)$
• $Assis{t}_{\left(w1\right)}^2=\left(p_1,n_1\right)$

In world w₂, there is a different patient p₂ who is diagnosed with a different disease d₂ by physician ph₂. Nurse n₂ provides assistance to p₂. The relations in this world can be represented using the function ρ as follows:

• $Patien{t}_{\left(w2\right)}^1=p_2$
• $Physicia{n}_{\left(w2\right)}^1=p{h}_2$
• $Nurs{e}_{\left(w2\right)}^1=n_2$
• $Diagnosi{s}_{\left(w2\right)}^2=\left(p_2,d_2\right)$
• $Assis{t}_{\left(w2\right)}^2=\left(p_2,n_2\right)$

This example illustrates how the proposed hybrid model for formal modeling of conceptualization in AI systems can be applied to represent the relations between patients, physicians, and nurses in the healthcare sector. By using the intensional structure ρ and the set of admittable extensions $E\rho$, we can represent the different possible states of affairs in the healthcare sector, including the different patients, physicians, nurses, and diseases that exist in each possible world, as well as the relationships between these entities.

Furthermore, by using modal logic, we can reason about the different beliefs and how they relate to each other in a more precise and formal manner than what is possible with traditional first-order logic (FOL) or description logic (DL). One of the limitations of FOL is that it lacks built-in mechanisms for representing modal notions such as necessity and possibility, which can be essential when reasoning about beliefs and perspectives. While it is possible to encode these notions in FOL using complex workarounds, this can lead to cumbersome and less intuitive representations. As for DL, it is typically focused on representing taxonomies and relationships between concepts, but it also lacks native support for modalities, which can hinder the representation of shared perspectives in a nuanced and flexible way. In contrast, modal logic provides a more natural and expressive formalism for representing and reasoning about perspectives, thanks to its built-in modal operators and richer semantics.

3.4.2. Example 2: Representing and Reasoning about Different Perspectives in the Healthcare Sector

Now, let us consider an agent, who is a nurse, who believes that patient p₁ is diagnosed with disease d₁ and is being assisted by nurse n1. We can represent this belief using the epistemic modal operator K and the accessibility relation R as follows:

$$K{p}_1\left(w_1\right)\wedge K{d}_1\left(w_1\right)\wedge K{n}_1\left(w1\right)\wedge R\left(w_1,w_2\right)$$

This means that the agent knows that patient p₁ is diagnosed with disease d₁ and is being assisted by nurse n₁ in world w₁, and also the agent believes that this is possible in world w₂ as well.

Alternatively, let us consider another agent, who is a physician, who believes that patient p₂ is diagnosed with disease d₂ and is being assisted by nurse n₂. We can represent this belief using the epistemic modal operator K and the accessibility relation R as follows:

$$K{p}_2\left(w_2\right)\wedge K{d}_2\left(w_2\right)\wedge K{n}_2\left(w_2\right)\wedge R\left(w_2,w_1\right)$$

This means that the agent knows that patient p₂ is diagnosed with disease d₂ and is being assisted by nurse n₂ in world w₂, and also the agent believes that this is possible in world w₁ as well.

In the domain of education, we can construct a conceptualization $C$, where the universe of discourse $D$ encompasses all conceivable entities within the domain. This includes students, teachers, subjects, and educational institutions. The set $W$ denotes the possible worlds within the conceptualization, symbolizing various states of affairs within the education sector. The set $R$ signifies the conceptual relations that are valid within each possible world. These relations include Student1 (denoting the set of students), Teacher1 (denoting the set of teachers), Subject1 (denoting the set of subjects), and Institution1 (denoting the set of educational institutions).

We can formulate a function ${\rho }^n:W\to 2^{D^n}$ that maps each possible world $w$ in $W$ to a set of extensional structures $\rho \left(w\right)$ that represent the entities and relationships that are valid within that world. Formally, for all $w\in W$, we have:

• $Studen{t}_{\left(w\right)}^1\subseteq D$, which denotes the set of students in world $w$.
• $Teache{r}_{\left(w\right)}^1\subseteq D$, which denotes the set of teachers in world $w$.
• $Subjec{t}_{\left(w\right)}^1\subseteq D$, which denotes the set of subjects in world $w$.
• $Institutio{n}_{\left(w\right)}^1\subseteq D$, which denotes the set of educational institutions in world $w.$
• $Teac{h}_{\left(w\right)}^2\subseteq D\times D$, which denotes the set of teaching relations between teachers and subjects in world $w$.
• $Lear{n}_{\left(w\right)}^2\subseteq D\times D$, which denotes the set of learning relations between students and subjects in world $w$.

3.4.3. Example 3: Formal Representation of Relations within the Education Sector

Consider two possible worlds, $w_1$ and $w_2$, within the education sector. In world w₁, a student $s_1$ is learning a subject $su{b}_1$ from a teacher $t_1$. The relations within this world can be represented using the function $\rho$ as follows:

• $Studen{t}_{\left(w1\right)}^1=s_1$
• $Teache{r}_{\left(w1\right)}^1=t_1$
• $Subjec{t}_{\left(w1\right)}^1=su{b}_1$
• $Teac{h}_{\left(w1\right)}^2=\left(t_1,su{b}_1\right)$
• $Lear{n}_{\left(w1\right)}^2=\left(s_1,su{b}_1\right)$

In world $w2$, a different student s₂ is learning a different subject sub₂ from a teacher t₂. The relations within this world can be represented using the function $\rho$ as follows:

• $Studen{t}_{\left(w2\right)}^1=s_2$
• $Teache{r}_{\left(w2\right)}^1=t_2$
• $Subjec{t}_{\left(w2\right)}^1=su{b}_2$
• $Teac{h}_{\left(w2\right)}^2=\left(t_2,su{b}_2\right)$
• $Lear{n}_{\left(w2\right)}^2=\left(s_2,su{b}_2\right)$

3.4.4. Example 4: Formal Representation and Reasoning about Different Perspectives within the Education Sector

Consider an agent, a teacher, who holds the belief that student s₁ is learning subject sub₁ from teacher t₁. This belief can be formally represented using the epistemic modal operator K and the accessibility relation R as follows:

$$K{s}_1\left(w_1\right)\wedge Ksu{b}_1\left(w_1\right)\wedge K{t}_1\left(w1\right)\wedge R\left(w_1,w_2\right)$$

This implies that the agent is aware that student s₁ is learning subject sub₁ from teacher t₁ in world w₁, and the agent also believes that this situation is plausible in world w₂.

Alternatively, consider another agent, a student, who holds the belief that they are learning subject sub₂ from teacher t₂. This belief can be formally represented using the epistemic modal operator K and the accessibility relation R as follows:

$$K{s}_2\left(w_2\right)\wedge Ksu{b}_2\left(w_2\right)\wedge K{t}_2\left(w_2\right)\wedge R\left(w_2,w_1\right)$$

This implies that the agent is aware that they are learning subject $su{b}_2$ from teacher $t_2$ in world $w_2$, and the agent also believes that this situation is plausible in world $w_1$.

The use of the epistemic modal operator K and the accessibility relation R allows us to reason about these different beliefs and how they relate to each other in a more precise and formal manner than what is possible with FOL. Additionally, by utilizing the intensional structure ρ, we are able to represent and reason about different perspectives in the healthcare sector in a more comprehensive and accurate way. This, in turn, can help improve the performance of AI systems in a decentralized environment.

3.5. Applying the Hybrid Model to a Multi-Specialist Healthcare Scenario

In complex and dynamic domains such as healthcare, effective decision making often requires the integration of multiple perspectives and expertise. A hybrid approach combining epistemology, ontology, and epistemic logic provides a powerful and flexible framework to represent and reason about these diverse perspectives in a structured manner. This paper explores the application of this hybrid approach to modeling and analyzes the shared conceptualization among various medical professionals involved in the treatment of a patient with diabetes. Specifically, we focus on how the primary care physician, endocrinologist, and nephrologist can collaborate and make informed decisions based on their respective areas of expertise. By employing a conceptualization structure that incorporates intensional and extensional components, we demonstrate how the hybrid approach can be used to capture the different possible world structures representing the perspectives and knowledge of the medical professionals involved. This approach enables a more comprehensive understanding of the patient’s condition and facilitates better coordination and decision making among the medical team. In the revised scenario, we will consider each specialist’s perspective as a separate possible world, reflecting their unique viewpoint and understanding of the diabetes treatment domain. For simplicity, let us assume that there are two specialists: an endocrinologist ($s_1$) and a nephrologist ($s_2$).

First, we define the conceptualization $C=⟨D,W,\mathfrak{R}⟩$ for the diabetes treatment scenario:

$D:$ patient, primaryCarePhysician, endocrinologist, nephrologist, treatmentPlan, insulinType, dosage

W:

• $w_1\left(endocrinologist\mathrm{’}s perspective\right)$
• $w_2\left(nephrologist\mathrm{’}s perspective\right)$

$\mathfrak{R}$:

• $Patient\left(x\right)$
• $PrimaryCarePhysician\left(x\right)$
• $Endocrinologist\left(x\right)$
• $Nephrologist\left(x\right)$
• $TreatmentPlan\left(x\right)$
• $InsulinType\left(x\right)$
• $Dosage\left(x\right)$
• $HasDiabetes\left(x\right)$
• $ResponsibleFor(x,y)$
• $ProvidesInput(x,y,z)$
• $TreatmentPlanFor(x,y)$
• $TreatmentPlanIncludes(x,y,z)$

Next, we define the intensional interpretation function I and vocabulary $V:$

• $V: p, d, e, n, t, i, dos$
• $\mathfrak{I}:V\to D\cup \mathfrak{R}$
• $\mathfrak{I}\left(p\right)=patient$
• $\mathfrak{I}\left(d\right)=primaryCarePhysician \mathfrak{I}\left(e\right)=endocrinologist \mathfrak{I}\left(n\right)=nephrologist$
• $\mathfrak{I}\left(t\right)=treatmentPlan$
• $\mathfrak{I}\left(i\right)=insulinType$
• $\mathfrak{I}\left(dos\right)=dosage$

Now, let us define the intensional semantic level (epistemology) $\mathsf{\Theta }=⟨C,\mathfrak{I}⟩.$

For each possible world $w\in W$, we can define the intended extensional structure $S_w,C$ as the set of extensional structures that hold within that world according to the conceptualization C.

$S_{w,C}$ for $w_1$ (the endocrinologist’s perspective):

• $S_w,C_w$ = $⟨D,R_w,C_{w1}⟩$

$S_{w,C}$ for $w_2$ (the nephrologist’s perspective):

• $S_w,C_w$ = $⟨D,R_w,C_{w1}⟩$

$R_w,C_{w1}$ and $R_w,C_{w1}$ represent the sets of extensions (relative to w₁ and w₂, respectively) of the elements of R. These sets of extensions will differ based on the perspectives of the two specialists, capturing their unique viewpoints and understanding of the domain.

By considering the different perspectives of the two specialists as separate possible worlds, we can better represent their individual contributions and knowledge in the context of the diabetes treatment domain. This approach can facilitate more effective communication and decision making among the medical team, ultimately leading to improved patient outcomes.

Let us define the intended extensional structures SwC_w1 and SwC_w2 for ${\mathsf{\Phi }}_1$ (endocrinologist’s perspective) and ${\mathsf{\Phi }}_2$ (nephrologist’s perspective), respectively, along with their sets of extensions $R_w{C}_{w1}$ and $R_w{C}_{w2}$:

• $S_w{C}_{w1}$ = $⟨D,R_w{C}_{w1}⟩$ (the intended extensional structure for w₁, the endocrinologist’s perspective)
• $S_w{C}_{w2}$ = $⟨D,R_w{C}_{w2}⟩$ (the intended extensional structure for w₂, the nephrologist’s perspective)

For w₁ (endocrinologist’s perspective on the ontological view₂), we can define the set of extensions RwC_w1 as follows:

• $Patient\left(p\right)$
• $PrimaryCarePhysician\left(d\right)$
• $Endocrinologist\left(e\right)$
• $TreatmentPlan\left(t\right)$
• $InsulinType(t,i)$
• $Dosage(t,dos)$
• $HasDiabetes\left(p\right)$
• $ResponsibleFor(d,p)$
• $ProvidesInput(e,d,t)$
• $TreatmentPlanFor(t,p)$
• $TreatmentPlanIncludes(t,i,dos)$

For w₂ (nephrologist’s perspective), we can define the set of extensions RwC_w2 as follows:

• $Patient\left(p\right)$
• $PrimaryCarePhysician\left(d\right)$
• $Nephrologist\left(n\right)$
• $TreatmentPlan\left(t\right)$
• $InsulinType(t,i)$
• $Dosage(t,dos)$
• $HasDiabetes\left(p\right)$
• $ResponsibleFor(d,p)$
• $ProvidesInput(n,d,t)$
• $TreatmentPlanFor(t,p)$
• $TreatmentPlanIncludes(t,i,dos)$

In these sets of extensions, RwC_w1 and RwC_w2, we capture the different perspectives of the two specialists, the endocrinologist (e) and nephrologist (n). The main difference between RwC_w1 and RwC_w2 is the type of specialist providing input to the primary care physician (d) regarding the treatment plan (t) for the patient (p).

In RwC_w1, the endocrinologist (e) provides input, while in RwC_w2, the nephrologist (n) provides input. These unique perspectives and inputs will contribute to the medical team’s overall understanding of the patient’s condition and inform their decision-making process for the treatment plan.

In order to apply modal logic to the scenario and identify the accessibility relation between the two possible worlds ($w_1$ and $w_2$), we can represent the treatment plan for a patient with diabetes by defining a set of modal operators and axioms. Let us consider the following modal operators:

• $K_e:$ Represents the knowledge of the endocrinologist (in $w_1$)
• $K_n:$ Represents the knowledge of the nephrologist (in $w_2$)
• R: Represents the accessibility relation between $w_1$ and $w_2$

Now, let us formally represent the scenario using these modal operators and the previously defined extensional structures RwC_w1 and RwC_w2:

For w₁ (endocrinologist’s perspective), we have:

• $K_e,Patient\left(p\right)$
• $K_e,PrimaryCarePhysician\left(d\right)$
• $K_e,Endocrinologist\left(e\right)$
• $K_e,TreatmentPlan\left(t\right)$
• $K_e,InsulinType\left(t,i\right)$
• $K_e,Dosage\left(t,dos\right)$
• $K_e,HasDiabetes\left(p\right)$
• $K_e,ResponsibleFor\left(d,p\right)$
• $K_e,ProvidesInput\left(e,d,t\right)$
• $K_e,TreatmentPlanFor\left(t,p\right)$
• $K_e,TreatmentPlanIncludes\left(t,i,dos\right)$

For w₂ (nephrologist’s perspective), we have:

• $K_n,Patient\left(p\right)$
• $K_n,PrimaryCarePhysician\left(d\right)$
• $K_n,Nephrologist\left(n\right)$
• $K_n,TreatmentPlan\left(t\right)$
• $K_n,InsulinType\left(t,i\right)$
• $K_n,Dosage\left(t,dos\right)$
• $K_n,HasDiabetes\left(p\right)$
• $K_n,ResponsibleFor\left(d,p\right)$
• $K_n,ProvidesInput\left(n,d,t\right)$
• $K_n,TreatmentPlanFor\left(t,p\right)$
• $K_n,TreatmentPlanIncludes\left(t,i,dos\right)$

Now, let us define the accessibility relation R between the two possible worlds:

$R\left(w_1,w_2\right)$: This relation signifies that the information in w₁ (endocrinologist’s perspective) is accessible from w₂ (nephrologist’s perspective), and vice versa.

$R\left(w_2,w_1\right)$: This relation signifies that the information in w₂ (nephrologist’s perspective) is accessible from w₁ (endocrinologist’s perspective).

By defining the accessibility relation R between w₁ and w₂, we allow the sharing of knowledge between the two specialists’ perspectives. This, in turn, helps the medical team to collaborate and make informed decisions about the patient’s treatment plan. By combining the knowledge from both perspectives, the primary care physician can consider the input from both specialists and adjust the treatment plan accordingly.

In this context, the accessibility relation R allows us to reason about the combined knowledge of the endocrinologist and the nephrologist. Using modal logic, we can define some additional axioms to describe the relationship between their knowledge:

To represent the axioms using modal logic, we can use the following notation:

$$\begin{array}{c}{K}_{e}ProvidesInput\left(e,d,t\right)\to K_{n}ProvidesInput\left(e,d,t\right)\\ K_{n}ProvidesInput\left(n,d,t\right)\to K_{e}ProvidesInput\left(n,d,t\right)\\ K_{e}TreatmentPlanIncludes\left(t,i,dos\right)\wedge K_{n}TreatmentPlanIncludes\left(t,i,dos\right)\\ K_{d}TreatmentPlanIncludes\left(t,i,dos\right)\end{array}$$

In this notation, $K_e$ and $K_n$ represent the knowledge of the endocrinologist and nephrologist, respectively.

These axioms use the modal operators defined earlier to represent the relationship between the knowledge of the endocrinologist and the nephrologist. The first two axioms state that if one specialist provides input for the treatment plan, the other specialist is aware of this. The third axiom states that if both specialists agree on the insulin type and dosage for the treatment plan, the primary care physician will include it in the final plan. With these axioms, the medical team can analyze the shared knowledge between the endocrinologist and nephrologist perspectives and make more informed decisions about the patient’s treatment plan. This approach ensures that the different perspectives and expertise of the specialists are taken into account, leading to a better overall understanding of the patient’s needs and a more effective treatment plan.

Summary of Hybrid Model for Formal Modeling of Conceptualization in AI Systems

In summary, the proposed hybrid model for formal modeling of conceptualization in AI systems integrates the principles and approaches from ontology and epistemology to create a comprehensive and robust representation framework that accommodates both intensions and extensions. By incorporating both ontological and epistemological perspectives, the model is able to provide a more comprehensive and precise representation of knowledge and beliefs within a given domain. The use of modal logic, specifically the epistemic modal operator K and the accessibility relation R, allows for reasoning about the different perspectives and beliefs within the system, providing a more robust and accurate representation of knowledge showing the potential of the model to be applied to any domain where there are different perspectives and beliefs that need to be represented and reasoned about.

4. Implications, Limitations, and Future Research

4.1. Implications for Future Research and Practice

The conclusions drawn from our literature review and the proposed hybrid model for formal modeling of conceptualization in AI systems have several implications for future research and practice in the field of AI systems, particularly in domains requiring the representation and reasoning of various perspectives and beliefs. This promising approach to representing knowledge and reasoning aims to address the limitations of existing models. Key implications include:

• Improved AI system performance: By providing a consistent and accurate representation of knowledge, beliefs, and relationships within a domain, the proposed model may contribute to enhanced decision-making and problem-solving capabilities in AI systems.
• Interdisciplinary collaboration: The integration of ontology, epistemology, and modal logic in the proposed model highlights the importance of interdisciplinary collaboration in addressing complex problems in AI systems. This approach can inspire future research to draw upon diverse fields to create innovative solutions.
• Scalability: The proposed model’s flexibility and adaptability can support the growth and expansion of AI systems in various domains, allowing for the seamless integration of new entities and relationships.
• Standardization: The formal modeling approach can contribute to the development of standard protocols and guidelines for representing knowledge and beliefs in AI systems, facilitating interoperability and compatibility among diverse systems.

4.2. Limitations

Despite the potential benefits of the proposed hybrid model, there are some limitations that should be considered:

• Complexity: The integration of ontology, epistemology, and modal logic in the proposed model may increase its complexity, which could present challenges in implementation and maintenance.
• Applicability: Although the patient treatment journey scenario demonstrated the effectiveness of the proposed model, its applicability to other sectors and use cases remains to be further explored.
• Evolution of knowledge: The proposed model may not fully account for the dynamic nature of knowledge and its continuous evolution in various domains, potentially requiring periodic updates to maintain accuracy and relevance.

4.3. Future Research Directions

To address these limitations and further refine the proposed hybrid model, future research could explore the following areas:

• Development of tools and frameworks: To facilitate the implementation and maintenance of the proposed model, future research could focus on developing tools, frameworks, and techniques that streamline the process. For example, in the healthcare domain using a graph database like Neo4j, researchers could define axioms in modal logic, design a graph schema capturing modal logic relationships, assign properties to nodes and relationships, import healthcare data adhering to the schema, and query the graph using Cypher to analyze the healthcare domain while incorporating modal logic. By developing tools, frameworks, and techniques that support these steps, future research can streamline the implementation and maintenance of the proposed model, making it more accessible and practical across various domains.
• Evaluation in diverse contexts: Additional case studies in various sectors and use cases could be conducted to assess the generalizability and robustness of the proposed model across different contexts.
• Adaptive modeling: Incorporating mechanisms for handling the dynamic nature of knowledge and its evolution in various domains could enhance the proposed model’s effectiveness and applicability.
• Integration with other AI techniques: Exploring the synergies between the proposed model and other AI techniques, such as machine learning and natural language processing, could provide additional insights and further improve the representation and reasoning capabilities in AI systems.

The proposed hybrid model can be employed in semantic integration, a process of combining and reconciling information from different sources to create a unified and coherent understanding. The model’s combination of ontology, epistemology, and modal logic enables it to effectively represent and reason about the knowledge, beliefs, and relationships within various domains. This makes it particularly well-suited for addressing the challenges posed by semantic integration.

When applied to semantic integration, the proposed model offers several advantages:

• Enhanced understanding: By representing the underlying structure and meaning of information from diverse sources, the model can facilitate a more comprehensive understanding of the data, leading to better decision making and problem solving.
• Conflict resolution: The model’s ability to represent and reason about different perspectives and beliefs can help identify and resolve inconsistencies or contradictions that may arise during the integration process.
• Improved interoperability: By providing a standardized and formal approach to representing knowledge and beliefs, the model can enhance the compatibility and interoperability of information from different systems, facilitating seamless integration.

5. Conclusions

This paper has presented a novel hybrid model for representing shared conceptualization in decentralized AI systems, integrating ontology, epistemology, and epistemic logic. The model’s potential applicability extends far beyond healthcare to encompass a wide range of domains and industries. In our rapidly evolving and interconnected world, the ability to reason about different perspectives and beliefs is of paramount importance. The proposed model rises to this challenge, offering a powerful and innovative tool for researchers and practitioners in the AI field. As AI advancements continue to redefine the boundaries of what is possible, this model is poised to play a pivotal role in realizing these possibilities. We firmly believe the proposed model will leave an indelible mark on the AI field, and we eagerly anticipate its continued development, refinement, and application.

The future research directions outlined in the subsequent section provide a roadmap for further enhancing the model’s effectiveness and broadening its applicability. By addressing these directions, we hope to contribute to the advancement of AI systems in decentralized environments. We look forward to seeing the innovative applications and refinements that will undoubtedly emerge from this exciting field of research.