Coquaternions, Metric Invariants of Biologic Systems and Malignant Transformations

Abstract

Different hypotheses of carcinogenesis have been proposed based on local genetic factors and physiologic mechanisms. It is assumed that changes in the metric invariants of a biologic system (BS) determine the general mechanisms of cancer development. Numerous pieces of data demonstrate the existence of three invariant feedback patterns of BS: negative feedback (NFB), positive feedback (PFB) and reciprocal links (RL). These base patterns represent basis elements of a Lie algebra $sl\left(2,R\right)$ and an imaginary part of coquaternion. Considering coquaternion as a model of a functional core of a BS, in this work a new geometric approach has been introduced. Based on this approach, conditions of the system are identified with the points of three families of hypersurfaces in R⁴₂: hyperboloids of one sheet, hyperboloids of two sheets and double cones. The obtained results also demonstrated the correspondence of an indefinite metric of coquaternion quadratic form with negative and positive entropy contributions of the base elements to the energy level of the system. From that, it can be further concluded that the anabolic states of the system will correspond to the points of a hyperboloid of one sheet, whereas catabolic conditions correspond to the points of a hyperboloid of two sheets. Equilibrium states will lie in a double cone. Physiologically anabolic and catabolic states dominate intermittently oscillating around the equilibrium. Deterioration of base elements increases positive entropy and causes domination of catabolic states, which is the main metabolic determinant of cancer. Based on these observations and the geometric representation of a BS’s behavior, it was shown that conditions related to cancer metabolic malfunction will have a tendency to remain inside the double cone.

1. Introduction

Much is known about the molecular mechanisms of the regulation of cell, organ and system functions. System mechanisms of interactions of these structural elements, mainly related to negative feedback and positive feedback circuits, have also been an object of discussions for decades. On the other hand, little is known about the general principles of organization of biologic systems as whole structures [1,2,3,4,5,6]. The lack of this knowledge prevents understanding of the basic mechanisms of the formation of pathologic derivatives of normal biologic systems, which includes cancer [7,8,9,10,11].

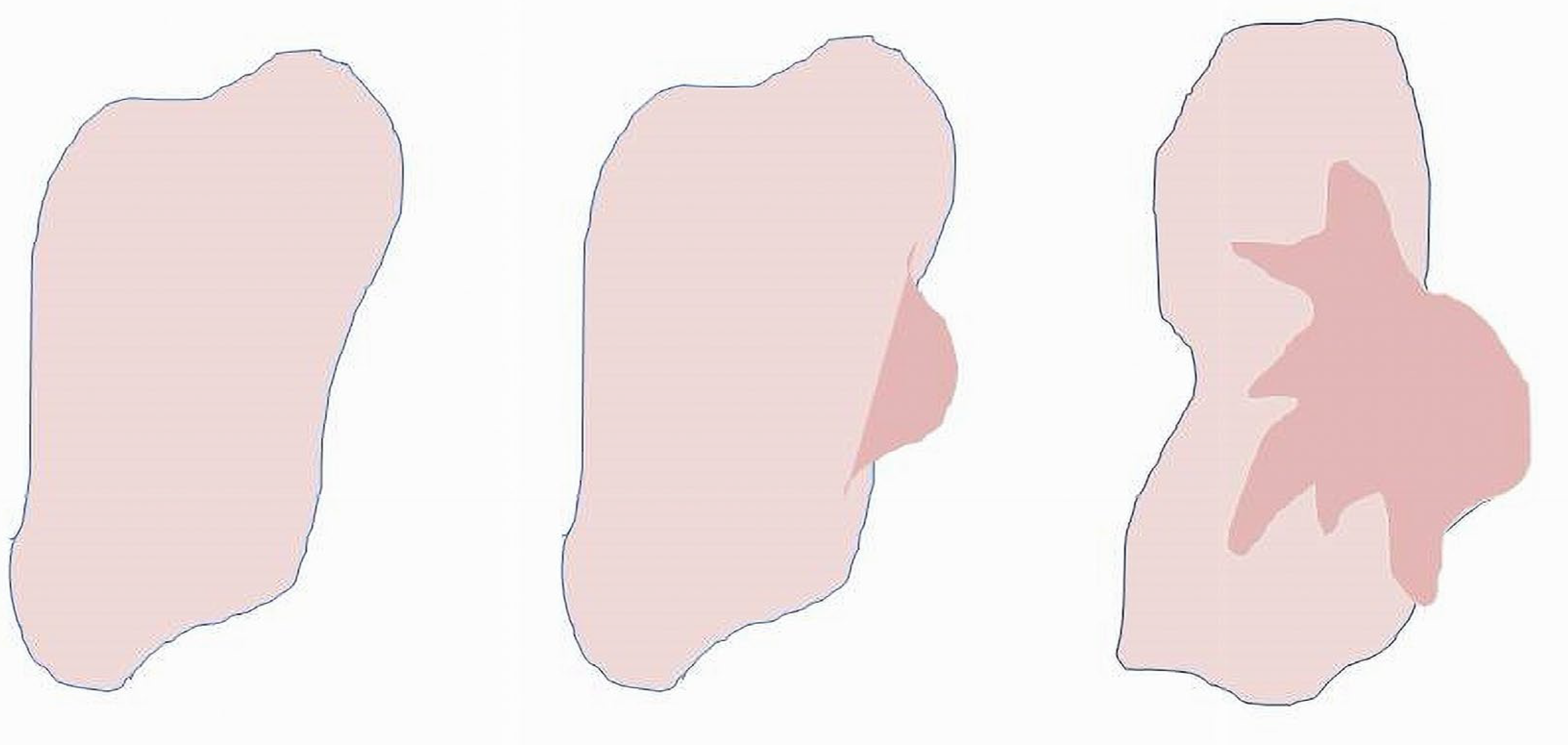
The uniqueness of cancer lies in its ability to invade and destroy normal biological tissue. Invasive growth is the single most important determinant of cancer. This property seems to be acquired by pathologic changes in the normal functional structure of BS, resulting in the inability of the deteriorated system to maintain its wholeness. Unlike the classical medico-biologic approaches based on local characteristics of cancer, and finding biochemical mechanisms and markers of pathologic proliferation of immature cells, encouraging results have also been obtained using mathematical methods. Mathematical models devoted to cancer development are mostly based on the properties of cancer cells, namely, their ability to multiply, and factors controlling pathologic proliferation [12,13,14,15]. On the other hand, malignant transformations considered as pathologic structures that originated from normal systemogenesis, were linked to the irreversible changes in the base mechanisms, mainly reciprocal interactions between proliferating cells [16].In the scope of this approach, functional invariants of BS determining the system as a functional module were also examined, whose properties could be modeled using algebraic structures. Lie algebra $sl\left(2,R\right)$ and coquaternions have natural representations in the known base regulatory elements of BS, namely, PFB, NFB and RL (PNR) [16,17].

The goal of this work is to continue the use of algebraic approaches with new applications related to the metabolic properties of BS. In the scope of this work, another aim is the development of new geometric methods describing the structural and functional changes in the basis PNR patterns of BS leading to cancer development (Figure 1).

2. Functional Properties of a Biologic System

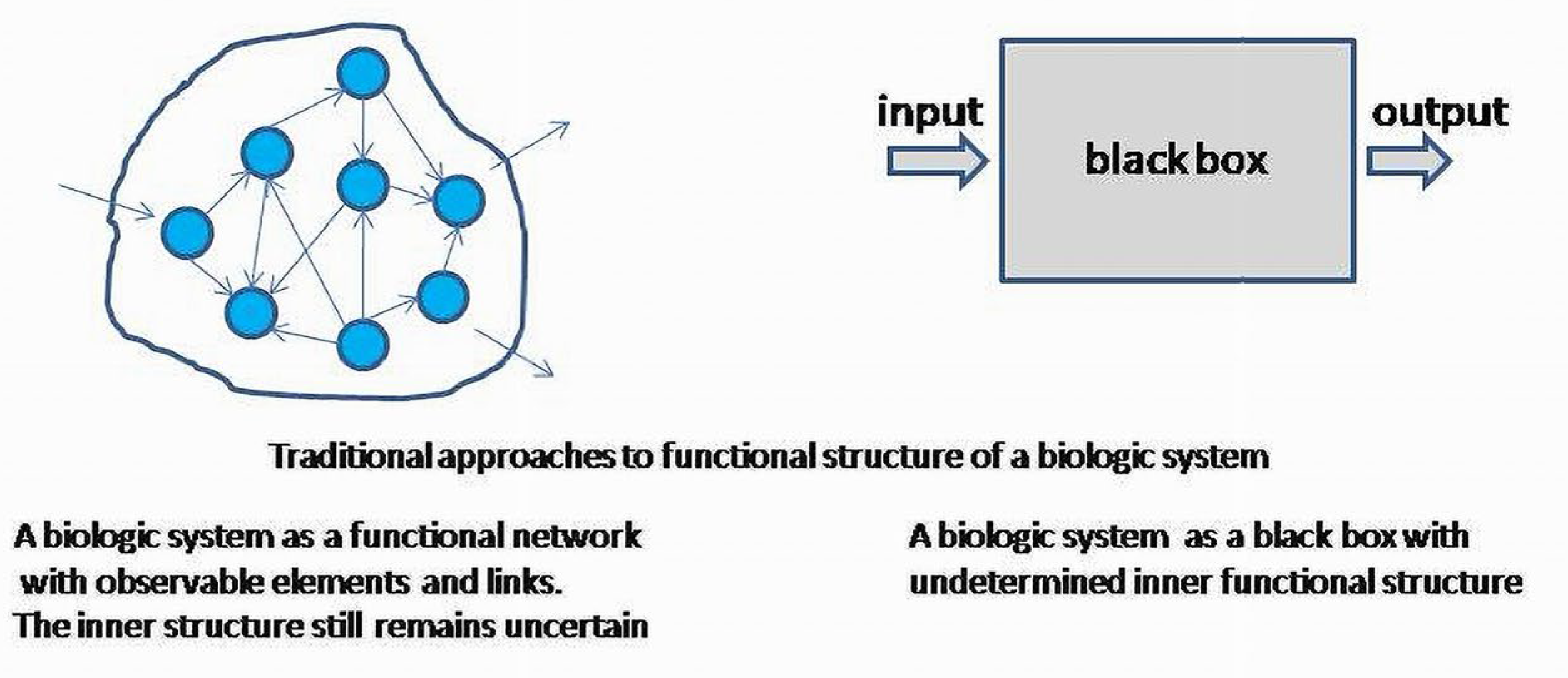
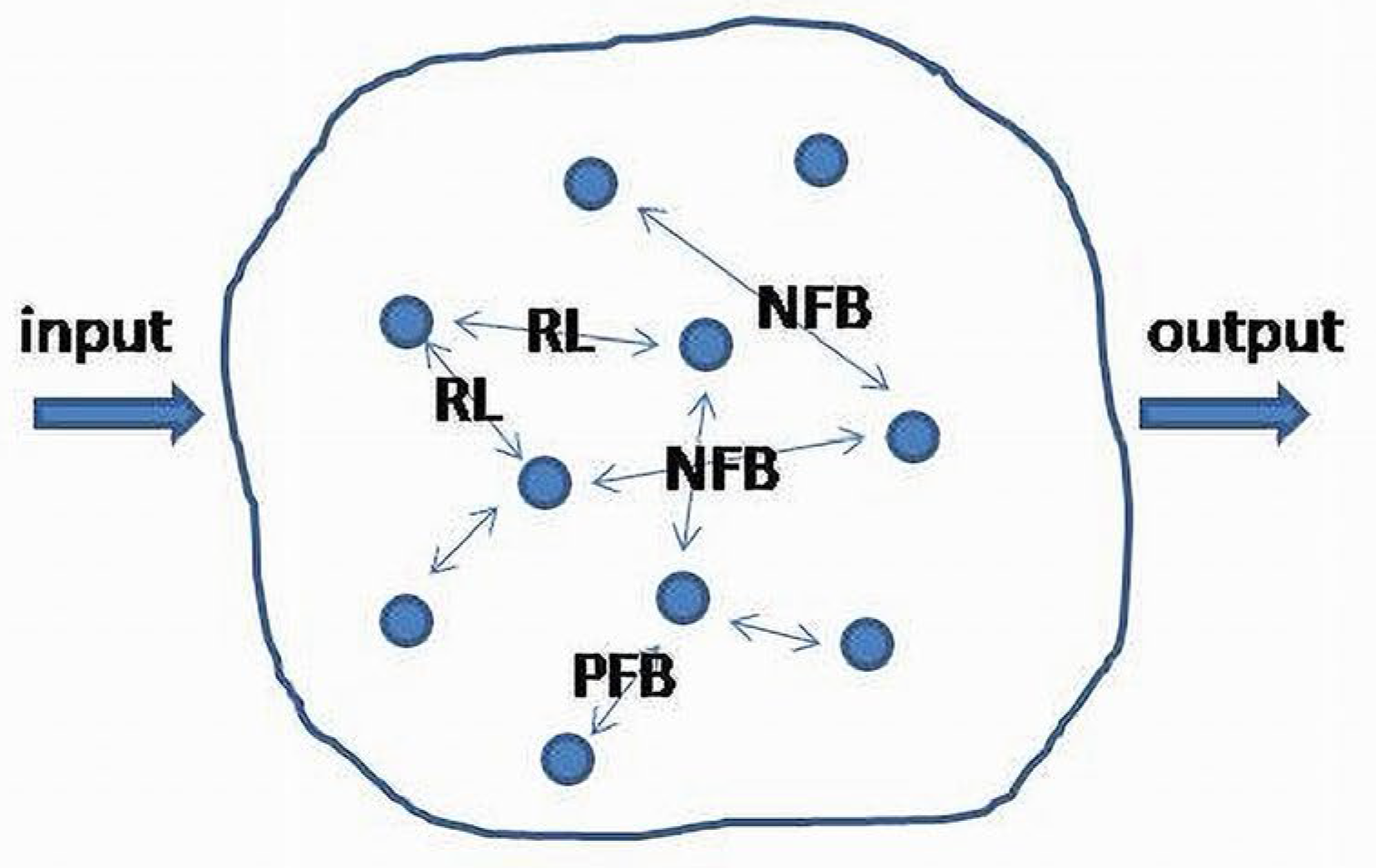
For the purposes of this work, the commonly used and poorly defined term “a biologic system (BS)” will be specified. A biologic system is a morphological and functional unit maintaining its internal structure and outcome. More formally, a BS is a set of morphologic elements and internal links, among them providing a BS with autoregulatory properties. Input and output relate a BS to the surrounding systems considered as its environment. Examples of a BS are biological cells, tissues, organs and functional systems, such as cardiovascular, endocrine, digestive systems, etc., (Figure 2).

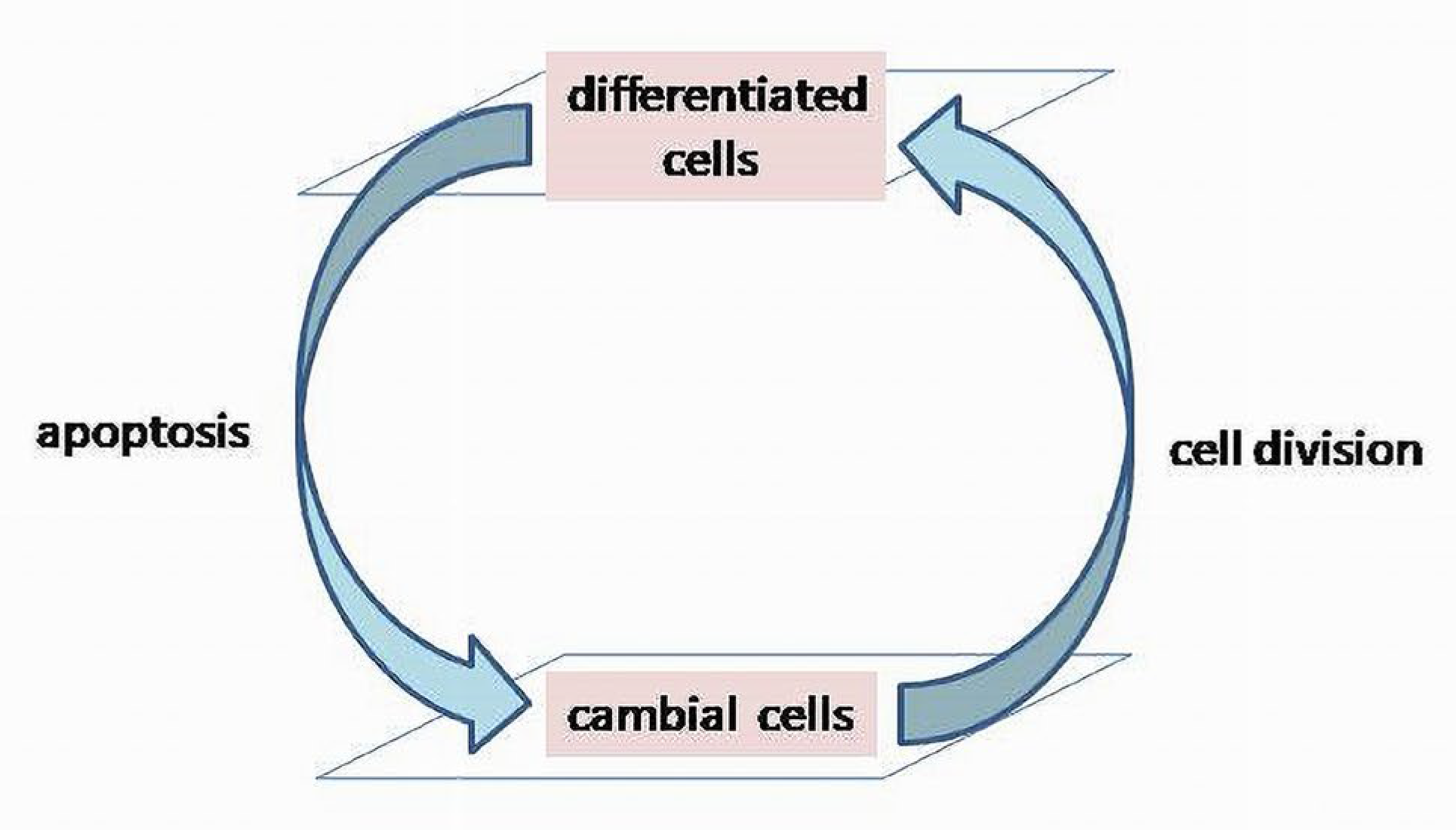
Life span of biologic matter is short, and the system’s reproductive mechanism provides its continuity in the development of species (phylogenesis) and individuals (ontogenesis). Through a reproductive mechanism, a BS maintains its functional and morphological wholeness. During the early stages of individual development (ontogenesis), it determines dominating proliferative activity of cells over the apoptosis (active elimination of malfunctioning cells) [18,19]. It is assumed that apoptotic and cell’s proliferation mechanisms are organized in a cycle and it will be termed a cell renewal cycle (CRC). It should not be confused with the cell’s mitotic cycles, which are included in the CRC as parts determining chromosomal changes before division.

A biologic cell is a minimal functional and morphological unit whose self-regulatory mechanisms possess certain levels of autonomy. The regeneration of biological tissues and organs after mechanical injury or microbial or viral invasion seems to also use features of the cell renewal mechanism [20].

Cell renewal processes embrace larger functional systems than cells themselves providing viability and integrity of tissues and organs. In this context, a CRC is a basic mechanism of reproduction of biological cells, tissues and organs, etc. The accuracy of the reproduction will determine the ability of a functional system to maintain the stability and longevity of its structural and functional units. The CRC is a dynamic process consisting of two main components: apoptosis (the elimination of malfunctioning cells) and cell divisions (Figure 3) [21,22].

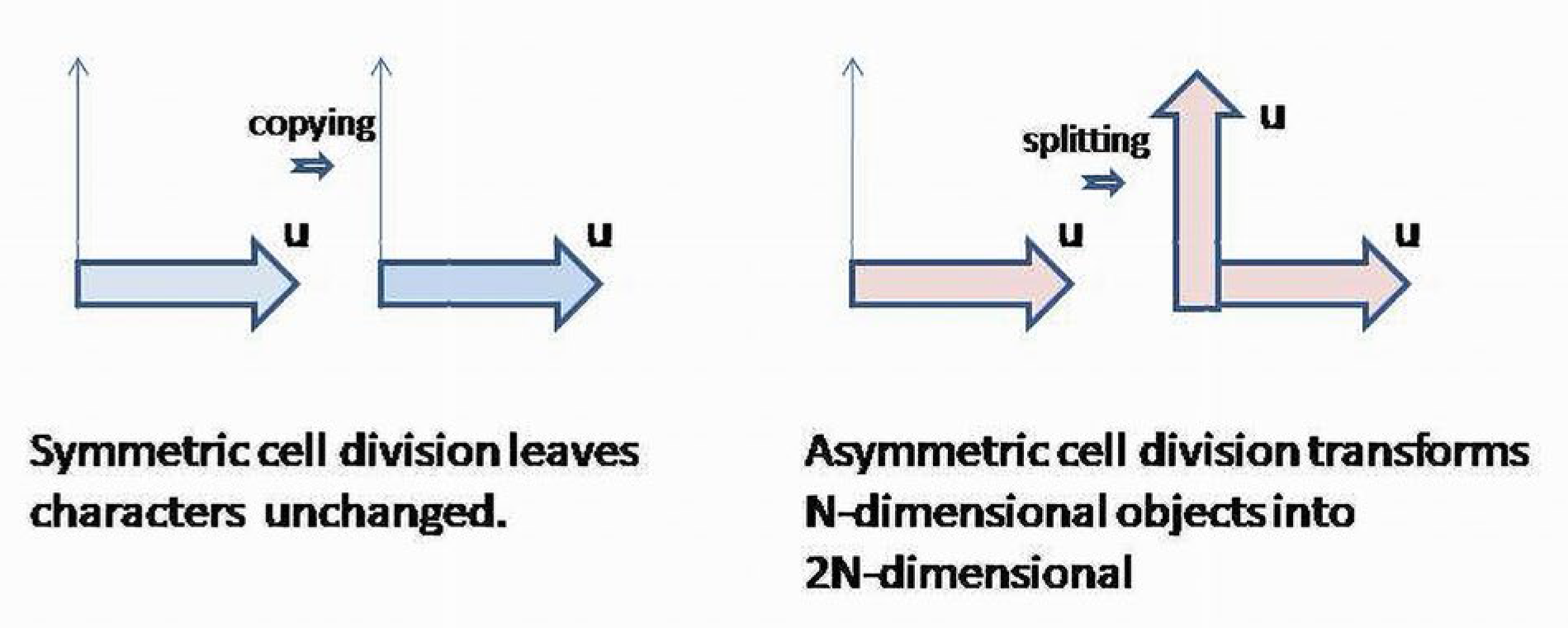
There are two major populations of cells: mature (differentiated) and cambial (stem) cells. Accordingly, there are two kinds of cell divisions: symmetric, when the result of the division is two identical cells, and asymmetric, when a cambial cell is divided into two complementary yet differentiated cells. Symmetric division simply copies the functional and morphological characteristics of a cell-progenitor, whereas asymmetric division splits the main characters of the cell precursors into two complementary classes [23,24]. A symmetric division keeps newly formed cells within the existing spectrum of functional properties, whereas asymmetric division increases the number of distinguishable characteristics of cells. In other words, asymmetric division increases the dimensionality of the space, where the newly formed cells could specifically contribute to the system’s outcome. It transforms the functional space of a cambial cell into a space containing two complementary subspaces, causing the cambial functions to be “distributed” between the two populations of differentiated cells. Thus, cell differentiation splits the characters controlled by cambial cells, and increases the number of distinguishable and separable characteristics of a BS (Figure 4).

Asymmetric division also bridges the functional levels of stem cells and differentiated cells. Mechanisms regulating the transformations from stem cells to mature differentiated cells may play a key role among the factors preventing malignant transformations.

Splitting is also considered to be a mechanism of the evolution of a species. It possibly follows the same strategy during the adaptation of the characters, which were drifting from their initial phenotypic and genotypic features. The links between the gaps, when compared with their ancestors, were possibly encoded in chromosomes, thus bridging separable stages of evolution within a species.

The existence of the separable stages of evolution is fairly well demonstrated by similarities of phenotype features of mammalian embryos of different species, indicating the possibility of having common roots of development. Ontogenesis mimics phylogenetic stages during the embryonic period, splitting functional levels into stem and differentiated cells. The CRC metabolic machine provides interactions between hierarchical levels, while maintaining them as separable systems.

It seems that only the core functions of BS can be reproduced during the life cycle of individuals. Other, supplemental, features being developed use additional functional mechanisms. The development and realization of these features strictly depend on the surrounding system environment. For instance, the anatomical and functional organization of the human body, the structure of regulations of cardiovascular (CV), endocrine, respiratory, etc., systems, including metabolic pathways and behavioral reactions such as conditional reflexes, are some examples of the genetically determined functions, then inherited by individuals. On the other hand, physical training will result in accelerated biochemical reactions and newly formed metabolic pathways. The same applies to the skills and behavioral patterns obtained through conditional reflexes, which are examples of traits developed additionally to the properties of the core functions. Morphological and functional features acquired during an individual life circle cannot be inherited.

The partition of the functional structure of a BS into two components makes sense not only because additional regulatory mechanisms (“periphery, superstructure”) make an ideal correspondence between the inherited (“core”) functions and specific environmental features, but also because supplementary functional mechanisms play a role in the formation of new, congruent to the environment and becoming genetically established characters. The “core” and “periphery” are two components that provide structural wholeness of the developing BS. A functional core has the “privilege” to provide the system with basic mechanisms, keeping a BS stable.

From clinical and experimental observations, it follows that the stability of the system and its components is determined by functional mechanisms capable of changing and even reversing the system’s current conditions. In other words, a system’s stability depends on its ability to redirect the deviated metabolic or other functional processes back towards equilibrium. If measured, these processes could be shown as fluctuations in the system’s conditions around the equilibrium. Equilibrium states are known as physiologic constants (the glucose level of the blood, concentration of hormones, electrolytes, body temperature, heart beats, respiratory rate, etc.). It is suggested that the behavior of a BS observed through the system’s regulatory mechanisms may have mathematical group properties. The group structure of regulatory mechanisms may be considered as one of the system’s core features [17,25]. Not every biochemical reaction is invertible; however, the normal system is capable of returning deviated states to the equilibrium, bypassing virtually existing reversal pathways. In the case of deterioration of a regulatory mechanism, the system will acquire this tendency in displacing the equilibrium from the acceptable margins. A displaced equilibrium is a direct cause for the development of pathological conditions. In practice, the equilibrium is considered as a state when all of the components of the system are balanced and do not require additional metabolic pathways. A normally functioning system is capable of returning currently deviating states back to equilibrium.

Regulatory mechanisms observed on different functional levels of a BS are supposed to have some properties additional to the mathematical group [16,17,25].

3. The Structure of Functional Invariants (Basis Patterns) of Biologic Systems

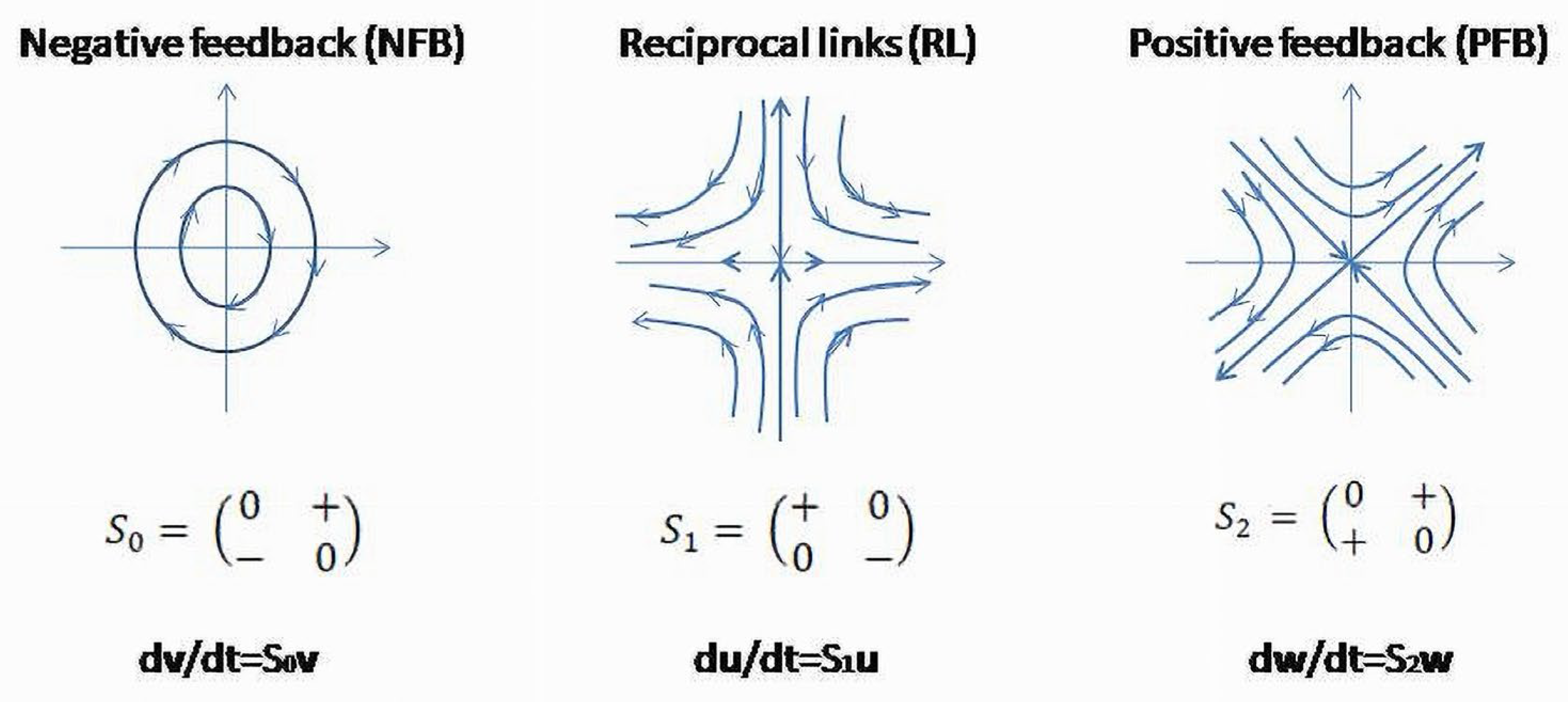
Clinical and physiologic observations demonstrate the existence of regulatory patterns which possess universal (invariant) functional properties. They have been found in different levels of the system’s organization- the level of biological cells [26] and the levels where cells are grouped in organs and functional systems such as CV, GI, respiratory endocrine systems, etc. The functional invariants are negative feedback (NFB), positive feedback (PFB) and reciprocal links (RL) [26,27,28,29,30,31]. The latter was recently introduced as a third functional invariant of the inner functional structure of a BS (Figure 5) [17,25].

These invariants presented in a matrix form in Figure 5 are linearized structures (phase flows) obtained as approximations of feedback circuits between the two subsystems.

Here are some examples demonstrating the existence of PNR links between subsystems at different functional levels. On the level of biological cells, NFB, PFB and RL (PNR) regulate the key functional properties of intracellular biochemical pathways [26]. Cardiovascular (CV), endocrine and gastrointestinal (GI) systems will be considered on the levels of biological organs and functional systems. NFB in a CV system determines the values of arterial blood pressure, depending on cardiac contractions during physical exercises. It also regulates atrial and ventricular volumetric strokes and pressure parameters, depending on cardiac preload and afterload values. In the endocrine system, NFB represents hypothalamic–pituitary, hypothalamic–suprarenal and pituitary–thyroid interactions. In the GI system, NFB controls the filling–emptying cycles of intestinal segments in different parts of the GI tract through the relationships between smooth muscle tone and stretching [32,33].

In the CVS, contraction and relaxation phases between the atria and ventricles occur reciprocally. Rheology of the blood is also regulated by reciprocally acting clot formation and clot degradation cascades. In the endocrine system, insulin- and glucagon-releasing mechanisms have reciprocal interactions. In the digestive system, contractions and relaxations of intestinal wall muscles and sphincters occur reciprocally during the filling–emptying cycle [32,33,34].

In the CV system, tachycardia causes ischemia of the conductive system, which in turn may cause its progression up to severe forms of cardiac arrhythmias (PFB). Tachycardia could also be a form of PFB mechanism accelerating oxygen supply to the muscles during strenuous physical exercises. In the reproductive system, during the first stage of delivery, the release of oxytocin stimulates uterus contractions, which, in turn, accelerates oxytocin-releasing mechanisms causing more oxytocin production. In GI system, during rectal emptying, the contractions of rectal wall and pelvic floor musculature occur simultaneously with the relaxation of anal sphincters (RL). The contractile forces and degree of relaxation become more pronounced during the following propulsive waves (PFB).

4. Ordinary Differential Equations and Matrix Structure of Functional Base Elements

The properties of NFB, PFB and RL acquire more functional details, if these patterns are expressed in a matrix form relative to a standard basis. $S_0=\left(\begin{array}{cc}0& 1\\ -1& 0\end{array}\right)$, $S_1=\left(\begin{array}{cc}1& 0\\ 0& -1\end{array}\right)$, $S_2=\left(\begin{array}{cc}0& 1\\ 1& 0\end{array}\right)$ are matrices of NFB, RL and PFB, respectively [25]. These matrices have some special properties as basis elements of a Lie algebra $sl\left(2,R\right)$ of a Special Linear Group $SL\left(2,R\right)$ ($SL$ for the group is in capital letters) [17,35,36,37,38]. The physiologic properties corresponding to these functional patterns could be demonstrated by the integral curves which are one-parameter group of diffeomorphisms $f_t:t\to \exp \left(t{S}_i\right)$ determinedby infinitesimal generators of these groups, which are the Lie algebra elements equipped by the defined basis $\left\{S_0, S_1, S_2\right\}$ [16,25,36]. Integral curves are solutions of the ordinary differential equations (ODE) $\dot{\mathit{u}}=S\mathit{u},$ where the matrix of the operator $S$ is an element of the algebra $sl\left(2,R\right)$. Each element of the basis $\left\{S_0, S_1, S_2\right\}$ is a non-singular (invertible), traceless $\left(Tr{S}_i=0\right)$ matrix, determining neither convergent nor divergent processes. This means that for the closed, isolated system and ideal conditions, these subsystems are autonomous functional structures whose actions do not require additional (external) sources of energy. Their integral curves lie in the same energy level that confirms the system’s autonomy (Figure 6) [39].

Besides the $\left\{S_0, S_1, S_2\right\}$ basis, $sl\left(2,R\right)$ may also be equipped with other bases. For example, the $\left\{S_i, N_{+}, N_{-}\right\}$ basis contains nilpotent elements $N_{+}, N_{-}$, which are singular (not invertible) and related to the non-reproducible regulatory elements; thus, they cannot serve as base functions of a BS. The space created by the PNR basis is a three-dimensional space comprising regulatory patterns of a BS.

It is assumed that the basis $\left\{S_0, S_1, S_2\right\}$ determines the structure of a functional core of a BS [24]. Because of the distinguishable morphological features of a BS (cells, organs, etc.), it is also proposed that formation of steady morphological structures with established functional links provided by the base patterns is a property of a BS to reproduce its own elements, which must be encoded in chromosomes [40,41,42]. Depending on the context, either terms “base” or “basis” regarding PNR patterns can be used.

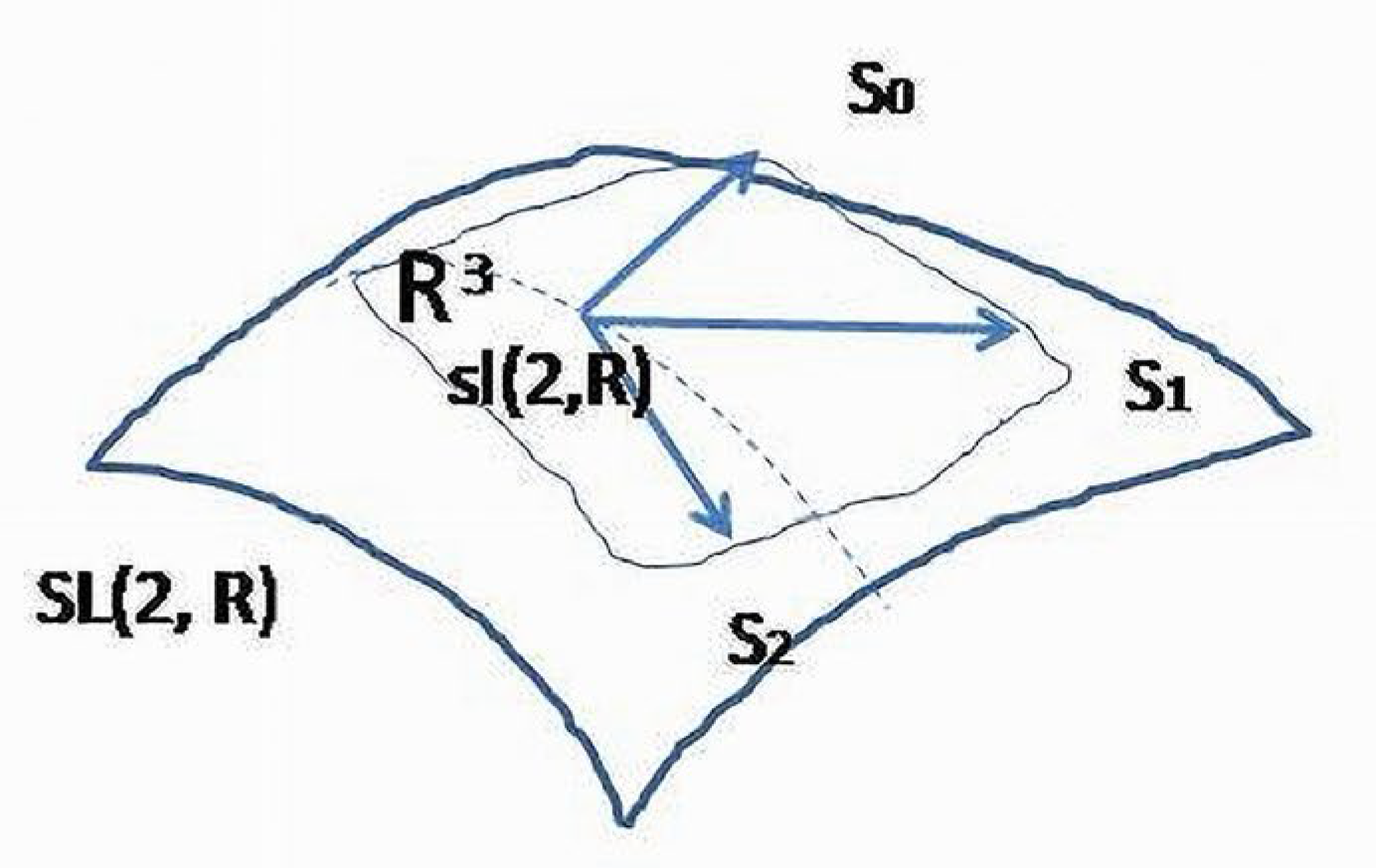
5. A Functional Superstructure and Hierarchy Built from Base Elements

For two-element dynamical systems, only three types of matrices satisfy the conditions to be traceless, invertible (non-singular) and contain a minimal number of non-zero entries- $\pm S_0, \pm S_1, \pm S_2$. These matrices are the basis elements of a Lie algebra $sl\left(2,R\right)$ and formal expressions for NFB, RL and PFB, respectively.

Lie algebra $sl\left(2,R\right)$ is a linear approximation of the $SL\left(2,R\right)$ group. Elements of $sl\left(2,R\right)$ lie in the tangent to the $SL\left(2,R\right)$ space, and in this sense, $SL\left(2,R\right)$ are “closer” to real physiologic processes. In a small neighbourhood, these two structures describe similar relationships between variables, and, for simplicity, the algebra elements are considered as functional patterns adequately describing the internal structure of a BS (Figure 7). The dynamical relationships between variables of a BS (2D carrier space) could be visualized through integral curves obtained as solutions of (linearized) differential equations. Each curve belongs to a 1-dimensional manifold of $M\left(2,ℝ\right)$-related variables and will determine behavior of a system considered as a whole structure on some hierarchical level.

It was mentioned before that integral curves corresponding to ${\mathit{S}}_0, {\mathit{S}}_1, \mathrm{and} {\mathit{S}}_2$ operators lie in the same energy level, so that the corresponding functional structures will require no additional sources of energy. Thus, these patterns determine the functional flows inherent or naturally possessed by for conservative (autonomous) systems. It indicates the system’s independence from the environment. The system’s autonomy also implies the stability of $S_i$ patterns as intrinsic regulatory elements providing the whole system with a unique self-regulatory mechanism.

On each level of functional systems (molecular, cell, organ, etc.), a set of variables always exists, which are related to each other by functional patterns ($S_i$), so that they are $S_i$-linked. $S_i$-linked pairs form steady groups of elements united (using physiologic language) by reciprocal links, negative feedback loops or positive feedback. Because of the functional stability of $S_i$ patterns, morphological units being grouped by each of these patterns may be considered as separable subsystems and potentially new variables belonging to the next level of morphological and functional organization. These groups, considered as whole structures, will represent morphological units of the next level formed as classes of equivalent elements. Examples of the established distinguishable classes include molecules, cells, tissues, organs, etc. Formation of the steady functional triplets $\left(S_0, S_1, S_2\right)$ makes a corresponding structural level functionally closed; this is a required condition for the beginning of the creation of the next, higher in the hierarchical scale, level.

Formation of hierarchical levels of a BS could agree with the following scenario: consider an initial level as a homogeneous space of structural (biochemical) units related to each other through the chaotic interactions. Due to the permanent forces of the surrounding environment, some elements will form steady, resistant to the destructive environmental forces, pairs involved in the orbits of the united by $S_i$-pattern elements. Only the three steady, orthogonal to each other, two-dimensional spaces (independent vector fields) could be formed according to $S_0, S_1, \mathrm{and} S_2$ invariants. Thus, the next to the homogeneous space functional level will be presented by a three-dimensional space spanned by $\left\{S_0, S_1, S_2\right\}$ basis acting on the elements of two-dimensional space of morphologic elements. Because two components are finalizing the stages of phylo-ontogenetic splitting, $S_i$-linked elements (subsystems, systems) will be named splitors. These pairs of elements considered as separable variables will fill the newly formed hierarchical level (3-dimensional $ℂ$-module) or (6-dimensional ℝ-module). Before the system is able to reproduce $S_i$-linked morphological structures, temporary morphological associations and functional relationships, including nilpotent patterns, will also be formed.

Between temporary elements, all theoretically possible relations could be created that may be formally demonstrated by any of $M\left(2,ℝ\right)$ matrices used in ODE, where temporary elements may also play the role of variables. These relationships form a superstructure linking the current and the next in the hierarchical scale levels. Thus, the formation of the next to the homogeneous space functional level will correspond to the mapping: $f: ℝ\times ℝ$→$ℂ.$ Formally, if an operator (matrix) and its related variables (vector-variable) are to be considered as a single new variable, it will belong to the set of elements representing functional subsystems of the next level. Thus, a functional hierarchy is being formed, where the whole (irreducible) functional pattern with its corresponding carrier space will represent a single variable or character. In other words, if the $M\left(2,ℝ\right)$ module is substituted by the $M\left(2,ℂ\right)$ module, then $M\left(2,ℂ\right)$ will represent a regulatory structure of the new carrier space and new irreducible variables for two-element systems and matrix operations on them.

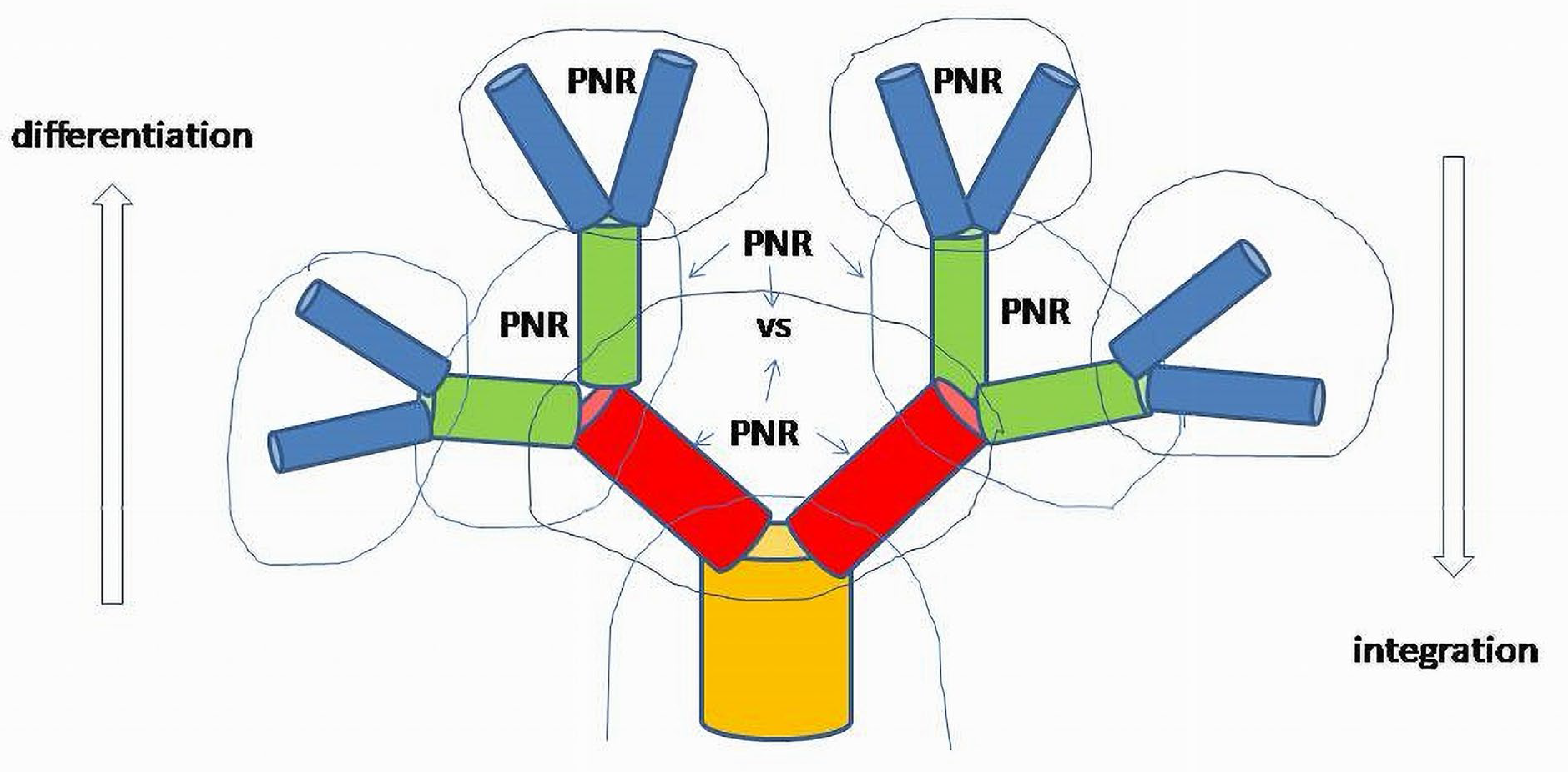
Reciprocal Splitting and Hierarchical Structure of Biologic Functions

A BS is a complex multi-element structure, and because of its complexity the system’s reproductive mechanisms should presume hierarchy in organizing its structural elements. The formation of a hierarchical structure seems to be a part of a long phylo-ontogenetic development.

Phylogenetic tree is an acceptable model of development of species. It is organized in a sequence of split taxonomic units. Splitting is a characteristic feature of a large-scale development. Ontogenesis mimics phylogenesis as a stage-dependent process of individual development; thus, they both follow the same principles of development.

A phylo-ontogenetic tree is also a graph where each branch with its input and output is represented by a functional system(Figure 8).

The splitting mechanism differentiates the system into two autonomous reciprocal subsystems. As a system integrated from two components, it possesses a PNR basis, whereas each component, due to its autonomy, must also be operated through the functional space spanned by its own PNR elements. A two-element system of split branches determines the primary hierarchy between the regulatory structures of differentiated elements and the integrated system. The progenitor’s functional structure existing in a relatively rudimental form will be transformed into a two-element system. Thus, the vertical sequence of the layers of split branches, especially in cases of asymmetric divisions of stem cells, will explicitly show hierarchy, for instance, between the level of cambial cells (initial branch) and the next level in a row of differentiated cells (split branches).

If a system is viewed as a part of another system, the inner structural elements of subsystems can be considered indistinguishable. In this case, the system is involved as the whole undifferentiated element in another, more complex, differentiated, system; structural (inner) properties of subsystems will be characterized only by input and output as signaling agents for other subsystems. Signaling agents will form the whole space of a regulatory network determining an inner functional structure of the integrated system. The inner structure of the whole system is also formed by functional links reducible to invariant patterns in any level as PNR base or basis elements. PFB, NFB and RL (PNR) can always be observed directly, or as enucleated, linearized patterns obtained from the complex system at each level.

Consider a biologic system with undetermined internal structure, associated with a branch of a phylo-ontogenetic tree. In this case, a system will only be characterized by input and output and realize its function by a single operator (a) (scalar), which transforms the input (x) to the output (ax).

For differentiation, not yet separated morphologically, a two-element system, a in an orthonormal basis, will be presented by a 2 × 2 in a general configuration matrix over $ℝ$,$A=\left(\begin{array}{cc}\mu & \xi \\ \nu & o\end{array}\right). A$ as a matrix of a second-order ODE represents the simple (linear) internal functional structure of a BS of two elements. Elements should satisfy the system’s requirements, i.e., together, they must form a self-regulatory unit. Similar to $A$ diagonal matrix $A^{\prime }$ will have entries obtained as solutions (roots) of the characteristic equation. ${\lambda }_{1,2}=1/2\left[\left(\mu +o\right)\pm \sqrt{{\left(\mu -o\right)}^2+4\xi \nu }\right]. A^{\prime }$ will indicate the property of the system to be presented as two separable subsystems with eigenvalues as input–output characteristics of split subsystems. Formally, it could be finalized as a direct sum of the operators, dividing the carrier space into two invariant subspaces. This property can be considered as a physiologic basis for biologic differentiation involved in a systemogenesis as a program of individual development towards more complex structures.

To describe mechanisms of hierarchical transformations we should relate outer links of the split elements with the internal functional structure of a system originating from the cambial element (branch–progenitor). Two differentiated elements comprise a system because they originated from the system: a common branch possesses the system’s structure by definition. Therefore, two differentiated, relatively autonomous, elements form a two-element system, which is also an auto regulatory unit of two separable elements. The system’s structure implies the existence of a 3D space of regulatory patterns between two elements spanned by PNR base represented by $\left\{Si\right\}$ matrices. Expressed as a system of two ODEs, a second-order (linearized) operator will determine “infinitesimal” relations between variables representing main characters or outcomes of the split branches.

The second-order self-adjoint (traceless) operators S over ℝ on the 2D space of biologic variables V are considered in this case. Because operators are acting on pseudo-Euclid space, being discussed further, they may have either diagonal or skew-symmetric spectrum (form) over ℝ. The spectrum of an operator will determine the partition of the space V; thus, it will tell us whether it may separate the space into two 1D invariant subspaces and act on each of them independently, or considered operating on a 2D space as irreducible over $ℝ$.

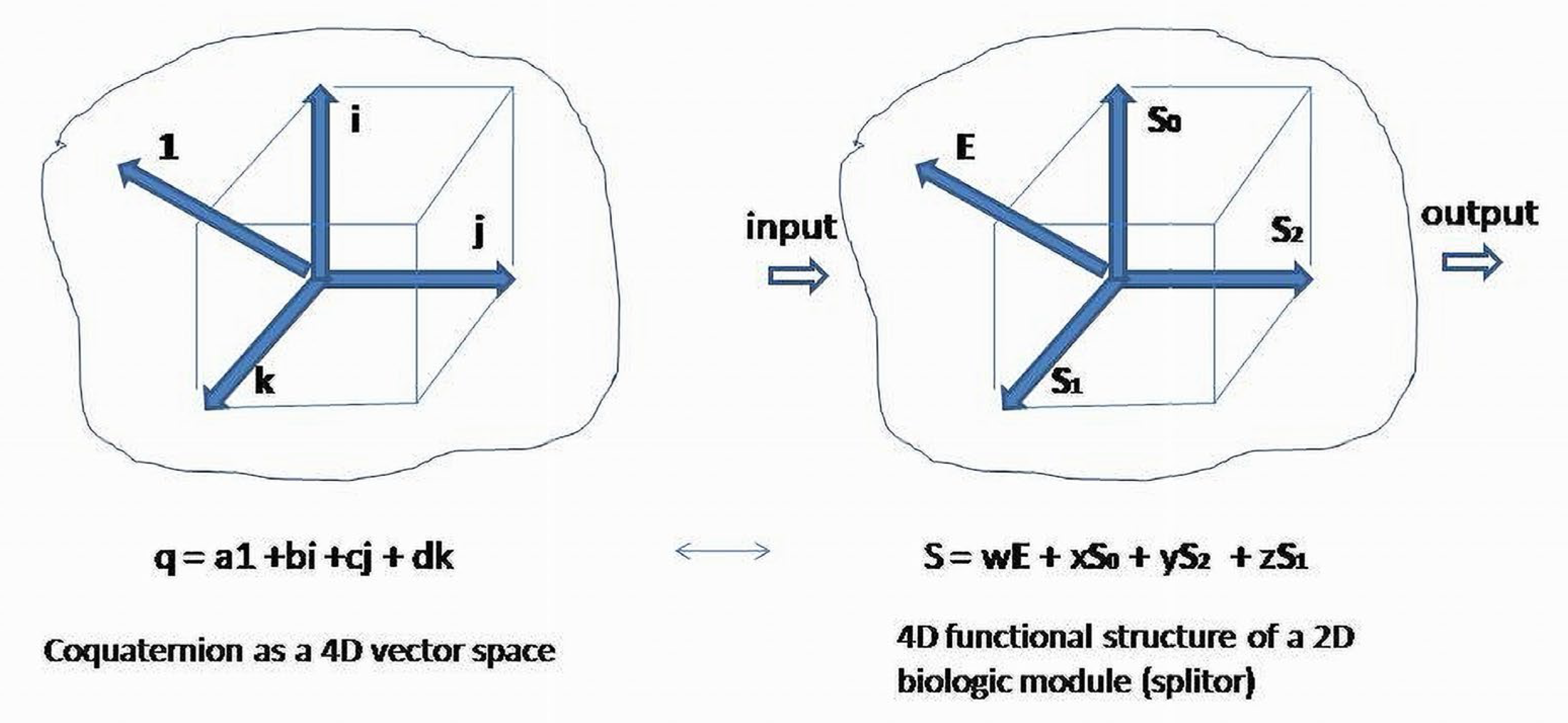
On an orthonormal basis, a matrix of an operator S for a two-element system having separable (not obviously separate) subsystems, has the form $A=\left\{\left(\begin{array}{cc}\mu & \xi \\ \nu & o\end{array}\right): \left(\mu ,\nu ,\xi ,o\right)\in ℝ\right\}.$ The space of the second-order matrices $M\left(2,ℝ\right)$, $A\in M\left(2,ℝ\right)$ is isomorphic to the space of coquaternions $\mathrm{c}ℍ$:

$$A\leftrightarrow q=\frac{1}{2}\left[\left(\begin{array}{cc}\mu +o& 0\\ 0& \mu +o\end{array}\right)+\left(\begin{array}{cc}0& \xi -\nu \\ \nu -\xi & 0\end{array}\right)+\left(\begin{array}{cc}0& \nu +\xi \\ \nu +\xi & 0\end{array}\right)+\left(\begin{array}{cc}\mu -o& 0\\ 0& -\mu +o\end{array}\right)\right].q\in \mathrm{c}ℍ.$$

Basis elements of coquaternion are presented as four second-order unit matrices with entries combined from coefficients of $A:\frac{1}{2}\left[\left(\mu +o\right)\left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right)+\left(\xi -\nu \right)\left(\begin{array}{cc}0& 1\\ -1& 0\end{array}\right)+\left(\nu +\xi \right)\left(\begin{array}{cc}0& 1\\ 1& 0\end{array}\right)+\left(\mu -o\right)\left(\begin{array}{cc}1& 0\\ 0& -1\end{array}\right)\right].$ Thus, a coquaternion $q$ can be associated with the regulatory (functional) structure of a two-element system, and $A$ can be written in the equivalent form $A\cong q=\left(\begin{array}{cc}a+d& b+c\\ b-c& a-d\end{array}\right).$ The obtained matrix represents regulatory structure of the system as combination of four basis regulatory patterns. Similarity transformation of $A$ will present coquaternion coefficients as diagonal or skew diagonal real entries in cases where the roots of the characteristic equation are complex numbers. For the second-order matrices over $ℝ$, only four Jordan canonical forms exist. The roots (eigenvalues) of the characteristic equation associated with $A$ or coquaternion $q$ are ${\lambda }_{1,2}=a\pm \sqrt{b^2+d^2-c^2}$.${\lambda }_{1,2}$ are the eigenvalues of the similar to $q$ diagonal matrix $q^{\prime }$ acting on the simultaneously transformed basis vectors. New vectors are splitors (eigenvectors) obtained as linear combinations of the initial basis elements.

For simplicity, we can skip the unit element of coquaternion and leave the imaginary part provided by the $\left\{Si\right\}$ basis, making $q^{\prime }$ traceless $(a=0$).

This technique assigns invariant subspaces to scalars (eigenvalues), which can only be interpreted as the values of the outcomes associated with the subsystems. The internal functional structure of subsystems remains uncertain, and can only be treated as a black box for each subsystem.

In order to demonstrate the splitting of each base element and actions on differentiated subsystems as separate patterns, we have to present their entries as matrix coefficients associated with the newly formed separable regulatory structures. In this case, coefficients (the matrices entries) of the initial basis patterns should be transformed and serve as new coefficients of some independent linear quantities not united under the square root, as in the expressions for the roots of the characteristic equation.

The following is according to Dirac’s approach in his relativistic energy equation [43].

Consider an equation ± $\sqrt{b^2+d^2-c^2}=\alpha b+\beta d+\gamma c,$ where the left side is the roots of the characteristic equation. The question is whether and what $\alpha , \beta , \gamma$ quantities may satisfy it. It follows that, if $\alpha \beta =-\beta \alpha , \alpha \gamma =-\gamma \alpha , \beta \gamma =-\gamma \beta$, then for the non-commuting quantities the simpler expression for the right side of the equation after both sides are being squared is ${\alpha }^2{b}^2+{\beta }^2{d}^2+{\gamma }^2{c}^2$. Moreover, if ${\alpha }^2=+1, {\beta }^2=+1, {\gamma }^2=-1,$ then the required conditions for the coefficients are obtained. It means that “eigenvalues” for diagonal elements can be presented not only as scalars, but also as linear combinations of some quantities with scalar coefficients $b, c, d$.

In fact, $\alpha , \beta , \gamma$ quantities are 4 × 4 Hermit (unitary) matrices:

$$\alpha =i\left(\begin{array}{cc}0& \left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right)\\ \left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right)& 0\end{array}\right); \beta =i\left(\begin{array}{cc}\left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right)& 0\\ 0& \left(\begin{array}{cc}-1& 0\\ 0& -1\end{array}\right)\end{array}\right); \gamma =i\left(\begin{array}{cc}0& \left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right)\\ \left(\begin{array}{cc}-1& 0\\ 0& -1\end{array}\right)& 0\end{array}\right)$$

These matrices show that 1D operators with scalar entries for each of two differentiated subsystems are equivalent to the second-order operators (2 × 2 matrices) whose entries are same scalars as for previously considered, not differentiated, functional patterns or base elements. It is easy to see that obtained 4 × 4 matrices also have 2 × 2 block-matrix structures isomorphic to $\left\{Si\right\}$ basis elements. Therefore, the hierarchy of a regulatory structure of a BS is provided by PNR invariant patterns applied to a structural module, which, in this case, includes two hierarchical levels. Together or separately, the levels characterize a BS as a universal structural and functional module (see Appendix A).

There are some examples of the uniformity of regulatory elements comprising a hierarchical functional structure of gastrointestinal (GI) and cardiovascular (CV) systems. These elements are PNR invariant regulatory patterns coordinating motility and circulatory functions of these systems. Physiologically, these patterns can be reduced and viewed as two-element graphs where elements are anatomic segments or organs.

The GI tract consists of organs and segments providing digestion, absorption and propagation of the content down the tract until it is evacuated from the body. Organs (for instance, large and small bowels) and their anatomically and functionally separated segments have accumulation and evacuation components as parts of their function, which are regulated by PNR circuits. Within the intestinal segments, smooth muscle contractions and relaxations occur in an alternating fashion with corresponding changes in the muscle tone. This mechanism includes NFB loops related to the basic flow pattern regulating the filling–emptying function [32,34].

Movements of the content from one segment to another are mainly regulated by the RL mechanism. Reciprocal interactions of neighbor segments are provided by contractions of proximal smooth muscles and relaxation of the distal muscles occurring simultaneously. On the macro level, it can be observed as peristaltic waves. The motility function of the GI tract is also regulated by reciprocal interactions (through the neuronal web) between distantly located, differentiated organs. Gastro-colic reflex is a classic example of a hierarchical functional structure of GI tract provided by reciprocal interactions (RL) between the distant organs, the stomach and the large intestine [44]. It follows from the existing data, in that the division of the GI tract on segments with specialized function (differentiation) is accompanied by invariant functional patterns, namely, reciprocal mechanisms, coordinating function inside and between hierarchical levels of differentiated elements. It points to reciprocal splitting as a leading mechanism of differentiation during individual development.

The same PNR mechanisms regulate blood circulation provided by a cardio-vascular system (CVS).The heart as a blood pumping machine phylogenetically was divided onto two reciprocally functioning parts- atria and ventricles, both having accumulating and emptying functional components. However, the left atrium collects oxygenated blood, whereas the right atrium is venous, thus preparing the right ventricle for making efficient contractions to pump the blood through the large area occupied by the alveolar–capillary system for CO₂–O₂ exchange. Similar advantages of functional and anatomical splitting for the large circle give collaboration with the left heart chambers. Collection of the blood in the left and right atria during diastole and pumping it into the ventricles make contractile forces of the ventricles more efficient due to Starling’s law: the more the heart musculature is stretched, the stronger the contractile forces are. The mechanism of Starling’s law is analogous to the regulations of the filling–emptying cycles of intestinal segments and operated mainly by NFB.

There are also neuronal and hormonal regulatory pathways linking the heart and arterial vessels through the NFB and PFB loops and providing the organs with adequate blood supply. For example, during physical activity, striated muscles demand more oxygen that, in turn, through the NFB loops, increases the rates of heart bits and increases arterial blood pressure caused by squeezed vessels. Another example is a centralization of blood circulation accompanied by contractions of peripheral arteries and increased heart rate in cases of severe blood loss. Emotional conditions increase the heart rate which, through the PFB loops, may increase it further; thus, a vicious circle can be formed. This defence mechanism may cause palpitations.

Functional differentiation of the systems occurs simultaneously with the integration of functional components.

The existence of reciprocally related anatomic branches of CVS and the GI tract is a result of morphological and functional differentiation. For example, the formation of a specialised chamber with enforced musculature, a blood pumping machine, undergoes further phylogenetic splitting into the atrium and the ventricle. The existence of anatomically distinguishable reciprocally related specialized parts of the GI tract (oesophagus, stomach, intestine) confirms phylo-ontogenetic splitting as a means of developing functionally more efficient and stable integrated structures during evolution. The division of the whole system into two reciprocal parts is provided by the formation of NFB and PFB regulatory mechanisms. For example, atriums and ventricles reciprocally related to one another also have NFB links with the nervous and endocrine systems controlling preload. Ventricular function also depends on afterload and is also regulated through the NFB loops within the arteries of the large circle.

The filling–emptying cycle of an intestinal segment includes NFB loops as an addition to the RL regulatory mechanism. The action of PFB patterns may be seen in increasing the strength of the smooth muscle contractions in response to the increase in the muscle tone [32]. The PFB mechanism also regulates rectal emptying, when the first evacuated portion of stool initiates the next, more strenuous, contractions of the rectum. At the same time, rectal contractions occur simultaneously with the relaxations of the smooth and voluntary sphincters of the anal canal. These two subsystems also have reciprocal relationships (RL).

These examples indicate the universality of physiologic functions of PNR patterns (PFB, NFB and RL) and distinguish them as the core regulatory structures presented in integrated anatomical systems at differentiated (hierarchical) levels.

6. Coquaternion as a Model of Inner Functional Structure of a Biologic System

In reality, a BS is not an isolated functional unit: PNR, considered as a basis for the 3D space of regulatory elements, describes the inner functional structure of the autonomous biologic systems in ideal conditions not affected by external (environmental) forces.

A special linear Lie group $SL\left(2,R\right)$ and Lie algebra $sl\left(2,R\right)$ are adequate algebraic structures to give an analytical description of behavior of BS in idealized conditions. $sl\left(2,R\right)$ provides infinitesimal characteristics of functional elements of BS and can be considered as approximation and a convenient toolfor investigating the complex structure of biologic objects.

Lie algebra $sl\left(2,R\right)$ is an additive group, and scalar quantities may appear as a result of multiplication of the group elements. Coquaternion contains real and imaginary parts and is closed as an algebraic structure under the multiplication of elements of a Lie algebra $sl\left(2,R\right)$= span{$S_0$, $S_1, S_2$}, whose basis is also an imaginary coquaternion basis (

Table 1. Coquaternion q = a1 + bi + cj + dk multiplication.

x	1	i	j	k
1	1	i	j	k
i	i	−1	k	−j
j	j	−k	1	−1
k	k	j	i	1

ij = k, ji = −k, ki = j, ik = −j, kj = i, jk = −i, ii = −1, jj = 1, kk = 1, ijk = 1. Coquaternions are four-element structures over $ℝ$ equipped with {1, i, j, k} basis. They form four-dimensional vector space over $ℝ$. Multiplication of basis elements shows coquaternions as closed algebraic structures.

) [45,46,47,48,49].

Coquaternion $cℍ$, is a set of elements $q=a1+bi+cj+dk$, where $a$, $b$, $c$, $d$ are real numbers $ℝ$. Elements of a coquaternion form a four-dimensional real space. Basis elements of a real part of coquaternion are represented by an identity matrix $1$. The imaginary part $\left\{i, j, k\right\}$ of four basis elements $\left\{1, i, j, k\right\}$ is presented by the matrices $S_0, S_2, S_1,$ respectively.

Quadratic function $\langle ,\rangle$ on covector $q^{\prime }=\{a$, $b$, $c$, $d\}$ gives an isotropic quadratic form $\langle q^{\prime },q^{\prime }\rangle =a^2+b^2-c^2-d^2.$ It provides the space in which coquaternions act with indefinite metric and a signature $\left(++--\right).$ Due to two negative signs of the elements of the form, the metric of the corresponding space is indefinite of index 2. The value of the form can be either positive $\langle q^{\prime },q^{\prime }\rangle >0$, negative $\langle q^{\prime },q^{\prime }\rangle <0$ or zero $\langle q^{\prime },q^{\prime }\rangle =0$, which is formally analogous to spacelike, timelike and lightlike vectors, respectively, with regard to the indefinite metric $ℝ$⁴₁$\left(-+++\right)$ of Minkowski’s spacetime and terminology used in physics [37,38]. The scalar product on this space with the signature (4,1) determines the Lorentz manifold and one of three causal characters to which the physical vectors belong.

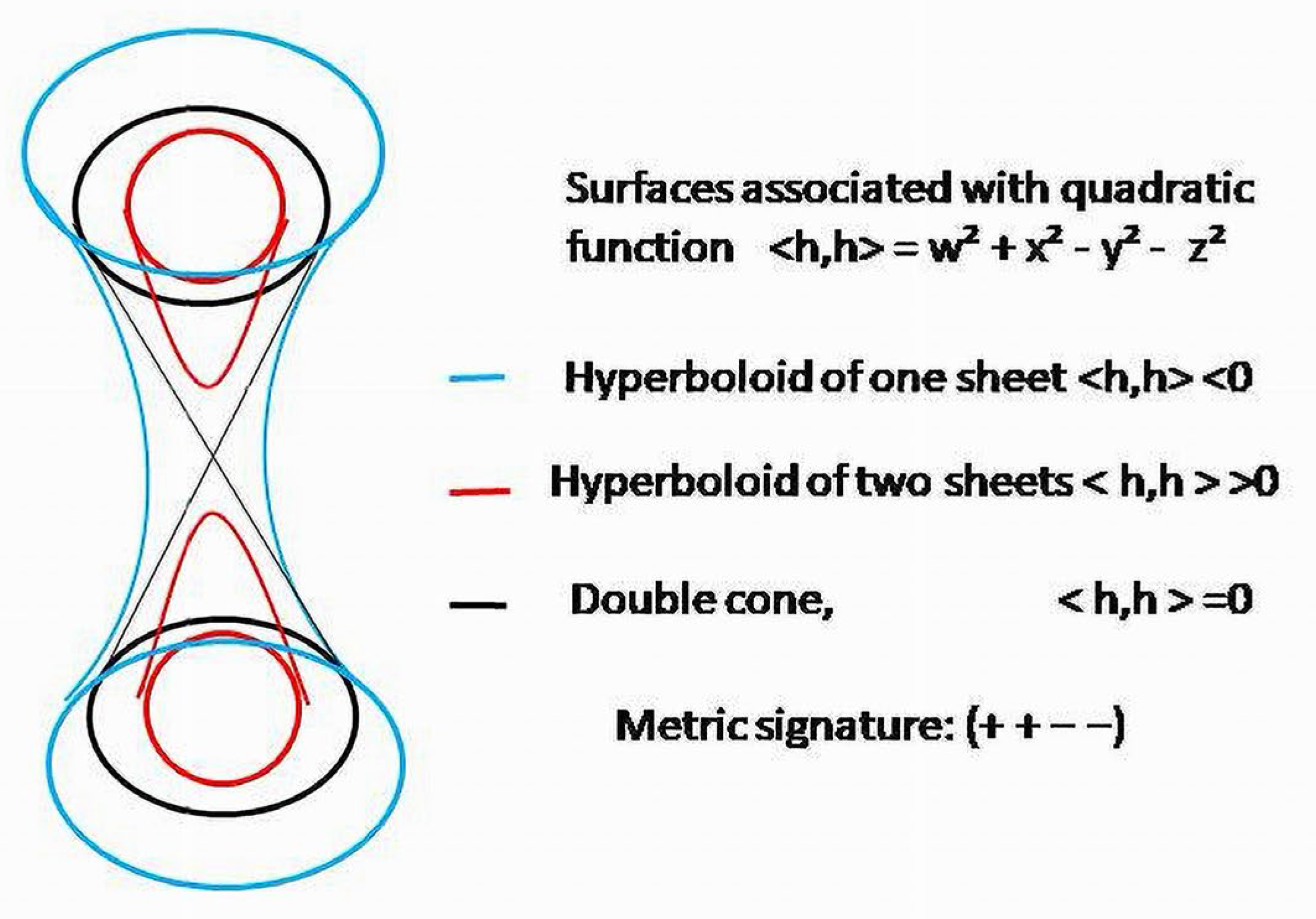
Due to the indefinite metric of BS, three families of hypersurfaces will pack pseudo-Euclidean space $ℝ$⁴₂—one sheet of hyperboloids for positive values of quadratic function, two sheets of hyperboloids for negative values and doublecones for vectors withzero lengths.

There is no natural correspondence with the time coordinate in Minkowski’s spacetime and any of the coordinates in pseudo-Euclidean space $ℝ$⁴₂ of biologic objects. In should be mentioned that terms “timelike”, “spacelike” and “lightlike” were initially used for the vectors applied to the physical systems, and as the names for vectors characterizing BS, they have no biologic sense. The space-time of the physical models and the space of biologic systems are the objects of different nature. Substantial feature of the metric of biological objects is its indefinite character and, more importantly, the signature (2, 2), having two positive and two negative components.

6.1. Indefinite Metric, Geometry of a Functional Core and Entropy of a Biologic System

It is important to mention that the metric signature (2, 2) of the coquaternions corresponds to the internal functional structure of biologic objects obtained in a natural manner through the intrinsic properties of $S_0$, $S_1, S_2$ matrices expressed by a determinant function $det{S}_i: sl\left(2,R\right)\to ℝ$. It may be recalled that $S_0$ denotes NFB, $S_1$ RL and $S_2$ PFB.

Coquaternion representation of biologic objects [16] endows a BS with the property of a closed functional structure due to the correspondence with the algebraically closed set of coquaternions.

This provides a BS with the additional base element—a unit vector $E$. Its properties are determined by the non-traceless identity matrix that functionally differentiates it from the imaginary part of the coquaternion. It is a divergence-positive (not a divergence-free) element. Now, each element of the expanded basis of a BS $\left\{E, S_0, S_2, S_1\right\}$ represents an element of a coquaternion basis {$1, i, j, k$}, and is associated with a set of one-forms $h\left(w, x, y, z\right)$ as coordinates of the basis elements of the vector $S=wE+x S_0+y S_2+z S_1$. (Figure 9). Thus, basis functional patterns contribute to the absolute value and sign of the associated BS quadratic form on covectors: $h\left(w, x, y, z\right)=\langle h,h\rangle =+w^2+x^2 –y^2–z^2$. It shows that coquaternion representation induces indefinite metric in (autonomous) biologic objects.

Due to the nature of the indefinite metric signature (2, 2) in BS, it cannot be interpreted in terms of space–time curves and velocities used for descriptions of the physical objects. The entropy of the system will be considered for reading the metric structure in terms of contribution of the components of the quadratic form to the energy status of biologic objects. Entropy will also be used to emphasize two directional metabolic processes of BS as self-regulatory reproducible units. For instance, it will endow apoptosis and cell divisions components of CRC with the additional structural and functional properties.

In the context of metric function, the term entropy [50,51,52] will be used as a quantitative measure of functional and morphological structural characteristics leading either to the system formation (negative entropy) or destruction (positive entropy). The values of four components of the quadratic function will show energy contributions of each of the basis patterns in the form of positive or negative entropy. The sign of the elements will also indicate direction of metabolic processes towards the accumulation or consumption of the energy.

For example, catabolism as a programmable destruction of a biologic tissue increases entropy, whereas anabolism, the creation of the structural components of the system, decreases the total entropy of the system. Functional disturbances (disorders) affecting the system’s outcome, physical destruction of morphological elements of the system, etc., will also increase entropy. Entropy can also be a measure of pathologic, non-systemic links that predispose the formation of chimerical and defective elements. Therefore, any process leading to destruction of the normal structure will increase the positive entropy of the system. Thus, disease, metabolic disturbances, changing the balance between anabolism and catabolism towards the latter, and any functional activity of cells or tissues, leading to the dissipation of energy used for biochemical reactions, will also increase (positive) entropy.

The entropy of a BS may have a negative sign (negentropy) that characterizes the system’s formation and development. Even at the stages of functional decline, the system is still capable of renovating morphological elements and partially maintaining their functions. Negative entropy, for example, is related to the growing and developing organisms whose functional systems are improving their adaptive properties. All proliferation activities of cells directed to the reproduction of normal (!) morphological structures after apoptosis contribute to negentropy. Balance between positive and negative entropy will be determined by the contributions of the two opposite groups of physiologic processes to its total value. For example, the consumption of food requires energy for digestion, and it increases entropy. However, the energy used for digestion is overweight by potential energy of consumed elements used for the maintenance of normal functions and anatomical structures (contribution to the negative entropy). A two-directional cell renewal process depends on how the system regulates its metabolic function combining two opposite processes—catabolism (destruction) and anabolism (formation). Thus, the sum of positive and negative components (total value) will tell us about the system’s status and how the balance between system destruction and formation is maintained.

$\langle h,h\rangle =+w^2+x^2 –y^2–z^2$ is obtained from the functional structure of a BS quadratic form, and has two positive and two negative components, which are the signs of the determinant values of the matrices of the base elements, $E, S_0, S_2, S_1$. The values of four summands and their signs indicate the amount of energy that each component can contribute, if considered as an isolated subsystem.

$\mathit{E}$ represents a scalar part of a coquaternion. It adds a positive value +w² to the quadratic form. A non-zero trace and positive value of $detE$ implies a permanent increase in positive entropy related to its actions. Considered as a part of the inner functional structure of the system, a functional contribution of $E$ is determined by a non-reversible, dissipated energy amount coming from the permanent energy input needed for feedback metabolic loops of the base patterns. Therefore, its actions under the system’s conditions reflect the forces of the internal environment created by the structural elements. Its functional contribution is also determined by the impacts of the physical environment, which destroys a biological tissue directly in a natural way. A BS adapts to the external environment (forces) by intrinsic mechanisms that initially stream metabolism in a way when the system builds its components (anabolism dominates catabolism) until it reaches mature stages, and after that from the mature stages up to the regression it only maintains its own structure through the use of self-renewal loops. A functional meaning and contribution of this component is based on the balance between permanently acting destructive forces of the external environment and non-reversible “heat” due to the system’s functionality maintaining mechanisms.

${\mathit{S}}_0$ (NFB) has positive value +x², and, formally, it contributes to the positive entropy. NFB is considered as a main regulatory element optimizing the functions of other members of the “imaginary” family, as well as elements of a carrier space involved in NFB relationships. Looped regulatory structure acts on two-dimensional invariant spaces. NFB only consumes energy and does not create new morphological elements. From this context it is assumed that NFB increases positive entropy.

${\mathit{S}}_2$ (PFB) corresponds to the negative element –z² of quadratic function. It accelerates functional processes and consumes much energy, but, in contrast to NFB, has creative features. PFB generates extreme conditions helping the system to transform its conditions to the higher energy and functional levels. It could possibly feed NFB with the additional energy [26].

${\mathit{S}}_1$ is a basis element representing RL. It is presented in the quadratic function as an element with negative value –y². The main functional feature of RL is the reciprocal regulation of subsystems. Overall, it splits a carrier and functional spaces into two autonomous subspaces, so that one-dimensional subspaces can be regulated by its own operator. Each subspace considered as an independent branch for further development makes structural and functional differentiation a substantial factor of evolution. RL is a major system-forming functional pattern determining morphologic and functional development of cells and tissues. Similar to PFB, RL facilitates transformations of potential energy and conserves it in the newly formed functional and morphological structures. The amount of potential energy conserved in specialized biomolecules, anatomical structures and links overweighs the amount of the energy required for performing a RL function itself.

The functionality of BS depends on the potential energy obtained from biological substrates for structural elements of a BS and its functions. The difference between available sources of energy and natural processes resulted in a decay of biological tissues reflecting Gibb’s law

$$G=N-TS$$

$G$—available energy accumulated by the system;

$N$—total energy from the available sources processed by the system; this amount is required to perform system’s actions and the maintenance of structural and functional elements of BS;

$S$—entropy of the system reflecting not reusable portion of energy dissipated from chemical reaction;

$T$—temperature.

As it was mentioned before, the values of main biologic variables fluctuate around physiologic constants. Equalizing the flows of energy should also follow the principles of regulations of BS according to which anabolic and catabolic states will fluctuate around equilibrium. Thus, fluctuations reflect the system’s actions towards neutralizing excessive anabolic and catabolic flows.

Assuming that the value of quadratic function is associated with the amount of available potential energy of the system (having positive and negative entropy characteristic), and this amount is determined by the energy being contributed by the components, a hypothetical equation is formulated:

$$+w^2+x^2-y^2-z^2=-\upsilon G$$

(1)

$G$—available energy accumulated by the system; $\upsilon$—coefficient; $w$, $x, y, z$ are one-forms associated with coquaternion representation of BS considered in Section 6.1.

The minus sign of the right-hand part reflects the suggestion that potential energy accumulated in the system (the sum of negative and positive components on the left) is equal to the consumed energy ($–N$) used to build and provide functionality of the system plus dissipated energy ($+TS$). Thus, the system is considered to be conservative.

The 1-forms $\left\{w, x, y, z\right\}$ of the vector $S=wE+x{S}_0+y{S}_2+z{S}_1$ are coordinates of the functional base elements of the system. Each condition of the system can be characterized by a convector $h=\left(w, x, y, z\right), w, x, y, z\in$ ℝ as a function of coordinates in a dual to $T_h\left(expS\right)$ cotangent space $T_h^{*}\left(expS\right)$. Points in the hypersurface $w^2+x^2-y^2-z^2=R=const$ are equipotential for the system. Corresponding to the covector energy of the system may take positive, negative or zero values due to the isotropic quadratic form.

It is known that each phase trajectory of $S_i$ elements (see Figure 6) is the same energy level curve of the described physical system. The same character of phase portraits of the base biologic patterns as in physical systems may provide biologic systems with behavioral features similar to physical objects, depending on the energy flow pattern associated with $S_i$.

Let 1-forms $\left\{w, x, y, z\right\}$ determine a parameterized smooth curve $\phi :t\to \phi \left(t\right);t\in ℝ;\phi \left(t\right)=\left(w\left(t\right), x\left(t\right), y\left(t\right), z\left(t\right)\right)$ in $ℝ$⁴₂. Traveling along the curve will change the values of the potential energy of the system $G$, except when the curve lies in the surface of the equipotential points $G=c$ (constant).

If $h+dh$ is infinitesimal displacement from $h$ and $∆h=\left(∆w, ∆x, ∆y, ∆z\right)$ is small enough, $∆h\cong dh$, then $Ah=h+∆h$ is a new systems condition obtained by the displacement of $h$, resulting in a new vector $Ah$ in $T_h^{*}\left(expS\right)$.

In Euclidean space $ℝ$ⁿ, the potential energy $U$ of the system x (mathematical pendulum) can be defined by a matrix of the symmetrical operator $A^{\prime }$ and positive definite identity matrix of quadratic form $\langle ,\rangle$, such that $U=\frac{1}{2}\langle A^{\prime }x,x\rangle , x\in ℝ$ⁿ [39].

In pseudo-Euclidean space ℝ⁴₂, which is considered a carrier space for BS, potential energy, according to (1), can also be defined by quadratic form associated with some operator $A, G_A=k\langle Ah,h\rangle ;$ k-coefficient; in this case a matrix of quadratic form is a diagonal matrix $g=diag\left(1, 1,-1,-1\right)$ of the metric signature $\left(++--\right)$.$h=\left(w, x, y, z\right)$—covector of the system’s condition.

For simplicity, $A=diag\left(a_1,a_2,a_3,a_4\right)$, $a_i>0,$ so that in orthonormal basis $h=w{e}^{1 }+x{e}^2+y{e}^3+z{e}^4,G_A=k\left(a_1{w}^2+a_2{x}^2-a_3{y}^2-a_4{z}^2\right)$ and coefficients $a_i$ will change the shape of a geometrical image of $G_A$ along the principal axes, leaving the metric signature unchanged.

$G_A$ represents the potential energy of the system related to the action of operator $A$ and the system will respond to this action depending on the ability to maintain an equilibrium state.

It seems to be a genetically programmed feature of a BS also to maintain its own functional characteristics which formally related to the (metric) structure, and which is only possible through the balancing of energy capacities and capabilities of the components to perform the actions. The ability of a BS to generate the inner forces directed towards neutralizing the factors which caused functional changes (deviations) can be expressed in a dynamical equation:

$$\ddot{h}=-grad\langle Ah,h\rangle$$

(2)

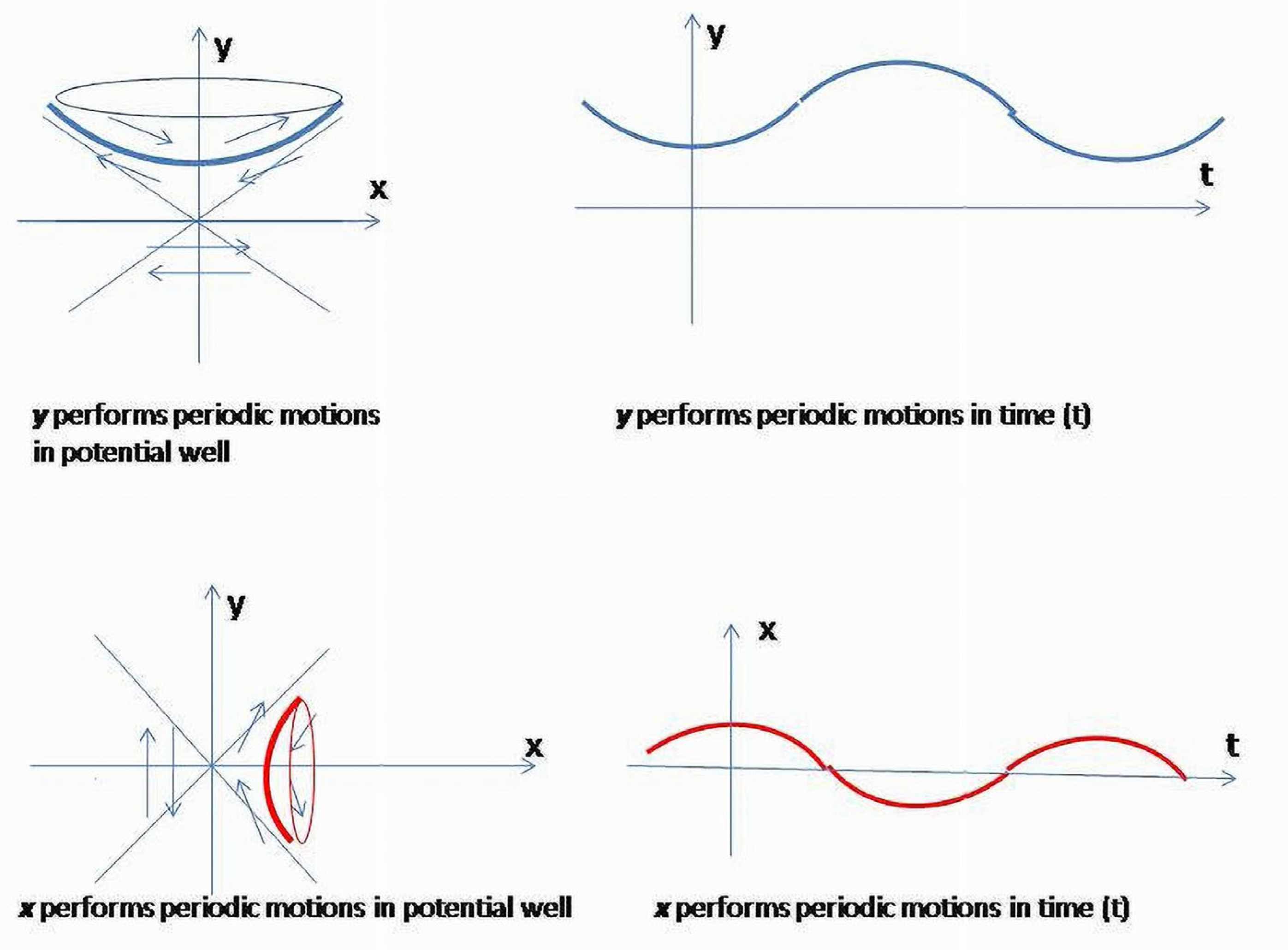
It falls into the system of four second-order ODE (k = 2)

$$\ddot{w}=-a_{1}w$$

(2a)

$$\ddot{x}=-a_{2}x$$

(2b)

$$\ddot{y}=+a_{3}y$$

(2c)

$$\ddot{z}=+a_{4}z$$

(2d)

The phase curves of the first two Equations (2a) and (2b) are periodic motions having elliptic trajectories on the phase plane, and the second two (2c), (2d) represent hyperbolic rotations.

6.2. Geometric Structure and Images of a Biologic System: Balance between Negative and Positive Entropy; Prevalence of Catabolic Processes (Positive Entropy) in Cancer

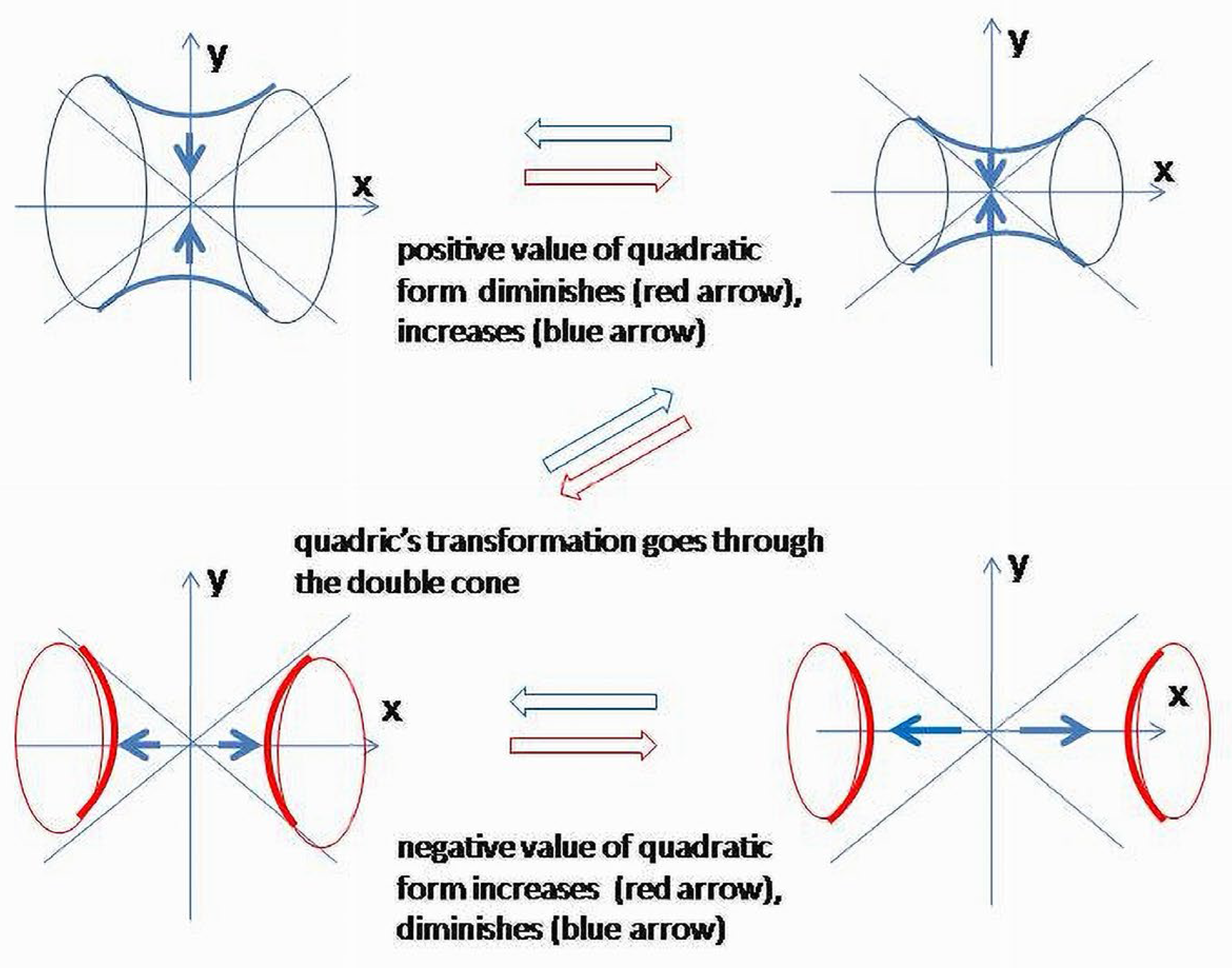
On an orthonormal basis {$1, i, j, k$} = {$E,$ S₀$,$ S₂$,$ S₁}, consider a coframe of normalized 1-forms (denoted by the same letters) as a coordinate system oriented along the principal axes of the quadratic form $w=w\left(t\right), x=x\left(t\right), y=y\left(t\right), z=z\left(t\right).$ The potential energy of the system will depend on the values of coefficients $a_i$ of the elements of the quadric $\frac{G_A}{\mathrm{k}}=\langle h^{\prime },h^{\prime }\rangle =\left(a_1{w}^2+a_2{x}^2-a_3{y}^2-a_4{z}^2\right).$ Each component will contribute separately. Therefore, coefficients applied to the elements of quadratic form will change the values of orthogonal coordinates and shapes of corresponding images of quadrics. Topology of the manifolds representing geometric images will not change due to the “undisturbed” metric signature (2, 2). This is quite an idealized model which will help to gain insights into the basic mechanisms of the regulation of normal systems.

Normalized expression of potential energy $\langle h,h\rangle$ = $s\left(w, x, y, z\right)=\left(w^2+x^2-y^2-z^2\right);s$ is a $ℝ$⁴₂ surface (four-dimensional hyperbolic paraboloid) which will be projected in $ℝ$³.

First, consider $s=0$. It corresponds to the surface, which splits the $ℝ$⁴₂ space on subspaces corresponding to positive and negative values of the quadratic form. Physiologically, it can be interpreted as conditions when neither catabolism $(s>0)$ nor anabolism $(s<0)$ are the leading metabolic process. 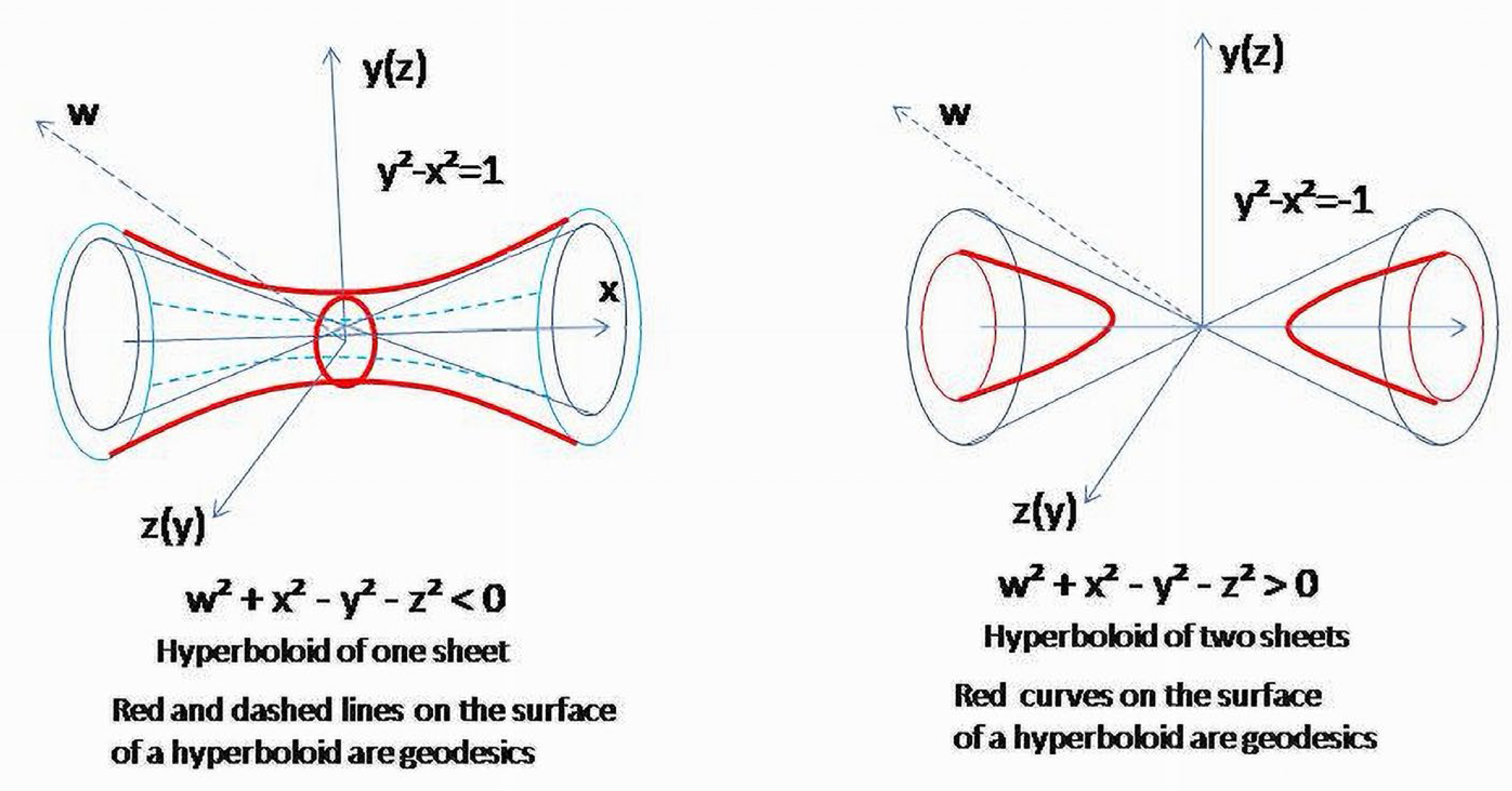Let $\tilde{x}=\frac{x}{w}, \tilde{y}=\frac{y}{w}, \tilde{z}=\frac{z}{w}$; $w\left(t\right)$ is also considered, slowly increasing within a short time interval, so that $w\left(t\right)\cong \mathrm{const}.$, and we could ignore the effect of its change on other variables. The result of projectivization is a hyperboloid of one sheet (Figure 10).

$$-{\tilde{x}}^2+{\tilde{y}}^2+{\tilde{z}}^2=1+l\left(t\right).$$

(3)

Formally, the right side of this equation should contain the dissipation of the energy ($TS$), from (1) which is added as the $l\left(t\right)>0$ parameter to the right side of (3). Its action increases the positive values of the quadric; thus, the required positive values for anabolic components as the threshold condition for the equilibrium $s=0 \mathrm{are} \mathrm{increased}$. For simplicity, further in the text, $l\left(t\right)$ can be omitted or considered depending on the context.

In (3), $ℝ$⁴₂ was projected in 3D manifold along the w axis. It displaces the equilibrium towards positive values, so that the lowest level of negative entropy component to obtain equilibrium becomes +1. Equilibrium conditions for the four-element system ($s=0)$ after projectivization will correspond to hyperboloid of one-sheet.

Vertical and horizontal sections of hyperboloid ($\tilde{z}=const$., $\tilde{y}=const$., respectively) will further restrict the image showing two branches of hyperbolas. The vertical sections ($x=const$) are ellipses (could be circles) related to the $\tilde{x}$ coordinate level. Above and below two asymptotes (or outside a double cone), there are areas where anabolism is dominating (Figure 11).

Due to the assumption $\ddot{h}=-grad\langle Ah,h\rangle$ (2) equivalent to the system of four differential Equations (2a)–(2d), it is easy to see that $\tilde{x}\left(t\right)$ will perform periodic motions (fluctuations) (2b), whereas $\tilde{y}$(t) and $\tilde{z}\left(t\right)$ will monotonously grow (2c, 2d). On the other hand, the expression for the energy (3) shows that $\tilde{x}\left(t\right)$ and $\tilde{y}\left(t\right)$ and $\tilde{z}\left(t\right)$ are reciprocally related due to opposite contributions to the values of the quadratic form. Reciprocal relations between $\tilde{x}\left(t\right)$ and $\tilde{y}$(t) and $\tilde{x}\left(t\right)$ and $\tilde{z}\left(t\right)$ would restrict the degrees of freedom of corresponding variables in (2b–2d).Therefore, two considerations will determine the system’s behavior, -dynamical equations (2a–2d) and equilibrium conditions between positive and negative entropy components ($s=0)$.

Sections of the hyperboloid corresponding to $\tilde{z}\left(t\right)=const.$ and $\tilde{y}\left(t\right)=const.$ are hyperbolas which are geodesics of a hyperboloid of one sheet (3) $+{\tilde{y}}^2-{\tilde{x}}^2=1-{\tilde{z}}^2;\left(1-{\tilde{z}}^2\right)>0$ and $+{\tilde{z}}^2-{\tilde{x}}^2=1-{\tilde{y}}^2;\left(1-{\tilde{y}}^2\right)>0$, or geodesics of a two-sheet hyperboloid, $\left(1-{\tilde{z}}^2\right)<0, \left(1-{\tilde{y}}^2\right)<0$ (Figure 12). Due to $s=0,$ the surface it determines in ℝ⁴₂ is a double cone, and obtained hyperbolas are geodesics of this surface.

On the $\left(\tilde{X},\tilde{Y}\right)$ plane, when the $\tilde{z}=0$ energy trajectories (3) are hyperbolas $+{\tilde{y}}^2-{\tilde{x}}^2=+1$. The curves $\tilde{y}=\pm \sqrt{1+{\tilde{x}}^2}$ are points of equal energy levels of the system restricted to the two variables. $\tilde{x}$(t) is a bounded periodic function. The maximum level of $\tilde{y}$(t) is achieved when $\tilde{x}$(t) reaches its highest value. This is not a steady equilibrium point for $\tilde{y}$. The upper branch is a constant speed parametrization curve through the point $p\left(t\right)=\left(\tilde{x}\left(t\right), \tilde{y}\left(t\right)\right)=\sinh t\tilde{x}+\cosh t\tilde{y}$ [37].

Due to periodic trajectories of $\tilde{x}\left(t\right)$,$\tilde{y}$(t) will demonstrate oscillations bounded by permissible energy levels (Figure 12). The lowest $\tilde{y}$(t) value is limited by the initial conditions on the energy level, which in our case is +1. If $l\left(t\right)$ parameter in (3) is not slowly increasing in time and cannot be ignored, it will cause a fast displacement of the $\tilde{y}$(t) trajectory toward the asymptotes.

Similar characteristics of curves and their behavior could be demonstrated as well on the $\left(\tilde{X},\tilde{Z}\right)$ plane $\left(\tilde{y}=0\right)$.

The constant speed parametrization curve on the plane $\left(\tilde{Y},\tilde{Z}\right),$($\tilde{x}=0)$ through the point $p^{\prime }\left(t\right)=\left(\tilde{z}\left(t\right), \tilde{y}\left(t\right)\right)=\cos t\tilde{z}+\sin t\tilde{y}$ is a closed trajectory (circle). This geodesic being in the subspace of a positive definite metric, shows that the energy contributions are bounded, and its total value is the sum of the components related to $\tilde{z}\left(t\right) \mathrm{and} \tilde{y}\left(t\right)$ variables having a similar metabolic nature.

Second, $s<0.$ Changing the zero value of the quadric s towards negative ones does not make a qualitative difference in the character of the obtained curves. It will only transform the lowest and highest values of the $\tilde{y}$(t) variable above the zero point.

Next, consider $s>0;$ following the same technique, the result of projectivization is

$$-{\tilde{x}}^2+{\tilde{y}}^2+{\tilde{z}}^2=r-1$$

(4)

Due to arbitrary $r>0$, there are three possibilities when $r-1>0, r-1<0, r-1=0$. The first one repeats the scenario discussed previously.

Let $\left(r-1\right)=-1$. This is a hyperboloid of two sheets (Figure 11 and Figure 12). Energy curves on $\left(\tilde{X},\tilde{Y}\right)$ plane $\left(\tilde{z}=0\right)$ are hyperbolas $+{\tilde{y}}^2-{\tilde{x}}^2=-1$. Similar to a previous case, the relations between catabolic $\tilde{x}$(t) and anabolic $\tilde{y}$(t) components are shown in time. Now, all hyperbolas are “inside” the branches of asymptotes; therefore, the process corresponds to the conditions when catabolism overweighs anabolism or, in other words, the destruction of the system dominates its formation. Depending on the ways in which the components are presented, functional relations are shown as closed curves (ovals or circles) or fluctuations (periodic function) of the catabolic component around the $\tilde{x}$ axis (Figure 12 and Figure 13). In fact, a comparison with the previous scenario gives similar images. Only now, the process is centered in the area bounded by asymptotes along the $\tilde{x}$ axis.

Similar to a previous case, the $\left(\tilde{X},\tilde{Z}\right)$ plane $\left(\tilde{y}=0\right)$ gives similar trajectories and behavior.

The third possibility, $r-1=0$, leads to the expression

$$-{\tilde{x}}^2+{\tilde{y}}^2+{\tilde{z}}^2=0$$

(5)

This is an expression for a double cone, which separates positive and negative values of the quadric. On the plane $\left(\tilde{X},\tilde{Y}\right)$,$\left(\tilde{z}=0\right)$, there are four asymptotes and a zero point satisfying $+{\tilde{y}}^2-{\tilde{x}}^2=0;\tilde{y}=\pm \sqrt{{\tilde{x}}^2}$. Similarly for $\left(\tilde{X},\tilde{Z}\right)$, $\left(\tilde{y}=0\right),+{\tilde{z}}^2-{\tilde{x}}^2=0;\tilde{z}=\pm \sqrt{{\tilde{x}}^2}$.

As it was mentioned before, regulations of metabolism should follow the same principles according to which balancing anabolic and catabolic processes will result in fluctuations in metabolic states around equilibrium, reflecting the system’s actions towards neutralizing excessive anabolic and catabolic flows.

Expression for the energy of the system (1) does not contain conditions when metabolism changes its directions from anabolism to catabolism and vice versa. Equation (2) also does not show it explicitly. It is logical to assume that the energy conditions of the systems undergo fluctuations such as practically all physiologic parameters of BS do. Modeling conditions applied to the system should, in this case, change the right side of (1) so that total available energy will, first, monotonously decrease, passing by the equilibrium until the lower acceptable level is reached. After that, the process reverses and returns to the initial point. Technically, the branches will first hold closer to the asymptotes, and after passing zero point and a double cone, the surface splits into two hyperboloids of two sheets which will initially move apart from one another; after reaching the threshold level, the process will move in the opposite direction (Figure 14).

Provided scenarios demonstrating relationships between system formation and destruction processes can be applied to the CRC whose functional structure consist of system destruction (apoptosis) and system formation (cell division) components.

7. Results

In [16], the transformation of the RL pattern (S₁) into the “environmental” matrix (E), similar to the real part of coquaternion, was related to the functional changes in BS associated with malignant transformations of normal cells. This transformation causes change in the metric structure of a normal BS: $\left(++--\right)\to \left(+++-\right)$. It was not clear, though, how the coquaternion structure as a functional module of BS is inherited and distributed between daughter elements after splitting the characters of BS during development, and which other functional elements provide hierarchical links between cambial and differentiated levels after splitting.

In the scope of this work, a question arose, namely, how two main metabolism components, anabolism and catabolism, are related to the base patterns providing structural wholeness of BS. This question is directly related to one well-known metabolic feature of cancer, which involves switching the balance of normal biochemical pathways towards the activation of anabolic processes of malignant tissues, and bypassing anabolic energy and increasing the catabolic rates of normal structural elements of the system. To answer these questions, the dynamics providing the balance of the main energy components contributing to the viability of a BS were described.

The reciprocal link (RL) is a main functional pattern linking split characters during development. Considering the cambial (progenitor) element as a functional system (module) with a coquaternion structure, it was shown that daughter elements inherit the coquaternion structure and are linked to the progenitors by 4 × 4 complex matrices isomorphic to the base elements of a functional module. (For simplicity the real part of the coquaternion structure was omitted.) The two-element “horizontal” structure of a functional module (a BS) being isomorphic to the two-element “vertical” structure of a BS clearly demonstrates the invariant character of functional links on horizontal and hierarchical (vertical) levels.

Obtained hierarchical links clarify the role of NFB linking cambial and differentiated levels as a functional pattern initiating and activating the proliferation of immature (malignant) cells following the deterioration of the RL structure.

The metric structure of a functional module provided by isotropic quadratic form was associated with the energy contributions of its components. By analogy with physical processes, quadratic functions of elements were considered as having entropy features related to the system formation and destruction processes. Thus, the value of the quadratic form was related to the domination of anabolic or catabolic processes. The physiological property of the system when returning deviated conditions to their equilibrium states was used in the formulation of modeling conditions regulating the system’s behavior. Anabolic and catabolic trajectories were shown as oscillations of the main contributing variables.

In case of domination of the system-formation processes related trajectory was mimicking geodesics of one-sheet hyperboloid until restricting actions from its metabolic counterpart resulted in the slow reversing the changes in initially increasing values of the variable. Thus, in time this process was shown as fluctuations bounded by the initial conditions. When the system-destruction processes are dominating, trajectories are geodesics of a two-sheet hyperboloid oscillating along the axis corresponding to the system-formation variable. Similar to a system–formation case, opposite actions of a metabolic counterpart will slowly reverse the process to the opposite.

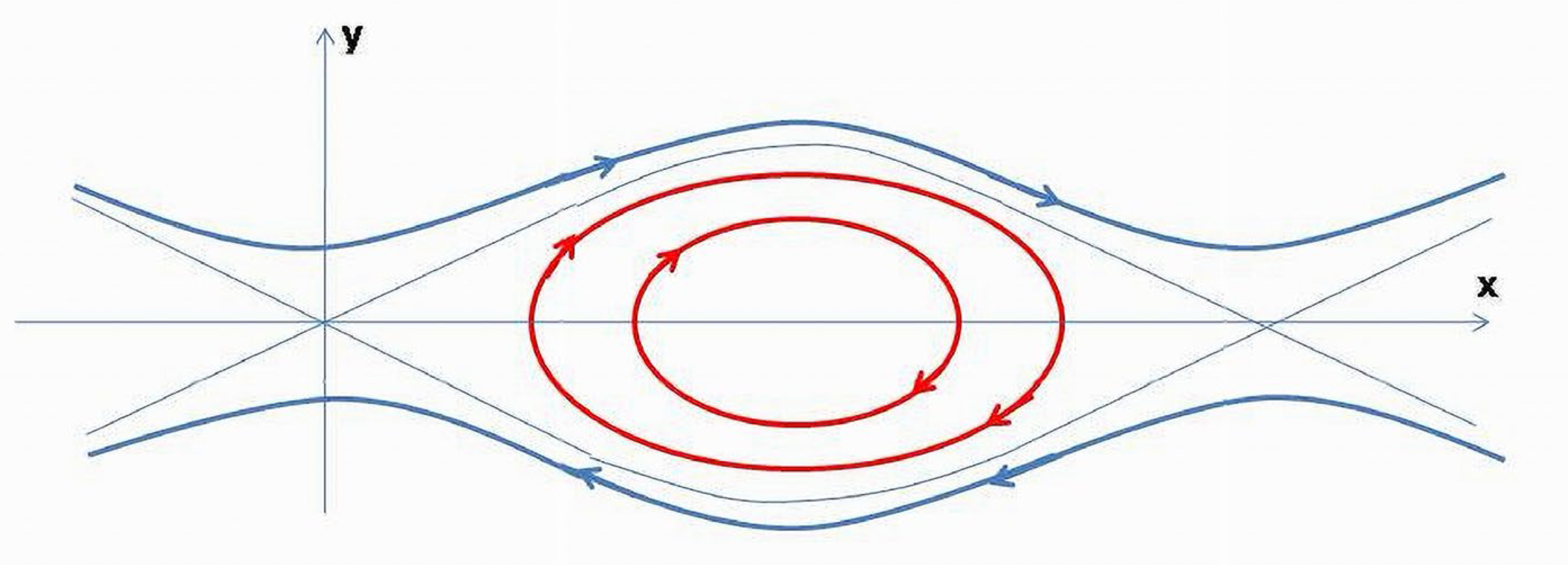
The interpretation of the trajectories demonstrated in Figure 12 is as follows: when anabolic states and negentropy processes are dominating the trajectory of the system‘s behavior are above the asymptotes of the equilibrium conditions. It requires some efforts from the RL and mostly PFB elements moving conditions of the system towards higher energy (negentropy) levels. Despite the environmental forces and naturally growing positive entropy related to the decay of biologic tissues and moving the system (inclining the trajectory) inside the area bounded by asymptotes and towards the domination of destructive processes, regulatory mechanisms of the normal system will be able to move the conditions and trajectory of the system through asymptotes towards anabolic states.

Although it was not shown explicitly, physiologic requirements dictate the necessity of interchanging of the anabolic and catabolic states in time, which could be demonstrated as fluctuations along the equilibrium surface of a double cone.

After the transformation of the reciprocal base element, the RL metric structure $\left(+++-\right)$ still possesses indefinite properties because of the remaining negative element related to the PFB. In all considered scenarios, changes in the metric signature toward increasing the number of positive components eventually will cause the inability of the system to compensate for destructive processes and increase negentropy to the level needed to maintain the normal system’s structure. On the other hand, the remaining systemic properties seem to be able to provide malignant tissue with enough energy required for growth. The mechanisms compensating for the flaws of the reciprocal interactions include NFB between cambial and differentiated levels. The obtained results show that the two-level hierarchical structure is supported by functional patterns isomorphic to the base patterns regulating the internal structure of the system. Therefore, the functional hierarchy resulting from the maturation of cambial cells is also formed and regulated by coquaternion elements. Thus, coquaternion can represent a functional module as a structural basis of the organization of BS as a hierarchical structure.

Dynamical changes in the conditions of the system related to the transformations of the elements determining metric structure reveal fluctuations in the conditions of the system considered as a normal physiologic reaction on intrinsic and extrinsic factors by adjusting anabolic and catabolic flows of energy required for maintaining the viability of the system.

The main structural characteristic of the steadiness of the system is a metric signature (2, 2). Until the metric is preserved, the system, for instance, a biological cell, is able to perform its function determined by the sequence of strict morphologic and biochemical changes forming the CRC.

Changes in the metric structure of a functional module caused by transformations of the base functional elements, namely, RL and PFB, into the environmental element ($E^{\prime }$) will raise the threshold for the minimum negentropy level required to maintain equilibrium and the viability of the system.

For example, consider the changes in the metric structure caused by the transformation of the RL base element $S_1$→$E^{\prime }$. A functional structure of the deteriorated system will correspond to the new vector $S^{\prime }=wE+x{S}_0+y{S}_2+k E^{\prime }$ and quadratic form $s^{\prime }\left(w, x, y, k\right)=\left(w^2+x^2-y^2+k^2\right)$. An alteration of the $S_1$ base element linked to the z variable responsible for the increase in negentropy will cause changes in the sign of the coefficient in (2d) so that it becomes $\ddot{w^{\prime }}=-a_4{w}^{\prime }$ (2d*), and together with (2b), $\ddot{x}=-a_{2}x$ and (2c) $\ddot{y}=+a_{3}y$ it will determine a one-sheet hyperboloid as a surface corresponding to the equilibrium conditions of the newly formed quadric whose metric became $\left(+++-\right).$ It is easy to see that the obtained system will demonstrate an increase in the threshold of the required negentropy on the $+{w^{\prime }}^2$ value to equilibrate system formation and the destruction processes. Similar metric changes can be caused by PFB transformation to either NFB or E elements.

In these scenarios, a change in the metric signature would cause changes in metabolism, and despite the attempts to compensate the structural transformations, eventually catabolism will overweigh the anabolic reactions; being preserved, “intact”, subsystems responsible for their own functions and links with other subsystems will work to compensate for the lack of response from the recipients.

It follows from the obtained results that RL–NFB interactions play a key role in functional and morphologic adaptations following metabolic changes. Transformations of RL in a way that it loses its split function led to a disbalance between anabolic and catabolic processes towards the latter. Clinically, it is manifested as tissue destruction caused by compensatory proliferative activity of cells of the cambial level resulted in synthesizing of malfunctioning (anaplastic) cells. Eventually, it causes active bypassing of the energy required for normal tissues.

The deterioration of base elements of a functional BS is related to scenarios when any of the $S_i$ base elements are replaced, omitted or excluded from the system and, formally, _cH structure. It means that the basis physiologic mechanisms and matrices related to them became singular. $A$ is singular, if $det\left(A\right)=0$. It reduces a 4D space of _cℍ to 3D with uncertain (algebraic) structure. From the possible changes it follows that the corresponding linear spaces: $span\left\{E, S_0, S_2\right\}$, $span${$E, S_0$,$S_1$} and $span${E, $S_1$, $S_2$}, lose functional wholeness or systemic mechanisms of regulations. Compositions of the remaining base elements resulting in a singular element will be modified or eliminated from metabolic pathways creating atypical morphologic structures and non-systemic regulatory mechanisms. Morphologically and functionally related “conjugates” (splitors) of deteriorated “systems” will also be affected due to the pathologic regulatory structure represented by singular operators (matrices).

On the other hand, being involved in a network with other functional systems, a deteriorated system not being able to send adequate signals about its current conditions, will instead receive the activating stimuli (positive input) due to the negative feedback signaling the lack of its output. Negative feedback from the elements at the malfunctioning level is a major regulatory pattern between cambial and differentiated levels. Despite a very simplified scenario, the result of NFB regulation will be a stimulation of malfunctioning cambial elements which did not reach the differentiated level of “reciprocal splitors”, but instead were involved in remaining self-reproductive renewal mechanisms linked to DNA.

8. Discussion

This work is based on algebraic and geometric approaches to the structural changes in base patterns of a BS which affect functional interactions between subsystems in general and can be linked to the deterioration of normal architecture and functions of the system. Due to the general structural and functional changes related to them, pathologic deviations can be associated with the unique biologic phenomenon of malignant transformations.

A BS is a hierarchical functional structure. Each hierarchical level is presented by a functional core as an inherited component and adjoining functions (not inherited) as a part of adaptation of the system to the environment. In the longer time scale, adjoining functions (functional superstructure) are responsible for the process of formation of characters, which will be encoded in chromosomes as a core, basis functional patterns determining the characteristic features of species. In ontogenesis, the core functions determine the genotypic properties of individuals and the system’s longevity through the cell renewal cycle (CRC). CRC restores a functional efficacy of the differentiated layer of a BS. The accuracy of a CRC mechanism, which includes apoptosis and cell proliferation, will determine functional stability and normal morphological features of the system.

A functional structure of the core is presented by negative feedback (NFB), positive feedback (PFB) and reciprocal links (RL) as base functional patterns, which, being presented in a matrix form, have a mathematical structure of the imaginary part of a coquaternion $q=a1+bi+cj+dk$, where the basis elements $\left(i, j, k\right)$ are represented by NFB, PFB and RL, respectively.

The strategy of biologic development, which includes phylogenesis and ontogenesis (individual development), predisposes the splitting of characters as a leading mechanism for obtaining more details of the existing functional features. The splitting has its functional representation in the RL mechanism. NFB, PFB and RL provide a BS with the same, stable structure of a functional core in each hierarchical level of biologic organization. The base elements considered are infinitesimal characteristics (patterns) obtained as approximations of feedback regulatory circuits, including reciprocal interactions between systems. They provide the considered functional models with a convenient tool to form 3D and 4D spaces of functional elements of BS endowed by integrative properties. Functional integration of the split anatomical structures representing separable organs of CV and GI systems is an example.

Formally, a functional structure of the base regulatory elements corresponds to a Lie algebra $sl\left(2,R\right)=span\left\{S_0, S_1, S_2\right\}$ of a Special Linear Group, where the basis elements of the algebra are represented by the core functional patterns. As an algebraic structure $sl\left(2,R\right)$ is subalgebra of General Linear Group algebra $gl\left(2,R\right)$ containing all 2 × 2 real matrices. A $gl\left(2,R\right)$ provides a BS with temporary functional links (functional superstructure), that add flexibility to the core patterns and resistance to the fluctuations in the environment.

The permanent impact of the environment finds its representation in addition to the $sl\left(2,R\right)$ basis, the element of a coquaternion, being an identity matrix. It makes physiologic sense, because from now on, a functional system will be considered to be not completely isolated, but a two-element structure with an inner environment element $\left(E\right)$. Moreover, a set of coquaternions is an algebraically closed structure under multiplication of its elements, and, because of that, formal operations between regulatory elements of the system are not restricted by matrices addition as the only group operation for Lie algebra.

Entropy is a qualitative characteristic of the system’s functionality and viability. Each of the four components of a (split quaternion) coquaternion is supposed to contribute to the total entropy. It is assumed that a matrix-determinant function can provide a new meaning and have a sense in defining entropy through the system’s formation and destruction parameters as elements of a bilinear form representing the system’s functional structure. Each coquaternion $q=a1+bi+cj+dk$ and its representation $S=wE+x{S}_0+y{S}_2+z{S}_1$ are related to a geometrical hypersurface described by a quadratic function: $\langle h,h\rangle =+w^2+x^2-y^2-z^2.$ The first two positive signs reflect contributions to the entropy of the system made by the environment $\left(E\right)$ and negative feedback (NFB = $S_0$). While any impact of the environment naturally increases the positive entropy of the system, positive contribution of NFB can be considered because of the energy consuming a non-creative, coordinating function inherent to this pattern. Contributions to the negative entropy of the system by PFB ($S_2$) and RL ($S_1$) are related to their direct system-formation functional properties.

Due to the indefinite metric, which seems to be a natural structural characteristic of a BS, current conditions of the system will belong to one of three families of hypersurfaces, depending on the sign of the form: $\langle h,h\rangle >0; h$ is a point in a two-sheet hyperboloid in ℝ⁴₂; $\langle h,h\rangle <0;h$ belongs to a one-sheet hyperboloid; $\langle h,h\rangle =0; h$ is a point in a doublecone embedded in $ℝ$⁴₂.

The trajectory of the system’s behavior should normally penetrate quadrics’ families and oscillate around the surface of the double cone. Indeed, normally functioning BS do not have tendencies to remain in either anabolic (negative entropy) or catabolic (positive entropy) states. Thus, the system’s behavior will demonstrate oscillations around the equilibrium, which is the surface of a double cone, and where the system’s destructive and creative forces are equilibrated.

Only in the case of transformation (deterioration) of the base elements, which may occur on any functional level, the system’s behavior will acquire some irreversible pathologic features.

Among other possible transformations, structural changes in the $S_1$ (RL) pattern, considered within the frames of an individual development, would deteriorate the mechanism of differentiation of stem cells during CRC. One of the possible scenarios is $S_1\to E^{\prime }$. In this case, the functional element ($S_1$) responsible for the system-formation features and negative entropy is transformed to the non-systemic regulatory pattern mimicking destructive environmental forces. If other functional elements remain unchanged, the system will have preserved its indefinite metric, except for the metric signature, which becomes (3, 1). Formally, these changes in the geometry of the normal space, (2, 2)$\to$(3, 1), can be associated with malignant transformations. Indeed, cancer cells possess not only the autonomy of a normal system due to preserved indefinite metric features, but also acquire high rates of proliferative function, resulting in the formations of conglomerates of cells destroying the surrounding tissue. When splitting (RL) is eliminated from the system’s functions by substituting it for the environment pattern, missing feedback from differentiated layer will activate the NFB response, resulting in the proliferation of immature cambial elements. Corresponding changes in the realization of the cell renewal mechanisms usually begin in a single cambial layer and will then continue up along the differentiated layers. The balance between apoptosis and cell proliferation will be displaced towards the proliferation of malfunctioning cells. Thus, due to corresponding changes in the metric signature, the system’s behavior will have a tendency to remain in a pseudo hyperbolic space (inside a double cone). Because a coquaternion structure represents the core features in each hierarchical level of a BS, the deeper the layer where the stem cells’ structure becomes deteriorated, the more differentiated levels will be omitted for normal transformations, and therefore the more aggressive form the malignancy will have.

To understand the place of malignant transformations in normal functional structure of a BS, first, chromosome loci responsible for base patterns organized in a hierarchy should be found; second, deteriorated pattern(s) corresponding to malignancy should then be linked to the related loci of a genome.

9. Conclusions

The system structure of complex biologic objects predisposes a hierarchy where each level (module) is supposed to have uniform organization. Coquaternion as an algebraically closed structure represents the base functional patterns of biologic systems, namely, PFB, NFB and RL on the levels of biological cells, tissues and organs. Geometrically, coquaternion is represented by 4D hyperbolic paraboloid due to its metric signature (2, 2). The stability of a BS is based on the reproducibility of base elements in onto-phylogenesis and CRC. Considering the self-organizing properties of a BS (a functional module) the value of the metabolic components associated with the isotropic quadratic form is supposed to have an oscillating character. This behavior confirms the general principle of dynamical organization of normal BS, demonstrating the fluctuations in biologic variables around physiologic constants. In cases of irreversible deterioration of the basis functional patterns and corresponding changes in the normal metric structure, the system will lose the ability to maintain the wholeness of the corresponding functional module. Pathologic behavior will demonstrate its inability to collaborate and adjust functional properties to the surrounding tissues. The most general feature of non-systemic structures with the functional advantages to survive is invasive growth and bypassing the energy for anabolic reactions from the surrounding systems. In general, malignant transformations of the normal functional structure of a BS are the result of unconvertible changes in its base functional patterns.