A New Hybrid Multi-Objective Scheduling Model for Hierarchical Hub and Flexible Flow Shop Problems
Abstract
1. Introduction
2. Literature Review
2.1. Hierarchical Hub Problems
2.2. Flexible Flow Shop
2.3. Research Contribution
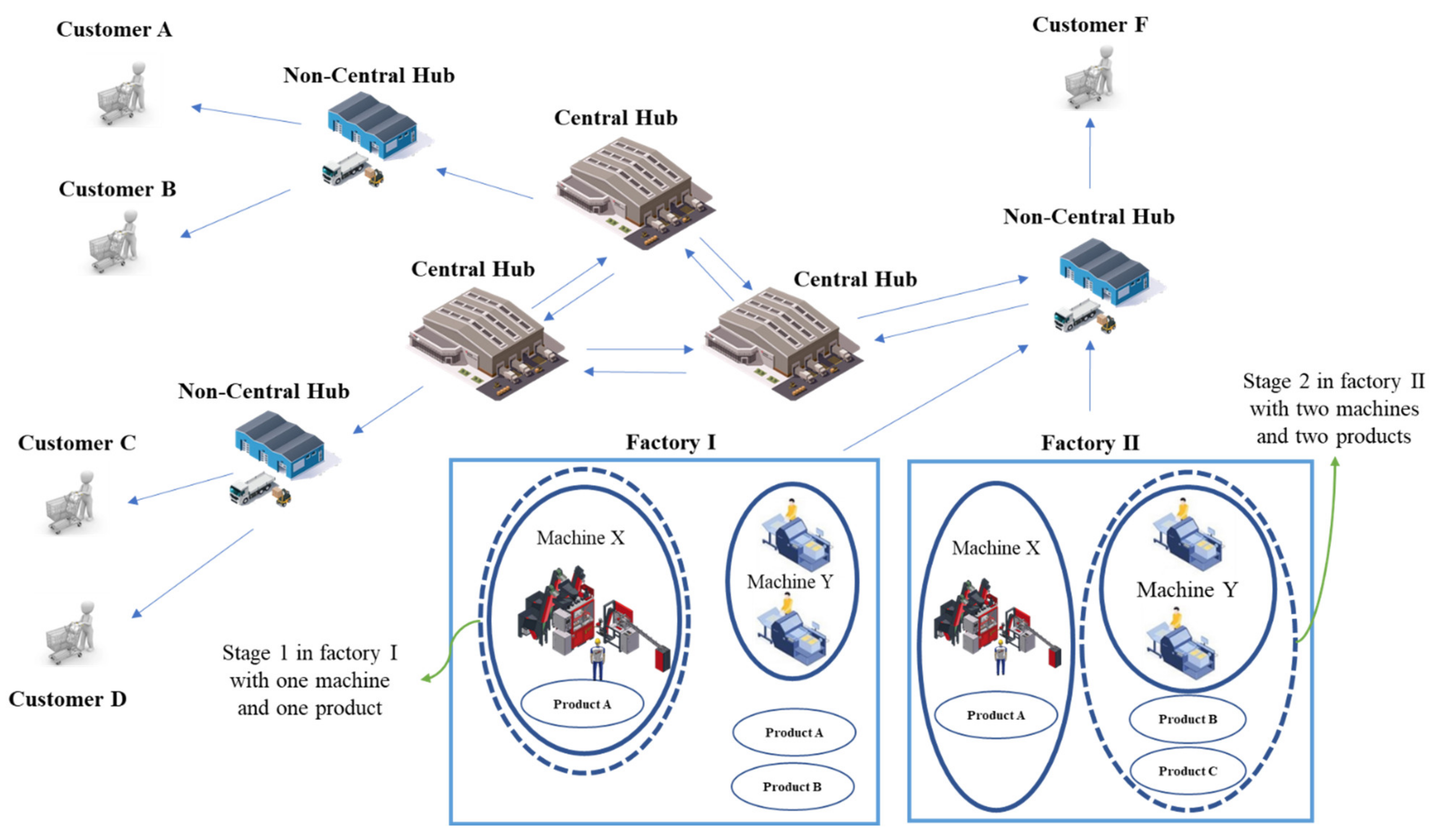
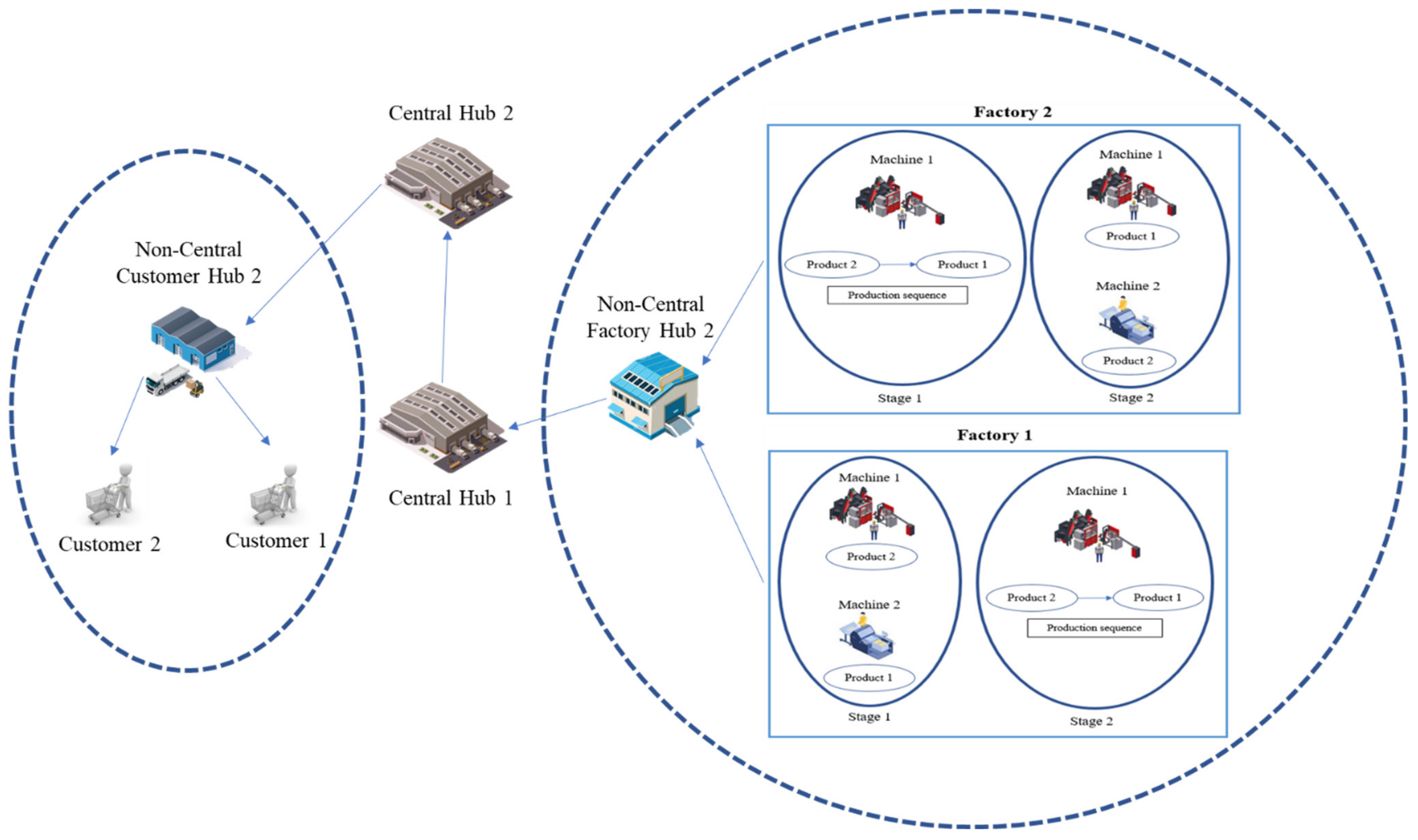
3. Problem Definition
4. Solution Approach
Subject to:
x belongs S
Subject to:
f2(x) ≥ e2
f3(x) ≥ e3
…
fp(x) ≥ ep
x belongs S
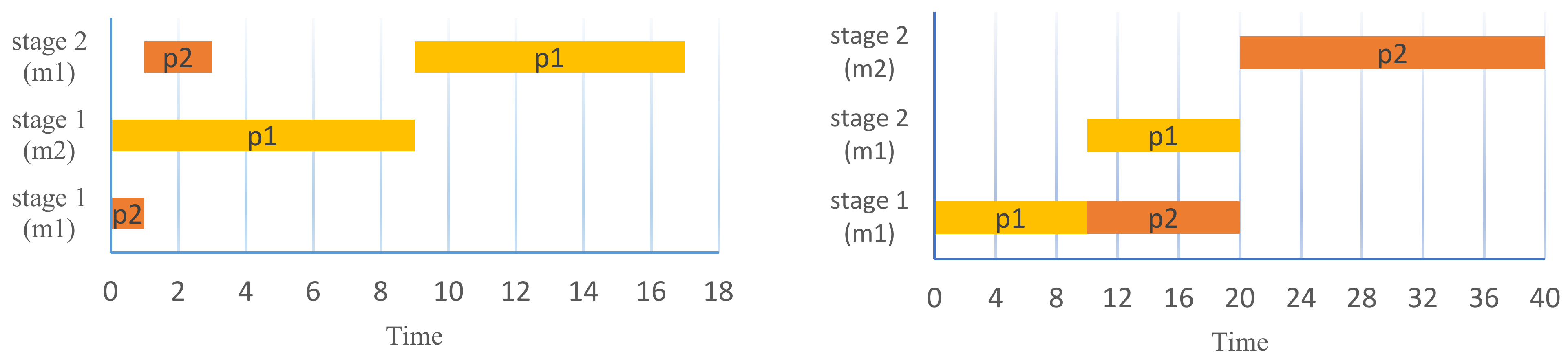
4.1. Validation of the Model
4.2. Numeral Experiments
5. Discussion
6. Managerial Insights and Practical Implications
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Sets | |
| Set of stages | |
| Set of non-central hubs connected to customers | |
| Set of products | |
| Set of factories | |
| Set of non-central hubs connected to factories | |
| Set of the central hubs | |
| Set of customers | |
| Indices | |
| Index of stages | |
| Index of non-central hubs connected to customers | |
| Index of products | |
| Index of factories | |
| Index of non-central hubs connected to factories | |
| Index of the central hubs | |
| Index of customers | |
| Parameters | |
| Cost of produced product p in factory f connected to non-central hub j | |
| Cost of sending products from non-central hub j (NCHF) to central hub k (CH), then from central hub k to another central hub , and, finally, from the central hub to non-central hub h (NCHC) | |
| Product sending cost from non-central hub j to central hub k then to non-central hub | |
| Cost of connecting customer node c to non-central hub h | |
| Cost of connecting non-central hub h to central hub k | |
| Cost of connecting factory f to non-central hub j | |
| Cost of connecting non-central hub j to central hub k | |
| The demand of customer c for product p | |
| Period of time between factory f and non-central hub j for product p | |
| Period of time between non-central hub j and central hub k for product p | |
| Period of time between the central hub and non-central hub h for product p | |
| Period of time between the central hub and central hub k for product p | |
| The number of the machine at stage s in factory f | |
| Period of time between non-central hub k and customer c for product p | |
| Binary variables | |
| If customer c connects to the non-center hub h is 1, otherwise 0 | |
| If product p is processed (produced) in factory f by machine m at stage s is 1, otherwise 0 | |
| If factory f is assigned to non-center hub j is 1, otherwise 0 | |
| If non-central hub j is assigned to central hub k is 1, otherwise 0 | |
| If customer c is assigned to non-central hub h is 1, otherwise 0 | |
| If non-central hub h is assigned to customer k is 1, otherwise 0 | |
| If the product is processed (produced) immediately after p in factory f on machine m at stage s is 1, otherwise 0 | |
| If the variable is positive, this variable will be 1, otherwise 0 | |
| If the variable is positive, this variable will be 1, otherwise 0 | |
| Positive variables | |
| The number of produced product p in factory f connected to non-central hub j | |
| The number of product p sent from non-central hub j (NCHF) to central hub k (CH), then from central hub to another central hub to non-central hub h (NCHC) | |
| The number of product p sent from non-central hub j (NCHF) to central hub k, then from central hub k to non-central hub h (NCHC) | |
| Maximum arrival time of product p to non-central hub j (NCHF) | |
| Maximum arrival time of product p to non-central hub h (NCHC) | |
| Maximum completion time of products in factory f | |
| Maximum arrival time of product p to customer c connected to non-central hub h |
References
- Alderighi, M.; Cento, A.; Nijkamp, P.; Rietveld, P. Assessment of New Hub-and-Spoke and Point-to-Point Airline Network Configurations. Transp. Rev. 2007, 27, 529–549. [Google Scholar] [CrossRef]
- Pels, E. Optimality of the hub-spoke system: A review of the literature, and directions for future research. Transp. Policy 2021, 104, A1–A10. [Google Scholar] [CrossRef]
- Yaman, H. The hierarchical hub median problem with single assignment. Transp. Res. Part B Methodol. 2009, 43, 643–658. [Google Scholar] [CrossRef]
- Lotfi, R.; Kargar, B.; Gharehbaghi, A.; Afshar, M.; Rajabi, M.S.; Mardani, N. A data-driven robust optimization for multi-objective renewable energy location by considering risk. Environ. Dev. Sustain. 2022, 24, 1–22. [Google Scholar] [CrossRef]
- Rajabi, M.S.; Beigi, P.; Aghakhani, S. Drone Delivery Systems and Energy Management: A Review and Future Trends. arXiv 2022, arXiv:2206.10765. [Google Scholar]
- Beigi, P.; Rajabi, M.S.; Aghakhani, S. An Overview of Drone Energy Consumption Factors and Models. arXiv 2022, arXiv:2206.10775. [Google Scholar]
- Shakerian, M.; Rajabi, M.S.; Tajik, M.; Taghaddos, H. Hybrid Simulation-based Resource Planning and Constructability Analysis of RCC Pavement Projects. arXiv 2022, arXiv:2204.05659. [Google Scholar]
- Rajabi, M.S.; Radzi, A.R.; Rezaeiashtiani, M.; Famili, A.; Rashidi, M.E.; Rahman, R.A. Key Assessment Criteria for Organizational BIM Capabilities: A Cross-Regional Study. Buildings 2022, 12, 1013. [Google Scholar] [CrossRef]
- Rajabi, M.S.; Rezaeiashtiani, M.; Radzi, A.R.; Famili, A.; Rezaeiashtiani, A.; Rahman, R.A. Underlying Factors and Strategies for Organizational BIM Capabilities: The Case of Iran. Appl. Syst. Innov. 2022, 5, 109. [Google Scholar] [CrossRef]
- Naderi, H.; Shojaei, A. Civil Infrastructure Digital Twins: Multi-Level Knowledge Map, Research Gaps, and Future Directions. IEEE Access 2022, 10, 122022–122037. [Google Scholar] [CrossRef]
- Rajabi, M.S.; Taghaddos, H.; Zahrai, M. Improving Emergency Training for Earthquakes Through Immersive Virtual Environments and Anxiety Tests: A Case Study. Buildings 2022, 12, 1850. [Google Scholar] [CrossRef]
- Moeinifard, P.; Rajabi, M.S.; Bitaraf, M. Lost Vibration Test Data Recovery Using Convolutional Neural Network: A Case Study. AUT J. Civ. Eng. 2021, 5, 701–714. [Google Scholar] [CrossRef]
- Omer, M.M.; Adeeq, N.M.; Ezazee, M.; Lee, Y.S.; Sadra Rajabi, M.; Rahman, R.A. Constructive and Destructive Leadership Behaviors, Skills, Styles and Traits in BIM-Based Construction Projects. Buildings 2022, 12, 2068. [Google Scholar] [CrossRef]
- Dindar, A.; Ourang, S.; Ghadikola, E.G. Development of a Communication-Assisted Adaptive Overcurrent Protection Scheme in Smart Distribution Networks in Presence of Wind and Solar Generation. 2022. Available online: https://www.researchgate.net/profile/Shiva-Ourang-2/publication/359191101_Development_of_a_Communication-Assisted_Adaptive_Overcurrent_Protection_Scheme_in_Smart_Distribution_Networks_in_Presence_of_Wind_and_Solar_Generation/links/625d928d9be52845a90d1e39/Development-of-a-Communication-Assisted-Adaptive-Overcurrent-Protection-Scheme-in-Smart-Distribution-Networks-in-Presence-of-Wind-and-Solar-Generation.pdf (accessed on 31 October 2022).
- Saaty, M.; Haqq, D.; Toms, D.B.; Eltahir, I.; McCrickard, D.S. A Study on Pokémon GO: Exploring the Potential of Location-based Mobile Exergames in Connecting Players with Nature. In Extended Abstracts, Proceedings of the 2021 Annual Symposium on Computer-Human Interaction in Play, Virtual Event Austria, 18–21 October 2021; ACM: New York, NY, USA, 2021; pp. 128–132. [Google Scholar] [CrossRef]
- Saaty, M.; Patel, J.V.; Abdelgawad, N.; Marion, J.; McCrickard, D.S.; Misra, S.; Wernstedt, S. Note: Studying Sustainable Practices of Appalachian Trail Community based on Reddit Topic Modelling Analysis. In Proceedings of the ACM SIGCAS/SIGCHI Conference on Computing and Sustainable Societies (COMPASS), Seattle, WA, USA, 29 June–1 July 2022; ACM: New York, NY, USA, 2022; pp. 560–563. [Google Scholar] [CrossRef]
- Gelareh, S.; Nickel, S.; Pisinger, D. Liner shipping hub network design in a competitive environment. Transp. Res. Part E Logist. Transp. Rev. 2010, 46, 991–1004. [Google Scholar] [CrossRef]
- Lotfi, R.; Yadegari, Z.; Hosseini, S.H.; Khameneh, A.H.; Tirkolaee, E.B.; Weber, G.-W. A robust time-cost-quality-energy-environment trade-off with resource-constrained in project management: A case study for a bridge construction project. J. Ind. Manag. Optim. 2022, 18, 375. [Google Scholar] [CrossRef]
- Shang, X.; Yang, K.; Jia, B.; Gao, Z.; Ji, H. Heuristic algorithms for the bi-objective hierarchical multimodal hub location problem in cargo delivery systems. Appl. Math. Model. 2021, 91, 412–437. [Google Scholar] [CrossRef]
- Topcuoglu, H.; Corut, F.; Ermis, M.; Yilmaz, G. Solving the uncapacitated hub location problem using genetic algorithms. Comput. Oper. Res. 2005, 32, 967–984. [Google Scholar] [CrossRef]
- Boland, N.; Krishnamoorthy, M.; Ernst, A.T.; Ebery, J. Preprocessing and cutting for multiple allocation hub location problems. Eur. J. Oper. Res. 2004, 155, 638–653. [Google Scholar] [CrossRef]
- Abdinnour-Helm, S.; Venkataramanan, M.A. Solution approaches to hub location problems. Ann. Oper. Res. 1998, 78, 31–50. [Google Scholar] [CrossRef]
- Yazdani, M.; Khalili, S.M.; Jolai, F. A parallel machine scheduling problem with two-agent and tool change activities: An efficient hybrid metaheuristic algorithm. Int. J. Comput. Integr. Manuf. 2016, 29, 1075–1088. [Google Scholar] [CrossRef]
- Schultz, G.P. The logic of health care facility planning. Socioecon. Plann. Sci. 1970, 4, 383–393. [Google Scholar] [CrossRef]
- Calvo, A.B.; Marks, D.H. Location of health care facilities: An analytical approach. Socioecon. Plann. Sci. 1973, 7, 407–422. [Google Scholar] [CrossRef]
- Dokmeci, V.F. An optimization model for a hierarchical spatial system. J. Reg. Sci. 1973, 13, 439–451. [Google Scholar] [CrossRef]
- Chou, Y. The hierarchical-hub model for airline networks. Transp. Plann. Technol. 1990, 14, 243–258. [Google Scholar] [CrossRef]
- Alumur, S.A.; Yaman, H.; Kara, B.Y. Hierarchical multimodal hub location problem with time-definite deliveries. Transp. Res. Part E Logist. Transp. Rev. 2012, 48, 1107–1120. [Google Scholar] [CrossRef]
- Davari, S.; Zarandi, M.H.F. The single-allocation hierarchical hub median location problem with fuzzy demands. Afr. J. Bus. Manag. 2012, 6, 347–360. [Google Scholar] [CrossRef]
- Dukkanci, O.; Kara, B.Y. Routing and scheduling decisions in the hierarchical hub location problem. Comput. Oper. Res. 2017, 85, 45–57. [Google Scholar] [CrossRef]
- Khodemani-Yazdi, M.; Tavakkoli-Moghaddam, R.; Bashiri, M.; Rahimi, Y. Solving a new bi-objective hierarchical hub location problem with an M/M/c queuing framework. Eng. Appl. Artif. Intell. 2019, 78, 53–70. [Google Scholar] [CrossRef]
- Bhattacharjee, A.K.; Mukhopadhyay, A. Solving Multi-Objective Hierarchical Hub Facility Location Problem Using GA-Based Approaches. In Proceedings of the 2021 IEEE 18th India Council International Conference (INDICON), Guwahati, India, 19–21 December 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Yazdani, M.; Aleti, A.; Khalili, S.M.; Jolai, F. Optimizing the sum of maximum earliness and tardiness of the job shop scheduling problem. Comput. Ind. Eng. 2017, 107, 12–24. [Google Scholar] [CrossRef]
- Ikar, E.; Grinshpoun, T.; Ilani, H.; Shufan, E. Reentrant Flow Shop with Identical Jobs and Unit Processing Times. In Proceedings of the 9th Multidisciplinary International Conference on Scheduling: Theory and Applications (MISTA 2019), Ningbo, China, 12–15 December 2019; pp. 125–140. [Google Scholar]
- Zhu, Z.; Zhou, X. Flexible job-shop scheduling problem with job precedence constraints and interval grey processing time. Comput. Ind. Eng. 2020, 149, 106781. [Google Scholar] [CrossRef]
- Jenabi, M.; Fatemi Ghomi, S.M.T.; Torabi, S.A.; Karimi, B. Two hybrid meta-heuristics for the finite horizon ELSP in flexible flow lines with unrelated parallel machines. Appl. Math. Comput. 2007, 186, 230–245. [Google Scholar] [CrossRef]
- Ruiz, R.; Stützle, T. An Iterated Greedy heuristic for the sequence dependent setup times flowshop problem with makespan and weighted tardiness objectives. Eur. J. Oper. Res. 2008, 187, 1143–1159. [Google Scholar] [CrossRef]
- Jayamohan, M.S.; Rajendran, C. New dispatching rules for shop scheduling: A step forward. Int. J. Prod. Res. 2000, 38, 563–586. [Google Scholar] [CrossRef]
- Kianfar, K.; Fatemi Ghomi, S.M.T.; Karimi, B. New dispatching rules to minimize rejection and tardiness costs in a dynamic flexible flow shop. Int. J. Adv. Manuf. Technol. 2009, 45, 759–771. [Google Scholar] [CrossRef]
- Gupta, J.N.D.; Tunc, E.A. Schedules for a two-stage hybrid flowshop with parallel machines at the second stage. Int. J. Prod. Res. 1991, 29, 1489–1502. [Google Scholar] [CrossRef]
- Bertel, S.; Billaut, J.-C. A genetic algorithm for an industrial multiprocessor flow shop scheduling problem with recirculation. Eur. J. Oper. Res. 2004, 159, 651–662. [Google Scholar] [CrossRef]
- Fu, Y.; Tian, G.; Fathollahi-Fard, A.M.; Ahmadi, A.; Zhang, C. Stochastic multi-objective modelling and optimization of an energy-conscious distributed permutation flow shop scheduling problem with the total tardiness constraint. J. Clean. Prod. 2019, 226, 515–525. [Google Scholar] [CrossRef]
- Lee, T.-S.; Loong, Y.-T. A review of scheduling problem and resolution methods in flexible flow shop. Int. J. Ind. Eng. Comput. 2019, 10, 67–88. [Google Scholar] [CrossRef]
- Tan, Y.; Mönch, L.; Fowler, J.W. A hybrid scheduling approach for a two-stage flexible flow shop with batch processing machines. J. Sched. 2018, 21, 209–226. [Google Scholar] [CrossRef]
- Juárez-Pérez, F.; Cruz-Chávez, M.A.; Rivera-López, R.; Ávila-Melgar, E.Y.; Eraña-Díaz, M.L.; Cruz-Rosales, M.H. Grid-Based Hybrid Genetic Approach to Relaxed Flexible Flow Shop with Sequence-Dependent Setup Times. Appl. Sci. 2022, 12, 607. [Google Scholar] [CrossRef]
- Zhang, B.; Pan, Q.; Meng, L.; Lu, C.; Mou, J.; Li, J. An automatic multi-objective evolutionary algorithm for the hybrid flowshop scheduling problem with consistent sublots. Knowl. Based Syst. 2022, 238, 107819. [Google Scholar] [CrossRef]
- Wu, X.; Shen, X.; Cui, Q. Multi-Objective Flexible Flow Shop Scheduling Problem Considering Variable Processing Time due to Renewable Energy. Sustainability 2018, 10, 841. [Google Scholar] [CrossRef]
- Li, J.; Sang, H.; Han, Y.; Wang, C.; Gao, K. Efficient multi-objective optimization algorithm for hybrid flow shop scheduling problems with setup energy consumptions. J. Clean. Prod. 2018, 181, 584–598. [Google Scholar] [CrossRef]
- Lin, D.; Lee, C.K.M.; Wu, Z. Integrating analytical hierarchy process to genetic algorithm for re-entrant flow shop scheduling problem. Int. J. Prod. Res. 2012, 50, 1813–1824. [Google Scholar] [CrossRef]
- Hosseini, S.M.H.; Sana, S.S.; Rostami, M. Assembly flow shop scheduling problem considering machine eligibility restrictions and auxiliary resource constraints. Int. J. Syst. Sci. Oper. Logist. 2021, 9, 512–528. [Google Scholar] [CrossRef]



| Notations | Value | Notations | Value |
|---|---|---|---|
| 2 | 2 | ||
| 2 | 2 | ||
| 2 | 2 | ||
| 2 |
| Parameters | Value | Parameters | Value | Parameters | Value |
|---|---|---|---|---|---|
| Test Problem | Sets | Parameter | ||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | |
| 2 | 3 | 2 | 2 | 2 | 3 | 2 | 2 | |
| 3 | 2 | 2 | 3 | 2 | 2 | 3 | 2 | |
| 4 | 2 | 2 | 3 | 2 | 2 | 3 | 2 | |
| 5 | 2 | 2 | 2 | 1 | 3 | 3 | 2 | |
| 6 | 2 | 2 | 2 | 2 | 3 | 3 | 2 | |
| 7 | 2 | 2 | 2 | 2 | 1 | 2 | 3 | |
| 8 | 3 | 2 | 3 | 2 | 1 | 2 | 3 | |
| 9 | 2 | 1 | 3 | 1 | 1 | 3 | 4 | |
| 10 | 3 | 3 | 2 | 3 | 1 | 4 | 2 | |
| Number of Weights | Weight of Cost Functions (W1) | Weight of Time Function (W2) |
|---|---|---|
| 1 | 0.0001 | 0.9999 |
| 2 | 0.091 | 0.909 |
| 3 | 0.1 | 0.9 |
| 4 | 0.2 | 0.8 |
| 5 | 0.4 | 0.6 |
| 6 | 0.9 | 0.1 |
| Number of Instance | MID | |
|---|---|---|
| Weighted Sum Method | ε-Constraint | |
| 1 | 1366.04 | 1456.67 |
| 2 | 2392.25 | 2793.64 |
| 3 | 2264.26 | 2393.91 |
| 4 | 2265.29 | 2395.61 |
| 5 | 2254.99 | 2279.10 |
| 6 | 2178.88 | 2261.40 |
| 7 | 1471.04 | 1547.63 |
| 8 | 1525.28 | 1737.77 |
| 9 | 2623.40 | 2670.86 |
| 10 | 2794.20 | 2942.09 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aghakhani, S.; Rajabi, M.S. A New Hybrid Multi-Objective Scheduling Model for Hierarchical Hub and Flexible Flow Shop Problems. AppliedMath 2022, 2, 721-737. https://doi.org/10.3390/appliedmath2040043
Aghakhani S, Rajabi MS. A New Hybrid Multi-Objective Scheduling Model for Hierarchical Hub and Flexible Flow Shop Problems. AppliedMath. 2022; 2(4):721-737. https://doi.org/10.3390/appliedmath2040043
Chicago/Turabian StyleAghakhani, Sina, and Mohammad Sadra Rajabi. 2022. "A New Hybrid Multi-Objective Scheduling Model for Hierarchical Hub and Flexible Flow Shop Problems" AppliedMath 2, no. 4: 721-737. https://doi.org/10.3390/appliedmath2040043
APA StyleAghakhani, S., & Rajabi, M. S. (2022). A New Hybrid Multi-Objective Scheduling Model for Hierarchical Hub and Flexible Flow Shop Problems. AppliedMath, 2(4), 721-737. https://doi.org/10.3390/appliedmath2040043








