Hydrogenation of Aromatic Ethers and Lactones: Does the Oxygen Functionality Really Improve the Thermodynamics of Reversible Hydrogen Storage in the Related LOHC Systems?
Abstract
1. Introduction
2. Approach
3. Results and Discussion
3.1. Step I: Quantum Chemical Calculations of the Gas-Phase Enthalpies of Formation
| Compound | (g) b G3MP2/AT | (g) c G3MP2//B3LYP | (g) d G3MP2 | (g)QC e | (g) f (exp) |
|---|---|---|---|---|---|
| 2,3-benzofuran | 17.2 | 16.6 | 16.9 | 13.9 ± 0.7 | |
| 2,3-dihydrobenzofuran | −47.1 | −45.5 | −46.3 | −46.7 ± 0.9 | |
| isobenzofuran | 67.3 | 79.3 ± 4.1 | |||
| 1,3-dihydro-isobenzofuran | −26.3 | −26.0 | −26.1 | −30.6 ± 1.2 | |
| dibenzofuran | 50.1 | 48.9 | 49.5 | 52.9 ± 0.7 | |
| 2-coumaranone | −222.7 | −217.5 d | −218.1 | −218.7 | (−210.8 ± 4.0) |
| 3-coumaranone | −166.3 | −162.1 d | −162.3 | −162.9 | −168.8 ± 2.4 |
| phthalide | −224.1 | −220.4 d | −220.7 | −221.4 | −220.6 ± 2.8 |
| Compounds | (liq or cr) | b | (g)exp c | (g)QC d |
|---|---|---|---|---|
| 2,3-benzofuran [271-89-6] (liq) | −34.8 ± 0.7 [11] | |||
| −35.3 ± 1.6 [12] | ||||
| −34.9 ± 0.6 | 48.4 ± 0.4 | 13.9 ± 0.7 | 16.9 ± 2.9 | |
| 2,3-dihydro-benzofuran [496-16-2] (liq) | −99.8 ± 0.7 [11] | |||
| −100.6 ± 1.9 [13] | ||||
| −99.9 ± 0.8 | 53.2 ± 0.3 | −46.7 ± 0.9 | −46.3 ± 2.9 | |
| 1,3-dihydro-isobenzofuran [496-14-0] (liq) | −83.8 ± 0.9 [14] | 53.2 ± 0.8 | −30.6 ± 1.2 | −26.1 ± 2.9 |
| dibenzofuran [132-64-9] (cr) | −29.1 ± 0.6 [15] | 82.0 ± 0.3 [16] | 52.9 ± 0.7 | 49.5 ± 2.9 |
| fluorene [86-73-7] (cr) | 89.9 ± 1.4 [17] | 86.1 ± 0.1 [18] | 176.0 ± 1.4 | - |
| 2-coumaranone [553-86-6] (cr) | (−292.4 ± 3.7) [10] | 81.6 ± 1.4 f | (−210.8 ± 4.0) | −218.7 ± 1.9 |
| 3-coumaranone [7169-34-8] (cr) | −254.9 ± 2.0 [10] | 86.1 ± 1.4 g | −168.8 ± 2.4 | −162.9 ± 1.9 |
| phthalide [87-41-2] (cr) | (−366 ± 10) [19] | |||
| −312.4 ± 1.5 [20] | 92.0 ± 2.2h | −220.6 ± 2.8 | −221.4 ± 2.3 |
| Compounds | Method a | T-Range/ K | Tav | 298.15 K b | |
|---|---|---|---|---|---|
| 2,3-benzofuran [271-89-6] | n/a | 323–403 | 45.0 ± 1.5 | 47.9 ± 1.6 | [21] |
| E | 273.2–488.1 | 45.1 ± 0.1 | 48.0 ± 0.6 | [11] | |
| T | 278.7–313.4 | 49.0 ± 0.4 | 48.8 ± 0.6 | [12] | |
| 48.4 ± 0.4 c | average | ||||
| Jx | 49.4 ± 1.0 | Table 4 | |||
| 2,3-dihydro-benzofuran [496-16-2] | E | 285.0–503.2 | 48.7 ± 0.1 | 53.0 ± 0.9 | [11] |
| T | 278.7–333.0 | 52.7 ± 0.2 | 53.2 ± 0.4 | [13] | |
| BP | 341–465 | 47.8 ± 0.8 | 53.2 ± 1.3 | Table S4 | |
| 53.2 ± 0.3 c | |||||
| Jx | 52.7 ± 1.0 | Table 4 | |||
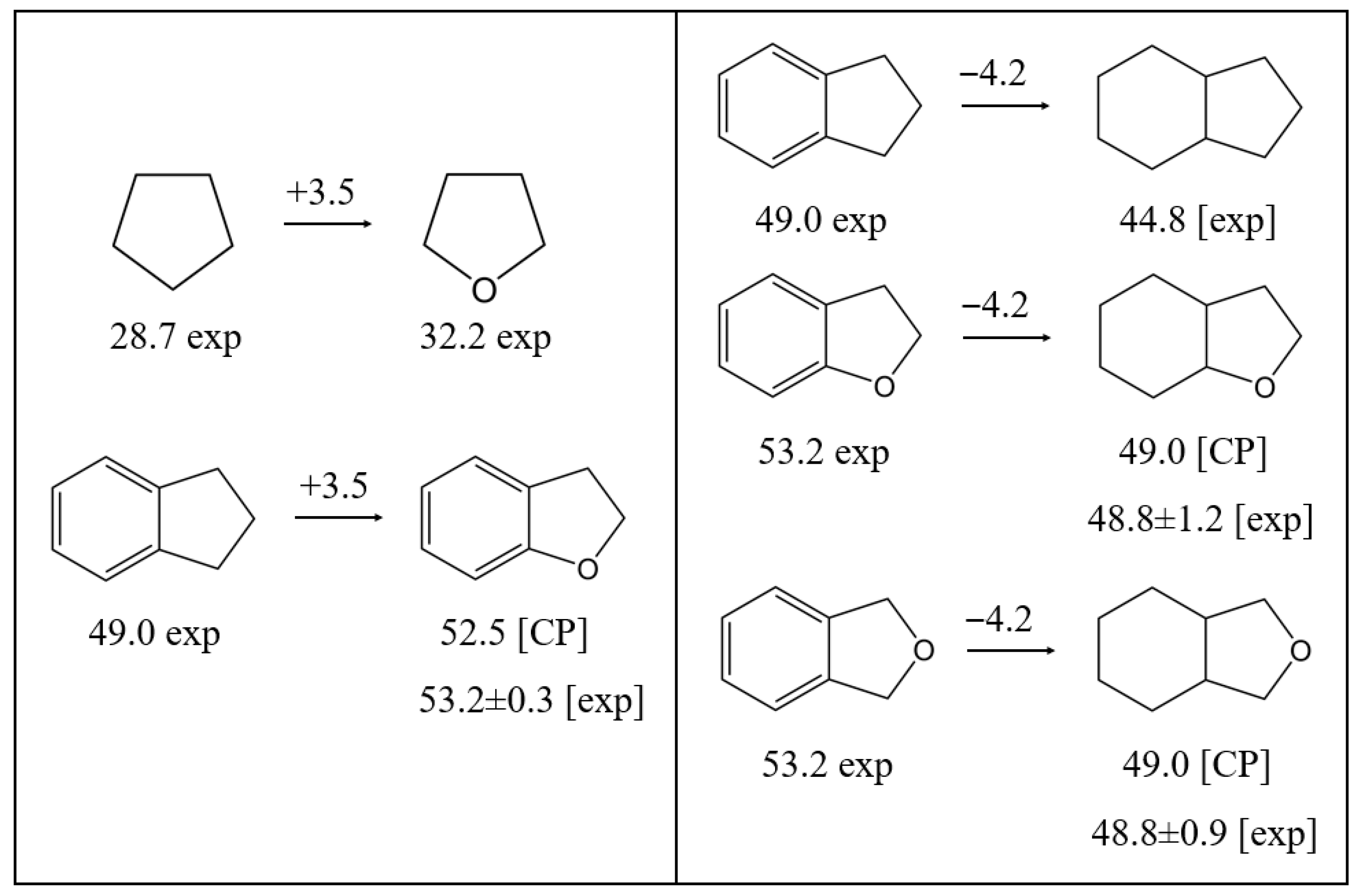
| CP | 52.5 ± 1.5 | Figure 3 | |||
| 1,3-dihydro-isobenzofuran [496-14-0] | E | 285.0–503.2 | 48.9 ± 0.1 | 53.3 ± 0.9 | [14] |
| phthalan | CGC | 298 | 52.7 ± 2.9 | [22] | |
| BP | 318–465 | 48.0 ± 1.1 | 53.1 ± 1.5 | Table S4 | |
| 53.2 ± 0.8 c | average | ||||
| Jx | 52.6 ± 1.0 | Table 4 | |||
| 8H-octahydro-benzofuran | BP | 337–446 | 44.5 ± 0.8 | 48.8 ± 1.9 | Table S4 |
| [13054-97-2] | Tb | 48.8 ± 1.5 | Equation (7) | ||
| 48.8 ± 1.2 c | average | ||||
| CP | 49.0 ± 1.5 | Figure 3 | |||
| CP | 48.3 ± 1.5 | Figure S3 | |||
| CP | 48.4 ± 1.5 | Figure 3 | |||
| GA | 48.9 ± 1.5 | Figure S3 | |||
| 8H-octahydro-isobenzofuran | BP | 324–453 | 43.8 ± 0.8 | 48.1 ± 1.2 | Table S4 |
| [4743-54-8] | Tb | 49.9 ± 1.5 | Equation (7) | ||
| 48.8 ± 0.9 c | average | ||||
| CP | 48.8 ± 1.5 | Figure 3 | |||
| CP | 48.3 ± 1.5 | Figure 3 | |||
| CP | 48.3 ± 1.5 | Figure S4 | |||
| GA | 48.8 ± 1.5 | Figure S4 | |||
| 12H-dodecahydro-dibenzofuran | BP | 381–532 | 52.2 ± 1.4 | 63.8 ± 2.7 | Table S4 |
| [13054-98-3] | |||||
| 2(3H)-benzofuranone [553-86-6] | PhT | 298 | 61.9 ± 2.0 | Table S3 | |
| 2-coumaranone | BP | 384–521 | 57.0 ± 1.8 | 65.3 ± 2.4 | Table S4 |
| Jx | 65.7 ± 1.5 | Table S7 | |||
| Jx | 65.7 ± 2.0 | Table S8 | |||
| CP | 67.3 ± 1.5 | Figure S5 | |||
| CP | 66.2 ± 1.5 | Figure S5 | |||
| 65.7 ± 0.7 | average | ||||
| benzofuran-3(2H)-one [7169-34-8] | PhT | 298 | 67.8 ± 2.3 | Table S3 | |
| 3-coumaranone | BP | 425–551 | 60.3 ± 1.5 | 68.8 ± 2.3 | Table S4 |
| CP | 66.7 ± 1.5 | Figure S6 | |||
| CP | 67.3 ± 1.5 | Figure S6 | |||
| CP | 65.5 ± 1.5 | Figure S6 | |||
| 66.9 ± 0.8 c | average | ||||
| 2-benzofuran-1(3H)-one [87-41-2] | n/a | 368.7–563.0 | 58.7 ± 1.5 | (66.9 ± 2.2) | [23] |
| phthalide | PhT | 298 | 71.5 ± 4.6 | Table S3 | |
| BP | 346–563 | 69.0 ± 2.0 | 76.3 ± 2.5 | Table S4 | |
| CP | 74.7 ± 1.5 | Figure S7 | |||
| CP | 75.4 ± 1.5 | Figure S7 | |||
| CP | 73.6 ± 1.5 | Figure S7 | |||
| 74.7 ± 0.8 c | average | ||||
| 6H-hexahydro-2-coumaranone | BP | 327–537 | 56.3 ± 1.7 | 64.3 ± 2.3 | Table S4 |
| [6051-03-2] | |||||
| 6H-hexahydro-3-coumaranone | BP | 353–626 | 54.2 ± 0.7 | 65.2 ± 2.3 | Table S4 |
| [1206676-08-5] | CP | 62.5 ± 1.5 | Figure S8 | ||
| CP | 63.0 ± 1.5 | Figure S8 | |||
| CP | 62.2 ± 1.5 | Figure S8 | |||
| 62.9 ± 0.8 c | average | ||||
| 6H-hexahydro-phthalide | BP | 337–503 | 72.3 ± 0.8 | 77.6 ± 1.3 | Table S4 |
| [2611-01-0] | |||||
| octahydro-benzofuran-2-ol | CP | 66.5 ± 2.0 | Figure S9 | ||
| [36871-99-5] | CP | 67.2 ± 2.0 | Figure S9 | ||
| 66.9 ± 1.4 c | average | ||||
| 8H-octahydro-benzofuran-3-ol | BP | 354–513 | 63.8 ± 1.6 | 73.2 ± 2.5 | Table S4 |
| [99769-38-7] | CP | 73.0 ± 2.0 | Figure S9 | ||
| CP | 73.5 ± 2.0 | Figure S9 | |||
| 73.2 ± 1.2 c | average | ||||
| 8H-octahydro-isobenzofuran-1-ol | CP | 66.7 ± 2.0 | Figure S9 | ||
| [59901-42-7] | CP | 66.5 ± 2.0 | Figure S9 | ||
| 66.6 ± 1.4 c | average | ||||
| methoxy-benzene [100-66-3] | 46.4 ± 0.2 | [24] | |||
| methoxy-cyclohexane [931-56-6] | 43.0 ± 0.5 | [25] |
3.2. Step II: Evaluation of the Thermodynamic Functions of Vaporisation
3.2.1. Absolute Vapour Pressures and Vaporisation Enthalpies
3.2.2. Validation of Vaporisation Enthalpies by Structure–Property Correlations
3.2.3. Validation of Vaporisation Enthalpies Using Correlation with the Kovats Indices Jx
| CAS | Compound | Jx a | (298.15 K)exp b | (298.15 K)calc c | Δ d |
|---|---|---|---|---|---|
| 109-99-9 | tetrahydrofuran | 611 | 32.6 ± 0.2 [33] | 33.1 | −0.5 |
| 110-00-9 | furan | 468 | 27.7 ± 0.2 [33] | 27.8 | −0.1 |
| 1191-99-7 | 2,3-dihydrofuran | 564 | 31.3 ± 0.3 [34] | 31.3 | 0.0 |
| 1708-29-8 | 2,5-dihydrofuran | 614 | 32.6 ± 0.2 [33] | 33.2 | −0.6 |
| 534-22-5 | 2-methyl-furan | 603 | 32.7 ± 0.2 [33] | 32.7 | 0.0 |
| 625-86-5 | 2,5-dimethyl-furan | 729 | 37.7 ± 0.2 [33] | 37.4 | 0.3 |
| 3208-16-0 | 2-ethyl-furan | 720 | 37.1 ± 0.2 [33] | 37.1 | 0.0 |
| 271-89-6 | 2,3-benzofuran | 1054 | 48.8 ± 0.3 [12] | 49.4 | −0.6 |
| 496-16-2 | 2,3-dihydrobenzofuran | 1144 | 53.2 ± 0.4 [13] | 52.7 | 0.5 |
| 496-14-0 | phthalan | 1142 e | 53.7 ± 0.4 [14] | 52.6 | 1.1 |
| 4265-25-2 | 2-methyl-benzofuran | 1158 | 53.3 ± 1.5 [35] | 53.2 | 0.1 |
| 132-64-9 | dibenzofuran | 1537 | 66.3 ± 0.6 [16] | 67.2 | −0.9 |
| Compound | a | (g) b | (liq) c | (liq) d |
|---|---|---|---|---|
| 2,3-benzofuran [271-89-6] | 111.3 ± 0.1 [11] | 328.3 | 215.6 [36] | 217.0 |
| isobenzofuran [270-75-7] | 102.4 ± 8.0 g | 330.7 | 228.3 | |
| 2,3-dihydro-benzofuran [496-16-2] | 119.2 ± 3.0 | 344.1 | 226.4 [36] | 224.9 |
| 1,3-dihydro-isobenzofuran [496-14-0] | 119.2 ± 0.1 [14] | 357.5 | 238.3 | |
| dibenzofuran [132-64-9] | 128.4 ± 2.0 [16] | 384.0 | 248.5 e | 255.6 |
| fluorene [86-73-7] | 136.7 ± 0.4 [37] | 392.0 | 257.8 f | 255.3 |
| 2-coumaranone [553-86-6] | 132.4 ± 3.0 | 353.8 | 221.4 | |
| 3-coumaranone [7169-34-8] | 132.2 ± 5.1 | 355.8 | 223.6 | |
| phthalide [87-41-2] | 144.5 ± 0.2 | 353.6 | 209.1 | |
| furan [110-00-9] | 93.4 ± 0.2 [38] | 272.7 | 176.7 [38] | 179.3 |
| 2,3-dihydro-furan [1191-99-7] | 95.8 ± 0.1 [34] | 294.7 | 198.9 | |
| tetrahydrofuran [109-99-9] | 96.5 ± 0.2 [39] | 301.7 | 203.9 [40] | 205.2 |
| 8H-benzofuran [13054-97-2] | 113.1 ± 2.6 | 365.5 | 252.4 | |
| 8H-isobenzofuran [4743-54-8] | 110.7 ± 1.4 | 364.2 | 253.5 | |
| 12H-dibenzofuran [13054-98-3] | 135.5 ± 4.6 | 430.7 | 295.2 | |
| 12H-fluorene | 136.0 ± 2.7 | 434.7 | 298.7 | |
| 6H-2-coumaranone [6051-03-2] | 127.6 ± 5.6 | 373.9 | 246.3 | |
| 6H-3-coumaronone [1206676-08-5] | 119.8 ± 2.4 | 377.9 | 258.1 | |
| 6H-phthalide [2611-01-0] | 162.5 ± 2.9 | 374.1 | 211.6 | |
| 8H-benzofuran-2-ol [36871-99-5] | 152.0 ± 8.0 g | 385.9 | 233.9 | |
| 8H-benzofuran-3-ol [99769-38-7] | 151.9 ± 5.5 | 390.3 | 238.4 | |
| 8H-isobenzofuran-1-ol [59901-42-7] | 172.0 ± 8.0 g | 387.8 | 215.8 | |
| 1,3-cyclopentadiene [542-92-7] | 274.5 [41] | 182.7 [40] | ||
| cyclopentene [142-29-0] | 289.7 [42] | 201.3 [43] | ||
| cyclopentane [287-92-3] | 292.9 | 204.1 [44] | ||
| indene [95-13-6] | 115.4 ± 0.6 [13] | 335.9 | 214.2 [45] | 220.5 |
| indane [496-11-7] | 110.8 ± 0.8 [13] | 345.9 | 234.4 [45] | 235.1 |
| trans-8H-indene [3296-50-2] | 106.2 ± 0.1 | 371.6 | 258.9 [46] | 265.4 |
3.2.4. Standard Molar Vaporisation Entropies
3.3. Step III: Thermodynamic Analysis of the LOHC Systems Based on Aromatic Ethers
3.3.1. Reaction Enthalpies, Entropies, and Gibbs Energies of the LOHC Hydrogenation
3.3.2. Comparison of the Thermodynamics of Hydrogenation Reactions with and Without Oxygen Functionality
3.3.3. Comparison of Reactions Involving Five-Membered Aliphatic Rings
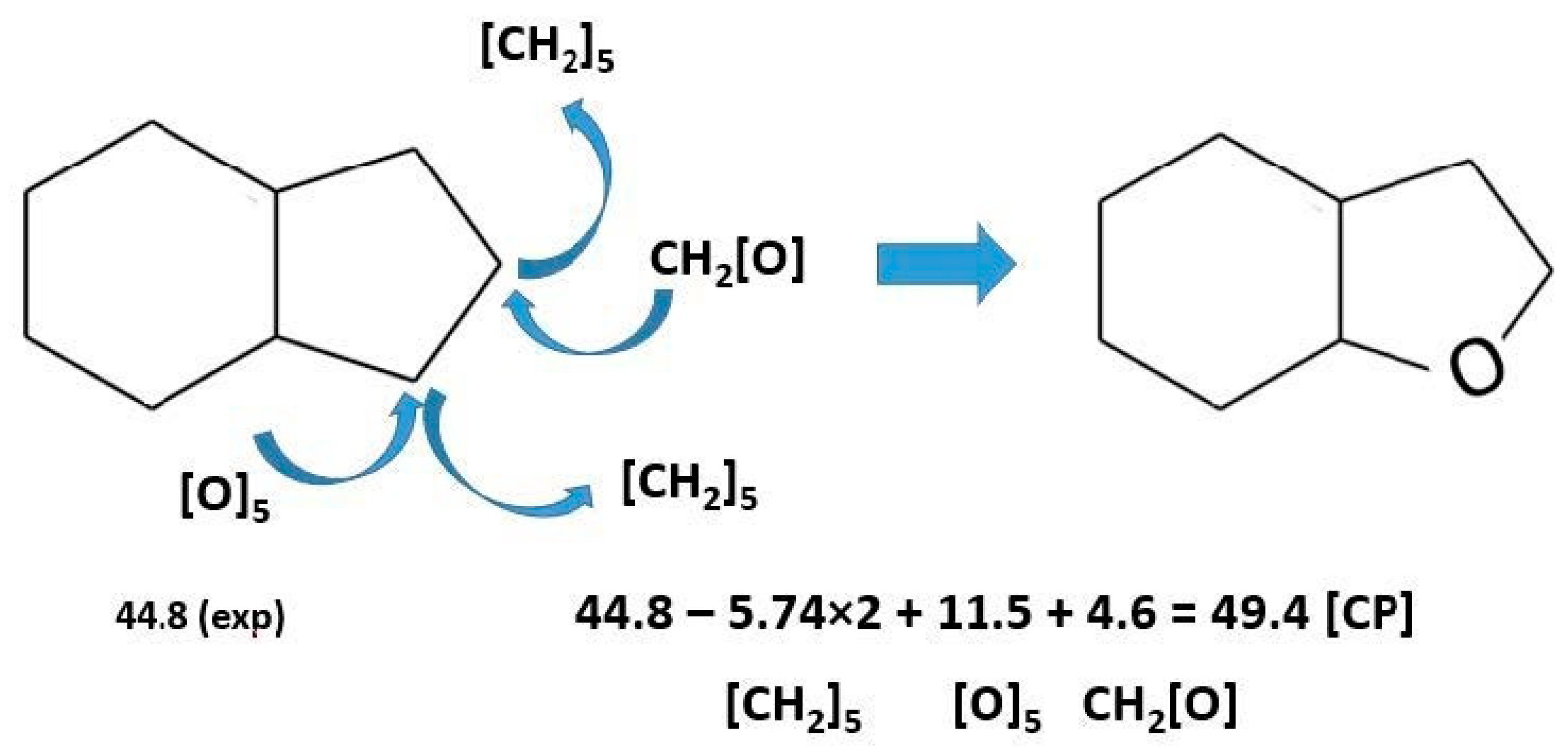
3.3.4. Comparison of Reactions Involving Aromatic Ethers with Attached Five-Membered Aliphatic Ring
3.3.5. Comparison of Reactions Involving a Five-Membered Aliphatic Ring Fused to Two Benzene Rings
3.3.6. Could the Lactone Ring Improve Hydrogen Storage Thermodynamics?
3.3.7. Thermodynamic Analysis of the Reversible Hydrogenation/Dehydrogenation Process
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Teichmann, D.; Arlt, W.; Wasserscheid, P.; Freymann, R. A Future Energy Supply Based on Liquid Organic Hydrogen Carriers (LOHC). Energy Environ. Sci. 2011, 4, 2767. [Google Scholar] [CrossRef]
- Zakgeym, D.; Hofmann, J.D.; Maurer, L.A.; Auer, F.; Müller, K.; Wolf, M.; Wasserscheid, P. Better through Oxygen Functionality? The Benzophenone/Dicyclohexylmethanol LOHC-System. Sustain. Energy Fuels 2023, 7, 1213–1222. [Google Scholar] [CrossRef]
- Verevkin, S.P.; Samarov, A.A.; Vostrikov, S.V. Does the Oxygen Functionality Really Improve the Thermodynamics of Reversible Hydrogen Storage with Liquid Organic Hydrogen Carriers? Oxygen 2024, 4, 266–284. [Google Scholar] [CrossRef]
- Ghahremanpour, M.M.; van Maaren, P.J.; Ditz, J.C.; Lindh, R.; van der Spoel, D. Large-Scale Calculations of Gas Phase Thermochemistry: Enthalpy of Formation, Standard Entropy, and Heat Capacity. J. Chem. Phys. 2016, 145, 114305. [Google Scholar] [CrossRef]
- Pracht, P.; Bohle, F.; Grimme, S. Automated Exploration of the Low-Energy Chemical Space with Fast Quantum Chemical Methods. Phys. Chem. Chem. Phys. 2020, 22, 7169–7192. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision C.01; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Wheeler, S.E.; Houk, K.N.; Schleyer, P.v.R.; Allen, W.D. A Hierarchy of Homodesmotic Reactions for Thermochemistry. J. Am. Chem. Soc. 2009, 131, 2547–2560. [Google Scholar] [CrossRef] [PubMed]
- Verevkin, S.P.; Emel’yanenko, V.N.; Notario, R.; Roux, M.V.; Chickos, J.S.; Liebman, J.F. Rediscovering the Wheel. Thermochemical Analysis of Energetics of the Aromatic Diazines. J. Phys. Chem. Lett. 2012, 3, 3454–3459. [Google Scholar] [CrossRef] [PubMed]
- Notario, R.; Victoria Roux, M.; Castaño, O. The Enthalpy of Formation of Dibenzofuran and Some Related Oxygen-Containing Heterocycles in the Gas Phase. A GAUSSIAN-3 Theoretical Study. Phys. Chem. Chem. Phys. 2001, 3, 3717–3721. [Google Scholar] [CrossRef]
- Sousa, C.C.S.; Matos, M.A.R.; Santos, L.M.N.B.F.; Morais, V.M.F. Reprint of: Energetics of 2- and 3-Coumaranone Isomers: A Combined Calorimetric and Computational Study. J. Chem. Thermodyn. 2014, 73, 283–289. [Google Scholar] [CrossRef]
- Steele, W.V.; Chirico, R.D. Cooperative Agreement No. FC22-83FE60149 (NIPEP-457); IIT Research Institute, NIPEP: Bartlesville, OK USA, 1990; pp. 1–75. [Google Scholar]
- Verevkin, S.P.; Emel’yanenko, V.N.; Pimerzin, A.A.; Vishnevskaya, E.E. Thermodynamic Analysis of Strain in Heteroatom Derivatives of Indene. J. Phys. Chem. A 2011, 115, 12271–12279. [Google Scholar] [CrossRef]
- Verevkin, S.P.; Emel’yanenko, V.N.; Pimerzin, A.A.; Vishnevskaya, E.E. Thermodynamic Analysis of Strain in the Five-Membered Oxygen and Nitrogen Heterocyclic Compounds. J. Phys. Chem. A 2011, 115, 1992–2004. [Google Scholar] [CrossRef]
- Steele, W.V.; Chirico, R.D.; Knipmeyer, S.E.; Nguyen, A.; Smith, N.K.; Tasker, I.R. Thermodynamic Properties and Ideal-Gas Enthalpies of Formation for Cyclohexene, Phthalan (2,5-Dihydrobenzo-3,4-Furan), Isoxazole, Octylamine, Dioctylamine, Trioctylamine, Phenyl Isocyanate, and 1,4,5,6-Tetrahydropyrimidine. J. Chem. Eng. Data 1996, 41, 1269–1284. [Google Scholar] [CrossRef]
- Chirico, R.; Gammon, B.; Knipmeyer, S.; Nguyen, A.; Strube, M.; Tsonopoulos, C.; Steele, W. The Thermodynamic Properties of Dibenzofuran. J. Chem. Thermodyn. 1990, 22, 1075–1096. [Google Scholar] [CrossRef]
- Verevkin, S.P. Enthalpy of Sublimation of Dibenzofuran: A Redetermination. Phys. Chem. Chem. Phys. 2003, 5, 710–712. [Google Scholar] [CrossRef]
- Rakus, K.; Verevkin, S.P.; Schätzer, J.; Beckhaus, H.; Rüchardt, C. Thermolabile Hydrocarbons, 33. Thermochemistry and Thermal Decomposition of 9,9′-Bifluorenyl and 9,9′-Dimethyl-9,9′-bifluorenyl—The Stabilization Energy of 9-Fluorenyl Radicals. Chem. Ber. 1994, 127, 1095–1103. [Google Scholar] [CrossRef]
- Verevkin, S.P. Vapor Pressure Measurements on Fluorene and Methyl-Fluorenes. Fluid Phase Equilib. 2004, 225, 145–152. [Google Scholar] [CrossRef]
- Tavernier, P. Donnees Thermochimiques Relatives Aux Constituants Des Poudres. Mem. Poudres 1956, 301–327. [Google Scholar]
- Freitas, V.L.S.; Santos, C.P.F.; Ribeiro da Silva, M.D.M.C.; Ribeiro da Silva, M.A.V. The Effect of Ketone Groups on the Energetic Properties of Phthalan Derivatives. J. Chem. Thermodyn. 2016, 96, 74–81. [Google Scholar] [CrossRef]
- Stephenson, R.M.; Malanowski, S. Handbook of the Thermodynamics of Organic Compounds; Springer: Dordrecht, The Netherlands, 1987; ISBN 978-94-010-7923-5. [Google Scholar]
- Gobble, C.; Chickos, J.S. The Vapor Pressure and Vaporization Enthalpy of R-(+)-Menthofuran, a Hepatotoxin Metabolically Derived from the Abortifacient Terpene, (R)-(+)-Pulegone by Correlation Gas Chromatography. J. Chem. Thermodyn. 2016, 98, 135–139. [Google Scholar] [CrossRef]
- Stull, D.R. Vapor Pressure of Pure Substances. Organic and Inorganic Compounds. Ind. Eng. Chem. 1947, 39, 517–540. [Google Scholar] [CrossRef]
- Verevkin, S.P. Weaving a Web of Reliable Thermochemistry around Lignin Building Blocks: Phenol, Benzaldehyde, and Anisole. J. Therm. Anal. Calorim. 2022, 147, 6073–6085. [Google Scholar] [CrossRef]
- Verevkin, S.P.; Samarov, A.A.; Vostrikov, S.V. Thermodynamics of Reversible Hydrogen Storage: Are Methoxy-Substituted Biphenyls Better through Oxygen Functionality? Hydrogen 2023, 4, 862–880. [Google Scholar] [CrossRef]
- Samarov, A.A.; Verevkin, S.P. Hydrogen Storage Technologies: Methyl-Substituted Biphenyls as an Auspicious Alternative to Conventional Liquid Organic Hydrogen Carriers (LOHC). J. Chem. Thermodyn. 2022, 165, 106648. [Google Scholar] [CrossRef]
- Verevkin, S.P.; Andreeva, I.V.; Zherikova, K.V.; Pimerzin, A.A. Prediction of Thermodynamic Properties: Centerpiece Approach—How Do We Avoid Confusion and Get Reliable Results? J. Therm. Anal. Calorim. 2022, 147, 8525–8534. [Google Scholar] [CrossRef]
- Benson, S.W. Thermochemical Kinetics, 2nd ed.; John Wiley & Sons: New York, NY, USA; London, UK; Sydney, Australia; Toronto, ON, Canada, 1976; pp. 1–320. [Google Scholar]
- Verevkin, S.P.; Emel’yanenko, V.N.; Diky, V.; Muzny, C.D.; Chirico, R.D.; Frenkel, M. New Group-Contribution Approach to Thermochemical Properties of Organic Compounds: Hydrocarbons and Oxygen-Containing Compounds. J. Phys. Chem. Ref. Data 2013, 42, 033102. [Google Scholar] [CrossRef]
- Kováts, E. Gas-chromatographische Charakterisierung Organischer Verbindungen. Teil 1: Retentionsindices Aliphatischer Halogenide, Alkohole, Aldehyde Und Ketone. Helv. Chim. Acta 1958, 41, 1915–1932. [Google Scholar] [CrossRef]
- Verevkin, S.P. Vapour Pressures and Enthalpies of Vaporization of a Series of the Linear N-Alkyl-Benzenes. J. Chem. Thermodyn. 2006, 38, 1111–1123. [Google Scholar] [CrossRef]
- NIST Chemistry WebBook. Available online: https://webbook.nist.gov/chemistry/ (accessed on 15 June 2025).
- Majer, V.; Svoboda, V. Enthalpies of Vaporization of Organic Compounds: A Critical Review and Data Compilation; Blackwell Scientific Publications: Oxford, UK, 1985; pp. 1–300. Available online: http://old.iupac.org/publications/books/author/majer.html (accessed on 15 June 2025).
- Steele, W.V.; Chirico, R.D.; Knipmeyer, S.E.; Nguyen, A. Measurements of Vapor Pressure, Heat Capacity, and Density along the Saturation Line for Cyclopropane Carboxylic Acid, N, N -Diethylethanolamine, 2,3-Dihydrofuran, 5-Hexen-2-One, Perfluorobutanoic Acid, and 2-Phenylpropionaldehyde. J. Chem. Eng. Data 2002, 47, 715–724. [Google Scholar] [CrossRef]
- Steele, W.V.; Chirico, R.D.; Knipmeyer, S.E.; Nguyen, A.; Tasker, I.R. Determination of Ideal Gas Enthalpies of Formation for Key Compounds the 1991 Project Results; DIPPR Project, NIPER-716; National Inst. for Petroleum and Energy Research: Bartlesville, OK, USA, 1993.
- Chirico, R.D.; Nguyen, A.; Steele, W.V.; Strube, M.M.; Hossenlopp, I.A.; Gammon, B.E. Thermochemical and Thermophysical Properties of Organic Compounds Derived from Fossil Substances. Chemical Thermodynamic Properties of Organic Oxygen Compounds Found in Fossil Materials. NIPER Rep. 1986, 135, 1–42. [Google Scholar]
- Sasse, K.; Jose, J.; Merlin, J.-C. A Static Apparatus for Measurement of Low Vapor Pressures. Experimental Results on High Molecular-Weight Hydrocarbons. Fluid Phase Equilib. 1988, 42, 287–304. [Google Scholar] [CrossRef]
- Guthrie, G.B.; Scott, D.W.; Hubbard, W.N.; Katz, C.; McCullough, J.P.; Gross, M.E.; Williamson, K.D.; Waddington, G. Thermodynamic Properties of Furan. J. Am. Chem. Soc. 1952, 74, 4662–4669. [Google Scholar] [CrossRef]
- Parsana, V.M.; Parikh, S.; Ziniya, K.; Dave, H.; Gadhiya, P.; Joshi, K.; Gandhi, D.; Vlugt, T.J.H.; Ramdin, M. Isobaric Vapor–Liquid Equilibrium Data for Tetrahydrofuran + Acetic Acid and Tetrahydrofuran + Trichloroethylene Mixtures. J. Chem. Eng. Data 2023, 68, 349–357. [Google Scholar] [CrossRef]
- Lebedev, B.V.; Lityagov, V.Y. Calorimetric Study of Tetrahydrofuran and Its Polymerization in the Temperature Range 0–400 °K. Vysok. Soedin. 1977, A19, 2283–2290. [Google Scholar] [CrossRef]
- Furuyama, S.; Golden, D.M.; Benson, S.W. Thermochemistry of Cyclopentene and Cyclopentadiene from Studies of Gas-Phase Equilibria. J. Chem. Thermodyn. 1970, 2, 161–169. [Google Scholar] [CrossRef]
- Beckett, C.W.; Freeman, N.K.; Pitzer, K.S. The Thermodynamic Properties and Molecular Structure of Cyclopentene and Cyclohexene 1. J. Am. Chem. Soc. 1948, 70, 4227–4230. [Google Scholar] [CrossRef]
- Huffman, H.M.; Eaton, M.; Oliver, G.D. The Heat Capacities, Heats of Transition, Heats of Fusion and Entropies of Cyclopentene and Cyclohexene. J. Am. Chem. Soc. 1948, 70, 2911–2914. [Google Scholar] [CrossRef]
- Douslin, D.R.; Huffman, H.M. The Heat Capacities, Heats of Transition, Heats of Fusion and Entropies of Cyclopentane, Methylcyclopentane and Methylcyclohexane 1. J. Am. Chem. Soc. 1946, 68, 173–176. [Google Scholar] [CrossRef]
- Stull, D.R.; Sinke, G.C.; McDonald, R.A.; Hatton, W.E.; Hildebrand, D.L. Thermodynamic Properties of Indane and Indene. Pure Appl. Chem. 1961, 2, 315–322. [Google Scholar] [CrossRef]
- Finke, H.; McCullough, J.; Messerly, J.; Osborn, A.; Douslin, D. Cis- and Trans-Hexahydroindan. Chemical Thermodynamic Properties and Isomerization Equilibrium. J. Chem. Thermodyn. 1972, 4, 477–494. [Google Scholar] [CrossRef]
- Verevkin, S.P.; Samarov, A.A.; Vostrikov, S.V.; Wasserscheid, P.; Müller, K. Comprehensive Thermodynamic Study of Alkyl-Cyclohexanes as Liquid Organic Hydrogen Carriers Motifs. Hydrogen 2023, 4, 42–59. [Google Scholar] [CrossRef]
- Müller, K.; Völkl, J.; Arlt, W. Thermodynamic Evaluation of Potential Organic Hydrogen Carriers. Energy Technol. 2013, 1, 20–24. [Google Scholar] [CrossRef]
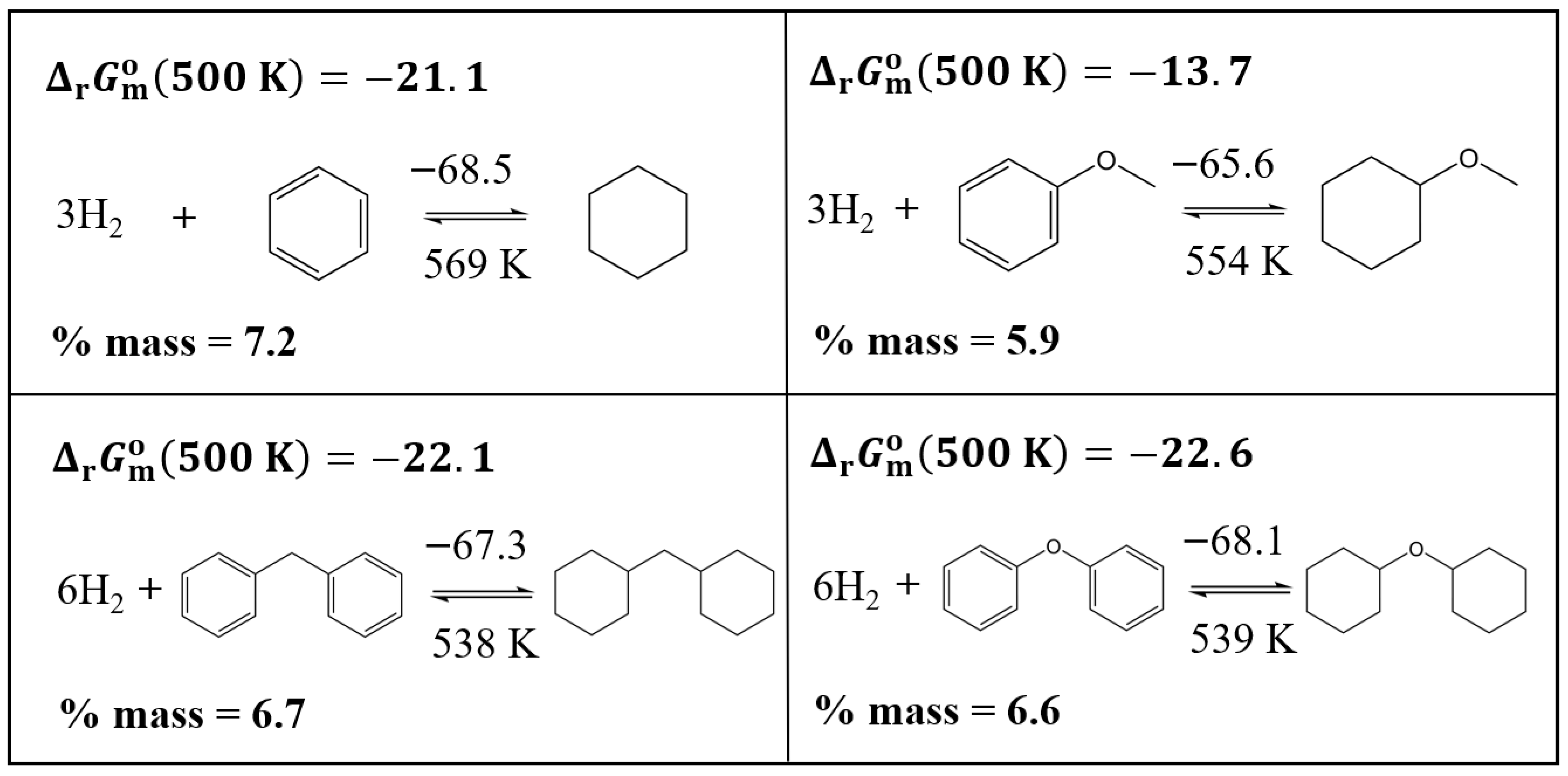
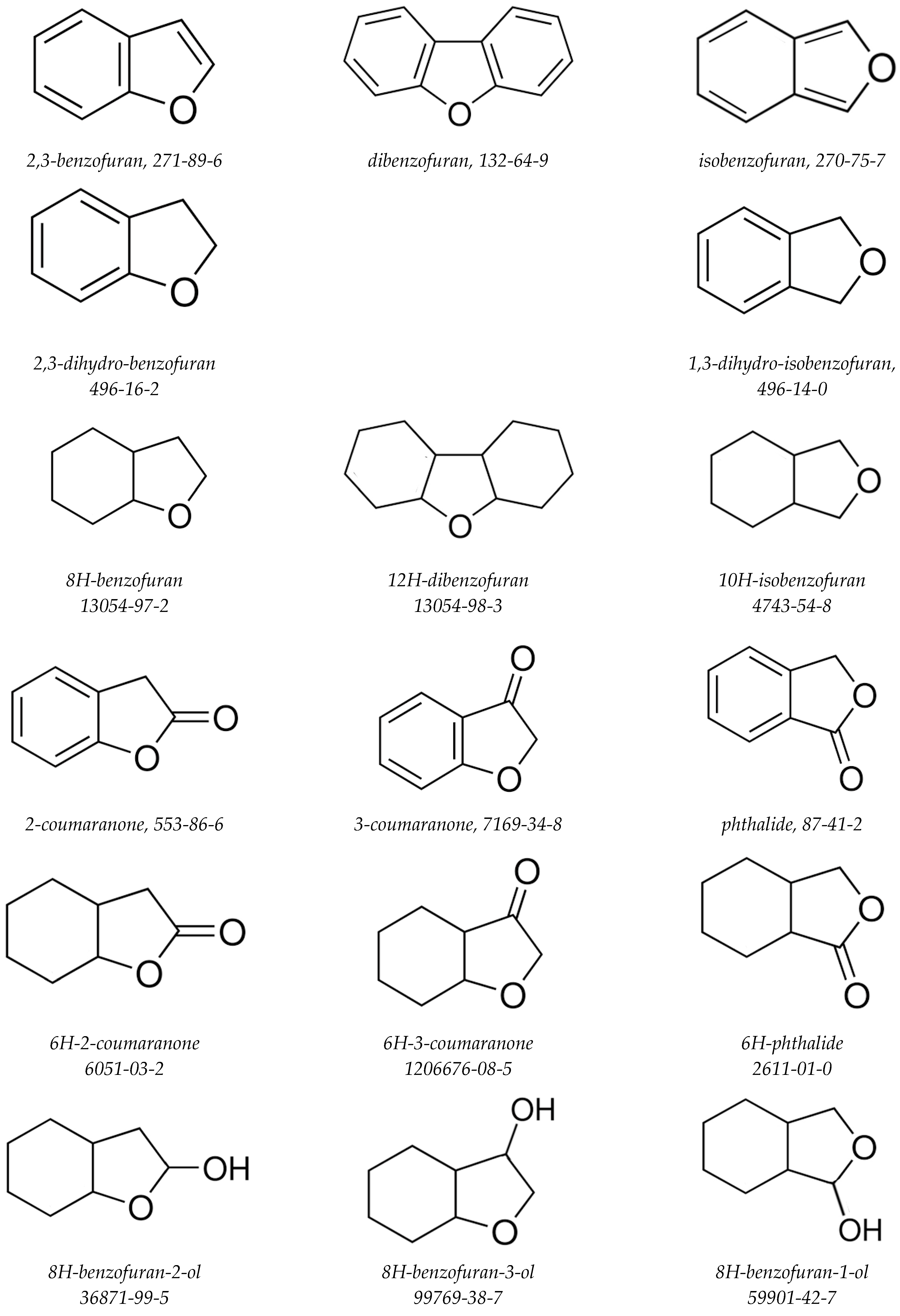
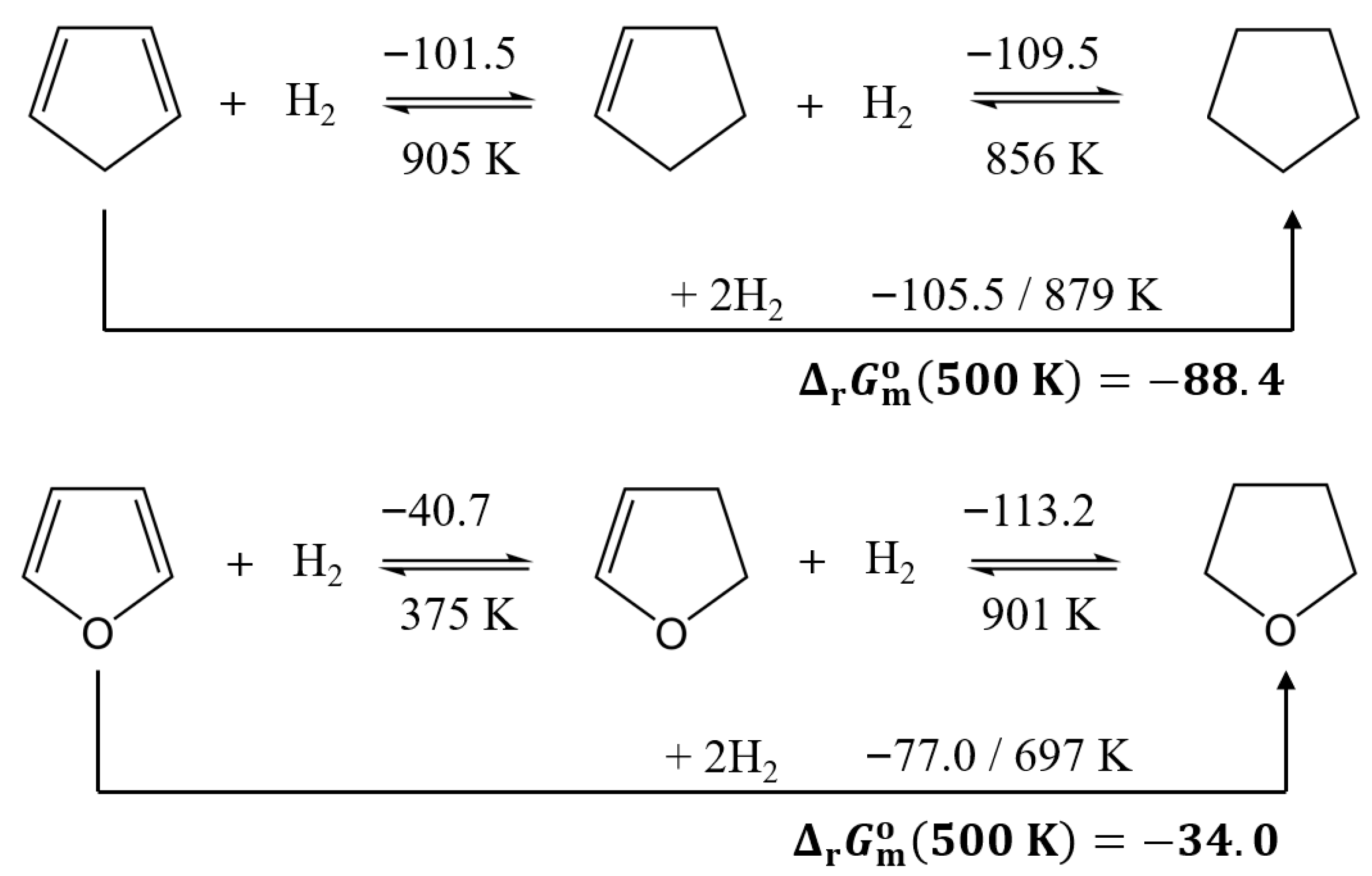
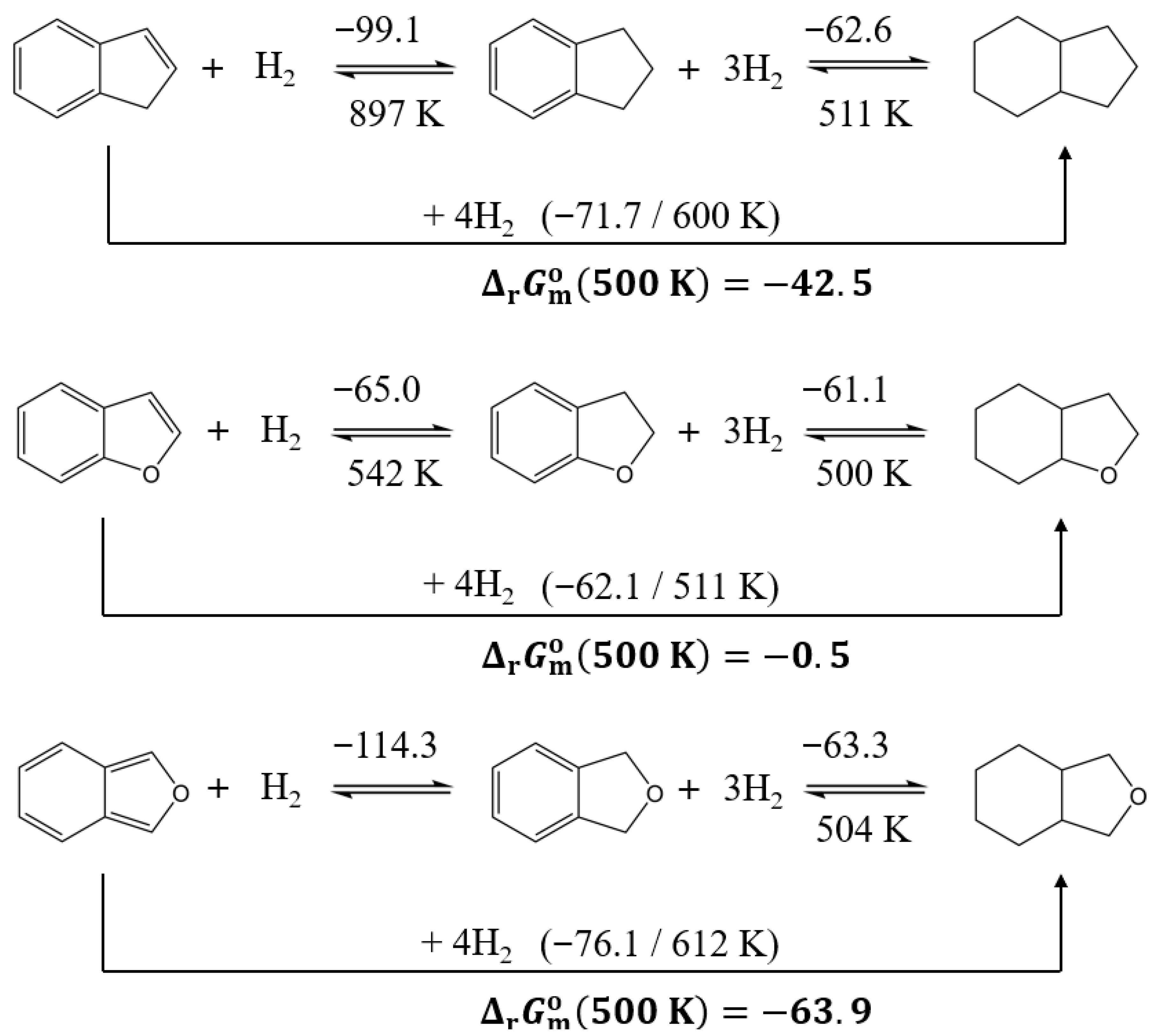
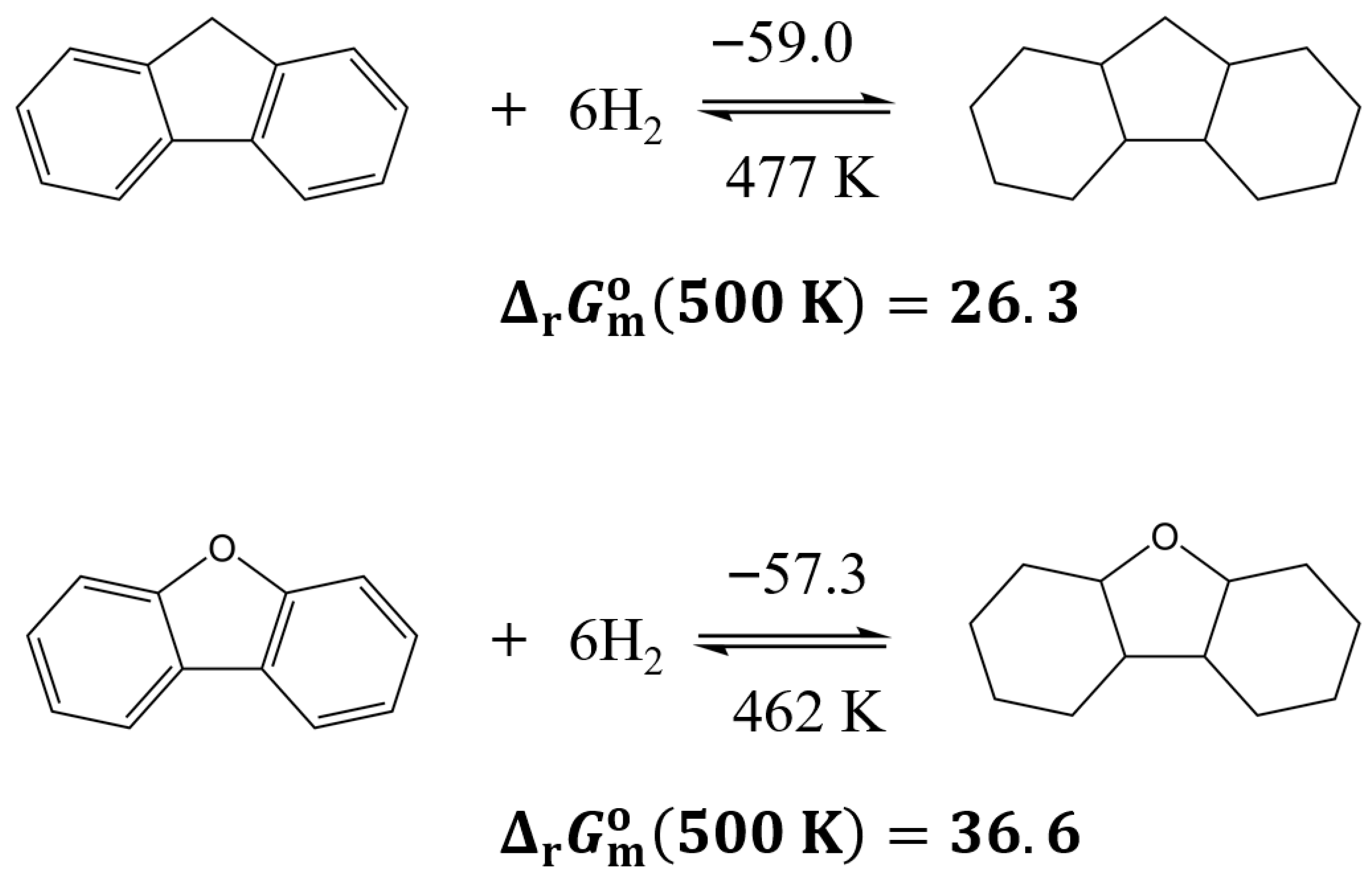
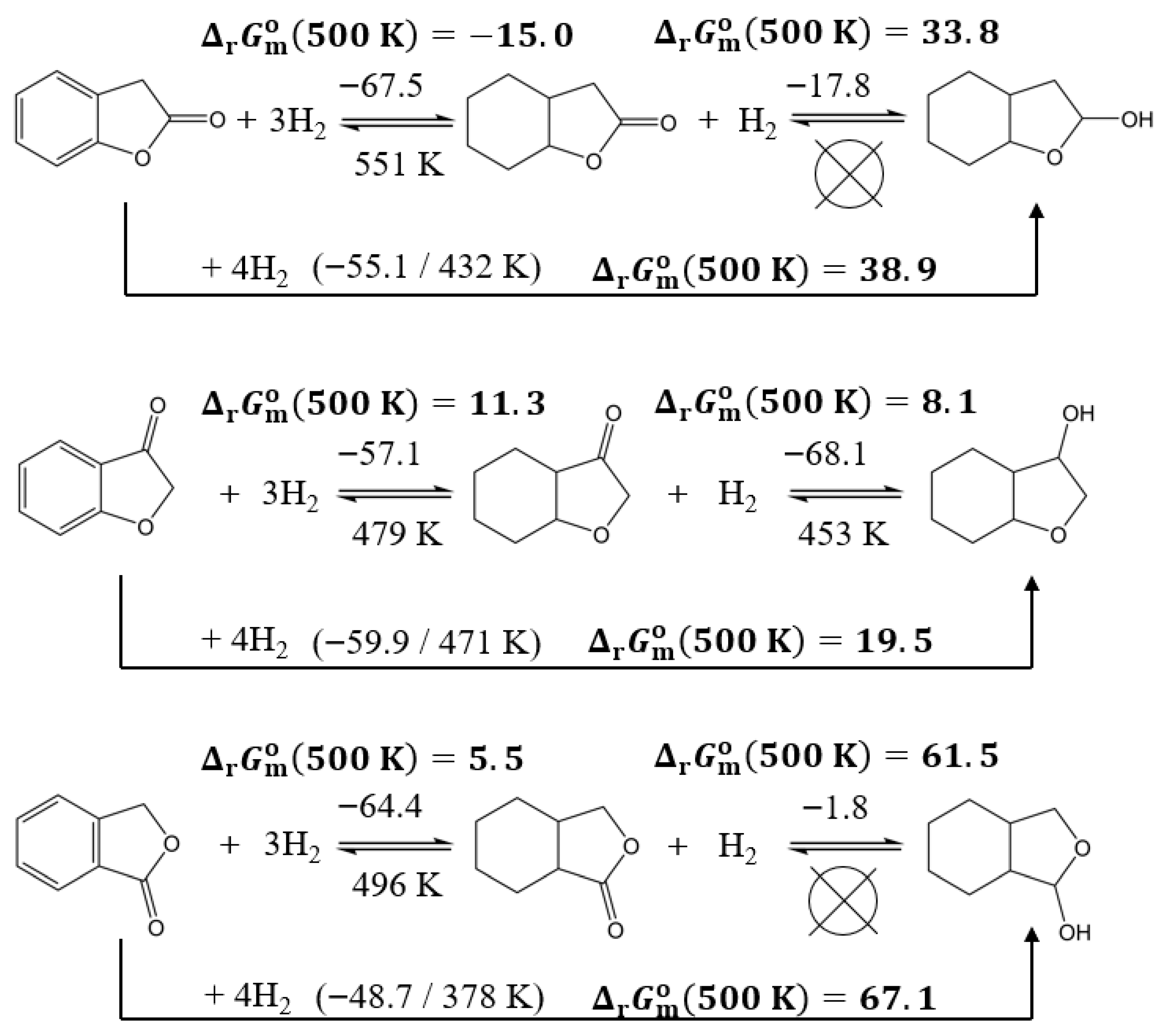
| Compound | (298 K)/H2 d | (298 K)/H2 | (298 K)/H2 b | (500 K)/H2 b | (298 K) | (298 K) | (298 K) b | (500 K) b | |
|---|---|---|---|---|---|---|---|---|---|
| kJ·mol−1 | J·K−1·mol−1 | kJ·mol−1 | kJ·mol−1 | kJ·mol−1 | J·K−1·mol−1 | kJ·mol−1 | kJ·mol−1 | K | |
| (aliphatic)5 | |||||||||
| 1,3-cyclopentadiene | −105.5 | −120.0 | −69.7 | −44.2 | −211.0 | −240.0 | −139.4 | −88.4 | 879 |
| furan | −77.0 | −117.1 | −42.0 | −17.0 | −153.9 | −234.2 | −84.1 | −34.0 | 697 |
| (aromatic)6 + (aliphatic)5 | |||||||||
| indene | −71.7 | −119.5 | −72.1 | −10.6 | −286.8 | −478.1 | −144.3 | −42.5 | 600 |
| 2,3-benzofuran | −62.1 | −121.5 | −25.8 | −0.1 | −248.2 | −486.0 | −103.3 | −0.5 | 511 |
| 2,3-dihydrobenzofuran | −61.1 | −122.0 | −24.7 | 1.2 | −183.2 | −366.1 | −74.0 | 3.5 | 500 |
| isobenzofuran | −76.1 | −124.4 | −39.0 | −16.0 | −304.3 | −497.6 | −155.9 | −63.9 | 612 |
| 1,3-dihydro-isobenzofuran | −63.3 | −125.6 | −25.9 | −2.6 | −190.0 | −376.9 | −77.6 | −7.7 | 504 |
| (aromatic)6 + (aliphatic)5 +(aromatic)6 | |||||||||
| fluorene | −59.0 | −123.9 | −22.1 | 4.1 | −354.2 | −743.3 | −132.6 | 24.6 | 477 |
| dibenzofuran | −57.3 | −124.1 | −20.3 | 6.1 | −343.7 | −744.6 | −121.7 | 36.6 | 462 |
| (aromatic)6 + (lactone)5 | |||||||||
| indene | −71.7 | −119.5 | −72.1 | −10.6 | −286.8 | −478.1 | −144.3 | −42.5 | 600 |
| 2-coumaranone | −55.1 | −127.6 | −17.0 | 9.7 | −220.2 | −510.3 | −68.1 | 38.9 | 432 |
| 3-coumaranone | −59.9 | −127.0 | −22.0 | 4.9 | −239.4 | −508.0 | −87.9 | 19.5 | 471 |
| phthalide | −48.7 | −129.0 | −10.3 | 16.8 | −194.9 | −516.1 | −41.0 | 67.1 | 378 |
| open-chained ethers | |||||||||
| benzene | −68.5 | −120.3 | −32.6 | −7.0 | −205.4 | −360.9 | −97.8 | −21.1 | 569 |
| methoxy-benzene | −65.6 | −118.9 | −30.1 | −4.6 | −196.8 | −356.8 | −90.4 | −13.7 | 552 |
| diphenyl ether | −68.1 | −126.2 | −30.5 | −3.8 | −408.5 | −757.3 | −182.7 | −22.6 | 539 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Siewert, R.; Samarov, A.A.; Vostrikov, S.V.; Müller, K.; Wasserscheid, P.; Verevkin, S.P. Hydrogenation of Aromatic Ethers and Lactones: Does the Oxygen Functionality Really Improve the Thermodynamics of Reversible Hydrogen Storage in the Related LOHC Systems? Oxygen 2025, 5, 18. https://doi.org/10.3390/oxygen5030018
Siewert R, Samarov AA, Vostrikov SV, Müller K, Wasserscheid P, Verevkin SP. Hydrogenation of Aromatic Ethers and Lactones: Does the Oxygen Functionality Really Improve the Thermodynamics of Reversible Hydrogen Storage in the Related LOHC Systems? Oxygen. 2025; 5(3):18. https://doi.org/10.3390/oxygen5030018
Chicago/Turabian StyleSiewert, Riko, Artemiy A. Samarov, Sergey V. Vostrikov, Karsten Müller, Peter Wasserscheid, and Sergey P. Verevkin. 2025. "Hydrogenation of Aromatic Ethers and Lactones: Does the Oxygen Functionality Really Improve the Thermodynamics of Reversible Hydrogen Storage in the Related LOHC Systems?" Oxygen 5, no. 3: 18. https://doi.org/10.3390/oxygen5030018
APA StyleSiewert, R., Samarov, A. A., Vostrikov, S. V., Müller, K., Wasserscheid, P., & Verevkin, S. P. (2025). Hydrogenation of Aromatic Ethers and Lactones: Does the Oxygen Functionality Really Improve the Thermodynamics of Reversible Hydrogen Storage in the Related LOHC Systems? Oxygen, 5(3), 18. https://doi.org/10.3390/oxygen5030018








