Abstract
The aim of this work was to investigate the evolutionary mechanisms of an artificial sedimentary agglomerate formed by cathodic polarization in natural seawater during its abandonment to a natural environment. Previous studies indicate that the mineralogical evolution of the material is controlled by kinetic factors and/or the local precipitation of aragonite on the brucite surface. However, the observation of the precipitation of metastable phase precipitation during the initial immersion of this material (in powder form) has suggested the possibility of a more complex mechanism. The present study builds upon previous experimental work and includes thermogravimetric analysis and infrared spectrometry. The results are analyzed using numerical experimentation to evaluate the proposed hypotheses. Findings show that the transformation mechanism is characterized by the precipitation of metastable calcium carbonate phases. Under supersaturation conditions, these hydrated phases form on the brucite surface, limiting the mineral’s contact with the solution. The subsequent transformation of these amorphous phases into aragonite further reduces brucite–solution interaction, which explains the persistence of brucite both in the residual powder after 120 h of immersion and in the consolidated material after more than 20 years of exposure to natural seawater.
1. Introduction
Coastal areas are complex ecosystems that are subjected to human activities, which cause erosion and are intensified by the rise in sea levels due to climate change. Recently, an innovative solution was proposed to mitigate coastal degradation in addition to classical engineering solutions such as rockfill dikes [1,2,3,4,5]. This solution consists of cementing shoreline sediments in submerged or tidal zones. In practice, a metallic grid is buried in the marine sediments (Figure 1). The cathodic polarization of this grid changes the local pH, leading to the precipitation of brucite () and aragonite (). This calco-magnesium deposit serves as a matrix, and the cemented sediments form an artificial agglomerate with a compressive strength up to 10 MPa [2]. After several months, the polarization is stopped. The application of such a process raises the question of the chemical stability of the formed agglomerate in seawater over time.
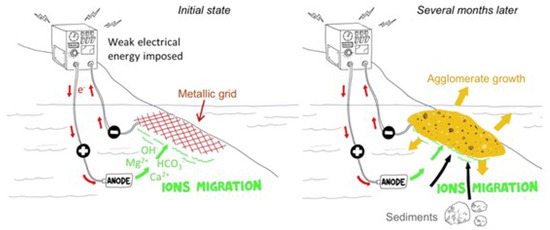
Figure 1.
Principle of the calco-magnesium agglomerate formation from a polarized metallic grid buried in seawater sediments (schemes adapted from [2]).
Although the phenomenon has been known for a long time and has been investigated in recent studies dealing with the cathodic protection of steels in marine environments (e.g., [6,7]), or as a reverse process to prevent natural scaling phenomena [8], the number of studies on calco-magnesian deposits as materials for cementing aggregates remains limited. In the case of our study, the issue of the agglomerate durability was addressed by laboratory investigations in a previous work [9]. Centimeter-sized blocks of agglomerate formed by the polarization of a grid buried in a siliceous sand were kept in natural seawater for 18 months in a state of abandonment, i.e., after the polarization was switched off. Thanks to mineralogical characterizations, we observed a dissolution of brucite accompanied by the precipitation of aragonite, as described by the following chemical reactions:
The molar ratio of these two phases composing the matrix appeared to be stationary after 12 months of immersion. A slight decrease in porosity of the agglomerate was also observed. Both mineralogical and physical stability after an 18-month immersion in seawater indicate that the calco-magnesium agglomerate should remain durable after abandonment. However, some results appeared to be unclear. In particular, not all brucite dissolved, even though it is thermodynamically unstable in seawater due to a pH lower than 9.3 [10,11,12]. We then resorted to tests on powders obtained from grinding agglomerates. Samples of powder were immersed in natural seawater under agitation for 4 days. These tests revealed, once again, that brucite does not dissolve completely in solution. The persistence of brucite can be explained by the precipitation of aragonite at the brucite surface, reducing its contact with the solution [1,3]. However, the kinetics of aragonite precipitation are slower than the kinetics of brucite dissolution. Furthermore, the powder form offers a high chemical contact with the solution. Moreover, mineral phases precipitated during the test were not clearly identified. These phases were observed only in the case of powders and not in agglomerate blocks after 18 months of immersion in seawater. This suggests complex transformation mechanisms of the agglomerate.
From a numerical point of view, modeling the durability of porous materials composed of a binder and aggregates can be an effective tool for understanding the mechanisms leading to the physicochemical degradation and durability of materials. It is particularly widely used for cementitious materials exposed to seawater [13]. These reactive transport models encourage the adoption of an approach that takes into account the physicochemical reactions occurring within the materials during the transport of aggressive agents or during their exposure in powdered form. The importance of considering the kinetics of dissolution and precipitation is also highlighted [14]. However, whereas a model was found in the literature describing the influence of parameters on the formation of calcareous deposits on cathodically protected steel in seawater [15], the modeling of the durability of the present material is, to the authors’ knowledge, still lacking. It was, therefore, implemented in this study to gain a better understanding of the mechanisms involved.
The aim of the present study is to further investigate the transformation mechanisms of a calco-magnesium agglomerate in seawater. To accelerate aging, powders ground from the agglomerate were tested in natural seawater under laboratory conditions. Mineralogical changes were monitored through thermogravimetric analysis (TGA), X-ray diffraction (XRD) and diffuse reflection infrared by Fourier transformation (DRIFT). The experimental results were compared with numerical simulations performed with the geochemical calculation code PHREEQC (version 3) coupled to the Thermoddem database [16]. In the following, the results of both experiments and modeling are discussed in order to formulate a scenario for the calco-magnesium agglomerate’s evolution in seawater.
2. Material and Methods
2.1. Material
Experiments were carried out on powder samples obtained from a sedimentary agglomerate. The latter was formed in the laboratory from a bed of a silica sand placed in a basin filled with natural seawater. A galvanized steel grid was buried in the sand bed and polarized with a current density of the order of mA/cm2 for 10 months duration. At the anodic site, acidification happens. In fact, in this experiment, a platinum wire is used as counter electrode. Then, we have electrolyte oxidation and then O2 and Cl2 degassing. More details on the formation process are available in [4,9]. Figure 2a shows an example of an agglomerate obtained using this method. For the present study, samples were taken from the formed agglomerate and then ground into powder with a particle size of less than 100 m. The powder was composed of approximately 88% of silica, 11.5% of and 0.5% of (aragonite).
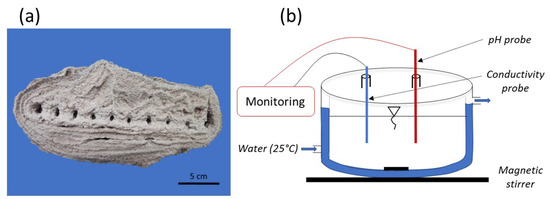
Figure 2.
Experimental protocol: (a) laboratory material formation scheme; (b) double wall chemical reactor.
2.2. Experimental Methods
The studied powder was placed in a double-walled reactor of 300 cm3 containing natural seawater solution, as shown in Figure 2b. The mixture was homogenized by magnetic stirring at 450 rpm. The reactor temperature was maintained at 25 °C. The same solid-to-liquid ratio as that found in [1] was used, i.e., 200 mg of powder per 200 cm3 of solution. Solution pH and conductivity were monitored over time using probes.
The test was repeated for different durations, i.e., 1, 24, 48 and 120 h. At the end of the test, the solution was filtered with a 0.54 m pore-size filter paper and the residual powder was dried at 105 °C in an oven for 1 h. The mineralogical composition of the dry powder was determined by X-ray tube (Bruker, ) using a sample mass of around 1 g. Samples of around 100 mg were also tested by thermogravimetric analysis (TGA) using a Setaram Setsys Evolution device. The samples were heated from 20 to 1000 °C at 10 °C/min in an argon atmosphere. To better identify possible hydrated phases, the dry powder was tested by Fourier transform diffuse infrared reflectance (DRIFT) spectrometry. Potassium bromide powder () was used as the standard.
For this purpose, we focused the thermogravimetric analysis on the qualitative variation of the differential thermogravimetric (DTG) curve over time. In fact, in the literature, the mass loss due to aragonite decarbonation begins on the TGA curve at a minimum temperature of 600 °C [17,18,19]. This mass loss was observed below 600 °C in the previous analysis of Zadi et al. [9] and may indicate particular transformations during the dissolution/precipitation process.
2.3. Numerical Contribution
2.3.1. Phases and Kinetics Models Choices
The dissolution/precipitation kinetics of mineral phases are modeled in general terms on the basis of transition state theory and are defined as follows [20]:
where R (mol/s) represents the dissolution/precipitation rate, associated with an empirical model represented by the constant k (mol/m2/s), A0 (m2) is the specific surface area of the mineral under consideration and p and q are constants. The saturation index (), expressed as the logarithm of the ratio between the ionic activity product (IAP) and the solubility product (K), reflects the deviation from equilibrium between the mineral and the contacting solution.
According to previous studies [1,9], the reactive phases in the system studied are brucite (Equation (1)) and aragonite (Equation (2)). Other phases, such as magnesite (MgCO3), could also be considered. Indeed, from thermodynamic considerations, magnesite is four orders of magnitude more stable than calcite and aragonite [21,22]. It should, therefore, be the primary precipitated phase but because of the very high dehydration energy of magnesium, it leads to the formation of poorly stable hydrated magnesium carbonates such as hydromagnesite and nesquehonite [23]. At room temperature (25 °C), magnesite precipitation is 10 times slower than that of calcite [24]. The main mineral phases to be considered are, therefore, brucite, aragonite and calcite. However, as calcite precipitation is inhibited by the high magnesium concentration in natural seawater, the numerical model can reasonably be limited to the first two phases.
There are several calcium carbonate models in the literature, but most of them concern calcite kinetics [22]. Few studies have been related to the dissolution/precipitation kinetics of aragonite, making the development of a numerical model challenging. In the literature, only two models have been applied for the specific case of aragonite. These are the non-linear kinetic model [25,26] and the mechanistic model based on the combination of several elementary reactions [21,27].
In the non-linear model, the dissolution/precipitation rate, R (mol/s), is estimated from Equation (Equation (3)) with a unit coefficient p and q as an empirical kinetic constant independent of the system’s reaction progress. In contrast, the mechanistic model suggests a series of intermediate reactions during the dissolution/precipitation of calcium carbonate, involving several empirical dissolution/precipitation constants (mol/m2/s), so that the kinetic constant depends on the evolution of the system. In this model, this constant is expressed as follows (Equation (5)).
with a(i) activity of species i.
This model, developed by Plummer et al. [28], has been widely used for calcite dissolution/precipitation kinetics. Few authors, such as Busenberg and Plummer [27], determined the kinetic parameters in the case of aragonite, but only in a solution supersaturated with and a partial pressure of of 320 ppm. Although this partial pressure is close to that used in the present study, the solutions employed differ. Furthermore, the empirical aragonite precipitation constant () has not been determined by these authors. Chou et al. [21] determined the parameters of this kinetic model for aragonite, but in a fluidized-bed reactor experiment, which leads to accelerated chemical reactions and, therefore, very rapid reaction kinetics. Moreover, such a model neglects the nucleation time of nuclei in solutions supersaturated with carbonates, as is the case for natural seawater.
As part of the numerical experimentation carried out in this study, we will use the nonlinear model for aragonite precipitation with the kinetic parameters of Burton and Walter [26]. This model is simple to implement and the experimental conditions of these authors [22] are similar to those of the present study.
For the brucite phase, two main precipitation/dissolution models exist in the literature. The first is based on transition-state theory (Equation (3)), with a kinetic constant driven by either protons (Equation (6)) [29] or by the concentration of complexed species at the - interface [30]. As the first case is valid only for acidic to neutral pH values, it is not suitable for modeling brucite dissolution/precipitation in seawater. The second case, described in the work of Pokrovsky et al. [30], is characterized by brucite dissolution/precipitation kinetics that are proportional to the concentration of complexed species (>) (Equation (7)).
with n the reaction order.
However, these two models do not take into account the existence of organic and inorganic ligands in solution, which may act as catalysts or inhibitors of the dissolution or precipitation reactions [31]. Based on this observation, Pokrovsky et al. [30] developed a second, more comprehensive model considering the presence of ligands in solution. In the case of brucite dissolution, assuming that the most active inorganic ligand is the bicarbonate ion, the dissolution/precipitation kinetics of brucite can be expressed as follows:
According to the work of Pokrovsky et al. [32], this equation remains valid for pH values below 11, which is the case for the solution used in the experiments conducted. This model will, therefore, be used in the present study to simulate brucite dissolution. The different kinetic constants of the various models used are summarized in Table 1.

Table 1.
Phases kinetics parameters.
2.3.2. Dissolution Model
The system studied is the solution placed in the double-walled cell and closed by an airtight lid. This system can be modeled either as a closed system or as an open system. The closed-system model assumes that the system is depleted in as the carbonates precipitate. This can occur when the reaction system is isolated from the atmosphere, or when the mechanical agitation is not sufficiently strong to ensure continuous equilibrium of dissolved with atmospheric . In contrast, the open-system model assumes that the solution is continuously in equilibrium with the atmosphere, so that atmospheric is available to maintain the solution’s calcium-carbonate balance. This equilibrium is ensured by the dissolution of gaseous into aqueous phase , and is implicitly enforced under the Phreeqc calculation code environment, based on Henry’s law:
With , the partial pressure in gas phase, the Henry constant at considerate temperature and the activity in solution.
2.3.3. Summary of Numerical Model Parameters
The chosen solution is that of Mediterranean seawater. The composition was measured by ion chromatography and is as follows (in g/l):, , , , , and trace species as . The initial pH and conductivity was and mS/cm, respectively. This solution is initially thermodynamically equilibrated with of 450 ppm at 25 °C.
The kinetics models mentioned above have been validated by their authors. Any modification of these laws, in particular, the reaction orders of the reactive species or the kinetic constants, for the purpose of adjusting simulations to experimental data, should, therefore, be avoided, as it is not rigorous [33]. The only adjustable parameter is the specific surface area of these phases. This choice is difficult, since there are several reported values for a given mineral in the literature, depending on the measurement or approximation method (BET or geometric method). These methods can either overestimate or underestimate the specific surface measurement, depending on whether the phase has a rough surface, is characterized by internal porosity, or was formed in a natural environment or synthesized in the laboratory.
For example, Habte et al. [34] reported specific surface areas ranging from 2 to 18 m2/g for a particle size between 10 and 30 µm on a synthetic aragonite. More commonly, this specific surface area varies between 0.1 and 3 m2/g [26,35,36,37,38,39]. The brucite specific surface varies from 5 to 15 m2/g [30,40,41,42,43].
In the present work, it is first assumed that the system is always in equilibrium with the ambient atmosphere, so that the partial pressure of dissolved in solution is equivalent to the ambient concentration (in 1 atm). In this configuration, two numerical models were run to analyze the effect of reaction kinetics on system evolution, with reference to experimental data. The first model, called HRSM, uses the maximum specific surface areas reported in the literature for these two phases. The second model, called LRSM, uses minimum specific surface area values based on literature data (Table 1). Analysis of the results obtained should allow identification of the most decisive parameters for model fitting, particularly the solution pH.
3. Results
3.1. Experiment Analysis
The results of previous experimental work by Zadi et al. [9] are shown in Figure 3a,b. The evolution of pH and conductivity shows three main phases: (i) a very rapid increase of pH and conductivity during the first hour of immersion, (ii) a subsequent decrease of these two parameters, and (iii) stabilization after 48 h of immersion (Figure 3a). The XRD analyses shown in Figure 3b revealed a decrease in brucite peaks (dissolution) and an increase in aragonite peaks (precipitation). These analyses also revealed the formation of unidentified mineral phases.
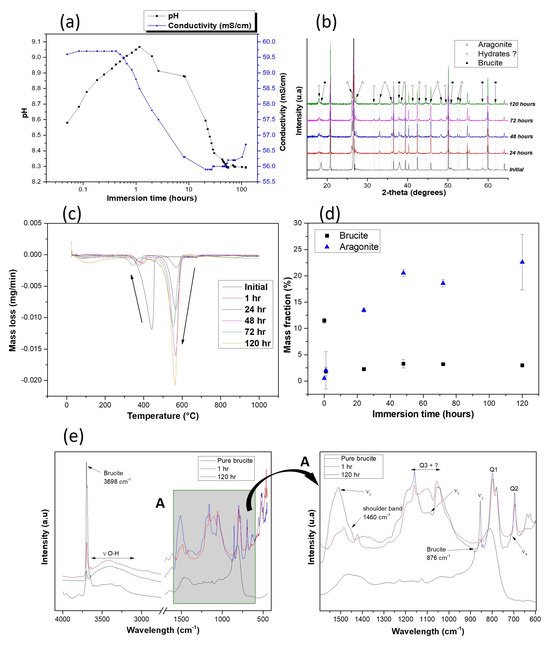
Figure 3.
Analysis of the evolution of the powdery sedimentary agglomerate: (a) pH and conductivity evolution, (b) X-ray diffractogram after different immersion times, (c) DTG curve, (d) qualitative evolution of the assumed phases and (e) comparison of infrared diffuse reflection spectra at different immersion times.
In fact, the DTG curves (Figure 3c) initially reveal two peaks located between 320 and 470 °C and between 630 °C and 680 °C, which may correspond to brucite and aragonite, respectively. These peaks evolve inversely over time, shifting towards lower temperatures and eventually moving outside the expected temperature ranges for the crystalline forms of these phases, especially in the case of aragonite. If these peaks correspond to brucite and aragonite, Figure 3d shows a rapid decrease in brucite mass from the first hour, ranging from 11.5% to 1.8%, followed by stabilization after 48 h of immersion at a proportion of around 3%. The curve associated with the evolution of brucite mass in solution can be likened to the concentration profile of active chemical species in a reaction kinetically controlled by surface reactions [20]. This is in line with the work of Jordan and Rammensee [44], who established that the dissolution/precipitation mechanism of brucite is controlled by surface reactions. Aragonite (or the phase assumed to be aragonite) varies less rapidly, which could be explained by slower precipitation kinetics rather than by brucite dissolution. Its mass proportion rises gradually from 0.5% to over 22% within 48 h of immersion and stabilizes later (Figure 3d).
The DRIFT results presented in Figure 3e show a curvature of the spectrum between 2700 and 3700 cm−1, a small peak at 1645 cm−1 and a shoulder at 1460 cm−1 at the peak (1490 cm−1), corresponding to the aragonite vibration signature [45]. The first two peaks correspond to the elongation vibration of the O-H bonds of the bound water contained in the mineral phases and the deformation vibration of the water molecule. According to Rodriguez-Blanco et al. [46], the observation of these different wave numbers is a signature of the presence of hydrated forms of calcium carbonates. The other aragonite characteristic wavelengths ( at 1080 cm−1, at 856 cm−1 and at 713 cm−1) [45,47,48,49], those of brucite (3698 cm−1 and 876 cm−1) [50] and those of silica (695 cm−1, 780 cm−1 to 800 cm−1 and 1050 cm−1 to 1200 cm−1) [51,52,53] can also be identified on zoom A in Figure 3e.
The shape of the peak attributed to silica is not perfectly consistent with the literature and could correspond to a coupling with aragonite () and other unidentified phases. The results show the coexistence of commonly known phases, namely, aragonite, brucite and silica, with hydrated calcium carbonate phases and other unidentified phases. In fact, the succession of peaks recorded at 1420 cm−1 and 1484 cm−1 can be related to the elongation vibration of monohydrocalcite [45].
3.2. Numerical Experiments
The results of the numerical modeling of sediment agglomerate evolution are shown in Figure 4, which compares experimental measurements with the HRSM numerical simulations (Figure 4a,b) and the LRSM numerical model (Figure 4c,d). Like the experimental results, the different simulated configurations show a dissolution of brucite accompanied by precipitation of the carbonate phase. The pH evolution presented in Figure 4b follows the trend of the experimental results, i.e., an increase during the first hours of immersion, followed by a rapid decrease up to 24 h, and a quasi-stable pH until the end of the experiment (120 h). However, the values obtained are significantly lower than the experimental pH values. For example, the maximum pH reached in the numerical model is around 8.4, compared with an experimental pH close to 9.1 at its maximum.
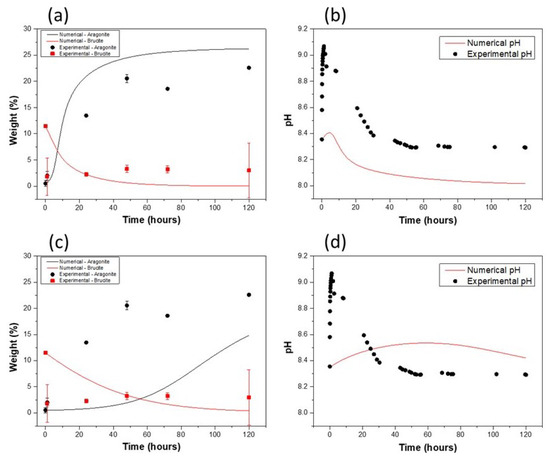
Figure 4.
Numerical simulation of sediment agglomerate powder evolution upon abandonment in natural seawater (high (a,b) and low (c,d) reactive surface model): (a,c) variation in the mass proportion of cementitious phases and (b,d) variation in solution pH.
In the second configuration (LRSM), i.e., considering the lowest values of the specific surface areas of the mineral phases, the evolution of the calculated pH differs from that obtained experimentally. It can also be noted that in this model, although the reactions are relatively slow, the proportion of brucite is around 0.24% after 120 h of immersion. In the fast kinetics configuration, the proportion is virtually nil after just 48 h of immersion. Thus, in both numerical configurations, brucite dissolves completely after 120 h of immersion, even assuming a low brucite reactive surface. As for the mass proportion of aragonite formed in both configurations, it is either far too high (HRSM) or too low (LRSM) compared with experimental data, at least if the mineral phase formed is almost exclusively aragonite.
Coupling the cementitious phase and pH profiles in the two configurations shows, on the one hand, that the rate of carbonate precipitation controls the overall shape of the pH curve, with pH decay being observed only from the onset of aragonite precipitation. Since experimental data show a pH decrease after around 10h of immersion, it follows that carbonate precipitation kinetics must be sufficiently rapid. However, the minimum level reached is determined by the equilibrium of dissolved gas in solution with atmospheric , so the low pH level reached in the HRSM model indicates that the quantity of available considered in the numerical experiment, i.e., that measured in the measurement laboratory is much greater than the actual quantity in the gas phase inside the cell. Indeed, the presence of a lid on the cell could lead to a very high relative humidity inside the cell and, therefore, to a lower concentration than that measured in the test laboratory. This limit to availability due to the closure of the cell with a lid has also been previously observed in the work of Prevot [3].
On the other hand, to better account for the rapid increase in solution pH in the first few hours, brucite dissolution kinetics must be very rapid and coupled with slower aragonite precipitation. If we consider pH as the parameter for fitting the numerical model to the experimental data, carbonate precipitation kinetics cannot be too slow. It follows that the most influential fitting parameters are, therefore, the amount of available and the rate of brucite dissolution. However, it should be noted that, in the HRSM model configuration, although brucite dissolution kinetics are already high, in line with literature data, the model adjusts very little to brucite proportion measured after an hour. The reaction kinetics must, therefore, be faster than those chosen, which could be due to non-uniformity in brucite grain size after material manual grinding of the material.
By modifying these various parameters, the numerically obtained pH values were adjusted to match those measured experimentally. The results of this model are shown in Figure 5. They are based on a reactive surface area of 150 m2/g for brucite (10 times higher than the literature maximum) and 1 m2/g for aragonite. The partial pressure of was progressively reduced until a better fit with experimental pH was obtained, with an arbitrary lower limit of 100 ppm.
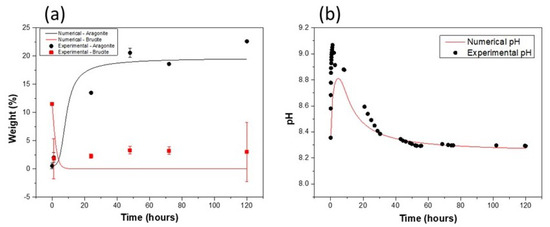
Figure 5.
Numerical model adjusted to the pH solution: (a) evolution of mass proportions and (b) pH profile of the solution.
In contrast to previous numerical results, the results presented in Figure 5b show that pH of the “optimized” model follows a trend more consistent with experimental measurements, especially after 24 h of immersion. The model also reproduces the data well at the beginning of the system’s evolution, although it does not reach the maximum experimental pH value, despite the excessively rapid dissolution of brucite (Figure 5a). As in the previous models, this phase dissolves entirely in solution, contrary to the experimental measurements. Fitting the pH value to those of experimental data highlights a semi-open character of the studied system, contrary to initial assumption. Indeed, the results indicate that, for a better adjustment of the solution pH, partial pressure in the cell must be much lower than in the laboratory. This reduction in partial pressure can be explained by the increase in relative humidity within the cell. Despite this limitation in availability, the optimized model remains consistent with thermodynamic predictions of total brucite dissolution (Figure 5a), which contrasts with the experimental measurements.
3.3. Discussion
The optimized numerical model highlighted partial pressure in the system as an additional variable influencing system equilibrium. The conditions required to align the numerical pH with experimental measurements raise questions about availability in the system. Among these conditions, reduction over time in the reactor could call into question the reliability of this type of protocol for the accelerated study of material durability.
Furthermore, despite this probable decrease in partial pressure, experimental measurements have shown that maximum pH measured is below thermodynamic equilibrium pH of brucite. Also, the LRSM model using very slow kinetics leads to total brucite dissolution. These two observations show that the persistence of brucite in solution is related neither to the scarcity of in solution, nor to the kinetics effects or solution saturation.
On the other hand, experimental observations have highlighted the formation of hydrated phases (Figure 3e). In the literature, calcium carbonates can also occur in monohydrate (monohydrocalcite), hexahydrate or even amorphous forms [54]. The latter, commonly referred to as amorphous calcium carbonates (ACCs) and with the chemical formula , have been widely studied [45,46,54,55,56,57,58]. These nanoparticles, smaller than 50 nm, are difficult to observe by XRD analysis. XRD analyses of Rodriguez-Blanco et al. [46] showed that the products formed are characterized by two broad bumps approximately centered at incidence angles of and . Others mentions the existence of hydromagnesite a precipitation phase in addition to calcium carbonates [59]. However, hydromagnesite is less stable thermodynamically than calcium carbonates.
In TGA, the work of Brečević & Nielsen [54] showed that ACCs are characterized by two temperature ranges: a first located between and 300 °C, where a third of the bound water is evaporated, and a second, broader range (from 100 to 500 °C), where all the remaining water is released. Regarding thermogravimetric analyses in this study, the mass loss signatures show a shoulder between below 300 °C especially in DTG diagram obtained after 120 h of powder immersion. The mass loss signature of ACC can also be masked by that of brucite, as the thermogravitry signature of the latter mineral corresponds to the release temperature of its maximum water content.
On the other hand, Ihli and al. [58] note that the presence of silica in solution, as in this study, increases the thermal stability of these phases. Furthermore, in the experimental protocol used here, a filter with a porosity of around 500 nm was employed, whereas ACCs are composed of aggregates of spherical particles of the order of a few tens of nanometers in diameter. Some of these particles may therefore have been lost during filtration.
Rodriguez-Diego et al. [46] also point out that the transformation of ACCs into crystalline calcium carbonate polymorphs is very rapid (a few minutes), which can make their observation difficult. Clarkson et al. [60] note that homogeneous nucleation of ACCs occurs when their solubility product is lower than the ionic product of the solution. This solubility product is expressed as a function of temperature, between 16 and 60 °C, by equation Equation (10):
At 25 °C, we obtain pKs = 6.04. For this same temperature, this value is slightly lower than that reported by Brečević and Nielsen [54] (pKs = 6.39). From numerical ionic species activities, at the maximum pH reached during experimentation (pH = 9.1), we obtain , i.e., supersaturated conditions compared with literature data. Nucleation can also occur heterogeneously as solution saturation decreases. In this case, the products formed are hexahydrate crystalline phases. These various metastable hydrated phases then transform into anhydrous crystalline phases whose allotropic shapes are strongly controlled by the presence of inhibitors, notably magnesium.
Thus, the thermodynamic conditions in the present study may favor the precipitation of ACC, whose XRD and thermogravimetry signatures could be masked by the presence of silica, brucite and aragonite.
In addition, the optimized numerical model indicates that calcium is not the limiting factor of the reaction, which is, rather, the carbonate ions in solution. Consequently, the overall shape of the aragonite mass-proportion evolution curve remains valid, with similar precipitation kinetics, for any other form of carbonate. However, it seems obvious that, regardless of the aragonite precipitation rate, the model cannot accurately reproduce the mass proportions observed during the initial stages of immersion. Likewise, even if brucite dissolution kinetics are varied, the numerical model cannot reach the experimental maximum pH while maintaining a consistent trend for the carbonate phase evolution.
This limitation may arise from the model’s omission of a carbonate nucleation stage, whose duration depends on saturation index of specific precipitated phases [30]. Yet, such an assumption does not explain the early growth of the carbonate peak upon first immersion, particularly when the amount of material decreases (180 mg against less than 100 mg after immersion).
The combined analysis of numerical simulations and experimental data, therefore, raises concerns about the reliability of this type of test for assessing material durability. Moreover, the results suggest that the mineral phases detected during the initial immersion period cannot correspond solely to aragonite. This is consistent with the presence of hydrated carbonate phases, whose precipitation supports the new mechanism of material evolution proposed in the next section and helps explain the persistence of brucite in solution.
3.4. Evolution Mechanism Proposal Under Accelerated Conditions
During the evolution of the studied material powder in seawater, brucite dissolution promotes the formation of aragonite. This transformation, however, proceeds through intermediate steps involving the formation of metastable phases. A quantitative analysis of the abandonment evolution of the agglomerate cannot be fully assessed with the method used here, as the probable evolution of available would require aging experiments in a well-controlled environment with respect to amospheric exchange.
Furthermore, the identification of these metastable phases would necessitate the use of more sophisticated analytical techniques. From a mineralogical standpoint, the persistence of brucite in solution remains a reliable indicator of the material’s self-stabilization. This stabilization is consistent with the previous analyses of material blocks exposed for 18 months, which revealed only minor variations in the molar ratio as well as negligible changes in porosity and density [9].
Despite the measurement uncertainties observed, these results provide valuable insight into the mechanisms governing the material’s evolution under abandonment conditions (i.e., without polarization current density) and confirm its mineralogical stability.
The present study shows that, under conditions of local supersaturation, as may occur within the pore solution of the material, the precipitation of aragonite proceeds through the quasi-spontaneous formation of metastable amorphous phases during the first hours of material evolution. As supersaturation decreases, brucite becomes entrapped within aggregates of particles formed by heterogeneous nucleation. The precipitation of this amorphous phase cannot be attributed to a reduction in partial pressure, which would instead lower their saturation index and, thus, hinder their formation. However, the gradual scarcity of over time can influence the transformation of these metastable phases into crystalline calcium carbonates by limiting their saturation index.
In all cases, due to their intrinsic metastability, these phases eventually transform into crystalline calcium carbonate polymorphs—either aragonite or calcite—depending on the local magnesium concentration. This transformation could explain both the strong thermogravimetric signatures of carbonate phases and the absence of unidentified peaks in the XRD diffractograms of the same material in block form, as previously analyzed by Zadi et al. [9]. In this scenario, the localized precipitation of aragonite acts as an impermeable layer that almost completely inhibits brucite dissolution, thereby ensuring the material’s long-term stability. This mechanism is analogous to the protection of portlandite in Portland cement-based materials, where carbonation promotes the precipitation of polycrystalline calcium carbonate around portlandite crystals [61].
The persistence of brucite was previously highlighted by Zadi and al. [9] and Zanibellato [1]. The latter author hypothesized that aragonite precipitates on the surface of brucite, thereby preventing its dissolution. Zadi et al. [9] proposed that local saturation within the material’s pores, combined with subsurface aragonite precipitation, limits the diffusive processes controlling its evolution. A similar mechanism of calcium carbonate was also suggested by Prevot [3]. However, the relatively slow precipitation rate of aragonite compared with the rapid dissolution of brucite can restrict the validity of this hypothesis, particularly in low-permeability materials. The observations of the present study overcome this limitation by providing new insights into the mineralogical transformations occurring within the porous medium. This findings clarify the mechanisms governing the long-term evolution of the sedimentary agglomerate, whose mineralogical stability is a key factor in its potential qualification as a sustainable alternative solution for mitigating coastal erosion.
4. Conclusions
The objective of this study was to investigate the mechanisms governing the evolution of a sedimentary agglomerate formed by cathodic polarization in natural seawater during its abandonment. Previous studies have highlighted the transformation of brucite into aragonite, the two main cementitious phases of this agglomerate. However, these studies provided only a global assessment of the transformation and did not elucidate the intermediate steps, leaving unresolved the question of brucite persistence during material abandonment in the marine environment. To address this gap, the present work implemented an accelerated aging protocol to reproduce and study the material’s evolution under controlled laboratory conditions. The experimental results were coupled with numerical experiments performed using the Geochemical calculation code PHREEQC, enabling a detailed interpretation of the observations and a deeper understanding of the underlying transformation mechanisms.
Experimental analyses revealed a very rapid dissolution of brucite, followed by stabilization at non-zero mass proportion, in contradiction with thermodynamic predictions. Brucite dissolution promotes the precipitation of carbonate and other hydrated phases that remain only partially identified. Numerical simulations likewise indicate that the persistence of brucite in solution conflicts with thermodynamic predictions. The combined interpretation of experimental data and modeling supports a mechanism in which brucite undergoes an almost spontaneous intermediate transformation into hydrated amorphous phases that precipitate heterogeneously on the surface of the brucite, thereby limiting its direct contact with seawater. These metastable amorphous phases, unstable in seawater, are progressively replaced by more stable crystalline phases, namely, aragonite. Such transformation pathways not only explain the persistence of brucite over long immersion times but also clarify the successive steps leading to the mineralogical stabilization of the agglomerate, as suggested in previous studies.
Furthermore, analysis of the conditions required to match simulated and measured pH values highlights the limitations of the experimental protocol, notably, a progressive reduction of levels in the vapor phase inside the cell. This decrease—attributable to the semi-open nature of the system, which increases relative humidity during water evaporation—lowers the partial pressure of dissolved , buffering solution pH and constraining carbonation reactions. However, given the rapid precipitation of carbonate phases (within the first 24 h), this limitation does not appear to significantly affect the formation of the observed phases or the proposed mechanism.
Since this work did not allow the characterization of the intermediate mineral phases, additional analytical techniques—such as chromatographic analyses or induction mass spectrometry—could be coupled to the protocol to refine the results. However, as the nature and composition of these intermediate phases may strongly depend on the solution chemistry, the generalization of the present findings remais challenging.
Author Contributions
Conceptualization, L.Z., A.S., P.T. and A.Z.; investigation, L.Z.; methodology, L.Z.; visualization, L.Z.; writing—original draft preparation, L.Z., A.S., P.T., A.Z., R.S. and M.J.; writing—review and editing, L.Z., A.S., P.T., A.Z., P.-Y.M., R.S. and M.J.; funding acquisition, A.S. and P.T.; project administration, A.S., P.T. and A.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work is a part of a Ph.D. project related to “the numerical modelling of the mechanisms governing the growth and the durability of calcareous based material formed by cathodic polarization”, funded by Association Nationale de la Recherche et de la Technologie (ANRT, France).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
Louis Zadi hereby disclose his conflict of interest as outlined by the MDPI guidelines. He is currently employed by “IRT-M2P” and was employed by “Geocorail” while contributing to this manuscript. His contributions to this work and manuscript were made independently without any requirement, guidance or input by his employer. He received no financial compensation from any source for the contributions he made to the scientific work and manuscript. Alaric Zanibellato hereby disclose his conflict of interest as outlined by the MDPI guidelines. He is currently employed by “Seacure” and was employed by “Geocorail” while contributing to this manuscript. His contributions to this work and manuscript were made independently without any requirement, guidance or input by his employer. He received no financial compensation from any source for the contributions he made to the scientific work and manuscript. Anthony Soive, Philippe Turcry, Pierre-Yves Mahieux, René Sabot and Marc Jeannin have no conflicts of interest.
References
- Zanibellato, A. Synthèse et études Physico-Chimiques d’un Agglomérat Calcomagnésien Formé sur acier en Milieu Marin: Un éco-Matériau Pour la Protection du Littoral. Ph.D. Thesis, La Rochelle Université, La Rochelle, France, 2016. [Google Scholar]
- Carré, C.; Zanibellato, A.; Achgare, N.; Mahieux, P.Y.; Turcry, P.; Jeannin, M.; Sabot, R. Electrochemical limestone synthesis in seawater binds metal grids and sediments for coastal protection. Environ. Chem. Lett. 2020, 18, 1685–1692. [Google Scholar] [CrossRef]
- Prevot, J. Etude du Conglomérat dépôt Calcomagnésien/Scories: Formation, Propriétés et Applications. Ph.D. Thesis, Université de la Nouvelle-Calédonie, Nouméa, France, 2020. [Google Scholar]
- Zadi, D.L. Mécanismes Physico-Chimiques Impliqués Dans la Formation et l’évolution à l’Abandon d’un Matériau Sédimentaire Innovant généré en Milieu Marin par Polarisation Cathodique. Ph.D. Thesis, Université de La Rochelle, La Rochelle, France, 2022. [Google Scholar]
- Marais, C. Formation d’un agglomérat calcomagnésien en écoulement à base de granulats recyclés pour la protection côtière. Acad. J. Civ. Eng. 2024, 42, 880–889. [Google Scholar] [CrossRef]
- Sharker, T.; Simonsen, K.R.; Margheritini, L.; Kucheryavskiy, S.V.; Simonsen, M.E. Optimisation of electrochemical deposition of calcareous material during cathodic protection by implementing response surface methodology (RSM). Electrochim. Acta 2023, 444, 141960. [Google Scholar] [CrossRef]
- Mahlobo, M.G.R.; Seadira, T.W.P.; Mabuza, M.M.; Olubambi, P.A. Application of voltammetry as a technique to monitor cathodic protection performance of steel in simulated soil solution. Electrochem. Commun. 2024, 166, 107777. [Google Scholar] [CrossRef]
- Souiad, F.; Bendaoud-Boulahlib, Y.; Rodrigues, A.S.; Fernandes, A.; Ciríaco, L.; Pacheco, M.J.; Lopes, A. Electrodeposition of Calcium Carbonate and Magnesium Carbonate from Hard Water on Stainless-Steel Electrode to Prevent Natural Scaling Phenomenon. Water 2021, 13, 2752. [Google Scholar] [CrossRef]
- Zadi, L.; Turcry, P.; Soive, A.; Zanibellato, A.; Mahieux, P.Y.; Sabot, R.; Jeannin, M. Physico-chemical stability evaluation of a sedimentary. J. Coast. Conserv. 2023, 27, 8. [Google Scholar] [CrossRef]
- Deslouis, C.; Festy, D.; Gil, O.; Maillot, V.; Touzain, S.; Tribollet, B. Characterization of calcareous deposits in artificial sea water by impedances techniques: 2-deposit of Mg(OH)2 without CaCO3. Electrochim. Acta 2000, 45, 1837–1845. [Google Scholar] [CrossRef]
- Barchiche, C.; Deslouis, C.; Gil, O.; Refait, P.; Tribollet, B. Characterisation of calcareous deposits by electrochemical methods: Role of sulphates, calcium concentration and temperature. Electrochim. Acta 2004, 49, 2833–2839. [Google Scholar] [CrossRef]
- Gautier, Q. Cinétiques de Précipitation de Minéraux Carbonatés Magnésiens, Influence de Ligands Organiques, et Conséquences Pour la Séquestration Minérale de CO2. Ph.D. Thesis, Université Paris-Est, Paris, France, 2012. [Google Scholar]
- Marchand, J.; Samson, E. Predicting the service-life of concrete structures - Limitations of simplified models. Cem. Concr. Compos. 2009, 31, 515–521. [Google Scholar] [CrossRef]
- Tran, V.Q.; Soive, A.; Baroghel-Bouny, V. Modelisation of chloride reactive transport in concrete including thermodynamic equilibrium, kinetic control and surface complexation. Cem. Concr. Res. 2018, 110, 70–85. [Google Scholar] [CrossRef]
- Yan, J.F.; White, R.E.; Griffin, R.B. Parametric Studies of the Formation of Calcareous Deposits on Cathodically Protected Steel in Seawater. J. Electrochem. Soc. 1993, 140, 1275–1280. [Google Scholar] [CrossRef]
- Blanc, P.; Lassin, A.; Piantone, P.; Azaroual, M.; Jacquemet, N.; Fabbri, A.; Gaucher, E.C. Thermoddem: A geochemical database focused on low temperature water/rock interactions and waste materials. Appl. Geochem. 2012, 27, 2107–2116. [Google Scholar] [CrossRef]
- Thiery, M. Modelling of Atmospheric Carbonation of Cement Based Materials Considering the Kinetic Effects and Modifications of the Microstructure and the Hydric State Mickaël Thiery to Cite This Version: HAL Id: Pastel-00001517 Modélisation de la Carbonatation Atm. Ph.D. Thesis, Ecole Nationale des Ponts et Chaussées, Champs-sur-Marne, France, 2005. [Google Scholar]
- Villain, G.; Thiery, M.; Platret, G. Measurement methods of carbonation profiles in concrete: Thermogravimetry, chemical analysis and gammadensimetry. Cem. Concr. Res. 2007, 37, 1182–1192. [Google Scholar] [CrossRef]
- Shafiu Kamba, A.; Ismail, M.; Tengku Ibrahim, T.A.; Zakaria, Z.A.B. Synthesis and characterisation of calcium carbonate aragonite nanocrystals from cockle shell powder (Anadara granosa). J. Nanomater. 2013, 2013, 9. [Google Scholar] [CrossRef]
- Appelo, C.A.J.; Postma, D. Geochemistry, Groundwater and Pollution, 2nd ed.; A. A. Balkema Publishers: Rotterdam, The Netherlands, 2005; p. 649. [Google Scholar]
- Chou, L.; Garrels, R.M.; Wollast, R. Comparative study of the kinetics and mechanisms of dissolution of carbonate minerals. Chem. Geol. 1989, 78, 269–282. [Google Scholar] [CrossRef]
- Sanjuan, B.; Girard, J.P. Review of Kinetic Data on Carbonate Mineral Precipitation; Technical Report 4; BRGM: Orléans, France, 1996. [Google Scholar]
- Saldi, G.D.; Jordan, G.; Schott, J.; Oelkers, E.H. Magnesite growth rates as a function of temperature and saturation state. Geochim. Cosmochim. Acta 2009, 73, 5646–5657. [Google Scholar] [CrossRef]
- Grandjean, M. Étude De La Réactivité Et De L’Hydratation Des Particules Obtenues Par Carbonatation De Saumures Alcalines. Ph.D. Thesis, Université de Lorraine, Nancy, France, 2013. [Google Scholar]
- Zhong, S.; Mucci, A. Calcite and aragonite precipitation from seawater solutions of various salinities: Precipitation rates and overgrowth compositions. Chem. Geol. 1989, 78, 283–299. [Google Scholar] [CrossRef]
- Burton, E.A.; Walters, L.M. The role of pH in phosphate inhibition of calcite and aragonite precipitation rates in seawater. Geochim. Cosmochim. Acta 1990, 54, 797–808. [Google Scholar] [CrossRef]
- Busenberg, E.; Plummer, L.N. A comparative study of the dissolution and crystal growth kinetics of calcite and aragonite. US Geol. Surv. Bull. 1987, 1578, 139–168. [Google Scholar]
- Plummer, L.; Wigly, T.; Parkhurst, D. The Kinetics of calcite dissolution in CO2-Water systems at 5° to 60 °C and 0.0 to 1.0 Atm CO2. J. Sci. 1978, 278, 179–216. [Google Scholar]
- Palandri, J.L.; Kharaka, Y.K. A Compilation of Rate Parameters of Water-Mineral Interaction Kinetics for Application to Geochemical Modeling; Technical report; Survey, U.S. Department of the Interior U.S. Geological Survey: Reston, VA, USA, 2004. [Google Scholar]
- Pokrovsky, O.S.; Schott, J. Experimental study of brucite dissolution and precipitation in aqueous solutions: Surface speciation and chemical affinity control. Geochim. Cosmochim. Acta 2004, 68, 31–45. [Google Scholar] [CrossRef]
- Stumm, W. Reactivity at the mineral-water interface: Dissolution and inhibition. Colloids Surfaces A Physicochem. Eng. Asp. 1997, 120, 143–166. [Google Scholar] [CrossRef]
- Pokrovsky, O.S.; Schott, J.; Castillo, A. Kinetics of Brucite Dissolution at 25 °C in the Presence of Organic and Inorganic Ligands and Divalent Metals. Geochem. Cosmochim. Acta 2005, 69, 905–918. [Google Scholar] [CrossRef]
- Saldi, G.D.; Knauss, K.G.; Spycher, N.; Oelkers, E.H.; Jones, A.P. A combined experimental and modelling study of granite hydrothermal alteration. Geothermics 2023, 108, 102633. [Google Scholar] [CrossRef]
- Habte, L.; Khan, M.D.; Shiferaw, N.; Farooq, A.; Hye Lee, M.; Ho Jung, S.; Ahn, J.W. Synthesis, characterization and mechanism study of green aragonite crystals fromwaste biomaterials as calcium supplement. Sustainability 2020, 12, 5062. [Google Scholar] [CrossRef]
- Reddy, M.M.; Plummer, L.N.; Busenberg, E. Crystal growth of calcite from calcium bicarbonate solutions at constant Pco2 and 25 °C: A test of a calcite dissolution model. Geochim. Cosmochim. Acta 1981, 45, 1281–1289. [Google Scholar] [CrossRef]
- Prieto, M.; Cubillas, P.; Fernandez-Gonzalez, A. Uptake of dissolved Cd by biogenic and abiogenic aragonite: A comparison with sorption onto calcite. Geochim. Cosmochim. Acta 2003, 67, 3859–3869. [Google Scholar] [CrossRef]
- Cubillas, P.; Köhler, S.; Prieto, M.; Chaïrat, C.; Oelkers, E.H. Experimental determination of the dissolution rates of calcite, aragonite, and bivalves. Chem. Geol. 2005, 216, 59–77. [Google Scholar] [CrossRef]
- Alkhatib, M.; Eisenhauer, A. Calcium and Strontium Isotope Fractionation during Precipitation from Aqueous Solutions as a Function of Temperature and Reaction Rate; II. Aragonite. Geochim. Cosmochim. Acta 2017, 209, 320–342. [Google Scholar] [CrossRef]
- Tadier, S.; Rokidi, S.; Rey, C.; Combes, C.; Koutsoukos, P.G. Crystal growth of aragonite in the presence of phosphate. J. Cryst. Growth 2017, 458, 44–52. [Google Scholar] [CrossRef]
- Kumada, N.; Yonesaki, Y.; Takei, T.; Kinomura, N. Hydrothermal conversion of chrysotile to amorphous silica or brucite. J. Ceram. Soc. Jpn. 2009, 117, 1240–1242. [Google Scholar] [CrossRef]
- Harrison, A.L.; Power, I.M.; Dipple, G.M. Accelerated carbonation of brucite in mine tailings for carbon sequestration. Environ. Sci. Technol. 2013, 47, 126–134. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Pang, H.; Chen, W.; Lin, Y.; Zong, L.; Ning, G. Controllable Fabrication of Zinc Borate Hierarchical Nanostructure on Brucite Surface for Enhanced Mechanical Properties and Flame Retardant Behaviors. ACS Appl. Mater. Interfaces 2014, 6, 7223–7235. [Google Scholar] [CrossRef] [PubMed]
- Tutolo, B.M.; Luhmann, A.J.; Tosca, N.J.; Seyfried, W.E. Serpentinization as a reactive transport process: The brucite silicification reaction. Earth Planet. Sci. Lett. 2018, 484, 385–395. [Google Scholar] [CrossRef]
- Jordan, G.; Rammensee, W. Dissolution rates and activation energy for dissolution of brucite (001): A new method based on the microtopography of crystal surfaces. Geochim. Cosmochim. Acta 1996, 60, 5055–5062. [Google Scholar] [CrossRef]
- Zhang, Z.; Xie, Y.; Xu, X.; Pan, H.; Tang, R. Transformation of amorphous calcium carbonate into aragonite. J. Cryst. Growth 2012, 343, 62–67. [Google Scholar] [CrossRef]
- Rodriguez-Blanco, J.D.; Shaw, S.; Benning, L.G. The kinetics and mechanisms of amorphous calcium carbonate (ACC) crystallization to calcite, via vaterite. Nanoscale 2011, 3, 265–271. [Google Scholar] [CrossRef]
- Chakrabarty, D.; Mahapatra, S. Aragonite crystals with unconventional morphologies. J. Mater. Chem. 1999, 9, 2953–2957. [Google Scholar] [CrossRef]
- Wang, C.; Xu, Y.; Liu, Y.; Li, J. Synthesis and characterization of lamellar aragonite with hydrophobic property. Mater. Sci. Eng. C 2009, 29, 843–846. [Google Scholar] [CrossRef]
- Carteret, C.; De La Pierre, M.; Dossot, M.; Pascale, F.; Erba, A.; Dovesi, R. The vibrational spectrum of CaCO3 aragonite: A combined experimental and quantum-mechanical investigation. J. Chem. Phys. 2013, 138. [Google Scholar] [CrossRef]
- Frost, R.L.; Kloprogge, J.T. Infrared emission spectroscopic study of brucite. Spectrochim. Acta-Part A Mol. Biomol. Spectrosc. 1999, 55, 2195–2205. [Google Scholar] [CrossRef]
- Reig, F.B.; Adelantado, J.V.; Moya Moreno, M.C. FTIR quantitative analysis of calcium carbonate (calcite) and silica (quartz) mixtures using the constant ratio method. Application to geological samples. Talanta 2002, 58, 811–821. [Google Scholar] [CrossRef]
- Saikia, B.J.; Parthasarathy, G.; Sarmah, N.C. Fourier transform infrared spectroscopic estimation of crystallinity in SiO2 based rocks. Bull. Mater. Sci. 2008, 31, 775–779. [Google Scholar] [CrossRef]
- Bandopadhyay, A.K. Determination of quartz content for Indian coals using an FTIR technique. Int. J. Coal Geol. 2010, 81, 73–78. [Google Scholar] [CrossRef]
- Brečević, L.; Nielsen, A.E. Solubility of amorphous calcium carbonate. J. Cryst. Growth 1989, 98, 504–510. [Google Scholar] [CrossRef]
- Rodriguez-Blanco, J.D.; Shaw, S.; Benning, L.G. How to make ’stable’ ACC: Protocol and preliminary structural characterization. Mineral. Mag. 2008, 72, 283–286. [Google Scholar] [CrossRef]
- Goodwin, A.L.; Michel, F.M.; Phillips, B.L.; Keen, D.A.; Dove, M.T.; Reeder, R.J. Nanoporous structure and medium-range order in synthetic amorphous calcium carbonate. Chem. Mater. 2010, 22, 3197–3205. [Google Scholar] [CrossRef]
- Bots, P.; Benning, L.G.; Rodriguez-Blanco, J.D.; Roncal-Herrero, T.; Shaw, S. Mechanistic insights into the crystallization of amorphous calcium carbonate (ACC). Cryst. Growth Des. 2012, 12, 3806–3814. [Google Scholar] [CrossRef]
- Ihli, J.; Wong, W.C.; Noel, E.H.; Kim, Y.Y.; Kulak, A.N.; Christenson, H.K.; Duer, M.J.; Meldrum, F.C. Dehydration and crystallization of amorphous calcium carbonate in solution and in air. Nat. Commun. 2014, 5, 3169. [Google Scholar] [CrossRef]
- Landivar Macias, A.; Jacobsen, S.D.; Rotta Loria, A.F. Electrodeposition of calcareous cement from seawater in marine silica sands. Commun. Earth Environ. 2024, 5, 442. [Google Scholar] [CrossRef]
- Clarkson, J.R.; Price, T.J.; Adams, C.J. Role of metastable phases in the spontaneous precipitation of calcium carbonate. J. Chem. Soc. Faraday Trans. 1992, 88, 243–249. [Google Scholar] [CrossRef]
- Galan, I.; Glasser, F.P.; Baza, D.; Andrade, C. Assessment of the protective effect of carbonation on portlandite crystals. Cem. Concr. Res. 2015, 74, 68–77. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).