Impact Assessment of Beach Nourishment on Hot Spring Groundwater on Ibusuki Port Coast
Abstract
1. Introduction
1.1. Background and Aims of the Present Study
1.2. Review of Related Studies
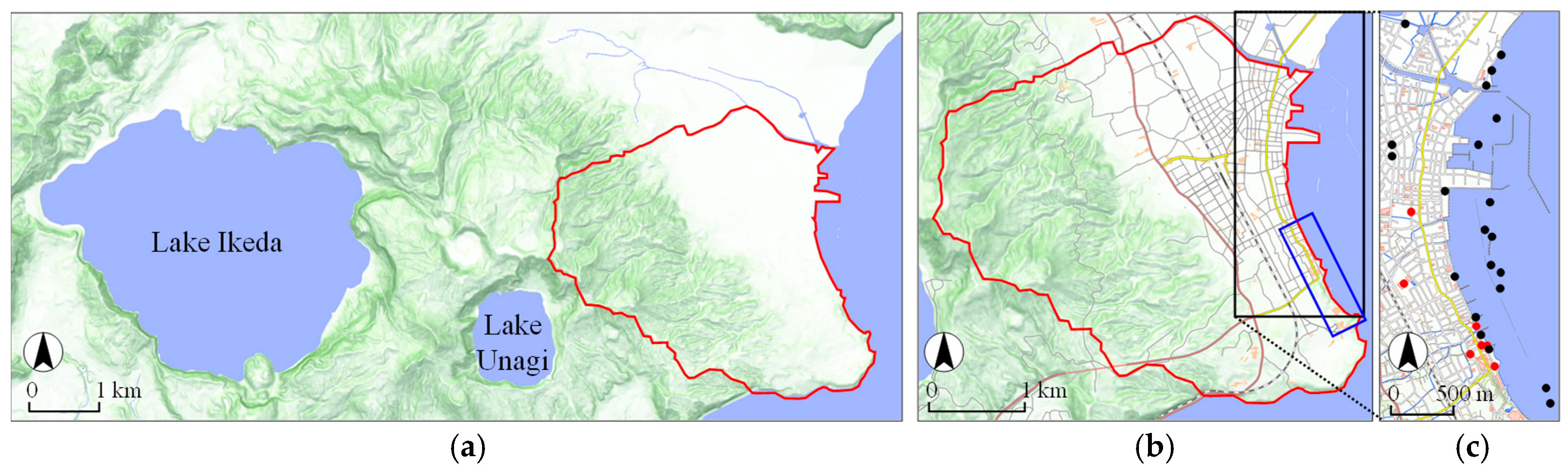
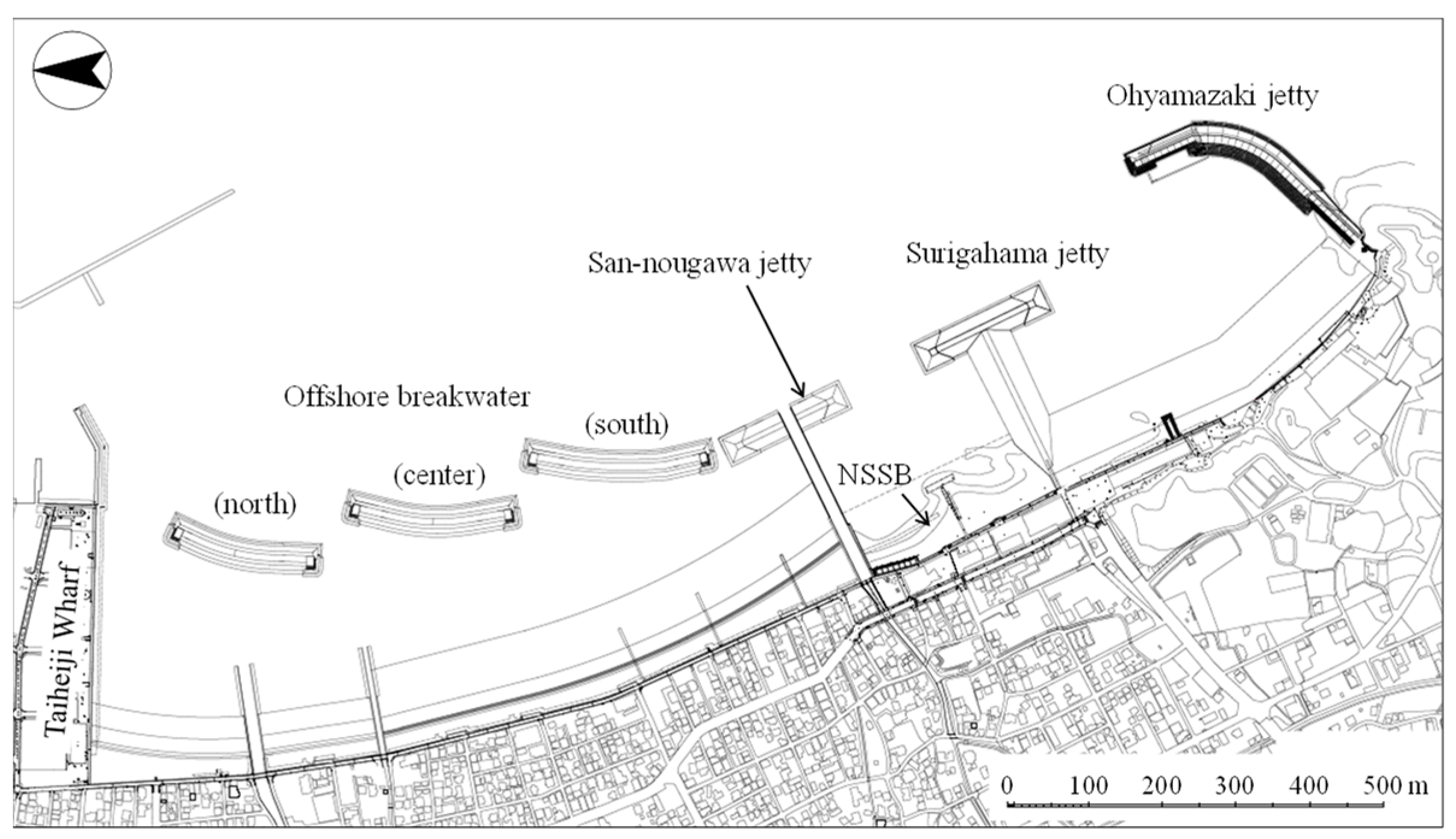
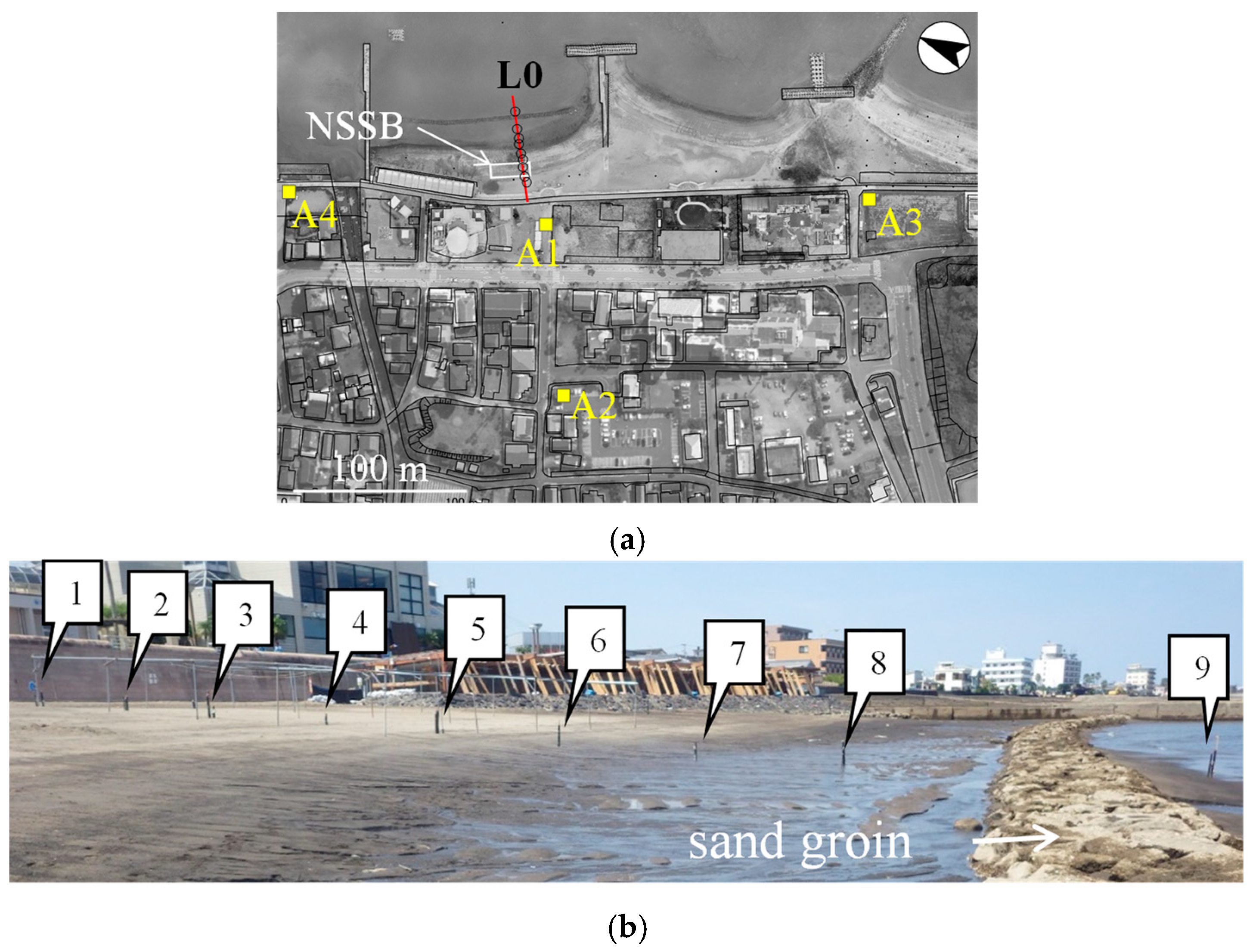
2. Study Site
3. Materials and Methods
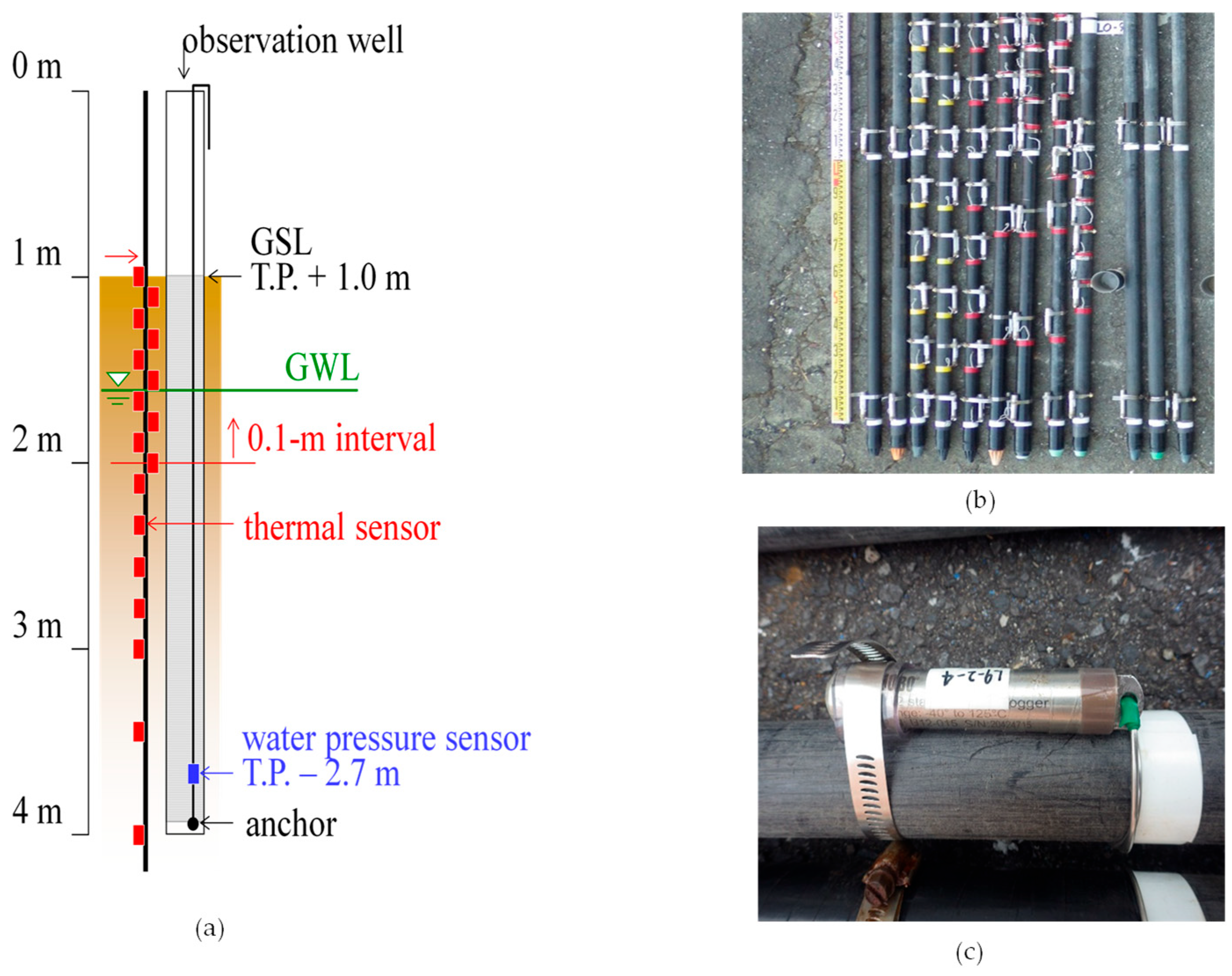
3.1. Field Observations
3.1.1. Overview of the Observations
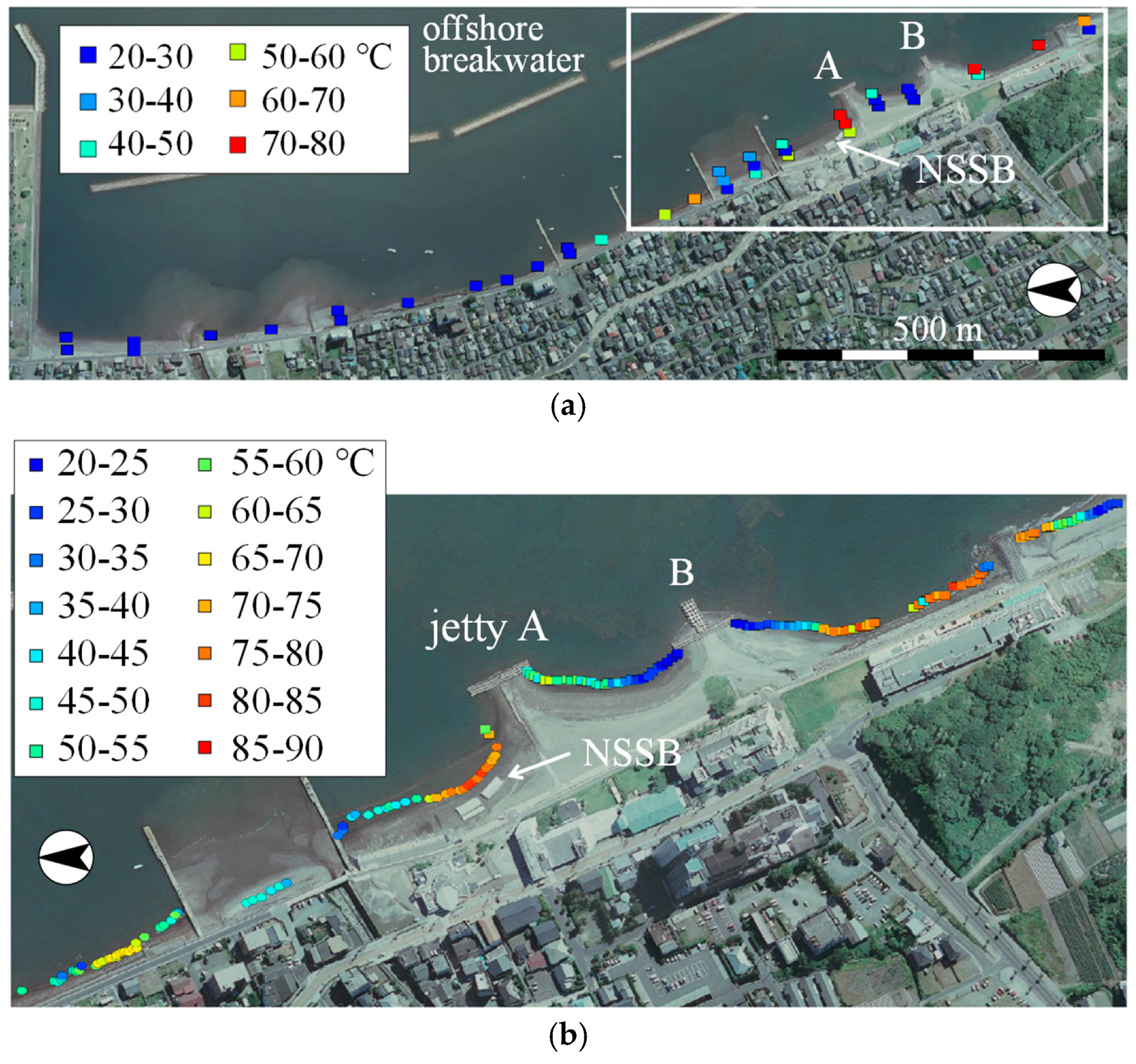
3.1.2. Alongshore Measurements
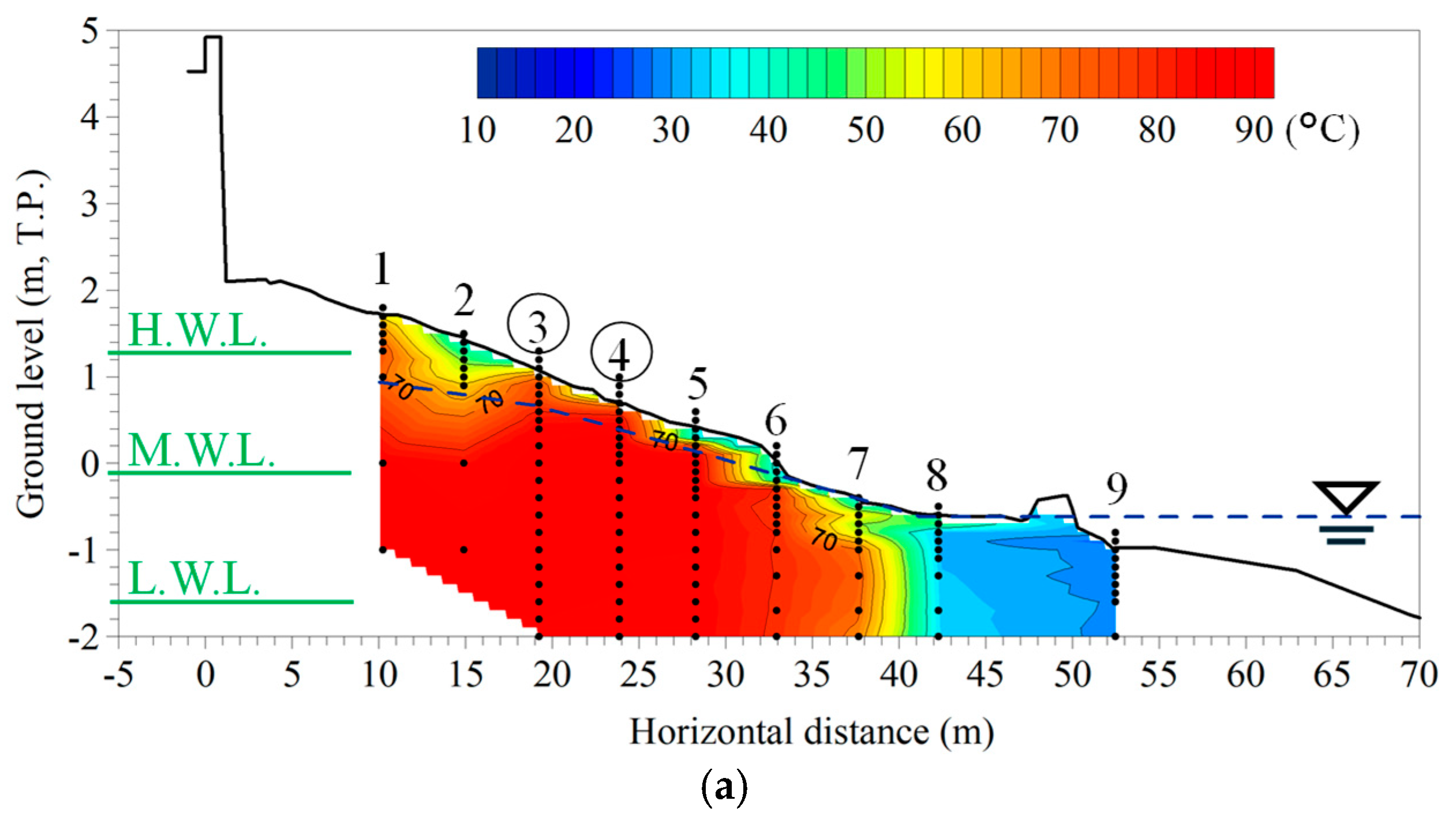
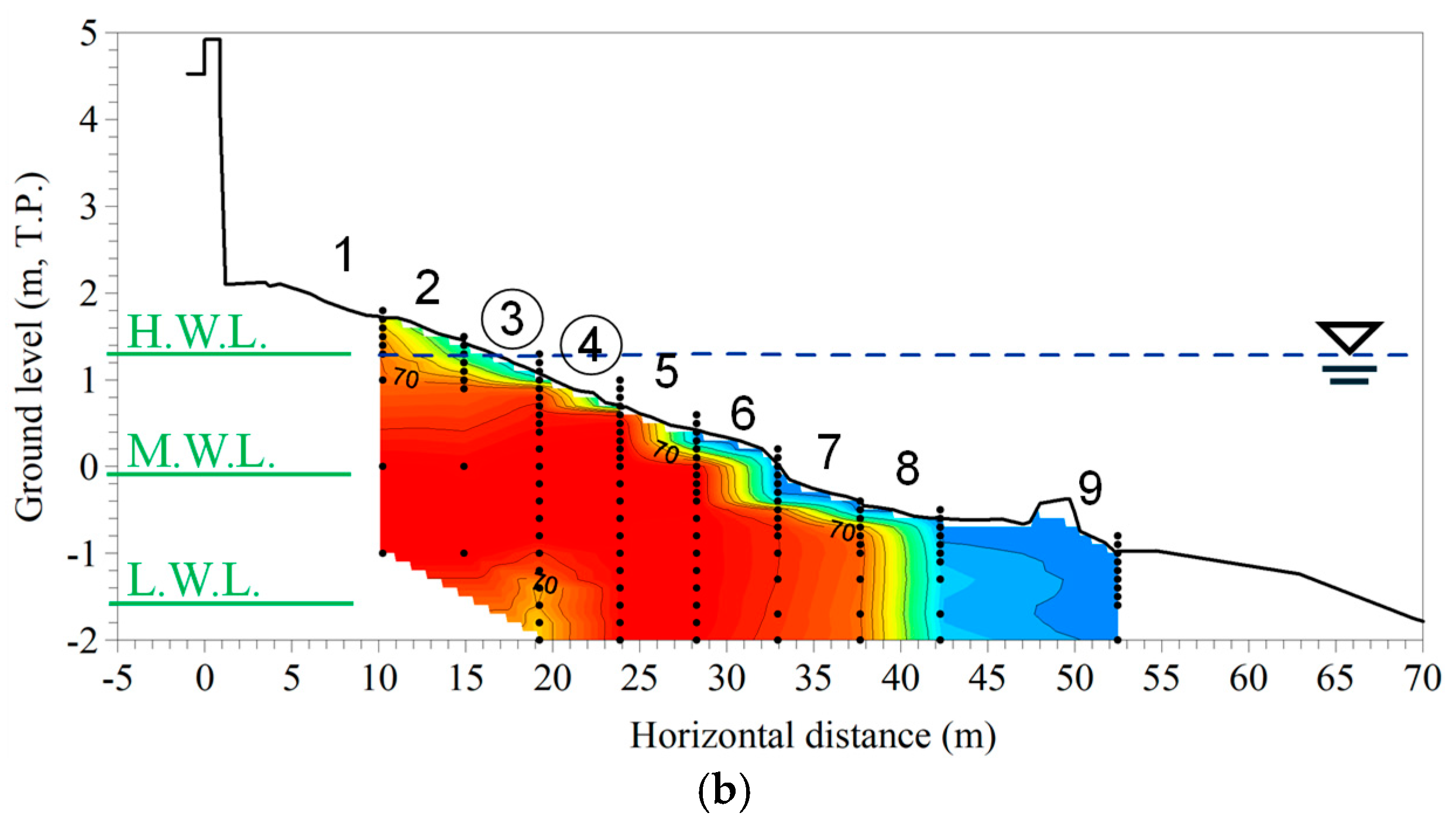
3.1.3. Cross-Sectional Measurements Along the NSSB Transect
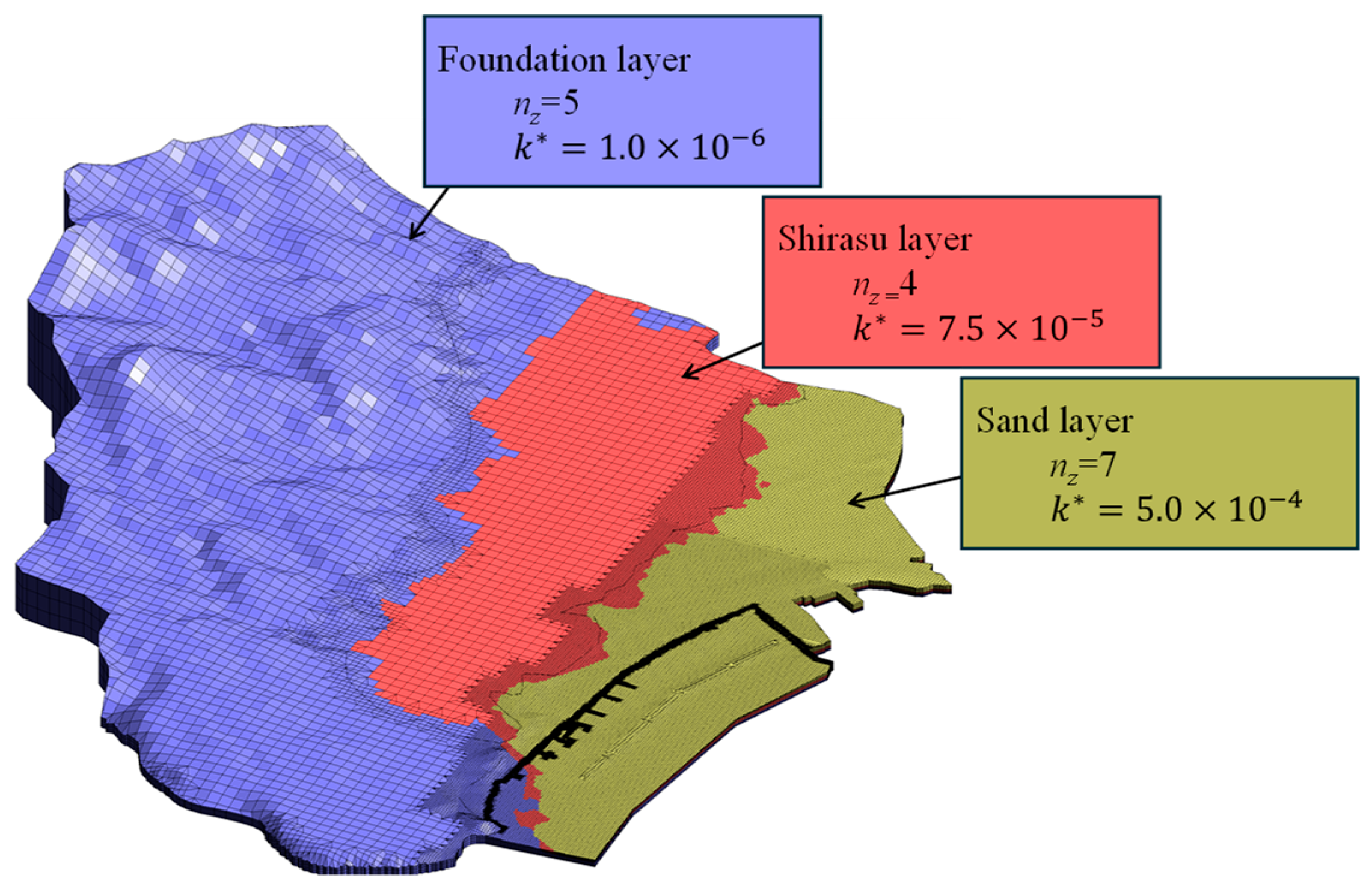
3.2. Numerical Analysis
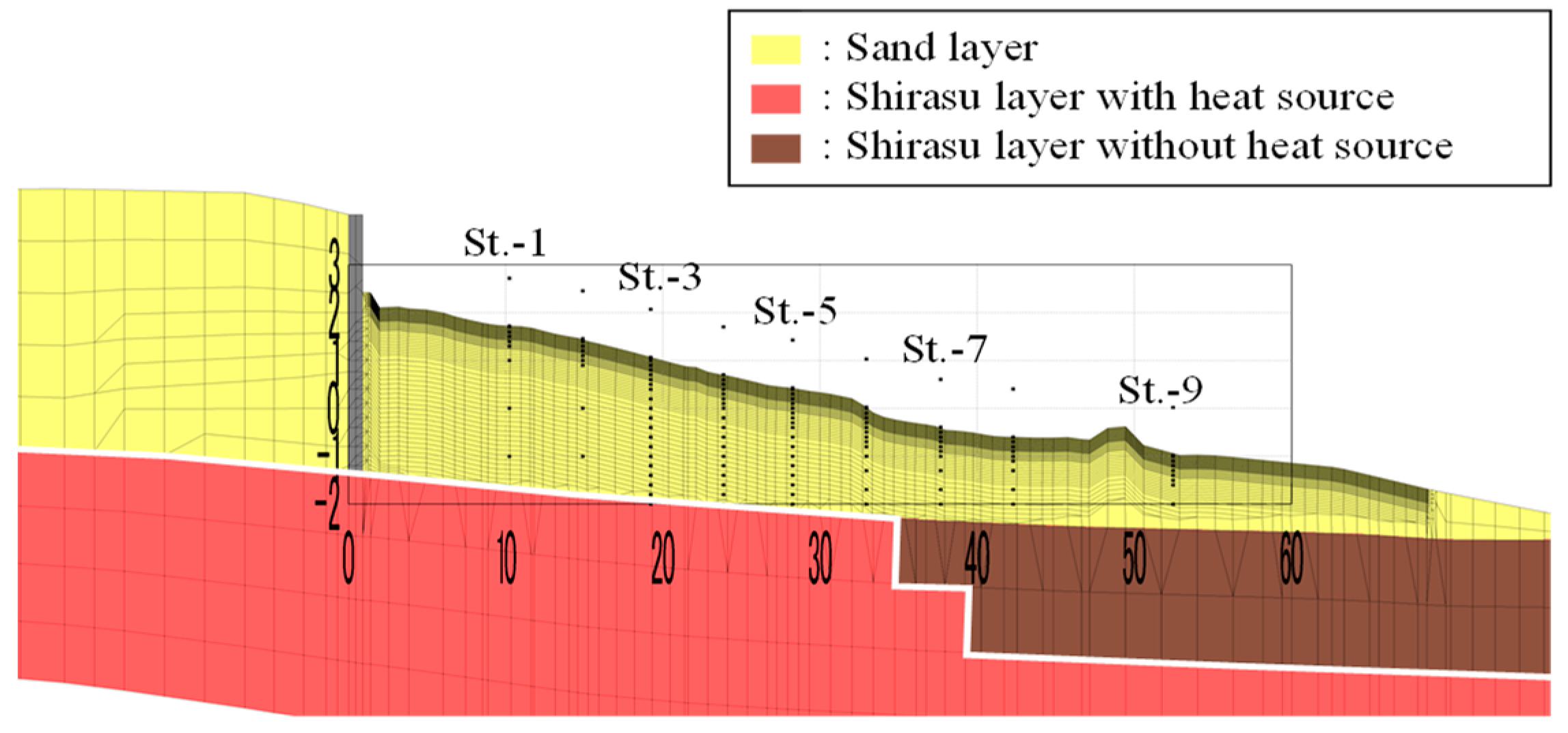
3.2.1. Computational Domain
3.2.2. Boundary Conditions
3.2.3. Basic Equations
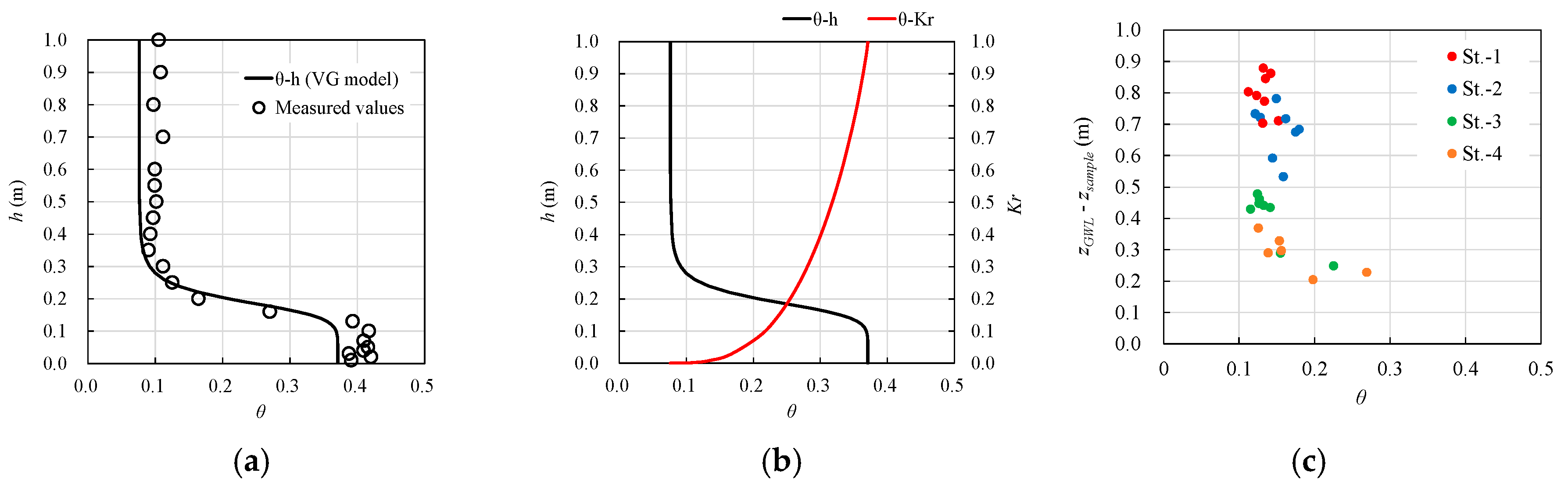
3.2.4. Saturation/Unsaturation Characteristics
4. Results
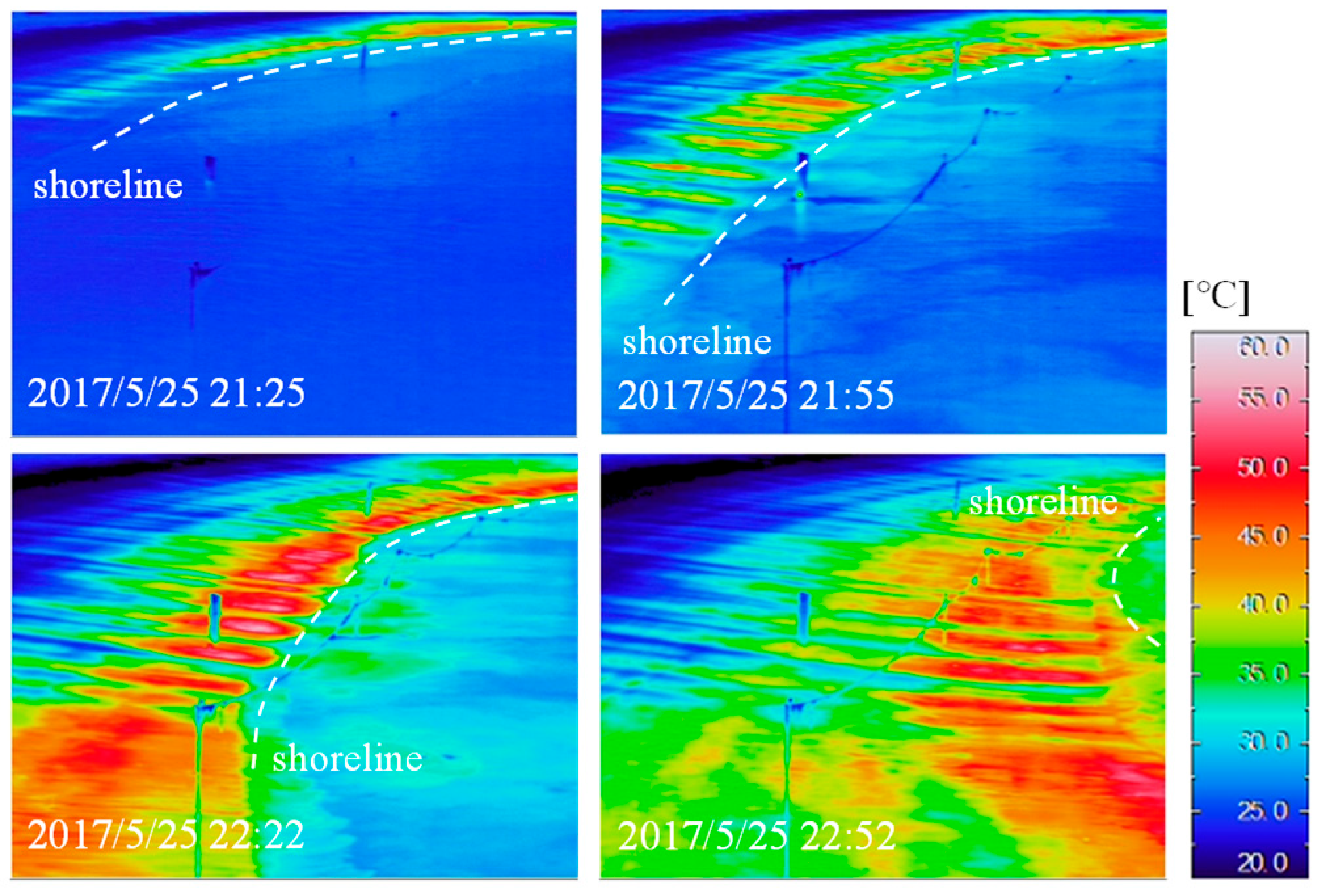
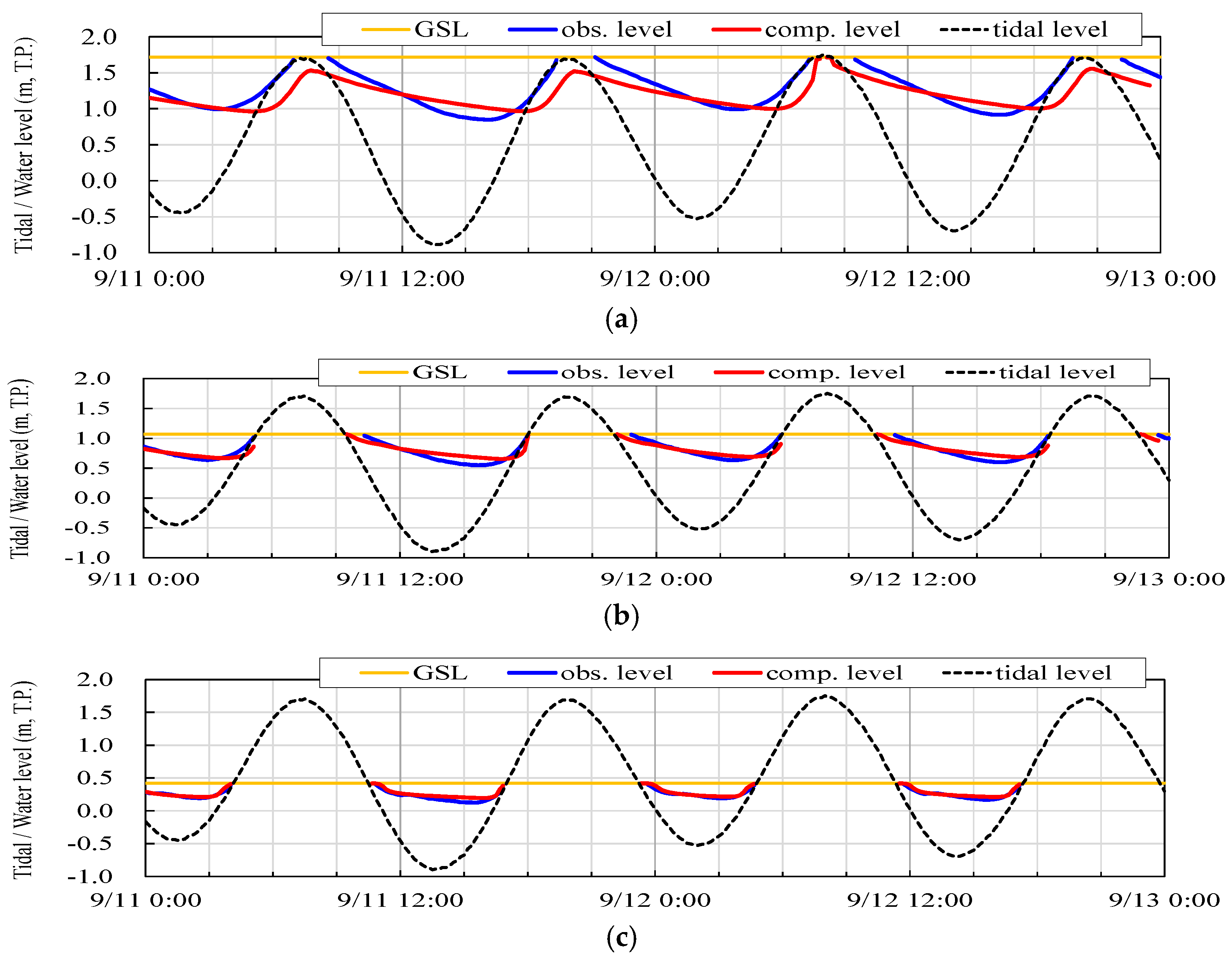
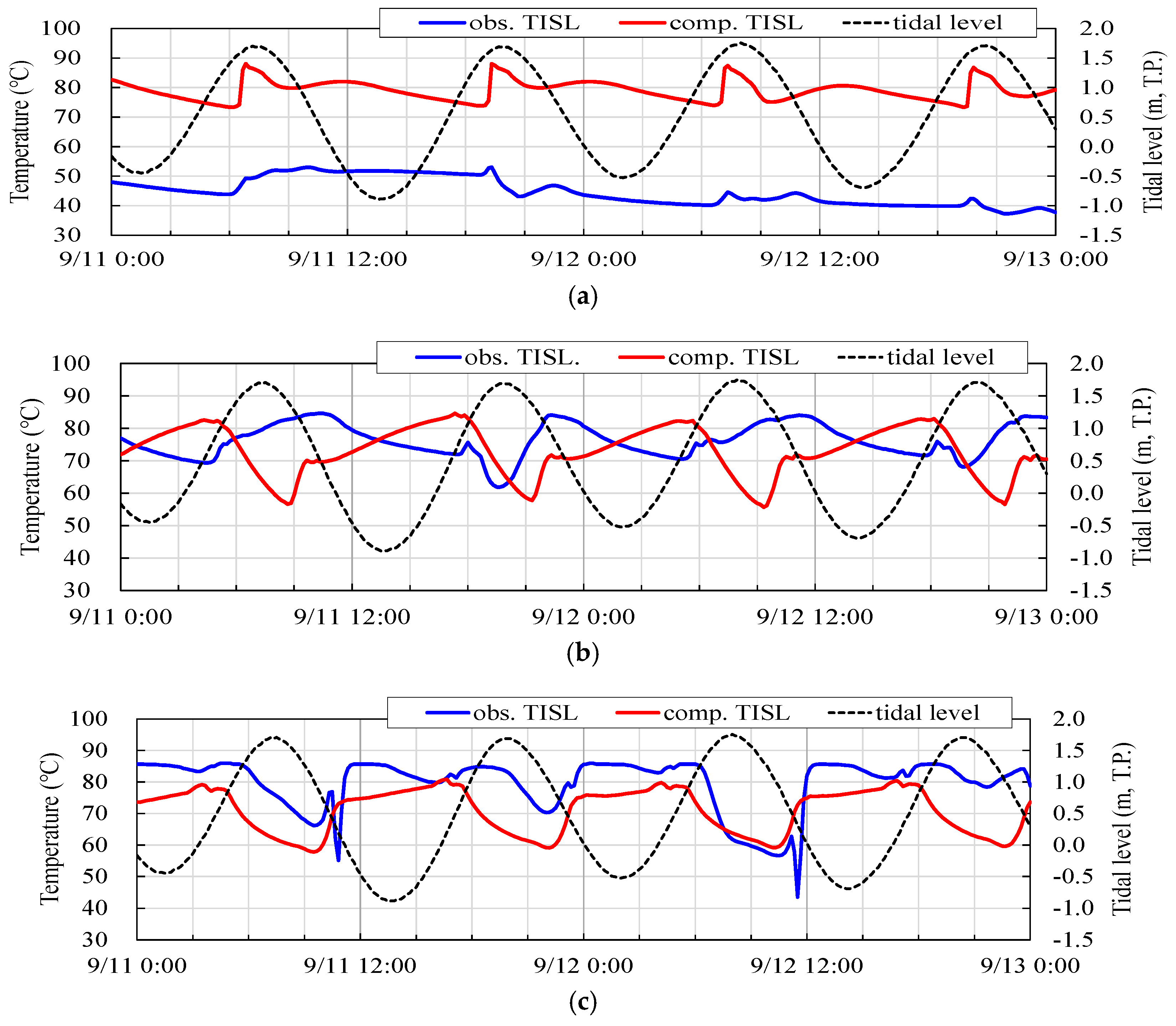
4.1. Observational Results
4.2. Computational Results
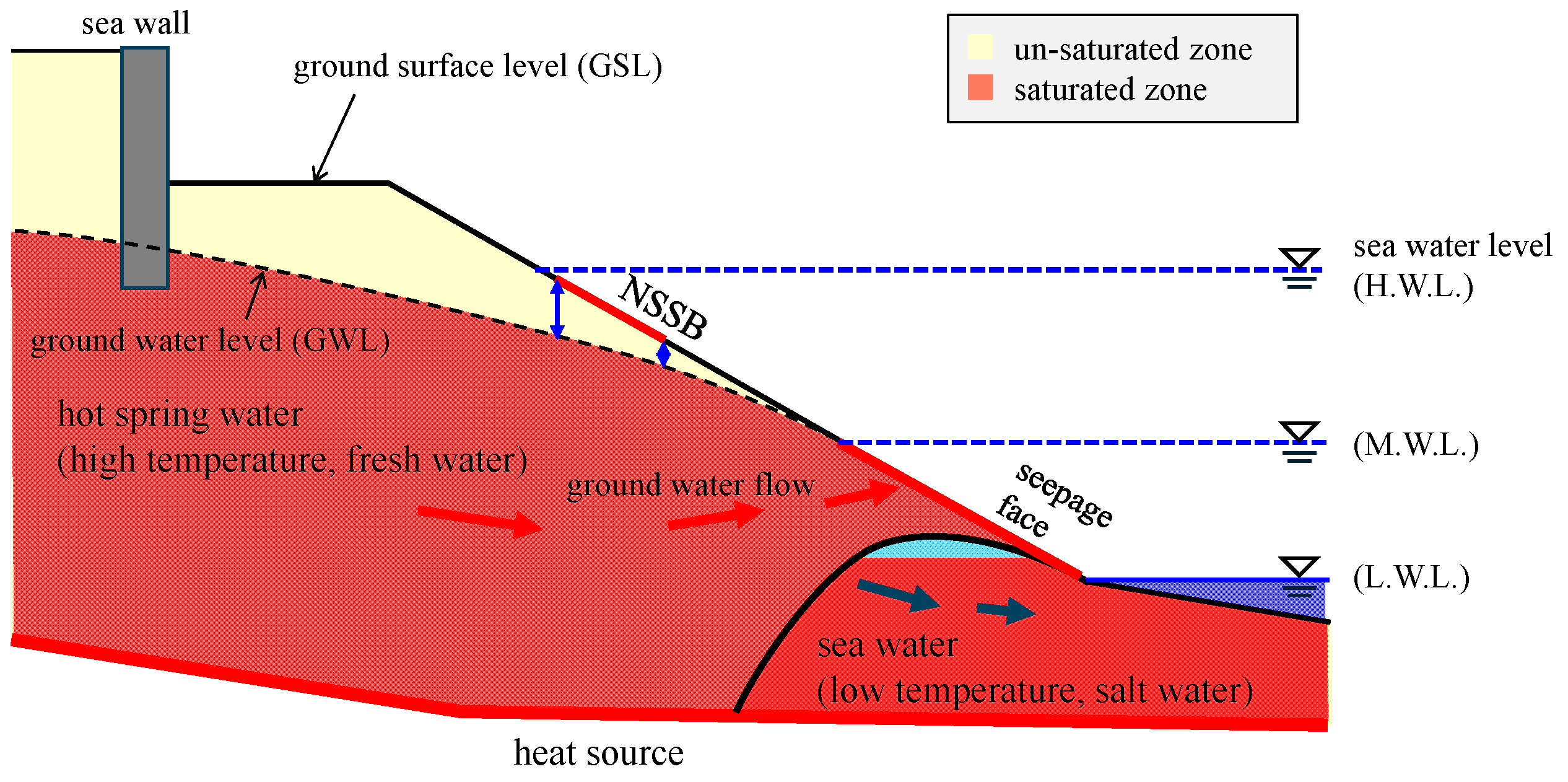
5. Discussion
5.1. Assessment of Reproducibility of Groundwater Table and Sand Temperature
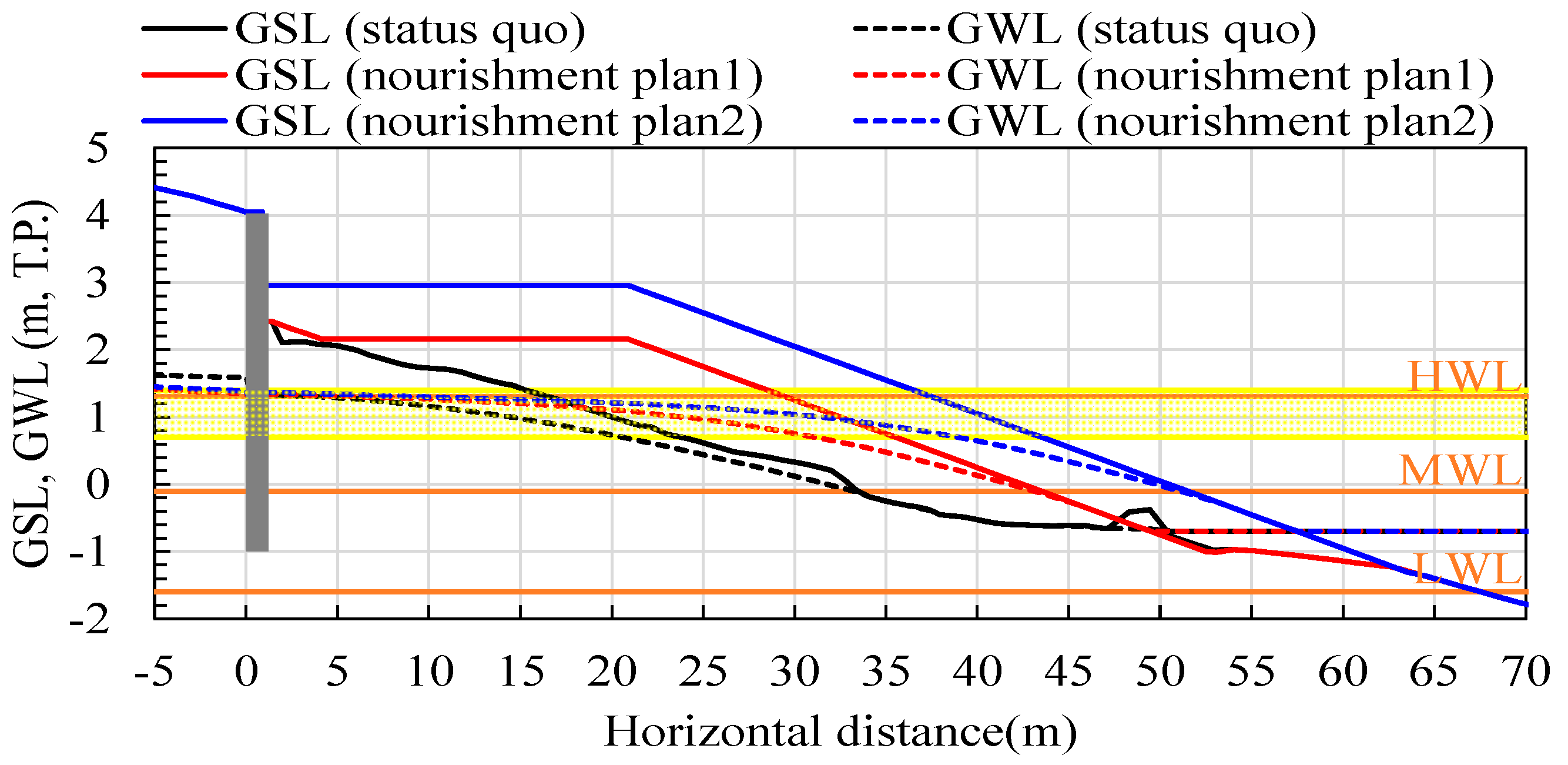
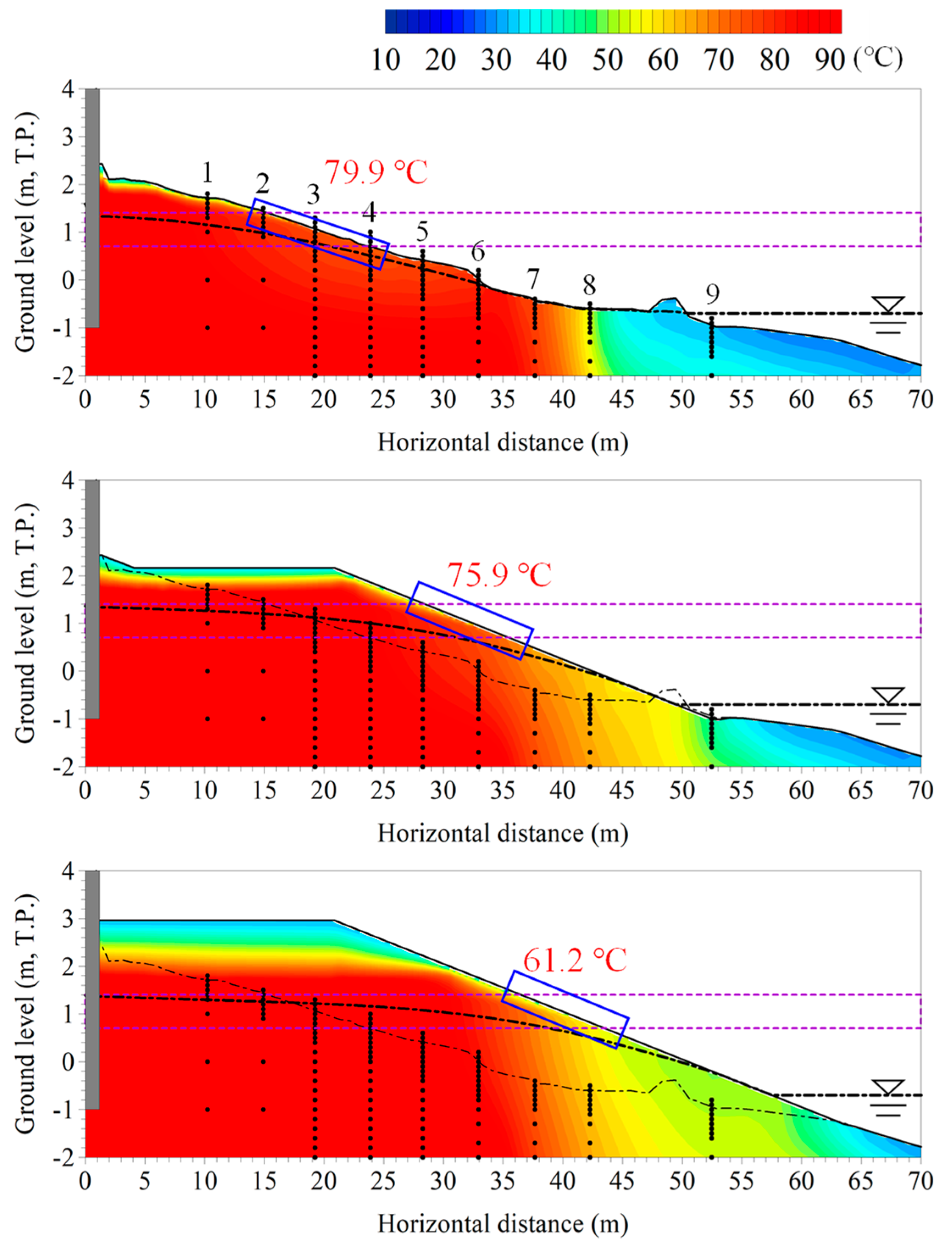
5.2. Impact Assessment of Beach Nourishment Work on the NSSB Site
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Emery, K.O.; Foster, J.F. Water table in beaches. J. Mar. Res. 1948, 7, 644–654. [Google Scholar]
- Grant, U.S. Influence of the water table on beach aggradation and degradation. J. Mar. Res. 1948, 7, 655–660. [Google Scholar]
- Turner, I. Water table outcropping on macro-tidal beaches: A simulation model. Mar. Geol. 1993, 115, 227–238. [Google Scholar] [CrossRef]
- Turner, I.L.; Masselink, G. Swash infiltration-exfiltration and sediment transport. J. Geophys. Res. 1998, 103, 30813–30824. [Google Scholar] [CrossRef]
- Nielsen, P.; Chritiansen, R.B.M.; Oliva, P. Infiltration effects on sediment mobility under waves. Coast. Eng. 2001, 42, 105–114. [Google Scholar] [CrossRef]
- Butt, T.; Russell, P.; Turner, I. The influence of swash infiltration-exfiltration on beach face sediment transport: Onshore or offshore? Coast. Eng. 2001, 42, 35–52. [Google Scholar] [CrossRef]
- Hoque, M.A.; Asano, T. Filtration effects on sediment transport in a swash zone. In Coastal Engineering 2002: Solving Coastal Conundrums; World Scientific: Singapore, 2002; pp. 2981–2993. [Google Scholar]
- Ochi, M.; Miyatake, M.; Kimura, K. Characteristics of sediment transport in swash zone due to saturated-unsaturated sloped beach. Coast. Eng. Proc. 2014, 1, sediment.39. [Google Scholar] [CrossRef]
- Bear, J. Dynamics of Fluid in Porous Media; Dover Publications: Mineola, NY, USA, 1988; p. 437. [Google Scholar]
- Uchiyama, Y. Numerical analysis on groundwater flow in sandy beaches considering tidal fluctuation and density distribution. Rep. Port Harb. Res. Inst. 1999, 38, 7–27. (In Japanese) [Google Scholar]
- Uchiyama, Y.; Nadaoka, N.; Rolke, P.; Adachi, K.; Yagi, H. Submarine groundwater discharge into the sea and associated nutrient transport in a sandy beach. Water Resour. Res. 2000, 36, 1467–1479. [Google Scholar] [CrossRef]
- Karambas, T.V.; Ioannidis, D. ‘Soft’ shore protection by a beach drain system. Glob. NEST J. 2013, 15, 295–304. [Google Scholar]
- Sato, M.; Fukushima, T.; Nishi, R.; Fukunaga, M. On the change of velocity field in nearshore zone due to coastal drain and consequent beach transformation. In Coastal Engineering 1996; ASCE Library: Reston, VA, USA, 1996; pp. 2666–2676. [Google Scholar]
- Law, A.W.-K.; Lim, S.-Y.; Liu, B.-Y. A note on transient beach evolution with artificial seepage in the swash zone. J. Coast. Res. 2002, 18, 379–387. [Google Scholar]
- Horn, D.P. Measurements and modelling of beach groundwater flow in the swash-zone: A review. Cont. Shelf Res. 2006, 26, 622–652. [Google Scholar] [CrossRef]
- Hallin, C.; van Ijzendoorn, C.; Homberger, J.; de Vries, S. Simulating surface soil moisture on sandy beaches. Coast. Eng. 2023, 185, 104376. [Google Scholar] [CrossRef]
- Zheng, Y.; Yang, M.; Liu, H. Coastal groundwater dynamics with a focus on wave effects. Earth-Sci. Rev. 2024, 256, 104869. [Google Scholar] [CrossRef]
- Allice, R.G.; Yusa, Y. Fluid flow processes in the Beppu geothermal system. Japan. Geothermics 1989, 18, 743–759. [Google Scholar] [CrossRef]
- Yusa, Y. Numerical experiment of groundwater motion under geothermal condition—Vying between potential flow and thermal convective flow. J. Geotherm. Soc. Jpn. 1983, 5, 23–38. (In Japanese) [Google Scholar]
- Pasquale, V.; Verdoya, M.; Chiozzi, P. Groundwater flow analysis using different geothermal constraints: The case study of Acqui Termi area, northwestern Italy. J. Volcanol. Geotherm. Res. 2011, 199, 38–46. [Google Scholar] [CrossRef]
- Kaya, E.; O’Sullivan, M.J.; Hochstein, M.P. A three dimensional numerical model of the Waiotapu, Waikite and Reporoa geothermal area, New Zealand. J. Volcanol. Geotherm. Res. 2014, 283, 127–142. [Google Scholar] [CrossRef]
- Tsang, C.F.; Buscheck, T.; Doughty, C. Aquifer thermal energy storage: A numerical simulation of Auburn University field experiments. Water Resour. Res. 1981, 17, 647–658. [Google Scholar] [CrossRef]
- Buscheck, T.; Doughty, C.; Tsang, C.F. Prediction and analysis of a field experiment on a multilayered aquifer—Thermal energy storage system with strong buoyancy flow. Water Resour. Res. 1983, 19, 1307–1315. [Google Scholar] [CrossRef]
- Hecht-Mendez, J.; Molina-Giraldo, N.; Blum, P.; Bayer, P. Evaluating MT3DMS for heat transport simulation of closed geothermal systems. Ground Water 2010, 48, 741–756. [Google Scholar] [CrossRef] [PubMed]
- White, J.T.; Karakhanian, A.; Connor, C.B.; Connor, L.; Hughes, J.D.; Malservisi, R.; Wetmore, P. Coupling geophysical investigation with hydrothermal modeling to constrain the enthalpy classification of a potential geothermal resource. J. Volcanol. Geotherm. Res. 2015, 298, 59–70. [Google Scholar] [CrossRef]
- Deb, S.K.; Shukka, M.K.; Sharma, P.; Mexal, J.G. Coupled liquid water, water vapor, and heat transport simulations in an unsaturated zone of a sandy loam filed. Soil Sci. 2011, 176, 387–398. [Google Scholar] [CrossRef]
- Haruyama, M. Geological physical and mechanical properties of “Shirasu” and its engineering classification. Jpn. Soc. Soil Mech. Found. Eng. 1973, 13, 45–60. [Google Scholar] [CrossRef] [PubMed]
- Moritz, A.R.; Henriques, F.C. Studies of thermal injury: II. The relative importance of time and surface temperature in the causation of cutaneous burns. Am. J. Pathol. 1947, 23, 695–720. [Google Scholar]
- Nishigaki, M.; Hishiya, T.; Hashimoto, N.; Kohno, I. The numerical method for saturated-unstaturated fluid-density-dependent groundwater flow with mass transport. Jpn. Soc. Civ. Eng. 1995, 511, 135–144. (In Japanese) [Google Scholar]
- Nakano, M.; Miyazaki, T.; Shiozono, S.; Nishimura, T. Physical and Environmental Analysis of Soil (Soil Column Method); University of Tokyo Press: Tokyo, Japan, 1995; pp. 77–79. [Google Scholar]
- Seki, K. SWRC fit—A Nonlinear Fitting Program with a Water Retention Curve for Soils Having Unimodal and Bimodal Pore Structure. Hydrol. Earth Syst. Sci. Discuss. 2007, 4, 407–437. [Google Scholar]
- van Genuchten, M.T. A Closed-Form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]




| Coefficient | Value | ||
|---|---|---|---|
| Foundation Layer | Shirasu Layer | Sand Layer | |
| Effective Porosity (-) | 0.100 | 0.100 | 0.393 |
| Specific storage coefficient m−1) | 1.0 × 10−5 | 1.0 × 10−5 | 1.0 × 10−5 |
| Thermal diffusion coefficient m2/s) | 1.0 × 10−6 | 1.0 × 10−6 | 1.0 × 10−6 |
| Longitudinal dispersion length (m) | 5.0 | 5.0 | 5.0 |
| Transverse dispersion length m) | 2.5 | 2.5 | 2.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ono, N.; Miyake, T.; Kasamo, K.; Ishimoto, K.; Asano, T. Impact Assessment of Beach Nourishment on Hot Spring Groundwater on Ibusuki Port Coast. Coasts 2025, 5, 1. https://doi.org/10.3390/coasts5010001
Ono N, Miyake T, Kasamo K, Ishimoto K, Asano T. Impact Assessment of Beach Nourishment on Hot Spring Groundwater on Ibusuki Port Coast. Coasts. 2025; 5(1):1. https://doi.org/10.3390/coasts5010001
Chicago/Turabian StyleOno, Nobuyuki, Takatomo Miyake, Kenki Kasamo, Kenji Ishimoto, and Toshiyuki Asano. 2025. "Impact Assessment of Beach Nourishment on Hot Spring Groundwater on Ibusuki Port Coast" Coasts 5, no. 1: 1. https://doi.org/10.3390/coasts5010001
APA StyleOno, N., Miyake, T., Kasamo, K., Ishimoto, K., & Asano, T. (2025). Impact Assessment of Beach Nourishment on Hot Spring Groundwater on Ibusuki Port Coast. Coasts, 5(1), 1. https://doi.org/10.3390/coasts5010001





