Abstract
Hydrogen-bond-like M···H–C interactions in square-planar d8 metal complexes have recently gained attention as structure-directing elements and design motifs in asymmetric catalysis. In this study, we explore these weak interactions not as static features, but as key modulators of molecular motion. We synthesized four cis-[N,N′-pentamethylenebis(iminomethylazolato)]M(II) (M = Pt, Pd), including iminomethyl-2-imidazole, iminomethyl-5-imidazole, and iminomethylpyrrolato Pt(II) complexes and an iminomethylpyrrolato Pd(II) analog. All complexes display reversible flipping of the alkylene bridge across the coordination plane, with the M···H–C interaction alternately engaging from above or below. This dynamic motion was characterized by variable-temperature 1H NMR spectroscopy, revealing activation parameters for the flipping process. X-ray crystallography confirmed geometries consistent with hydrogen-bond-like interactions, while NBO analysis based on DFT calculations provided insight into their electronic nature. Interestingly, although Pt and Pd display comparable M···H–C distances, solvent effects dominate the flipping kinetics over metal identity. These findings highlight the role of hydrogen-bond-like M···H–C interactions not only in structural stabilization, but also in regulating conformational dynamics.
1. Introduction
Metal···hydrogen–carbon (M···H–C) interactions play a crucial role in controlling the structure and reactivity of transition metal complexes [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20]. Among these, agostic interactions—representing a typical form of M···H–C bonding—have attracted significant attention as a key concept in the elementary steps of various catalytic and transformation reactions, such as C–H activation [8], β-hydrogen elimination [9], polymerization [10,11], and cyclometallation [12,13]. In contrast, non-covalent metal–C–H interactions, referred to as anagostic interactions or hydrogen-bond-type M···H–C interaction, have also been reported [14,15,16,17,18,19,20]. Structurally, agostic interactions are characterized by M···H–C distances of 1.8–2.3 Å and M···H–C angles of 90–140°, with the corresponding 1H NMR signals of agostic hydrogens typically observed in the upfield region. On the other hand, anagostic interactions exhibit longer M···H–C distances (2.3–2.9 Å) and wider bond angles (110–170°), and the associated 1H NMR signals appear downfield, providing a clear distinction between the two types of interactions.
While agostic interactions are widely recognized as key intermediates in catalytic processes, hydrogen-bond-type M···H–C interactions have traditionally been regarded as secondary interactions that arise when structural constraints bring a C–H bond into close proximity with a metal center [21,22,23,24,25,26]. However, recent studies have begun to reevaluate these hydrogen-bond-type M···H–C interactions not merely as structural features, but as active design elements that can influence conformational control and catalytic selectivity. Notably, a chiral biaryl-based imidazo[1,5-a]pyridine carbene–palladium complex (ImPy–Pd) reported in 2024 demonstrated that a hydrogen-bond-type Pd···H–C interaction can rigidify the steric environment around the ligand, thereby enabling high enantioselectivity in asymmetric C–N cross-coupling reactions of malonamide derivatives [27]. In this system, the hydrogen-bond-type M···H–C formed between the bulky aryl group and the metal center was suggested to suppress rotational flexibility within the ligand framework, serving as a key factor in reaction selectivity. Although molecular design strategies that purposefully utilize M···H interactions remain relatively rare, their potential is expected to garner increasing attention in the future.
We have previously developed a series of three-dimensional molecular designs for square-planar platinum(II) and palladium(II) complexes, aimed at endowing them with expanded functions such as molecular aggregation and dynamic motion [28,29,30,31,32,33,34,35,36,37,38,39,40]. This strategy has led to the emergence of unique molecular functions, including ultrasound-induced gelation [29,31,39], aggregation-induced emission [28,34,40], chiroptical properties [37,38], and precisely regulated molecular dynamics [30,32,35]. In the course of these studies, we discovered that in trans-configured platinum(II) complexes bridged by a polymethylene chain, a hydrogen-bond-type M···H–C interaction is formed between the platinum center and a methylene hydrogen atom on the alkyl chain [19]. This Pt···H–C interaction occurred in a site-selective manner depending on the chain length, suggesting its role in stabilizing specific conformers of the flexible methylene chain.
In this study, we investigated the role of hydrogen-bond-type M···H–C interactions in regulating dynamic structural changes, focusing on the flipping motion of polymethylene chains in square-planar metal complexes. Regulated molecular motions accompanied by specific structural transformations, especially in transition metal complexes, have garnered attention as elementary units of molecular machines and as key determinants in stimulus-responsive functional systems [41,42,43,44,45,46,47,48,49,50]. A series of cis-configured platinum(II) and palladium(II) complexes (1–4), each bearing a N,N′-pentylene-bridged bis(iminomethylazole) scaffold coordinating to Pt(II) or Pd(II), were synthesized to enable comparative analysis of different ligand and metal centers (Figure 1, upper). The dynamic behavior of the pentylene bridge was examined by variable-temperature 1H NMR line-shape analysis. The activation parameters associated with the flipping motion were examined in relation to the presence of M···H interactions (Figure 1, lower). The results revealed that while the M···H interaction stabilizes specific conformations, the activation enthalpy (ΔH‡) and entropy (ΔS‡) of the flipping process are more strongly influenced by the solvent environment than by the metal center or chain length. This study demonstrates that metal–hydrogen interactions can function not only as static conformational constraints but also as dynamic control elements, providing a new conceptual framework for regulating molecular motion in coordination systems with flexible architectures.
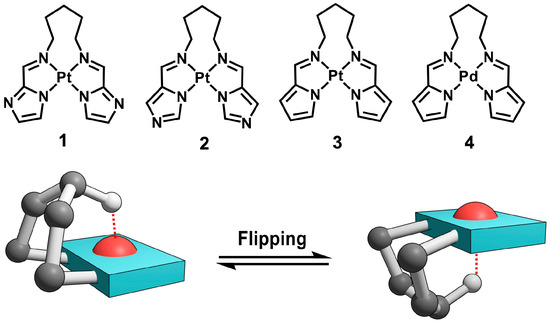
Figure 1.
Molecular structures of complexes 1–4 and schematic illustration of the flipping motion between two representative conformers. The red dashed line indicates the H(γ) atom interacting with the metal center in one conformer.
2. Materials and Methods
General: Melting points were measured on a glass plate on micro melting point apparatus (Yanagimoto Manufacturing Co., Ltd., Kyoto, Japan). IR spectroscopy was performed using a FT/IR-410 spectrometer (JASCO Corporation, Tokyo, Japan). 1H and 13C NMR spectra were recorded on a Unity–Inova 500 spectrometer (Varian Inc., Palo Alto, CA, USA; 500 MHz for 1H, 125 MHz for 13C). Chemical shifts are denoted in δ-unit (ppm) relative to tetramethylsilane. The splitting patterns are designated as follows: s (singlet), d (doublet), t (triplet), q (quartet), m (multiplet), and br (broad). High-resolution mass spectroscopy (HRMS) was performed using a microTOF spectrometer (Bruker Daltonics, Billerica, MA, USA, APCI mode).
X-ray structure determination: Crystals employed for X-ray diffraction studies were obtained by recrystallization from chloroform/benzene solution for 1, chloroform/toluene solution for 2, acetonitrile solution for 3, and chloroform solution for 4, and data were collected using a XtaLAB P-200 diffractometer (Rigaku Corporation, Tokyo, Japan) with graphite-monochromated Mo Kα radiation (λ = 0.71075 Å). Their structures were solved by direct methods and refined using the full-matrix least-squares method. In the subsequent refinement, the function ∑ω(Fo2–Fc2)2 was minimized, where Fo and Fc are the observed and calculated structure factor amplitudes, respectively. The positions of non-hydrogen atoms were determined from difference Fourier electron-density maps and refined anisotropically. All the ORTEP illustrations [51] were generated using ORTEP-3 [52]. Crystallographic data for compounds 1 (CCDC 2475822), 2 (CCDC 2475823), 3 (CCDC 2475824), and 4 (CCDC 2475825) can be obtained free of charge from the Cambridge Crystallographic Data Centre.
Computational Methods: All calculations were performed using the ORCA 6.0.0 program package [53]. Geometry optimizations and vibrational frequency analyses were carried out using density functional theory (DFT) with the B3LYP functional [54]. The def2-TZVP basis set [55] was employed for all atoms. To reduce computational cost, the RIJCOSX approximation was applied in conjunction with the def2/J auxiliary basis set. Solvent effects were taken into account using the CPCM model with chloroform as the solvent. Natural bond orbital (NBO) analyses were performed using the NBO 7.0 program [56] interfaced with ORCA. The second-order perturbation theory analysis was used to evaluate donor–acceptor interactions. Second-order perturbation theory was used to estimate donor–acceptor interactions. Noncovalent interaction (NCI) analyses [57] were conducted using the Multiwfn 3.8 program [58], and the reduced density gradient (RDG) isosurfaces were visualized using VMD [59].
Synthesis of Ligands:

- All Schiff-base ligands L1–3 were synthesized via condensation reactions between the corresponding diamines and pyrrole-2-carbaldehyde. As a representative example, the synthesis of N,N′-bis((1H-pyrrolyl)methylene)-1,5-pentanediamine (L3) is described below. Pyrrole-2-carbaldehyde (0.954 g, 10.0 mmol) and 1,5-pentanediamine (0.513 g, 5.0 mmol) were dissolved in 99% ethanol (50 mL) and refluxed for 20 h in a 100 mL round-bottom flask equipped with a condenser. After the reaction, the solvent was removed under reduced pressure, and the resulting gray solid was dried under vacuum to afford L3 (1.14 g, 4.4 mmol, 88%) without further purification.
Synthesis of Pt Complexes: All Pt complexes were synthesized via reactions between the corresponding ligands and PtCl2(CH3CN)2. As a representative example, the synthesis of 1 is described below. In a 100 mL round-bottomed flask equipped with a reflux condenser, ligand L1 (0.129 g, 0.50 mmol), PtCl2(CH3CN)2 (0.174 g, 0.50 mmol), K2CO3 (0.829 g, 6.00 mmol), toluene (60 mL), and DMSO (15 mL) were placed. The reaction mixture was refluxed at 120 °C for 28 h. After the reaction, toluene was removed under reduced pressure. The resulting precipitate was filtered off, and ethyl acetate (100 mL) was added to the solution. Afterwards, the organic layer was washed with brine (100 mL × 3) to remove DMSO. The organic layer was dried over Na2SO4, then removed with ethyl acetate under reduced pressure to afford the crude product. This crude product was purified by column chromatography (NH–SiO2, CH2Cl2/MeOH = 95:5) to obtain 1 (0.135 g, 59%) as an orange solid.
cis-[N,N′-pentamethylenebis(2-iminomethylimidazolato)]platinum(II) (1): Yellow solid (59%). M.p.: 249.6-250.2 °C (decomp.). 1H NMR (CDCl3, 12 °C, 500 MHz): δ 1.31 (br, 1H, Hγ2), 2.06 (br, 4H, Hβ), 3.18 (br, 1H, Hγ1), 3.08 (br, 2H, Hα), 4.34 (br, 2H, Hα), 7.39 (s, 2H, H4), 7.43 (s, 2H, H5), 7.98 (s, 2H, H6). 13C NMR (CDCl3, 125 MHz): δ 17.0, 32.7, 59.2, 129.9, 133.7, 155.2, 162.4 ppm. HRMS (FAB+): m/z calcd for C13H17N6195Pt: 452.1162; found: 452.1161 [M+H]+. Anal. Calcd for C13H16N6Pt: C, 34.59; H, 3.57; N, 18.62, found: C, 34.45; H, 3.23; N, 18.37. IR (KBr): 783 (s), 831 (s), 932 (s), 1095 (s), 1146 (s), 1157 (s), 1214 (s), 1273 (s), 1346 (s), 1415 (s), 1559 (s), 1584 (s), 2328 (m), 2342 (m), 2361 (m), 2842 (w), 2917 (w), 2973 (w), 3011 (w), 3106 (w).
cis-[N,N′-butamethylenebis(2-iminomethylimidazolato)]platinum(II) (1′): Yellow solid (22%). M.p.: 241.0 °C (decomp.). 1H NMR (CDCl3, 25 °C, 500 MHz): δ 2.12 (tm, J = 4.6 Hz, 4 H, Hβ), 4.06 (tm, J = 4.6 Hz, 4 H, Hα), 7.33 (s, 2 H, H4), 7.40 (s, 2 H, H5), 7.99 (s, 2 H, H6). 13C NMR (CDCl3, 125 MHz): δ 25.2, 56.8, 130.1, 133.8, 155.6, 160.5 ppm. HRMS (FAB+): m/z calcd for C12H14N6195Pt: 438.1023; found: 438.1001 [M]+. IR (KBr): 766 (s), 1147 (s), 1345 (s), 1409 (s), 1592 (s), 2946 (w), 2999 (w), 3207 (w), 3279 (w).
cis-[N,N′-propamethylenebis(2-iminomethylimidazolato)]platinum(II) (1″): Red solid (89%). M.p.: 235.0 °C (decomp.). 1H NMR (CDCl3, 25 °C, 500 MHz): δ 2.21 (quin, J = 5.2 Hz, 2 H, Hβ), 3.88 (t, J = 5.2 Hz, 4 H, Hα), 7.27 (s, 2 H, H4), 7.42 (s, 2 H, H5), 8.14 (s, 2 H, H6). 13C NMR (CDCl3, 125 MHz): δ 30.9, 55.0, 130.5, 133.9, 155.5, 158.9 ppm. HRMS (FAB+): m/z calcd for C11H12N6195Pt: 424.0882; found: 424.0844 [M]+. IR (KBr): 797 (s), 877 (s), 944 (s), 1151 (s), 1257 (s), 1411 (s), 1591 (s), 2991 (w), 3116 (w), 3332 (w).
cis-[N,N′-pentamethylenebis(5-iminomethylimidazolato)]platinum(II) (2): Yellow solid (11%). M.p.: 229.8-230.2 °C (decomp.). 1H NMR (CDCl3, 10 °C, 500 MHz): δ 1.49 (br, 1H, Hγ2), 1.94 (br, 4H, Hβ), 3.05 (br, Hγ1), 3.56 (br, 2H, Hα), 4.12 (br, 2H, Hα), 7.68 (s, 2H, H3), 7.72 (s, 2H, H6), 7.90 (s, 2H, H5). 13C NMR (CDCl3, 125 MHz): δ 16.9, 32.5, 59.0, 137.2, 139.8, 147.6, 161.8 ppm. HRMS (FAB+): m/z calcd for C13H17N6195Pt: 452.1162; found: 452.1164 [M+H]+. IR (KBr): 655 (s), 944 (s), 1129 (s), 1258 (s), 1274 (s), 1456 (s), 1593 (s), 2322 (m), 2357 (m), 2694 (w), 2838 (m), 2900 (m), 2924 (m), 3101 (w), 3129 (w).
cis-[N,N′-pentamethylenebis(iminomethylpyrrolato)]platinum(II) (3): Yellow solid (10%). M.p.: 248.2-250.4 °C (decomp.). 1H NMR (CDCl3, 10 °C, 500 MHz): δ 1.44 (br, 1H, Hγ2), 1.92 (br, 4H, Hβ), 3.21 (br, 1H, Hγ1), 3.61 (br, 2H, Hα), 4.22 (br, 2H, Hα), 6.32 (dd, J = 3.9 Hz, 2.0 Hz, 2H, H4), 6.74 (dd, J = 3.9 Hz, 1.0 Hz, 2H, H3), 7.35 (br, 2H, H5), 7.61 (s, 2H, H6). 13C NMR (CDCl3, 125 MHz): δ 17.1, 32.9, 58.5, 110.8, 135.8, 140.1, 162.6 ppm. HRMS (FAB+): m/z calcd for C15H19N4195Pt: 450.1257; found: 450.1261 [M+H]+. Anal. Calcd for C15H18N4Pt: C, 40.09; H, 4.04; N, 12.47, found: C, 39.84; H, 3.75; N, 12.28. IR (KBr): 674 (w), 735 (s), 1040 (s), 1224 (s), 1326 (s), 1396 (s), 1591 (s), 2328 (m), 2339 (m), 2357 (m), 2693 (m), 2839 (w), 2917 (m), 2969 (w), 2993 (w), 3078 (w).
Synthesis of cis-[N,N′-pentamethylenebis(iminomethylpyrrolato)]palladium(II) (4): In this study, only complex 4 was prepared as a representative Pd(II) analog, since it bears the same ligand framework as complex 3 and thus enables direct comparison of the effect of metal substitution. The ligand L3 (55.2 mg, 0.22 mmol), Pd(OAc)2 (49.7 mg, 0.22 mmol), and acetonitrile (50 mL) were placed in a 100 mL round-bottomed flask equipped with a reflux condenser. This reaction mixture was refluxed under an Ar atmosphere at 60 °C for 3 h. After the reaction, acetonitrile was removed under reduced pressure. The resulting precipitate was filtered the solid was washed with acetonitrile (5 mL). This product was purified by recrystallization from acetonitrile and Et2O (1:1) and GPC to afford 4 (19.8 mg, 0.055 mmol 25%) as a yellow solid. M.p. 220–222 °C. 1H NMR (CDCl3, 4 °C, 500 MHz): δ 1.42 (br, 1H, Hγ2), 1.85 (br, 4H, Hβ), 3.07 (br, Hγ1), 3.36 (br, 2H, Hα), 3.99 (br, 2H, Hα), 6.23 (dd, J = 3.8 Hz, 2.0 Hz, 2H, H4), 6.71 (dd, J = 3.8 Hz, 1.1 Hz, 2H, H3), 7.27 (br, 2H, H5), 7.42 (s, 2H, H6). 13C NMR (CDCl3, 125 MHz): δ 17.1, 32.9, 58.5, 110.8, 135.8, 140.1, 162.6 ppm. IR (KBr): 669 (w), 736 (s), 1035 (s), 1225 (s), 1325 (s), 1394 (s), 1594 (s), 2329 (m), 2357 (m), 2854 (s), 2917 (s), 3078 (w), 3133 (w). HRMS (APCI): m/z calcd for C15H18N4Pd: 360.0544; found: 360.0567 [M]+.
3. Results and Discussion
A series of cis-[N,N′-pentamethylenebis(iminomethylazolato)]M(II) complexes (M = Pt, Pd), including iminomethyl-2-imidazole (1), iminomethyl-5-imidazole (2), and iminomethylpyrrolato Pt(II) (3), as well as an iminomethylpyrrolato Pd(II) analog (4), were synthesized and structurally characterized by single-crystal X-ray diffraction (XRD, Table 1) and NMR (see Supplementary Materials, Figures S1–S12). Figure 2 shows the ORTEP drawings obtained from XRD (left) alongside the corresponding geometries optimized by density functional theory (DFT) calculations. Geometry optimizations were performed with the ORCA 6.0.0 program package using the B3LYP functional and the def2-TZVP basis set for all atoms, together with the RIJCOSX approximation and the def2/J auxiliary basis set. Solvent effects were taken into account with the CPCM model (chloroform). As the optimized structures showed good agreement with the experimental geometries, the calculated structures were used for subsequent discussion of structural parameters (Table 2), particularly for locating hydrogen atoms. All complexes exhibit a unique three-dimensional conformation in which the bridging alkyl chain bends away from the coordination plane and reaches toward the axial region above the metal center.

Table 1.
Crystallographic data for 1–4.
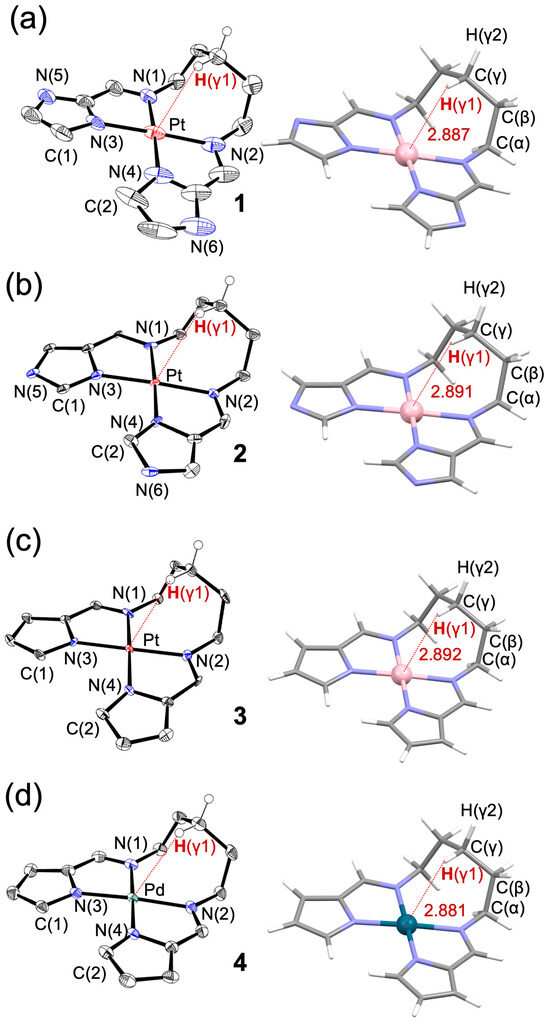
Figure 2.
ORTEP drawings (left) and DFT-optimized structures (right) of (a–d) 1–4, respectively. Thermal ellipsoids are shown at the 50% probability level. In the DFT structures, calculated at the B3LYP/TZVP level of theory, close contacts between the Pt or Pd center and the γ-position hydrogen H(γ) are highlighted by red dotted lines, with the corresponding distances in Å.

Table 2.
Selected structural parameters for complexes 1–4 optimized at the B3LYP/TZVP level [a].
The bond lengths between the metal center (Pt or Pd) and the coordinating nitrogen atoms were generally consistent across complexes 1–4. The distances to the neutral nitrogen atoms (N1 and N2) were approximately 2.09 Å, while those to the anionic nitrogen atoms (N3 and N4) were around 2.03 Å. The planarity of the coordination environment was assessed by examining the dihedral angles N3–Pt–N4–C2 and N4–Pt–N3–C1. In the imidazole-based complexes 1 and 2, the twist angles were close to 1°, indicating an almost planar geometry. In contrast, the pyrrole-based complexes 3 and 4 exhibited slightly larger dihedral angles of around 5°, suggesting a modest deviation from planarity.
Furthermore, in the propylene-bridged ligands, the γ-position C–H bond (H(γ1)) was found to be oriented toward the metal center in an unusual manner. In the DFT-optimized structures, the H(γ1)–M (Pt or Pd) distances were calculated to be 2.887, 2.891, 2.892, and 2.881 Å for complexes 1–4, respectively. These values are substantially shorter than the sum of the van der Waals radii for Pt–H (3.49 Å) and Pd–H (3.35 Å) [60]. Although the H(γ1)–M distance in Pd complex 4 is approximately 0.01 Å shorter than those in the Pt complexes 1–3, this difference becomes negligible when considering that the typical van der Waals contact distance for a Pd–H interaction is about 0.1 Å shorter than that for a Pt–H interaction. Thus, the slightly shorter distance in the Pd complex does not necessarily reflect a stronger interaction, and the Pt–H contacts in complexes 1–3 are likely more significant. These observations suggest the presence of an attractive interaction between the metal center and the γ-position hydrogen atom on the pentylene bridging chain. In contrast, such close M···H–C contacts are not observed in the shorter-chain analogs (chain length n = 3 or 4; see Figures S9 and S11), indicating that this interaction is chain-length dependent.
In the 1H NMR spectrum of 1 in CDCl3 (Figure 3a), the signals corresponding to the bridged alkyl chain appeared broadened, and no clear coupling patterns indicative of structural information were observed. Nonetheless, the α- and γ-protons were resolved as chemically nonequivalent signals, with the γ-protons in particular (H(γ1) and H(γ2)) exhibiting a pronounced difference in chemical shift. This nonequivalence can be explained by the molecular conformation revealed in the X-ray crystal structure, where the bridging alkyl chain is positioned above the platinum coordination plane and undergoes a dynamic flipping motion (Figure 3b). The flipping process interchanges the spatial relationship of the chain with respect to the coordination plane, thereby causing the coalescence of either the α- or the γ-proton signals into a single averaged resonance. Because each conformer has a sufficiently long lifetime at room temperature, the interconversion is slow on the NMR timescale, resulting in distinct, non-averaged signals for the γ-protons. Notably, the H(γ1) signal in 1 is significantly downfield-shifted due to its interaction with the platinum center, suggesting the presence of a hydrogen-bonding-type M···H–C interaction. Such nonequivalent protons were not observed in the shorter-chain analogs (chain length n = 3 or 4; see Figures S9 and S11).
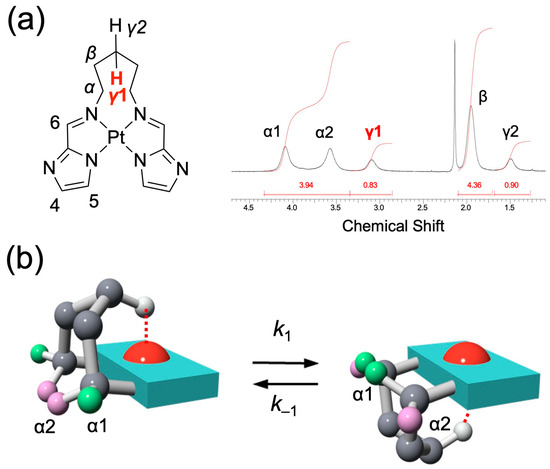
Figure 3.
(a) 1H NMR spectrum (aliphatic region) of 1 in CDCl3 at 298 K, showing distinct nonequivalent signals for H(α) and H(γ). (b) Schematic representations of two representative conformers of 1, where the polymethylene bridge flips above and below the coordination plane.
To further investigate the flipping motion of the bridging chain in 1, variable-temperature 1H NMR measurements were performed, focusing on the nonequivalent proton signals (Figure 4a, black traces). At 285 K, two distinct peaks corresponding to H(α1) and H(α2) were clearly observed, each with a different chemical shift. As the temperature increased, these peaks gradually broadened and eventually coalesced into a single broad peak at 301 K. This behavior is attributed to accelerated flipping motion of the bridging chain at elevated temperatures, leading to exchange between the environments of H(α1) and H(α2) and thus to signal averaging. The α-protons were chosen for quantitative analysis rather than the γ-protons, because the γ-signals, although clearly nonequivalent, become too broadened and weak near coalescence, making accurate rate constant determination unreliable. Similar temperature-dependent behavior was also observed for 2–4. To quantitatively analyze the peak broadening behavior, line shape simulations were performed at each temperature to determine the exchange rate constant k (Figure 4a, red traces). The simulated spectra showed good agreement with the experimental spectra at all temperatures, providing reliable values of the rate constant. Furthermore, an Eyring plot constructed using the obtained k values exhibited excellent linearity (R2 = 0.999), supporting the reliability of the activation parameters derived from the data (Figure 4b).
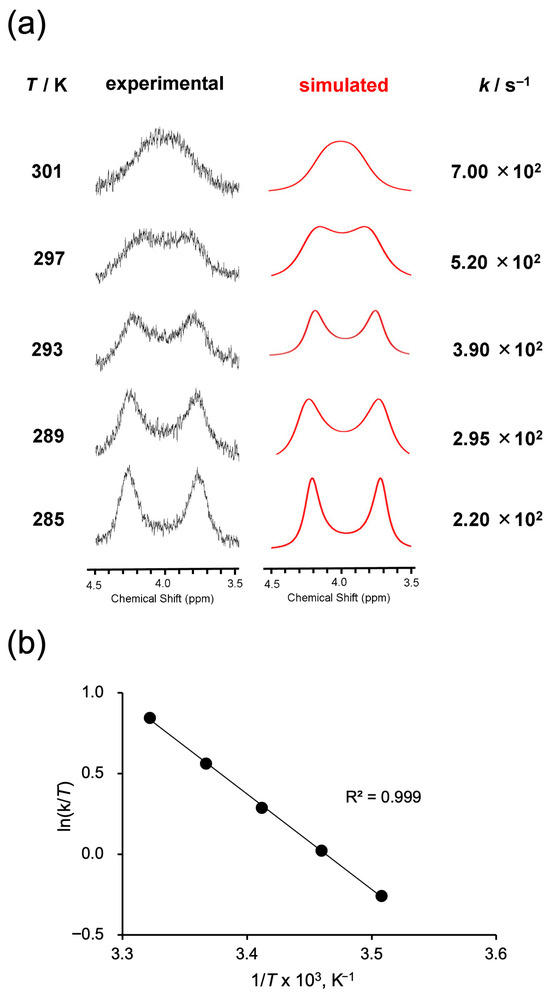
Figure 4.
(a) Variable-temperature 1H NMR spectra (black) of 1 recorded in CDCl3. The spectra exhibit coalescence behavior of the α-protons. Simulated line shapes (red) were fitted to determine exchange rate constants k at each temperature. (b) Eyring plot constructed from the temperature-dependent exchange rate constants obtained from (a).
From the variable-temperature 1H NMR line shape analysis and the resulting Eyring plots, activation parameters (ΔH‡, ΔS‡, and ΔG‡) for the flipping motion of the bridged alkyl chains in 1–4 were determined (Figure 5). The ΔH‡ values ranged from 49 to 51 kJ mol−1, with no significant differences observed within the experimental error. In contrast, all complexes exhibited negative ΔS‡ values (ranging from –27.6 to –14.1 J mol−1 K−1), indicating increased ordering in the transition state. Notably, the palladium complex 4 showed the smallest entropy change (ΔS‡ = –14.1 J mol−1 K−1), suggesting a more conformationally flexible transition state compared to the platinum analogs 1–3. The calculated ΔG‡ at 298 K ranged from 55 to 58 kJ mol−1, a variation that lies within the experimental uncertainty and thus cannot be considered significant. The fact that the difference in ΔS‡ for the Pd complex did not result in a distinguishable difference in ΔG‡ indicates a typical enthalpy–entropy compensation effect between ΔH‡ and ΔS‡ [61,62,63,64,65]. The smaller ΔS‡ value observed in the Pd complex is compensated by a higher ΔH‡ value, resulting in a ΔG‡ value that remains comparable to those of the Pt analogs.
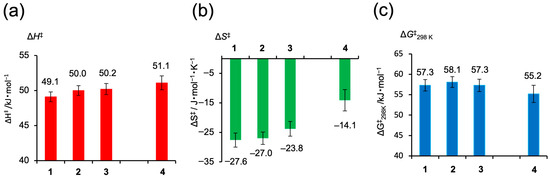
Figure 5.
Activation parameters derived from line-shape analysis of variable-temperature 1H NMR spectra for the flipping motion of the alkyl bridge in complexes 1–4. (a) Activation enthalpy (ΔH‡, red), (b) activation entropy (ΔS‡, green), and (c) Gibbs activation free energy at 298 K (ΔG‡, blue).
The distinct trend in ΔS‡ among the complexes implies that, in Pt complexes 1–3, the relatively strong Pt···H(γ1) interaction imposes structural constraints on the transition state, reducing its conformational freedom. In contrast, the weaker Pd–H interaction in complex 4 allows for greater flexibility in the transition state, leading to a smaller entropy loss. These findings suggest that the strength of the noncovalent metal–hydrogen interaction influences the dynamic behavior and activation profile of the bridged alkyl chain.
To evaluate the strength of the metal–hydrogen interactions, NBO and NCI analyses were performed on complexes 1–4 (Figure 6). In the NBO second-order perturbation analysis, carried out with the NBO7.0 program interfaced with ORCA 6.0.0, a stabilizing interaction of approximately 5.3–5.4 kJ mol−1 was observed in the Pt complexes 1–3 between a nonbonding dz2 orbital on the metal center and the antibonding orbital of the γ-position C–H bond on the bridging chain. In contrast, the corresponding interaction in the Pd complex 4 was significantly weaker, with an energy of only 2.3 kJ mol−1. Although these values are modest, they are consistent with the experimentally observed trend in ΔS‡, where the Pd complex shows a markedly smaller entropy change than the Pt analogs, suggesting that the M···H interaction contributes to the conformational restriction in the transition state. The NCI analysis, based on reduced density gradient (RDG) plots, was performed using Multiwfn 3.8 and visualized with VMD 1.9.4. It further revealed green isosurfaces between the metal center and the interacting hydrogen atom in all complexes, providing visual evidence of weak but definite noncovalent interactions. Together with the NBO analysis, which offered a quantitative estimate of interaction strength, these results demonstrate that the metal–hydrogen contacts can be visually identified as weak noncovalent interactions.
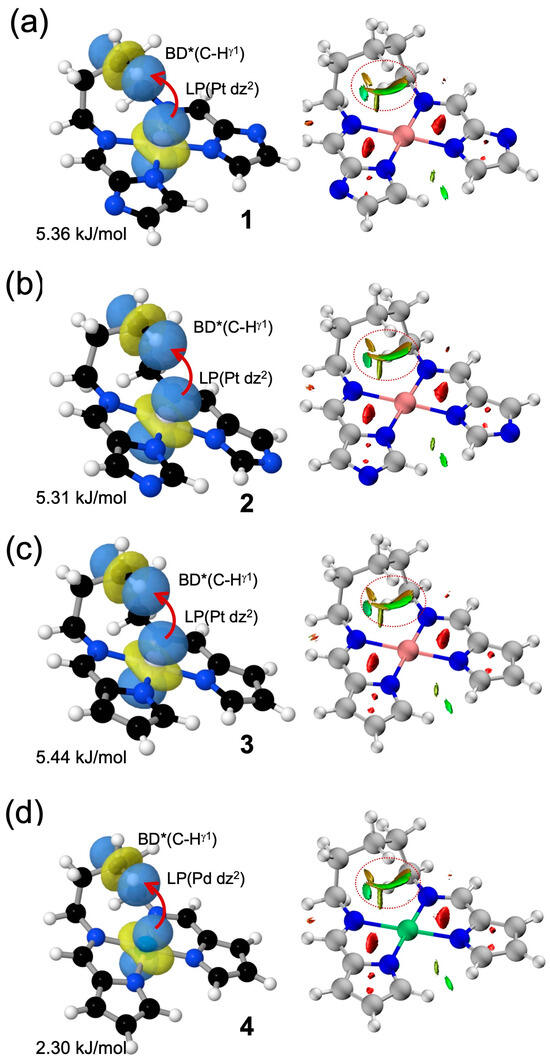
Figure 6.
Computational analysis of weak metal–hydrogen interactions in (a–d) 1–4. Left panels: Representative NBO illustrating the interaction between the metal-centered lone pair (LP; dz2 orbital) and the antibonding orbital of the γ-positioned C–H bond [BD* (C–Hγ1)], along with their corresponding second-order perturbation energies. Right panels: NCI (Non-Covalent Interaction) plots showing the reduced density gradient (RDG) mapped onto isosurfaces. Green surfaces represent weak attractive interactions consistent with through-space Pt···H (or Pd···H) contacts. Red circles highlight the regions of Pt···H (or Pd···H) interactions.
To further investigate the relationship between the enthalpic and entropic components of the flipping motion, an enthalpy–entropy compensation analysis was conducted using the thermodynamic parameters obtained from variable-temperature 1H NMR line-shape analyses in various solvents (Figure 7). A clear linear correlation between ΔH‡ and TΔS‡ at 298 K was observed, indicating that despite variations in enthalpy and entropy, the activation free energy barrier (ΔG‡) remains relatively constant. This behavior reflects a typical enthalpy–entropy compensation phenomenon, suggesting that the structure of the transition state is modulated by a balance between conformational order and noncovalent M···H interaction strength. Moreover, the fact that all data points fall on a single compensation line indicates that the observed flipping motions share a common mechanistic origin and belong to a related dynamic regime.
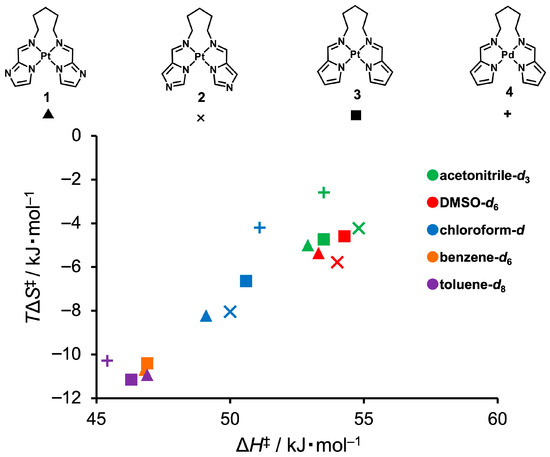
Figure 7.
Enthalpy–entropy compensation plot for the flipping dynamics of complexes 1–4, obtained from variable-temperature 1H NMR line-shape analysis at 298 K. Marker shapes represent different complexes (▲: 1, ×: 2, ■: 3, +: 4), and marker colors indicate the deuterated solvents used (green: acetonitrile-d3, red: DMSO-d6, blue: chloroform-d, orange: benzene-d6, purple: toluene-d8).
Notably, the Pd-containing complex, denoted by the “+” symbol in Figure 7, is positioned noticeably higher than the other related data points along the vertical axis (TΔS‡). This clearly indicates a smaller absolute value of entropy change (ΔS‡), suggesting a more conformationally flexible transition state in Pd complex 4. This trend aligns well with the weaker Pd–H interactions inferred from both the structural parameters and NBO analysis. These results underscore that even weak noncovalent interactions can modulate the dynamic behavior of flexible molecular frameworks, although their energetic contributions may be obscured by enthalpy–entropy compensation effects.
4. Conclusions
In this study, we investigated the role of hydrogen bond-like M···H–C interactions in the flipping motion of the bridging alkyl chain in cis-[N,N′-pentamethylenebis(iminomethylazolato)]Pt(II)/Pd(II) complexes by combining single-crystal X-ray diffraction, variable-temperature 1H NMR, NBO, and NCI analyses. Variable-temperature 1H NMR measurements confirmed the presence of a thermally activated flipping motion, and the corresponding activation parameters were extracted from Eyring analysis. Notably, a significant difference was observed in ΔS‡, with the Pd complex exhibiting the smallest entropy loss, suggesting a more flexible transition state. The results revealed that Pt–H interactions increase the entropic cost of the flipping process by imposing conformational constraints, whereas the weaker Pd–H interactions allow for greater conformational freedom. However, these effects are offset by corresponding enthalpy changes, resulting in comparable activation free energies (ΔG‡) across the series, consistent with an enthalpy–entropy compensation mechanism.
To further assess the nature and strength of the metal–hydrogen interactions, NBO and NCI analyses were performed. The NBO second-order perturbation analysis identified a weak but non-negligible stabilizing interaction (5.3–5.4 kJ mol−1) between the Pt center and the γ-position C–H bond in 1–3, whereas the corresponding interaction in the Pd complex 4 was substantially weaker (2.3 kJ mol−1). In parallel, the NCI analysis provided visual confirmation of these interactions through characteristic RDG isosurfaces between the metal center and the interacting hydrogen atom. Taken together, these computational results confirm the presence of weak but significant M···H–C interactions that modulate conformational dynamics. This highlights the potential of hydrogen-bond-type M···H–C interaction as a design element for controlling molecular motion in flexible systems. Attempts to locate a discrete transition state structure by quantum chemical calculations were unsuccessful, likely due to the conformational flexibility of the alkyl chain. We regard this as an important subject for future investigation, which will require more advanced sampling approaches.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/appliedchem5040025/s1, Figure S1: 1H NMR spectra (500 MHz) of 1 in CDCl3; Figure S2: 13C NMR spectra (125 MHz) of 1 in CDCl3; Figure S3: 1H NMR spectra (500 MHz) of 2 in CDCl3; Figure S4: 13C NMR spectra (125 MHz) of 2 in CDCl3; Figure S5: 1H NMR spectra (500 MHz) of 3 in CDCl3; Figure S6: 13C NMR spectra (125 MHz) of 3 in CDCl3; Figure S7: 1H NMR spectra (500 MHz) of 4 in CDCl3; Figure S8: 13C NMR spectra (125 MHz) of 4 in CDCl3; Figure S9: 1H NMR spectra (500 MHz) of 1′ in CDCl3; Figure S10: 13C NMR spectra (125 MHz) of 1′ in CDCl3; Figure S11: 1H NMR spectra (500 MHz) of 1″ in CDCl3; Figure S12: 13C NMR spectra (125 MHz) of 1″ in CDCl3.
Author Contributions
Conceptualization, N.H.-T.L., S.K. and T.N.; methodology, M.N. and N.H.-T.L.; software, S.K.; validation, S.K.; formal analysis, M.N., N.H.-T.L. and S.K.; investigation, M.N., N.H.-T.L. and K.N.; data curation, S.K., M.N. and N.H.-T.L.; writing—original draft preparation, S.K.; writing—review and editing, S.K.; visualization, M.N. and S.K.; supervision, T.N.; project administration, T.N.; funding acquisition, S.K. and T.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by a Kakenhi Grant-in-Aid (No. JP20H02753) (T.N.) from the Japan Society for the Promotion of Science (JSPS), the Iketani Science and Technology Foundation (S.K.), the Toyota Physical and Chemical Research Institute (S.K.), and the Chubei Itoh Foundation (S.K.).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article. Computational input and output files supporting the conclusions of this article are openly available in Zenodo at 10.5281/zenodo.16899726. Further inquiries can be directed to the corresponding authors.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Brookhart, M.; Green, M.L.H.; Parkin, G. Agostic Interactions in Transition Metal Compounds. Proc. Natl. Acad. Sci. USA 2007, 104, 6908–6914. [Google Scholar] [CrossRef]
- Brammer, L. Metals and Hydrogen Bonds. Dalton Trans. 2003, 3145–3157. [Google Scholar] [CrossRef]
- Brookhart, M.; Green, M.L.H. Carbon-Hydrogen-Transition Metal Bonds. J. Organomet. Chem. 1983, 250, 395–408. [Google Scholar] [CrossRef]
- Dawoodi, Z.; Green, M.L.H.; Mtetwa, V.S.B.; Prout, K.; Schultz, A.J.; Williams, J.M.; Koetzle, T.F. Evidence for Carbon–Hydrogen–Titanium Interactions: Synthesis and Crystal Structures of the Agostic Alkyls [TiCl3(Me2PCH2CH2PMe2)R] (R = Et or Me). J. Chem. Soc. Dalton Trans. 1986, 1629–1637. [Google Scholar] [CrossRef]
- Brookhart, M.; Green, M.L.H.; Pardy, R.B.A. Two-Electron, Three-Centre Carbon–Hydrogen–Cobalt Bonds in the Compounds [Co(η-C5Me4R)(η-C2H4)(η-C2H4-µ-H)]BF4, R = Me and Et. J. Chem. Soc. Chem. Commun. 1983, 691–693. [Google Scholar] [CrossRef]
- Brookhart, M.; Lamanna, W.; Humphrey, M.B. Structural Characterization and Fluxional Behavior of Cyclohexenylmanganese Tricarbonyl. Intramolecular Carbon-Hydrogen Bond Activation via a 2-Electron, 3-Center Manganese...Hydrogen...Carbon Interaction. J. Am. Chem. Soc. 1982, 104, 2117–2126. [Google Scholar] [CrossRef]
- Dawoodi, Z.; Green, M.L.H.; Mtetwa, V.S.B.; Prout, K. Evidence for a Direct Bonding Interaction Between Titanium and a β-C–H Moiety in a Titanium–Ethyl Compound; X-ray Crystal Structure of [Ti(Me2PCH2CH2PMe2)EtCl3]. J. Chem. Soc. Chem. Commun. 1982, 802–803. [Google Scholar] [CrossRef]
- Altus, K.M.; Love, J.A. The Continuum of Carbon–Hydrogen (C–H) Activation Mechanisms and Terminology. Commun. Chem. 2021, 4, 173. [Google Scholar] [CrossRef]
- Xu, H.; White, P.B.; Hu, C.; Diao, T. Structure and Isotope Effects of the β-H Agostic (α-Diimine) Nickel Cation as a Polymerization Intermediate. Angew. Chem. Int. Ed. 2017, 56, 1535–1538. [Google Scholar] [CrossRef]
- Grubbs, R.H.; Coates, G.W. α-Agostic Interactions and Olefin Insertion in Metallocene Polymerization Catalysts. Acc. Chem. Res. 1996, 29, 85–93. [Google Scholar] [CrossRef]
- Talarico, G.; Budzelaar, P.H.M. α-Agostic Interactions and Growing Chain Orientation for Olefin Polymerization Catalysts. Organometallics 2016, 35, 47–54. [Google Scholar] [CrossRef]
- Sajjad, M.A.; Christensen, K.E.; Rees, N.H.; Schwerdtfeger, P.; Harrison, J.A.; Nielson, A.J. Chasing the Agostic Interaction in Ligand Assisted Cyclometallation Reactions of Palladium(II). Dalton Trans. 2017, 46, 16126–16138. [Google Scholar] [CrossRef]
- Beck, R.; Camadanli, S.; Klein, H. Spontaneous Bicyclometalation of a Single Cobalt(I) Complex Stabilized by a δ-C–H Agostic Interaction. Eur. J. Inorg. Chem. 2018, 2018, 608–611. [Google Scholar] [CrossRef]
- Yao, W.; Eisenstein, O.; Crabtree, R.H. Interactions Between C–H and N–H Bonds and d8 Square Planar Metal Complexes: Hydrogen Bonded or Agostic? Inorg. Chim. Acta 1997, 254, 105–111. [Google Scholar] [CrossRef]
- Braga, D.; Grepioni, F.; Tedesco, E.; Biradha, K.; Desiraju, G.R. Hydrogen Bonding in Organometallic Crystals. 6. X−H---M Hydrogen Bonds and M---(H−X) Pseudo-Agostic Bonds. Organometallics 1997, 16, 1846–1856. [Google Scholar] [CrossRef]
- Sini, G.; Eisenstein, O.; Yao, W.; Crabtree, R.H. Intermolecular Re–H·H–X Hydrogen Bonding (X =N, C) Involving ReH5(PPh3)3. Inorg. Chim. Acta 1998, 280, 26–29. [Google Scholar] [CrossRef]
- Zhang, Y.; Lewis, J.C.; Bergman, R.G.; Ellman, J.A.; Oldfield, E. NMR Shifts, Orbitals, and M···H−X Bonding in d8 Square Planar Metal Complexes. Organometallics 2006, 25, 3515–3519. [Google Scholar] [CrossRef]
- Scherer, W.; Dunbar, A.C.; Barquera-Lozada, J.E.; Schmitz, D.; Eickerling, G.; Kratzert, D.; Stalke, D.; Lanza, A.; Macchi, P.; Casati, N.P.M.; et al. Anagostic Interactions under Pressure: Attractive or Repulsive? Angew. Chem. Int. Ed. 2015, 54, 2505–2509. [Google Scholar] [CrossRef]
- Komiya, N.; Hosokawa, T.; Adachi, J.; Inoue, R.; Kawamorita, S.; Naota, T. Regiospecific Remote Pt–H Interactions in Oligomethylene-Vaulted (N^C^N)-Pincer PtII Complexes. Eur. J. Inorg. Chem. 2018, 2018, 4771–4778. [Google Scholar] [CrossRef]
- Schmitz, D.; Kalter, M.; Dunbar, A.C.; Vöst, M.; Fischer, A.; Batke, K.; Eickerling, G.; Ruhland, K.; Ebad-Allah, J.; Kuntscher, C.; et al. Pressure-Enhanced C–H Bond Activation in Chloromethane Platinum(II) Complexes. Eur. J. Inorg. Chem. 2020, 2020, 79–83. [Google Scholar] [CrossRef]
- Iglesias-Sigüenza, J.; Ros, A.; Díez, E.; Alcarazo, M.; Álvarez, E.; Fernández, R.; Lassaletta, J.M. Synthesis, Structure and Properties of [1,2,4]Triazolo[4,3-a]Pyridin-3-Ylidene Rhodium and Palladium Complexes. Dalton Trans. 2009, 7113–7120. [Google Scholar] [CrossRef]
- Teci, M.; Brenner, E.; Matt, D.; Toupet, L. N-Heterocyclic Carbenes Functioning as Monoligating Clamps. Eur. J. Inorg. Chem. 2013, 2013, 2841–2848. [Google Scholar] [CrossRef]
- Teci, M.; Brenner, E.; Matt, D.; Gourlaouen, C.; Toupet, L. N-Alkylfluorenyl-Substituted N-Heterocyclic Carbenes as Bimodal Pincers. Dalton Trans. 2015, 44, 9260–9268. [Google Scholar] [CrossRef]
- Race, J.J.; Burnage, A.L.; Boyd, T.M.; Heyam, A.; Martínez-Martínez, A.J.; Macgregor, S.A.; Weller, A.S. ortho-Aryl Substituted DPEphos Ligands: Rhodium Complexes Featuring C–H Anagostic Interactions and B–H Agostic Bonds. Chem. Sci. 2021, 12, 8832–8843. [Google Scholar] [CrossRef]
- Lagunas-Simón, B.; González-Montiel, S.; Salazar-Pereda, V.; Vásquez-Pérez, J.M.; Cruz-Borbolla, J. An Structural Study of Pt•••Hδ–C(Sp3) Anagostic Interaction in Heteroscorpionate Complexes. J. Mol. Struct. 2024, 1300, 137289. [Google Scholar] [CrossRef]
- Bouley, B.S.; Garvey, I.J.; Na, H.; Byeong Chae, J.; Mirica, L.M. Anagostic Axial Interactions Inhibit Cross-Coupling Catalytic Activity in Square Planar Pyridinophane Nickel Complexes. ChemCatChem 2024, 16, e202301677. [Google Scholar] [CrossRef]
- Han, W.; Ryu, H.; Kang, C.; Hong, S. Chiral Biaryl N-Heterocyclic Carbene–Palladium Catalysts with Anagostic C–H···Pd Interaction for Enantioselective Desymmetric C–N Cross-Coupling. Org. Lett. 2024, 26, 9891–9896. [Google Scholar] [CrossRef] [PubMed]
- Komiya, N.; Okada, M.; Fukumoto, K.; Jomori, D.; Naota, T. Highly Phosphorescent Crystals of Vaulted trans-Bis(Salicylaldiminato)Platinum(II) Complexes. J. Am. Chem. Soc. 2011, 133, 6493–6496. [Google Scholar] [CrossRef] [PubMed]
- Komiya, N.; Muraoka, T.; Iida, M.; Miyanaga, M.; Takahashi, K.; Naota, T. Ultrasound-Induced Emission Enhancement Based on Structure-Dependent Homo- and Heterochiral Aggregations of Chiral Binuclear Platinum Complexes. J. Am. Chem. Soc. 2011, 133, 16054–16061. [Google Scholar] [CrossRef]
- Naito, M.; Souda, H.; Koori, H.; Komiya, N.; Naota, T. Binuclear trans-Bis(Β-iminoaryloxy)Palladium(II) Complexes Doubly Linked with Pentamethylene Spacers: Structure-Dependent Flapping Motion and Heterochiral Association Behavior of the Clothespin-Shaped Molecules. Chem. Eur. J. 2014, 20, 6991–7000. [Google Scholar] [CrossRef]
- Naito, M.; Inoue, R.; Iida, M.; Kuwajima, Y.; Kawamorita, S.; Komiya, N.; Naota, T. Control of Metal Arrays Based on Heterometallics Masquerading in Heterochiral Aggregations of Chiral Clothespin-Shaped Complexes. Chem. Eur. J. 2015, 21, 12927–12939. [Google Scholar] [CrossRef] [PubMed]
- Inoue, R.; Kawamorita, S.; Naota, T. Single-Point Remote Control of Flapping Motion in Clothespin-Shaped Bimetallic Palladium Complexes Based on the N(Sp2)–N(Sp3) Interconversion in Amide Functionalities. Chem. Eur. J. 2016, 22, 5712–5726. [Google Scholar] [CrossRef]
- Matsuoka, T.; Li, Z.; Ikeshita, M.; Kawamorita, S.; Naota, T. Linker Length Dependence of the Chromogenic Properties of Polymethylene-Vaulted trans-Bis(2-Aminotroponato)Palladium(II) Complexes. J. Mol. Struct. 2018, 1165, 217–222. [Google Scholar] [CrossRef]
- Le, N.H.-T.; Inoue, R.; Kawamorita, S.; Komiya, N.; Naota, T. Phosphorescent Molecules That Resist Concentration Quenching in the Solution State: Concentration-Driven Emission Enhancement of Vaulted trans-Bis[2-(Iminomethyl)Imidazolato]Platinum(II) Complexes. Inorg. Chem. 2019, 58, 9076–9084. [Google Scholar] [CrossRef]
- Adachi, J.; Mori, T.; Inoue, R.; Naito, M.; Le, N.H.; Kawamorita, S.; Hill, J.P.; Naota, T.; Ariga, K. Emission Control by Molecular Manipulation of Double-Paddled Binuclear PtII Complexes at the Air-Water Interface. Chem. Asian J. 2020, 15, 406–414. [Google Scholar] [CrossRef] [PubMed]
- Adachi, J.; Naito, M.; Sugiura, S.; Le, N.H.-T.; Nishimura, S.; Huang, S.; Suzuki, S.; Kawamorita, S.; Komiya, N.; Hill, J.P.; et al. Coordination Amphiphile: Design of Planar-Coordinated Platinum Complexes for Monolayer Formation at an Air-Water Interface Based on Ligand Characteristics and Molecular Topology. Bull. Chem. Soc. Jpn. 2022, 95, 889–897. [Google Scholar] [CrossRef]
- Ikeshita, M.; Hara, N.; Imai, Y.; Naota, T. Chiroptical Response Control of Planar and Axially Chiral Polymethylene-Vaulted Platinum(II) Complexes Bearing 1,1′-Binaphthyl Frameworks. Inorg. Chem. 2023, 62, 13964–13976. [Google Scholar] [CrossRef]
- Ikeshita, M.; Ma, S.C.; Muller, G.; Naota, T. Linker-Dependent Control of the Chiroptical Properties of Polymethylene-Vaulted trans-Bis[(β-Iminomethyl)Naphthoxy]Platinum(II) Complexes. Dalton Trans. 2024, 53, 7775–7787. [Google Scholar] [CrossRef]
- Ikeshita, M.; Takahashi, K.; Hara, N.; Kawamorita, S.; Komiya, N.; Imai, Y.; Naota, T. Ultrasound-induced Circularly Polarized Luminescence Based on Homochiral Aggregation of Clothespin-shaped Pt(II) Complexes. Responsive Mater. 2024, 2, e20240017. [Google Scholar] [CrossRef]
- Kawamorita, S.; Huang, S.; Yoshida, A.; Suzuki, S.; Naota, T. Aggregation-Induced Phosphorescence of a trans-Bis(iminomethylpyrolato)platinum Complex Bearing a Polymethylene Vaulted Structure: Chain Length–Dependent Solid-State Emission. Chem. Eur. J. 2025, 31, e01670. [Google Scholar] [CrossRef]
- Sauvage, J.-P. Molecular Machines and Motors; Springer: Berlin, Germany, 2001. [Google Scholar]
- Tashiro, K.; Konishi, K.; Aida, T. Metal Bisporphyrinate Double-Decker Complexes as Redox-Responsive Rotating Modules. Studies on Ligand Rotation Activities of the Reduced and Oxidized Forms Using Chirality as a Probe. J. Am. Chem. Soc. 2000, 122, 7921–7926. [Google Scholar] [CrossRef]
- Huang, C.-Y.; Klemke, J.W.; Getahun, Z.; DeGrado, W.F.; Gai, F. Temperature-Dependent Helix−Coil Transition of an Alanine Based Peptide. J. Am. Chem. Soc. 2001, 123, 9235–9238. [Google Scholar] [CrossRef]
- Hiraoka, S.; Shiro, M.; Shionoya, M. Heterotopic Assemblage of Two Different Disk-Shaped Ligands through Trinuclear Silver(I) Complexation: Ligand Exchange-Driven Molecular Motion. J. Am. Chem. Soc. 2004, 126, 1214–1218. [Google Scholar] [CrossRef]
- Muraoka, T.; Kinbara, K.; Aida, T. Mechanical Twisting of a Guest by a Photoresponsive Host. Nature 2006, 440, 512–515. [Google Scholar] [CrossRef]
- Nawara, A.J.; Shima, T.; Hampel, F.; Gladysz, J.A. Gyroscope-like Molecules Consisting of PdX2 /PtX2 Rotators Encased in Three-Spoke Stators: Synthesis via Alkene Metathesis, and Facile Substitution and Demetalation. J. Am. Chem. Soc. 2006, 128, 4962–4963. [Google Scholar] [CrossRef]
- Ihalainen, J.A.; Bredenbeck, J.; Pfister, R.; Helbing, J.; Chi, L.; Van Stokkum, I.H.M.; Woolley, G.A.; Hamm, P. Folding and Unfolding of a Photoswitchable Peptide from Picoseconds to Microseconds. Proc. Natl. Acad. Sci. USA 2007, 104, 5383–5388. [Google Scholar] [CrossRef]
- Balzani, V.; Credi, A.; Venturi, M. Molecular Devices and Machines: Concepts and Perspectives for the Nanoworld, 1st ed.; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2008. [Google Scholar]
- Feringa, B.L.; Browne, W.R. (Eds.) Molecular Switches, 1st ed.; Wiley-VCH & Co. KGaA: Weinheim, Germany, 2011. [Google Scholar]
- Rodríguez-Molina, B.; Pérez-Estrada, S.; Garcia-Garibay, M.A. Amphidynamic Crystals of a Steroidal Bicyclo[2.2.2]Octane Rotor: A High Symmetry Group That Rotates Faster than Smaller Methyl and Methoxy Groups. J. Am. Chem. Soc. 2013, 135, 10388–10395. [Google Scholar] [CrossRef]
- Johnson, C.K. ORTEP: A Fortran Thermal-Ellipsoid Plot Program for Crystal Structure Illustrations; Report ORNL-3794; Oak Ridge National Laboratory: Oak Ridge, TN, USA, 1965. [Google Scholar] [CrossRef]
- Burnett, M.N.; Johnson, C.K. ORTEP-III: Oak Ridge Thermal Ellipsoid Plot Program for Crystal Structure Illustrations; Report ORNL-6895; Oak Ridge National Laboratory: Oak Ridge, TN, USA, 1996. [Google Scholar] [CrossRef]
- Neese, F.; Wennmohs, F.; Becker, U.; Riplinger, C. The ORCA Quantum Chemistry Program Package. J. Chem. Phys. 2020, 152, 224108. [Google Scholar] [CrossRef] [PubMed]
- Becke, A.D. Density-Functional Thermochemistry. III. The Role of Exact Exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Weigend, F.; Ahlrichs, R. Balanced Basis Sets of Split Valence, Triple Zeta Valence and Quadruple Zeta Valence Quality for H to Rn: Design and Assessment of Accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef] [PubMed]
- Glendening, E.D.; Landis, C.R.; Weinhold, F. NBO 7.0; Theoretical Chemistry Institute, University of Wisconsin: Madison, WI, USA, 2018. [Google Scholar]
- Johnson, E.R.; Keinan, S.; Mori-Sánchez, P.; Contreras-García, J.; Cohen, A.J.; Yang, W. Revealing Noncovalent Interactions. J. Am. Chem. Soc. 2010, 132, 6498–6506. [Google Scholar] [CrossRef] [PubMed]
- Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef] [PubMed]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD–Visual Molecular Dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Alvarez, S. A Cartography of the van Der Waals Territories. Dalton Trans. 2013, 42, 8617–8636. [Google Scholar] [CrossRef]
- Liu, L.; Guo, Q.-X. Isokinetic Relationship, Isoequilibrium Relationship, and Enthalpy−Entropy Compensation. Chem. Rev. 2001, 101, 673–696. [Google Scholar] [CrossRef]
- Rekharsky, M.V.; Mori, T.; Yang, C.; Ko, Y.H.; Selvapalam, N.; Kim, H.; Sobransingh, D.; Kaifer, A.E.; Liu, S.; Isaacs, L.; et al. A Synthetic Host-Guest System Achieves Avidin-Biotin Affinity by Overcoming Enthalpy–Entropy Compensation. Proc. Natl. Acad. Sci. USA 2007, 104, 20737–20742. [Google Scholar] [CrossRef] [PubMed]
- Chodera, J.D.; Mobley, D.L. Entropy-Enthalpy Compensation: Role and Ramifications in Biomolecular Ligand Recognition and Design. Annu. Rev. Biophys. 2013, 42, 121–142. [Google Scholar] [CrossRef]
- Ryde, U. A Fundamental View of Enthalpy–Entropy Compensation. Med. Chem. Commun. 2014, 5, 1324–1336. [Google Scholar] [CrossRef]
- Peccati, F.; Jiménez-Osés, G. Enthalpy–Entropy Compensation in Biomolecular Recognition: A Computational Perspective. ACS Omega 2021, 6, 11122–11130. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).