Abstract
Rotating electrical machine maintenance is a core component of engineering education curricula worldwide. Within this context, vibration monitoring represents a widespread methodology for electrical rotating machinery monitoring. However, the multi-physical nature of vibration monitoring presents a complex learning scenario, including concepts from both mechanical and electrical engineering domains. This article proposes a novel knowledge-based educational experience design leveraging an integrated FEA-assisted test bench aimed at comprehensively addressing the electromechanical link between stator current and frame vibration. To this aim, a Finite Element Analysis (FEA) model is utilized to link excitation electrical signals with airgap radial forces acting in the stator. The subsequent correlation of these FEA predictions with measured frame vibrations on a physical test bench provides students with the theoretical concepts and practical tools to adequately comprehend this complex multi-physical phenomenon of wide application in real industrial scenarios. The pedagogical potential of the method also includes the development of critical thinking and problem-solving soft skills, and foundational understanding for digital twin concepts. A Delphi-style expert survey conducted with 25 specialists yielded strong support for the pedagogical robustness and relevance of the method, with mean ratings between 4.32 and 4.64 out of 5 across key dimensions. These results confirm the potential to enhance deep understanding and practical skills in vibration-based electrical machine diagnosis.
1. Introduction
In various economic sectors such as automotive, energy, and industry, there is a growing focus on electrifying numerous applications. While rotating electrical machines are reliable for electromechanical energy conversion, they are still prone to failures, presenting a significant maintenance challenge [1]. The consequences of machine failures can be severe, leading to substantial economic costs and risking operational safety. Traditionally, maintenance has been carried out periodically or reactively, waiting until a failure occurs. However, new maintenance strategies are emerging to address the limitations of these approaches. Predictive maintenance, also known as condition-based maintenance, allows for continuous monitoring of machinery, reducing downtime and preventing critical failures that could compromise safety [2]. This monitoring involves gathering and analyzing various physical parameters such as vibrations, temperature, and phase current using appropriate tools [3]. There is ongoing extensive research in both academia and industry aimed at advancing predictive maintenance techniques. Additionally, university curricula increasingly incorporate specialized courses on this topic.
Works on electrical machinery maintenance education are found in the literature, where the authors highlight the presence of maintenance courses in different engineering curricula [4]. These courses partially address machine monitoring via frame vibrations, which represents a widespread industrial technique to detect and diagnose several faults [5]. Mechanical signals (e.g., vibrations) in electrical machines possess an inherent multi-physical nature, including concepts of mechanical and electrical engineering. Thus, the understanding of electromagnetically excited vibrations for diagnosis purposes poses an educational challenge [6]. To aid in the understanding of electrical machine electromagnetic-borne vibration, a hybrid practical approach is proposed including the exploration of a real induction motor specimen together with its virtual model. This is achieved through practical sessions including both Finite Element Analysis (FEA) modeling and laboratory signal acquisition and analysis. The present manuscript significantly extends the work presented in [7] by (i) significantly expanding the technical content of the methodology; (ii) providing the complete educational framework within existing theories; (iii) deeply discussing the expected pedagogical features with an early validation of the main outcomes; (iv) providing insights regarding scalability, limitations, and future work on the topic.
The work is organized as follows. Section 2 poses the main theoretical basis for knowledge construction and the specifics of the educational context. Section 3 meticulously describes the proposed methodology including the demonstration of the main technical outcomes. Section 4 discusses the expected pedagogical outcomes including a Delphi survey validation based on an expert panel. Moreover limitations and scalability aspects are discussed in this section. Section 5 closes the work and provides future steps of this research to be implemented in future stages.
2. Educational Context and Theoretical Background
2.1. Theoretical Background and Literature Review
The present section is aimed at describing the theoretical educational theories that frame the proposed learning methodology and performing a thorough literature review of related methodologies. Specifically, this section will detail the pedagogical principles that underpin the design and expected effectiveness of the FEA-assisted test bench, grounding the approach in established educational research.
At the broadest philosophical level, the proposed methodology is deeply rooted in constructivism, the theory asserting that learners actively build their own understanding and knowledge by making sense of new information in light of their existing cognitive frameworks, rather than passively receiving it [8,9]. This foundational principle naturally leads to the adoption of active learning strategies, which encompass any instructional method requiring students to engage in meaningful activities and critical thinking about what they are doing [10,11].
In this context, experiential learning has emerged as a significant area of pedagogical development over the past several decades, extending beyond engineering into a wide range of academic disciplines [12]. This approach represents a shift from traditional didactic methods, such as lecture-based instruction, towards a more active, student-centered learning experience [13]. By engaging learners directly in tasks and activities that reinforce theoretical concepts, experiential learning has been shown to enhance both understanding and retention. Although long embedded in engineering education, interest in experiential learning has recently intensified, reflecting broader trends in higher education [14]. Building upon the principles of experiential learning, which states that knowledge is actively constructed through a cyclical process of concrete experience, reflective observation, abstract conceptualization, and active experimentation, problem-based learning (PBL) emerges as a highly effective pedagogical methodology [15,16]. PBL provides a structured framework where students engage with complex, authentic problems that serve as the initial concrete experience. This problem then drives the entire learning process, compelling students to actively seek out and apply knowledge (i.e., active experimentation), critically analyze information (i.e., reflective observation), and develop deeper theoretical understanding (i.e., abstract conceptualization) as they work towards a solution [17]. In this way, PBL inherently integrates the core principles of experiential learning, enhancing critical thinking, problem-solving skills, and a deeper, contextually relevant comprehension of the subject matter. Figure 1 illustrates the pedagogic framework of the proposed learning experience.

Figure 1.
Pedagogic framework of the proposed learning experience.
PBL is often integrated within engineering curricula, which provide students with the fundamental principles and core knowledge necessary for professional practice [18]. While continued professional experience will further develop and refine this knowledge, the initial engineering education plays a critical role in establishing a solid base upon which future learning and professional growth are built [19]. Some examples of PBL in engineering education can be found in [20,21,22]. Specifically, several authors explored the integration of simulation and virtual tools to enhance PBL in the engineering context. This integration brings significant advantages such as increased engagement and motivation, enhanced critical thinking and reflection, improved conceptual understanding, and increased access and safety during the experiences [23]. Additionally, this integration mirrors authentic engineering teamwork by fostering collaborative problem-solving, and contextualized simulated environments are used as PBL effectively bridging the gap between classroom and professional practice [24]. Some notorious examples of simulation and virtual integration for engineering education are found in recent literature. Terkaj et al. [25] present a Virtual Reality (VR) learning factory designed for industrial engineering labs. The immersive environment enables students to simulate manufacturing systems, fostering hands-on learning in a safe, fully controlled setting. Norambuena et al. [26] explore multi-user VR labs with digital twins for topics like fluid mechanics and thermodynamics. Students collaboratively manipulate virtual equipment in real time, promoting authentic interaction in teaching and technical skill development. In [27] the authors propose real-world thermal experiments with simulated scenarios and a VR visualization of the actual lab. Students use Comsol/Unreal Engine to set up thermographic tests, receive real-time feedback, and interact within a 3D digital replica of the laboratory workspace, bridging simulation and physical learning experiences. Some PBL learning examples utilizing FEA analysis are found in recent literature, where students apply ANSYS to solve real-world problems [28]. This hybrid approach combines structured instruction with hands-on simulation in a professional software environment, promoting engagement and mastery of FEA principles.
The integration of simulations and VR tools for PBL is also utilized to strengthen the understanding of multiphysics concepts. These simulation tools allow students to model and simulate real-world systems that involve complex multiphysics interactions [29,30]. By adjusting parameters and observing outcomes in a controlled virtual environment, students can explore the effects of various factors on system behavior, enhancing their understanding of underlying principles at a reduced economic cost and in a safe environment [31]. Several recent examples of simulation-assisted engineering educational experiences focused on a better understanding of underlying physical principles are found in [32,33,34].
In the field of electrical machines and drives education, it is usual to find PBL methodologies in education curricula [21,35]. Education in electrical machines and drives takes advantage of interactive models to integrate control algorithms, power electronics, and rotating electrical machines in a safe manner [36,37,38,39]. The sole virtual experimentation to understand the basic principles of control algorithms constitutes a stand-alone experience [40]. Experimental experiences on electrical machines present significant challenges, including increased maintenance requirements, critical safety risks, and limitations in acquiring certain physical quantities. Nevertheless, some authors propose tools to aid in the understanding of real laboratory experiments. VR tools for education in electrical machines are utilized in [41], where the authors describe a VR-based training tool using Oculus Go for hands-on assembly, disassembly, and performance testing of electrical machines. Checa et al. [42] propose a virtual laboratory to provide a safe environment in electrical machine maintenance courses. Moreover, the utilization of virtual resources for laboratory sessions is present in the literature, even if not widespread [43,44]. Romero et al. [45] describe the implementation of a virtual laboratory that enables broader experimentation in a safe environment. Practical virtual experiences on electrical machines through the utilization of FEA are found in literature [33], which allow the visualization of different electromagnetic fields within the experiments. In [46] the authors propose a simulation module complementing traditional induction motor labs. The combination of simulation and experiments is also present in the literature. Some authors propose methods focusing on the difference between experiments and FEA in electrical machines with the objective of bridging the empirical and theoretical knowledge gap [47,48]. Hybrid experiences combining real laboratory specimens with their virtual representation are gaining increased attention due to the emergence of Industry 4.0 and digital twin concepts as highlighted in [49,50]. Despite extensive research in electrical machine and drives education, the explicit educational integration of the electromagnetically induced vibration including virtual resources remains underexplored in the literature. Yet, deep comprehension of this coupled phenomenon is essential in electrical machine curricula, especially for maintenance and diagnostics-related courses. The integration of virtual tools in this context represents a key knowledge-focused asset to represent non-measurable physical quantities.
2.2. Educational Context and Learning Objectives
The conceived educational experience is initially motivated by different master’s courses in Universitat Politècnica de València (UPV). The first course is named “Maintenance of Electrical Machines and Installations”, which is included within an official UPV master’s degree named “Master on Maintenance Engineering”. This course includes a fundamental learning objective:
- Apply preventive and predictive maintenance techniques to industrial electrical machines and installations, leveraging appropriate instrumentation and analytical methods.
The second course is named “Electric Traction and Electrical Machine Technology”, included in the official UPV program “Master of Science in Industrial Engineering”. It encompasses a broad range of learning objectives, including those focused on testing and diagnosing electrical machines:
- Ability to design and test electrical machines.
- Develop and carry out practical or experimental projects and research, interpreting data and drawing conclusions grounded in the fundamental principles of the discipline.
The specific topics covered in both courses include motor current signature analysis, conducting partial discharge tests, and performing offline tests to assess insulation condition, among other techniques. These span from traditional maintenance practices, like corrective and breakdown maintenance, to advanced preventive and predictive methods. The latter are examined in depth, particularly focusing on modern electrical monitoring techniques. Vibration monitoring applied to electrical machines is sometimes neglected due to its inner complexity and the predominantly mechanical nature of such signals. Nevertheless, the present practical experience is engineered to bridge the knowledge gap between the mechanical and electrical worlds in the frame of education on electrical machine maintenance. The PBL experience is oriented to tackle a common industrial scenario, where induction motors are the most common machine type due to their outstanding cost/performance ratio. This method is intended to substantially contribute to the courses’ learning objectives and to boost student motivation and professional outlook. Specific pedagogical outcomes of the methodology are analyzed in Section 4.2.
3. Methodology
The present section represents the main core of the presented work. It introduces and details each part of the whole knowledge-based methodology including evaluation nuances. The study begins with a comprehensive presentation of the fundamental theoretical principles. Subsequently, the FEA model is introduced, enabling students to engage with a virtual representation of the machine specimen within a controlled and risk-free environment. The experimental component involves the acquisition of multiple signals during the actual operation of the induction motor under investigation. In the data processing phase, students analyze both the experimentally acquired signals and those derived from the FEA model. The method ends with a thorough evaluation of the results, upon which the students formulate well-supported conclusions regarding the conducted activities. Figure 2 shows the activity flow of the proposed knowledge-based pedagogical experience. The section ends by proposing an adaptable evaluation strategy.
Figure 2.
Overview of the proposed knowledge-based didactic experience.
3.1. Theoretical Knowledge
The present section is intended to set the main theoretical concepts prior to the session execution in a summarized way. Basic knowledge about induction machine working principles and constructive elements is assumed as a prerequisite. The presented formulation is based on a well-known reference book in the field of noise and vibrations of electrical machines [51]. The explanation of concepts is separated into electromagnetic and mechanical domains.
3.1.1. Electromagnetic Domain
An ideal system and a perfectly sinusoidal three-phase voltage wave exciting the stator winding are first assumed. Depending on the dynamic model of induction machine including stator and rotor resistances and inductances, stator phase current flows through the stator windings and rotor current is induced within the rotor bars [52]. A possible dynamic model in the three-phase reference frame of the machine is described by
where is a diagonal matrix containing the resistances of the stator and rotor windings, and represent the stator and rotor winding inductances respectively, represents stator and rotor voltages, is the current matrix containing the system output, represents the geometrical position along the airgap, and is the flux linkage of the machine winding. Stator and rotor current electrical frequencies are related through the slip, which is a basic induction machine parameter. Currents flowing within the stator and rotor conductors create an airgap magnetomotive force, which depends on the conductor distribution along the machine periphery and on the properties of the input wave . Thus, by assuming a fixed frequency stator current , two-dimensional rotor and stator magnetomotive force waves for -th and -th stator and rotor spatial harmonics, respectively, are defined as
where represents the rotor electrical frequency, Q is the number of rotor slots, s represents the slip, and p is the number of pole pairs. Note that these equations include backward and forward propagating waves.
The airgap geometry includes stator and rotor slots, while the ferromagnetic material is saturated along some sections of the airgap. These effects are accounted for by defining the airgap permeance function, which can be simplified as solely dependent on the airgap angle (). By multiplying the magnetomotive force sum and the permeance, the two-dimensional airgap flux density wave is obtained:
The airgap magnetic flux density wave can be separated into tangential and radial components. Tangential forces mainly contribute to the torque generation, while the radial counterpart mainly contributes to the generation of electromagnetic noise. According to Maxwell’s stress tensor approach, the radial force density wave (i.e., force per unit area) is approximated as
where represents the radial airgap flux density wave and is the airgap vacuum permeability. Figure 3 shows a comprehensive block chart where all electromagnetic waves are interrelated in a sequential manner.

Figure 3.
Relationships between electromagnetic magnitudes for airgap radial force density computation.
3.1.2. Mechanical Domain
Electromagnetic radial forces excite the stator teeth, creating vibrations in the housing surface. Nevertheless, the stator including windings and the housing constitutes mechanical elements with a non-ideal vibrating transfer path. The mechanical transfer path amplifies or damps the vibrating forces depending on a transfer function , which depends on the mechanical system mass, stiffness, and damping. This mechanical transfer function can be assimilated to the electrical domain, where mass, stiffness, and damping are compared with inductances, capacitances, and resistances of an RLC resonant circuit with an impedance. By assimilating the stator structure to a mass–spring–damper system, the governing equation of the mechanical system is defined as
where m represents the system mass, c is the damping coefficient, k is the stiffness, is the system displacement, and the force function, which in this case represents the radial force. The mechanical transfer path can be broadly estimated by utilizing analytical methods [51], and FEA [53]. Nevertheless, the most common and accurate methodology is to perform experimental modal analysis to estimate the mechanical system parameters and thus, obtain the mechanical transfer path between excitation and acquisition point [54]. The problem is simplified from a machine diagnosis perspective, where a limited amount of housing points is available to perform vibration acquisition due to the presence of cooling fins, connection boxes, etc. Thus, the acceleration is sampled at single points, where the radial force excitation and the acceleration measurement are related by an unknown transfer function:
where represents the acceleration measured in the sampling point, and is the electromagnetic exciting force in the radial direction. Note that the single-point acquisition of vibration eliminates the dependence on the airgap position . Figure 4 shows an overview of the most important theoretical concepts to bridge electrical and mechanical domains.
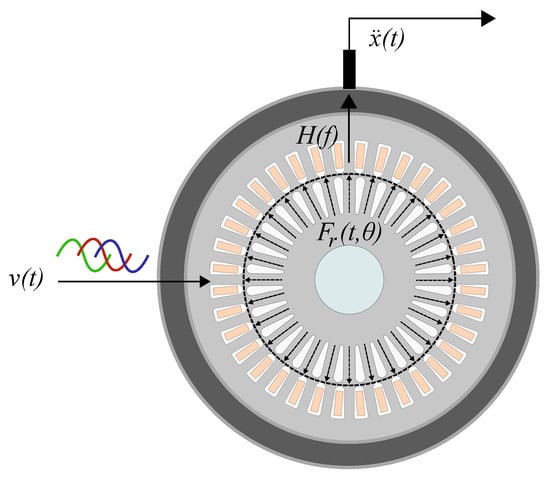
Figure 4.
Description of relationships between electrical input and mechanical measured output.
3.2. Machine Specimen and FEA Model
The machine specimen selected for electromagnetic and mechanical assessment is a 4-pole commercial IE3 1.1 kW squirrel cage induction machine, the main data of which are summarized in Table 1.

Table 1.
Main data of the selected 1.1 kW commercial IM specimen.
The machine is virtually modeled via FEA, which is a widespread technique in industry. The physical machine specimen is subjected to reverse engineering to develop an accurate model that closely replicates both its real-world and simulated responses. A 2D FEA model in Ansys Electronics Desktop platform was devised to evaluate relevant performance indicators of the machine, as presented schematically in Figure 5, including high density mesh in the airgap, slot opening, and rotor bar areas to correctly obtain the transient and steady-state machine response. The proposed 2D model was validated by means of experimental testing at rated conditions, as described in Table 2. A good agreement may be appreciated in terms of rated performance, while current response was further verified by assessing 12 different operating points at different motor speeds and line voltage values.

Figure 5.
Two-dimensional FE model devised to represent the electromagnetic and mechanical response of a 1.1 kW IE3 commercial machine. The left side represents a section of the real machine, the upper-right side shows the magnetic flux density contour plot, and the bottom-right side shows the implemented mesh.

Table 2.
Performance comparison between the developed FE model and experimental results at rated conditions.
The main function of the model is to provide key insights into airgap magnitudes such as radial magnetic flux density and radial force waves, which are not readily available in a standard test bench. In order to evaluate such magnitudes by means of the proposed model, a circumferential path was created in the airgap, from which flux density values were obtained both in space and time. Transient mechanical simulation was considered to this end, starting the machine from rest and imposing a variable load torque depending on the desired operation conditions. Simulation time step was set to 0.5 ms in order to obtain relevant information from the harmonic analysis of electromagnetic signals up to 1000 Hz, and 10 s of steady state were recorded to provide a frequency spacing of 0.1 Hz when assessing harmonic content of signal waveforms. It is important to note that these parameters are the default values used in the baseline simulation. However, both the simulation and time step duration serve as adjustable parameters that students can explore. This exploration facilitates a deeper understanding of the limitations inherent in the simulation.
Aiming to showcase to learners the relationship between the easily measurable vibrations and the complex formulation of radial force density wave in the machine airgap, a simulation is devised to extract the RFD from the circumferential path created in the machine airgap. Two distinct signal types are defined, corresponding to steady-state conditions and start-up transients. Figure 6a,d illustrate the phase current signals under steady-state and transient conditions. Similarly, Figure 6d,e and Figure 6c,f present the airgap radial magnetic flux density and force density, respectively. From obtained signals, a diagnosis-oriented assessment can be performed and presented to the students, taking into account (i) the harmonic content of the RFD by means of conventional Fast Fourier Transform (FFT) tools in steady state, (ii) the evolution of the RFD frequency spectrum in transient operation, and (iii) the relationship between the observed physical quantities and vibration/force generation.

Figure 6.
Electromagnetic variables estimated through FEA from the studied IM, steady-state (a) phase current, (b) radial flux density, and (c) radial force density estimated in an equidistant point between a stator tooth and rotor surface. Simulated transient start-up evolutions in (d) phase current, (e) airgap b-field, and (f) radial force density.
It should be noted that the 2D FE simulation was created in tight agreement with the actual 1.1 kW machine specimen, and that the devised simulation set is bundled in such a way that students can interact with relevant data of the machine and focus on the applicability of this tool to specific learning outcomes. Particularly, dimensional data of the 2D model are locked, and interaction is oriented towards changing the motor inertia, load torque, supply voltage, and simulation settings such as time step and total simulation time. Since the simulation environment is risk-free and allows a significant repeatability degree, the simulation can be used for assessing a healthy machine, and can be further extended to evaluate bar breakage, eccentricity, and other related faults if desired.
3.3. Experimental Work
The present section describes the hands-on activities, equipment, and setup for the proposed method. Initially, the students are provided with a sectioned induction motor, which is identical to the modeled and tested specimen. Figure 7 shows the sectioned motor in detail. The provided material includes the machine stator, die-cast squirrel cage rotor and short-circuit ring, and a disassembled bearing, which is normally allocated in the end bell. This experience greatly supports the comprehensive analysis of the different constructive parts of the machine and their different roles. In addition, it allows the students to co-relate the experimental motor specimen to the provided 2D FEA model.

Figure 7.
(a) Sectioned squirrel cage induction motor with its main components. (b) Detail of squirrel cage machine stator.
The experimental setup is envisioned to provide the students with a safe-operating real scenario in accordance with the defined simulation framework. The test bench for data acquisition is formed by the induction machine under test coupled via flexible mechanical coupling to a 3.3 kW DC generator, which supplies a resistive load for power dissipation. The induction machine is directly connected to the grid and thus, fed at mains frequency 50 Hz and 400 V line-to-line. An auto-transformer is installed at the initial section of the three-phase circuit to facilitate reduced voltage operation. The schematic of the test bench is shown in Figure 8, while the real description of the working space is provided in Figure 9. The imposed resistive torque is controlled by manually varying the DC generator field current. The load point is set by monitoring the non-drive-end shaft speed via a laser manual tachometer to obtain the desired slip value.
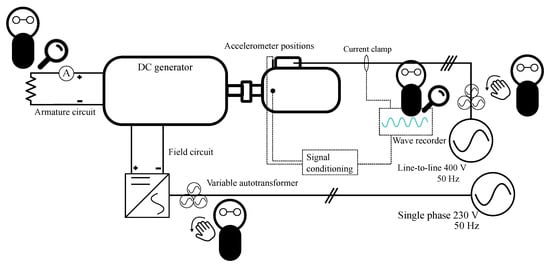
Figure 8.
Test bench schematic and student interface description.

Figure 9.
Didactic test bench description including sensor position and acquisition system.
Acceleration is acquired in two different circumferential positions (i.e., 12 o’clock and 3 o’clock) at the induction machine drive-end, and attached via tack-it adhesive. The accelerometers are then connected to a signal conditioning unit that allows the direct interface with the wave recorder. Measuring vibration in the drive-end of the motor is a common industrial practice since it allows the detection of common mechanical faults such as misalignment and mass unbalances. The two different circumferential positions are selected to showcase the effect of the mechanical transfer path of the motor structure. Phase current is measured by utilizing an inductive current clamp. Figure 9 shows the location of the accelerometers and current clamp. A wave recorder is utilized to simultaneously acquire the vibration and current signals. The students are provided with the basic acquisition setup, while sampling frequency and total signal duration are left as a degree of freedom. This allows the students to experiment with different sampling frequencies defining the Nyquist frequency (or maximum observable frequency), and the frequency resolution depending on the total acquisition time.
The measurement campaign is conducted at various load points to assess the impact of slip and applied resistive torque. Table 3 serves as a reference to guide the laboratory measurements, where voltage readings are taken by the instructor using a safety multimeter. This is performed to account for small fluctuations in the voltage level supply. The load current is read in the multimeter supplying the generator resistive load as shown in Figure 9. Furthermore, a transient analysis of the induction machine’s start-up process is conducted. To achieve this, multiple experiments are performed under reduced voltage excitation to extend the transient duration. The analysis of transient start-up magnitudes is performed to assess the nature of certain slip-dependent components. Figure 10 shows phase current and vibration signals obtained during steady state and transient start-up at rated slip and line-to-line voltage.

Table 3.
Measurement guide example.
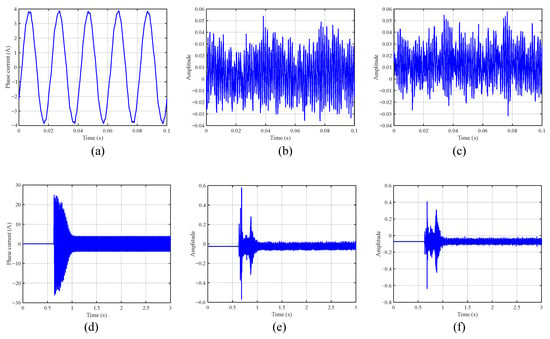
Figure 10.
Acquired signals at 100% rated line-to-line voltage and rated slip, steady-state (a) phase current, (b) 12 o’clock radial vibration, (c) 3 o’clock radial vibration, and transient signals corresponding to (d) phase current, (e) 12 o’clock radial vibration-field, and (f) 3 o’clock radial vibration.
3.4. Signal Postprocessing
The signals are analyzed both in the time and frequency domains. The time-domain analysis is performed on the raw acquired and simulated signals. In this way, Root Mean Squared (rms) and peak magnitudes can be readily compared. The transformation into the frequency domain for single-frequency component analysis is performed using the FFT, a computationally efficient implementation of the Discrete Fourier Transform (DFT). This technique is widely employed across various engineering fields to analyze the frequency spectrum of steady-state signals.
Transient signal analysis poses increased complexity due to their not non-stationary nature. To this aim, the well-known Short-Time Fourier Transform (STFT) is utilized, which is a windowed version of the FFT. The continuous STFT is defined as
where represents the signal under analysis in the time domain, is the window function, and the window duration. The practical implementation of the STFT includes the definition of the window duration, and overlap between windows, which is kept at 95% to ease the student interaction. The obtained frequency resolution heavily depends on the defined time window, which is left as an open degree of freedom. The scripts to perform the mentioned analysis are provided to the students to ease the analysis.
3.5. Target Components
The present exercise is aimed at the identification and quantification of healthy components in the vibration and phase current spectra. The spectrum of the phase current includes the fundamental at supply frequency (i.e., 50 Hz), winding harmonics (WHs), and Principal Slot Harmonics (PSHs). The WHs originate from the discrete distribution of conductors around the stator and the presence of supply voltage harmonics. These are allocated in odd multiples of the supply frequency (e.g., 150 Hz, 250 Hz, etc.) and their magnitude normally decreases for increased orders. The PSHs are related to the rotor slotting, which induces some specific harmonics in the airgap b-field, thus affecting the current spectra. These are slip-dependent and their frequency locus is defined according to [2]:
where k is a positive integer , Q is the number of rotor slots, represents the supply frequency, and is an odd integer, which defines the order of the component. The spectra of vibration signals include both mechanical and electromagnetic-borne components. The most relevant inherent vibration mechanical components are rotating frequency multiples (i.e., 1 × , 2 × , etc.). Another prominent component is the twice-supply frequency component derived from the radial force excitation and its multiples [5]. Additionally, electromagnetic components related to PSH appear in the vibration spectrum. These components are described by Equation (8), with the parameter taking even values instead of odd integers [55]. Note that depending on the vibration acquisition location these components adopt different amplitude values due to the mechanical structural response.
3.6. Synthesis and Analysis—Demonstration of the Learning Experience
The present subsection serves to showcase the expected result analysis and to demonstrate the outcomes of the learning experience overall. The analysis is structured into several parts and is envisioned to foster students’ analytical and critical thinking. It is particularly important that the learners relate the results to theoretical principles related to induction machines, electromagnetic vibrations, and maintenance concepts. In this way, new knowledge is acquired by means of reflection and hands-on tasks. First, steady-state experimental signals are used to identify the main components in both vibration and current spectra. Next, the effect of different load points is examined. Subsequently, transient evolutions during machine start-up are analyzed using the Short-Time Fourier Transform (STFT). Finally, simulated and experimental signals are compared, relating the airgap radial force to the measured housing vibration in both steady-state and transient conditions.
3.6.1. Steady-State Analysis at Rated Slip
Figure 11 shows the steady-state analysis by utilizing the provided FFT. This spectrum contains the characteristic frequencies described in Section 3.5. The main objective of the analysis is to find and quantify the most significant components. A model table should be completed as shown in Table 4, which presents the frequency locus and amplitude of the main components for all acquired magnitudes. Note that the amplitude of the current signal is normalized with respect to the fundamental. The first emphasis is placed on the difference in amplitude of the vibration signals. These possess the same characteristic frequencies but different amplitudes. These differences are mainly due to different sensor placements in the circumferential direction. The most significant PSHs of the vibration signal are found in for . The next emphasis is placed on the characteristic phase current components, which are found in the main WH and the PSH for . Note that the provided script provides the normalized amplitude for the current with respect to the fundamental.
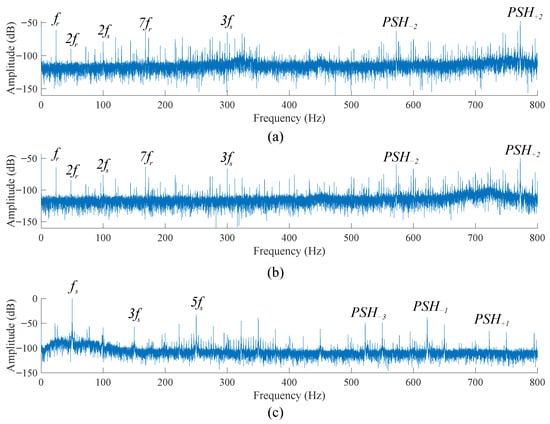
Figure 11.
Frequency-domain spectra and main components for (a) 12 o’clock vibration, (b) 3 o’clock vibration, and (c) phase current.

Table 4.
Steady-state frequency locus and amplitude of main vibration and current components at rated load.
3.6.2. Steady-State Analysis at Different Load Levels
The present analysis is designed to demonstrate to learners the effect of load on a directly fed induction motor. As the DC generator field supply increases, a higher resistive torque is imposed, causing the rotor to decrease its speed. This, in turn, increases slip, affecting both rotational frequencies and slip-dependent frequency components. Figure 12 shows the effect of slip change for different signals and frequency windows. Figure 12a shows the 12 o’clock frequency locus around , where rotating frequencies vary from nearly 25 Hz to 24 Hz for rated load (i.e., 100% load). Figure 12b shows the same magnitude around . This figure shows how the component remains unchanged for different load levels, while the varies significantly. Figure 12c,d depict the frequency locus of two different PSHs in the 12 o’clock vibration and phase current signals, respectively. These figures clearly illustrate the frequency shift at different load levels, highlighting their strong dependence on slip. The learners are encouraged to identify load-dependent components in the acquired signals. Figure 12 provides an example of several such components, though the results are not limited to these.
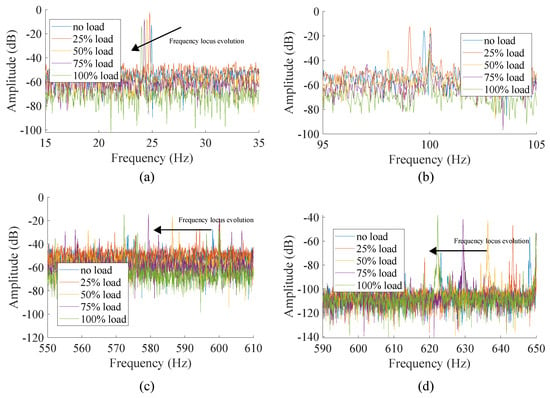
Figure 12.
Frequency locus for different load levels, (a) 12 o’clock vibration rotating frequency, (b) 12 o’clock vibration locus, (c) 12 o’clock vibration PSH-2 locus, and (d) phase current PSH-1 locus.
3.6.3. Transient Analysis of Reduced Voltage Transient Start-Up
The transient analysis of experimental signals is performed under reduced voltage conditions to enlarge the duration of the induction motor start-up as highlighted in Section 5. The main objective of this analysis is to qualitatively identify the main components of the vibration and current spectrum. The analysis of start-up signals further strengthens the identification and analysis of slip-dependent components. The provided script yields the results depicted in Figure 13 for two different vibrations and the current signals. Figure 13a shows the phase current signal transient and its most significant components. The winding harmonics are readily observable for odd multiples of . Additionally, various PSHs are detected, with the main ones located at . Figure 13b,c show the two acquired vibration signals in two different circumferential positions. The first observation is the discrepancies in harmonic content. While low-order rotating frequencies are readily observable in the 12 o’clock signal, these present a weaker signature at the 3 o’clock position. Additionally, the differences in amplitude of the different components are clearly visible. This is partially due to the slightly different vibration mechanical transmission paths. The main observable components in both vibration signals are located in and two main PSHs for .
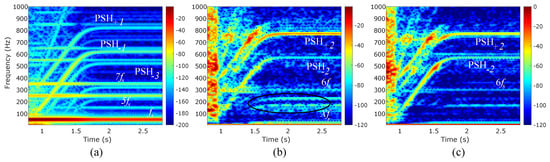
Figure 13.
STFT representation of acquired current and vibration signals; (a) phase current, (b) 12 o’clock housing vibration, and (c) 3 ’clock housing vibration. Circled components represent rotating components .
3.6.4. Comparison Between Simulated and Real Signals
The present analysis represents the main core of the conceived experience, where students compare the experimental analysis with the FEA-obtained results. The comparison is divided into two parts. First, steady-state simulation signals are processed via the provided FFT. Figure 14 shows the steady-state analysis of three different simulated signals. Figure 14a shows the simulated phase current spectrum. The characteristic winding harmonics are readily observable in agreement with the experimental spectrum in Figure 11c. However, the simulated signal only presents the PSHs corresponding to , while experimental results also show the PSH with . Figure 14b shows the b-field spectrum at a fixed airgap point. The WHs are observable in the b-field together with the main PSHs. Figure 14c shows the radial force wave spectrum in a discrete airgap point. The twice-supply frequency component is observable together with its multiples (i.e., ). Three slip-dependent components are observed in this case corresponding to PSHs with . The PSHs are coincident with the acquired vibration signals shown in Figure 11. This highlights the relationship between the radial force and the acquired radial vibration spectra.

Figure 14.
Frequency-domain spectra of simulated signals; (a) phase current, (b) airgap b-field acquired in a single point, and (c) airgap radial force wave acquired in a single point.
Figure 15 shows the simulated transient signals during the induction motor start-up by utilizing the provided STFT script. Slip-dependent evolutions are clearly visible. In addition, the airgap field and radial force evolutions show components that are not observable in the vibration and current signals. The main conclusion of the comparison is the absence of several simulated components in the real acquired signals. The reason behind these differences lies in the possible imperfections of the FEA, and in the case of the vibrations, in the influence of the mechanical transfer path of the stator-housing assembly. The origin identification of these discrepancies represents the main critical component of the students’ job.

Figure 15.
STFT representation of simulated start-up current and vibration signals; (a) phase current, (b) airgap b-field acquired in a single point, and (c) airgap radial force wave acquired in a single point.
3.7. Proposed Evaluation
An evaluation of the FEA-assisted test bench activity was devised to align with the skill sets defined in the master’s programs at the UPV and to reflect the core pedagogical principles of the proposed methodology. The assessment strategy aims to emphasize the integration of theory and practice, experiential learning, and continuous feedback, consistent with modern engineering education standards.
As mentioned in the introduction, recent studies and educational frameworks highlight the importance of experiential learning implemented through PBL in engineering education as a foundation for knowledge construction. Since students must simulate, experiment, and analyze the behavior of an induction motor through both FEA and laboratory measurements, the learning outcomes are assessed to quantify these dimensions. This is, (i) to integrate theoretical concepts with practical skills, as students apply principles of induction machine theory, FEA modeling, and vibration analysis to understand real-world scenarios; (ii) to help develop problem-solving and design skills, as students design experiments and troubleshoot discrepancies between simulated and experimental data, which contributes to their analytical and design abilities; (iii) to interact proficiently with industrially relevant experimental and simulation tools; and (iv) to lay the foundation for comprehension and assimilation of digital twin concepts, by understanding the principles of virtual model creation, validation, and their correlation with physical system behavior.
While these core learning dimensions are central to the methodology, the specific implementation and detailed metrics of the evaluation are intentionally left as a degree of freedom to be adapted by each course instructor and institution. This flexibility allows for tailoring the assessment to diverse curricula, student backgrounds, and local resources, ensuring the methodology’s broad applicability and scalability. Examples of assessment methods could include laboratory reports, problem-solving assignments requiring both FEA and experimental data analysis, and presentations demonstrating critical interpretation of results.
4. Discussion and Pedagogical Implications
This section critically discusses the educational contribution of the proposed FEA-assisted test bench methodology, articulating its alignment with established pedagogical theories and detailing the expected learning outcomes for students. Furthermore, the proposed methodology is validated at its design stage through a Delphi-style survey conducted with an expert panel. Finally, scalability and limitations are discussed.
4.1. Contextualization of the Proposed Methodology Within Theoretical Educational Concepts
The methodology is closely related to the pedagogical framework introduced in Figure 1. The methodology’s foundation in constructivism is evident in its emphasis on the student’s active role in knowledge creation. The students are encouraged to build their understanding by engaging directly with both virtual and physical phenomena. For instance, by first predicting force distributions via FEA and then challenging these predictions with real-world vibration measurements, students actively construct their own mental model of how electrical inputs translate into mechanical responses. This iterative process of hypothesis, experimentation, and reflection allows learners to integrate new observations with their existing knowledge, refining their comprehension in a deeply personalized and meaningful way. This inherent constructivist approach naturally leads to the inter-relation with active learning strategies. Students are continuously engaged in tasks that demand higher-order thinking, moving beyond simple memorization. Activities such as setting up experimental parameters, interpreting complex spectral data, troubleshooting discrepancies between simulation and reality, and formulating conclusions based on integrated evidence all require active participation. Furthermore, the entire methodology is a prime example of experiential learning. The cycle begins with a concrete experience as students operate the physical test bench and collect raw vibration and current data from a real electrical machine. This is followed by reflective observation, where they critically compare these empirical measurements with the theoretical predictions derived from the FEA model, analyzing similarities, differences, and potential sources of error. This reflection leads to abstract conceptualization, as students synthesize their observations to refine their understanding of the underlying physics and the electromechanical link. Lastly, the methodology can be effectively structured as a form of PBL. By presenting students with authentic challenges, such as identifying the source of a specific vibration signature or predicting the impact of a simulated fault on machine behavior, the learning becomes highly contextualized and purposeful. The problem acts as the driving force, compelling students to independently and collaboratively utilize the FEA tool, the physical test bench, and their analytical skills to derive solutions. This problem-centric approach not only develops critical diagnostic abilities but also cultivates self-directed learning and interdisciplinary problem-solving, which are vital for future engineering careers.
4.2. Expected Pedagogical Outcomes
The presented FEA-assisted test bench methodology represents a significant contribution to engineering education, particularly in the domain of electrical machine education and vibration analysis. Traditional approaches often present theoretical concepts of electromagnetic forces and mechanical vibrations in a fragmented manner, leaving students to struggle with synthesizing the complex multi-physical interactions. This methodology addresses a critical pedagogical gap by providing a unique and integrated learning environment that explicitly bridges the gap between theoretical prediction and empirical observation of the electromechanical link. Additionally, this experience moves beyond conventional lab exercises to create a cohesive learning experience that reflects the interdisciplinary nature of modern engineering challenges. Thus, the proposed method is expected to deliver the following learning outcomes:
- Enhanced conceptual understanding supporting knowledge-based education. By enabling direct comparison between FEA-predicted force spectra and experimentally measured vibration responses, students can tangibly observe how electrical phenomena translate into mechanical effects. This visualization and correlation deepen their understanding beyond abstract equations.
- Development of integrated problem-solving skills. The methodology requires students to apply knowledge from both electrical and mechanical engineering, fostering an integrated problem-solving approach essential for real-world diagnostic scenarios.
- Hands-on engagement with industry-relevant tools including FEA software, vibration sensors, acquisition systems, and signal processing techniques.
- Foundation for digital twin concepts related to the interaction with a physical asset’s model, which directly mirrors the fundamental principles underlying digital twin technology.
4.3. Delphi Method
To validate the pedagogical robustness and scalability of the proposed hybrid practical approach, a structured expert consultation was carried out using a modified Delphi method. The Delphi method is a structured communication technique originally developed for systematic forecasting through expert consensus. In the educational context, it provides early-stage validation by leveraging the informed judgment of a panel of experts [56]. In this study, a modified version was used consisting of a single quantitative round to collect structured feedback on key pedagogical dimensions of the proposed methodology, without iterative rounds or qualitative feedback. A panel of 25 external experts was considered, each holding either a master’s or PhD degree in relevant domains such as electrical engineering, engineering education, educational technologies, and mechanical diagnostics.
Experts were asked to evaluate six core aspects of the methodology through a structured survey. Each item was rated on a five-point Likert scale (1 = Strongly disagree, 5 = Strongly agree). The aspects assessed included the integration of simulations and lab work, support for diagnostic skill development, instructional coherence, theoretical alignment with constructivist and experiential learning principles, support for digital twin understanding, and methodological scalability. Table 5 presents the statistical summary of the survey results. The mean scores for all aspects ranged between 4.32 and 4.64, indicating a strong consensus on the value of the proposal. The highest-rated item was “The combination of FEA simulations and lab experiments has strong potential” (M = 4.64, SD = 0.79), while the lowest, though still favorable, was “The sequence of activities is well structured” (M = 4.32, SD = 0.84). The low standard deviations across all items reflect a high level of agreement among respondents, with minimal divergence in expert opinion.

Table 5.
Summary of expert responses using the Delphi method (N = 25).
These results provide robust external validation of the educational soundness of the methodology at this design stage. The strong support across experts from diverse backgrounds reinforces the relevance of the experience not only for electrical engineering curricula but also for broader interdisciplinary educational contexts.
4.4. Methodology Scalability
While the presented FEA-assisted test bench offers a comprehensive learning experience, its core pedagogical principles are highly adaptable to diverse institutional contexts and resource availability. Institutions with limited physical laboratory resources, for instance, could prioritize the in-depth exploration of FEA modeling and simulation, potentially utilizing open-source software or cloud-based platforms to visualize the electromechanical link. Conversely, those with robust experimental facilities could focus on refining the data acquisition and correlation aspects, integrating simpler analytical models if advanced FEA tools are not readily accessible. This modularity allows for a phased implementation, leveraging existing infrastructure and gradually expanding the integrated approach. The versatility of the methodology extends to its applicability across various course levels and types. For introductory courses, the focus could be on simplified FEA models and guided exercises to illustrate fundamental electromechanical principles. In contrast, advanced students could engage in more complex fault diagnosis scenarios, explore multi-domain coupling phenomena, or undertake student-led design projects using the integrated platform. Furthermore, the inherent digital nature of the FEA component makes this methodology particularly amenable to hybrid or online learning environments, where virtual simulations can be extensively utilized, complemented by remote access to data or condensed in-person lab sessions. Beyond its current application, the underlying framework of integrating FEA with experimental validation is highly transferable. This methodology can be readily expanded to study different types of electrical machines (e.g., synchronous machines, axial-flux machines, etc.) and a wider array of fault conditions, each presenting unique electromechanical signatures. This adaptability ensures the long-term relevance and broad utility of the pedagogical approach across the diverse landscape of education in electrical engineering and, particularly, education in the field of electrical machines and drives.
4.5. Limitations
While the proposed FEA-assisted test bench methodology offers a novel and pedagogically sound approach, the work at hand presents several limitations. Firstly, a primary limitation is the absence of a comprehensive empirical study to quantify the methodology’s effectiveness on student learning outcomes (e.g., conceptual understanding, skill development, engagement, and retention). This manuscript focuses on the design, development, and pedagogical rationale of this early-stage knowledge-based innovation. Future research will prioritize rigorous empirical studies with diverse student groups, employing robust assessment strategies (e.g., pre/post-tests, comparative analyses, and qualitative feedback) to formally evaluate its impact after the formal deployment. Secondly, the full implementation of a dedicated FEA-assisted test bench can be resource-intensive. While adaptable, achieving the full integrated experience may challenge some institutions. Finally, as a detailed “educational case study” of a specific design for an induction motor, broader generalization to other machine types and excitation setups requires further validation.
5. Closure
The present manuscript presents a novel educational workflow utilizing an FEA-assisted experimental test bench to significantly enhance engineering students’ comprehension of multi-physical fault diagnosis in electrical machines via vibration signals. By integrating virtual FEA simulations with hands-on experimental validation, the proposed methodology enables students to tangibly link electromagnetic signatures with measured vibration signals, thereby boosting active knowledge construction. Rooted in constructivism, experiential learning, active learning, and PBL principles, this approach additionally develops critical thinking and problem-solving skills, while also laying a foundational understanding for digital twin concepts. The early-stage validation of the methodology through a Delphi-style expert survey supports its significant pedagogical value.
Future work will focus on the comprehensive empirical evaluation of this methodology with diverse student groups to quantify its impact on learning outcomes, including comparative studies against traditional methods. This should be performed in the next steps of implementation of the proposed methodology. Future work will also include the exploration of strategies for more accessible deployment, such as integrating open-source tools and virtual lab environments, and extending the methodology’s application to other electrical machine types and fault conditions to establish broader generalization.
Author Contributions
Conceptualization, J.E.R.-S. and C.M.-C.; methodology, J.E.R.-S. and C.M.-C.; software, J.E.R.-S. and C.M.-C.; validation, C.M.-C.; formal analysis, J.E.R.-S.; investigation, J.E.R.-S.; resources, J.A.A.-D.; data curation, J.E.R.-S. and C.M.-C.; writing—original draft preparation, J.E.R.-S. and C.M.-C.; writing—review and editing, J.A.A.-D.; visualization, J.E.R.-S.; supervision, J.A.A.-D.; project administration, J.A.A.-D.; funding acquisition, J.A.A.-D. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the European Commission (HORIZON program) within the context of the DITARTIS Project (“Network of Excellence in Digital Technologies and AI Solutions for Electromechanical and Power Systems Applications”) under the call HORIZON-WIDERA-2021-ACCESS-03 (Grant Number 101079242).
Institutional Review Board Statement
In accordance with Chilean national guidelines on research ethics (Guía de Buenas Prácticas de Investigación del Consejo de Rectores), this study does not require approval from a Research Ethics Committee, as it involves anonymous expert opinions on non-sensitive topics and poses no risk to participants. Informed consent was obtained from all participants through an online consent question presented before the survey. In accordance with the ethical guidelines of Spanish universities and national regulations (e.g., Organic Law 3/2018 and EU GDPR), this study did not require evaluation by a Research Ethics Committee. The survey was anonymous, voluntary, and collected no personal or sensitive data.
Informed Consent Statement
All participants provided informed consent prior to participation.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Thorsen, O.V.; Dalva, M. Failure identification and analysis for high-voltage induction motors in the petrochemical industry. IEEE Trans. Ind. Appl. 1999, 35, 810–818. [Google Scholar] [CrossRef]
- Thomson, W.T.; Culbert, I. Current Signature Analysis for Condition Monitoring of Cage Induction Motors: Industrial Application and Case Histories; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Antonino-Daviu, J. Electrical monitoring under transient conditions: A new paradigm in electric motors predictive maintenance. Appl. Sci. 2020, 10, 6137. [Google Scholar] [CrossRef]
- Antonino-Daviu, J.; Dunai, L. Software tool for training on electric motors condition monitoring. In Proceedings of the 2022 IEEE 9th International Conference on e-Learning in Industrial Electronics (ICELIE), Brussel, Belgium, 17–20 October 2022; pp. 1–6. [Google Scholar]
- Mistry, R.; Finley, W.R.; Kreitzer, S. Induction motor vibrations. IEEE Ind. Appl. Mag. 2010, 16, 37–46. [Google Scholar] [CrossRef]
- Khawaja, H.A. Multiphysics in Engineering Education: Bridging Theory and Practice; UiT The Arctic University of Norway: Tromsø, Norway, 2024. [Google Scholar]
- Ruiz-Sarrio, J.E.; Madariaga-Cifuentes, C.; Antonino-Daviu, J.A. Understanding Stator Current and Frame Vibrations for Electrical Machine Maintenance: An Educational Approach Using FEA-Assisted Test Bench. In Proceedings of the 2024 IEEE 11th International Conference on E-Learning in Industrial Electronics (ICELIE), Chicago, IL, USA, 3–6 November 2024; pp. 1–6. [Google Scholar]
- Jones, M.G.; Brader-Araje, L. The impact of constructivism on education: Language, discourse, and meaning. Am. Commun. J. 2002, 5, 1–10. [Google Scholar]
- Thampinathan, S. The application of the constructivism learning theory to physician assistant students in primary care. Educ. Health 2022, 35, 26–30. [Google Scholar] [CrossRef] [PubMed]
- Hernández-de Menéndez, M.; Vallejo Guevara, A.; Tudón Martínez, J.C.; Hernández Alcántara, D.; Morales-Menendez, R. Active learning in engineering education. A review of fundamentals, best practices and experiences. Int. J. Interact. Des. Manuf. (IJIDeM) 2019, 13, 909–922. [Google Scholar] [CrossRef]
- Jaroenkhasemmeesuk, C.; Lima, R.M.; Horgan, K.; Mesquita, D.; Supeekit, T. Active learning in engineering education: Case study in mechanics for engineering. In Leveraging Transdisciplinary Engineering in a Changing and Connected World; IOS Press: Amsterdam, The Netherlands, 2023; pp. 633–642. [Google Scholar]
- Holden, M.; Worthington, P.; Searle, M.; Mak, C. Examining an Interdisciplinary Experiential Learning Program for Doctoral Students: Expanding our conception of the advanced degree. Exp. Learn. Teach. High. Educ. 2024, 7. [Google Scholar] [CrossRef]
- Steele, A.L. Experiential Learning in Engineering Education; CRC Press: Boca Raton, FL, USA, 2023. [Google Scholar]
- Duchatelet, D.; Cornelissen, F.; Volman, M. Features of experiential learning environments in relation to generic learning outcomes in higher education: A scoping review. J. Exp. Educ. 2024, 47, 400–423. [Google Scholar] [CrossRef]
- Sims, R.R. Kolb’s experiential learning theory: A framework for assessing person-job interaction. Acad. Manag. Rev. 1983, 8, 501–508. [Google Scholar] [CrossRef]
- Abdulwahed, M.; Nagy, Z.K. Applying Kolb’s experiential learning cycle for laboratory education. J. Eng. Educ. 2009, 98, 283–294. [Google Scholar] [CrossRef]
- Affandy, H.; Sunarno, W.; Suryana, R.; Harjana. Integrating creative pedagogy into problem-based learning: The effects on higher order thinking skills in science education. Think. Ski. Creat. 2024, 53, 101575. [Google Scholar] [CrossRef]
- Edström, K. Integrating the academic and professional values in Engineering education–ideals and tensions. In Technical Universities: Past, Present and Future; Springer: Cham, Switzerland, 2020; pp. 145–164. [Google Scholar]
- Akinci-Ceylan, S.; Ahn, B. ‘I think it’s probably one of the most important skills we could ever know’: Insights from early-career engineers on the preparedness of undergraduate degrees for the aerospace industry. Eur. J. Eng. Educ. 2025, 50, 320–341. [Google Scholar] [CrossRef]
- Sedaghat, A.; AlJundub, M.; Eilaghi, A.; Bani-Hani, E.; Sabri, F.; Mbarki, R.; Assad, M.E.H. Application of pbl in the course fluid and electrical drive systems, case study: Manufacturing an automated punch machine. J. Probl. Based Learn. High. Educ. 2017, 5, 1–11. [Google Scholar]
- Mahtani, K.; Guerrero, J.M.; Decroix, J. Implementing innovation in project-based learning in electro-mechanical engineering education. Int. J. Mech. Eng. Educ. 2024, 03064190241284600. [Google Scholar] [CrossRef]
- Lara-Bercial, P.J.; Gaya-López, M.C.; Martínez-Orozco, J.M.; Lavado-Anguera, S. PBL Impact on Learning Outcomes in Computer Engineering: A 12-Year Analysis. Educ. Sci. 2024, 14, 653. [Google Scholar] [CrossRef]
- Li, J.; Liang, W. Effectiveness of virtual laboratory in engineering education: A meta-analysis. PLoS ONE 2024, 19, e0316269. [Google Scholar] [CrossRef]
- Lavado-Anguera, S.; Velasco-Quintana, P.J.; Terrón-López, M.J. Project-based learning (PBL) as an Experiential Pedagogical Methodology in Engineering Education: A review of the literature. Educ. Sci. 2024, 14, 617. [Google Scholar] [CrossRef]
- Terkaj, W.; Urgo, M.; Kovács, P.; Tóth, E.; Mondellini, M. A framework for virtual learning in industrial engineering education: Development of a reconfigurable virtual learning factory application. Virtual Real. 2024, 28, 148. [Google Scholar] [CrossRef]
- Norambuena, N.; Ortega, J.; Muñoz-La Rivera, F.; Covarrubias, M.; Valín Rivera, J.L.; Ramírez, E.; Ketterer, C.I.G. Integrating Digital Twins of Engineering Labs into Multi-User Virtual Reality Environments. Appl. Sci. 2025, 15, 3819. [Google Scholar] [CrossRef]
- Strazzeri, I.; Notebaert, A.; Barros, C.; Quinten, J.; Demarbaix, A. Virtual Reality Integration for Enhanced Engineering Education and Experimentation: A Focus on Active Thermography. Computers 2024, 13, 199. [Google Scholar] [CrossRef]
- Srinivasan, S.; Centea, D. Problem based learning in finite element analysis. In Proceedings of the Visions and Concepts for Education 4.0: Proceedings of the 9th International Conference on Interactive Collaborative and Blended Learning (ICBL2020), Hamilton, ON, Canada, 14–16 October 2020; Springer: Berlin/Heidelberg, Germany, 2021; pp. 240–246. [Google Scholar]
- Huang, C.; Cai, W.; Cui, L.; Zhu, C.; Tang, Y. Enhancing Geotechnical Engineering Education Based on Multiphysics Enriched Mixed Reality Game. In Proceedings of the 2023 Fall Mid Atlantic Conference: Meeting Our Students Where They Are and Getting Them Where They Need to Be, Ewing, NJ, USA, 27 October 2023–10 January 2024. [Google Scholar]
- Cellupica, A.; Cirelli, M.; Saggio, G.; Gruppioni, E.; Valentini, P.P. An interactive digital-twin model for virtual reality environments to train in the use of a sensorized upper-limb prosthesis. Algorithms 2024, 17, 35. [Google Scholar] [CrossRef]
- Weistroffer, V.; Keith, F.; Bisiaux, A.; Andriot, C.; Lasnier, A. Using physics-based digital twins and extended reality for the safety and ergonomics evaluation of cobotic workstations. Front. Virtual Real. 2022, 3, 781830. [Google Scholar] [CrossRef]
- Wang, S.; Wang, X.; Yu, H. Simulation of material mechanics tensile experiment based on finite element technology. In Proceedings of the 2023 9th International Conference on Frontiers of Educational Technologies, Bali, Indonesia, 9–11 June 2023; pp. 109–114. [Google Scholar]
- Prasad, N.; Jain, S.; Gupta, S. An educational tool based on finite element method for electromagnetic study. Int. J. Electr. Eng. Educ. 2021, 58, 828–848. [Google Scholar] [CrossRef]
- Zhu, K.; Ma, Z.; Wang, F.; Geng, L.; Wu, R.; Meng, X.; Wang, L.; Gao, H. Finite Element Software Analysis of Engineering Structure Test and Teaching Reform of Integration of Production and Teaching. In Proceedings of the 2023 4th International Conference on Education, Knowledge and Information Management (ICEKIM 2023); Atlantis Press: Dordrecht, The Netherlands, 2023; pp. 1621–1631. [Google Scholar]
- Cobos-Torres, J.C.; Reyes, P.A.; Mendez, C.F. Problem-based learning for an electrical machines course. Int. J. Emerg. Technol. Learn. (iJET) 2020, 15, 192–203. [Google Scholar] [CrossRef]
- Li, S.; Challoo, R. Restructuring an electric machinery course with an integrative approach and computer-assisted teaching methodology. IEEE Trans. Educ. 2006, 49, 16–28. [Google Scholar] [CrossRef]
- Duran, M.J.; Barrero, F.; Pozo-Ruz, A.; Guzman, F.; Fernandez, J.; Guzman, H. Understanding power electronics and electrical machines in multidisciplinary wind energy conversion system courses. IEEE Trans. Educ. 2012, 56, 174–182. [Google Scholar] [CrossRef]
- O’Keeffe, H.; Masoud, M.; Panagiotou, P.; Toqeer, R.; Griffo, A.; Lazari, P. A versatile and low-cost approach to power electronics practical training. In Proceedings of the 13th International Conference on Power Electronics, Machines and Drives (PEMD 2024), Hertfordshire, UK, 6–13 October 2024; IET: Hertfordshire, UK, 2024; Volume 2024, pp. 653–658. [Google Scholar]
- Wray, T.; Panagiotou, P.; Masoud, M.; O’Keeffe, H.; Toqeer, R.; Griffo, A.; Lazari, P. A compact and modular remote access platform for enhanced practical education in power electronics, machines, and drives. In Proceedings of the 13th International Conference on Power Electronics, Machines and Drives (PEMD 2024), Nottingham, UK, 10–13 June 2024; IET: Hertfordshire, UK, 2024; Volume 2024, pp. 646–652. [Google Scholar]
- Lei, Z.; Zhou, H.; Hu, W.; Deng, Q.; Zhou, D.; Liu, Z.W.; Gao, X. 3-D interactive control laboratory for classroom demonstration and online experimentation in engineering education. IEEE Trans. Educ. 2020, 64, 276–282. [Google Scholar] [CrossRef]
- Cvetkovski, G.; Petkovska, L.; Digalovski, M.; Celeska, D.K.; Firych-Nowacka, A.; Wiak, S.; Sapiński, T.; Lefik, M.; Zwoliński, G.; Di Barba, P.; et al. Virtual reality as a tool for electrical machines assembling and testing. In Proceedings of the 7th Symposium on Applied Electromagnetics SAEM18, Maribor, Slovenia, 17–20 June 2018; University of Maribor Press: Lexington, MA, USA, 2018; p. 151. [Google Scholar]
- Checa, D.; Saucedo-Dorantes, J.J.; Osornio-Rios, R.A.; Antonino-Daviu, J.A.; Bustillo, A. Virtual reality training application for the condition-based maintenance of induction motors. Appl. Sci. 2022, 12, 414. [Google Scholar] [CrossRef]
- Belu, R. Virtual laboratory for study of the electric machines parameters and characteristics. In Proceedings of the 2010 Annual Conference & Exposition, Louisville, KY, USA, 20–23 June 2010; pp. 15–1351. [Google Scholar]
- Dong, J.; Soeiro, T.B.; Koeners, J.; Bauer, P. Online laboratory sessions for the education of electrical machines and drives. In Proceedings of the 2020 IEEE 29th International Symposium on Industrial Electronics (ISIE), Delft, The Netherlands, 17–19 June 2020; pp. 430–435. [Google Scholar]
- Romero, J.M.R.; Tellez, S.; Rivera, S. Implementing virtual laboratories: Remote teaching of electrical machines. Rev. Int. Métodos Numér. Cálc. Diseño Ing. 2021, 37, 20–36. [Google Scholar]
- Chiguano, E.; Hidalgo, L.; Otero, P.; Granda, N. Virtual Laboratory for Induction Motor Simulation. In Proceedings of the International Conference on Science, Technology and Innovation for Society, Guayaquil, Ecuador, 22–24 June 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 430–438. [Google Scholar]
- Tsunata, R.; Takemoto, M. Teaching Method for Electrical Machines Focusing on Differences Between Simulation and Experimental Verification. In Proceedings of the 2023 IEEE 10th International Conference on E-Learning in Industrial Electronics (ICELIE), Singapore, 16–19 October 2023; pp. 1–6. [Google Scholar]
- Ruíz Rodríguez, F.J.; Torreglosa, J.P. Evaluating the effect of using synchronous machine simulations to support traditional teaching methodology in electrical engineering degree courses. Comput. Appl. Eng. Educ. 2020, 28, 556–567. [Google Scholar] [CrossRef]
- Liljaniemi, A.; Paavilainen, H. Using digital twin technology in engineering education–course concept to explore benefits and barriers. Open Eng. 2020, 10, 377–385. [Google Scholar] [CrossRef]
- Hazrat, M.; Hassan, N.; Chowdhury, A.A.; Rasul, M.; Taylor, B.A. Developing a skilled workforce for future industry demand: The potential of digital twin-based teaching and learning practices in engineering education. Sustainability 2023, 15, 16433. [Google Scholar] [CrossRef]
- Gieras, J.F.; Wang, C.; Lai, J.C. Noise of Polyphase Electric Motors; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Boldea, I. Induction Machines Handbook: Transients, Control Principles, Design and Testing; CRC Press: Boca Raton, FL, USA, 2020. [Google Scholar]
- Chauvicourt, F.; van der Auweraer, H. The application of vibration synthesis on electric machines for skewed designs. In Proceedings of the 2020 23rd International Conference on Electrical Machines and Systems (ICEMS), Hamamatsu, Japan, 24–27 November 2020; pp. 91–96. [Google Scholar]
- Chauvicourt, F. Vibro-Acoustics of Rotating Electric Machines: Prediction, Validation and Solution. Ph.D. Thesis, Katholieke Universiteit Leuven, Leuven, Belgium, 2018. [Google Scholar]
- Cameron, J.; Thomson, W.; Dow, A. Vibration and current monitoring for detecting airgap eccentricity in large induction motors. IEE Proc. B Electric Power Appl. 1986, 133, 155–163. [Google Scholar] [CrossRef]
- Green, R.A. The Delphi technique in educational research. Sage Open 2014, 4, 2158244014529773. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).