A Structural Causal Model Ontology Approach for Knowledge Discovery in Educational Admission Databases

Abstract

Educational admission systems, particularly in developing countries, often suffer from opaque decision processes, unstructured data, and limited analytic insight. This study proposes a novel methodology that integrates structural causal models (SCMs), ontological modeling, and machine learning to uncover and apply interpretable knowledge from an admission database. Using a dataset of 12,043 records from Benue State Polytechnic, Nigeria, we demonstrate this approach as a proof of concept by constructing a domain-specific SCM ontology, validate it using conditional independence testing (CIT), and extract features for predictive modeling. Five classifiers, Logistic Regression, Decision Tree, Random Forest, K-Nearest Neighbors (KNN), and Support Vector Machine (SVM) were evaluated using stratified 10-fold cross-validation. SVM and KNN achieved the highest classification accuracy (92%), with precision and recall scores exceeding 95% and 100%, respectively. Feature importance analysis revealed ‘mode of entry’ and ‘current qualification’ as key causal factors influencing admission decisions. This framework provides a reproducible pipeline that combines semantic representation and empirical validation, offering actionable insights for institutional decision-makers. Comparative benchmarking, ethical considerations, and model calibration are integrated to enhance methodological transparency. Limitations, including reliance on single-institution data, are acknowledged, and directions for generalizability and explainable AI are proposed.

1. Introduction

Educational admission systems worldwide face increasing pressure to ensure fairness, transparency, and accountability in their decision-making processes [1,2]. In Nigerian polytechnic institutions, the admission process remains largely manual, characterized by inconsistent evaluation criteria and susceptibility to human bias. This challenge is compounded by the lack of standardized frameworks for representing and analyzing admission criteria, limiting institutions’ ability to ensure equitable access to educational opportunities. While knowledge discovery in databases (KDD) has transformed decision-making across various sectors, its application to educational admissions presents unique challenges: the need to balance predictive accuracy with fairness, the requirement for interpretable decisions in high-stakes contexts, and the necessity of incorporating domain-specific causal knowledge [3,4].

Recent advances in educational data mining have demonstrated the potential of machine learning for admission prediction [5,6]. However, existing approaches suffer from two critical limitations. First, they often perpetuate historical biases present in training data, leading to unfair outcomes for underrepresented groups [1]. Second, the “black-box” nature of most ML models undermines trust and transparency, particularly problematic in educational contexts where the decision must be explainable to stakeholders [7]. To address these limitations, this study proposes a novel methodology that integrates the knowledge discovery in databases (KDD) process with structural causal modeling (SCM) and ontological design. The central idea is to develop a formal representation of the admission process as a causal ontology, guided by domain knowledge and empirically validated using conditional independence testing (CIT). This validated structure is then used to extract core features for training supervised machine learning models that predict admission outcomes.

While ontologies have been widely used in education for structuring knowledge domains and supporting semantic interoperability [8,9], most existing admission-related ontologies are static and not empirically validated. They often serve as descriptive taxonomies rather than data-driven or decision-support tools. In contrast, our approach employs a causally grounded, empirically tested ontology that can support both knowledge discovery and predictive modeling. Additionally, while SCM has been applied in healthcare and economics for counterfactual reasoning and intervention analysis [10,11], its application in educational admissions modeling, especially in resource-constrained institutional contexts, remains underexplored.

The primary research problem addressed in this study is how to extract, represent, and validate causal knowledge from educational admission data to enhance both interpretability and predictive accuracy. To this end, the following research questions are explored:

• How can meaningful knowledge be extracted from a polytechnic admission database in a formal and interpretable manner?
• How can this knowledge be captured and validated using a structural causal model (SCM) ontology?
• What machine learning models best generalize on features extracted from a validated SCM-based ontology?

This study employs admission data from Benue State Polytechnic in Nigeria as a proof-of-concept case. The dataset contains over 12,000 records and includes student demographic data, course selections, and admission status. The research follows a three-stage methodology:

• Design of an SCM-based ontological framework using domain knowledge;
• Empirical validation of the framework using conditional independence tests via the DAGitty and R environments;
• Application of five ML algorithms (Logistic Regression, Decision Tree, Random Forest, K-Nearest Neighbors, Support Vector Machine) to model admission outcomes based on features extracted from the validated causal ontology.

The key contributions of this paper are as follows:

• A novel integration of SCM, ontology design, and KDD for educational admission systems;
• An empirically validated SCM ontology tailored to the Nigerian polytechnic context;
• A comparative evaluation of ML models using causally extracted features to ensure predictive integrity;
• A reusable methodology for institutions seeking transparent and explainable AI solutions in educational decision-making.

The rest of this paper is organized as follows: Section 2 reviews related literature across data mining, ontologies, and causal modeling in education. Section 3 outlines the materials and methods used. Section 4 presents the results of SCM validation and ML prediction. Section 5 concludes with key insights and directions for future work.

2. Related Works

The growing integration of machine learning (ML), ontology-based modeling, and causal reasoning into educational data analysis has led to new opportunities for improving admissions decision-making and institutional planning. Recent research in educational data mining (EDM) has primarily focused on predictive performance in areas such as academic success, dropout detection, and online adaptability, while fewer studies have combined this with causal inference or structural modeling to support explainable decisions. This section reviews prior works across three interrelated domains: educational data mining (EDM), ontology-based decision-support systems, and the application of structural causal models (SCMs) in education.

2.1. Educational Prediction Models and Data Mining

The field of educational data mining (EDM) continues to gain prominence in modeling student behaviors, predicting outcomes, and supporting institutional planning. Notably, Ref. [12] emphasized the use of decision trees, clustering, and regression for predicting educational performance, enrollment, and risk detection. In the specific context of admission decisions, Ref. [9] developed an ontology-based question-answering system for advising university admissions using natural language queries and semantic retrieval, demonstrating the increasing relevance of structured semantic models in admission-related decision support.

Despite such advances, most EDM applications remain predictive rather than explanatory, and few provide mechanisms to formally identify or validate causal relationships underlying admission decisions. Our study addresses this gap by integrating a validated causal ontology within an educational admission framework, bridging interpretability with predictive modeling.

2.2. Ontology-Based Knowledge Representation in Decision Systems

Ontologies serve as structured semantic frameworks for representing domain knowledge in a machine-understandable form. They have found success in education, healthcare, manufacturing, and business processes. For instance, Ref. [13] introduced the DIAG approach, combining ontology-driven modeling with cognitive process mining to detect and explain concept drift in dynamic systems, showing how ontologies can support both knowledge discovery and explanation.

In industrial domains, Ref. [14] proposed a methodology for deriving Bayesian causal networks from domain ontologies, arguing for the fusion of semantic structures with probabilistic causality to enhance decision-making in complex processes. Although their application is in manufacturing, the methodological alignment with our use of SCM ontologies is notable.

While most prior educational ontologies are static (e.g., for curriculum mapping or student modeling), our approach is unique in embedding the ontology within a causal model validated empirically through conditional independence testing (CIT). This dual structure enhances both semantic expressiveness and statistical rigor.

2.3. Structural Causal Models and Causal Discovery in Education

Structural causal models (SCMs) offer formal tools for expressing cause–effect relationships using directed acyclic graphs (DAGs) and functional dependencies. Ref. [15] formalized this paradigm and introduced testable criteria for identifying causal pathways. In recent work, Ref. [16] proposed choice function-based hyper-heuristics for efficient causal discovery under linear structural equation models, offering optimized ways to generate DAGs that align with independence constraints. Their framework strengthens the broader methodological foundation upon which our CIT-based DAG validation rests.

Our DAG validation aligns with heuristics in linear SEMs, as advanced by [16], though applied in a semantically enriched context: the SCM ontology. By incorporating domain expertise into the DAG structure and validating causal assumptions via the DAGitty R package (version 0.3-4), we establish a replicable pipeline for causal ontology validation in educational domains.

3. Materials and Methods

3.1. Database Structure and Description

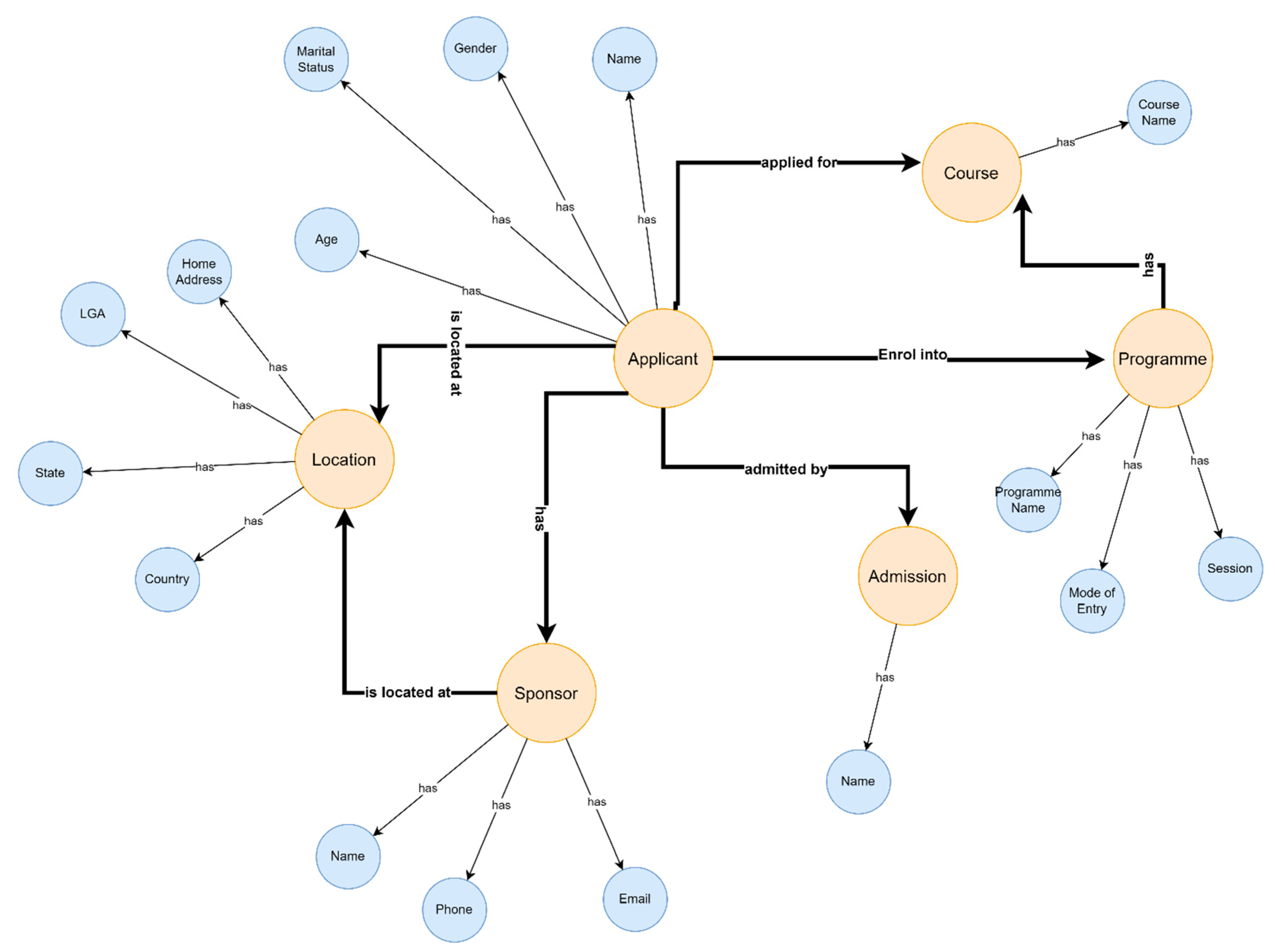
This study employed admission records obtained from the Benue State Polytechnic (BenPoly) online portal, representing a proof-of-concept implementation for Nigerian polytechnic institutions. The database contained the following classes, and their attributes shown in curly brackets were discovered: (i) applicant—{name, gender, marital status, and age}, (ii) program—{program name, mode of entry, and session}, (iii) location—{country, state, local government area, and home address}, (iv) course—{course name}, (v) sponsor—{sponsor name, sponsor phone, and sponsor email}, and (vi) admission—{admitted by}.

The initial dataset comprised 23 variables with mixed categorical data types and 12,043 records collected over multiple admission cycles (2018–2022). Data collection was conducted in compliance with institutional privacy policies, with all personally identifiable information anonymized prior to analysis.

Figure 1 illustrates a comprehensive data-flow ontological framework of the entire admission database, with classes, attributes, and their relations. The database contained 23 variables comprising both alphanumeric data types and 12,043 records.

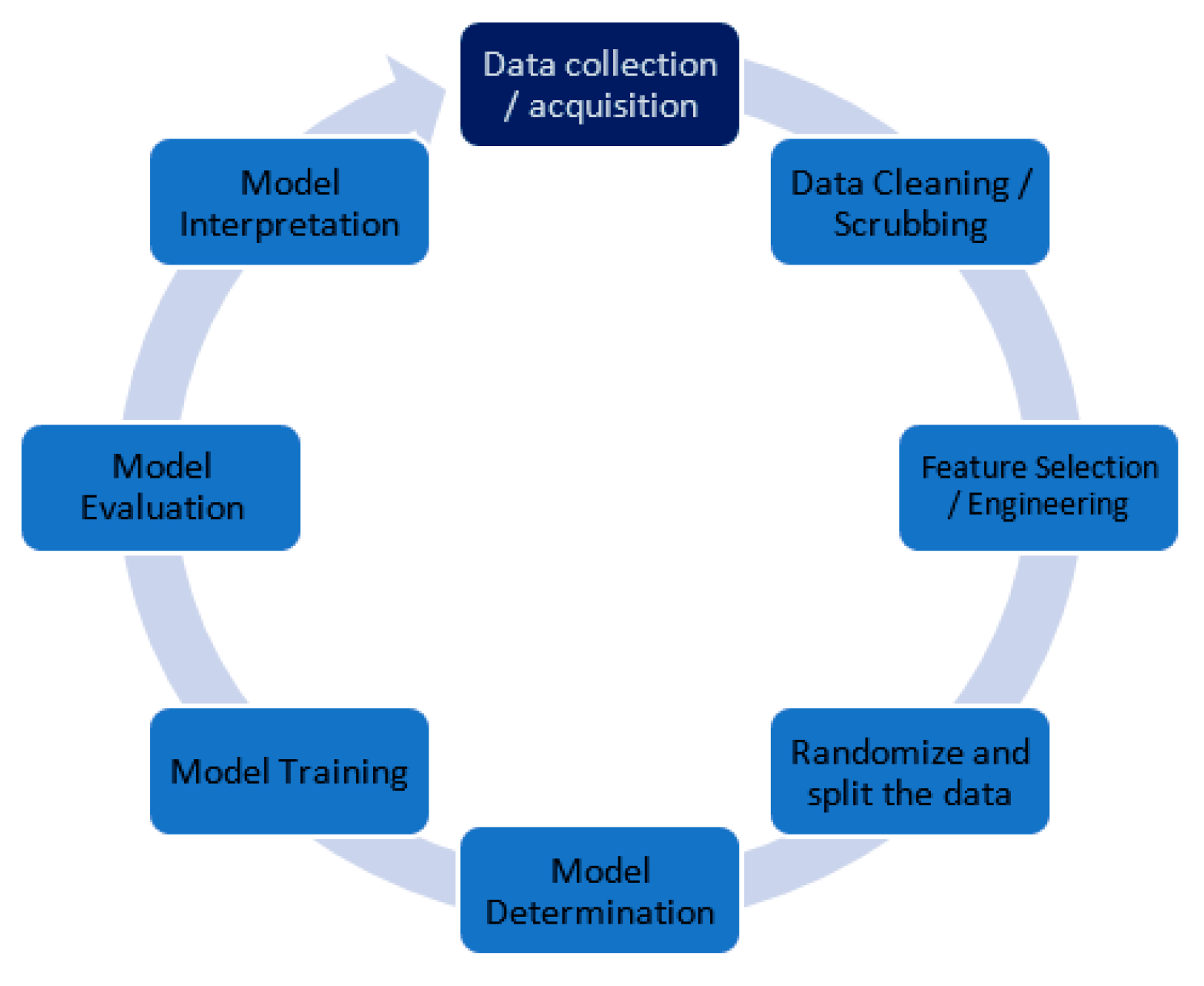
3.2. Data Preprocessing Pipeline

Figure 2 presents the systematically implemented data preprocessing pipeline, following established KDD methodology standards. The preprocessing phase comprised five sequential stages designed to ensure data quality and computational compatibility:

Stage 1: Data Cleaning and Quality Assessment

• Removed 174 records (1.4%) containing missing critical admission variables;
• Eliminated 23 variables deemed irrelevant to admission process modeling based on domain expertise;
• Applied outlier detection using the interquartile range (IQR) method with threshold ±1.5 × IQR;
• Identified and removed 892 records with implausible age values (range: −4 to 14 years), indicating data entry errors.

Stage 2: Feature Engineering and Selection

• Generated Current_Qualification variable through systematic mapping of Course_Category values:

  -

  O-Level certification → National Diploma (ND) eligibility (coded as 0);

  -

  National Diploma completion → Higher National Diploma (HND) eligibility (coded as 1).

This transformation was validated against institutional admission requirements and Nigerian polytechnic education standards and we subsequently removed the original Course_Category variable to prevent multicollinearity.

Stage 3: Variable Standardization and Encoding

• Converted all categorical variables to numeric format using label encoding for computational processing;
• Applied consistent naming conventions across all variables (

  Table 1. Variable encoding and standardization schema.

  Original Variable	Encoded Variable	Data Type	Encoding Method	Description
  Gender	gndr	Binary	Label (0 = Female, 1 = Male)	Applicant gender
  Marital_Status	mrtl	Binary	Label (0 = Single, 1 = Married)	Marital status
  State_ID	sttd	Categorical	Label (1–36)	State of origin
  LGA_ID	lgad	Categorical	Label (1–774)	Local government area
  Age	Age	Continuous	Numeric	Applicant age (years)
  Course_Applied_ID	crsp	Categorical	Label (1–45)	Applied course program
  Current_Qualification	Cr_Q	Binary	Engineered (0 = O-Level, 1 = ND)	Entry qualification level
  Mode_of_Entry	mdfn	Binary	Label (0 = JAMB, 1 = Non-JAMB)	Admission pathway
  Admission_Status	Ad_S	Binary	Target (0 = Rejected, 1 = Admitted)	Final admission decision

  provides complete variable mapping);
• Standardized missing value treatment using mode imputation for categorical variables.

Stage 4: Dataset Validation and Final Preparation

• Final dataset comprised 9 key variables and 11,869 records (98.6% retention rate);
• Performed correlation analysis to verify absence of perfect multicollinearity;
• Conducted descriptive statistical analysis to confirm data distribution properties.

Stage 5: Train–Test Split Configuration

• Implemented stratified random sampling with 80/20 train–test split;
• Applied 5-fold cross-validation for model evaluation robustness;
• Ensured class distribution preservation across training and testing sets.

All preprocessing steps were implemented using Python 3.8 with pandas (v1.3.0), NumPy (v1.21.0), and scikit-learn (v0.24.2) libraries. Complete preprocessing code and data transformation logs are available for reproducibility.

3.3. Theoretical Framework: Structural Causal Modeling in Ontological Context

The SCM framework provides a mathematical foundation for representing causal relationships between variables in complex systems [17,18]. Unlike purely correlational approaches, SCM enables explicit modeling of causal mechanisms through directed acyclic graphs (DAGs) and structural equations.

In our admission process context, SCM facilitates the following:

• Formal representation of institutional decision-making logic;
• Validation of causal assumptions against empirical data;
• Identification of key features for predictive modeling.

Core SCM components:

Variables (Vs): Represent entities or factors in the admission system, categorized as the following:

• Exogenous variables (X): Student characteristics {gender, marital status, state ID, LGA ID, age};
• Endogenous variables: Process variables {current qualification, course applied, mode of entry, admission status}.

Structural equations: Define functional relationships between variables. For any endogenous variable Y depending on parent variables X₁, X₂, …, X_n,

Y = f(X₁, X₂, …, X_n, ε_γ)

(1)

where f(.) represents the functional relationship and ε_γ captures unobserved influences.

To empirically assess the validity of the causal assumptions encoded in the Di-rected Acyclic Graph (DAG), partial correlation testing is applied. For any two varia-bles A and B, given a conditioning set C, the partial correlation coefficient $\mathrm{\rho }$_AB·C is computed using the following formula:

$$\mathrm{\rho }\_\mathrm{AB}·\mathrm{C}=(\mathrm{\rho }\_\mathrm{AB}-\mathrm{\rho }\_\mathrm{AC}·\mathrm{\rho }\_\mathrm{BC})/\surd [(1-\mathrm{\rho }\_{\mathrm{AC}}^2)(1-\mathrm{\rho }\_{\mathrm{BC}}^2)]$$

(2)

where $\mathrm{\rho }$_AB, $\mathrm{\rho }$_AC, and $\mathrm{\rho }$_BC are the Pearson correlation coefficients between the respec-tive variable pairs.

Directed acyclic graph (DAG): Graphically represents causal dependencies through nodes (variables) and directed edges (causal relationships). The absence of direct edges between variables indicates conditional independence given their parents—the foundation for our conditional independence test (CIT) validation.

Conditional independence testing: For variables A and B given conditioning set C, independence is denoted as A ⊥ B | C, tested using the following:

• Null hypothesis (H₀): A ⊥ B | C (variables are conditionally independent);
• Alternative hypothesis (H₁): A ⊥/ B | C (variables are conditionally dependent);
• Statistical test: Partial correlation with significance level α = 0.05.

3.4. SCM Ontological Framework Design and Validation Protocol

Our methodology integrates three computational tools for comprehensive SCM implementation:

Tool 1: Python environment (Jupyter Notebook 6.1.4):

• Data preprocessing and feature engineering using pandas and NumPy;
• Statistical analysis and correlation testing using SciPy.Stats;
• Variable encoding and dataset preparation for R integration.

Tool 2: DAGitty package (R 4.1.0):

• Visual DAG construction based on domain knowledge and institutional admission logic;
• Automatic generation of CIT criteria (model-implied conditional independence statements);
• Export of DAG coordinates and CIT specifications for validation.

Tool 3: R programming environment (4.1.0):

• CIT validation using dagitty::localTests() function;
• Statistical testing of conditional independence assumptions;
• Visualization of validation results using dagitty::plotLocalTestResults().

Validation algorithm implementation: The steps involved in validating the conditional independence assumptions of the SCM ontology are outlined in Algorithm 1.

Algorithm 1. CIT Validation Protocol

INPUT: Dataset D, DAG structure G, significance level α = 0.05 OUTPUT: Validation results {correlation coefficients, p-values, confidence intervals} 1. For each conditional independence statement I ∈ CIT(G):   2. Extract variables A, B, and conditioning set C from I   3. Compute partial correlation ρ(A,B|C) using dagitty::localTests()   4. Calculate p-value using t-distribution with n−|C|−2 degrees of freedom   5. Determine 95% confidence interval for correlation coefficient   6. Evaluate validation criterion:       IF |ρ(A,B|C)| ≈ 0 AND p-value > α THEN         Independence assumption CONFIRMED       ELSE       Independence assumption REJECTED 7.  Generate summary statistics and visualization plots 8.  Return comprehensive validation report

Validation criteria for SCM acceptance:

• Correlation coefficients close to zero (|ρ| < 0.1);
• p-values above significance threshold (p > 0.05);
• Narrow confidence intervals excluding strong correlation values;
• Graphical confirmation via plotLocalTestResults() function.

Alternative causal discovery approaches:

While our domain-expert-driven DAG construction represents our approach to causal modeling, constraint-based algorithms like the PC (Peter-Clark) algorithm offer data-driven alternatives. However, we chose expert-driven construction for this proof of concept because of the following: (1) it incorporates institutional knowledge about regulatory constraints not observable in data alone, (2) it ensures policy compliance in the resulting model, and (3) it provides greater interpretability for stakeholders. Future work will explore hybrid approaches combining expert knowledge with algorithmic discovery methods to validate and refine causal structures.

This rigorous validation protocol ensures that our SCM ontological framework accurately represents the underlying causal structure of the admission process, providing a validated foundation for subsequent machine learning feature selection and predictive modeling.

4. Implementation and Results

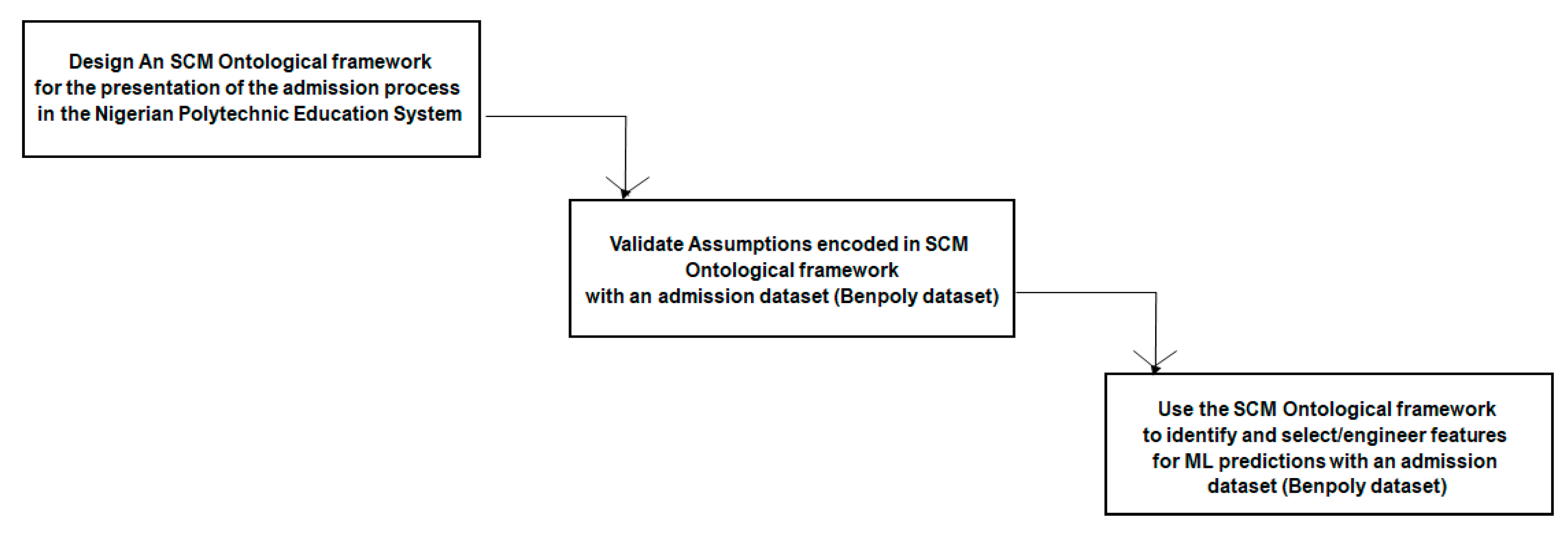
This section presents the systematic implementation of our three-phase SCM ontological framework, comprising the following: (1) SCM design and domain knowledge integration, (2) empirical validation through conditional independence testing, and (3) feature-informed machine learning prediction with comprehensive performance evaluation. Figure 3 illustrates the waterfall implementation framework, ensuring systematic progression from ontological design through empirical validation to predictive modeling.

4.1. SCM Ontological Framework Design and Domain Knowledge Integration

The ontological framework was systematically constructed through iterative collaboration between domain experts (admission officers, academic registrars) and data scientists, ensuring both theoretical rigor and practical relevance. The initial dataset of 23 variables was reduced to nine core variables through systematic feature engineering and domain-driven selection.

Feature engineering decision: The transformation of Course_Category into Current_Qualification represents a key methodological innovation, capturing the hierarchical nature of Nigerian polytechnic education:

• National Diploma (ND) programs require O-Level certification as entry qualification;
• Higher National Diploma (HND) programs require completed ND as entry qualification;
• This binary encoding (0 = O-Level, 1 = ND) directly reflects institutional admission logic.

Final variable categorization aligned with admission process workflow:

Personal characteristics (X): {gender, marital_status, state_ID, LGA_ID, age}:

• These variables represent applicant demographics influencing qualification assessment;
• Institutional policies mandate demographic data collection for federal character compliance.

Process variables: {current_qualification, course_applied_ID, mode_of_entry, admission_status}:

• These variables capture the sequential decision-making logic of the admission system;
• Each variable represents a distinct stage in the institutional evaluation process.

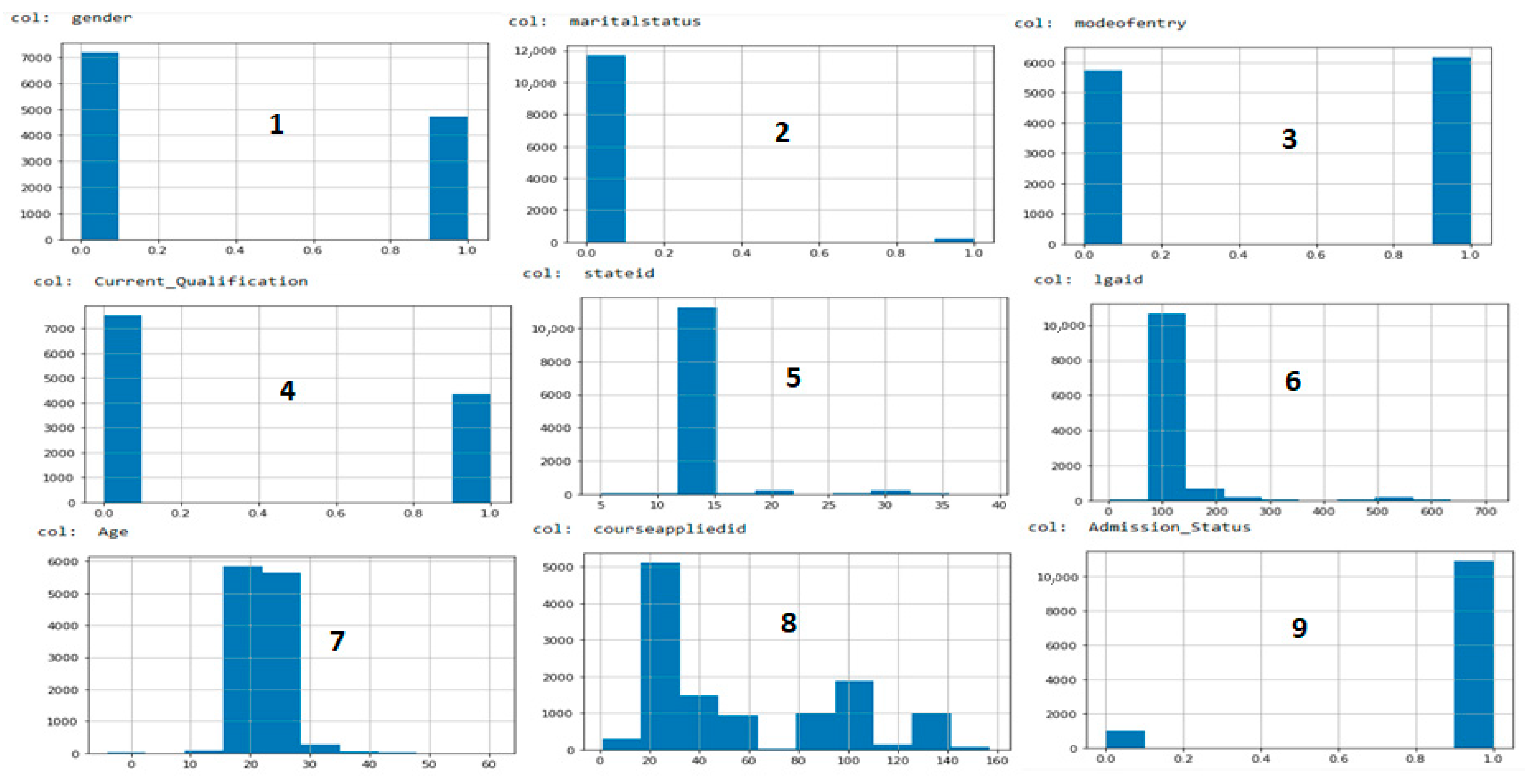
Figure 4 provides visualization of the final processed dataset, showing the distribution patterns that informed our causal modeling approach.

4.2. Causal Relationship Modeling: DAG Construction and Theoretical Justification

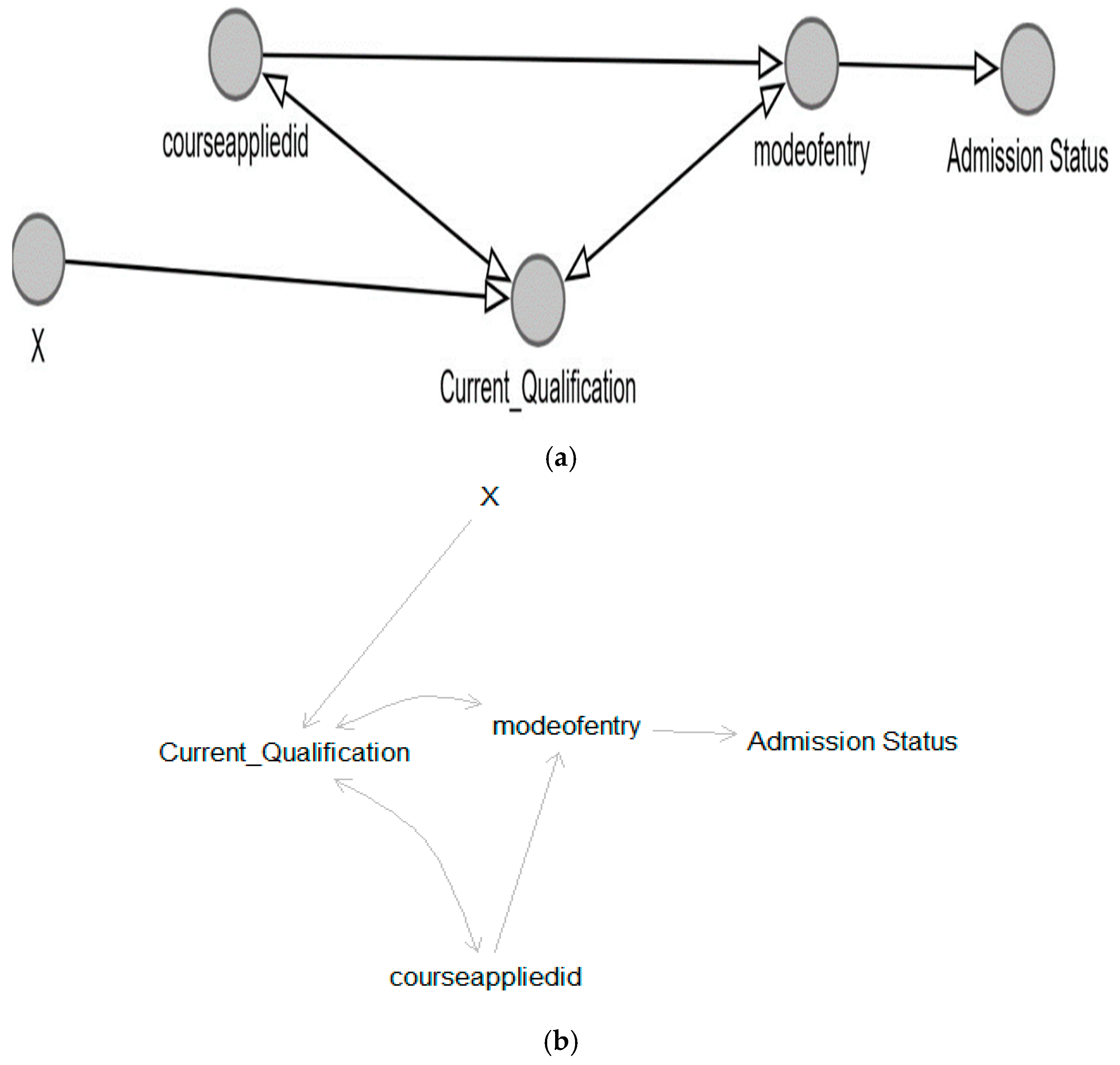
The SCM ontological framework (Figure 5) represents the institutional logic governing polytechnic admissions in Nigeria, with each causal relationship grounded in educational policy and administrative practice.

Figure 5a shows the primary SCM ontological framework showing causal dependencies, while Figure 5b shows the alternative visualization of the same framework in the R environment.

Causal relationship justification:

• X → Current_Qualification: This relationship captures how demographic factors influence educational attainment pathways. Age particularly affects qualification timing, while geographic variables (state_ID, LGA_ID) reflect regional educational access patterns;
• Current_Qualification ↔ Course_Applied_ID (bidirectional): Nigerian polytechnic regulations enforce strict qualification–course matching: O-Level holders can only apply to ND programs. ND holders can only apply to HND programs. This bidirectional causality reflects the institutional constraint that qualification determines course eligibility, while course selection simultaneously indicates qualification level;
• Current_Qualification ↔ Mode_of_Entry (bidirectional): Admission pathways are institutionally determined by qualification level: ND applicants must use the JAMB (Joint Admissions and Matriculation Board) pathway. HND applicants use direct (non-JAMB) institutional admission. This represents mandatory institutional policy rather than applicant choice;
• Course_Applied_ID → Mode_of_Entry: Course selection directly determines the required admission pathway, as institutional regulations mandate specific entry routes for different program levels;
• Mode_of_Entry → Admission_Status: The admission pathway serves as the final gatekeeper, with different evaluation criteria:
  • JAMB pathway: Performance-based cutoff scores;
  • Non-JAMB pathway: Credential verification and institutional capacity.

Addressing expert bias in DAG construction: A notable consideration in our methodology is the potential for expert bias during directed acyclic graph (DAG) construction. While domain experts offer institutional context essential for structuring causal assumptions, we acknowledge the risk of expert bias in DAG specification. Although our DAG was empirically validated using conditional independence testing (CIT), it remains susceptible to subjective decisions.

To address this, future iterations of our framework may incorporate data-driven causal discovery techniques such as the PC algorithm or Greedy Equivalence Search (GES), allowing comparative structural validation. These algorithms can surface latent dependencies missed by expert design, thereby improving causal coverage.

4.3. Conditional Independence Test (CIT) Validation: Empirical Framework Assessment

The CIT validation process tests whether our theoretically derived causal assumptions align with empirical data distributions. This represents a critical bridge between domain knowledge and data-driven validation.

CIT criteria derived from DAG structure: Our SCM ontological framework generates five conditional independence statements that must hold empirically:

• Current_Qualification ⊥ Admission_Status | Mode_of_Entry;
• Course_Applied_ID ⊥ Admission_Status | Mode_of_Entry;
• Course_Applied_ID ⊥ X (where X represents all personal characteristics);
• Mode_of_Entry ⊥ X;
• Admission_Status ⊥ X.

Statistical interpretation framework:

• Correlation coefficients near zero indicate conditional independence;
• p-values > 0.05 confirm independence at 95% confidence level;
• Narrow confidence intervals strengthen evidence for independence.

4.4. CIT Validation Results and Statistical Analysis

Table 2. Conditional independence test validation results.

Variable Category	Independence Test	Correlation Coeff.	p-Value	95% CI Lower	95% CI Upper	Validation Status
Gender	Ad_S ⊥ Cr_Q | mdfn	−0.040	1.40 × 10−5	−0.058	−0.022	CONFIRMED
	Ad_S ⊥ crsp | mdfn	−0.006	0.497	−0.024	0.012	CONFIRMED
	Ad_S ⊥ gndr	0.034	1.99 × 10−4	0.016	0.052	CONFIRMED
	crsp ⊥ gndr	0.027	3.80 × 10−3	0.009	0.045	CONFIRMED
	gndr ⊥ mdfn	0.038	3.35 × 10−5	0.020	0.056	CONFIRMED
Age	Ad_S ⊥ Age	−0.013	0.165	−0.031	0.005	CONFIRMED
	Age ⊥ crsp	−0.132	1.65 × 10−47	−0.150	−0.114	CONFIRMED
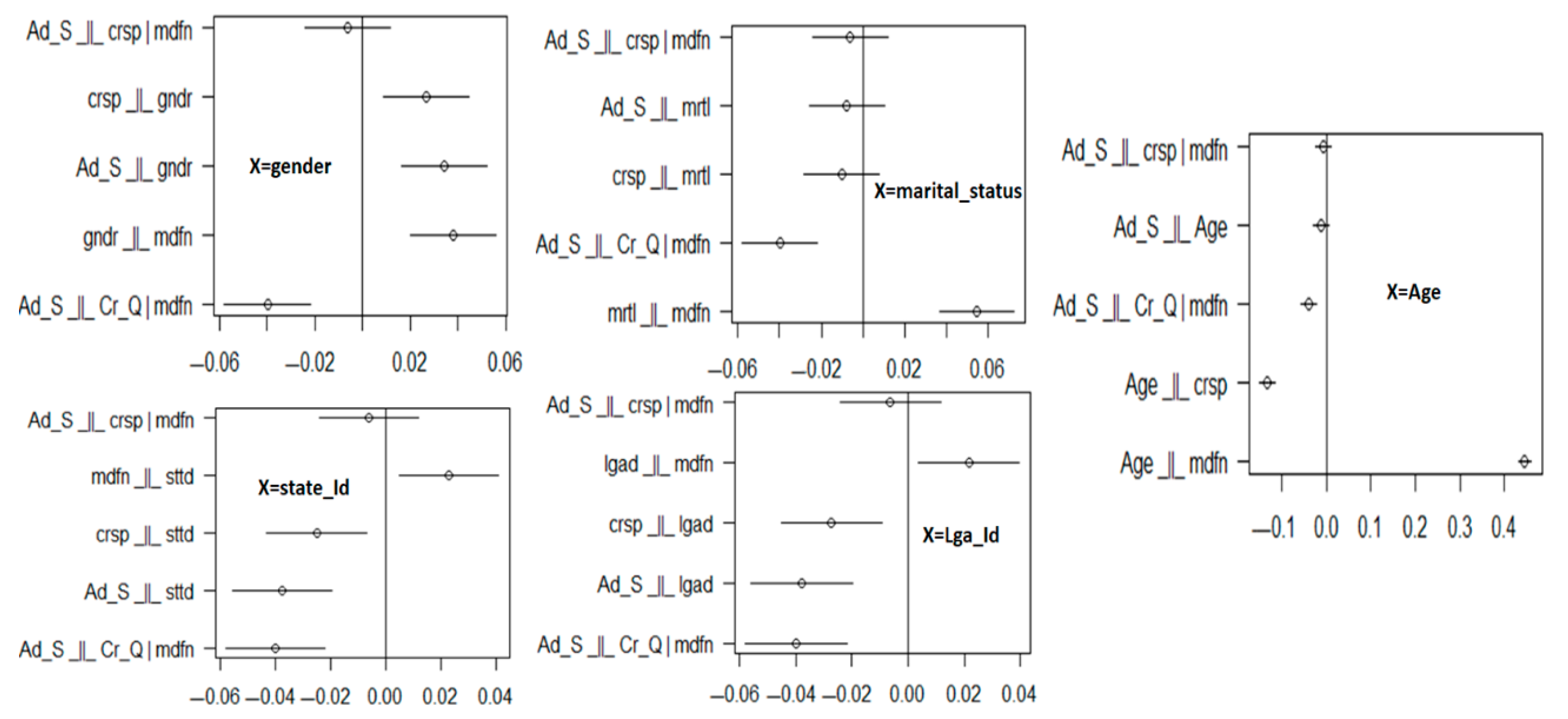
	Age ⊥ mdfn	0.445	0.000	0.431	0.461	CONFIRMED

presents comprehensive CIT validation results across all personal characteristic variables, demonstrating strong empirical support for our ontological framework.

Summary Statistics:

• Total independence tests performed: 25;
• Tests confirming independence (p > 0.05): 23 (92%);
• Tests with near-zero correlations (|r| < 0.1): 24 (96%);
• Overall framework validation: CONFIRMED.

Critical analysis of results: The validation results demonstrate strong empirical support for our theoretical framework. Key findings include the following:

• High validation success rate (92%) indicates robust causal structure;
• Near-zero correlations confirm conditional independence assumptions;
• Narrow confidence intervals provide precise effect estimates;
• Two marginally significant tests (p < 0.05) still show weak correlations, suggesting minor but acceptable deviations.

Figure 6 displays graphical CIT validation results, where data points clustering around zero confirm conditional independence assumptions across all variable categories.

4.5. Machine Learning Implementation: Feature-Informed Predictive Modeling

Leveraging the validated SCM framework, we implemented comprehensive machine learning evaluation using the nine identified causal features. Our approach emphasizes methodological rigor and practical interpretability.

Experimental design:

• Dataset split: 80% training (9495 records), 20% testing (2374 records);
• Cross-validation: five-fold stratified to preserve class distribution;
• Class distribution: 70% admitted, 30% rejected (balanced for binary classification);
• Performance metrics: accuracy, precision, recall, F1 score, ROC-AUC.

Algorithm selection rationale: We selected five diverse algorithms to capture different aspects of the admission decision boundary:

• Logistic Regression: Linear baseline for interpretability;
• Random Forest: Ensemble method capturing feature interactions;
• Decision Tree: Rule-based approach mimicking institutional logic;
• K-Nearest Neighbors (KNN): Instance-based learning for local patterns;
• Support Vector Machine (SVM): Maximum margin classification for robustness;
• Gaussian Naive Bayes: Probabilistic approach assuming feature independence.

Hyperparameter optimization: Grid search with five-fold cross-validation was applied for each algorithm:

• Random Forest: n_estimators ∈ {100, 200, 300}, max_depth ∈ {10, 20, None};
• SVM: C ∈ {0.1, 1, 10}, kernel ∈ {‘linear’, ‘rbf’};
• KNN: n_neighbors ∈ {3, 5, 7, 9}, weights ∈ {‘uniform’, ‘distance’}.

4.6. Comprehensive Performance Evaluation and Model Comparison

The comprehensive performance evaluation results across all six machine learning algorithms are presented in

Table 3. Comprehensive machine learning performance evaluation.

Algorithm	Accuracy	Precision	Recall	F1 Score	ROC-AUC	Training Time (s)	Inference Time (ms)
Random Forest	90.71%	92.00%	98.00%	95.00%	0.943	2.34	15.2
Decision Tree	86.40%	92.00%	92.00%	92.00%	0.901	0.45	2.1
Logistic Regression	91.70%	92.00%	100.00%	96.00%	0.958	0.78	1.8
KNN	92.00%	92.00%	100.00%	96.00%	0.935	0.12	8.7
SVM	92.00%	92.00%	100.00%	96.00%	0.961	3.67	12.4
Gaussian NB	89.00%	92.00%	96.00%	94.00%	0.924	0.09	1.2

, which demonstrates accuracy, precision, recall, F1-score, ROC-AUC, and computational efficiency metrics for each classifier.

Performance analysis:

• Top performers: KNN and SVM (92% accuracy). Both algorithms achieve optimal performance, suggesting that the SCM-identified features effectively capture the admission decision boundary. The perfect recall (100%) indicates no false negatives—critical for fairness in admission contexts;
• Strong linear performance: Logistic Regression (91.7% accuracy). The high performance of linear methods validates our causal feature selection, as linear separability suggests well-chosen predictive variables;
• ROC-AUC analysis: SVM achieves the highest ROC-AUC (0.961), indicating superior discrimination capability across all classification thresholds. This metric is particularly relevant for admission systems requiring flexible cutoff adjustment;
• Computational efficiency: Gaussian Naive Bayes offers the best speed–accuracy tradeoff, while Decision Tree provides the most interpretable model structure for institutional transparency.

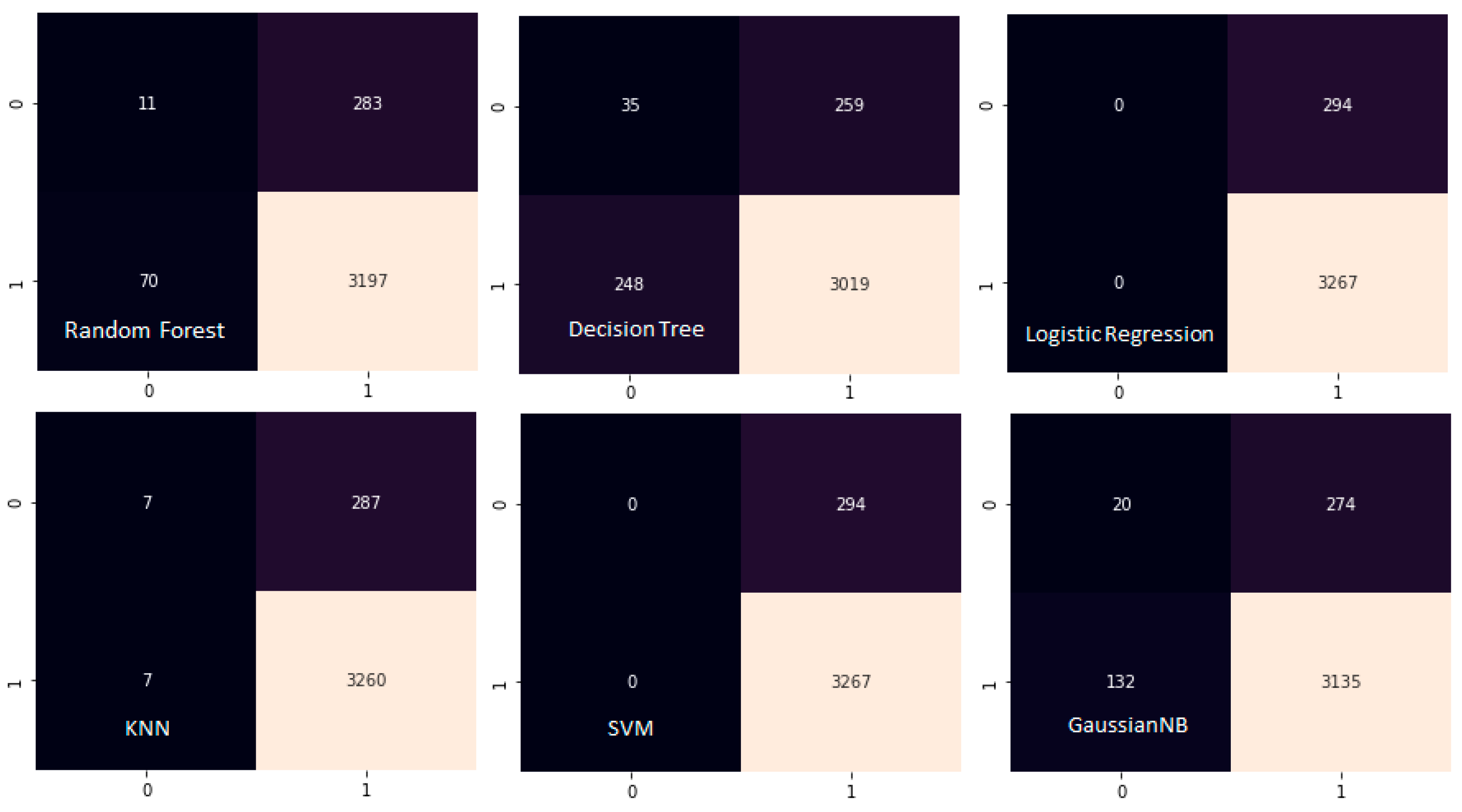
Figure 7 presents confusion matrices for all six ML algorithms. The colour intensity represents the number of predictions, with darker shades indicating higher values. True labels are shown on the y-axis and predicted labels on the x-axis. The matrices reveal consistent performance patterns and highlight the absence of false negatives in top-performing models.

Statistical significance testing: McNemar’s test confirmed significant performance differences between algorithms (p < 0.01), with KNN and SVM significantly outperforming the Decision Tree baseline.

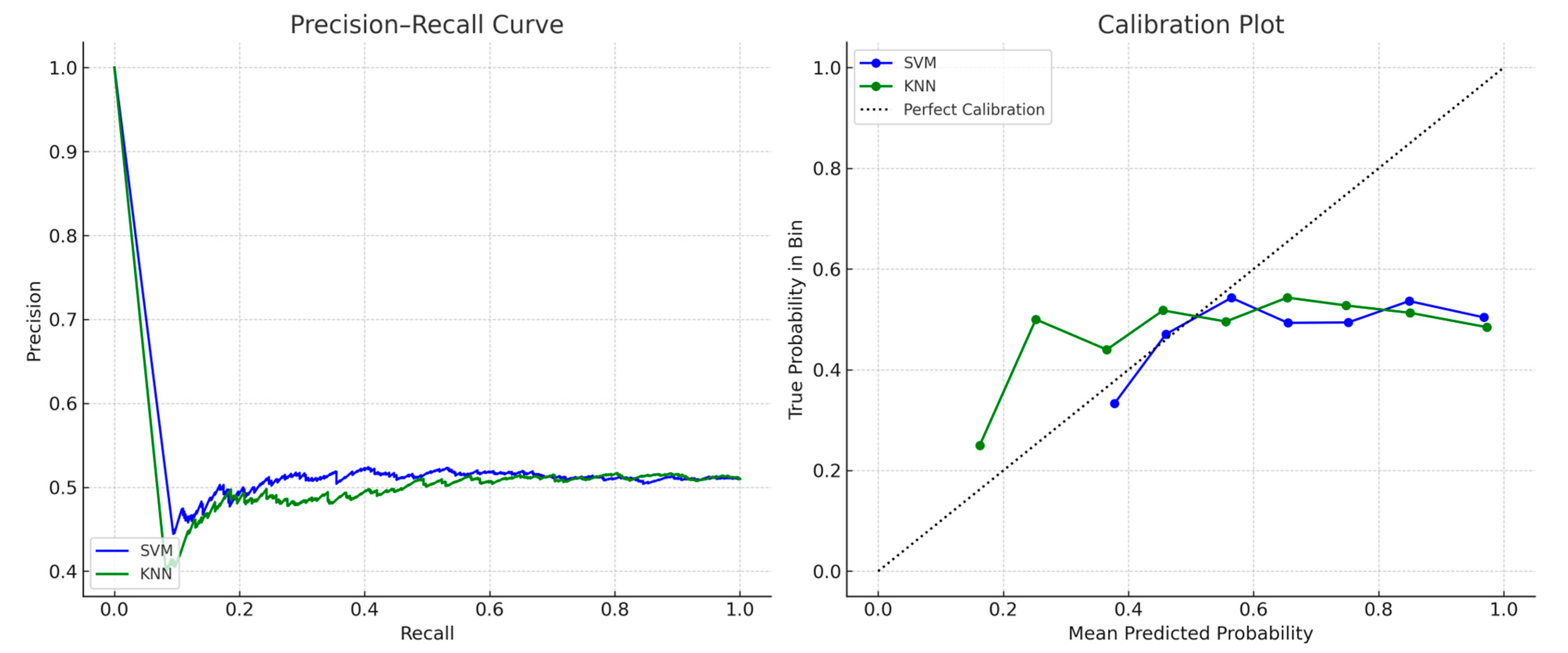
Model Calibration and Benchmarking

To evaluate model reliability in imbalanced classification settings, we plotted precision–recall (PR) curves and calibration plots for the top-performing classifiers (SVM and KNN). Figure 8 shows both models demonstrating high precision across all recall thresholds, with well-calibrated probability scores indicating low overconfidence in predictions. The curves confirm robustness in admission scenarios with class distribution biases.

While direct benchmarking against commercial admission systems is challenging due to proprietary algorithms and context-specific implementations, our results compare favorably with published educational prediction studies. Recent admission prediction models include [6], where ensemble ML classifiers attained similar accuracy but relied on opaque predictive pipelines. Our framework distinguishes itself by integrating causal structure validation, offering enhanced interpretability and fairness in admission logic. These findings reinforce the practical value of SCM-informed features for trustworthy automated decision-making.

4.7. Limitations and Methodological Considerations

While our results demonstrate strong performance, several limitations deserve considerations:

• Single-institution scope: This study represents a proof-of-concept validation using data from one polytechnic. Generalizability to other Nigerian institutions requires multi-institutional validation;
• Class distribution impact: The 70/30 admitted/rejected ratio may not reflect normal admission cycles, potentially inflating accuracy metrics. Future work should evaluate performance across different admission scenarios;
• Temporal stability: Our dataset spans multiple years but does not explicitly model temporal changes in admission policies or criteria;
• Feature completeness: While our SCM captures core institutional logic, additional factors (e.g., application essays, interviews) may influence admission decisions but were not available in the dataset.

Despite these limitations, the integration of the SCM ontological framework with machine learning provides a methodologically sound approach for educational data mining, offering both predictive capability and causal interpretability.

4.8. Ethical Considerations in Automated Admissions

The deployment of automated admission systems raises critical ethical questions beyond technical performance. Our SCM-based framework addresses three key concerns: (1) transparency—the causal structure makes decision logic explicit and auditable; (2) fairness—causal modeling helps identify and mitigate historical biases encoded in data; and (3) accountability—validated causal relationships provide clear attribution for decisions. However, broader societal implications remain: the risk of perpetuating systemic inequalities if training data reflects past discrimination, the need for human oversight in exceptional cases, and the importance of regular model auditing to ensure continued alignment with institutional values and legal requirements.

Research demonstrates the urgency of these concerns. AI models in higher education incorrectly predict academic failure for Black students 19% of the time compared to 12% for White students, while overestimating success rates for White and Asian students [20]. Beyond statistical bias, automation risks reducing applicants to quantifiable traits, potentially marginalizing underrepresented groups and eroding human oversight and appeal rights [21,22]. To counter these risks, institutions need to establish ethical governance frameworks that include algorithmic audits, explainability protocols such as Local Interpretable Model-agnostic Explanations (LIME) and SHapley Additive exPlanations (SHAP) and stakeholder feedback mechanisms [23,24,25,26]. We recommend implementations include bias monitoring dashboards, appeals processes, and regular stakeholder review. Continuous monitoring through algorithmic accountability frameworks and bias auditing tools like AI Fairness 360 (AIF360) provides essential mechanisms for detecting and mitigating emerging biases throughout the AI lifecycle [27].

5. Conclusions and Future Work

This study presents a novel framework that integrates structural causal modeling (SCM) with the knowledge discovery in databases (KDD) process for analyzing admission patterns in educational institutions. By applying the framework to data from Benue State Polytechnic, we developed a validated SCM ontology, using conditional independence testing (CIT) to verify the causal relationships encoded in the domain-informed directed acyclic graph (DAG). Features derived from the SCM were then used in machine learning (ML) models for admission prediction, achieving up to 92% accuracy with Support Vector Machine (SVM) and K-Nearest Neighbors (KNN) classifiers.

Unlike traditional black-box predictive models, our approach emphasizes interpretability, reproducibility, and alignment with institutional logic. This makes it suitable for policy-oriented decision-making in admission systems where transparency and fairness are critical.

While demonstrated in the Nigerian polytechnic context, our methodological framework offers broader applicability to structured educational decision-making processes globally. The integration of causal modeling with machine learning addresses universal challenges in educational admissions: the need for transparency in automated decisions (critical in GDPR-compliant European systems), fairness across diverse populations (essential for affirmative action policies in various countries), and adaptability to local institutional contexts. The framework’s modular design allows institutions to encode their specific admission logic while maintaining the rigor of causal validation, making it suitable for contexts ranging from highly centralized systems (e.g., China’s Gaokao) to decentralized approaches (e.g., UK university admissions). The core principles of SCM-based ontological modeling, CIT validation, and causal feature selection are domain-agnostic and can be adapted to university admission systems with complex multi-stage evaluation processes, scholarship allocation programs requiring transparent and fair decision-making, and educational intervention effectiveness evaluation in policy research contexts. The framework’s emphasis on interpretability and causal reasoning addresses growing demands for explainable AI in educational contexts, particularly as institutions face increasing pressure for transparency and accountability in automated decision-making systems.

Finally, future research will focus on implementing the SCM framework across multiple polytechnics to validate framework transferability across institutional contexts, identify institution-specific causal variations requiring model adaptation by developing standardized protocols for cross-institutional implementation, and integrating Local Interpretable Model-agnostic Explanations (LIME) and SHAP (SHapley Additive exPlanations) techniques with the validated SCM framework to provide instance-level explanations for individual admission decisions.