Nonignorable Consequences of (Partially) Ignoring Missing Item Responses: Students Omit (Constructed Response) Items Due to a Lack of Knowledge
Abstract
1. Introduction
2. Analysis of the Critique of Traditional Approaches to Handling Missing Item Responses
2.1. Aleatoric and Epistemic Uncertainty
2.2. Reasoning Based on Foundations of Psychometric Test Theory
3. Model-Based Treatment of Missing Item Responses
4. Two Alternative Item Response Models for Nonignorable Item Responses: Approaches for a Sensitivity Analysis
4.1. Pseudo-likelihood Approach for Partially Correct Scoring of Missing Item Responses
4.2. Modeling the Missing Response Process
5. Comparison of Four Countries in PIRLS 2011
5.1. Data
5.2. Analysis
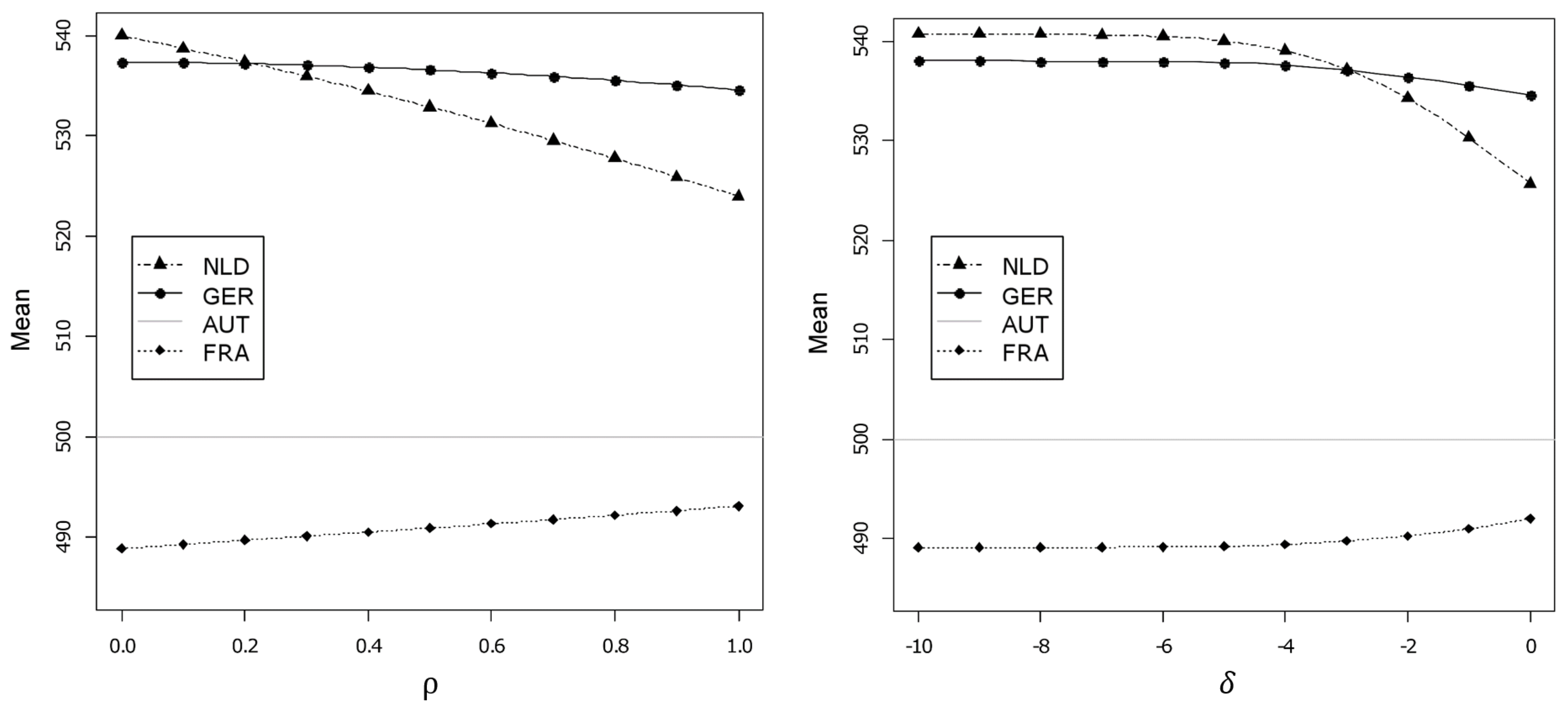
5.3. Results
6. Discussion
7. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lietz, P.; Cresswell, J.C.; Rust, K.F.; Adams, R.J. (Eds.) Implementation of Large-scale Education Assessments; Wiley: New York, NY, USA, 2017. [Google Scholar] [CrossRef]
- Foy, P.; Yin, L. Scaling the PIRLS 2016 achievement data. In Methods and Procedures in PIRLS 2016; Martin, M.O., Mullis, I.V., Hooper, M., Eds.; IEA: Paris, France; Boston College: Chestnut Hill, MA, USA, 2017. [Google Scholar]
- Foy, P.; Yin, L. Scaling the TIMSS 2015 achievement data. In Methods and Procedures in TIMSS 2015; Martin, M.O., Mullis, I.V., Hooper, M., Eds.; IEA: Paris, France; Boston College: Chestnut Hill, MA, USA, 2016. [Google Scholar]
- OECD. PISA 2018. Technical Report; OECD: Paris, France, 2020; Available online: https://bit.ly/3zWbidA (accessed on 7 March 2023).
- Pohl, S.; Ulitzsch, E.; von Davier, M. Reframing rankings in educational assessments. Science 2021, 372, 338–340. [Google Scholar] [CrossRef] [PubMed]
- Mislevy, R.J.; Wu, P.K. Missing Responses and IRT Ability Estimation: Omits, Choice, Time Limits, and Adaptive Testing; Research Report No. RR-96-30; Educational Testing Service: Princeton, NJ, USA, 1996. [Google Scholar] [CrossRef]
- Mislevy, R.J. Missing responses in item response modeling. In Handbook of Item Response Theory, Volume 2: Statistical Tools; van der Linden, W.J., Ed.; CRC Press: Boca Raton, FL, USA, 2016; pp. 171–194. [Google Scholar] [CrossRef]
- Bernshausen, H.; Fuhrmann, C.; Harney, H.L.; Harney, K. Form invariance—An alternative answer to the measurement problem of item response theory. Math. Stat. 2022, 10, 690–700. [Google Scholar] [CrossRef]
- Bock, R.D.; Moustaki, I. Item response theory in a general framework. In Handbook of Statistics, Volume 26: Psychometrics; Rao, C.R., Sinharay, S., Eds.; CRC Press: Boca Raton, FL, USA, 2007; pp. 469–513. [Google Scholar] [CrossRef]
- van der Linden, W.J.; Hambleton, R.K. (Eds.) Handbook of Modern Item Response Theory; Springer: New York, NY, USA, 1997. [Google Scholar] [CrossRef]
- van der Linden, W.J. Unidimensional logistic response models. In Handbook of Item Response Theory, Volume 1: Models; van der Linden, W.J., Ed.; CRC Press: Boca Raton, FL, USA, 2016; pp. 11–30. [Google Scholar] [CrossRef]
- Wagner, W. Item-Response-Theorie (IRT) [Item response theory]. In Handbuch Geschichts- und Politikdidaktik; Weißeno, G., Ziegler, B., Eds.; Springer: Wiesbaden, Germany, 2022; pp. 377–393. [Google Scholar] [CrossRef]
- Graham, J.W. Missing data analysis: Making it work in the real world. Annu. Rev. Psychol. 2009, 60, 549–576. [Google Scholar] [CrossRef]
- Schafer, J.L.; Graham, J.W. Missing data: Our view of the state of the art. Psychol. Methods 2002, 7, 147–177. [Google Scholar] [CrossRef] [PubMed]
- Rose, N.; von Davier, M.; Xu, X. Modeling Nonignorable Missing Data with Item Response Theory (IRT); Research Report No. RR-10-11; Educational Testing Service: Princeton, NJ, USA, 2010. [Google Scholar] [CrossRef]
- Rose, N.; von Davier, M.; Nagengast, B. Commonalities and differences in IRT-based methods for nonignorable item nonresponses. Psych. Test Assess. Model. 2015, 57, 472–498. [Google Scholar]
- Pohl, S.; Gräfe, L.; Rose, N. Dealing with omitted and not-reached items in competence tests: Evaluating approaches accounting for missing responses in item response theory models. Educ. Psychol. Meas. 2014, 74, 423–452. [Google Scholar] [CrossRef]
- OECD. PISA 2012. Technical Report; OECD: Paris, France, 2014; Available online: https://bit.ly/2YLG24g (accessed on 7 March 2023).
- Foy, P.; Fishbein, B.; von Davier, M.; Yin, L. Implementing the TIMSS 2019 scaling methodology. In Methods and Procedures: TIMSS 2019 Technical Report; Martin, M.O., von Davier, M., Mullis, I.V., Eds.; IEA: Paris, France; Boston College: Chestnut Hill, MA, USA, 2020. [Google Scholar]
- Mislevy, R.J. Randomization-based inference about latent variables from complex samples. Psychometrika 1991, 56, 177–196. [Google Scholar] [CrossRef]
- von Davier, M.; Sinharay, S. Analytics in international large-scale assessments: Item response theory and population models. In A Handbook of International Large-Scale Assessment: Background, Technical Issues, and Methods of Data Analysis; Rutkowski, L., von Davier, M., Rutkowski, D., Eds.; Chapman Hall/CRC Press: London, UK, 2013; pp. 155–174. [Google Scholar] [CrossRef]
- De Ayala, R.J.; Plake, B.S.; Impara, J.C. The impact of omitted responses on the accuracy of ability estimation in item response theory. J. Educ. Meas. 2001, 38, 213–234. [Google Scholar] [CrossRef]
- Pohl, S.; Carstensen, C.H. NEPS Technical Report—Scaling the Data of the Competence Tests; NEPS Working Paper No. 14; Otto-Friedrich-Universität, Nationales Bildungspanel: Bamberg, Germany, 2012; Available online: https://bit.ly/2XThQww (accessed on 7 March 2023).
- Pohl, S.; Carstensen, C.H. Scaling of competence tests in the national educational panel study —Many questions, some answers, and further challenges. J. Educ. Res. Online 2013, 5, 189–216. Available online: https://bit.ly/39AETyE (accessed on 7 March 2023).
- Rose, N. Item Nonresponses in Educational and Psychological Assessment. Unpublished Dissertation, Friedrich-Schiller-Universität Jena, Jena, Germany, 2013. Available online: https://bit.ly/3i6eaOS (accessed on 7 March 2023).
- von Davier, M. Omitted response treatment using a modified Laplace smoothing for approximate Bayesian inference in item response theory. PsyArXiv 2023. [Google Scholar] [CrossRef]
- Denoeux, T. Maximum likelihood estimation from fuzzy data using the EM algorithm. Fuzzy Sets Syst. 2011, 183, 72–91. [Google Scholar] [CrossRef]
- Senge, R.; Bösner, S.; Dembczyński, K.; Haasenritter, J.; Hirsch, O.; Donner-Banzhoff, N.; Hüllermeier, E. Reliable classification: Learning classifiers that distinguish aleatoric and epistemic uncertainty. Inf. Sci. 2014, 255, 16–29. [Google Scholar] [CrossRef]
- Denoeux, T. Maximum likelihood estimation from uncertain data in the belief function framework. IEEE Trans. Knowl. Data Eng. 2011, 25, 119–130. [Google Scholar] [CrossRef]
- Rohwer, G. Making Sense of Missing Answers in Competence Tests; (NEPS Working Paper No. 30); Otto-Friedrich-Universität, Nationales Bildungspanel: Bamberg, Germany, 2013; Available online: https://bit.ly/3AGfsr5 (accessed on 7 March 2023).
- Robitzsch, A. On the treatment of missing item responses in educational large-scale assessment data: An illustrative simulation study and a case study using PISA 2018 mathematics data. Eur. J. Investig. Health Psychol. Educ. 2021, 11, 117. [Google Scholar] [CrossRef] [PubMed]
- Robitzsch, A.; Lüdtke, O. Some thoughts on analytical choices in the scaling model for test scores in international large-scale assessment studies. Meas. Instrum. Soc. Sci. 2022, 4, 9. [Google Scholar] [CrossRef]
- Hennig, C. Some thoughts on simulation studies to compare clustering methods. Arch. Data Sci. Ser. A 2018, 5, 1–21. [Google Scholar] [CrossRef]
- Rose, N.; von Davier, M.; Nagengast, B. Modeling omitted and not-reached items in IRT models. Psychometrika 2017, 82, 795–819. [Google Scholar] [CrossRef]
- Birnbaum, A. Some latent trait models and their use in inferring an examinee’s ability. In Statistical Theories of Mental Test Scores; Lord, F.M., Novick, M.R., Eds.; MIT Press: Reading, MA, USA, 1968; pp. 397–479. [Google Scholar]
- Holland, P.W. On the sampling theory foundations of item response theory models. Psychometrika 1990, 55, 577–601. [Google Scholar] [CrossRef]
- Wainer, H. Visual revelations: Schrödinger’s cat and the conception of probability in item response theory. Chance 2010, 23, 53–56. [Google Scholar] [CrossRef]
- Molenaar, I.W. Some background for item response theory and the Rasch model. In Rasch Models: Foundations, Recent Developments, and Applications; Fischer, G.H., Molenaar, I.W., Eds.; Springer: New York, NY, USA, 1995; pp. 3–14. [Google Scholar] [CrossRef]
- Rasch, G. Probabilistic Models for Some Intelligence and Attainment Tests; Danish Institute for Educational Research: Copenhagen, Denmark, 1960. [Google Scholar]
- Naumann, A.; Hartig, J.; Hochweber, J. Absolute and relative measures of instructional sensitivity. J. Educ. Behav. Stat. 2017, 42, 678–705. [Google Scholar] [CrossRef]
- Robitzsch, A. Methodische Herausforderungen bei der Kalibrierung von Leistungstests [Methodological challenges in calibrating performance tests]. In Bildungsstandards Deutsch und Mathematik; Bremerich-Vos, A., Granzer, D., Köller, O., Eds.; Beltz Pädagogik: Weinheim, Germany, 2009; pp. 42–106. [Google Scholar]
- Meredith, W.; Teresi, J.A. An essay on measurement and factorial invariance. Med. Care 2006, 44, S69–S77. [Google Scholar] [CrossRef]
- van Bork, R.; Rhemtulla, M.; Sijtsma, K.; Borsboom, D. A causal theory of error scores. Psychol. Methods, 2022; epub ahead of print. [Google Scholar] [CrossRef]
- Frey, A.; Hartig, J.; Rupp, A.A. An NCME instructional module on booklet designs in large-scale assessments of student achievement: Theory and practice. Educ. Meas. 2009, 28, 39–53. [Google Scholar] [CrossRef]
- Molenaar, P.C.M. A manifesto on psychology as idiographic science: Bringing the person back into scientific psychology, this time forever. Meas. Interdiscip. Res. Persp. 2004, 2, 201–218. [Google Scholar] [CrossRef]
- Fischer, G.H.; Molenaar, I.W. (Eds.) Rasch Models: Foundations, Recent Developments, and Applications; Springer: New York, NY, USA, 1995. [Google Scholar] [CrossRef]
- Yen, W.M.; Fitzpatrick, A.R. Item response theory. In Educational Measurement; Brennan, R.L., Ed.; Praeger Publishers: Westport, CT, USA, 2006; pp. 111–154. [Google Scholar]
- Holman, R.; Glas, C.A.W. Modelling non-ignorable missing-data mechanisms with item response theory models. Br. J. Math. Stat. Psychol. 2005, 58, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Frey, A.; Spoden, C.; Goldhammer, F.; Wenzel, S.F.C. Response time-based treatment of omitted responses in computer-based testing. Behaviormetrika 2018, 45, 505–526. [Google Scholar] [CrossRef]
- Debeer, D.; Janssen, R.; De Boeck, P. Modeling skipped and not-reached items using IRTrees. J. Educ. Meas. 2017, 54, 333–363. [Google Scholar] [CrossRef]
- Glas, C.A.W.; Pimentel, J.L.; Lamers, S.M.A. Nonignorable data in IRT models: Polytomous responses and response propensity models with covariates. Psych. Test Assess. Model. 2015, 57, 523–541. Available online: https://bit.ly/3EOcX8M (accessed on 7 March 2023).
- Rosas, G.; Shomer, Y. Models of nonresponse in legislative politics. Legis. Stud. Q. 2008, 33, 573–601. [Google Scholar] [CrossRef]
- Fu, Z.H.; Tao, J.; Shi, N.Z. Bayesian estimation of the multidimensional graded response model with nonignorable missing data. J. Stat. Comput. Simul. 2010, 80, 1237–1252. [Google Scholar] [CrossRef]
- Santos, V.L.F.; Moura, F.A.S.; Andrade, D.F.; Gonçalves, K.C.M. Multidimensional and longitudinal item response models for non-ignorable data. Comput. Stat. Data Anal. 2016, 103, 91–110. [Google Scholar] [CrossRef]
- Kuha, J.; Katsikatsou, M.; Moustaki, I. Latent variable modelling with non-ignorable item nonresponse: Multigroup response propensity models for cross-national analysis. J. R. Stat. Soc. Ser. A Stat. Soc. 2018, 181, 1169–1192. [Google Scholar] [CrossRef]
- Okumura, T. Empirical differences in omission tendency and reading ability in PISA: An application of tree-based item response models. Educ. Psychol. Meas. 2014, 74, 611–626. [Google Scholar] [CrossRef]
- Pohl, S.; Becker, B. Performance of missing data approaches under nonignorable missing data conditions. Methodology 2020, 16, 147–165. [Google Scholar] [CrossRef]
- Köhler, C.; Pohl, S.; Carstensen, C.H. Investigating mechanisms for missing responses in competence tests. Psych. Test Assess. Model. 2015, 57, 499–522. Available online: https://bit.ly/3zOCcEp (accessed on 7 March 2023).
- Ulitzsch, E.; von Davier, M.; Pohl, S. Using response times for joint modeling of response and omission behavior. Multivar. Behav. Res. 2020, 55, 425–453. [Google Scholar] [CrossRef]
- Kreitchmann, R.S.; Abad, F.J.; Ponsoda, V. A two-dimensional multiple-choice model accounting for omissions. Front. Psychol. 2018, 9, 2540. [Google Scholar] [CrossRef]
- Zhou, S.; Huggins-Manley, A.C. The performance of the semigeneralized partial credit model for handling item-level missingness. Educ. Psychol. Meas. 2019, 80, 1196–1215. [Google Scholar] [CrossRef]
- Lu, J.; Wang, C. A response time process model for not-reached and omitted items. J. Educ. Meas. 2020, 57, 584–620. [Google Scholar] [CrossRef]
- Weeks, J.P.; von Davier, M.; Yamamoto, K. Using response time data to inform the coding of omitted responses. Psych. Test Assess. Model. 2016, 58, 671–701. Available online: https://bit.ly/3AG33U7 (accessed on 7 March 2023).
- Harel, O.; Schafer, J.L. Partial and latent ignorability in missing-data problems. Biometrika 2009, 96, 37–50. [Google Scholar] [CrossRef]
- Bartolucci, F.; Montanari, G.E.; Pandolfi, S. Latent ignorability and item selection for nursing home case-mix evaluation. J. Classif. 2018, 35, 172–193. [Google Scholar] [CrossRef]
- Beesley, L.J.; Taylor, J.M.G.; Little, R.J.A. Sequential imputation for models with latent variables assuming latent ignorability. Aust. N. Z. J. Stat. 2019, 61, 213–233. [Google Scholar] [CrossRef]
- Jung, H.; Schafer, J.L.; Seo, B. A latent class selection model for nonignorably missing data. Comput. Stat. Data Anal. 2011, 55, 802–812. [Google Scholar] [CrossRef]
- Köhler, C.; Pohl, S.; Carstensen, C.H. Taking the missing propensity into account when estimating competence scores: Evaluation of item response theory models for nonignorable omissions. Educ. Psychol. Meas. 2015, 75, 850–874. [Google Scholar] [CrossRef]
- Bertoli-Barsotti, L.; Punzo, A. Rasch analysis for binary data with nonignorable nonresponses. Psicologica 2013, 34, 97–123. Available online: https://bit.ly/3agqA2g (accessed on 7 March 2023).
- Bacci, S.; Bartolucci, F. A multidimensional finite mixture structural equation model for nonignorable missing responses to test items. Struct. Equ. Model. 2015, 22, 352–365. [Google Scholar] [CrossRef]
- Bacci, S.; Bartolucci, F.; Grilli, L.; Rampichini, C. Evaluation of student performance through a multidimensional finite mixture IRT model. Multivar. Behav. Res. 2017, 52, 732–746. [Google Scholar] [CrossRef] [PubMed]
- Lord, F.M. Estimation of latent ability and item parameters when there are omitted responses. Psychometrika 1974, 39, 247–264. [Google Scholar] [CrossRef]
- Resseguier, N.; Giorgi, R.; Paoletti, X. Sensitivity analysis: When data are missing not-at-random. Epidemiology 2011, 22, 282–283. [Google Scholar] [CrossRef] [PubMed]
- van Buuren, S. Flexible Imputation of Missing Data; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar] [CrossRef]
- Gruhl, J.; Erosheva, E.A. A tale of two (types of) memberships: Comparing mixed and partial membership with a continuous data example. In Handbook of Mixed Membership Models and Their Applications; Airoldi, E.M., Blei, D., Erosheva, E.A., Fienberg, S.E., Eds.; Chapman & Hall: Boca Raton, FL, USA, 2015; pp. 15–38. [Google Scholar] [CrossRef]
- Warm, T.A. Weighted likelihood estimation of ability in item response theory. Psychometrika 1989, 54, 427–450. [Google Scholar] [CrossRef]
- Aitkin, M. Expectation maximization algorithm and extensions. In Handbook of Item Response Theory, Volume 2: Statistical Tools; van der Linden, W.J., Ed.; CRC Press: Boca Raton, FL, USA, 2016; pp. 217–236. [Google Scholar] [CrossRef]
- Rosas, G.; Shomer, Y.; Haptonstahl, S.R. No news is news: Nonignorable nonresponse in roll-call data analysis. Am. J. Pol. Sci. 2015, 59, 511–528. [Google Scholar] [CrossRef]
- Guo, J.; Xu, X. An IRT-based model for omitted and not-reached items. arXiv 2019, arXiv:1904.03767. [Google Scholar]
- Robitzsch, A.; Lüdtke, O. An item response model for omitted responses in performance tests. In Proceedings of the International Meeting of the Psychometric Society (IMPS 2017), Switzerland, Zurich, 18–21 July 2017; Available online: https://bit.ly/3u8rgjy (accessed on 7 March 2023).
- Deribo, T.; Kroehne, U.; Goldhammer, F. Model-based treatment of rapid guessing. J. Educ. Meas. 2021, 58, 281–303. [Google Scholar] [CrossRef]
- Sportisse, A.; Boyer, C.; Josse, J. Imputation and low-rank estimation with missing not at random data. Stat. Comput. 2020, 30, 1629–1643. [Google Scholar] [CrossRef]
- Hanson, B. IRT Parameter Estimation Using the EM Algorithm. Technical Report. 2000. Available online: https://bit.ly/3i4pOdg (accessed on 7 March 2023).
- R Core Team. R: A Language and Environment for Statistical Computing; R Core Team: Vienna, Austria, 2022; Available online: https://www.R-project.org/ (accessed on 11 January 2022).
- Robitzsch, A. Sirt: Supplementary Item Response Theory Models. R Package Version 3.12-66. 2022. Available online: https://CRAN.R-project.org/package=sirt (accessed on 17 May 2022).
- Arts, I.; Fang, Q.; Meitinger, K.; van de Schoot, R. Approximate measurement invariance of willingness to sacrifice for the environment across 30 countries: The importance of prior distributions and their visualization. Front. Psychol. 2021, 12, 624032. [Google Scholar] [CrossRef] [PubMed]
- Asparouhov, T.; Muthén, B. Multiple-group factor analysis alignment. Struct. Equ. Model. 2014, 21, 495–508. [Google Scholar] [CrossRef]
- Robitzsch, A. Exploring the multiverse of analytical decisions in scaling educational large-scale assessment data: A specification curve analysis for PISA 2018 mathematics data. Eur. J. Investig. Health Psychol. Educ. 2022, 12, 54. [Google Scholar] [CrossRef]
- Kolen, M.J.; Brennan, R.L. Test Equating, Scaling, and Linking; Springer: New York, NY, USA, 2014. [Google Scholar] [CrossRef]
- Robitzsch, A.; Kiefer, T.; Wu, M. TAM: Test Analysis Modules. R Package Version 4.1-4. 2022. Available online: https://CRAN.R-project.org/package=TAM (accessed on 28 August 2022).
- Siddique, J.; Harel, O.; Crespi, C.M. Addressing missing data mechanism uncertainty using multiple-model multiple imputation: Application to a longitudinal clinical trial. Ann. Appl. Stat. 2012, 6, 1814–1837. [Google Scholar] [CrossRef]
- Dai, S. Handling missing responses in psychometrics: Methods and software. Psych 2021, 3, 43. [Google Scholar] [CrossRef]
- Huisman, M. Imputation of missing item responses: Some simple techniques. Qual. Quant. 2000, 34, 331–351. [Google Scholar] [CrossRef]
- Sinharay, S. Reporting proficiency levels for examinees with incomplete data. J. Educ. Behav. Stat. 2022, 47, 263–296. [Google Scholar] [CrossRef]
- Yucel, R.M. Multiple imputation inference for multivariate multilevel continuous data with ignorable non-response. Philos. Trans. R. Soc. A 2008, 366, 2389–2403. [Google Scholar] [CrossRef] [PubMed]
- Audet, L.A.; Desmarais, M.; Gosselin, É. Handling missing data through prevention strategies in self-administered questionnaires: A discussion paper. Nurse Res. 2022, 30, 9–18. [Google Scholar] [CrossRef] [PubMed]
- Shultz, K.S.; Whitney, D.J.; Zickar, M.J. Measurement Theory in Action: Case Studies and Exercises; Routledge: New York, NY, USA, 2020. [Google Scholar] [CrossRef]
- Wainer, H.; Braun, H.I. (Eds.) Test Validity; Routledge: New York, NY, USA, 1988. [Google Scholar] [CrossRef]
- Kane, M.T. Validating the interpretations and uses of test scores. J. Educ. Meas. 2013, 50, 1–73. [Google Scholar] [CrossRef]
- Gorgun, G.; Bulut, O. A polytomous scoring approach to handle not-reached items in low-stakes assessments. Educ. Psychol. Meas. 2021, 81, 847–871. [Google Scholar] [CrossRef] [PubMed]
- Robitzsch, A.; Lüdtke, O. Reflections on analytical choices in the scaling model for test scores in international large-scale assessment studies. PsyArXiv 2021. [Google Scholar] [CrossRef]
| Model | AUT | GER | FRA | NLD |
|---|---|---|---|---|
| M1: missing = incorrect | 500 | 537.5 | 488.7 | 540.3 |
| M2: missing = ignorable | 500 | 534.2 | 492.4 | 523.4 |
| M3: 2-dim. model | 500 | 534.9 | 492.5 | 524.8 |
| M4: pseudo-likelihood (for multiple-choice items) | 500 | 537.6 | 489.4 | 539.5 |
| M5: pseudo-likelihood | ||||
| 500 | 537.3 | 488.9 | 539.9 | |
| 500 | 537.0 | 490.1 | 535.9 | |
| 500 | 535.9 | 491.8 | 529.5 | |
| 500 | 534.6 | 493.1 | 524.0 | |
| M6: 2-dim. model | ||||
| 500 | 538.0 | 489.1 | 540.7 | |
| 500 | 535.9 | 490.6 | 532.4 | |
| 500 | 535.1 | 491.5 | 528.0 | |
| 500 | 534.6 | 492.1 | 525.7 |
| Model | AUT | DEU | FRA | NLD |
|---|---|---|---|---|
| N1: , | 47,741 | 36,366 | 45,029 | 33,142 |
| N2: , | 47,827 | 36,414 | 45,263 | 33,144 |
| N3: estimated, | 47,722 | 36,365 | 45,028 | 33,130 |
| N4: , estimated | 47,677 | 36,285 | 44,888 | 33,127 |
| N5: , estimated | 47,790 | 36,355 | 45120 | 33134 |
| N6: estimated, estimated | 47,666 | 36,288 | 44,887 | 33,120 |
| Model | AUT | DEU | FRA | NLD |
|---|---|---|---|---|
| N1: , | 500 | 535.4 | 494.1 | 526.9 |
| N2: , | 500 | 537.6 | 489.8 | 542.0 |
| N3: estimated, | 500 | 537.1 | 497.9 | 530.9 |
| N4: , estimated | 500 | 535.1 | 493.3 | 526.9 |
| N5: , estimated | 500 | 537.6 | 489.9 | 542.0 |
| N6: estimated, estimated | 500 | 537.4 | 495.8 | 530.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Robitzsch, A. Nonignorable Consequences of (Partially) Ignoring Missing Item Responses: Students Omit (Constructed Response) Items Due to a Lack of Knowledge. Knowledge 2023, 3, 215-231. https://doi.org/10.3390/knowledge3020015
Robitzsch A. Nonignorable Consequences of (Partially) Ignoring Missing Item Responses: Students Omit (Constructed Response) Items Due to a Lack of Knowledge. Knowledge. 2023; 3(2):215-231. https://doi.org/10.3390/knowledge3020015
Chicago/Turabian StyleRobitzsch, Alexander. 2023. "Nonignorable Consequences of (Partially) Ignoring Missing Item Responses: Students Omit (Constructed Response) Items Due to a Lack of Knowledge" Knowledge 3, no. 2: 215-231. https://doi.org/10.3390/knowledge3020015
APA StyleRobitzsch, A. (2023). Nonignorable Consequences of (Partially) Ignoring Missing Item Responses: Students Omit (Constructed Response) Items Due to a Lack of Knowledge. Knowledge, 3(2), 215-231. https://doi.org/10.3390/knowledge3020015






