1. Introduction
Representation is one of the essential abilities in mathematics learning [
1,
2,
3,
4]. Representation can reduce difficulties in solving word problems, for example, communicating ideas between signs, words or symbols, expressions, or images [
2,
3,
4]. Representation serves as a medium to assist students in understanding and integrating remembered information with new information presented in the problem [
1]. Furthermore, representation is the process of modeling tangible things in the real world into abstract concepts or symbols [
5,
6]. Filloy, Rojano, and Solares [
7] argue that representation is a mental picture of mental development visualized in mathematical thinking, which helps solve word problems. Representation has a role in strengthening students’ understanding to build concepts and solve problems, especially in word problems [
8] and as a forum for mathematical thinking [
9]. Therefore, representation is needed to solve the word mathematics problems.
Previous studies have focused on identifying student representations in solving word problems and categorizing the types of representations proposed by students and teachers [
10,
11,
12]. Students who produce representations mean they conduct relationship processing and understand interpreting word problems [
10]. Boonen, Wesel, Jolles, and School [
13] describe that students who produce accurate schematic visual representations have better problem-solving abilities than students who make schematic representations of visuals and inaccurate images. Therefore, students with low spatial knowledge tend to build image representations in solving word problems.
Furthermore, Poch, Garderen, and Scheuermann [
12] add that visual representations are needed to interpret verbal problems and when students produce representations. Özsoy [
11] found that students with high spatial abilities build schematic structured representations. At the same time, Rahmah and Irawati [
14] analyzed students’ mathematical representations in solving mathematical problems, which included pictorial, symbol, and verbal–written representations. Then, Cromley et al. [
15] formulated the stages of coordinating representation in three main aspects: matching, comparing, and concluding. However, from the results of the above studies, few researchers have yet to find out about students’ different representation processes in solving word problems.
There are still many students experiencing difficulties in representing word problems [
16,
17,
18]. Difficulties experienced by students when solving word problems are due to a lack of understanding in interpreting problems and the inability to represent mathematical terms in word problems. Hackenberg [
16], through “Student and Professor Problems,” found that most students mistakenly interpret mathematical terms when understanding word problems. This finding is like inquiry, which conducts investigations on middle-level students; about 70% of students erroneously construct word problems for proportional and fractional situations [
17]. Additionally, Beckmann and Izsak [
18] found that there was a tendency for students to solve problems that were operational rather than descriptive. However, there are fifth-grade elementary school students in Makassar, Indonesia. When given the task to solve word problems, namely “There are 28 students in fifth grade. Many female students in grade five, four more than male students. How many female students are in grade 5?” Students solve these word problems by producing different representations and finding the correct answer. However, this is not suitable for some mathematics teachers who only focus on the accuracy and correctness of the mathematical content in the answers written by students [
19]. Based on previous findings, researchers suspect that the different representational processes produced by students play a role in solving word problems. In contrast, previous studies have not explored the students’ other representation processes in solving word problems.
Representing mathematical word problem solving is not just writing formulas, symbols, or operations to produce answers [
5]. However, students need to form different expressions in describing solutions to problems. The resulting representation will be incorrect if students do not have good representation knowledge [
20]. Research shows that students need to know many ways to obtain successful solutions in solving mathematical problems [
21,
22]. Therefore, students need to know several forms of representation and some ways of carrying out a good representation process in solving word problems.
In this article, we revealed the different representation processes of students in solving word problems. This study aims to describe the representation process of diverse students in solving word problems. The representation process intended to produce representations in this article starts with students being given word problem assignments to be solved until finding the correct answer.
2. Methods
This research used a qualitative approach with a case study design. The researcher determined whether students have already solved word problems, either in class or in additional coursework classes. It is essential to ensure that prospective subjects have the knowledge and experience in solving mathematical word problems. The instruments used in this study were word problem assignments adapted from Kaur, Ban-har, and Kapur [
23] and interview instruments for the mathematical problem solving were from the yearbook of the association of mathematics educators. Word problems are translated into Indonesian. These word problems are used as assignments for problem-solving in grades 3 and 5 of primary schools in Singapore. Word problems are presented by Yeap [
24] in
Figure 1. Meanwhile, word problems result from adaptations used in this study in
Figure 2.
Considerations were made for adapting problem-posing mathematical tasks according to the elementary school level. In addition, the school-level curriculum in Singapore has a problem submission model, while the primary school-level curriculum in Indonesia is still at the level of problem solving. Therefore, problems were simplified from problem solving to mathematical word problem solving. In addition, changing scores of many male and female students were adjusted according to student data at the study site. This makes it more contextual, makes it easier for students to solve word problems, and can attract students’ attention to solve word problems, as shown in
Figure 2.
This study involved 75 grade 5 elementary school students (10–11 years old) in Makassar City, Indonesia. Students were asked to complete word problem assignments given by researchers. Students’ answers were grouped based on the resulting representations, namely symbol representations and correct answers, symbol representations but incorrect answers, and different representations to find the right solutions. The two subjects chosen in this study produced other representations, namely (verbal–written–table–symbol) and (verbal–written–graphic–symbol), for more in-depth interviews related to the representation process to create different representations. Students were selected based on good communication skills, confidence, and willingness to participate in research. The teacher helped researchers to choose students who met these requirements. Interviews were conducted to more closely track the different representations produced.
The research procedure involved the stages of giving word problem assignments, identifying, and grouping students’ answers based on the representations produced in solving word problems, interviewing students regarding the resulting representations, and analyzing data on assignment results and student interviews. Student interviews were recorded audio–visually, then transcribed. The data analysis technique used was qualitative data analysis and was carried out exploratively and continuously, which requires continuous reflection until the data are saturated. Data analysis steps include processing, preparing, reading, analyzing more details, coding, describing, presenting data in the narrative form, and interpreting data [
25].
3. Results
The initial activity carried out by researchers involved giving word problems to 75 students. After students solved the word problems, student answers were collected, then identified, and grouped based on the representations produced in solving word problems. Based on the student results identification, 75% students solved word problems that produced one or two forms and some even produced three different representations and found the right answer. A total of 25% of students solved word problems with one form of representation and incorrect answers. In this article, the researcher focuses on the work of two students who were found to solve word problems and find the correct answer by using different representations (verbal–written–graphic–symbol and verbal–written–symbol–table). It was decided because it was considered that student representation was different from other students and resulted in three forms of representation in solving word problems. Here are the results of solving word problems and interviewing the subject using different representations with the coding of Subject 1 (S1) and Subject 2 (S2) then described to be understood and interpreted.
A description of the process of representing different subjects (S1) in solving word problems based on observations and interviews of researchers follows. The first activity undertaken by S1 after being given word problems was reading the text word problems repeatedly. After reading, S1 identified the text in word problems. Before solving the word problems until finding an answer, the student wrote some things that were considered important and marked things that were known. Important things that were marked were “male = L” and “female = P. The reason for S1 in writing these important things was that it was easier to distinguish men from women and to be a reference in solving word problems. In solving word problems, S1 used three forms of representation in solving word problems, namely verbal–written–table–symbol. The following are the different representations produced by S1 in
Figure 3.
The first representation presented by S1 in solving word problems was for written–verbal representation. S1 interpreted that the text in the word problems “women 4 more than men”, was suitable using the checked method and it was converted into a 2 × 2 table. However, before drawing the table, S1 outlined in the form of written–verbal. From the first representation, the researcher asked “why to start by writing” the checked method, because there are four more women than men, then the table is 2 × 2 as follows. The researcher asked while showing the written verbal representation of S1 “why don’t you draw a straight picture of the table? Why does it have to be written again? S1 paused for a moment and answered: “as an explanation for drawing tables (while pointing to the table in
Figure 3)”. The researcher responded and asked again “I mean, why is not the table drawn directly? S1 answered, “so that the table is clearer based on this description while pointing to the verbal representation written in
Figure 3. The researcher asked “Why is there a 2 × 2 operation? “. S1 answered, “Because the table that I made is 2 columns and 2 rows”.
S1 realized the first representation (written–verbal) into a graphical image as the second representation, from the table. The researcher asked, “What do you think, why do you want to draw a table in solving these word problems?”. S1 answered, “Because I often draw when solving questions like this. The researcher asked again“. Then why the table picture, why not other images such as circles, graphs, or others?”. S1 answered, “Because the picture that I usually use in solving problems like this is a table”. S1 indeed needed to produce a (second) table representation, because the first representation (verbal) with the second representation (table) were interrelated. When the table representation was not made, the S1 representation was incomplete. This was revealed by S1 when the researcher asked: “if you do not make a table what?”. S1 paused for a moment and answered: “if I do not draw this picture (pointing at the graphic image), then this does not apply pointing at the verbal representation, because the two are interrelated”. In addition, the researcher asked about the existence of the symbols B1 and B2 written by S1, on the left side of the table, and the symbols P, L, and number 4 in
Figure 3. S1 answered, “B1 = first row is P (female) and B2 = line the second is L (male), while the number 4 in B2 indicates that women are equal to many men. I added 4 according to the text word problems that said (four women more than men)”. Furthermore, S1 utilizes the text word problems that are understood to produce two equations namely “P = L + 4 … (1)” as the first equation and “P + L = 28”, as the second equation.” S1 revealed that the source “P = L + 4 … (1)”, because it would be counted “four women more than men”. Whereas “P + L = 28”, because “the total number of students in the class is 28.” This equation is used in symbol representations in algebraic arithmetic operations to find the correct answer.
Representation of S1 symbols to find solutions for solving word problems. It made it clear that the word problems given were well understood. S1 proved that producing different and interrelated representations could find the right answer. This evidence was presented through a research interview. The researcher’s question is related to the representation “B1 = B2”. S1 answered, “B1 = B2 because of 2 × 2, two columns of two rows. While the origin of “L = P − 4”, the researcher did not ask again because it was written in the answer, that it came from Equation 1 in
Figure 3. So, the researcher immediately asked the source of “P + (P − 4) = 28”. S1 answered, “From here (pointing to Equation 1) and from here (pointing to Equation 2)”. The next research question “why from” P + (P − 4) = 28 “you immediately write P = 16? How do get it?” S2 immediately answered quickly and said that “from P + (P − 4) = 28, keep opening the brackets so we get P + P − 4 = 28, then it becomes 2P − 4 = 28, then 2P − 4 = 28, then respectively − each segment is added 4, so that 2P = 28 + 4, becomes 2P = 32, then 32 divided by 2, the result is P = 16. So many female students are 16.” The researcher asked after S1 found the answer “why don’t you immediately finish with performing a count operation to quickly find out the answer to these word problems? S1 answered, “because I want my answer to be different from other friends. Aside from the results of the test-based interviews, researchers also conducted interviews on S1 based on the subject’s movements or style. The final question the researcher had was the movement of the finger up and down while pointing at the answer sheet when answering the researcher’s question, and after the subject found the answer to word problems. S1 answered, “oh… if that’s the case, I look back at the completion of the answer that I’m working on. Besides that, I want to know whether my process and answers are correct or not”.
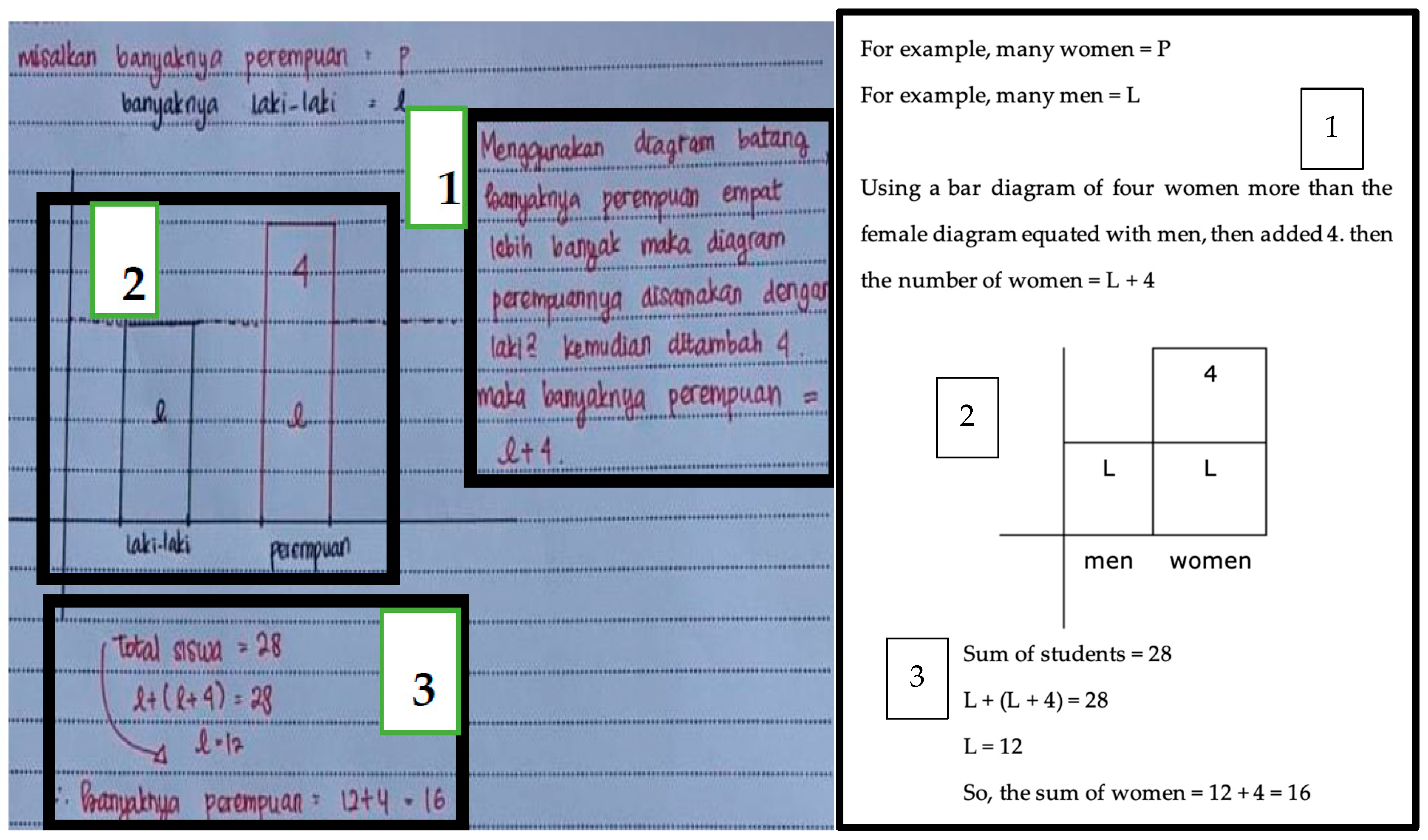
Based on observations and interviews of the researchers, the first activity undertaken by S2 was the same as the activity of S1 after they were given word problems, that is, reading text word problems repeatedly. After reading the word problems, S2 identified text in word problems, then wrote things that were considered important and marked them as known, before solving word problems until finding the correct answer. Important things to be noted include “male = L” marked with black ink while “female = P” marked with red ink. The reason S2 used two different inks was so that someone who sees the completion of these word problems, can more easily distinguish objects that are stated in the text word problems. S2 marked, by writing down these important things, to distinguish between men and women and the sign, used in solving word problems. In solving word problems, S2 produced three forms of representation in solving word problems, namely (verbal–written–graphic–symbol). The following are the different representations produced by S2 in
Figure 4.
The next activity involved S2 interpreting the text in word problems. With verbal–written representations as to the first representation produced in solving word problems accompanied by equations. From the first (verbal–written) representation produced by S2 “using a bar diagram, there are four women more than the female diagram compared to men, then added 4, so the number of women = L + 4”. The researcher asked, “Why should it be written down again, why not directly draw a graph”. S2 answered “This paper (pointing to a verbal representation in
Figure 4), as a guide for the second representation (graph)”. The researcher asked again “Why graphic images, why not circles, tables or others”. S2 answered “because I used to use graphs when answering story questions, and if it is graphical, it is easier to draw to compare things. The researcher asked, “Compare what how?”. S2 answered “comparing objects expressed in word problems. The researcher asked, “what kind of object? S2 answered, “like a person or thing to a problem, and this question is said,” there are four women more than men, then the image of the female rod that I drew is higher than the image of the male bar”.
Furthermore, from the verbal representation produced first, S2 drew a graphical representation based on the instruction of the first (verbal) representation, which was both interrelated. So, both needed to be shown by S2. It was revealed by S2 from the researcher’s question, “if, you did not draw this graphical form (while pointing to
Figure 4) what do you think?”. S2 answered, “it cannot be absent (while pointing to the graphical representation in
Figure 4) because it is explained by these words (while pointing to the verbal representation in
Figure 4), are related”. The researcher again asked for the use of two different writing colors, namely black and red ink. S1 answered, “to distinguish men and women”. Furthermore, S2 utilized equations written on verbal representations and graphical representations to be used in symbol representations in algebraic arithmetic operations to find answers.
The last representation produced by S2 was the completion of word problems until finding the correct answer, which was the symbol representation. Based on the short symbol representation of S2, the researcher assumed that S2 understood word problems. Because of the two previous representations, it was realized in algebraic arithmetic operations to obtain the right answer. It is evidenced by the results of interviews with several researchers’ questions related to S2’s algebra representation. The researcher asked, “why is the answer short?”. Are you aware of the process?”. S2 answered, “yes, I already knew the process because I was used to working on problems like this (while pointing to word problems)”. The researcher asked, “what questions do you usually answer?”. S2 answered, “math Olympics questions”. The researcher asked again, “who asked you to answer questions about the Olympics?”. S2 answered, “my wish, because I often participate in the Math Olympiad, both regional and national level”. The researcher said “wow, amazing”. Then the researcher continued the question “where did L + (L + 4) = 28 come from”? S2 answered, “because there are four women more than men”, and many women asked. The researcher asked, “Try to decipher L + (L + 4) = 28 to get L = 12”, without thinking, S2 answered, “from L + (L + 4) = 28, then I group the same term into (L + L) + 4 = 18. So, we get 2L + 4 = 28. Then 2L + 4 − 4 = 28 − 4, it becomes 2L = 24, then L = 12”. The researcher then asked the origin of 12 + 4 = 16. S2 answered, “from here (while pointing to the equation P = 1 + 4 in verbal representations)”. The researcher asked, “what do you think about solving this word problem, using three forms of representation? S2 answered, “I am trying to make it different from the others, and those who see this solution can be learned to be used to answer questions of the same type as this problem.” The researcher asked, “are you sure about your answer?” S2 answered “yes, uh … wait for me to check again (students only need about 10 s and say” yes, I am sure that the answers I found were correct.”.
4. Discussion
The use of representation is significant in solving word problems because students represent problem solving by carrying out the process of modeling tangible things in the real world into abstract concepts or symbols [
5]. Representation has a role in strengthening students’ understanding to build ideas and solve problems, especially in word problems [
8]. Then, representation serves as a medium to assist students in learning and integrating recalled information with new information presented in the problem [
1]. Furthermore, representation reduces the difficulty in solving word problems, for example, communicating ideas between signs, words or symbols, expressions, or images [
2,
3,
4]. Therefore, representation is needed in solving word problems.
This study aims to describe students’ different processes of representation in mathematical word problems. The study was conducted by giving assignments to 75 elementary school students in Makassar, Indonesia. Then, two subjects were chosen to be interviewed in depth, based on the different representations produced: S1 representation (verbal–table–symbol) and S2 representation (verbal–graphic–symbol), to find the correct answer. Different representations of students analyzed were verbal–written representations, picture representations, and symbol representations.
Based on the analysis of the different representation processes produced by students, four methods were found: translation, integration, solution, and evaluation. In the translation process, students expressed this before answering the word problem assignments. Students read word problem text repeatedly. Students identified the quantity by marking 28 students in class and four more female students than male students. Furthermore, the results of determining the amount in the transformation were in the form of images, equations, and algebraic operations. Students showed the integration process by connecting two different forms of representation, namely the verbal–written representation with the representation of corresponding images and connecting the statement “four female students are more than male students” with the same comparison. The solution process was shown by students using the equations “P = L + 4” and “P + L = 28” to carry out computational approaches based on students’ conceptual and procedural knowledge of algebraic arithmetic operations until finding the correct answer.
The evaluation process revealed by students that in solving word problems, the gesture of finger movements fluctuated on the assignment sheet, each response to the researcher’s questions from the resulting representation, and after the overall representation was generated. Students re-checked the truth of the representations produced, and the answers obtained. Students carried out this process, so they were not wrong in converting statements into operations. Hegarty, Mayer, and Monk [
26] state that conversion errors are incorrect operations, for example, adding when the relational information in the problem is “more” and the correct answer involves reduction. Next, student identification of the quantity in transformations into images, equations, and algebraic arithmetic operations results was carried out. Nunes and Bryant [
27] found that transforming relational statements into equivalent statements helps students think about solving word problems differently.
Students showed the integration process by connecting two different forms of representation, namely the verbal–written representation with the representation of corresponding images and connecting the statement “four female students are more than male students” with the same comparison. Hegarty, Mayer, and Green [
28] found that integrating information in the word problem text is necessary before constructing representations. Then, Abdullah, Zakaria, and Halim [
1] found that completing representations can successfully demonstrate mathematical concepts and procedures to solve word problems.
The solution process was shown by students using the equations “P = L + 4” and “P + L = 28” to carry out computational techniques based on students’ conceptual and procedural knowledge in algebraic counting operations until finding the correct answer, that is “P = 16”. Students can identify simple solutions by making schemes and describing the proper relations between relevant statements [
9,
10,
29].
The evaluation process was shown from the students’ gestures, finger movements up and down on the word problem assignment sheet, each representation produced, and the representation made until obtaining an answer. Students carried this process out to re-check the truth of the resulting representations and the validity of the solutions obtained. Students re-checked the correctness of the decision obtained from the representation produced and after the overall representation was generated. Swartz [
30] revealed that decision making in the problem-solving process needs to be re-evaluated. The aim is to find out whether the decision we made is suitable or not. In addition, it was essential to re-evaluate activities after solving word problems [
31,
32]. The aim is to convince us by translating the resulting problem.
Lastly, mathematical literacy was found based on the interview results, and other findings supporting this result. Students were carrying out the processes of translation, integration, and solutions in solving word problems because of their mathematical literacy ability. Bednarz and Dufour-Janvier [
33] explain that translation ability is essential for mathematics learning and problem solving. Two types of transformation of semiotic representations: treatment and conversion, correspond to quite different cognitive processes [
34]. They are two distinct sources of misunderstanding in mathematics learning. If treatment is more crucial from a mathematical standpoint, conversion is essentially the decisive factor in learning. Smith, Hardman, and Higgins [
35] found that mathematics literacy benefits teachers and students in the learning process in the classroom. In addition, Smith, Hardman, Wall, and Mroz [
36] found that literacy can affect traditional student interaction patterns throughout the class. Furthermore, Beard [
37] found that reading literacy in the course helps students learn and offers a significant promise for improving living standards and opportunities for thousands of children. Therefore, students develop different representations based on their experience and habits of solving Math Olympiad questions, part of mathematical literacy, such as these word problems.
5. Conclusions
This study found three forms of representation produced by students: verbal–written, image representation, and symbol representation. Furthermore, these findings carried out the three forms of representation through four representation processes, namely the processes of translation, integration, solution, and evaluation. In addition, there are other findings used by students in solving word problems, namely, students’ mathematical literacy in solving word problems. Students’ mathematical literacy in the different representation processes of students in solving word problems can be studied in subsequent studies or by other researchers.
The relevance of this research to teaching and learning mathematics produces several findings, namely, directing students to think creatively. In addition, teachers need to be aware of the translation, integration, solution, and evaluation process in producing different representations in solving word problems. It can be considered to convey additional knowledge in solving various word problems to students. The teacher can use it in the learning process in the classroom, especially in solving word problems. This should be introduced earlier at the elementary school level using simple problems and be a reference for other researchers to study the different representation processes.