Knots in Polymer Molecules Under Poiseuille Flow
Abstract
1. Introduction
2. Model
3. Results
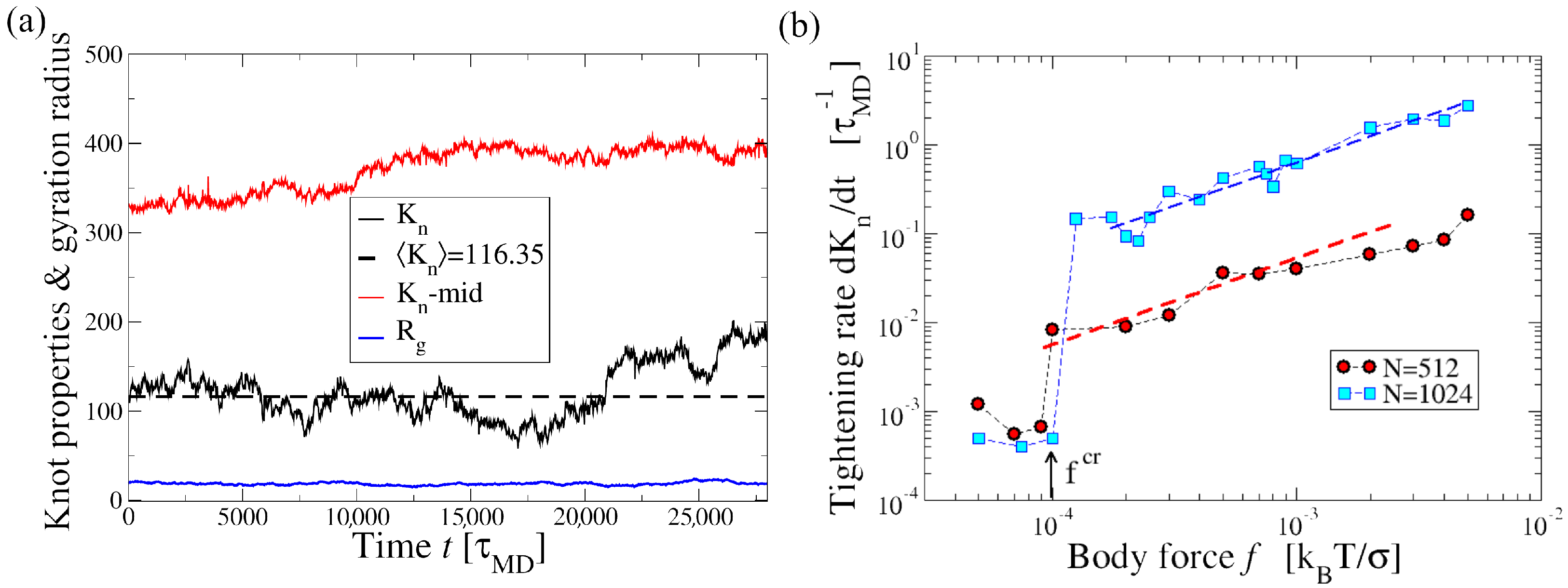
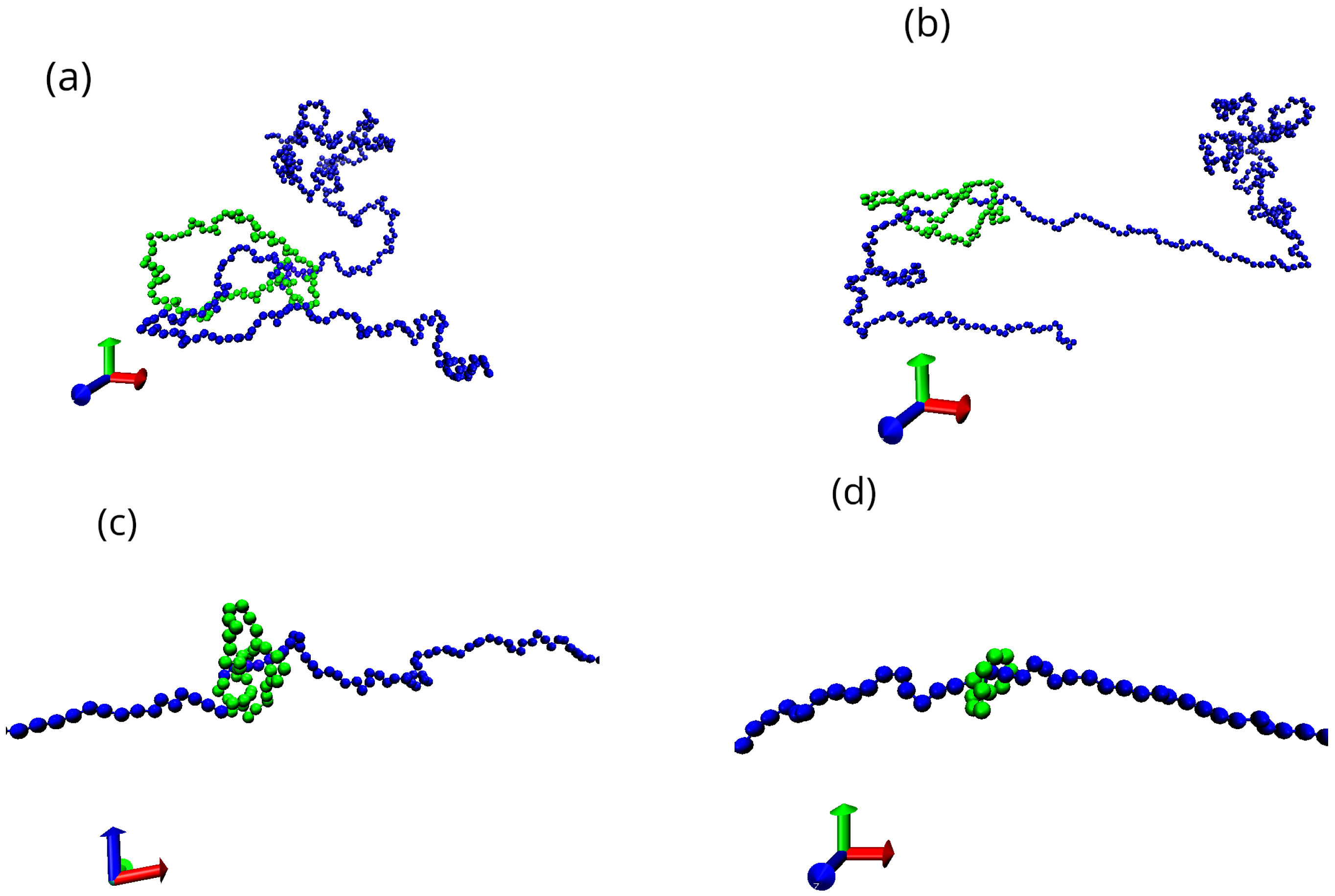
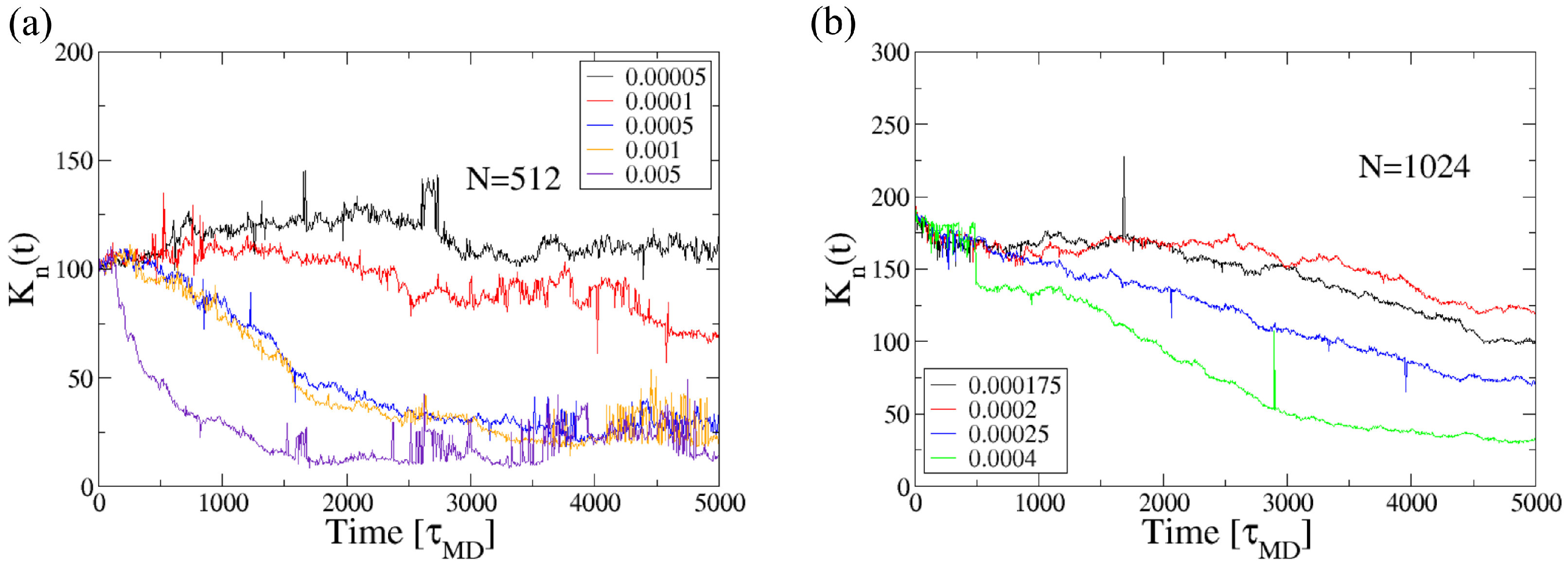
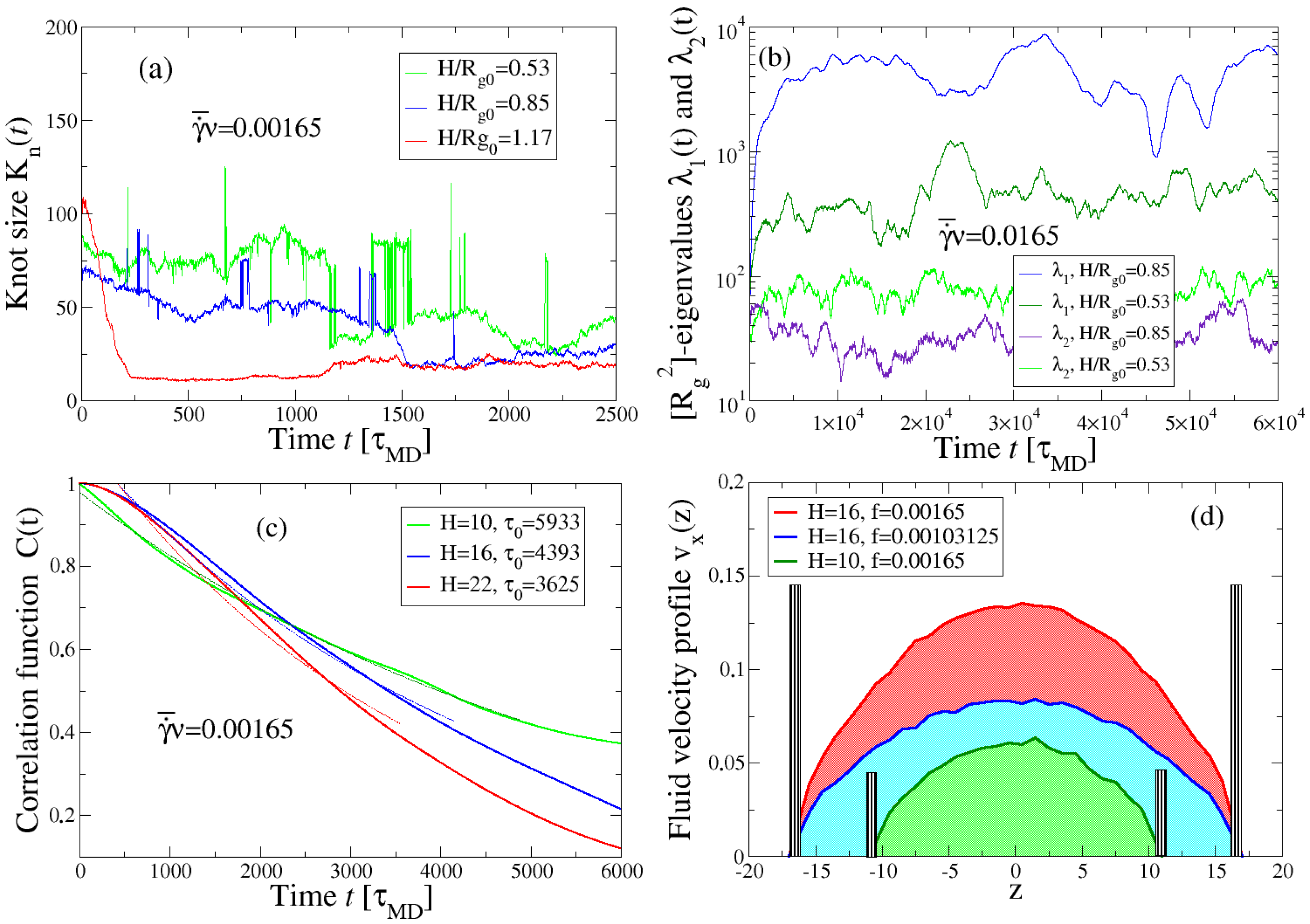
3.1. Effect of Shear on Knot Size in a Poiseuille Flow
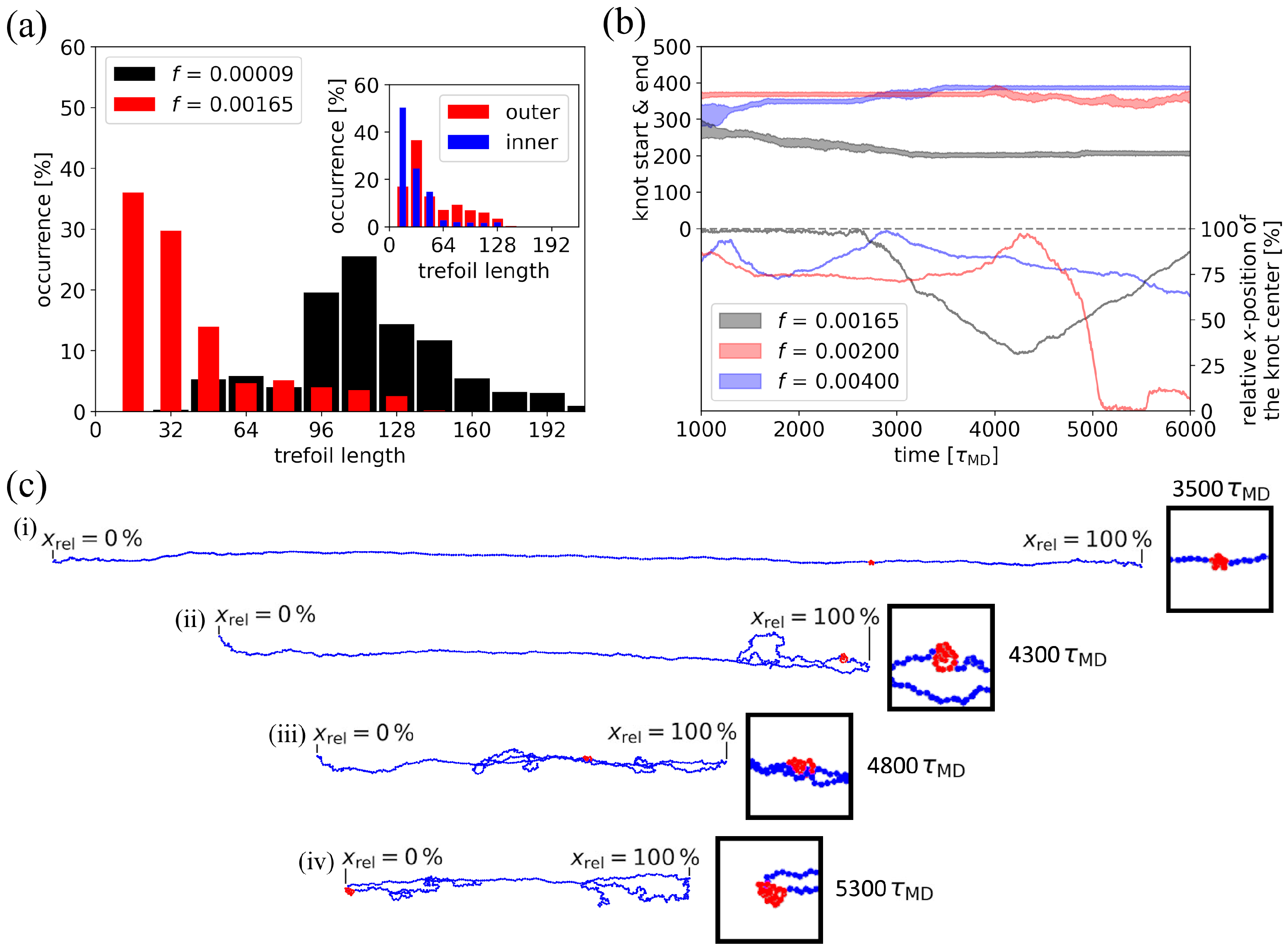
3.2. Cross-Correlation Between Chain Tumbling and Knot Size
3.3. Effect of the Channel Width on Knot Tightening
4. Methods for Experimental Verification
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Faísca, P.F. Knotted proteins: A tangled tale of Structural Biology. Comput. Struct. Biotechnol. J. 2015, 13, 459–468. [Google Scholar] [CrossRef]
- Micheletti, C.; Marenduzzo, D.; Orlandini, E. Polymers with spatial or topological constraints: Theoretical and computational results. Phys. Rep. 2011, 504, 1–73. [Google Scholar] [CrossRef]
- Tubiana, L.; Alexander, G.P.; Barbensi, A.; Buck, D.; Cartwright, J.H.; Chwastyk, M.; Cieplak, M.; Coluzza, I.; Čopar, S.; Craik, D.J.; et al. Topology in soft and biological matter. Phys. Rep. 2024, 1075, 1–137. [Google Scholar] [CrossRef]
- Arsuaga, J.; Vazquez, M.; Trigueros, S.; Sumners, D.W.; Roca, J. Knotting probability of DNA molecules confined in restricted volumes: DNA knotting in phage capsids. Proc. Natl. Acad. Sci. USA 2002, 99, 5373–5377. [Google Scholar] [CrossRef] [PubMed]
- Arsuaga, J.; Vazquez, M.; McGuirk, P.; Trigueros, S.; Sumners, D.W.; Roca, J. DNA knots reveal a chiral organization of DNA in phage capsids. Proc. Natl. Acad. Sci. USA 2005, 102, 9165–9169. [Google Scholar] [CrossRef]
- Marenduzzo, D.; Orlandini, E.; Stasiak, A.; Sumners, D.W.; Tubiana, L.; Micheletti, C. DNA–DNA interactions in bacteriophage capsids are responsible for the observed DNA knotting. Proc. Natl. Acad. Sci. USA 2009, 106, 22269–22274. [Google Scholar] [CrossRef]
- Plesa, C.; Verschueren, D.; Pud, S.; van der Torre, J.; Ruitenberg, J.W.; Witteveen, M.J.; Jonsson, M.P.; Grosberg, A.Y.; Rabin, Y.; Dekker, C. Direct observation of DNA knots using a solid-state nanopore. Nat. Nanotechnol. 2016, 11, 1093–1097. [Google Scholar] [CrossRef]
- Kumar Sharma, R.; Agrawal, I.; Dai, L.; Doyle, P.S.; Garaj, S. Complex DNA knots detected with a nanopore sensor. Nat. Commun. 2019, 10, 4473. [Google Scholar] [CrossRef]
- Taylor, W.R. A deeply knotted protein structure and how it might fold. Nature 2000, 406, 916–919. [Google Scholar] [CrossRef]
- Virnau, P.; Mirny, L.A.; Kardar, M. Intricate Knots in Proteins: Function and Evolution. PLoS Comput. Biol. 2006, 2, e122. [Google Scholar] [CrossRef]
- Potestio, R.; Micheletti, C.; Orland, H. Knotted vs. Unknotted Proteins: Evidence of Knot-Promoting Loops. PLoS Comput. Biol. 2010, 6, e1000864. [Google Scholar] [CrossRef] [PubMed]
- Mallam, A.L.; Rogers, J.M.; Jackson, S.E. Experimental detection of knotted conformations in denatured proteins. Proc. Natl. Acad. Sci. USA 2010, 107, 8189–8194. [Google Scholar] [CrossRef]
- Boelinger, D.; Sulkowska, J.; Hsu, H.-P.; Mirny, L.; Kardar, M.; Onuchic, J.; Virnau, P. A Stevedore’s Protein Knot. PLoS Comput. Biol. 2010, 6, e1000731. [Google Scholar] [CrossRef]
- Virnau, P.; Mallam, A.; Jackson, S. Structures and folding pathways of topologically knotted proteins. J. Phys. Cond. Matter 2011, 23, 033101. [Google Scholar] [CrossRef]
- Jarmolinska, A.I.; Perlinska, A.P.; Runkel, R.; Trefz, B.; Ginn, H.M.; Virnau, P.; Sulkowska, J.I. Proteins’ Knotty Problems. J. Mol. Biol. 2019, 431, 244–257. [Google Scholar] [CrossRef]
- Brems, M.A.; Runkel, R.; Yeates, T.O.; Virnau, P. AlphaFold predicts the most complex protein knot and composite protein knots. Protein Sci. 2022, 31, e4380. [Google Scholar] [CrossRef]
- Frisch, H.L.; Wasserman, E. Chemical Topology 1. J. Am. Chem. Soc. 1961, 83, 3789–3795. [Google Scholar] [CrossRef]
- Delbrück, M. Knotting Problems in Biology; Bellman, R.E., Ed.; American Mathematical Society: Providence, RI, USA, 1962; Volume 14, p. 55. [Google Scholar]
- Vologodskii, A.V.; Lukashin, A.V.; Frank-Kamenetskii, M.D. Topological interaction between polymer chains. Sov. Phys.-JETP 1974, 40, 932–936. [Google Scholar]
- Sumners, D.W.; Whittington, S.G. Knots in self-avoiding walks. J. Phys. A Math. Gen. 1988, 21, 1689. [Google Scholar] [CrossRef]
- Mansfield, M.L. Knots in Hamilton cycles. Macromolecules 1994, 27, 5924–5926. [Google Scholar] [CrossRef]
- Virnau, P.; Kantor, Y.; Kardar, M. Knots in globule and coil phases of a model polyethylene. J. Am. Chem. Soc. 2005, 127, 15102–15106. [Google Scholar] [CrossRef]
- Adams, C.C. The Knot Book; American Mathematical Soc.: Providence, RI, USA, 1994. [Google Scholar]
- Virnau, P. Detection and visualization of physical knots in macromolecules. Phys. Procedia 2010, 6, 117–125. [Google Scholar] [CrossRef]
- Tubiana, L.; Orlandini, E.; Micheletti, C. Probing the Entanglement and Locating Knots in Ring Polymers: A Comparative Study of Different Arc Closure Schemes. Prog. Theor. Phys. Suppl. 2011, 191, 192–204. [Google Scholar] [CrossRef]
- Foteinopoulou, K.; Karayiannis, N.C.; Laso, M.; Kroeger, M.; Mansfield, M.L. Universal Scaling, Entanglements, and Knots of Model Chain Molecules. Phys. Rev. Lett. 2008, 101, 265702. [Google Scholar] [CrossRef] [PubMed]
- Meyer, H.; Horwath, E.; Virnau, P. Mapping onto Ideal Chains Overestimates Self-Entanglements in Polymer Melts. ACS Macro Lett. 2018, 7, 757–761. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Meyer, H.; Virnau, P.; Daoulas, K.C. Can Soft Models Describe Polymer Knots? Macromolecules 2020, 53, 10475–10486. [Google Scholar] [CrossRef] [PubMed]
- Coronel, L.; Orlandini, E.; Micheletti, C. Non-monotonic knotting probability and knot length of semiflexible rings: The competing roles of entropy and bending energy. Soft Matter 2017, 13, 4260–4267. [Google Scholar] [CrossRef]
- Bornschlögl, T.; Anstrom, D.M.; Mey, E.; Dzubiella, J.; Forest, K.T. Tightening the Knot in Phytochrome by Single-Molecule Atomic Force Microscopy. Biophys. J. 2009, 96, 1508–1514. [Google Scholar] [CrossRef]
- Ohta, S.; Alam, M.T.; Arakawa, H.; Ikai, A. Origin of mechanical strength of bovine carbonic anhydrase studied by molecular dynamics simulation. Biophys. J. 2004, 87, 4007. [Google Scholar] [CrossRef]
- Sułkowska, J.I.; Sułkowski, P.; Szymczak, P.; Cieplak, M. Untying Knots in Proteins. J. Am. Chem. Soc. 2010, 132, 13954–13956. [Google Scholar] [CrossRef]
- Liebetreu, M.; Ripoll, M.; Likos, C.N. Trefoil Knot Hydrodynamic Delocalization on Sheared Ring Polymers. ACS Macro Lett. 2018, 7, 447–452. [Google Scholar] [CrossRef]
- Kuei, S.; Słowicka, A.M.; Ekiel-Jezewska, M.L.; Weinryb, E.; Stone, H.A. Dynamics and topology of a flexible chain: Knots in steady shear flow. New J. Phys. 2015, 17, 053009. [Google Scholar] [CrossRef]
- Renner, C.B.; Doyle, P.S. Untying Knotted DNA with Elongational Flows. ACS Macro Lett. 2014, 3, 963–967. [Google Scholar] [CrossRef]
- Di Stefano, M.; Tubiana, L.; Di Ventra, M.; Micheletti, C. Driving knots on DNA with AC/DC electric fields: Topological friction and memory effects. Soft Matter 2014, 10, 6491–6498. [Google Scholar] [CrossRef]
- Narsimhan, V.; Klotz, A.R.; Doyle, P.S. Steady-state and Transient Behavior of Knotted Chains in Extensional Fileds. ACS Macro Lett. 2017, 6, 1285–1289. [Google Scholar] [CrossRef]
- Klotz, A.R.; Soh, B.W.; Doyle, P.S. Motion of knots in DNA stretched by elongational fields. Phys. Rev. Lett. 2018, 120, 188003. [Google Scholar] [CrossRef]
- Klotz, A.R.; Soh, B.W.; Doyle, P.S. An experimental investigation of attraction between knots in a stretched DNA molecule. Europhys. Lett. 2020, 129, 68001. [Google Scholar] [CrossRef]
- Soh, B.W.; Klotz, A.R.; Doyle, P.S. Untying of Complex Knots on Stretched Polymers in Elongational Fields. Mscromolecules 2018, 51, 9562–9571. [Google Scholar] [CrossRef]
- Milchev, A.; Schmitt, M.P.; Virnau, P. Effect of simple shear on knotted polymer coils and globules. J. Chem. Phys. 2024, 161, 224905. [Google Scholar] [CrossRef] [PubMed]
- Tan, S. Monte-Carlo simulation of polymers in shear flow. Polymer 1999, 40, 695–700. [Google Scholar] [CrossRef]
- Smith, D.E.; Babcock, H.P.; Chu, S. Single Polymer Dynamics in Steady Shear Flow. Science 1999, 283, 1724–1727. [Google Scholar] [CrossRef] [PubMed]
- Lyulin, A.V.; Adolf, D.B.; Davies, G.R. Brownian dynamics simulations of linear polymers under shear flow. J. Chem. Phys. 1999, 111, 758. [Google Scholar] [CrossRef]
- Kong, X.; Han, Y.; Chen, W.; Cui, F.; Li, Y. Understanding conformational and dynamical evolution of semiflexible polymers in shear flow. Soft Matter 2019, 15, 6353–6361. [Google Scholar] [CrossRef]
- Jeong, S.H.; Cho, S.; Baig, C. Chain rotational dynamics in dilute polymer solutions and melts under shear flow. Polymer 2023, 281, 126101. [Google Scholar] [CrossRef]
- Srivastva, D.; Nikoubashman, A. Flow Behavior of Chain and Star Polymers and Their Mixtures. Polymers 2018, 10, 599. [Google Scholar] [CrossRef]
- Cannavacciolo, L.; Winkler, R.G.; Gompper, G. Mesoscale simulations of polymer dynamics in microchannel flows. Europhys. Lett. 2008, 83, 34007. [Google Scholar] [CrossRef][Green Version]
- Grest, G.S.; Kremer, K. Molecular dynamics simulation for polymers in the presence of a heat bath. Phys. Rev. A 1986, 33, 3628(R). [Google Scholar] [CrossRef] [PubMed]
- Malevanets, A.; Kapral, R. Mesoscopic model for solvent dynamics. J. Phys. Chem. 1999, 110, 8605–8613. [Google Scholar] [CrossRef]
- Gompper, G.; Ihle, T.; Knoll, D.M.; Winkler, R.G. Multi-particle collision dynamics: A parrticle-based mesoscale simulation approach to the hydrodynamics of comlex fluids. Adv. Polym. 2009, 221, 1–87. [Google Scholar]
- Andersen, L.; Lorenz, C.; Travesset, J. General purpose molecular dynamics simulations fully implemented on graphics processing units. J. Comput. Phys. 2008, 227, 5342–5359. [Google Scholar] [CrossRef]
- Padding, J.T.; Louis, A.A. Hydrodynamic interactions and Brownian forces in colloidal suspensions: Coarse-grained over time and length svvales. Phys. Rev. E 2006, 74, 031402. [Google Scholar] [CrossRef]
- Ihle, T.; Knoll, D.M. Stochastic rotational dynamics: A Galilean-invariant mesoscopic model for fluid flow. Phys. Rev. E 2001, 63, 020201. [Google Scholar] [CrossRef]
- Jendrejack, R.M.; Dimalanta, E.T.; Schwartz, D.C.; Graham, M.D.; de Pablo, J.J. DNA Dynamics in a Microchannel. Phys. Rev. Lett. 2003, 91, 038102. [Google Scholar] [CrossRef]
- Ranguelov, B.; Petkov, P.; Milchev, A. Flow-Induced Vesicle Translocation through a Narrow Slit–Transit Time Scaling Relations. Langmuir 2025, 41, 15849–15856. [Google Scholar] [CrossRef] [PubMed]
- Tubiana, L.; Polles, G.; Orlandini, E.; Micheletti, C. Kymoknot: A web server and software package to identify and locate knots in trajectories of linear or circular polymers. Eur. Phys. J. E 2018, 41, 72. [Google Scholar] [CrossRef]
- Klotz, A.R.; Estabrooks, B. Revisiting the second Vassiliev (In) variant for polymer knots. J. Phys. A Math. Theor. 2024, 57, 245002. [Google Scholar] [CrossRef]
- Herschberg, T.; Pifer, K.; Panagiotou, E. A computational package for measuring Topological Entanglement in Polymers, Proteins and Periodic systems (TEPPP). Comp. Phys. Commun. 2023, 286, 108639. [Google Scholar] [CrossRef]
- Meluzzi, D.; Smith, D.E.; Arya, G. Biophysics of knotting. Annu. Rev. Biophys. 2010, 39, 349–366. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Winkler, R.G. Semiflexible Polymers in Shear Flow. Phys. Rev. Lett. 2006, 97, 128301. [Google Scholar] [CrossRef]
- Dai, L.; Doyle, P.S. Trapping a Knot into Tight Conformations by Intra-Chain Repulsions. Polymers 2017, 9, 57. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Li, H. Mechanically tightening, untying and retying a protein trefoil knot by single-molecule force spectroscopy. Chem. Sci. 2020, 11, 12512–12521. [Google Scholar] [CrossRef] [PubMed]
- Bikerdal, V. Folding and unfolding of G-rich DNA knots using single molecule. Biophys. J. 2024, 123, 4a. [Google Scholar] [CrossRef]
- Cebrián, J.; Kadomatsu-Hermosa, M.J.; Castán, A.; Martínez, V.; Parra, C.; Fernández-Nestosa, M.J.; Schaerer, C.; Martínez-Robles, M.-L.; Hernández, P.; Krimer, D.B.; et al. Electrophoretic mobility of supercoiled, catenated and knotted DNA molecules. Nucleic Acids Res. 2014, 43, e24. [Google Scholar] [CrossRef] [PubMed]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schmitt, M.P.; Milchev, A. Knots in Polymer Molecules Under Poiseuille Flow. Foundations 2025, 5, 28. https://doi.org/10.3390/foundations5030028
Schmitt MP, Milchev A. Knots in Polymer Molecules Under Poiseuille Flow. Foundations. 2025; 5(3):28. https://doi.org/10.3390/foundations5030028
Chicago/Turabian StyleSchmitt, Maurice P., and Andrey Milchev. 2025. "Knots in Polymer Molecules Under Poiseuille Flow" Foundations 5, no. 3: 28. https://doi.org/10.3390/foundations5030028
APA StyleSchmitt, M. P., & Milchev, A. (2025). Knots in Polymer Molecules Under Poiseuille Flow. Foundations, 5(3), 28. https://doi.org/10.3390/foundations5030028






