Beyond Classical Multipoles: The Magnetic Metapole as an Extended Field Source

Abstract

We introduce the concept of the magnetic metapole—a theoretical extension of classical multipole theory involving a fractional j pole count (related to the harmonic degree n as j = 2ⁿ). Defined by a scalar potential with colatitudinal dependence and no radial variation, the metapole yields a magnetic field that decays as 1/r and is oriented along spherical surfaces. Unlike classical multipoles, the metapole cannot be described as a point source; rather, it corresponds to an extended or filamentary magnetic distribution as derived from Maxwell’s equations. We demonstrate that pairs of oppositely oriented metapoles (up/down) can, at large distances, produce magnetic fields resembling those of classical monopoles. A regularized formulation of the potential resolves singularities for the potential and the field. When applied in a bounded region, it yields finite field energy, enabling practical modeling applications. We propose that the metapole can serve as a conceptual and computational framework for representing large-scale magnetic field structures particularly where standard dipole-based models fall short. This construct may have utility in both geophysical and astrophysical contexts, and it provides a new tool for equivalent source modeling and magnetic field decomposition.

1. Introduction

Classical electromagnetic theory [1] often describes magnetic fields through multipole expansions of scalar potentials, where each term corresponds to a distinct field geometry—monopoles, dipoles, quadrupoles, and so on. These expansions have proven foundational in physics particularly in the study of planetary and astrophysical magnetic fields [2]. However, they are traditionally limited to integer-valued j multipoles, and their application can be constrained in systems, such as those observed in astrophysical systems [3] and in shallow and deep Earth environments [4]—exhibiting non-standard field structures, such as long-range coherence, directional asymmetry, or non-radial decay patterns.

In this work, we propose an extension to this classical framework by introducing the magnetic metapole—a theoretical construct defined by a fractional multipole (j = 1/2, corresponding to n = −1 degree). The metapole arises naturally from potential field theory when the harmonic expansion is extended to non-integer j indices. The resulting scalar potential generates a magnetic field that is purely colatitudinal and exhibits a 1/r spatial decay, deviating from the radial field structures of classical dipoles or monopoles. The field satisfies Maxwell’s equations outside a singular polar axis, which we show corresponds to an extended, filament-like source rather than a point singularity.

Crucially, the metapole is not introduced as a new physical particle but as a modeling tool that may offer new insights into the organization of magnetic fields in complex systems. Its structure and behavior can help explain the emergence of monopole-like fields from composite or distributed sources. When metapoles are arranged in up/down pairs, they produce fields that, at large distances, closely approximate those of magnetic monopoles [5,6,7,8].

This concept complements our companion paper [9], which addresses the origin and amplification of seed magnetic fields (SMFs) in planetary and galactic contexts [10]. In that work, we propose that SMFs arise from the non-synchronous rotational dynamics of orbiting bodies and can be amplified via dynamo effects. However, such a framework still requires a foundational source structure capable of generating long-range magnetic coherence in the absence of localized currents. The metapole, as presented here, may serve as a theoretical candidate for that seed structure—providing a background magnetic topology that helps initiate or sustain dynamo processes [11].

The remainder of this paper is organized as follows: we define the metapole and its field analytically; we find the property of duality with monopoles and then explore metapole behavior in superposed configurations. Finally, we discuss applications in equivalent source modeling for geophysical magnetism and speculative extensions in astrophysical contexts. In parallel, in the appendices, we derive the corresponding source distribution using Maxwell’s equations, assess a possible regularization to remove divergences of the potential and the associated field, and explore more in detail the resulting behavior of a pair of metapoles.

2. The Metapole

Let us define the metapole in terms of its magnetic field potential in analogy with other more conventional multipoles in the framework of the potential field theory [1]. In general, we can define a magnetic multipole, i.e., a j-pole, as a magnetic source with a magnetic field potential (in the space outside the source):

$$V_n=-{\displaystyle \frac{k_n}{r^{n+1}}}{f}_n(\theta ,\lambda )$$

(1)

with j = 2ⁿ; k_n is an appropriate constant and f_n(θ,λ) is a function depending only on the colatitude (θ) and longitude (λ) but not on the radial distance r of the point of measurement from the location of the multipole, which is taken as the origin of the reference system. Their dimensions change accordingly with n. The latter parameter, in general, n ≥ 0, is the corresponding harmonic degree when we expand the magnetic field potential in spherical harmonics [11]. In this way, a monopole is defined with j = 1 and n = 0, a dipole with j = 2 and n = 1, a quadruple with j = 4 and n = 2, and so on. Therefore, the index j represents the number of poles (or the pole count) that compose the magnetic source. Consequently, we can define a magnetic field B_n = −grad V_n:

$${\mathit{{\rm B}}}_n=\left(-{\displaystyle \frac{k_n(n+1)}{r^{n+2}}}{f}_n,{\displaystyle \frac{k_n}{r^{n+2}}}{\displaystyle \frac{\partial f_n}{\partial \theta }},{\displaystyle \frac{k_n}{r^{n+2}\mathit{sin}\theta }}{\displaystyle \frac{\partial f_n}{\partial \lambda }}\right)$$

(2)

It is easy to see that the total intensity of this vector will be

$$B_n={\displaystyle \frac{k_n}{r^{n+2}}}{g}_n(\theta ,\lambda )$$

(2a)

i.e., the intensity decays with the radial distance as an inverse (n + 2)-power law; g_n is a known function of n, f_n and its partial derivatives. Actually, for n = 0 (monopole), there is no dependence on θ and λ, while for n = 1 (dipole), after an appropriate choice of the reference system (z-axis coinciding with the dipole axis), there is no dependence on λ.

We can extend the above definitions also to negative values of n, i.e., n = −2, −3, −4, …: in these cases, the corresponding sources are dipoles, quadrupoles, octupoles, …, respectively, placed at r = ∞. This is a typical way in geomagnetism to model external sources with respect to the Earth’s surface, ideally placed at infinity [11], with a field that goes to zero approaching the Earth’s center, as the origin of the reference system. However, there is yet another kind of “j-pole” that has been never taken into account—one with j = 1/2 and n = −1:

$$V_{-1}=-k_{-1}{f}_{-1}(\theta ,\lambda ),$$

(3)

so that the magnetic potential will not have any radial dependence. The corresponding total intensity will be in the general form:

$${\mathit{B}}_{-1}={\displaystyle \frac{k_{-1}}{r}}{g}_{-1}(\theta ,\lambda )$$

(4)

Because the value of j is fractional, in particular j = ½ = 0.5, in analogy with the names of the other multipoles, we will call this magnetic source a metapole where the prefix meta has the double meaning of “beyond” (from meta in ancient Greek) and “half” (from metà in modern Italian). Since the field is derived from a scalar potential, it is always rotB₋₁ = 0, while the null divergence, outside the sources, is satisfied for f₋₁ = log(tan(θ/2)), where log is the natural logarithm. Hence, the corresponding Equation (3) becomes

$$V_{-1}=-k_{-1}\mathit{log}\left(\mathit{tan}{\displaystyle \frac{\theta }{2}}\right)$$

(5)

The corresponding field is a vector

b₋₁ = (0, k₋₁/(rsin θ), 0),

(6)

which has only the θ-component.

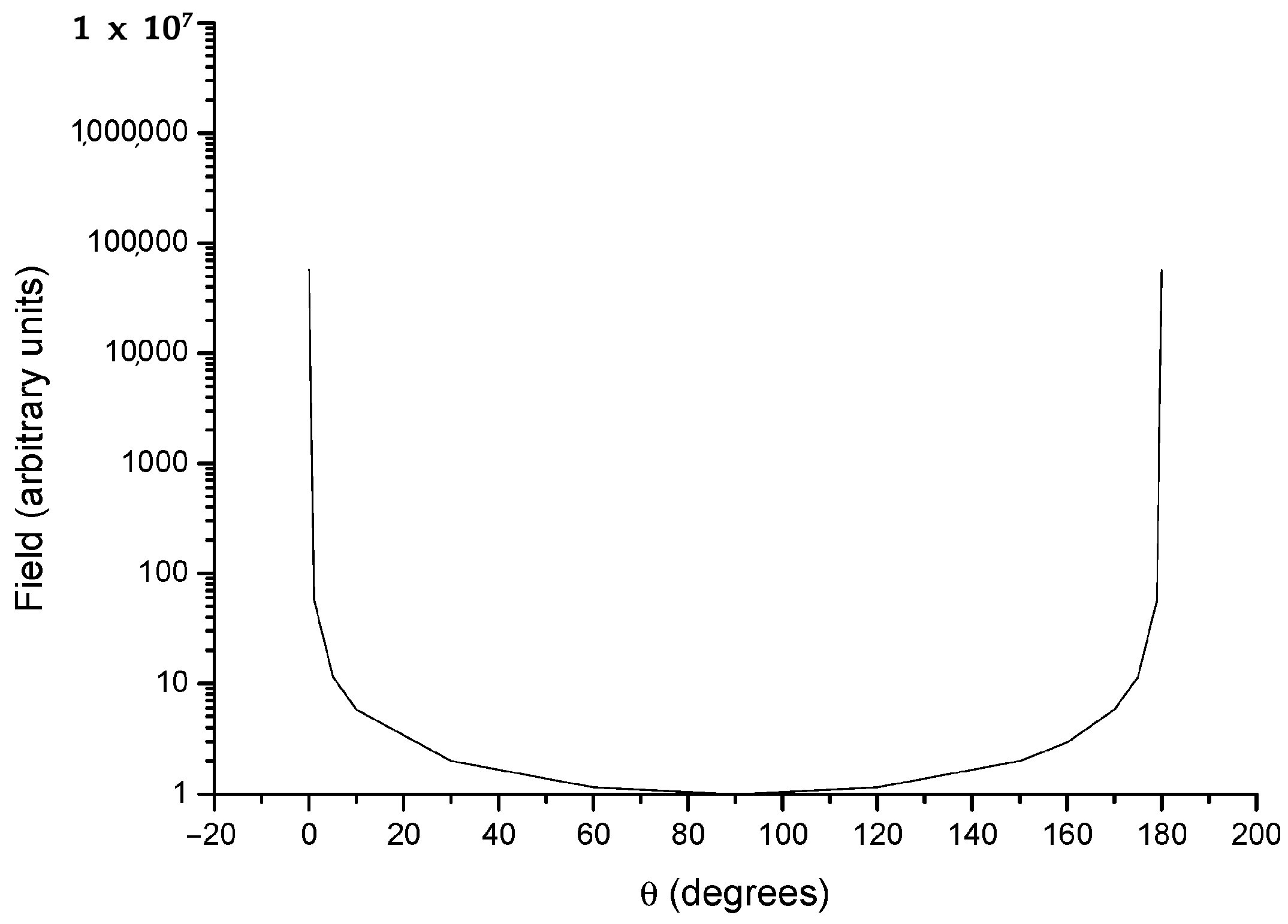
This hypothetical magnetic source has some important properties. Figure 1 shows the magnetic field of this kind of metapole, while Figure 2 and Figure 3 describe the behavior of its magnetic potential and field, respectively, with colatitude. Because the corresponding magnetic field is always positive and colatitudinal, the field vector is always directed toward increasing colatitudes, and the magnetic field lines of the metapole are along spherical surfaces. This means that the metapole has a preferential axis and direction: rotating the metapole by 180° changes the signs of both the potential and field. Both the field and potential are singular along all the entire z-axis, where they go to plus or minus infinity, so as the total magnetic energy diverges, too.

The metapole has been defined in the framework of potential field theory of multipoles, where each multipole is placed ideally at a defined point of the reference system (at the origin for n ≥ 0 or at infinity for n < −1), so in principle, we would expect a “point-like charge”, such as monopoles, dipoles, etc., but because of its singularity along the z-axis (see Figure 2), the metapole is more complicated, so we prefer to use the more general term of “source”. Appendix A.1 shows more detail on the source distribution and its physical realizability.

3. Duality and Superposition of Metapoles

The found divergence of the potential and the field along the polar z-axis could be prevented (see Appendix A.2), but for convenience, we continue with the simpler expressions for potential and magnetic field given by Equations (5) and (6), respectively. We can call the metapole defined above, i.e., with V = + ∞ in θ = 0, “up”, while the other kind of metapole (defined by the same potential but without the minus sign, i.e., with V = −∞ in θ = 0), can be called “down” (this nomenclature somewhat follows that used for the first two kinds of quarks [12], although the analogy is only conceptual). Figure 4 compares the equipotential surfaces and magnetic field lines of the metapole and the monopole. It is noteworthy that there is a striking duality between the two magnetic sources, i.e., the similarity between the equipotential surfaces of the monopole and the magnetic field lines of the metapole (Figure 4).

A couple of metapoles with opposite orientations, up with potential V(θ’) and down with potential –V(θ), placed at small distance s from each other, with the down metapole placed at the origin, provides a magnetic potential V_t at radial distance r (r ≫ s) (Appendix A.3; Figure 5):

$$V_t=-{\displaystyle \frac{k_{-1}s}{r}}$$

(5a)

and a magnetic field with the total intensity

$$B_t={\displaystyle \frac{k_{-1}s}{r^2}}$$

(6a)

Equations (5a) and (6a) resemble the general definitions (1-2a) for a negative magnetic monopole, whose field is directed toward the origin and decays as 1/r². An exception to the radial field occurs along the z-axis, where the field is only colatitudinal but still follows a 1/r² dependence. If we have a reverse combination of down–up metapoles, we will closely resemble a positive magnetic monopole. A complete resemblance can be achieved when a series of down–up pairs are rotated differently with respect to the original orientation. For instance, a couple of metapoles placed in the equatorial plane (θ = π/2) would resolve the issue along the z-axis.

If we relax the null divergence condition (this is also the case shown in the Appendix A.2 for regularizing the metapole potential at the poles), even a simpler potential with f₋₁ = θ provides another metapole-like field: the corresponding field b₋₁ = (0, k₋₁/r, 0) satisfies the general condition established by Equation (4). By the way, this potential, with an appropriate factor, is a good approximation of Equation (5) for colatitudes in the interval 150° > θ > 30° (5π/6 > θ > π/6, in radians). A couple of this kind of metapoles can also generate, at distances r>>s, a monopole-like potential and field (although non-completely radial): $V_t=-{\displaystyle \frac{k_{-1}s}{r}}\mathit{sin}\theta$ and ${\mathit{B}}_t=\left(-{\displaystyle \frac{k_{-1}s}{r^2}}\mathit{sin}\theta ,{\displaystyle \frac{k_{-1}s}{r^2}}\mathit{cos}\theta ,0\right)$, respectively. The total intensity is $B_t={\displaystyle \frac{k_{-1}s}{r^2}}$ and decays as a monopole. It is interesting to notice that there is a preferential plane θ = π/2, where the field divergence is also null. This is obvious because in this plane, this simpler potential is the same as the log-tan potential of Equation (5).

This raises the question: Could magnetic monopoles, if they exist, actually be bound metapole pairs? This hypothesis could have implications for high-energy physics and early-universe magnetic field generation [13].

More in general, we can think that metapoles might form the building blocks of larger magnetic structures. This would provide an alternative to monopole-based explanations of cosmic magnetism [14].

4. Discussion

The concept of the magnetic metapole, introduced here as a fractional extension of classical multipole theory, offers a novel perspective on how magnetic fields with non-dipolar geometries might be described within a coherent theoretical framework. Unlike standard multipoles, which are typically associated with integer harmonic degrees and radial decay patterns (e.g., 1/r³ for dipoles), the metapole exhibits a colatitudinal field orientation and a slower 1/r decay. This behavior aligns with certain large-scale astrophysical observations, such as the radial profiles of magnetic fields in galaxies that are difficult to reconcile with dipole-only models [15,16,17,18].

Importantly, our formulation demonstrates that the metapole field can be derived from a scalar potential that is consistent with Maxwell’s equations outside the singularity axis. The corresponding divergence is confined to a narrow region along the poles, implying an extended, filamentary source rather than a localized or point-like magnetic charge. In this regard, the metapole is not a proposal for a new elementary particle but rather a conceptual modeling tool. The regularized version of the potential introduced in Appendix A.2 confirms that the field can be made finite and smooth, supporting its potential utility in numerical modeling and equivalent source applications.

A particularly intriguing feature is the ability of metapole pairs to replicate the behavior of magnetic monopoles at large distances. When configured in oppositely oriented up and down pairs, the net field becomes effectively radial and decays as 1/r², matching the theoretical signature of a monopole field. This result mirrors the logic of composite charge models in other areas of physics—such as the construction of mesons from quark-antiquark pairs [19]—and invites further exploration into how field structures traditionally attributed to monopoles might arise from distributed, non-singular sources [20].

Moreover, we suggest that metapoles may exist at a cosmic scale possibly generating background magnetic fields. Cosmologically, metapoles may have formed under the extreme conditions of the early universe akin to the origin of light elements during primordial nucleosynthesis [13,21,22]. Due to their slower decay with distance, metapoles might still permeate deep space, contributing to a “cosmic magnetic background relic”. Observations of galactic and pulsar magnetic fields, which often show a 1/r spatial decay rather than the expected 1/r³ of dipoles, support this possibility [23].

Traditional explanations, such as the influence of interplanetary plasmas, struggle to account for the observed field strengths and structures [24]. The metapole model, described by Equation (6), provides a more consistent explanation for the persistent, large-scale magnetic fields seen in galaxies. Furthermore, this model could explain the apparent violation of Parker’s limit [3], which restricts the abundance of monopoles due to the total magnetic field energy density. If metapoles are responsible for much of the observed galactic field, this limit no longer applies in the same way.

This modeling framework also complements the hypothesis presented in our companion paper [9], where we argue that seed magnetic fields (SMFs) in astrophysical and planetary systems [23] may originate from the non-synchronous rotational dynamics of orbiting bodies. The SMF model requires a basic possibly persistent magnetic structure present even in the absence of local dynamo action. The metapole, with its extended field and slow decay, offers a candidate source configuration that could underlie such seed fields. Its non-dipolar geometry and axial orientation may help explain observed magnetic features in systems where traditional dynamo or solar wind explanations fall short [23].

Beyond astrophysics, the metapole could prove useful in geophysical applications, particularly in equivalent source modeling for deep Earth magnetic anomalies [4,25,26,27,28]. Current approaches often rely on dipole or monopole distributions to model long-wavelength magnetic features. The inclusion of metapole-like elements could improve these models’ accuracy where anomalous or directional field patterns are observed especially in regions with complex mantle conductivity or uncharacterized magnetized structures.

While the metapole remains a theoretical construct, it opens several avenues for exploration. These include the following:

• Numerical simulations incorporating metapole-based source terms into planetary or galactic field models.
• Analytical comparisons with empirical field data exhibiting non-dipolar or long-range coherence.
• Laboratory analogs using current loops or designed metamaterials to emulate metapole-like field structures.

Overall, the metapole concept expands the toolkit of magnetic field theory, offering a middle ground between the abstraction of the magnetic monopole and the limitations of traditional dipole-centric models.

5. Conclusions

In this paper, we have introduced the concept of the magnetic metapole as a novel extension to classical multipole theory [1]. Unlike standard multipoles, the metapole is defined by a fractional multipole index (specifically j = 1/2, corresponding to n = −1), resulting in a magnetic field with colatitudinal direction and 1/r decay.

Rather than treating the metapole as a new fundamental particle, our analysis shows that its field structure corresponds more closely to that of an extended magnetic source, which is possibly filamentary or sheet-like in nature. We demonstrated that the potential and field are consistent with Maxwell’s equations outside the singularity axis, and that regularization (Appendix A.2) yields finite energy in a limited region of the space: well-behaved fields that remain physically meaningful.

The most notable feature of the metapole is its ability to reproduce monopole-like behavior at large distances when paired in specific up–down configurations. This is mathematically demonstrated via the potential expansion around distant points (Section 2 and Appendix A.3) and has possible applications in astrophysical and geophysical modeling.

Our main conclusions are outlined below:

1.

Mathematical consistency: The metapole is a valid construct within potential field theory and satisfies Maxwell’s equations except at singularities, which can be regularized.

2.

Composite behavior: Pairs of metapoles can mimic monopole-like fields at macroscopic distances, providing a theoretical basis for constructing effective large-scale magnetic sources without invoking fundamental magnetic charges.

3.

Modeling applications: In geomagnetism and astrophysics, metapoles may serve as useful equivalent sources to describe long-wavelength anomalies or extended field structures where classical dipole models are insufficient [14,25,26,27,28].

4.

Not a fundamental particle: We emphasize that the metapole is not proposed as a fundamental elementary particle but rather as a conceptual and mathematical model useful in magnetic field theory.

Future work may focus on the following:

• Numerical simulations to test metapole source distributions against observed magnetic anomalies;
• Laboratory analogs using current loops or metamaterials to model colatitudinal fields;
• Exploring the role of metapole-like structures in explaining deviations from dipolar decay in astrophysical magnetic fields [17].

We understand that the present formulation of metapoles, although innovative and ingenious, has some limitations. Nevertheless, we are confident that what we have introduced and developed might have laid the foundations for new horizons in electromagnetism and theoretical physics, which will need further exploration.