Quantum Brain Dynamics: Optical and Acoustic Super-Radiance via a Microtubule
Abstract
1. Introduction
2. Super-Radiance in the Model of Quantum Brain Dynamics
2.1. Optical Super-Radiance
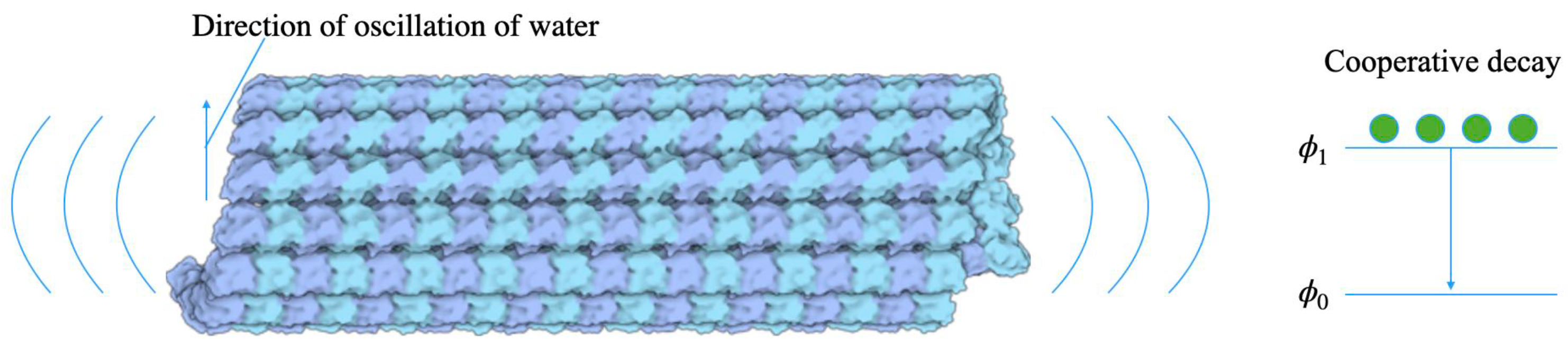
2.2. Acoustic Super-Radiance
3. Discussion
4. Concluding Remarks and Perspectives
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hawkins, J.; Blakeslee, S. On Intelligence; Macmillan: New York, NY, USA, 2004. [Google Scholar]
- Lashley, K.S. Brain Mechanisms and Intelligence: A Quantitative Study of Injuries to the Brain; University of Chicago Press: Chicago, IL, USA, 1929. [Google Scholar]
- Pribram, K.H. Languages of the Brain: Experimental Paradoxes and Principles in Neuropsychology; Prentice-Hall: Saddle River, NJ, USA, 1971. [Google Scholar]
- Pribram, K.H.; Yasue, K.; Jibu, M. Brain and Perception: Holonomy and Structure in Figural Processing; Psychology Press: London, UK, 1991. [Google Scholar]
- Gabor, D. A new microscopic principle. Nature 1948, 161, 777–778. [Google Scholar] [CrossRef]
- Jibu, M.; Yasue, K. Quantum Brain Dynamics and Consciousness; John Benjamins: Amsterdam, The Netherlands, 1995. [Google Scholar]
- Ricciardi, L.M.; Umezawa, H. Brain and physics of many-body problems. Kybernetik 1967, 4, 44–48. [Google Scholar] [CrossRef]
- Stuart, C.; Takahashi, Y.; Umezawa, H. On the stability and non-local properties of memory. J. Theor. Biol. 1978, 71, 605–618. [Google Scholar] [CrossRef]
- Stuart, C.; Takahashi, Y.; Umezawa, H. Mixed-system brain dynamics: Neural memory as a macroscopic ordered state. Found. Phys. 1979, 9, 301–327. [Google Scholar] [CrossRef]
- Fröhlich, H. Bose condensation of strongly excited longitudinal electric modes. Phys. Lett. A 1968, 26, 402–403. [Google Scholar] [CrossRef]
- Fröhlich, H. Long-range coherence and energy storage in biological systems. Int. J. Quantum Chem. 1968, 2, 641–649. [Google Scholar] [CrossRef]
- Nardecchia, I.; Torres, J.; Lechelon, M.; Giliberti, V.; Ortolani, M.; Nouvel, P.; Gori, M.; Meriguet, Y.; Donato, I.; Preto, J.; et al. Out-of-equilibrium collective oscillation as phonon condensation in a model protein. Phys. Rev. X 2018, 8, 031061. [Google Scholar] [CrossRef]
- Zhang, Z.; Agarwal, G.S.; Scully, M.O. Quantum fluctuations in the Fröhlich condensate of molecular vibrations driven far from equilibrium. Phys. Rev. Lett. 2019, 122, 158101. [Google Scholar] [CrossRef]
- Azizi, K.; Gori, M.; Morzan, U.; Hassanali, A.; Kurian, P. Examining the origins of observed terahertz modes from an optically pumped atomistic model protein in aqueous solution. PNAS Nexus 2023, 2, pgad257. [Google Scholar] [CrossRef]
- Davydov, A.; Kislukha, N. Solitons in One-Dimensional Molecular Chains. Phys. Status Solidi 1976, 75, 735–742. [Google Scholar] [CrossRef]
- Tuszyński, J.; Paul, R.; Chatterjee, R.; Sreenivasan, S. Relationship between Fröhlich and Davydov models of biological order. Phys. Rev. A 1984, 30, 2666. [Google Scholar] [CrossRef]
- Del Giudice, E.; Doglia, S.; Milani, M.; Vitiello, G. Spontaneous symmetry breakdown and boson condensation in biology. Phys. Lett. A 1983, 95, 508–510. [Google Scholar] [CrossRef]
- Del Giudice, E.; Doglia, S.; Milani, M.; Vitiello, G. A quantum field theoretical approach to the collective behaviour of biological systems. Nucl. Phys. B 1985, 251, 375–400. [Google Scholar] [CrossRef]
- Del Giudice, E.; Doglia, S.; Milani, M.; Vitiello, G. Electromagnetic field and spontaneous symmetry breaking in biological matter. Nucl. Phys. B 1986, 275, 185–199. [Google Scholar] [CrossRef]
- Del Giudice, E.; Preparata, G.; Vitiello, G. Water as a free electric dipole laser. Phys. Rev. Lett. 1988, 61, 1085. [Google Scholar] [CrossRef]
- Del Giudice, E.; Smith, C.; Vitiello, G. Magnetic Flux Quantization and Josephson Systems. Phys. Scr. 1989, 40, 786–791. [Google Scholar] [CrossRef]
- Jibu, M.; Yasue, K. A physical picture of Umezawa’s quantum brain dynamics. Cybern. Syst. Res. 1992, 92, 797–804. [Google Scholar]
- Jibu, M.; Yasue, K. Intracellular quantum signal transfer in Umezawa’s quantum brain dynamics. Cybern. Syst. 1993, 24, 1–7. [Google Scholar] [CrossRef]
- Jibu, M.; Pribram, K.H.; Yasue, K. From conscious experience to memory storage and retrieval: The role of quantum brain dynamics and boson condensation of evanescent photons. Int. J. Mod. Phys. B 1996, 10, 1735–1754. [Google Scholar] [CrossRef]
- Jibu, M.; Yasue, K. What is mind?—Quantum field theory of evanescent photons in brain as quantum theory of consciousness. Informatica 1997, 21, 471–490. [Google Scholar]
- Jibu, M.; Yasue, K. Magic without magic: Meaning of quantum brain dynamics. J. Mind Behav. 1997, 18, 205–227. [Google Scholar]
- Dicke, R.H. Coherence in spontaneous radiation processes. Phys. Rev. 1954, 93, 99. [Google Scholar] [CrossRef]
- Gross, M.; Haroche, S. Superradiance: An essay on the theory of collective spontaneous emission. Phys. Rep. 1982, 93, 301–396. [Google Scholar] [CrossRef]
- Benedict, M.G. Super-Radiance: Multiatomic Coherent Emission; CRC Press: Boca Raton, FL, USA, 1996. [Google Scholar]
- Jibu, M.; Hagan, S.; Hameroff, S.R.; Pribram, K.H.; Yasue, K. Quantum optical coherence in cytoskeletal microtubules: Implications for brain function. Biosystems 1994, 32, 195–209. [Google Scholar] [CrossRef]
- Treisman, A. The binding problem. Curr. Opin. Neurobiol. 1996, 6, 171–178. [Google Scholar] [CrossRef]
- Tsenkova, R. Aquaphotomics: Dynamic spectroscopy of aqueous and biological systems describes peculiarities of water. J. Near Infrared Spectrosc. 2009, 17, 303–313. [Google Scholar] [CrossRef]
- Stoilov, A.; Muncan, J.; Tsuchimoto, K.; Teruyaki, N.; Shigeoka, S.; Tsenkova, R. Pilot Aquaphotomic Study of the Effects of Audible Sound on Water Molecular Structure. Molecules 2022, 27, 6332. [Google Scholar] [CrossRef]
- Nishiyama, A.; Tanaka, S.; Tuszynski, J.A. Quantum Brain Dynamics and Holography. Dynamics 2022, 2, 187–218. [Google Scholar] [CrossRef]
- Nishiyama, A.; Tanaka, S.; Tuszynski, J.A. Non-equilibrium Quantum Brain Dynamics II: Formulation in 3+1 dimensions. Phys. A Stat. Mech. Appl. 2021, 567, 125706. [Google Scholar] [CrossRef]
- Vitiello, G. Dissipation and memory capacity in the quantum brain model. Int. J. Mod. Phys. B 1995, 9, 973–989. [Google Scholar] [CrossRef]
- Vitiello, G. Fractals, coherent states and self-similarity induced noncommutative geometry. Phys. Lett. A 2012, 376, 2527–2532. [Google Scholar] [CrossRef]
- Vitiello, G. Fractals as macroscopic manifestation of squeezed coherent states and brain dynamics. J. Phys. Conf. Ser. 2012, 380, 012021. [Google Scholar] [CrossRef]
- Cavaglià, M.; Deriu, M.A.; Tuszynski, J.A. Toward a holographic brain paradigm: A lipid-centric model of brain functioning. Front. Neurosci. 2023, 17, 1302519. [Google Scholar] [CrossRef]
- Brown, J.; Tuszyński, J. Dipole interactions in axonal microtubules as a mechanism of signal propagation. Phys. Rev. E 1997, 56, 5834. [Google Scholar] [CrossRef]
- Lee, G.; Leech, G.; Rust, M.J.; Das, M.; McGorty, R.J.; Ross, J.L.; Robertson-Anderson, R.M. Myosin-driven actin-microtubule networks exhibit self-organized contractile dynamics. Sci. Adv. 2021, 7, eabe4334. [Google Scholar] [CrossRef]
- Babcock, N.; Montes-Cabrera, G.; Oberhofer, K.; Chergui, M.; Celardo, G.; Kurian, P. Ultraviolet superradiance from mega-networks of tryptophan in biological architectures. J. Phys. Chem. B 2024, 128, 4035–4046. [Google Scholar] [CrossRef]
- Kim, J.H.; Aghaeimeibodi, S.; Richardson, C.J.; Leavitt, R.P.; Waks, E. Super-radiant emission from quantum dots in a nanophotonic waveguide. Nano Lett. 2018, 18, 4734–4740. [Google Scholar] [CrossRef]
- Solano, P.; Barberis-Blostein, P.; Fatemi, F.K.; Orozco, L.A.; Rolston, S.L. Super-radiance reveals infinite-range dipole interactions through a nanofiber. Nat. Commun. 2017, 8, 1857. [Google Scholar] [CrossRef]
- Kurian, P.; Obisesan, T.; Craddock, T.J. Oxidative species-induced excitonic transport in tubulin aromatic networks: Potential implications for neurodegenerative disease. J. Photochem. Photobiol. B Biol. 2017, 175, 109–124. [Google Scholar] [CrossRef]
- Zapata, F.; Pastor-Ruiz, V.; Ortega-Ojeda, F.; Montalvo, G.; Ruiz-Zolle, A.V.; García-Ruiz, C. Human ultra-weak photon emission as non-invasive spectroscopic tool for diagnosis of internal states—A review. J. Photochem. Photobiol. B Biol. 2021, 216, 112141. [Google Scholar] [CrossRef]
- Lin, C.; Top, D.; Manahan, C.C.; Young, M.W.; Crane, B.R. Circadian clock activity of cryptochrome relies on tryptophan-mediated photoreduction. Proc. Natl. Acad. Sci. USA 2018, 115, 3822–3827. [Google Scholar] [CrossRef]
- Preparata, G. QED Coherence in Matter; World Scientific: Singapore, 1995. [Google Scholar]
- Debye, P. Polar Molecules; The Chemical Catalog Co., Inc.: New York, NY, USA, 1929; Volume 89. [Google Scholar]
- Cornwall, J.M.; Jackiw, R.; Tomboulis, E. Effective action for composite operators. Phys. Rev. D 1974, 10, 2428. [Google Scholar] [CrossRef]
- Calzetta, E.; Hu, B.L. Nonequilibrium quantum fields: Closed-time-path effective action, Wigner function, and Boltzmann equation. Phys. Rev. D 1988, 37, 2878. [Google Scholar] [CrossRef]
- Smith, A.; Lawson, A. The velocity of sound in water as a function of temperature and pressure. J. Chem. Phys. 1954, 22, 351–359. [Google Scholar] [CrossRef]
- Gaiduk, V.I.; Crothers, D.S. Nonharmonic transverse vibration of the H-bonded molecules and the THz spectra in ice and water. J. Mol. Liq. 2006, 128, 145–160. [Google Scholar] [CrossRef]
- Cifra, M.; Pokornỳ, J.; Havelka, D.; Kučera, O. Electric field generated by axial longitudinal vibration modes of microtubule. BioSystems 2010, 100, 122–131. [Google Scholar] [CrossRef]
- Kučera, O.; Cifra, M. Cell-to-cell signaling through light: Just a ghost of chance? Cell Commun. Signal. 2013, 11, 87. [Google Scholar] [CrossRef]
- Scholkmann, F.; Fels, D.; Cifra, M. Non-chemical and non-contact cell-to-cell communication: A short review. Am. J. Transl. Res. 2013, 5, 586. [Google Scholar]
- Shannon, C.E. Communication in the presence of noise. Proc. IRE 1949, 37, 10–21. [Google Scholar] [CrossRef]
- Hariharan, P. Optical Holography: Principles, Techniques and Applications; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Jaeger, H.; Haas, H. Harnessing nonlinearity: Predicting chaotic systems and saving energy in wireless communication. Science 2004, 304, 78–80. [Google Scholar] [CrossRef]
- Lukosevicius, M.; Jaeger, H. Reservoir computing approaches to recurrent neural network training. Comput. Sci. Rev. 2009, 3, 127–149. [Google Scholar] [CrossRef]
- Komatsu, M.; Yaguchi, T.; Nakajima, K. Algebraic approach towards the exploitation of “softness”: The input–output equation for morphological computation. Int. J. Robot. Res. 2021, 40, 99–118. [Google Scholar] [CrossRef]
- Nishiyama, A.; Tanaka, S.; Tuszynski, J.A. Non-Equilibrium ϕ4 Theory in a Hierarchy: Towards Manipulating Holograms in Quantum Brain Dynamics. Dynamics 2023, 3, 1–17. [Google Scholar] [CrossRef]
- Agarwal, R.P.; Baleanu, D.; Nieto, J.J.; Torres, D.F.; Zhou, Y. A survey on fuzzy fractional differential and optimal control nonlocal evolution equations. J. Comput. Appl. Math. 2018, 339, 3–29. [Google Scholar] [CrossRef]
- Huang, C.; Liu, H.; Shi, X.; Chen, X.; Xiao, M.; Wang, Z.; Cao, J. Bifurcations in a fractional-order neural network with multiple leakage delays. Neural Netw. 2020, 131, 115–126. [Google Scholar] [CrossRef]
- Chinnamuniyandi, M.; Chandran, S.; Changjin, X. Fractional order uncertain BAM neural networks with mixed time delays: An existence and Quasi-uniform stability analysis. J. Intell. Fuzzy Syst. 2024, 46, 4291–4313. [Google Scholar] [CrossRef]
- Xu, C.; Lin, J.; Zhao, Y.; Cui, Q.; Ou, W.; Pang, Y.; Liu, Z.; Liao, M.; Li, P. New results on bifurcation for fractional-order octonion-valued neural networks involving delays. Netw. Comput. Neural Syst. 2024, 1–53. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nishiyama, A.; Tanaka, S.; Tuszynski, J.A. Quantum Brain Dynamics: Optical and Acoustic Super-Radiance via a Microtubule. Foundations 2024, 4, 288-305. https://doi.org/10.3390/foundations4020019
Nishiyama A, Tanaka S, Tuszynski JA. Quantum Brain Dynamics: Optical and Acoustic Super-Radiance via a Microtubule. Foundations. 2024; 4(2):288-305. https://doi.org/10.3390/foundations4020019
Chicago/Turabian StyleNishiyama, Akihiro, Shigenori Tanaka, and Jack A. Tuszynski. 2024. "Quantum Brain Dynamics: Optical and Acoustic Super-Radiance via a Microtubule" Foundations 4, no. 2: 288-305. https://doi.org/10.3390/foundations4020019
APA StyleNishiyama, A., Tanaka, S., & Tuszynski, J. A. (2024). Quantum Brain Dynamics: Optical and Acoustic Super-Radiance via a Microtubule. Foundations, 4(2), 288-305. https://doi.org/10.3390/foundations4020019






