Abstract
Building on previous work that considered gravity to emerge from the collective behaviour of discrete, pre-geometric spacetime constituents, this work identifies these constituents with gravitons and rewrites their effective gravity-inducing interaction in terms of local variables for Schwarzschild–de Sitter scenarios. This formulation enables graviton-level simulations of entire emergent gravitational systems. A first simulation scenario confirms that the effective graviton interaction induces the emergence of spacetime curvature upon the insertion of a graviton condensate into a flat spacetime background. A second simulation scenario demonstrates that free fall can be considered to be fine-tuned towards a geodesic trajectory, for which the graviton flux, as experienced by a test mass, disappears.
1. Introduction
Numerous attempts to construct a theory of quantum gravity starting from a quantum field theory (typically, string theory) or from general relativity (typically, loop quantum gravity) have so far not yielded decisive results. According to emergent gravity theorists, this must be due to the fact that both formalisms emerge rather independently from a more fundamental framework involving entities that are currently invisible for experimentation, but can be expected to be of the order of the Planck scale [1,2,3]. Correspondingly, the emergent gravity paradigm states that spacetime and its dynamics, in terms of an effective gravitational field, emerge from the interaction of more fundamental, i.e., pre-geometric and non-gravitational, degrees of freedom [4,5,6]. It is often understood in terms of induced gravity [7] or entropic gravity [8], but applies to many other approaches as well; see [9,10,11] and references therein.
In one of the more recent approaches, gravity is considered to emerge from (possibly pre-spatiotemporal) graviton interactions, which are typically obtained from standard model physics [12,13,14,15,16,17]. Relating this approach to general relativity theory, however, remains a difficulty; see [18] and the previous references. In this work, this complication is shortcut by the introduction of an effective local graviton interaction––think of an analogy with the Lennard–Jones potential for molecular interactions—that is obtained from a solution of the Einstein field equations directly. This is achieved by borrowing heavily from previous results in entropic gravity theory.
Building on entropic gravity theory, previous work has provided an exploration of the emergentist viewpoint on gravity by adopting an explicit complex systems approach [19]. This work conjectured that spacetime basically consists of indistinguishable constituents that fulfil the conditions for the emergence of a complex system, which are defined as ‘numerosity’ and (typically non-linear) ‘interactions’ that spontaneously result in persistent structures [20]. In line with other emergent and analogue gravity approaches [4,15,21], it was assumed that only one type of such ‘spacetime constituents’ exists, that they move at the speed of light (i.e., cannot define spacetime for themselves), and that a single interaction law connects them relationally.
In this work, the spacetime constituents proposed in [19] are taken to be standard model gravitons (spin-2 gauge bosons). However, instead of using the standard derivation involving a boson Lagrangian that has each term corresponding to an interaction-specific Feynman graph [13,14], the graviton self-interaction is here derived from a reverse-engineering argument, in analogy with [9,19]: As the emergent effective field dynamics of the gravitons must eventually obey Einstein’s field equations, an interaction law that yields the required diffeomorphism invariant field behaviour is obtained from a solution to these equations (also see Section 2). This means that the graviton interaction is eventually formulated within the emergent spacetime framework itself, and not in a more fundamental, pre-geometric framework. Conceived as such, this approach is complicated by the involvement of some external time that is tied to the pre-geometric dynamics of the constituents. However, this flaw seems familiar and acceptable when looking at the analogous issue in perturbative string theory [22].
The proposed graviton interaction makes spacetime a non-ideal and dissipative fluid that eventually has to obey the Navier–Stokes equations [23,24]. For the Schwarzschild–de Sitter (SdS) scenarios in particular, as considered in this work, the graviton dynamics must obey the optical anisotropy of the Schwarzschild–de Sitter metric [25,26,27] and exhibit a spherically symmetric spacetime curvature around massive objects. In order to simplify our discussion without giving in on this metric, the central masses are considered to represent graviton condensates in this work, as motived by [28,29]. Here, a parallel can be observed with the recent attempt to derive entropic gravity from the relativistic transactional interpretation (RTI) of quantum mechanics [30]: In both approaches, spacetime and gravity emerge to massive entities from a speed-of-light interaction between them. This transaction takes place in the pre-spatiotemporal quantum substratum according to the RTI. In this work, the graviton interaction is made locally explicit with respect to emerged spacetime, enabling proof-of-principle simulations.
The presented work first revisits the spacetime constituent interaction identified in [19], which is extended to Schwarzschild–de Sitter scenarios in such a way that it only depends on local variables (Section 2). This enables direct graviton-level simulations for two simulation scenarios that are presented afterwards, and which are intended to, respectively, address two research questions (Section 3): (1) Does spacetime curvature emerge upon introducing a graviton condensate into a flat graviton (spacetime) background, and (2) does a graviton density gradient induce free fall upon a test mass? The demonstration of this emergent gravity framework by simulations of radially moving gravitons immediately results therefrom (Section 4). To our knowledge, these are the first graviton-level simulations in support of emergent gravity theory. The last section summarizes this work’s main findings and provides additional discussion (Section 5).
2. Effective Graviton Interaction
The self-interaction of gravitons within emergent gravity theory is typically developed from a Lagrangian framework [13,14], but this does not allow for graviton-level simulations of entire gravitational systems. Alternatively, as the graviton-graviton interaction must eventually obey the Einstein field equations, it can be derived from a solution to these equations for a null interval [9,19]. Given our goal to simulate the emergence of the spacetime curvature from a flat spacetime background upon the insertion of a mass, we consider the simplest solution of Einstein’s equations in the presence of both central mass M and cosmological constant , known as the Schwarzschild–de Sitter (SdS) metric [25]:
with
as a general solution. This solution actually combines the Schwarzschild solution describing a central mass in empty spacetime (second term) with the de Sitter solution for a cosmological constant (third term). The reference radius is the Schwarzschild radius with the G gravitational constant and the speed of light at infinity for . Cosmological constant can be considered to originate from a possibly time-dependent integration term in the Einstein field equations [31,32] and as such, for , represents a flat graviton background in this work.
For radially moving gravitons in the absence of a cosmological constant (, , ), the effective graviton velocity as calculated from Equations (1) and (2) simplifies to:
In previous work, based on the degrees of freedom within entropic gravity theory, M was found to represent a number of spacetime constituents multiplied by ‘unit mass’ as a conversion factor [19,33]. Under the assumption that an emergent quantum gravity theory requires spacetime to be discretized at the Planck scale (see also Introduction), this turned out to be equal to half of the Planck mass if the constituent length was equal to the Planck length [19]. Insertion of into Equation (3) reproduces Equation (4) of [19]:
whereby the right term was identified with a ‘radial constituent density’ that expresses the number of spacetime constituents with respect to radial distance R in Planck units. The radial constituent density only equals unity at the Schwarzschild radius, whereupon each Planck length along the radius is covered by a single constituent: and hence .
In this work, Equation (4) is assumed to hold for gravitons as well, upon their explicit identification with the constituents of the emergent spacetime presented in [19]. However, an alternative expression for the radial graviton density is required, which should allow rewriting Equation (4) fully in terms of local variables, hence expressing a local graviton interaction law. By redefining the radial graviton density due to M as , the critical (or condensation) radial density at the Schwarzschild radius is given by:
Therefore, the critical radial density corresponds to the presence of one graviton per Planck length along the radius, in agreement with our earlier assumption that the constituent size equals the Planck length. As such, Equation (4) becomes:
In analogy with our rewriting of the second term of Equation (2) in terms of a relative local graviton density , the same can be achieved for the third term that introduces a flat graviton background by means of a positive cosmological constant. By expressing the latter in terms of an equivalent volumetric mass density within R and insertion of the corresponding conversion factor , one obtains:
given that, as before . The de Sitter term of Equation (2) thus obtains the same form as the Schwarzschild term in Equation (4). By defining the background graviton density as , in agreement with the definition of , and sticking to the critical density obtained in Equation (5), the effective radial graviton velocity for the full Schwarzschild–de Sitter solution can be rewritten from Equation (6) in terms of the combined radial density as:
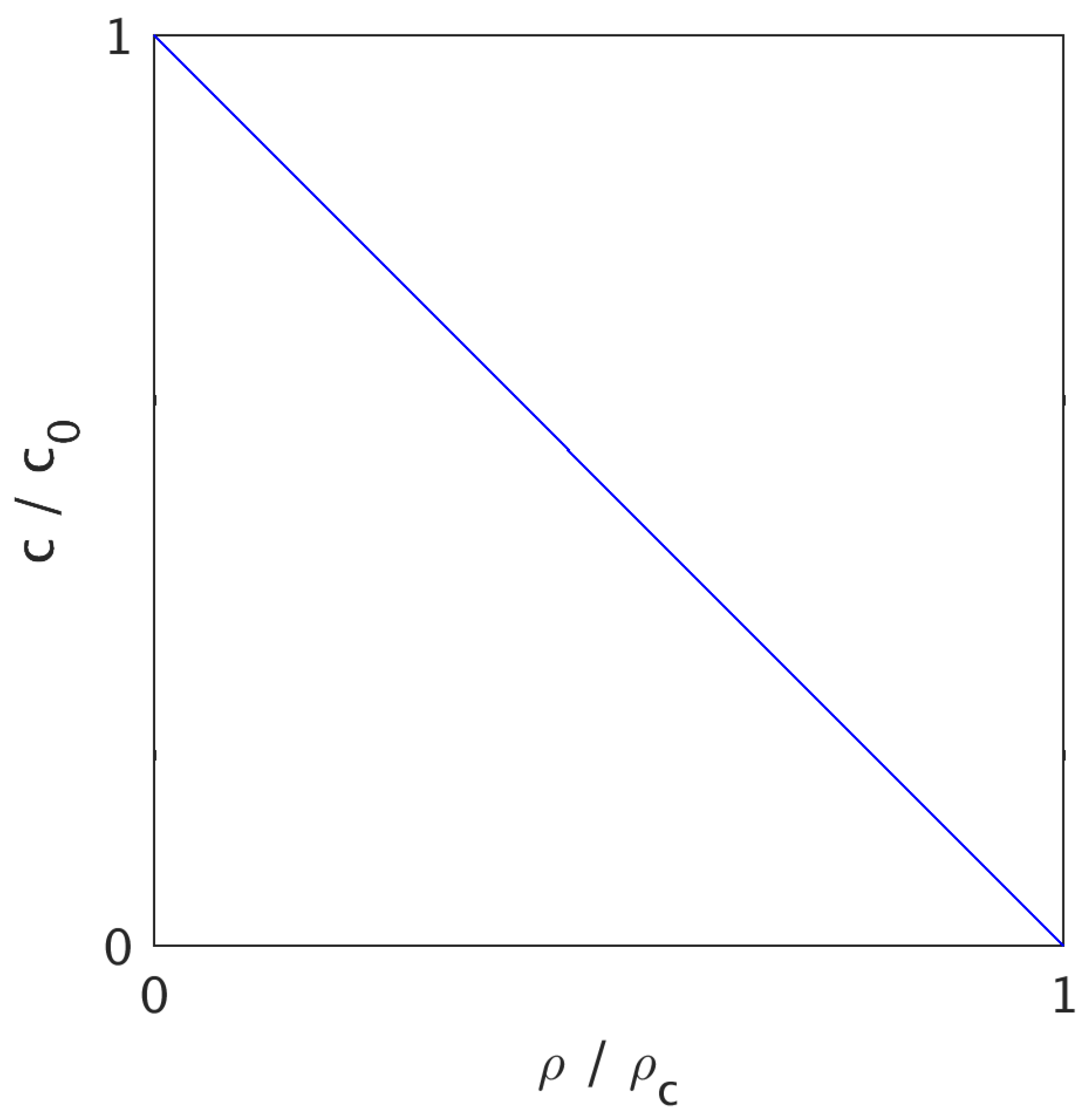
Equation (8) expresses a graviton interaction law based on local quantities, i.e., each graviton’s effective radial velocity is determined by the combined radial graviton density , including both a central graviton condensate (mass) and a constant graviton background. Therefore, this equation can be straightforwardly used for graviton-level simulations of Schwarzschild–de Sitter spacetimes (see next section). Moreover, it expresses a linear connection between graviton attributes c and that can be easily interpreted: The gravitons have a maximum speed in absolute (Fock) vacuum or , while they come to a standstill if there is no ‘room’ for movement, i.e., upon reaching , one has (see Figure 1). Moreover, from Equation (8), one also trivially has:
meaning that c and are recursively and symmetrically determined by an eventually non-linear interaction, resulting in a complex systems dynamic that shows a positive feedback mechanism (cf. Wheeler’s maxim [34]: "matter tells spacetime how to curve; spacetime tells matter how to move").
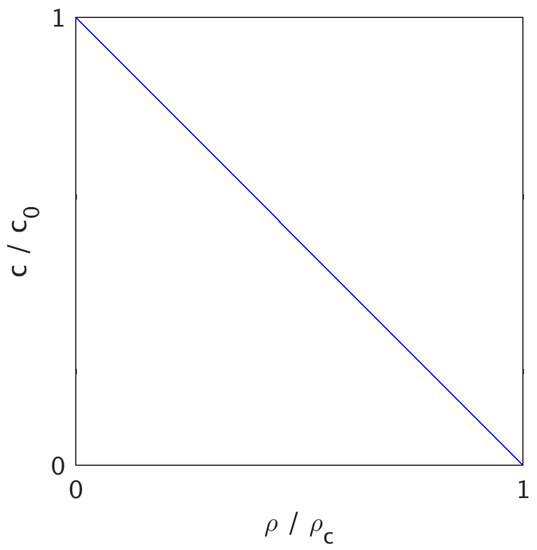
Figure 1.
Recursive linear connection between radial graviton density and radial graviton velocity c for an effective Schwarzschild–de Sitter spacetime.
3. Simulation Setup
Proof-of-principle for the emergence of gravity from a graviton interaction as obtained in the previous section is provided by straightforward graviton simulations. Two scenarios are considered addressing two research questions:
- Does spacetime curvature, i.e., a gravitational field in terms of a radial graviton density gradient, emerge upon introducing a mass (a graviton condensate) into a flat graviton background?
- Does the introduction of a test mass into a spherically symmetric gravitational field (a graviton density gradient) induce a geodesic trajectory (free fall)?
Conceived as such, both scenarios have spherically symmetric geometries around a central mass by construction. Through spherical integration, one can stick to radial simulations. For now, simulation parameter values are fine-tuned for proper visualization at short spatiotemporal scales of actually weak-field gravitational effects.
The radial simulations are performed by moving a conserved number of gravitons within an array of cells with a coarse-graining of choice and using circular edges. The central mass is considered a rigid graviton condensate that only contributes to the local graviton density. Apart from that, all gravitons in cell r are iteratively moved to cells by using the following implementation of Equation (8):
from with the current number of gravitons within cell r, and with randomly chosen between 0 and —mimicking spherical symmetry—for each graviton and within each iteration step with time interval , which is set to unity in practice. The graviton velocity c is determined by a sub-iteration within each , as is updated to each cell that is traversed by a graviton during a single time step.
According to the Schwarzschild–de Sitter solution to Einstein’s field equations, the introduction of a graviton condensate (central mass) into a flat graviton field (background cosmological constant) will go hand in hand with the emergence of a gravitational field in terms of a radial graviton density gradient outside of the central mass. This is demonstrated by the first simulation scenario addressing our first research question. The radial graviton density gradient can only emerge together with a radial graviton acceleration:
to a Rindler observer that is located at distance R from the mass centre. However, according to the equivalence principle for gravitational and inertial mass, a test object cannot distinguish between proper acceleration of its inertial mass and an acceleration in the opposite direction of the gravitons that constitute the local environment. Therefore, as in Einstein’s Gedankenexperiment [35], a gravitational field in terms of an acceleration of surrounding gravitons can be locally compensated for by the proper acceleration into a net flux-free (geodesic) trajectory, i.e., into the experience of a flat spacetime where the gradients of c and have disappeared. Conceived as such, free fall is a fine-tuning exercise by nature at (local) graviton speed: Due to the experience of a graviton flux, a graviton cluster is accelerated up to the point where the flux disappears. As a direct consequence, a test mass, which is a graviton condensate itself, can never be accelerated beyond the local graviton speed (of light). This is a well-known result from relativity theory.
In the second simulation scenario, a graviton condensate is introduced into a linearly curved spacetime background as a local, yet exaggerated, approximation to the previously emerged Schwarzschild–de Sitter spacetime. In the absence of a proper acceleration, this test mass will experience a gravitational pull in terms of a radial graviton density gradient . Our second research question addresses whether it can be accelerated up to and beyond a geodesic trajectory that has . According to the above, this can be achieved by adding a radial acceleration to Equation (10). Given the assumed rigidity of the test mass, however, this work sticks to radial acceleration that is independent of the location in simulation space. As such, the combined acceleration of the entire test mass is mimicked by a constant acceleration in the opposite direction of the curved spacetime background, leaving the test mass at the centre of the simulation space in practice. The second simulation scenario demonstrates that this acceleration can be fine-tuned to a free fall value whereupon the radial graviton density gradient indeed disappears at the location of the test mass.
4. Results
4.1. Spacetime Curvature
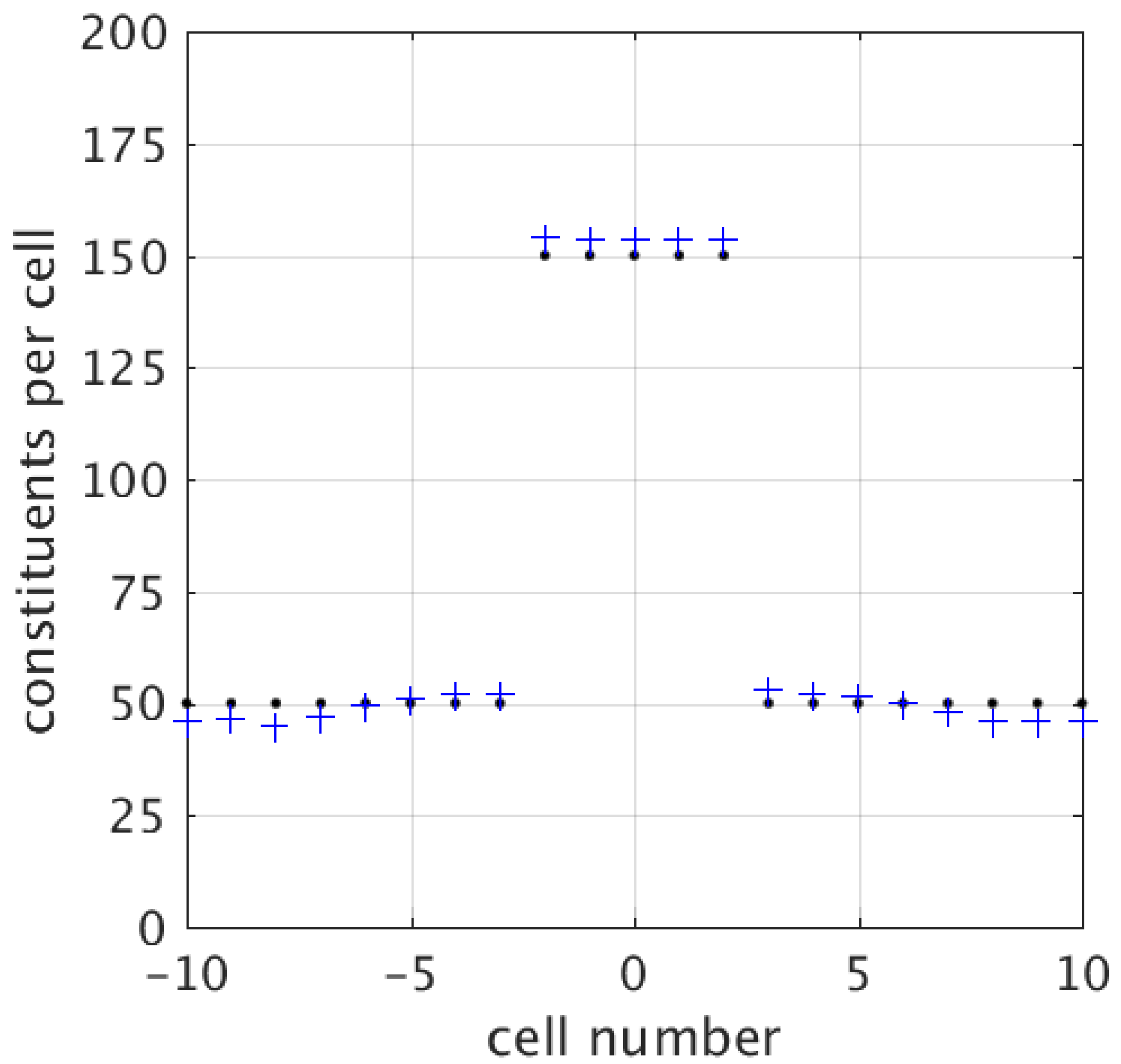
Considering simulation cells (to have a cell covering the mass centre at ) of size , and for of the spatial simulation range per , one has cells per time step . Introducing a flat spacetime background of 50 gravitons per cell and taking yields for the background. Adding a condensate of 100 gravitons per cell at the five central cells reduces the local graviton velocity to initially. Figure 2 contains simulation results for this first scenario, showing the emergence of a radial graviton density gradient outside of the central mass as a graviton condensate, i.e., outside of cells −2 to 2. The time-averaged graviton density is thereby plotted after 1000 iterations (blue crosses) and compared with the initially flat graviton density distribution (black dots). In every iteration step, any higher-order structure of is smoothed out from the condensate using linear fitting (while in reality the ratio between, e.g., a proton and a Planck-scale constituent, would be of the order of , allowing for tremendously complex internal dynamics, cf. QCD).
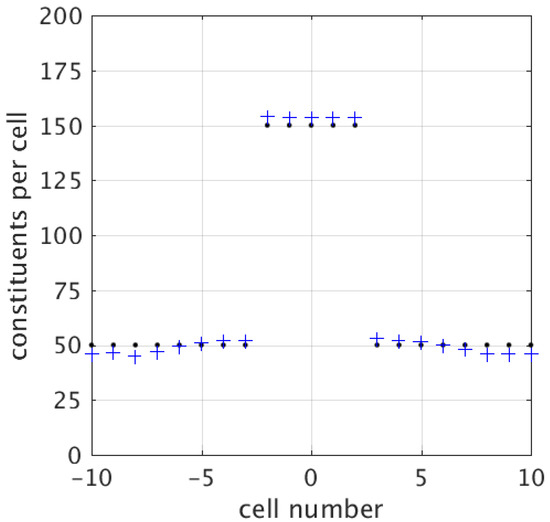
Figure 2.
Time-averaged number of constituents (gravitons) per cell before (black dots) and after (blue crosses) 1000 iterations for Scenario (1).
4.2. Geodesic Trajectory
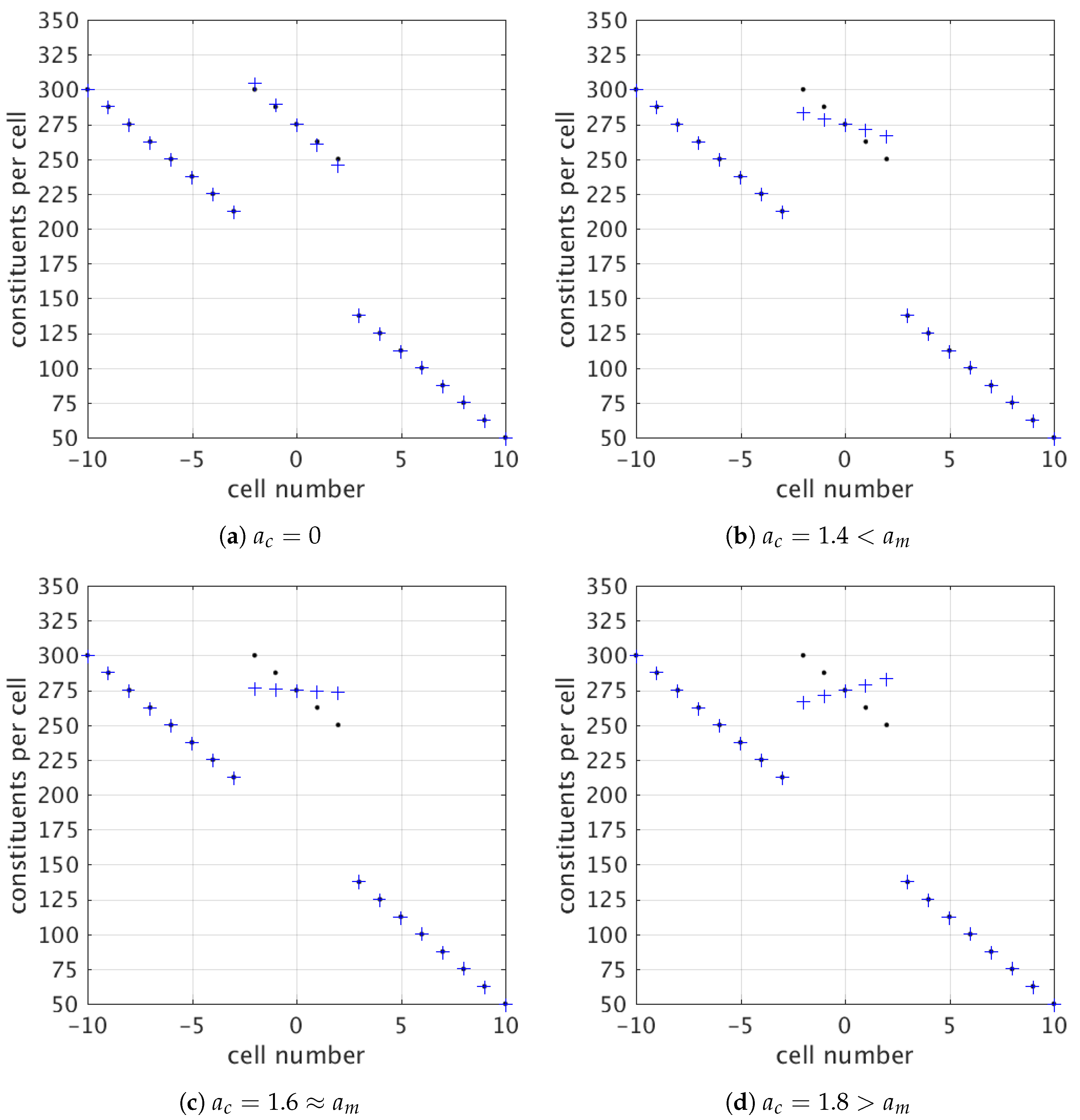
A linear background graviton density gradient, going from 300 () to 50 () gravitons per cell, is reintroduced upon every iteration step in the second scenario. As a result, the integrated number of gravitons of the central mass (with a distribution that is initially identical to that of the first scenario) has to be iteratively rescaled to keep the total graviton number conserved. Figure 3 displays the simulation results for this second scenario using the same settings as for Figure 2, for four values of acceleration term . The condensate experiences a graviton density gradient in agreement with the spacetime curvature for (Figure 3a), while the gradient decreases for increasing (Figure 3b) up to the point where a geodesic trajectory is reached, i.e., when the graviton acceleration matches the gravitational acceleration of the test mass (, Figure 3c). Acceleration beyond (Figure 3d) induces a graviton density gradient, and hence a gravitational pull according to the equivalence principle, in the opposite direction (cf. free fall as a fine-tuning exercise in the previous section).
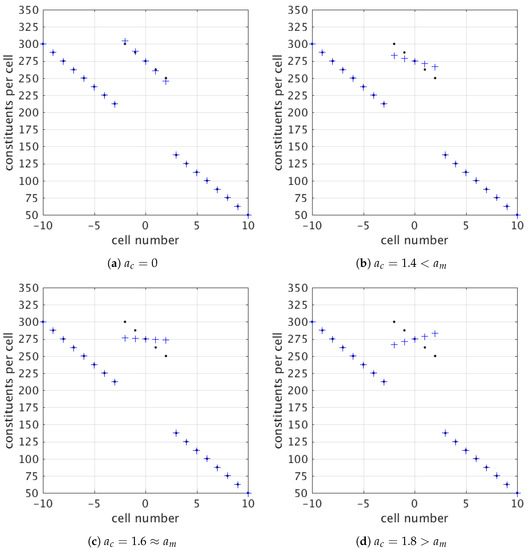
Figure 3.
Time-averaged number of constituents (gravitons) per cell before (black dots) and after (blue crosses) 1000 iterations for Scenario (2), for four values of the acceleration term in simulation units .
5. Discussion
In previous work, effective spacetime was considered to emerge from the collective behaviour of discrete, pre-geometric constituents, which were assumed to move at the speed of light with respect to massive constituent condensates (as observers) [19]. A constituent interaction (law) was defined in such way that general relativity’s Schwarzschild solution provided an effective description of the constituents’ emergent dynamics. Heavily building on these results, this work identifies spacetime’s constituents with gravitons and rewrites their effective gravity-inducing interaction in terms of local attributes (radial densities and velocities) for Schwarzschild–de Sitter scenarios. Actually, this formulation allows developing this emergent gravity framework without reference to the holographic principle—asserting that the number of fundamental degrees of freedom within a spacetime region is related to the area of its surface [36]—nor its artificial generalization to non-holographic surfaces, which were both assumed to be essential ingredients of entropic gravity theory [4,8,19,37,38,39]. Equation (8) indeed limits the gravitationally relevant degrees of freedom to the local graviton density along each graviton trajectory, which in turn determines the effective local graviton speed, as measured in a non-inertial coordinate system at fixed distance from the central mass. Most importantly, this localised formulation enables graviton-level emergent gravity simulations for the first time.
Two simulation scenarios are considered. Both scenarios show spherically symmetric (eventually Schwarzschild–de Sitter) geometries around a central mass by construction, and they address two research questions. The first simulation confirms that the graviton interaction proposed in Equation (8) indeed induces the emergence of a gravitational field in terms of a radial graviton density gradient as the spacetime curvature, upon introducing a graviton condensate (central mass) into a flat spacetime background. The second simulation addresses whether the introduction of a test mass into a (linearized) gravitational field induces a geodesic trajectory. By connecting with the equivalence principle, it is indeed found that the graviton flux, as experienced by the test mass, disappears upon proper acceleration, suggesting that free fall can be considered to be ‘fine-tuned’ towards a geodesic trajectory. Correspondingly, accelerating the test mass beyond the gravitational pull induces a graviton density gradient in the opposite direction.
The straightforward and successful insertion of a constant background graviton density in the simulations, as a substitute for a cosmological integration constant, indicates that the graviton fluid and the dark fluid, in terms of CDM cosmologies, could be one and the same, as already suggested in the literature [40]. The latter goes hand in hand with the study of Einstein’s field equations—including the cosmological constant—as a fully covariant representation of the graviton dynamics, i.e., without the need for their modification as for Verlinde’s entropic gravity [41]. Relatedly, it is remarkable that the absolute maximum mass density for which all gravitons come to a standstill (i.e., for ) equals , if represents the current (critical) density of the universe. This order of magnitude difference between the maximum density and the average observed density (corresponding to about six protons per ) points towards the cosmological constant problem: By construction, quantum field theories typically assign one condensed degree of freedom to each constituent-sized location at minimum, even in the vacuum state [42]. However, from the spacetime constituents considered here, it is concluded that on average the free graviton equivalent of one is distributed over possible locations. Thus, the universe is quite empty (in the Fock sense) with throughout, or, in other words, spacetime is mostly not. Moreover, within hadrons and black holes, which have comparable mass densities. In contrast with average spacetime, both can be considered graviton condensates indeed [43]. The ‘slow’ graviton movement ‘around’ and within these condensates must co-determine their (internal) dynamics.
The major drawbacks of the presented emergent gravity simulations are (1) their current limitation to Schwarzschild–de Sitter scenarios, (2) the need for the insertion of four-dimensional spacetime by hand, although the radial mass interpretation allows for reconsiderations in different dimensions, and (3) the lack of prospect towards a graviton-level falsification, i.e., at Planck energies [44]. Regarding (1), this work should be extendable to all Kerr–Newman-type surfaces by substitution of M with a total mass-equivalent that contains rotational and electric field energies. Generalizations of entropic gravity theory to geometries that are not necessarily asymptotically flat have been explored in the literature and will be related to this work in the future [45,46,47]. In order to compensate for (3), more extensive simulations involving fully realistic parameter values could demonstrate the applicability of this theory when compared to macro-scale observations. The latter also points to the necessity to connect with standard model quantum physics, although a possibility has already been outlined before [19]. Especially, the question of how graviton condensates acquire inertial mass, possibly through a connection to a Higgs field, has not been addressed in this work, and requires further examination.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The simulation code and data generated for this study can be obtained from the corresponding author upon request.
Acknowledgments
The author wishes to thank Christian Wüthrich (University of Geneva), Daniele Oriti (Max Planck Institute for Gravitational Physics, Potsdam), and their teams for insightful discussions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Adler, R.J. Six easy roads to the Planck scale. Am. J. Phys. 2010, 78, 925–932. [Google Scholar] [CrossRef]
- Hossenfelder, S. Minimal Length Scale Scenarios for Quantum Gravity. Living Rev. Relativ. 2013, 16, 2. [Google Scholar] [CrossRef] [PubMed]
- Linnemann, N.S.; Visser, M.R. Hints towards the emergent nature of gravity. Stud. Hist. Philos. Sci. B 2018, 64, 1–13. [Google Scholar] [CrossRef]
- Padmanabhan, T. Emergent gravity paradigm: Recent progress. Mod. Phys. Lett. A 2015, 30, 1540007. [Google Scholar] [CrossRef]
- Crowther, K. Effective Spacetime: Understanding Emergence in Effective Field Theory and Quantum Gravity; Springer International Publishing: Basel, Switzerland, 2016. [Google Scholar]
- Oriti, D. Levels of spacetime emergence in quantum gravity. arXiv 2018, arXiv:1807.04875. [Google Scholar] [CrossRef]
- Sakharov, A.D. Vacuum quantum fluctuations in curved space and the theory of gravitation. Dokl. Akad. Nauk SSSR 1967, 177, 70–71. [Google Scholar]
- Verlinde, E. On the origin of gravity and the laws of Newton. J. High Energy Phys. 2011, 29, 1–27. [Google Scholar] [CrossRef]
- Hu, B.L. Emergent/quantum gravity: Macro/micro structures of spacetime. J. Phys. Conf. Ser. 2009, 174, 012015. [Google Scholar] [CrossRef]
- Sindoni, L. Emergent models for gravity: An overview of microscopic models. Symmetry Integr. Geom. Methods Appl. 2012, 8, 027. [Google Scholar] [CrossRef]
- Mielczarek, J.; Trześniewski, T. Towards the map of quantum gravity. Gen. Relativ. Gravit. 2018, 50, 68. [Google Scholar] [CrossRef]
- Kawai, H.; Kawana, K.; Sakai, K. A note on graviton exchange in the emergent gravity scenario. Prog. Theor. Exp. Phys. 2017, 2017, 043B06. [Google Scholar] [CrossRef]
- Carone, C.D.; Erlich, J.; Vaman, D. Emergent gravity from vanishing energy-momentum tensor. J. High Energy Phys. 2017, 2017, 134. [Google Scholar] [CrossRef]
- Carone, C.D.; Claringbold, T.V.B.; Vaman, D. Composite graviton self-interactions in a model of emergent gravity. Phys. Rev. D 2018, 98, 024041. [Google Scholar] [CrossRef]
- Barceló, C.; Carballo-Rubio, R.; Garay, L.; García-Moreno, G. Toward a mechanism for the emergence of gravity. Appl. Sci. 2021, 11, 8763. [Google Scholar] [CrossRef]
- Betzios, P.; Kiritsis, E.; Niarchos, V. Emergent gravity from hidden sectors and TT deformations. J. High Energy Phys. 2021, 2021, 202. [Google Scholar] [CrossRef]
- Lee, S.S. Massless graviton in a model of quantum gravity with emergent spacetime. arXiv 2023, arXiv:2212.14011. [Google Scholar] [CrossRef]
- Padmanabhan, T. From Gravitons to Gravity: Myths and Reality. Int. J. Mod. Phys. D 2008, 17, 367–398. [Google Scholar] [CrossRef]
- Keppens, A. What constitutes emergent quantum reality? A complex system exploration from entropic gravity and the universal constants. Entropy 2018, 20, 335. [Google Scholar] [CrossRef]
- Ladyman, J.; Lambert, J.; Wiesner, K. What is a complex system? Eur. J. Philos. Sci. 2012, 3, 33–67. [Google Scholar] [CrossRef]
- Oriti, D. Spacetime as a Quantum Many-Body System. In Many-Body Approaches at Different Scales: A Tribute to Norman H. March on the Occasion of His 90th Birthday; Angilella, G.G.N., Amovilli, C., Eds.; Springer International Publishing: Berlin/Heidelberg, Germany, 2018; pp. 365–379. [Google Scholar] [CrossRef]
- Huggett, N.; Vistarini, T. Deriving General Relativity from String Theory. Philos. Sci. 2015, 82, 1163–1174. [Google Scholar] [CrossRef]
- Padmanabhan, T. Entropy density of spacetime and the Navier-Stokes fluid dynamics of null surfaces. Phys. Rev. D 2011, 83, 044048. [Google Scholar] [CrossRef]
- Chakraborty, S.; Padmanabhan, T. Thermodynamical interpretation of the geometrical variables associated with null surfaces. Phys. Rev. D 2015, 92, 104011. [Google Scholar] [CrossRef]
- Stuchlík, Z.; Hledík, S. Some properties of the Schwarzschild–de Sitter and Schwarzschild–anti-de Sitter spacetimes. Phys. Rev. D 1999, 60, 044006. [Google Scholar] [CrossRef]
- Gibbons, G.W.; Warnick, C.M.; Werner, M.C. Light bending in Schwarzschild–de Sitter: Projective geometry of the optical metric. Class. Quantum Gravity 2008, 25, 245009. [Google Scholar] [CrossRef]
- Khorasani, S.; Rashidian, B. Optical anisotropy of schwarzschild metric within equivalent medium framework. Opt. Commun. 2010, 283, 1222–1228. [Google Scholar] [CrossRef]
- Dvali, G.; Gomez, C. Black holes as critical point of quantum phase transition. Eur. Phys. J. C 2014, 74, 2752. [Google Scholar] [CrossRef] [PubMed]
- Alfaro, J.; Mancilla, R. Thermodynamics of graviton condensate. Eur. Phys. J. C 2021, 81, 871. [Google Scholar] [CrossRef]
- Schlatter, A.; Kastner, R.E. Gravity from Transactions: A Review of Recent Developments. arXiv 2022, arXiv:2209.04025. [Google Scholar] [CrossRef]
- Padmanabhan, T. The atoms of spacetime and the cosmological constant. J. Phys. Conf. Ser. 2017, 880, 012008. [Google Scholar] [CrossRef]
- Gallagher, P.; Koivisto, T. The Λ and the CDM as integration constants. Symmetry 2021, 13, 2076. [Google Scholar] [CrossRef]
- Abanto, J.A.Q. Information Theory of Gravity. 2021; Preprints. [Google Scholar] [CrossRef]
- Wheeler, J. Geons, Black Holes, and Quantum Foam: A Life in Physics; W. W. Norton & Co.: New York, NY, USA, 1998. [Google Scholar]
- Einstein, A. Über den Einfluß der Schwerkraft auf die Ausbreitung des Lichtes. Ann. Der Phys. 1911, 340, 898–908. [Google Scholar] [CrossRef]
- Bousso, R. The holographic principle. Rev. Mod. Phys. 2002, 74, 825–874. [Google Scholar] [CrossRef]
- Lee, J.W. On the Origin of Entropic Gravity and Inertia. Found. Phys. 2012, 42, 1153–1164. [Google Scholar] [CrossRef]
- Gao, S. Is Gravity an Entropic Force? Entropy 2011, 13, 936–948. [Google Scholar] [CrossRef]
- Wang, Z.W.; Braunstein, S.L. Surfaces away from horizons are not thermodynamic. Nat. Commun. 2018, 9, 2977. [Google Scholar] [CrossRef] [PubMed]
- Deur, A. Implications of graviton-graviton interaction to dark matter. Phys. Lett. B 2009, 676, 21–24. [Google Scholar] [CrossRef]
- Hossenfelder, S. Covariant version of Verlinde’s emergent gravity. Phys. Rev. D 2017, 95, 124018. [Google Scholar] [CrossRef]
- Hollands, S.; Wald, R.M. Essay: Quantum field theory is not merely quantum mechanics applied to low energy effective degrees of freedom. Gen. Relativ. Gravit. 2004, 36, 2595–2603. [Google Scholar] [CrossRef]
- Oriti, D.; Pranzetti, D.; Sindoni, L. Black holes as quantum gravity condensates. Phys. Rev. D 2018, 97, 066017. [Google Scholar] [CrossRef]
- Rothman, T.; Boughn, S. Can gravitons be detected? Found. Phys. 2006, 36, 1801–1825. [Google Scholar] [CrossRef]
- Myung, Y.S.; Kim, Y.W. Entropic force and entanglement system. Phys. Rev. D 2010, 81, 105012. [Google Scholar] [CrossRef]
- Nicolini, P. Entropic force, noncommutative gravity, and ungravity. Phys. Rev. D 2010, 82, 044030. [Google Scholar] [CrossRef]
- Sakalli, I. Dilatonic entropic force. Int. J. Theor. Phys. 2011, 50, 2426–2437. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).