Homotopy Perturbation Method for Pneumonia–HIV Co-Infection
Abstract
1. Introduction
2. Formulation of the Co-Infection Model
- (1)
- The disease-free equilibrium point:The disease-free equilibrium point is given by .The basic reproduction number is computed at the disease-free equilibrium by using the next-generation matrix method provided by [26]. The basic reproduction number is defined as the number of secondary infections caused by one infected individual in a susceptible population. The basic reproduction number is given bywhere
- (2)
- The endemic equilibrium point for pneumonia:The endemic equilibrium point for pneumonia is given by,whereThe endemic point for pneumonia exists if .
- (3)
- The endemic equilibrium point for HIV:The endemic equilibrium point for HIV is given by ,whereThe endemic point for HIV exists if .
- (4)
- Endemic equilibrium point:The endemic equilibrium point is denoted by :where
3. The Homotopy Perturbation Method (HPM) and Its Application in Our Model
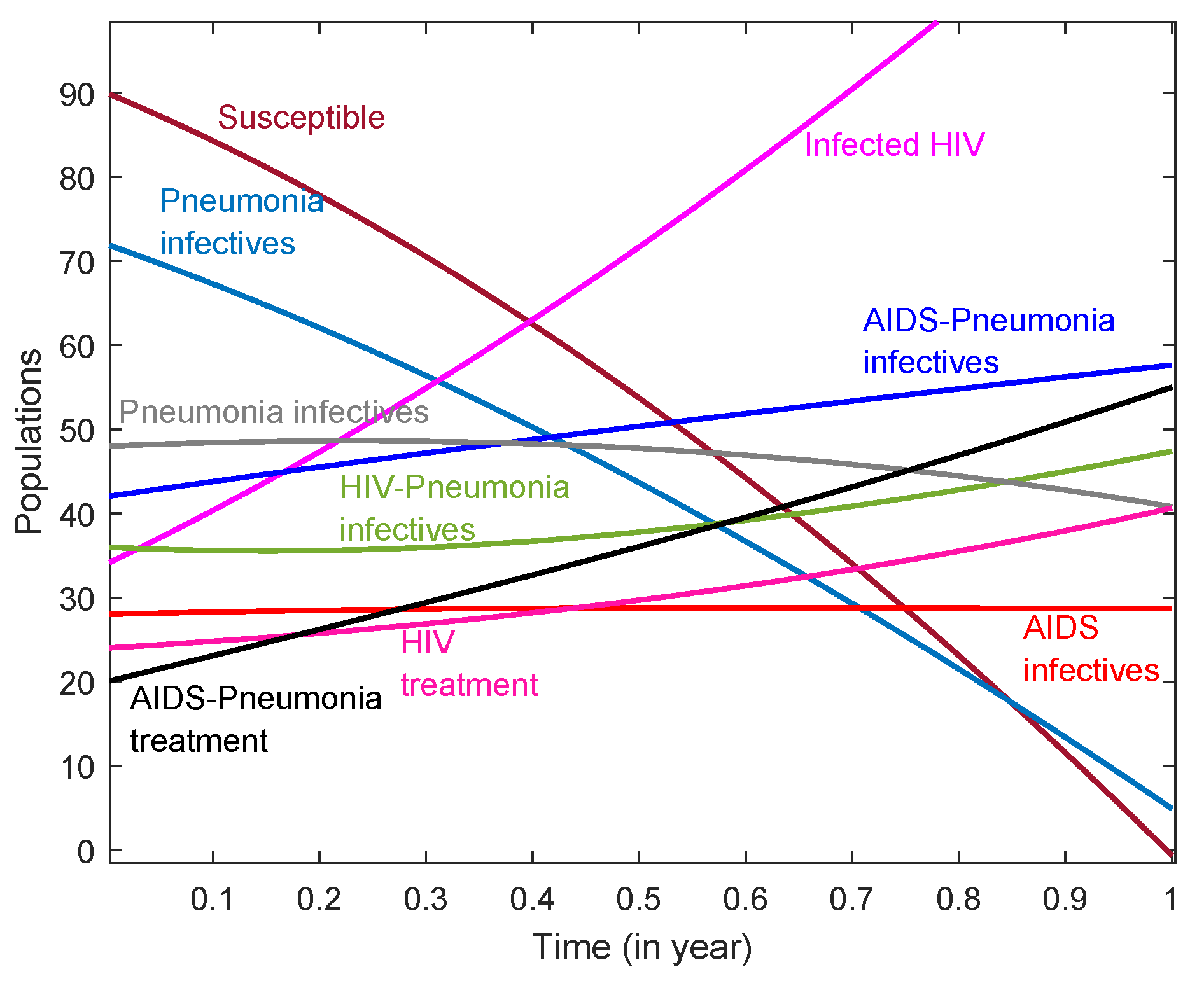
4. Numerical Simulation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mayilvaganan, S.; Balamuralitharan, S. Analytical solutions of influenza diseases model by HPM. AIP Conf. Proc. 2019, 2112, 020008. [Google Scholar] [CrossRef]
- Omondi, E.O.; Mbogo, R.W.; Luboobi, L.S. Mathematical analysis of sex-structured population model of HIV infection in Kenya. Lett. Biomath. 2018, 5, 174–194. [Google Scholar] [CrossRef]
- Khademi, F.; Yousefi-Avarvand, A.; Sahebkar, A.; Ghanbari, F.; Vaez, H. Bacterial co-infections in HIV/AIDS-positive subjects: A systematic review and meta-analysis. Folia Med. 2018, 60, 339–350. [Google Scholar] [CrossRef]
- Lutera, J.; Mbete, D.; Wangila, S. Co-infection model of HIV/AIDS-pneumonia on the effect of treatment at initial and final stages. IOSR J. Math. 2018, 14, 56–81. [Google Scholar]
- Huang, L.; Crothers, K. HIV-associated opportunistic pneumonias. Respirology 2009, 14, 474–485. [Google Scholar] [CrossRef]
- Teklu, S.W.; Kotola, B.S. The Impact of Protection Measures and Treatment on Pneumonia Infection: A Mathematical Model Analysis supported by Numerical Simulation. bioRxiv 2022. [Google Scholar] [CrossRef]
- Naveed, M.; Baleanu, D.; Raza, A.; Rafiq, M.; Soori, A.H.; Mohsin, M. Modeling the transmission dynamics of delayed pneumonia-like diseases with a sensitivity of parameters. Adv. Differ. Equations 2021, 2021, 1–19. [Google Scholar] [CrossRef]
- Tilahun, G.T.; Makinde, O.D.; Malonza, D. Modelling and optimal control of pneumonia disease with cost-effective strategies. J. Biol. Dyn. 2017, 11, 400–426. [Google Scholar] [CrossRef]
- Huo, H.F.; Chen, R. Stability of an HIV/AIDS treatment model with different stages. Discret. Dyn. Nat. Soc. 2015, 1–9. [Google Scholar] [CrossRef]
- Dutta, A.; Gupta, P.K. A mathematical model for transmission dynamics of HIV/AIDS with effect of weak CD4+ T cells. Chin. J. Phys. 2018, 56, 1045–1056. [Google Scholar] [CrossRef]
- de Carvalho, T.; Cristiano, R.; Goncalves, L.F.; Tonon, D.J. Global analysis of the dynamics of a mathematical model to intermittent HIV treatment. Nonlinear Dyn. 2020, 101, 719–739. [Google Scholar] [CrossRef]
- Nthiiri, J.K.; Lavi, G.O.; Mayonge, A. Mathematical model of pneumonia and HIV/AIDS coinfection in the presence of protection. Int. J. Math. Anal. 2015, 9, 2069–2085. [Google Scholar] [CrossRef]
- Onyinge, D.O.; Ongati, N.O.; Odundo, F. Mathematical model for co-infection of HIV/AIDS and pneumonia with treatment. Int. J. Sci. Eng. Appl. Sci. 2016, 2, 106–111. [Google Scholar]
- Teklu, S.W. Mathematical analysis of the transmission dynamics of COVID-19 infection in the presence of intervention strategies. J. Biol. Dyn. 2022, 16, 640–664. [Google Scholar] [CrossRef]
- Shen, C.; Xu, F.; Zhang, J.F. Periodic Solutions of an Infected-Age Structured HIV Model with the Latent Factor and Different Transmission Modes. Int. J. Bifurc. Chaos 2022, 32, 2250008. [Google Scholar] [CrossRef]
- Liu, H.; Xu, F.; Zhang, J.F. Analysis of an age-structured HIV-1 Infection Model with Logistic Target cell growth. J. Biol. Syst. 2020, 28, 927–944. [Google Scholar] [CrossRef]
- Wang, S.; Xu, F.; Rong, L. Bistability analysis of an HIV model with immune response. J. Biol. Syst. 2017, 25, 677–695. [Google Scholar] [CrossRef]
- Biazar, J. Solution of the epidemic model by Adomian decomposition method. Appl. Math. Comput. 2006, 173, 1101–1106. [Google Scholar] [CrossRef]
- Rafei, M.; Ganji, D.D.; Daniali, H. Solution of the epidemic model by homotopy perturbation method. Appl. Math. Comput. 2007, 187, 1056–1062. [Google Scholar] [CrossRef]
- He, J.H. Recent development of the homotopy perturbation method. Topol. Methods Nonlinear Anal. 2008, 31, 205–209. [Google Scholar]
- He, J.H. An elementary introduction to the homotopy perturbation method. Comput. Math. Appl. 2009, 57, 410–412. [Google Scholar] [CrossRef]
- Khan, M.A.; Islam, S.; Ullah, M.; Khan, S.A.; Zaman, G.; Arif, M.; Sadiq, S.F. Application of homotopy perturbation method to vector host epidemic model with non-linear incidences. Res. J. Recent Sci. 2013, 2, 90–95. [Google Scholar]
- Kolawole, M.; Ogunniran, M.; Alaje, A.; Kamiludeen, R.T. Simulating the Effect of Disease Transmission Coefficient on A Disease Induced Death Seirs Epidemic Model Using the Homotopy Perturbation Method. J. Appl. Comput. Sci. Math. 2022, 16, 40–43. [Google Scholar] [CrossRef]
- Rekha, S.; Balaganesan, P.; Renuka, J. Homotopy Perturbation Method for Mathematical Modeling of Listeriosis and Anthrax Diseases. Ann. Rom. Soc. Cell Biol. 2021, 25, 9787–9809. [Google Scholar]
- Omale, D.; Gochhait, S. Analytical solution to the mathematical models of HIV/AIDS with control in a heterogeneous population using Homotopy Perturbation Method (HPM). AMSE J. AMSE IIETA Ser. Adv. A 2018, 55, 20–34. [Google Scholar]
- Diekmann, O.; Heesterbeek, J.A.P.; Metz, J.A. On the definition and the computation of the basic reproduction ratio R 0 in models for infectious diseases in heterogeneous populations. J. Math. Biol. 1990, 28, 365–382. [Google Scholar] [CrossRef]
- He, J.H. Homotopy perturbation technique. Comput. Methods Appl. Mech. Eng. 1999, 178, 257–262. [Google Scholar] [CrossRef]
- Peter, O.J.; Awoniran, A.F. Homotopy perturbation method for solving sir infectious disease model by incorporating vaccination. Pac. J. Sci. Technol. 2018, 18, 133–140. [Google Scholar]
- Agbata, B.C.; Shior, M.M.; Olorunnishola, O.A.; Ezugorie, I.G.; Obeng-Denteh, W. Analysis of Homotopy Perturbation Method (HPM) and its Application for Solving Infectious Disease Models. Int. J. Math. Stat. Stud. 2021, 9, 27–38. [Google Scholar]
| Notation | Description | Parametric Values |
|---|---|---|
| N | Total human population | 0.5 |
| B | Birth rate | 0.0087 |
| The rate at which susceptible individuals acquire HIV infections | 0.024 | |
| The rate at which HIV-infected individuals are treated | 0.23 | |
| The rate at which HIV-infected individuals acquire pneumonia | 0.38 | |
| The rate at which HIV-infected individuals acquire AIDS | 0.125 | |
| The rate at which pneumonia-infected individuals join pneumonia treatment class | 0.42 | |
| The rate at which pneumonia-infected individuals acquire HIV | 0.006 | |
| The rate at which individuals suffering from pneumonia–HIV acquire AIDS and join the AIDS–pneumonia class | 0.08 | |
| The rate at which AIDS-infected individuals acquire pneumonia and join the pneumonia–AIDS class | 0.52 | |
| The rate at which pneumonia–HIV-infected individuals join the pneumonia–AIDS treatment class | 0.48 | |
| The rate at which AIDS–pneumonia-infected individuals join the treatment class | 0.33 | |
| The rate at which individuals treated for pneumonia are susceptible again | 0.5 | |
| Modification parameter responsible for increased co-infectivity | 0.04, 0.06 | |
| Contact rate with pneumonia-infected individuals | 0.125 | |
| HIV-related death | 0.01 | |
| Natural death rate | 0.02 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shah, N.H.; Sheoran, N. Homotopy Perturbation Method for Pneumonia–HIV Co-Infection. Foundations 2022, 2, 1101-1113. https://doi.org/10.3390/foundations2040072
Shah NH, Sheoran N. Homotopy Perturbation Method for Pneumonia–HIV Co-Infection. Foundations. 2022; 2(4):1101-1113. https://doi.org/10.3390/foundations2040072
Chicago/Turabian StyleShah, Nita H., and Nisha Sheoran. 2022. "Homotopy Perturbation Method for Pneumonia–HIV Co-Infection" Foundations 2, no. 4: 1101-1113. https://doi.org/10.3390/foundations2040072
APA StyleShah, N. H., & Sheoran, N. (2022). Homotopy Perturbation Method for Pneumonia–HIV Co-Infection. Foundations, 2(4), 1101-1113. https://doi.org/10.3390/foundations2040072






