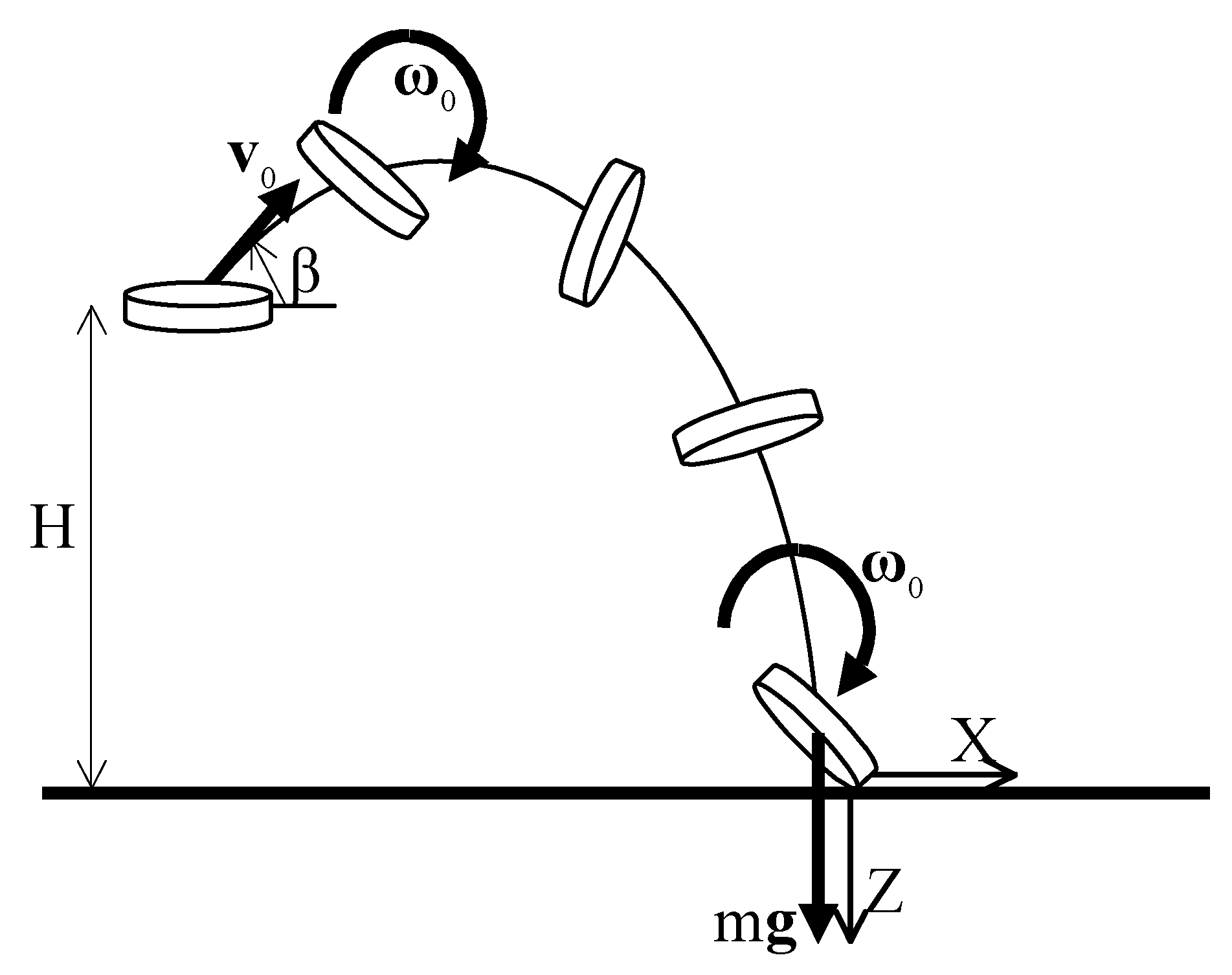Is The Probability of Tossing a Coin Really 50–50%? Part 2: Dynamic Model with Rebounds

Abstract

In the first part of this paper, we considered several theoretical models, a static and four dynamic models without rebounds, of the throw of a fair coin landing on its edge, to demonstrate that the probability of heads or tails is less than 50%, depending on the initial toss conditions, the coin geometry and conditions of the coin and landing surfaces. For the dynamic model with rebounds that is the subject of this second part of the paper, it is found that the probability that a 50 Euro cent coin thrown from a normal height with common initial velocity conditions and appropriate surface conditions will end up on its edge is in the order of one against several thousand.

1. Introduction

In the first part of this paper [1], several theoretical models, a static and four dynamic models without rebounds, were investigated to demonstrate that the throw of a fair coin can end with the coin on its edge, showing that the probability of heads or tails is less than 50%, depending on the initial conditions of the throw, the coin geometry and surface conditions of the coin and the landing area. The conclusion was that the probability of a coin landing on its edge is far from being nil, and in the order of one over several thousand.

In this second part of the paper, we consider a dynamic model with rebounds. The mechanical model equations are derived from a classic textbook [2].

It is found that the probability that a 50 Euro cent coin thrown from a normal height with common initial velocity conditions and appropriate surface conditions will end up on its edge is in the order of one against several thousand, but less than for the cases without rebounds.

2. Dynamic Model with Rebounds

2.1. General Model and Equations

All of the mechanical development of models and equations are detailed in the first part of the paper [1] and will not be repeated in this second paper. Only the main hypotheses and equations are recalled here.

We consider the following hypotheses (with bold characters denoting vectors):

-

the coin is fair, i.e., the coin is a homogeneous flat circular cylinder of mass $m$ and with thickness $h$ and diameter $d$;

-

the coin is thrown manually from an initial height $H$ with a velocity $v_0$ under an angle $\beta$ on the horizontal, and an initial angular velocity ${\omega }_0$; for a manual throw, the minimum and maximum possible values are considered to be:

$$d<H<2 \mathrm{m} ; 0<v_0<5 \mathrm{m}/\mathrm{s};-\frac{\pi }{2}<\beta <\pi /2 ; 0<{\omega }_0<10\pi \mathrm{rad}/\mathrm{s}$$

(1)

where $v_0$ and ${\omega }_0$ are the norms of the vectors $v_0$ and ${\omega }_0$;

-

the coin rotation axis is horizontal and passes through the coin center of mass at all times during the fall, until impacting the landing surface;

-

the coin angular velocity after the impact is along an undefined instantaneous axis of rotation that stays horizontal at all times;

-

the atmosphere is windless, without any disturbance and the air friction is negligible;

-

the landing surface is a perfectly horizontal plane, with a solid and immovable surface.

One considers further a referential frame with its origin at the impact point on the landing surface, its $Z$-axis perpendicular to the landing surface and directed downward, its $X$ and $Y$ axes in the horizontal plane of the landing surface with $X$ pointing in the direction of the throw (see Figure 1).

Using the impact equations [2] and developing then along the three axes X, Y, Z, one obtains:

$$along X: m u_x = m v_{0}cos \beta - T$$

(2)

$$along Y: I_a \left(\pm {\omega }_a\right) = I_b \left(\pm {\omega }_0\right) - N \rho \sin (\theta -\frac{\alpha }{2}), - T \rho \cos (\theta -\frac{\alpha }{2})$$

(3)

$$along Z: m u_z = m \sqrt{v_0^2{\sin }^2\beta +2gH}+ N$$

(4)

with

-

$v_0$ the norm of the velocity vector before impact;

-

$u_{\mathrm{x}}$ and $u_{\mathrm{z}}$ the components of the velocity vector after impact;

-

$\beta$ the angle of the initial velocity vector with the horizontal (see Figure 1);

-

T and N are the components of the impulse vector, respectively, along and normal to the surface at the point of contact;

-

$\rho =\frac{\sqrt{h^2+d^2}}{2}$ is the distance from the impact point to the coin center of mass (see Figure 2);

-

$I_{\mathrm{b}}$ and $I_{\mathrm{a}}$ are the moments of inertia of $m$ at the coin center of mass with respect to the instantaneous axis of rotation before and immediately after impact;

-

$\pm {\omega }_0$ and $\pm {\omega }_a$ are the coin angular velocity before and after impact, + (respectively, -) for a coin counterclockwise (respectively, clockwise) rotation;

2.2. The Case of Rebounds

The four cases analyzed in the first paper assumed that the coin is not rebounding after impact. This is obviously the case by definition for the first two cases with inelastic surfaces, the velocity component normal to the landing surface becomes nil, and the coin does not rebound.

For the last two cases, where elastic surfaces are involved, one has to be more cautious. A simple condition of no-rebound can be found by writing that the normal impulse of the landing surface at impact must be smaller than the integral over time of the coin weight considered as an impulsive force during the short period of impact, i.e.,

$$\left|N\right|=\left|{{\displaystyle \int }}_{t_0}^{t_f}mg dt\right|=mg \Delta t$$

(5)

For this condition to be respected in the two cases of elastic surfaces, the duration of impact $\Delta t$ must be such as:

$$\Delta t>\left|\left(\frac{1+e}{g}\right)\left(\left(\pm {\omega }_a\right)\rho \sin (\theta -\frac{\alpha }{2})-\sqrt{v_0^2{\sin }^2\beta +2gH}\right)\right|$$

(6)

where $e$ is the coefficient of restitution. Relation (6) yields, respectively, for the cases of elastic and perfectly smooth bodies and of elastic and partially rough bodies (with μ as the coefficient of friction)

$$\Delta t>\left|\frac{\kappa \left(\pm {\omega }_0\right)\sin (\theta -\frac{\alpha }{2})-\frac{{\kappa }_a}{\rho }\sqrt{v_0^2{\sin }^2\beta +2gH}}{g\left(\frac{{\kappa }_a}{\left(1+e\right)\rho }+{\sin }^2(\theta -\frac{\alpha }{2})\right)}\right|$$

(7)

$$\Delta t>\left|\frac{\kappa \left(\pm {\omega }_0\right)\sin (\theta -\frac{\alpha }{2})-\frac{{\kappa }_a}{\rho }\sqrt{v_0^2{\sin }^2\beta +2gH}}{g\left(\frac{{\kappa }_a}{\left(1+e\right)\rho }+{\sin }^2(\theta -\frac{\alpha }{2})+\frac{\mu }{2}\sin (2\theta -\alpha )\right)}\right|$$

(8)

where:

$$\kappa ={\kappa }_b=\frac{I_b}{\rho m}=\frac{\left(\frac{h^2}{3}+\frac{d^2}{4}\right)}{2\sqrt{h^2+d^2}}\hspace{1em}\hspace{1em}and\hspace{1em}{\kappa }_a=\frac{I_a}{\rho m}$$

For the numerical values given in (1) and assuming, for a 50 Euro cent coin, coefficients of restitution $e$ = 0.5 and of friction $\mu$ = 0.05, (7) and (8) yield impact duration $\Delta t$ longer than several seconds, which is practically impossible for usual surfaces. This shows that the condition (5) cannot be practically fulfilled, and the coin will rebound.

In this case, one can still calculate the probability that the coin will stay on its edge at the second impact by considering that the first impact will be such as to deliver the favorable initial conditions (Event 1) for the second impact to result in the coin staying on its edge (Event 2). The probability of the first event $E_1$ is obviously independent of the probability of the second event $E_2$. The opposite is, of course, not true and the probability of the second event $E_2$ depends on the first event $E_1$ having occurred. Therefore, the probability that the coin will stay on its edge at the second impact, knowing that the first impact has delivered the favorable conditions for the second event to occur, is:

$$P_{edge 2}=P\left(E_1\right) P\left(E_2 E_1\right)=P_{Fav.impact 1} P_{edge 2 1}$$

(9)

where indexes 1 and 2 refer, respectively, to the first and second impacts.

With the following hypotheses:

-

between the first and second impacts, the coin attains a maximum height:

$$H_{12}=e^{2}H$$

(10)

-

the rotation velocities and moments of inertia of the coin, respectively, before the second impact and after the first impact are the same, yielding:

$$\pm {\omega }_{b2}=\pm {\omega }_{a1}$$

(11)

$$I_{b2}=I_{a1}$$

(12)

and:

$${\kappa }_1={\kappa }_{b1}=\frac{I_{b1}}{\rho m}, {\kappa }_2={\kappa }_{b2}={\kappa }_{a1}=\frac{I_{a1}}{\rho m}=\frac{I_{b2}}{\rho m}$$

(13)

-

the vertical components of the coin velocity before and after the second impact are, respectively:

$$v_{z2}=e\sqrt{2gH}$$

(14)

$$u_{z2}=\left(\pm {\omega }_{a2}\right) {\rho }_x=\left(\pm {\omega }_{a2}\right)\rho \sin ({\theta }_2-\frac{\alpha }{2})$$

(15)

-

the coin and landing surface are elastic and partially rough bodies, such as the normal and tangential impulses read:

$$N_2=m \left(1+e\right) \left(\left(\pm {\omega }_{a2}\right) \rho \sin ({\theta }_2-\frac{\alpha }{2}\right)-e\sqrt{2gH})$$

(16)

$$T_2=m \mu \left(1+e\right) \left(\left(\pm {\omega }_{a2}\right) \rho \sin ({\theta }_2-\frac{\alpha }{2}\right)-e\sqrt{2gH})$$

(17)

and the impact equation reduces to:

$$I_{a2} \left(\pm {\omega }_{a2}\right)=I_{a1} \left(\pm {\omega }_{a1}\right)-N_2 {\rho }_x-T_2 {\rho }_z$$

(18)

yielding:

$$\left(\pm {\omega }_{a2}\right)=\frac{{\kappa }_2\left(\pm {\omega }_{a1}\right)+e\left(1+e\right)\sqrt{2gH}\left(\mu \cos ({\theta }_2-\frac{\alpha }{2})+\sin ({\theta }_2-\frac{\alpha }{2})\right)}{{\kappa }_{a2}+\left(1+e\right)\rho \sin ({\theta }_2-\frac{\alpha }{2})\left(\mu \cos ({\theta }_2-\frac{\alpha }{2})+\sin ({\theta }_2-\frac{\alpha }{2})\right)}$$

(19)

where:

$${\kappa }_{a2}=\frac{I_{a2}}{\rho m}$$

(20)

The coin will stay on its edge if the angular velocity after the second impact ${\omega }_{a2}$ is nil while $\left|{\theta }_2\right|<\frac{\alpha }{2}$. Solving the Equation (19) ${\omega }_{a2}$ = 0 for ${\theta }_2$ yields:

$${\theta }_2=\frac{\alpha }{2}-2\arctan \left(\frac{1\pm \sqrt{1+{\mu }^2-{\left(\frac{{\kappa }_2\left(\pm {\omega }_{a1}\right)}{e\left(1+e\right)\sqrt{2gH}}\right)}^2}}{\frac{{\kappa }_2\left(\pm {\omega }_{a1}\right)}{e\left(1+e\right)\sqrt{2gH}}-\mu }\right)$$

(21)

under the condition that the denominator of (19) is different from zero, i.e., for:

$${\theta }_2\ne \frac{\alpha }{2}-\arctan \left(\frac{\mu \left(1+e\right)\pm \sqrt{{\mu }^2{(1+e)}^2-4\frac{{\kappa }_{a2}}{\rho }\left(\frac{{\kappa }_{a2}}{\rho }+1\right)}}{2\left(\left(1+e\right)+\frac{{\kappa }_{a2}}{\rho }\right)}\right)$$

(22)

Note that this condition can be extended to the other configurations of the position of the instantaneous axis of rotation after impacts, as was discussed for (66) in [1]. This would introduce additional numerical coefficients in the expressions of the moments of inertia, but would not fundamentally alter the value of the angle ${\theta }_2$.

For ${\theta }_2$ to be real, the condition on the root in the numerator of (21) reads:

$$\frac{{\kappa }_2\left(\pm {\omega }_{a1}\right)}{\sqrt{2gH}}\le e\left(1+e\right)\sqrt{1+{\mu }^2}$$

(23)

For the condition $\left|{\theta }_2\right|<\frac{\alpha }{2}$ to hold, i.e.,

$$-\frac{\alpha }{2}<\theta <\frac{\alpha }{2}$$

(24)

the argument of the arctan function in (21) must be positive and smaller than $h/d$, i.e.,

$$0<\left(\frac{1\pm \sqrt{1+{\mu }^2-{\left(\frac{{\kappa }_2\left(\pm {\omega }_{a1}\right)}{e\left(1+e\right)\sqrt{2gH}}\right)}^2}}{\frac{{\kappa }_2\left(\pm {\omega }_{a1}\right)}{e\left(1+e\right)\sqrt{2gH}}-\mu }\right)<\tan \left(\frac{\alpha }{2}\right)=\frac{h}{d}$$

(25)

For the positive condition, the numerator and the denominator must be of the same sign. Considering the negative sign in front of the numerator root in (25):

-

both denominator and numerator are positive if

$$\frac{{\kappa }_2\left(\pm {\omega }_{a1}\right)}{\sqrt{2gH}}>e\left(1+e\right)\mu$$

(26)

that combined with (23) yields:

$$e\left(1+e\right)\mu <\frac{{\kappa }_2\left(\pm {\omega }_{a1}\right)}{\sqrt{2gH}}\le e\left(1+e\right)\sqrt{1+{\mu }^2}$$

(27)

which is true only for a positive sign in front of ${\omega }_{a1}$, i.e., a coin counterclockwise rotation;

-

both denominator and numerator are negative if:

$$\frac{{\kappa }_2\left(\pm {\omega }_{a1}\right)}{\sqrt{2gH}}<e\left(1+e\right)\mu$$

(28)

which includes condition (23), and is true either for a positive sign in front of ${\omega }_{a1}$, i.e., a coin counterclockwise rotation after the first impact, as long as values of ${\omega }_{a1}$ fulfil the condition (28), or for all of the negative values of ${\omega }_{a1}$, i.e., a coin clockwise rotation.

For the positive sign in front of the numerator root of (21), the denominator must be positive, which is true if condition (28) holds, meaning that the positive sign in front of ${\omega }_{a1}$ must be chosen, i.e., a coin counterclockwise rotation. However, the solution, in this case, yields a too large value of ${\theta }_2$.

The other part of the condition, i.e., the argument of the arctan in (21) smaller than $h/d$ yields, as in relations (72) to (74) in [1]:

$$if \mu <\frac{h}{d}: e\left(1+e\right)\mu <\frac{{\kappa }_2{\omega }_{a1}}{\sqrt{2gH}}<e\left(1+e\right)\left(\frac{2hd-\mu \left(d^2-h^2\right)}{h^2+d^2}\right)$$

(29)

$$\mathrm{if} \mu =\frac{h}{d}: \frac{{\kappa }_2{\omega }_{a1}}{\sqrt{2gH}}=e\left(1+e\right)\frac{h}{d}$$

(30)

$$\mathrm{if} \mu >\frac{h}{d}: e\left(1+e\right)\left(\frac{2hd-\mu \left(d^2-h^2\right)}{h^2+d^2}\right)<\frac{{\kappa }_2{\omega }_{a1}}{\sqrt{2gH}}<e\left(1+e\right)\mu$$

(31)

These three conditions include condition (23), as the right part of (23) is always greater than the right parts of (29) to (31).

Summarizing the conditions for this case:

-

if $\mu <\frac{h}{d}$, then (29) includes (27) and ${\omega }_{a1}$ must be positive, i.e., a coin counterclockwise rotation after first impact;

-

if $\mu =\frac{h}{d}$, then (30) is the limiting case of (26) and (27) and ${\omega }_{a1}$ is positive, i.e., a coin counterclockwise rotation after first impact;

-

if $\frac{h}{d}<\mu <\frac{2hd}{d^2-h^2}$, then (31) includes (27) and ${\omega }_{a1}$ is positive, i.e., a coin counterclockwise rotation after first impact;

-

if $\mu >\frac{2hd}{d^2-h^2}$, then (31) includes (28) and ${\omega }_{a1}$ can be either positive or negative, i.e., a coin counterclockwise rotation or clockwise rotation after first impact.

The three conditions (29) to (31) constrain the favorable values of ${\omega }_{a1}$, which can be translated into conditions on ${\theta }_1$ through (63) of [1] (where the index $1$ has been added to $\theta$, ${\omega }_a$ and $\kappa$).

Assuming that $\mu <\frac{h}{d}$, the left and right parts of (29) yield, respectively:

$${\sin }^2({\theta }_1-\frac{\alpha }{2})-\sin ({\theta }_1-\frac{\alpha }{2})\left(B-\mu \cos ({\theta }_1-\frac{\alpha }{2})\right)-\left(A+B\mu \cos ({\theta }_1-\frac{\alpha }{2})\right)<0$$

(32)

$${\sin }^2({\theta }_1-\frac{\alpha }{2})-\sin ({\theta }_1-\frac{\alpha }{2})\left(D-\mu \cos ({\theta }_1-\frac{\alpha }{2})\right)-\left(C+D\mu \cos ({\theta }_1-\frac{\alpha }{2})\right)>0$$

(33)

with

$$A={\kappa }_2\left(\frac{{\kappa }_1\left(\pm {\omega }_0\right)-e\left(1+e\right)\mu \sqrt{2gH}}{e{(1+e)}^2\mu \rho \sqrt{2gH}}\right)$$

(34)

$$B=\frac{{\kappa }_2\sqrt{v_0^2{\sin }^2\beta +2gH}}{e\left(1+e\right)\mu \rho \sqrt{2gH}}$$

(35)

and:

$$C={\kappa }_2\left(\frac{{\kappa }_1\left(\pm {\omega }_0\right)-e\left(1+e\right)\left(\frac{2hd-\mu \left(d^2-h^2\right)}{h^2+d^2}\right)\sqrt{2gH}}{e{(1+e)}^2\rho \left(\frac{2hd-\mu \left(d^2-h^2\right)}{h^2+d^2}\right)\sqrt{2gH}}\right)$$

(36)

$$D=\frac{{\kappa }_2\sqrt{v_0^2{\sin }^2\beta +2gH}}{e\left(1+e\right)\rho \left(\frac{2hd-\mu \left(d^2-h^2\right)}{h^2+d^2}\right)\sqrt{2gH}}$$

(37)

The analytical solutions of (32) and (33) for $\left({\theta }_1-\frac{\alpha }{2}\right)$ require solving analytically fourth-degree equations in $sin\left({\theta }_1-\frac{\alpha }{2}\right)$, which is not an easy task. However, the numerical solutions can be found to define the range $\left[{\theta }_{1min},{\theta }_{1max}\right]$ of the allowed values of ${\theta }_1$ at first impact to deliver favorable conditions. Relations (32) and (33) yield numerical values of, respectively, ${\theta }_{1min}$ and ${\theta }_{1max}$, involving functions ${\Phi }_{min}$ and ${\Phi }_{max}$ of ${\omega }_0$, $H$, $v_0$, $\beta$, $e, \mu , h$ and $d$, respectively, through $A$ and $B$ and through $C$ and $D$:

$${\theta }_{1min }=\frac{\alpha }{2}+{\Phi }_{min}\left(A,B,\mu \right);\hspace{1em}\hspace{1em} {\theta }_{1max }=\frac{\alpha }{2}+{\Phi }_{max}\left(C,D,\mu \right)$$

(38)

The probability that the first impact delivers favorable conditions for the second impact to bring the coin on its edge reads, then:

$$P_{Fav. impact 1}=\left(\frac{{\theta }_{1 max}-{\theta }_{1 min}}{\pi }\right)=\left(\frac{{\Phi }_{max}\left(C,D,\mu \right)-{\Phi }_{min}\left(A,B,\mu \right)}{\pi }\right)$$

(39)

For this case $\mu <\frac{h}{d}$, the condition (29) constrains the favorable coin rotation velocity ${\omega }_{a1}$ after the first impact between the minimum and maximum values ${\omega }_{a1min}$ and ${\omega }_{a1max}$ corresponding to ${\theta }_{1min}$ and ${\theta }_{1max}$ through (63) of [1]:

$${\omega }_{a1 min}=\frac{{\kappa }_1\left(\pm {\omega }_0\right)+\left(1+e\right)\sqrt{v_0^2{\sin }^2\beta +2gH}\left(\mu \cos {\Phi }_{min}+\sin {\Phi }_{min}\right)}{{\kappa }_2+\left(1+e\right)\rho \sin {\Phi }_{min}\left(\mu \cos {\Phi }_{min}+\sin {\Phi }_{min}\right)}$$

(40)

$${\omega }_{a1 max}=\frac{{\kappa }_1\left(\pm {\omega }_0\right)+\left(1+e\right)\sqrt{v_0^2{\sin }^2\beta +2gH}\left(\mu \cos {\Phi }_{max}+\sin {\Phi }_{max}\right)}{{\kappa }_2+\left(1+e\right)\rho \sin {\Phi }_{max}\left(\mu \cos {\Phi }_{max}+\sin {\Phi }_{max}\right)}$$

(41)

Replacing these two values ${\omega }_{a1min}$ and ${\omega }_{a1max}$ in (21) yield the two limiting values ${\theta }_{2min}$ and ${\theta }_{2max}$:

$${\theta }_{2min }=\frac{\alpha }{2}-\arctan \left(\frac{1-\sqrt{1+{\mu }^2-{\nu }_{min}^2}}{{\nu }_{min}-\mu }\right); {\theta }_{2max }=\frac{\alpha }{2}-\arctan \left(\frac{1-\sqrt{1+{\mu }^2-{\nu }_{max}^2}}{{\nu }_{max}-\mu }\right)$$

(42)

with:

$$v_{min}=\frac{{\kappa }_2{\omega }_{a1 min}}{e\left(1+e\right)\sqrt{2gH}}=\frac{\frac{{\kappa }_1\left(\pm {\omega }_0\right)}{\sqrt{2gH}}+\left(1+e\right)\sqrt{1+{\left(\frac{v_0\sin \beta }{\sqrt{2gH}}\right)}^2}\left(\mu \cos {\Phi }_{min}+\sin {\Phi }_{min}\right)}{e\left(1+e\right)\left(1+\left(1+e\right)\frac{\rho }{{\kappa }_2}\sin {\Phi }_{min}\left(\mu \cos {\Phi }_{min}+\sin {\Phi }_{min}\right)\right)}$$

(43)

and a similar expression for $v_{max}$ with ${\Phi }_{max}$ replacing ${\Phi }_{min}$.

The probability that the coin stays on its edge at the second impact, knowing that the first impact has delivered the appropriate favorable conditions is then:

$$\begin{array}{cc}{P}_{edge 2|1}\hfill & =\left(\frac{{\theta }_{2 max }-{\theta }_{2 min }}{\pi }\right)\hfill \\ & =\frac{2}{\pi }\left(\arctan \left(\frac{1-\sqrt{1+{\mu }^2-v_{min}^2}}{v_{min}-\mu }\right)-\arctan \left(\frac{1-\sqrt{1+{\mu }^2-v_{max}^2}}{v_{max}-\mu }\right)\right)\hfill \\ & =\frac{2}{\pi }\arctan \left(\frac{\left(v_{max}-\mu \right)\left(1-\sqrt{1+{\mu }^2-v_{min}^2}\right)-\left(v_{min}-\mu \right)\left(1-\sqrt{1+{\mu }^2-v_{max}^2}\right)}{\left(v_{min}-\mu \right)\left(v_{max}-\mu \right)+\left(1-\sqrt{1+{\mu }^2-v_{min}^2}\right)\left(1-\sqrt{1+{\mu }^2-v_{max}^2}\right)}\right)\hfill \end{array}$$

(44)

where the formula $\arctan \left(X\right) - \arctan \left(Y\right)= \arctan \left(\frac{X-Y}{1-XY}\right)$ was used.

The total probability that the coin stays on its edge at the second impact, after the first rebound has delivered the appropriate conditions, is given by (9).

Assuming coefficients of restitution $e$ = 0.5 and of friction $\mu$ = 0.05 for a 50 Euro cent coin yields that $\mu <\frac{h}{d}$. One considers further the two extreme cases of the position of the instantaneous rotation axis after the first impact, i.e., respectively, along the horizontal axis passing first through the coin center of mass, and second, through the coin contact point with the landing surface (see discussion leading to (66) in [1]), yielding values of ${\kappa }_2$ varying between 2.955 × 10⁻³ and 1.475 × 10⁻², while ${\kappa }_1$ = 2.955 × 10⁻³ under the initial hypothesis.

The condition (29) imposes a quite stringent range of values for the ratio $\frac{{\kappa }_2{\omega }_{a1}}{\sqrt{2gH}}$, namely:

$$12.689<\frac{{\kappa }_2{\omega }_{a1}}{\sqrt{2gH}}<30.381 \mathrm{and} 2.543<\frac{{\kappa }_2{\omega }_{a1}}{\sqrt{2gH}}<6.088$$

(45)

respectively, for ${\kappa }_{2min}$ = 2.955 × 10⁻³ m and ${\kappa }_{2max}$ = 1.475 × 10⁻² m, yielding, respectively, for $H=d$ and for $H=2$ m:

$$8.616<{\omega }_{a1}<20.629 \mathrm{and} 1.726<{\omega }_{a1}<4.134 (\mathrm{rad}/\mathrm{s})$$

(46)

$$79.490<{\omega }_{a1}<190.311 \mathrm{and} 15.928<{\omega }_{a1}<38.135 (\mathrm{rad}/\mathrm{s})$$

(47)

The allowed range for the coin angular velocities after the first impact thus increases for the increasing initial height $H$.

Within the value ranges (1) of initial parameters, the largest value of the probability $P_{edge2 max}$ is obviously attained for the largest values of $P_{Fav.Impact1 max}$ and $P_{edge21max}$. The largest value of $P_{Fav.Impact1}$ is obtained for the largest value of ${\Phi }_{max}$ and the smallest value of ${\Phi }_{min}$. ${\Phi }_{max}$ is the largest for $C_{min}$ and $D_{min}$, i.e., for ${\omega }_0$ = 0 and $v_0$ = 0, while ${\Phi }_{min}$ is the smallest for $A_{max}$ and $B_{max}$, i.e., for ${\omega }_0$ = 10π rad/s, $v_0$ = 5 m/s, $\beta =\pm \pi /2$ and $H=d$.

For the first case of ${\kappa }_1={\kappa }_{2min}$ = 2.955 × 10⁻³ m, a series of coin tosses having initial conditions in the ranges (1), one finds, successively:

${\Phi }_{max}$ = 0.0101, ${\Phi }_{min}$ = −0.0588 (rad)

${\theta }_{1max}$ = 0.0950, ${\theta }_{1min}$ = 0.0261 (rad)

${\omega }_{a1max}$ = 190.311, ${\omega }_{a1min}$ = 8.616 (rad/s)

${\theta }_{2max}$ = −0.0849, ${\theta }_{2min}$ = −0.0150 (rad)

$P_{Fav.Impact1max}$ = 2.193 × 10⁻², $P_{edge21max}$= 2.225 × 10⁻², $P_{edge2 max}$= 4.880 × 10⁻⁴

or approximately a throw every 2050 throws.

For the second case of ${\kappa }_{2max}$ = 1.475 × 10⁻² m, one has similarly:

${\Phi }_{max}$ = 0.0099, ${\Phi }_{min}$ = −0.0588 (rad)

${\theta }_{1max}$ = 0.0948, ${\theta }_{1min}$ = 0.0261 (rad)

${\omega }_{a1max}$ = 38.135, ${\omega }_{a1min}$ = 1.727 (rad/s)

${\theta }_{2max}$ = −0.0849, ${\theta }_{2min}$ = −0.0150 (rad)

$P_{Fav.Impact1max}$ = 2.188 × 10⁻², $P_{edge2 1 max}$ = 2.225 × 10⁻², $P_{edge2 max}$= 4.868 × 10⁻⁴

or approximately a throw every 2054 throws.

For more common values, a series of throws from an initial height $H$ = 1.5 m with a velocity $v_0$ = 1 m/s under an angle of $\beta =\pi /4$ and an initial rotation velocity ${\omega }_0$ varying between 0.5 and 5 turns/s yields, successively, first for ${\kappa }_{2min}$ = 2.955 × 10⁻³ m:

${\theta }_{1max}$ = 0.0829, ${\theta }_{1min}$ = 0.0585 (rad)

${\omega }_{a1max}$ = 164.814, ${\omega }_{a1min}$ = 68.840 (rad/s)

${\theta }_{2max}$ = −0.0849, ${\theta }_{2min}$ = −0.0150 (rad)

$P_{Fav.Impact1}$ = 7.774 × 10⁻³, $P_{edge21}$ = 2.224 × 10⁻² and $P_{edge2}$ = 1.729 × 10⁻⁴

or approximately a throw every 5783 throws, and second for ${\kappa }_{2max}$ = 1.475 × 10⁻² m:

${\theta }_{1max}$ = 0.0829, ${\theta }_{1min}$ = 0.0586 (rad)

${\omega }_{a1max}$ = 33.026, ${\omega }_{a1min}$ = 13.794 (rad/s),

${\theta }_{2max}$ = −0.0849, ${\theta }_{2min}$ = −0.0150 (rad),

$P_{Fav.Impact1}$ = 7.759 × 10⁻³, $P_{edge21}$ = 2.224 × 10⁻² and $P_{edge2}$ = 1.726 × 10⁻⁴

or approximately a throw every 5794 throws.

For the sake of completeness, for all of the above values, the term under the root sign in condition (22) is negative, yielding imaginary values for the argument of the arctan function, which shows that condition (22) is fulfilled for all of the practical values of ${\theta }_2$.

The cases of successive rebounds can be treated similarly, albeit with more and more complexity in the various relations.

3. Conclusions

To recall the man conclusions of the first paper:

-

there is a non-nil probability that a falling coin will not end up on one of its sides but on its edge, with decreasing probabilities for the models describing reality from closer;

-

probabilities calculated are independent of the coin mass but strongly depend on the coin’s vertical velocity before impact, on the initial height $H$ and on the initial angle $\beta$ of the throw;

-

increasing the initial height decreases the probability that the coin will end on its edge, while increasing the initial rotation will increase this probability;

-

depending on surface characteristics, tossing the coin vertically decreases the probability of the coin ending on its edge;

-

friction is of paramount importance: if the friction coefficient $\mu$ is increased above a certain value depending on surface conditions, the coin can no longer stop on its edge and will inevitably fall on one side.

The rebound case model shows that very limited initial conditions and surface conditions of the coin and landing would deliver the proper conditions for the coin to stop on its edge at the second impact. For a series of throws from an average height with common velocity values and appropriate surface conditions, the probability that a 50 Euro cent coin ends up on its edge is calculated to be in the order of one against several thousand, slightly larger than in the cases without rebounds.