Comparative Performance of NIR-Hyperspectral Imaging Systems
Abstract
:1. Introduction
2. Materials and Methods
2.1. Specimen Preparation and Testing
2.2. Hyperspectral Imaging
2.2.1. SWIR-HSI-I
2.2.2. SWIR-HSI-II
2.2.3. SWIR-HSI-III
2.2.4. NIR-HSI
2.3. Benchtop NIR (NIR-SPECT)
2.4. HSI Data Processing
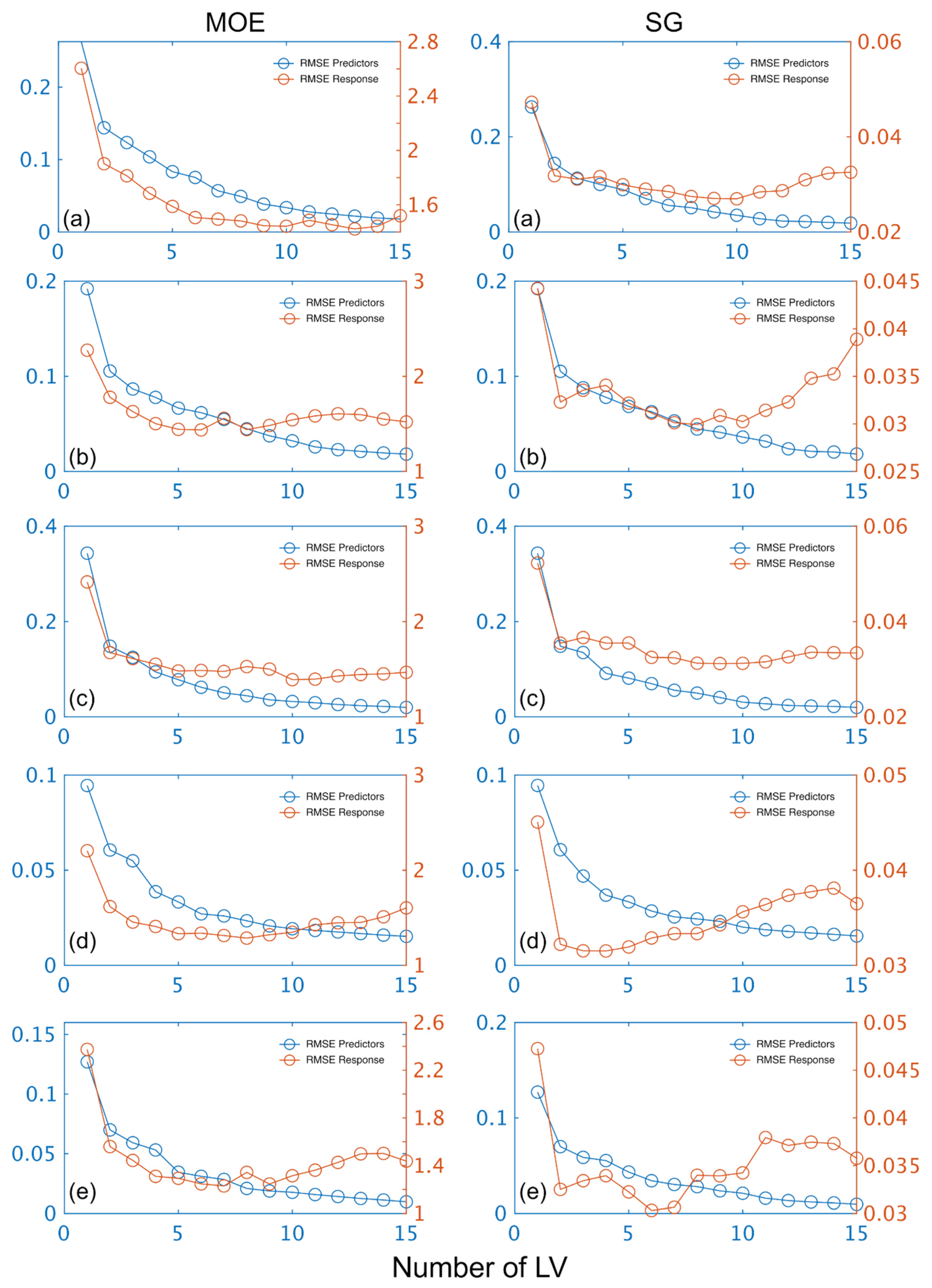
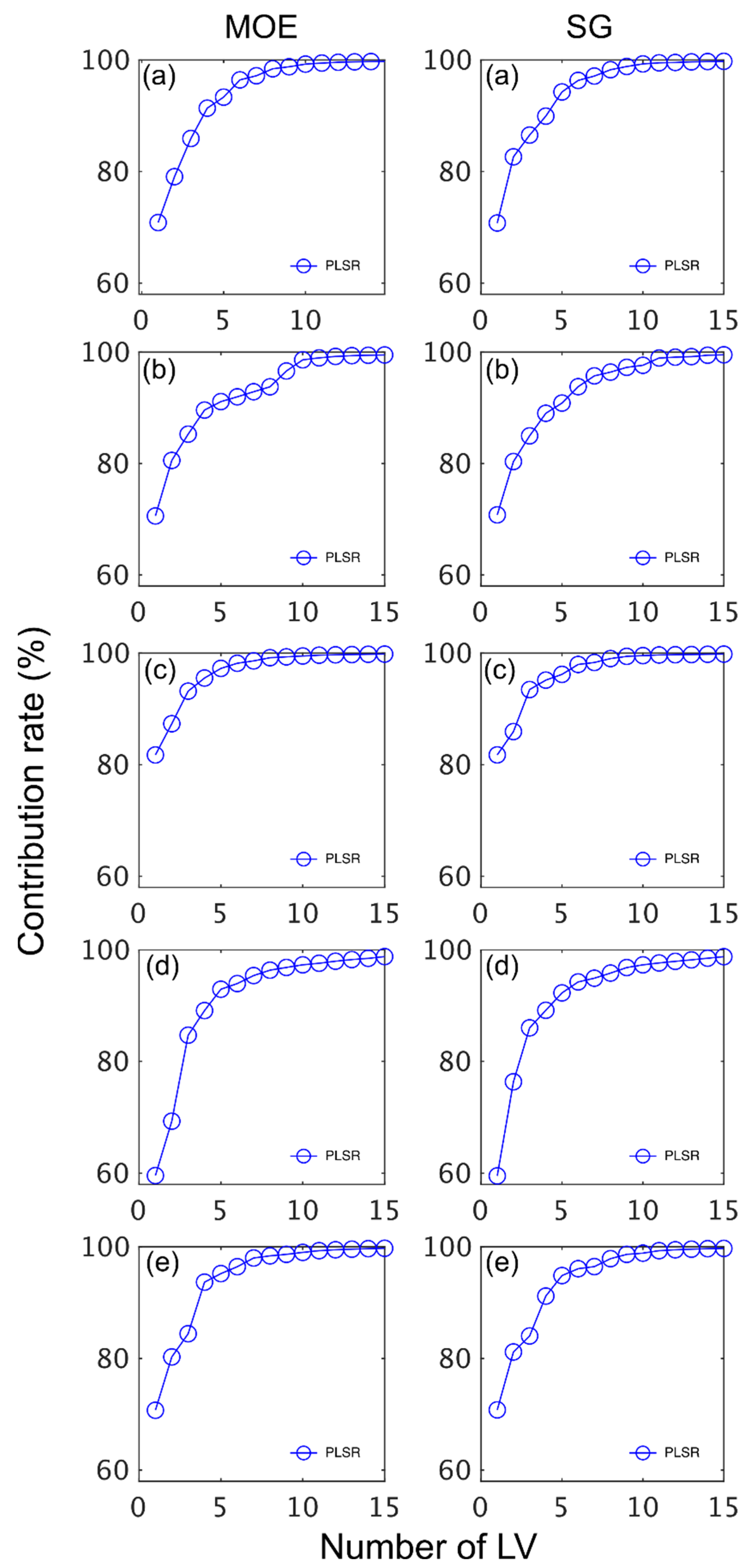
2.5. Wood Property Calibration and Prediction of Wood Properties
3. Results and Discussion
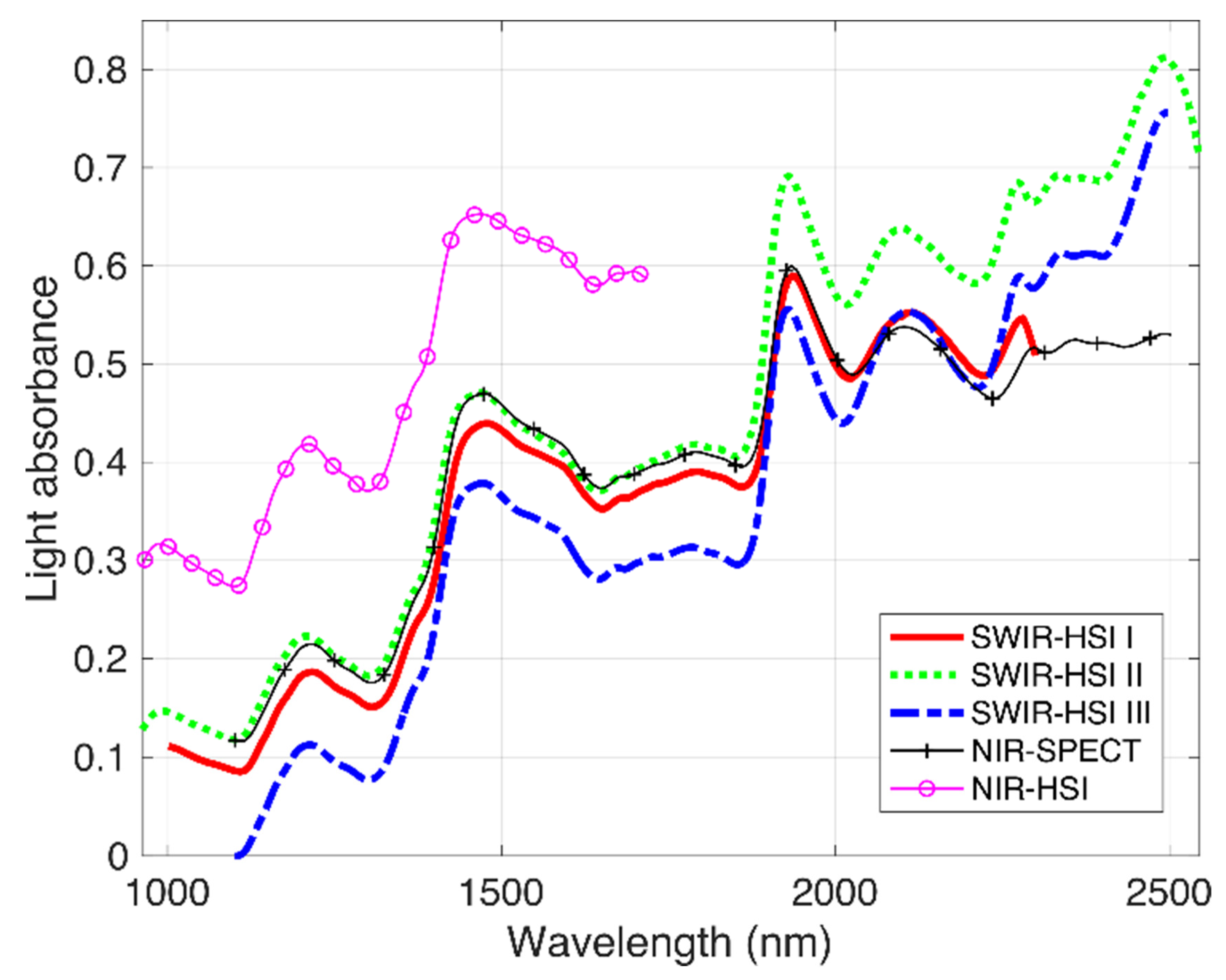
3.1. Comparison of Spectra
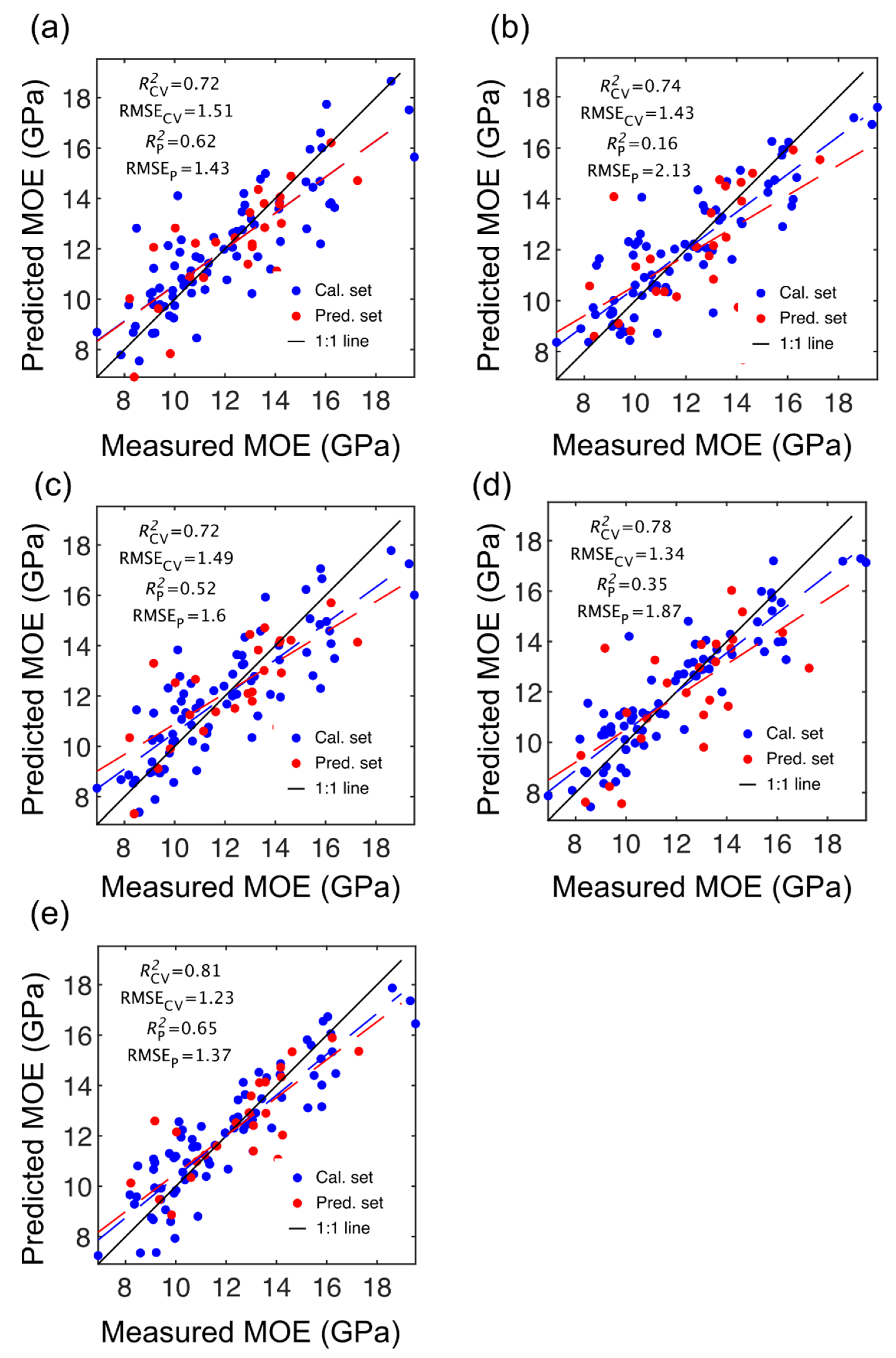
3.2. Calibration/Prediction—MOE and SG
3.3. Calibration/Prediction—MOE and SG Using 1100–1700 nm
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Schimleck, L.R.; Tsuchikawa, S. Application of NIR spectroscopy to wood and wood derived products. In The Handbook of Near-Infrared Analysis, 4th ed.; Ciurczak, E.W., Igne, B., Workman, J., Burns, D.A., Eds.; CRC Press: Boca Raton, FL, USA, 2021; Chapter 37; pp. 759–780. [Google Scholar]
- Meder, R.; Thumm, A.; Marston, D. Sawmill trial of at-line prediction of recovered lumber stiffness by NIR spectroscopy of Pinus radiata cants. J. Near Infrared Spectrosc. 2003, 11, 137–143. [Google Scholar]
- Thumm, A.; Meder, R. Stiffness prediction of radiata pine clearwood test pieces using near infrared spectroscopy. J. Near Infrared Spectrosc. 2001, 9, 117–122. [Google Scholar]
- Fujimoto, T.; Kurata, Y.; Matsumoto, K.; Tsuchikawa, S. Feasibility of near-infrared spectroscopy for online multiple trait assessment of sawn lumber. J. Wood Sci. 2010, 56, 452–459. [Google Scholar] [CrossRef]
- Kobori, H.; Inagaki, T.; Fujimoto, T.; Okura, T.; Tsuchikawa, S. Fast online NIR technique to predict MOE and moisture content of sawn lumber. Holzforschung 2015, 67, 329–335. [Google Scholar]
- Burger, J.; Gowen, A. Data handling in hyperspectral image analysis. Chemom. Intell. Lab. Syst. 2011, 108, 13–22. [Google Scholar] [CrossRef]
- Manley, M. Near-infrared spectroscopy and hyperspectral imaging: Non-destructive analysis of biological materials. Chemical Soc. Rev. 2014, 43, 8200–8214. [Google Scholar]
- Mishra, P.; Asaari, M.S.M.; Herrero-Langreo, A.; Lohumi, S.; Diezma, B.; Scheunders, P. Close range hyperspectral imaging of plants: A review. Biosyst. Eng. 2017, 164, 49–67. [Google Scholar]
- Elmasry, G.; Kamruzzaman, M.; Sun, D.W.; Allen, P. Principles and applications of hyperspectral imaging in quality evaluation of agro-food products: A review. Crit. Rev. Food Sci. Nutr. 2012, 52, 999–1023. [Google Scholar]
- Liu, Y.W.; Pu, H.B.; Sun, D.W. Hyperspectral imaging technique for evaluating food quality and safety during various processes: A review of recent applications. Trends Food Sci. Technol. 2017, 69, 25–35. [Google Scholar]
- Jones, P.D.; Schimleck, L.R.; So, C.-L.; Clark, A.; Daniels, R.F. High resolution scanning of radial strips cut from increment cores by near infrared spectroscopy. IAWA J. 2007, 28, 473–484. [Google Scholar] [CrossRef]
- Fernandes, A.; Lousada, J.; Morais, J.; Xavier, J.; Pereira, J.; Melo-Pinto, P. Comparison between neural networks and partial least squares for intra-growth ring wood density measurement with hyperspectral imaging. Comput. Electron. Agric. 2013, 94, 71–81. [Google Scholar] [CrossRef]
- Fernandes, A.; Lousada, J.; Morais, J.; Xavier, J.; Pereira, J.; Melo-Pinto, P. Measurement of intra-ring wood density by means of imaging VIS/NIR spectroscopy (hyperspectral imaging). Holzforschung 2013, 67, 59–65. [Google Scholar] [CrossRef]
- Ma, T.; Inagaki, T.; Tsuchikawa, S. Calibration of SilviScan data of Cryptomeria japonica wood concerning density and microfibril angles with NIR hyperspectral imaging with high spatial resolution. Holzforschung 2017, 71, 341–347. [Google Scholar] [CrossRef]
- Ma, T.; Inagaki, T.; Tsuchikawa, S. Non-destructive evaluation of wood stiffness and fiber coarseness, derived from SilviScan data, via near infrared hyperspectral imaging. J. Near Infrared Spectrosc. 2018, 26, 398–405. [Google Scholar] [CrossRef]
- Haddadi, A.; Burger, J.; Leblon, B.; Pirouz, Z.; Groves, K.; Nader, J. Using near-infrared hyperspectral images on subalpine fire board. Part 1: Moisture content estimation. Wood Mater. Sci. Eng. 2015, 10, 27–40. [Google Scholar] [CrossRef]
- Haddadi, A.; Burger, J.; Leblon, B.; Pirouz, Z.; Groves, K.; Nader, J. Using near-infrared hyperspectral images on subalpine fire board. Part 2: Density and basic specific gravity estimation. Wood Mater. Sci. Eng. 2015, 10, 41–56. [Google Scholar] [CrossRef]
- Schimleck, L.; Dahlen, J.; Yoon, S.-C.; Lawrence, K.; Jones, P. Prediction of Douglas-fir lumber properties: Comparison between a benchtop near-infrared spectrometer and hyperspectral imaging system. Appl. Sci. 2018, 8, 2602. [Google Scholar] [CrossRef] [Green Version]
- Meder, R.; Meglen, R.R. Near infrared spectroscopic and hyperspectral imaging of compression wood in Pinus radiata D. Don. J. Near Infrared Spectrosc. 2012, 20, 583–589. [Google Scholar] [CrossRef]
- Fujimoto, T.; Numa, T.; Kobori, H.; Tsuchikawa, S. Visualisation of spatial distribution of moisture content and basic density using near-infrared hyperspectral imaging method in sugi (Cryptomeria japonica). Int. Wood Prod. J. 2015, 6, 46–48. [Google Scholar] [CrossRef]
- Defoirdt, N.; Sen, A.; Dhaene, J.; De Mil, T.; Pereira, H.; Van Acker, J.; Bulcke, J.V.D. A generic platform for hyperspectral mapping of wood. Wood Sci. Technol. 2017, 51, 887–907. [Google Scholar] [CrossRef]
- Thumm, A.; Riddell, M. Resin defect detection in appearance lumber using 2D NIR spectroscopy. Eur. J. Wood Wood Prod. 2017, 75, 995–1002. [Google Scholar] [CrossRef]
- Mora, C.R.; Schimleck, L.R.; Yoon, S.C.; Thai, C.N. Determination of basic density and moisture content of loblolly pine wood disks using a near infrared hyperspectral imaging system. J. Near Infrared Spectrosc. 2011, 19, 401–409. [Google Scholar] [CrossRef]
- Kobori, H.; Gorretta, N.; Rabatel, G.; Bellon-Maurel, V.; Chaix, G.; Roger, J.M.; Tsuchikawa, S. Applicability of Vis-NIR hyperspectral imaging for monitoring wood moisture content (MC). Holzforschung 2013, 69, 307–314. [Google Scholar] [CrossRef]
- Chen, J.; Li, G. Prediction of moisture content of wood using Modified Random Frog and Vis-NIR hyperspectral imaging. Infrared Phys. Techn. 2020, 105, 103225. [Google Scholar] [CrossRef]
- Ma, T.; Inagaki, T.; Tsuchikawa, S. Rapidly visualizing the dynamic state of free, weakly, and strongly hydrogen-bonded water with lignocellulosic material during drying by near-infrared hyperspectral imaging. Cellulose 2020, 27, 4857–4869. [Google Scholar] [CrossRef]
- Ma, T.; Schimleck, L.; Inagaki, T.; Tsuchikawa, S. Rapid and nondestructive evaluation of hygroscopic behavior changes of thermally modified softwood and hardwood samples using near-infrared hyperspectral imaging (NIR-HSI). Holzforschung 2021, 75, 345–357. [Google Scholar] [CrossRef]
- Stefansson, P.; Thiis, T.; Gobakken, L.; Burud, I. Hyperspectral NIR time series imaging used as a new method for estimating the moisture content dynamics of thermally modified Scots pine. Wood Mater. Sci. Eng. 2021, 16, 49–57. [Google Scholar] [CrossRef]
- Thumm, A.; Riddell, M.; Nanayakkara, B.; Harrington, J.; Meder, R. Near infrared hyperspectral imaging applied to mapping chemical composition in wood samples. J. Near Infrared Spectrosc. 2010, 18, 507–515. [Google Scholar] [CrossRef]
- Thumm, A.; Riddell, M.; Nanayakkara, B.; Harrington, J.; Meder, R. Mapping within-stem variation of chemical composition by near infrared hyperspectral imaging. J. Near Infrared Spectrosc. 2016, 24, 605–616. [Google Scholar] [CrossRef]
- Colares, C.J.G.; Pastore, T.C.M.; Coradin, V.T.R.; Marques, L.F.; Moreira, A.C.O.; Alexandrino, G.L.; Poppi, R.J.; Braga, J.W.B. Near infrared hyperspectral imaging and MCR-ALS applied for mapping chemical composition of the wood specie Swietenia macrophylla King (Mahogany) at microscopic level. Microchem. J. 2016, 124, 356–363. [Google Scholar] [CrossRef]
- Burud, I.; Gobakken, L.R.; Flø, A.; Kvaal, K.; Thiis, T.K. Hyperspectral imaging of blue stain fungi on coated and uncoated wooden surfaces. Int. Biodeter. Biodegr. 2014, 88, 37–43. [Google Scholar] [CrossRef]
- Agresti, G.; Bonifazi, G.; Calienno, L.; Capobianco, G.; Lo Monaco, A.; Pelosi, C.; Picchio, R.; Serranti, S. Surface investigation of photo-degraded wood by colour monitoring, infrared spectroscopy, and hyperspectral imaging. J. Spectrosc. 2013, 2013, 380356. [Google Scholar] [CrossRef]
- Smeland, K.A.; Liland, K.H.; Sandak, J.; Sandak, A.; Gobakken, L.R.; Thiis, T.K.; Burud, I. Near infrared hyperspectral imaging in transmission mode: Assessing the weathering of thin wood samples. J. Near Infrared Spectrosc. 2016, 24, 595–604. [Google Scholar] [CrossRef] [Green Version]
- Sandak, A.; Burud, I.; Flø, A.; Thiis, T.; Gobakken, L.; Sandak, J. Hyperspectral imaging of weathered wood samples in transmission mode. Int. Wood Prod. J. 2017, 8 (Suppl. 1), 9–13. [Google Scholar] [CrossRef] [Green Version]
- Inagaki, T.; Mitsui, K.; Tsuchikawa, S. Visualisation of degree of acetylation in beechwood by near infrared hyperspectral imaging. J. Near Infrared Spectrosc. 2015, 23, 353–360. [Google Scholar] [CrossRef]
- Awais, M.; Altgen, M.; Mäkelä, M.; Altgen, D.; Rautkari, L. Hyperspectral near-infrared image assessment of surface-acetylated solid wood. ACS Appl. Bio. Mater. 2020, 3, 5223–5232. [Google Scholar] [CrossRef]
- Geladi, P.; Eriksson, D.; Ulvcrona, T. Data analysis of hyperspectral NIR image mosaics for the quantification of linseed oil impregnation in Scots pine wood. Wood Sci. Technol. 2014, 48, 467–481. [Google Scholar] [CrossRef]
- Myronycheva, O.; Sidorova, E.; Hagman, O.; Sehlstedt-Persson, M.; Karlsson, O.; Sandberg, D. Hyperspectral imaging surface analysis for dried and thermally modified wood: An exploratory study. J. Spectrosc. 2018, 2018, 10. [Google Scholar] [CrossRef] [Green Version]
- Stefansson, P.; Burud, I.; Thiis, T.; Gobakken, L.; Larnøy, E. Estimation of phosphorus-based flame retardant in wood by hyperspectral imaging—A new method. J. Spectr. Imaging 2018, 7, a3. [Google Scholar] [CrossRef] [Green Version]
- Kanayama, H.; Ma, T.; Tsuchikawa, S.; Inagaki, T. Cognitive spectroscopy for wood species identification: Near infrared hyperspectral imaging combined with convolutional neural networks. Analyst 2019, 144, 6438–6446. [Google Scholar] [CrossRef]
- Ma, T.; Inagaki, T.; Ban, M.; Tsuchikawa, S. Rapid identification of wood species by near-infrared spatially resolved spectroscopy (NIR-SRS) based on hyperspectral imaging (HSI). Holzforschung 2019, 73, 323–330. [Google Scholar] [CrossRef]
- Ruano, A.; Zitek, A.; Hinterstoisser, B.; Hermoso, E. NIR hyperspectral imaging (NIR-HI) and μxRD for determination of the transition between juvenile and mature wood of Pinus sylvestris L. Holzforschung 2019, 73, 621–627. [Google Scholar] [CrossRef]
- Sandak, A.; Sandak, J.; Janiszewska, D.; Hiziroglu, S.; Petrillo, M.; Grossi, P. Prototype of the near-infrared spectroscopy expert system for particleboard identification. J. Spectrosc. 2018, 2018, 11. [Google Scholar] [CrossRef]
- Sofianto, I.A.; Inagaki, T.; Ma, T.; Tsuchikawa, S. Effect of knots and holes on the modulus of elasticity prediction and mapping of sugi (Cryptomeria japonica) veneer using near-infrared hyperspectral imaging (NIR-HSI). Holzforschung 2019, 73, 259–268. [Google Scholar] [CrossRef]
- Lestander, T.A.; Geladi, P.; Larsson, S.H.; Thyrel, M. Near infrared image analysis for online identification and separation of wood chips with elevated levels of extractives. J. Near Infrared Spectrosc. 2012, 20, 591–599. [Google Scholar] [CrossRef]
- Serranti, S.; Gargiulo, A.; Bonifazi, G. The utilization of hyperspectral imaging for impurities detection in secondary plastics. Open Waste Manag. J. 2010, 3, 56–70. [Google Scholar] [CrossRef] [Green Version]
- Bonifazi, G.; Capobianco, G.; Palmieri, R.; Serranti, S. Hyperspectral imaging applied to the waste recycling sector. Spectrosc. Eur. 2019, 31, 8–11. [Google Scholar] [CrossRef]
- Xiao, W.; Yang, J.H.; Fang, H.Y.; Zhuang, J.T.; Ku, Y.D. Development of online classification system for construction waste based on industrial camera and hyperspectral camera. PLoS ONE 2019, 14, e0208706. [Google Scholar] [CrossRef] [Green Version]
- Gosselin, R.; Rodrigue, D.; Duchesne, C. A hyperspectral imaging sensor for on-line quality control of extruded polymer composite products. Comput. Chem. Eng. 2011, 35, 296–306. [Google Scholar] [CrossRef]
- Dahlen, J.; Jones, P.D.; Seale, R.D.; Shmulsky, R. Mill variation in bending strength and stiffness of in-grade Douglas-fir No. 2 2 × 4 lumber. Wood Sci. Technol. 2013, 47, 1167–1176. [Google Scholar] [CrossRef]
- Barnes, R.J.; Dhanoa, M.S.; Lister, S.J. Standard normal variate transformation and de-trending of near-infrared diffuse reflectance spectra. Appl. Spectrosc. 1989, 43, 772–777. [Google Scholar] [CrossRef]
- Williams, P.; Norris, K.H. Near-Infrared Technology in the Agricultural and Food Industries, 2nd ed.; American Association of Cereal Chemists: St. Paul, MN, USA, 2001; pp. 145–169. [Google Scholar]
- Wold, S.; Johansson, A.; Cochi, M. (Eds.) PLS-Partial Least Squares Projections to Latent Structures; ESCOM Science Publishers: Leiden, The Netherlands, 1993; pp. 523–550. [Google Scholar]
- Schwanninger, M.; Rodrigues, J.; Fackler, K. A review of band assignments in near infrared spectra of wood and wood components. J. Near Infrared Spectrosc. 2011, 19, 287–308. [Google Scholar] [CrossRef]

| Wavelength Range (nm) | # Wavebands | FWHM (nm) | SSI (nm) | |
|---|---|---|---|---|
| SWIR-HSI-I | 1000–2300 | 207 | 6.2 | 6.2 |
| SWIR-HSI-II | 1101–2503 | 185 | 8 to 10 | 7.4 |
| SWIR-HSI-III | 962–2545 | 228 | 12 | 5.6 |
| NIR-SPECT | 1100–2498 | 700 | 10 | 2 |
| NIR-HSI | 931–1718 | 224 | 8 | 3.5 |
| MOE (GPa) | SG | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| No. | Min | Max | Mean | SD | Min | Max | Mean | SD | |
| Calibration | 75 | 6.91 | 19.53 | 11.89 | 2.78 | 0.37 | 0.62 | 0.47 | 0.05 |
| Prediction | 25 | 8.44 | 18.61 | 12.58 | 2.57 | 0.37 | 0.60 | 0.48 | 0.06 |
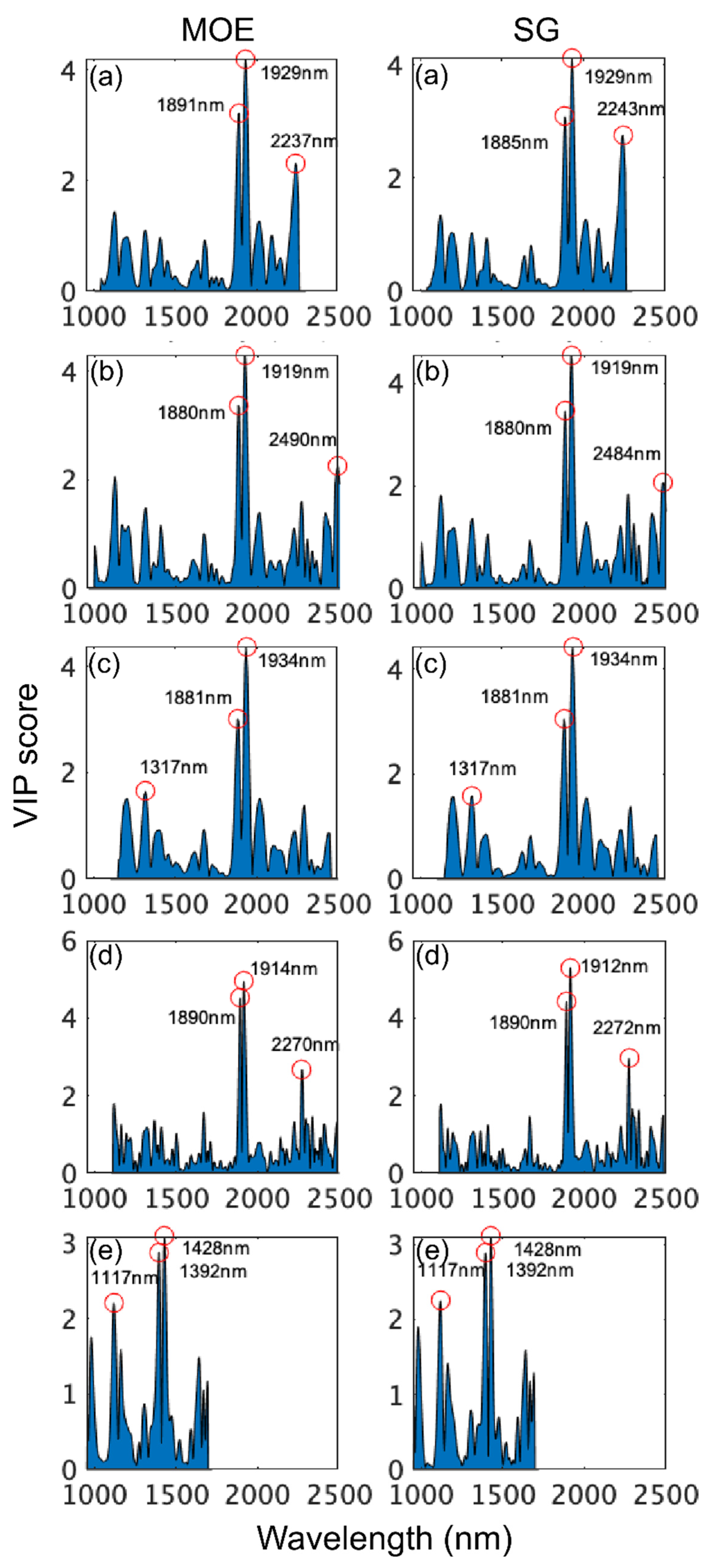
| Identified Wavelengths (nm) | Band Location (nm) | Bond Vibration | Wood Component |
|---|---|---|---|
| 1117 (MOE, SG) | NA | ||
| 1392 (MOE, SG) | 1386 | 1st OT O-H str. | None specified |
| 1st OT C-H str. + C-H def. | |||
| 1428 (MOE, SG) | 1428 | 1st OT O-H str. + H2O | Amorphous cellulose |
| 1317 (MOE, SG) | NA | ||
| 1880–1890 (MOE, SG) | NA | ||
| 1910–1940 (MOE, SG) | 1916–1942 | O-H asym. str. + O-H def. | Water |
| 1st OT C-H str. + C-H def. | |||
| 2237 (MOE) | NA | ||
| 2243 (SG) | NA | ||
| 2270 (MOE) | 2270 | O-H str. + C-O str. | Cellulose |
| 2272 (SG) | 2272 | C-H str. + C-H def. | Hemicellulose |
| 2484 (SG) | 2488 | C-H str. + C-C str. | Lignin t.a. |
| 2490 (MOE) | 2491 | C-H str. + C-C str. | Cellulose |
| Device Name | MOE (GPa) | SG | ||||||
|---|---|---|---|---|---|---|---|---|
| R2cv | RMSEcv | R2test | RMSEtest | R2cv | RMSEcv | R2test | RMSEtest | |
| SWIR-HSI-I | 0.68 | 1.54 | 0.75 | 1.36 | 0.64 | 0.03 | 0.44 | 0.04 |
| SWIR-HSI-II | 0.67 | 1.55 | 0.73 | 1.42 | 0.69 | 0.03 | 0.31 | 0.04 |
| SWIR-HSI-III | 0.61 | 1.7 | 0.43 | 2.06 | 0.60 | 0.04 | 0.25 | 0.05 |
| NIR-SPECT | 0.67 | 1.55 | 0.64 | 1.65 | 0.61 | 0.04 | 0.31 | 0.04 |
| NIR-HSI | 0.79 | 1.24 | 0.81 | 1.18 | 0.73 | 0.03 | 0.43 | 0.04 |
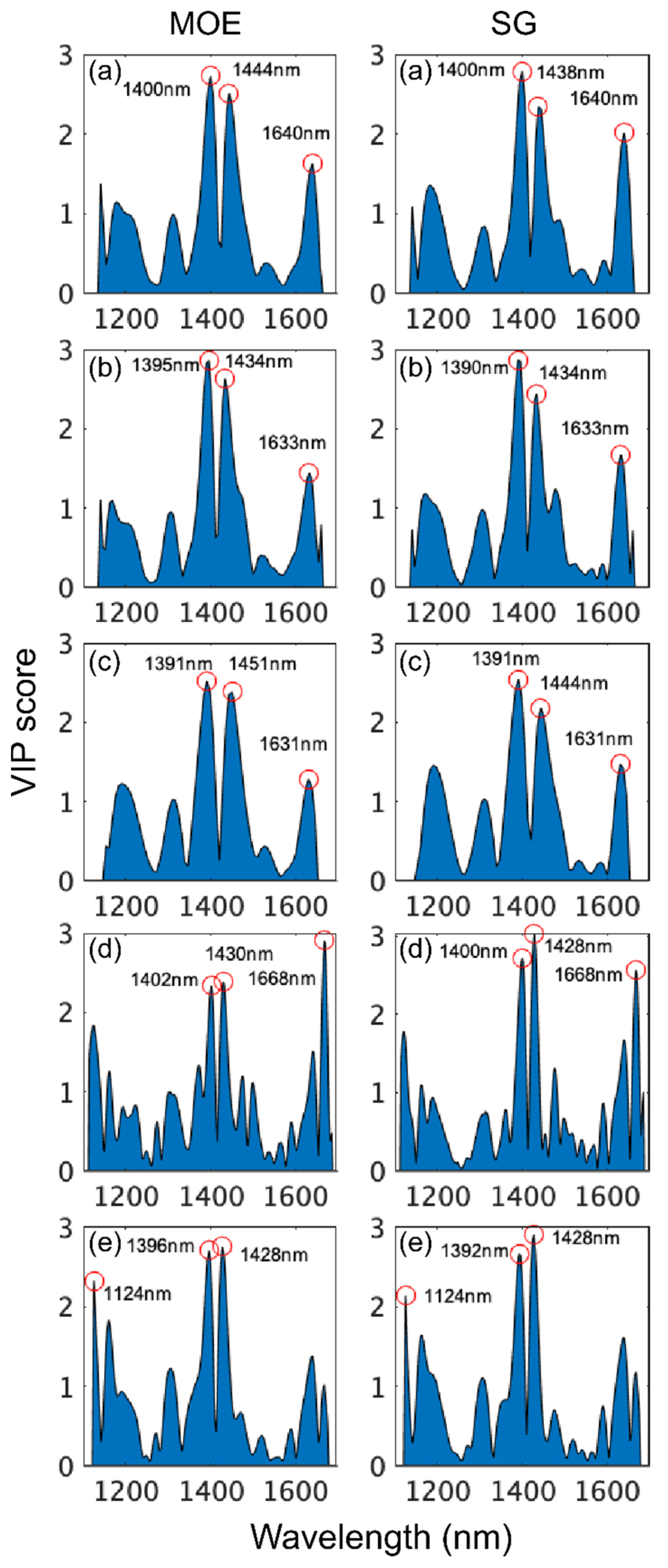
| Identified Wavelengths (nm) | Band Location (nm) | Bond Vibration | Wood Component |
|---|---|---|---|
| 1124 (MOE, SG) | NA | ||
| 1190 (MOE) | 1188–1195 | 2nd OT C-H str. | Lignin/(cellulose) |
| 1390–1402 (MOE, SG) | 1386 | 1st OT O-H str. | None specified |
| 1st OT C-H str. + C-H def. | |||
| 1428–1451 (MOE, SG) | 1428 | 1st OT O-H str. + H2O | Amorphous cellulose |
| 1440 | 1st OT C-H str. + C-H def. | Lignin | |
| 1447 | 1st OT O-H str. | Lignin | |
| 1448 | 1st OT O-H str. | Lignin/extractives | |
| 1630–1640 (MOE, SG) | 1632 | 1st OT O-H str. | Cellulose |
| 1668 (MOE, SG) | 1666 | 1st OT C-H str. | Hemicellulose |
| 1668 | 1st OT Car-H str. | Extractives | |
| 1672–1677 | 1st OT Car-H str. | Lignin | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, T.; Schimleck, L.; Dahlen, J.; Yoon, S.-C.; Inagaki, T.; Tsuchikawa, S.; Sandak, A.; Sandak, J. Comparative Performance of NIR-Hyperspectral Imaging Systems. Foundations 2022, 2, 523-540. https://doi.org/10.3390/foundations2030035
Ma T, Schimleck L, Dahlen J, Yoon S-C, Inagaki T, Tsuchikawa S, Sandak A, Sandak J. Comparative Performance of NIR-Hyperspectral Imaging Systems. Foundations. 2022; 2(3):523-540. https://doi.org/10.3390/foundations2030035
Chicago/Turabian StyleMa, Te, Laurence Schimleck, Joseph Dahlen, Seung-Chul Yoon, Tetsuya Inagaki, Satoru Tsuchikawa, Anna Sandak, and Jakub Sandak. 2022. "Comparative Performance of NIR-Hyperspectral Imaging Systems" Foundations 2, no. 3: 523-540. https://doi.org/10.3390/foundations2030035
APA StyleMa, T., Schimleck, L., Dahlen, J., Yoon, S.-C., Inagaki, T., Tsuchikawa, S., Sandak, A., & Sandak, J. (2022). Comparative Performance of NIR-Hyperspectral Imaging Systems. Foundations, 2(3), 523-540. https://doi.org/10.3390/foundations2030035










