Abstract
Neutron stars are the densest known objects in the universe and an ideal laboratory for the strange physics of super-condensed matter. Theoretical studies in connection with recent observational data of isolated neutron stars, as well as binary neutron stars systems, offer an excellent opportunity to provide robust solutions on the dense nuclear problem. In the present work, we review recent studies concerning the applications of various theoretical nuclear models on a few recent observations of binary neutron stars or neutron-star–black-hole systems. In particular, using a simple and well-established model, we parametrize the stiffness of the equation of state with the help of the speed of sound. Moreover, in comparison to the recent observations of two events by LIGO/VIRGO collaboration, GW170817 and GW190425, we suggest possible robust constraints. We also concentrate our theoretical study on the resent observation of a compact object with mass ∼ (GW190814 event), as a component of a system where the main companion was a black hole with mass ∼. There is scientific debate concerning the identification of the low mass component, as it falls into the neutron-star–black-hole mass gap. This is an important issue since understanding the nature of GW190814 event will offer rich information concerning the upper limit of the speed of sound in dense matter and the possible phase transition into other degrees of freedom. We systematically study the tidal deformability of a possible high-mass candidate existing as an individual star or as a component in a binary neutron star system. Finally, we provide some applications of equations of state of hot, dense nuclear matter in hot neutron stars (nonrotating and rapidly rotating with the Kepler frequency neutron stars), protoneutron stars, and binary neutron star merger remnants.
Keywords:
neutron stars; nuclear equation of state; gravitational waves; speed of sound; tidal polarizability PACS:
26.60.-c; 21.30.Fe; 21.65.Cd; 26.60.Kp
1. Introduction
One of the currently unsolved open problems in nuclear physics is the properties of dense nuclear matter. In particular, compact objects, such as white dwarfs and especially neutron stars, offer the opportunity to study the behavior of nuclear matter at high densities [1,2,3,4]. Neutron stars are a very promising tool for studying the properties of dense nuclear matter, such as the speed of sound and its possible upper bound.
The main assumption for the speed of sound is that it cannot exceed the speed of light because of the causality. However, this is not determinant, as Zel’dovich [5,6] showed the importance of defining a rigorous limit of speed of sound upon the equation of state (EoS). To be more specific, in the electromagnetic interaction, the main assumption is that is generally low in nature. Moreover, by considering the interaction of baryons through a vector field, he noticed that the upper limit of the speed of sound is the causality, . Therefore, the only restriction imposed by general principles is that [5,6]. On the other hand, Hartle noticed that the causality is not enough to constrain the high-density part of the EoS [7], while Weinberg pointed out that the speed of sound is much less than the speed of light for a cold nonrelativistic fluid [4]. In addition, for nonrelativistic and/or weakly coupled theories, the bound , according to Bedaque and Steiner seems to be valid, while in conformal theories, the upper bound is saturated [8]. According to these authors, the existence of a neutron star, in combination with the knowledge of the EoS of hadronic matter at the low density region, is not consistent with the limit . We notice that various recent studies have been conducted regarding the speed of sound and the tidal deformability of neutron stars [9,10,11,12].
One of the goals of this study is to apply a method that directly relates the observed tidal deformability, derived from binary neutron star mergers, to the maximum mass of neutron stars, aiming to obtain constraints on the upper bound of the speed of sound. The main idea is the fact that while the measured upper limit of the effective tidal deformability favors softer EoSs, recent measurements of high neutron star masses favor stiffer EoSs. As a basis in our study, we used a model in which we parametrized the EoS through the various bounds of the speed of sound (stiffness). Hence, the EoS is a functional of the transition density and the speed of sound bound. In our approach, we used the observation of two recent events, GW170817 [13] and GW190425 [14], as well as the current observed maximum neutron star masses ( [15], [16], [17], and [18]). The need for (a) a soft EoS for the low density region (to be in accordance with the observed upper limit of the effective tidal deformability) and (b) a stiff EoS for the high density region (to provide the high neutron star masses) leads to robust constraints on the EoS. In addition, this method allows making postulations about the kind of future measurements that would be more informative and help to improve our knowledge.
Furthermore, we highlight the very recent observation of the GW190814 event, where a gravitational wave has been detected from the merger of a 22.2–24.3 black hole with a non-identified compact object with mass 2.5–2.67 [19,20]. Although the authors of the mentioned references suggest that is unlikely for the second component’s mass to belong to a neutron star, they do leave open the window that the improved knowledge of the neutron star EoS and further observations of the astrophysical population of compact objects could alter this assessment.
It is worth pointing out that the observation of the GW190814 event has some additional general benefits, apart from the measurement of 2.6 of the second partner [19]. Firstly, this binary system has the most unequal mass ratio yet measured with gravitational waves close to the value of . Secondly, the dimensionless spin of the primary black hole is constrained to ≤0.07, where various tests of general relativity confirm this value, as well as its predictions of higher multiple emissions at high confidence intervals. Moreover, the GW190814 event poses a challenge for the understanding of the population of merging compact binaries. It was found, after systematic analysis, that the merger rate density of the GW190814-like binary system was Gpcyr [19]. More relevant to the present study, the observation of the GW190814 event led to the following conclusion: due to the source’s asymmetric masses, the lack of detection of an electromagnetic counterpart and of clear signature of tides or the spin-induced quadrupole effect in the waveform of the gravitational waves, we are not able to distinguish between a black-hole–black-hole and black-hole–neutron-star system [19]. In this case, one must count only the comparison between the mass of the second partner with the estimation of maximum neutron star mass [21]. This is one of the main subjects which has been revised in the present work. It should be emphasized that the measurements of neutron star mass can also inform us about a bound on the maximum gravitational mass independently of the assumptions of the specific EoS. For example, Alsing et al. [22], fitting the known population of neutron stars in binaries to double-Gaussian mass distribution, obtained the empirical constraint that (with confidence interval ).
Farr and Chatziionannou updated knowledge from previous studies, including recent measurements [23]. Their study constrains the maximum mass , leading to the conclusion that the posterior probability (for the mass of the second partner ) is around only . However, the prediction of is sensitive to the selection mass rules of neutron stars (not only on binary systems but also isolated) as well as to the discovery of new events, and this consequently remains an open problem. Finally, the conclusion of the recent GW190814 event in comparison with previous ones (for example the GW170817 event [24]) may shed light on the problem of the . For example, the spectral EoSs, which are conditioned by the GW170817 event, are once more elaborated to include the possibility that the prediction of is at least equal to . This approach leads to significant constraints on the radius and tidal deformability of a neutron star with mass of ( km and , respectively, [19]).
The matter of the finite temperature and its effect on the nuclear EoS, as well as astrophysical applications, has been extensively studied by Bethe et al. [25], Brown et al. [26], Lamb et al. [27], Lattimer and Ravenhall [28], and Lattimer [29]. Lattimer and Swesty [30], as well as Shen et al. [31], constructed the most used hot neutron star EoSs. The first one is based on the liquid drop-type model, and the second one is based on the relativistic mean field model. Afterwards, Shen et al. [31] broadened their study in order to study supernovae, binary neutron star mergers, and black hole formations by developing EoSs for various temperatures and proton fractions [32]. In addition, the density and temperature dependence of the nuclear symmetry free energy using microscopic two- and three-body nuclear potentials constructed from Chiral effective field theory have been studied in a series of works, including the one of Wellenhofer et al. [33]. Furthermore, hot neutron star and supernova properties have been studied by Constantinou et al. [34,35], where a suitable hot EoS is produced. Finally, the interplay between the temperature and the neutron star matter was probed by Sammarruca et al. [36], by considering the framework of chiral effective field theory.
EoSs at finite temperature constructed within the Brueckner–Hartree–Fock approach and the properties of hot -stable nuclear matter were studied in a series of papers [37,38,39,40,41,42,43,44,45]. In addition, a model for cold nucleonic EoSs, extended to include temperature and proton fractions for simulations of astrophysical phenomena, was constructed by Raithel et al. [46]. Pons et al. [47], as well as Prakash et al. [48], focused on describing the thermal and chemical evolution of protoneutron stars by considering neutrino opacities consistently calculated with the EoS. Finally, neutron stars, along with the hot EoS of dense matter, are presented in a recent review of Lattimer and Prakash [49].
The processes that occupy the stages of the merger and postmerger phases of a binary neutron star system have been extensively studied in recent years. However, matters that concern the remnant evolution are still under consideration or even unsolved. In particular, the remnant evolution contains (a) the collapse time, (b) the threshold mass, (c) the possible phase transition in the interior of the star, and (d) the disk ejecta and neutrino emission (for an extended discussion and applications, see Perego et al. [50]). It has to be noted here that the possibility of a phase transition will affect the signal of the emitted gravitational wave. Relevant previous work is also be available in Bauswein et al. [51], Kaplan et al. [52], Tsokaros et al. [53], Yasin et al. [54], Radice et al. [55], Sarin et al. [56], Soma and Bandyopadhyay [57], and Sen [58].
In the present work, we review some applications of the thermal effects on neutron star properties. In particular, we apply a momentum-dependent effective interaction (MDI) model, where thermal effects can be studied simultaneously on the kinetic part of the energy and also on the interaction one. In addition, the extension of the proposed model can lead to EoSs with varying stiffness with respect to the parameterized symmetry energy. In fact, Gale et al. [59] presented a model aimed at the influence of MDI on the momentum flow of heavy-ion collisions. However, the model has been successfully applied in studying the properties of cold and hot nuclear and neutron star matter (for an extensive review of the model, see References [60,61,62]).
Moreover, we review specific properties of neutron stars (including mainly the mass and radius, moment of inertia, Kerr parameter, etc.) with respect to the EoS, both at nonrotating and rapidly rotating (considering the mass-shedding limit) configurations. The above properties are well applied in studying hot neutron stars, protoneutron stars, and the remnants of binary neutron star systems.
To summarize, in the present work, we review the applications of various theoretical nuclear models on a few recent observations of binary neutron stars or neutron-star–black-hole systems, including mainly the GW170817, GW190425, and GW190814 events. Our results have been published recently in sections, in the following journals [63,64,65,66].
It has to be noted that the present study is mainly dedicated to the case of the emission of the gravitation waves due to the merger of a binary neutron star system. However, there are other mechanisms by which gravitational waves are emitted by a neutron star and thus, have additional ways of studying its internal structure (for a recent review, see Reference [67]). These mechanisms, which are considered as continuous gravitational waves sources, include, for example, (a) the case of radiation of gravitational waves by a rigidly rotating aligned triaxial ellipsoid (radiation of purely quadrupolar waves), (b) the emission of gravitational waves due to asymmetry in the magnetic field distribution in the interior of the neutron star, and (c) the radiation of gravitational waves from the rapidly rotating neutron stars. In this case, neutron stars may suffer a number of different instabilities with a general feature in common: they can be directly associated with unstable modes of oscillation (for exable g-modes, f-modes, w-modes, r-modes; for a review see Reference [68]). The more notable mechanism is the r-mode oscillations. In these oscillations, the restoring force is the Coriolis force. The r-mode mechanics have been proposed as an explanation for the observed relatively low spin frequencies of young neutron stars, as well as of accreting neutron stars in low-mass X-ray binaries. This instability only occurs when the gravitational radiation driving timescale is shorter compared to the ones of the various dissipation mechanisms, which occur in the neutron star matter [69]. The free procession may cause deformation of the neutron star, leading to a better understanding of some neutron star matter properties, including breaking strain, viscosity, rigidity, and elasticity [67]. We expect that in the future, the development of the sensitivity of LIGO and Virgo detectors in cooperation with and new instruments will help to significantly improve our knowledge of neutron star interiors with the detection of the emitted gravitational waves [67].
Another way to study the properties of dense nuclear matter that exists inside neutron stars can be done with the help of the statistical study of the observed properties of neutron stars. To be more specific, we refer to the observational data concerning both isolated neutron stars and those that exist in binary systems. In the first case, there are extensive studies where observational data are applied to estimations with the help of statistical studies, for example, the maximum possible mass of a neutron star, but mainly the radius of neutron stars with masses of about . In each case, valuable information and ideas can be extracted and utilized in terms of knowledge of the EoS of neutron star matter, in order to evaluate the reliability of the existing EoS (see the review article [70] and references therein). In the case of binary systems, the analysis of the emitted gravitational waves from the fusion of a binary system of neutron stars, where a large amount of information is received by studying the amplitude and phase of gravitational waves, is utilized. These studies mainly focus on the measurement (and utilization of the measurement) of tidal deformability. In any case, extensive and systematic statistical estimation of data can lead to valuable knowledge of the structure and composition of neutron stars (for a recent review see [71] and references therein).
The article is organized as follows: in Section 2, we present the theory concerning the EoS and the structure of cold neutron stars. In Section 3, we present the construction of the hot EoSs (both isothermal and isoentropic) and briefly discuss the stability equations of hot rapidly rotating neutron stars. The results and the discussion are provided in Section 4, while Section 5 includes the most noteworthy concluding remarks of the present review.
2. Cold Neutron Stars
2.1. The Momentum-Dependent Interaction Nuclear Model
The description of the interior structure of neutron stars demands the use of a nuclear model suitable to describe the properties of dense nuclear matter. In the present work, the EoS of nuclear matter is studied using the MDI model. In this model, the energy per baryon is given by the formulae [60,72]
where u is the baryon density normalized with respect to the saturation density , is the asymmetry parameter, , , , and . The parameters A, B, , , and appear in the description of symmetric nuclear matter (SNM) and are determined so that the relation holds. and are finite range parameters equal to and , respectively, where is the Fermi momentum at the saturation density. The remaining parameters, , , , appear in the description of asymmetric nuclear matter (ANM) and, with a suitable parametrization, are used in order to obtain different forms for the density dependence of symmetry energy, as well as the value of the slope parameter L and the value of the symmetry energy at the saturation density, defined as [63]
and consequently different parametrizations of the EoS stiffness.
The specific choice of the MDI model is based on the following: (a) it combines both density and momentum dependent interaction among the nucleons, (b) it is suitable for studying neutron star matter at zero and finite temperature (due to the momentum term), (c) it reproduces with high accuracy the properties of SNM at the saturation density, including isovector quantities, (d) it reproduces the microscopic properties of the Chiral model for pure neutron matter (PNM) and the results of state-of-the-art calculations of Akmal et al. [73] with suitable parametrizations, (e) it predicts higher maximum neutron star mass than the observed ones [16,17,18], and (f) it maintains the causal behavior of the EoS even at densities higher than the ones that correspond to the maximum mass configuration.
2.2. Speed of Sound Formalism
An EoS can be parametrized in order to reproduce specific values of the speed of sound in the interior of the neutron star. This parametrization is possible following the formula available from References [22,74,75,76,77,78,79,80]:
where P and denote the pressure and the energy density, respectively, and the corresponding subscript “tr” in energy density denotes the energy density at the transition density.
However, following the approach in Equation (3), only the continuity in the EoS is ensured. The artificial character of Equation (3) does not take into account the continuity in the speed of sound. Therefore, in order to ensure the continuity and a smooth transition, we followed the method presented in Reference [81]. We proceeded with the matching of the EoSs with the transition density by considering that, above this value, the speed of sound is parametrized as follows (for more details, see Reference [81]):
where the parameters and are fit to the speed of sound and its derivative at and also to the demands [74] according to the value of . The remaining parameter w controls the width of the curve, which in our case is equal to , in order to preserve the neutron star properties. Using Equation (4), the EoS for can be constructed with the help of the following [81]:
2.3. Construction of the EoS
The construction of the EoS for the interior of neutron stars is based on the MDI model and data provided by Akmal et al. [73]. More specifically, we utilized the data for the A18+UIX (hereafter APR-1) EoS from Akmal et al. [73] for the energy per particle of SNM and PNM in the density range . Due to the complexity of the microscopic data, we divided the density region into three sections—(a) low-density region , (b) medium-density region , and (c) high-density region —in order to acquire the best fitting using Equation (1). From this process emerged the coefficients for the SNM and ANM, and eventually the EoS, hereafter MDI-APR.
In the case of the speed-of-sound-parametrized EoSs, the construction of the EoSs follows the procedure: (a) in region , we used the equation of Feynman et al. [82] and also of Baym et al. [83] for the crust and low densities of neutron star; (b) in the intermediate region, , we employed the MDI-APR EoS; and (c) for region, the EoS is maximally stiff with the speed of sound, defined as (where S is the entropy) fixed in the present work in the range . The lowest allowed value of the speed of sound, that is , is introduced in order to be consistent with the possibility of a phase transition in quark matter. In this case, the theoretical predictions lead to this value as an upper bound of the speed of sound. The implementation of speed of sound values between the limited ones will lead to results well constrained by the two mentioned limits. Although the energy densities below the have negligible effects on the maximum mass configuration, we used them in calculations for the accurate estimation of the tidal deformability.
In this study, two cases, based on the transition density, and the speed of sound, are employed, in particular, (a) the ones where p takes the values while the speed of sound is parametrized in the two limiting cases, and , and (b) the ones where p takes the values while the speed of sound is parametrized in the range .
For reasons of completeness, the treatment with both discontinuity and continuity in the speed of sound is presented in Table V of Reference [74]. The main point was that the two approaches converge and consequently the effects of the discontinuity are negligible.
In Figure 1, we present the pressure as a function of the rest mass density () and the square speed of sound in units of speed of light as a function of the transition density for the EoSs constructed in cases (a) and (b). In addition, we display the credibility intervals proposed by Reference [24] from LIGO/Virgo collaboration for the GW170817 event. It is clear from these figures that the pure MDI-APR EoS is well-defined in the proposed limits of LIGO/Virgo collaboration and also fulfills the speed of light limit at high densities.
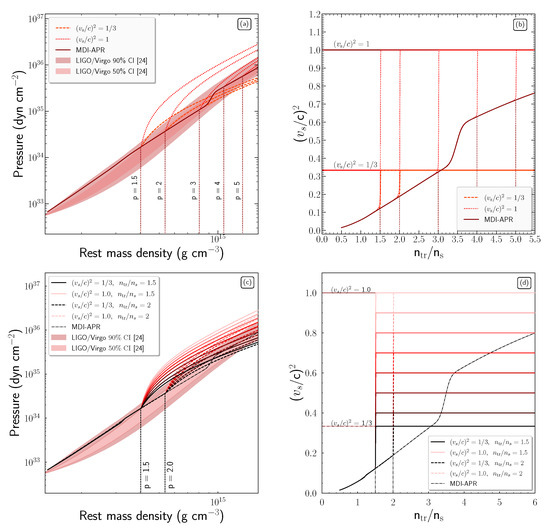
Figure 1.
(a,c) Dependence of the pressure on the rest mass density and (b,d) dependence of the square sound speed in units of light speed on the transition density. (a,b) The speed of sound is fixed at the two boundary cases, and , and the value p takes the arguments . (c,d) The value p takes the arguments , and the speed of sound is parametrized in the range (the lower values of the speed of sound correspond to the darker colored curves). In all figures, the vertical dotted lines indicate the transition cases, while the shaded regions note the credibility interval derived from Reference [24].
2.4. Structure Equations
2.4.1. Nonrotating Neutron Stars
For a static spherical symmetric system, which is the case of a nonrotating neutron star, the metric can be written as follows [1,2]:
The density distribution and the local pressure is related to the metric functions and according to the relations [1,2]
where derivatives with respect to the radius are denoted by . The combination of Equations (9) and (10) leads to the well known Tolman–Oppenheimer–Volkoff (TOV) equations [1,2]:
It is difficult to obtain exact solutions to TOV equations in closed analytical form, and they are solved numerically with an equation of state specified [84]. Actually, there are hundreds of analytical solutions of TOV equations, but there are three that satisfy the criteria that the pressure and energy density vanish on the surface of the star, and they also both decrease monotonically with increasing radius. These three solutions are the Tolman VII, the Buchdahl, and the Nariai IV. Actually, the Tolman VII and the Buchdahl have already been analyzed and employed in Reference [85]. It is worth pointing out that in the present work we use the Tolman VII solution, which contains two parameters, that is, the central density and the compactness parameter . All the mentioned solutions have been presented and analyzed in detail in References [85,86,87,88].
One of the most significant sources for the detectors of terrestrial gravitational waves is the gravitational waves from inspiraling binary neutron star systems before their merger [86,89,90,91,92,93,94,95,96]. The component masses of these binary systems can be measured. Additionally, during the last orbits before the merger, the tidal effects that are present can also be measured [90].
The dimensionless parameter that describes the response of a neutron star to the induced tidal field is called tidal Love number . This parameter depends on the neutron star structure (i.e., the mass of the neutron star, and the EoS). Specifically, the tidal Love number is a proportional parameter between the induced quadrupole moment and the applied tidal field [90,97] given below:
where R is the neutron star’s radius and is a key-role quantity, which is called tidal deformability. The tidal Love number is given by [90,91]
The quantity is determined by solving the following differential equation
with the initial condition [93]. and are functionals of , , and , defined as [86,93]
and
The Equation (15) must be integrated self-consistently with the TOV equations using the boundary conditions , and [86,91]. The numerical solution of these equations provides the mass M, the radius R of the neutron star, and the value of . The latter parameter along with the quantity are the basic ingredients of the tidal Love number .
Moving on to the parameters of a binary neutron star system, a well-measured quantity by the gravitational waves detectors is the chirp mass of the system [13,98]:
where and are the masses of the heavier and lighter components. Therefore, the binary mass ratio is within the range .
Another quantity that can be constrained from the analysis of the gravitational wave signal and is of great interest, is the effective tidal deformability [13,98]
where is the dimensionless tidal deformability, defined as [13,98]
By observing Equations (14) and (20), one can find that depends both on the star’s compactness and the value of . More specifically, depends directly on the stiffness of the EoS through the compactness and indirectly through the speed of sound which appears in Equation (17). In addition, the applied EoS also affects the behavior of regarding the neutron star’s mass M and radius R.
2.4.2. Rotating Neutron Stars
In a fully general relativistic framework, the rotating neutron stars are studied with the use of the stationary axisymmetric spacetime metric, which is given by [99]
where the metric functions , , , and depend only on the coordinates r and . In order to describe a rapidly rotating neutron star, in addition to the above metric, we need the matter inside the neutron star described as a perfect fluid. By neglecting sources of non-isotropic stresses, as well as viscous ones and heat transport, then the matter inside the neutron star can be fully described by the stress-energy tensor [99],
where is the fluid’s 4-velocity and and P are the energy density and pressure.
For the stability of cold rotating neutron stars, the turning-point criterion is being used. It has to be noted that this is only a sufficient and not a necessary condition. Actually, the neutral stability line is positioned to the left of the turning-point line in space, which implies that the star will collapse before reaching the turning-point line [100,101].
The numerical integration of the equilibrium equations was conducted under the RNS code [102] by Stergioulas and Friedman [103], which is actually based on the method developed by Komatsu, Eriguchi, and Hachisu [104] and modifications introduced by Cook, Shapiro, and Teukolsky [105].
3. Hot Neutron Stars
3.1. Thermodynamical Description of Hot Neutron Star Matter
The description of nuclear matter at finite temperature includes the Helmholtz free energy, where the differentials of the total free energy, as well as the total internal energy (assuming that the baryons are contained in volume V) are given by [106,107]
where is the total entropy of baryons, is the chemical potential of each species, and is the number of particles of each species, respectively. Furthermore, the free energy per particle can be expressed as
where and are the internal energy and entropy per particle, respectively. It has to be noted here that for , Equation (25) leads to the equality between free and internal energy.
In addition, the entropy density s has the same functional form as a noninteracting gas system, calculated through the form
with spin degeneracy . The first case corresponds to protons, neutrons, electrons, and muons, and the second case corresponds to neutrinos. Finally, the pressure and chemical potentials, which depend on the above quantities, are described as:
3.2. Bulk Thermodynamic Quantities
The pressure and chemical potentials, which are essential for the thermodynamical description of nuclear matter, can also be connected to the key quantity, that is, the free energy, as
where f denotes the free energy density. It is worth mentioning that the pressure P can also be determined by [106,107],
In this case, the calculation of the entropy per particle is possible by differentiating the free energy density f with respect to the temperature,
By applying Equation (30), the chemical potentials take the form [37,108,109]
The free energy and the internal energy , as well as the entropy, which depends on the latter quantities, can have the following quadratic dependence from the asymmetry parameter [37,109,110,111,112]:
as the parabolic approximation (PA) suggests, where
While the above approximation is valid for the specific model, in general, it is mandatory to check it. For completeness, the PA is satisfied in both the internal energy and the free energy, as References [37,109,110,111,112] state. However, there are studies [113] in which the PA contains uncertainties. In sum, the PA and its validity strongly depend on the specific character of the selected nuclear model.
Equation (35), which is mandatory for this approximation, can be acquired by substituting Equation (36) as
This equation is similar to that obtained for cold catalyzed nuclear matter by replacing with .
3.3. Lepton’s Contribution
Stable nuclear matter and a chemical equilibrium state are explicitly connected at high densities for all reactions. Specifically, electron capture and decay take place simultaneously
In consequence, a change in the electron fraction is in order. Considering that the generated neutrinos have left the system, a significant effect on the EoS is presented by changing the values of proton fraction [114,115]. In particular, the absence of neutrinos implies that
It is has to be mentioned that, in principle, the matter contains neutrons, protons, electrons, muons, photos, and antiparticles, which are in a thermal equilibrium state. However, in the present study, we consider only the contribution of neutron, protons, and electrons, as the contribution of the remaining particles is negligible [114]. As a consequence, the following relation holds:
The energy density and pressure of leptons are calculated through the following formulae:
The chemical potential of electrons is available through the Equations (42) and (45), as
which is crucial for the calculation of the proton fraction as a function of both the baryon density and the temperature. The construction of the EoS of hot nuclear matter in the -equilibrium state is provided through the calculation of the total energy density , as well as the total pressure . The total energy density (with all terms) is given by
where is the contribution of baryons, , are the contributions of particles and antiparticles of leptons, and is the contribution of photons. The total pressure (with all terms) is
where is the contribution of baryons,
while , are the contributions of particles and antiparticles of leptons, and is the contribution of photons.
3.4. Isothermal Configuration
In the isothermal temperature profile, by considering that for each value of temperature, the value of the proton fraction is a well-known function of the baryon density, the total energy density is evaluated as
where
is given by Equation (46), replacing the leptons with electrons and from Equation (48), and and are given by Equations (36) and (38), respectively. Moreover, the total pressure is evaluated as
where
and is given by Equation (47), replacing the leptons with the electrons and from Equation (48).
3.5. Isentropic Configuration and Neutrino Trapping
In an isentropic configuration, we assume that the entropy per baryon and lepton fraction are constant in the interior of the neutron star (protoneutron star). Specifically, according to Equation (43), the neutrinos are trapped in the interior of the star and the proton fraction is significantly increased. The relevant chemical equilibrium can be expressed in terms of the chemical potentials for the four species,
In addition, the charge neutrality demands the equality between proton and electron fraction, while the total fraction of leptons is equal to . Henceforth, the chemical equilibrium is expressed as
In this case too, the relevant system of equations can provide us with the density and temperature dependence of proton and neutrino fractions, and their chemical potentials, by assuming a constant entropy per baryon. Nonetheless, we applied the approximation of ( accuracy) introduced by Takatsuka et al. [114], in order to avoid computational complications. The ingredients for the construction of isentropic EoSs are given by the Equations (49) and (50).
3.6. Construction of the Hot EoSs
The construction of the EoS for the interior of neutron stars at finite temperature and entropy per baryon is based on the MDI model and data provided by Akmal et al. [73]. In particular, we utilized the APR-1 EoS data from Akmal et al. [73] for the energy per particle of SNM and PNM in the density range . The process leads to the evaluation of the coefficients for the symmetric and asymmetric nuclear matter, and finally, to the construction of the EoS, hereafter MDI+APR1.
In the case of the isothermal temperature profile, we have constructed 10 EoSs in the temperature range , while in the isentropic case, we have constructed nine EoSs in entropy per baryon and lepton fraction ranges and , respectively. For the crust region of the finite temperature cases and the low-density region , as well as the finite entropies per baryon and lepton fractions, the EoSs of Lattimer and Swesty [30] and the specific model corresponding to the incomprehensibility modulus at the saturation density of SNM are used (https://www.stellarcollapse.org, accessed on 4 March 2020).
3.7. Rapidly Rotating Hot Neutron Stars
The stability of hot neutron stars is acquired via a specific version of the secular instability criterion of Friedman et al. [116], which follows Theorem I of Sorkin [117]. In a continuous sequence of equilibria at a fixed baryon number and total entropy of the neutron star , the extremal point of the stability loss is found when [118]
where J and are the angular momentum and central baryon density of the star, respectively.
Furthermore, in a sequence, the turning-point appears in the case where three out of four following derivatives vanish,
with and denoting the gravitational and baryon mass [52,119]. In addition, the turning-point theorem shows that at this point, the fourth derivative also vanishes, and the sequence has transitioned from stable to unstable.
It has to be mentioned that the criterion for secularly stable/unstable configurations is essential only for constant entropy per baryon or temperature [119]. In this review, the entropy per baryon and the temperature in each case are constant throughout the neutron star. Therefore, the remaining criteria vanish at the maximum mass configuration (the last stable point). Furthermore, we considered that in the rotating configuration, the maximum mass and the maximum angular velocity coincide, which generally is not the case [99]. However, the existing difference is very small, and it could not be detected within the precision of our calculations [118].
The numerical integration of the equilibrium equations was conducted under the publicly available numerical code nrotstar from the C++ Lorene/Nrotstar library [120].
4. Results and Discussion
4.1. Speed of Sound and Tidal Deformability
In our study, we used two cases for the value of speed of sound, the lower bound of and the upper one of , and four transition densities [65].
In Figure 2, we display the corresponding mass-radius (M-R) diagram, which we obtained from the numerical solution to the TOV system of equations. The green colored lines correspond to the limit, while the blue ones correspond to the limit. One can observe that each transition density leads to bifurcations in the M-R diagram. Between the same kind of linestyle, the lower and upper bounds, and of speed of sound correspond to lower and higher masses, respectively. In general, the higher the transition density, the softer the EoS, with the lower bound of leading to a more soft EoS compared to the case. In addition, the estimation of the GW170817 event and the NICER’s data are also displayed [24,121]. We notice that while there is an accordance between the two observations, the GW170817 event (from the gravitational-waves perspective) is more informative for our study than the NICER’s detection, as it restricts the cases leading to the exclusion of EoS at least with transition density , for both bounds of speed of sound.
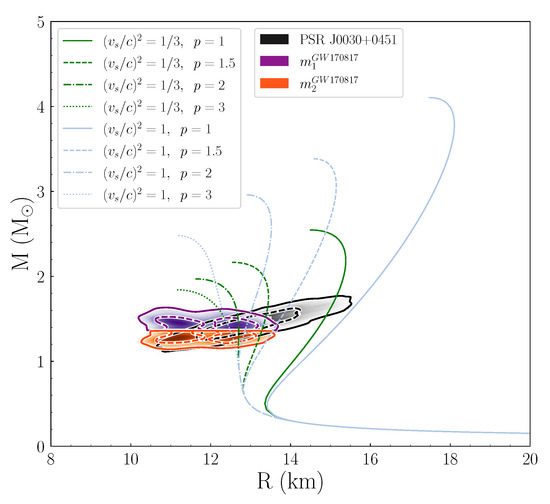
Figure 2.
Mass vs. radius for an isolated neutron star and for the two cases of speed of sound bounds. The blue (green) lines correspond to the upper (lower) bound. The black diagonal shaded region corresponds to NICER’s observation (data taken from Reference [121]), while the purple upper (orange lower) shaded region corresponds to the higher (smaller) component of GW170817 event (data taken from Reference [24]). The solid (dashed) contour lines describe the 90% (50%) confidence interval.
Our study takes into consideration the observation of binary neutron stars mergers from the gravitational waves detectors. Therefore, we used the measured upper limit of the effective tidal deformability provided by the events GW170817 and GW190425 [14,24,98]. The chirp masses for the two events are [13] and [14], respectively. The component masses vary in the ranges and [98] (GW170817) and and (GW190425). We notice that we modified the range of the component masses (especially in the second event) to have an equal mass boundary, i.e., .
In Figure 3, we display the effective tidal deformability as a function of q for both events. In Figure 3a, we observe that the upper limit on (derived from the GW170817 event) leads to the exclusion of both cases of speed of sound with transition density . By comparing to Figure 2, the constraints on the upper limit of in Figure 3 make more clear which cases must be excluded. For the second event in Figure 3b, we observe that all the EoSs are shifted to lower values of , compared to the GW170817 event. This is because of the higher value of chirp mass in the second event (GW190425). Contrary to the GW170817 event, the upper limit on , provided by GW190425 event, excludes only these EoSs with transition density , for both bounds of the speed of sound. In general, for both events, the EoSs corresponding to higher values of transition density lead to smaller values of . Therefore, the measured upper limits of favor softer EoSs. We have to notice that for the GW190425 event, we did not take into consideration the cases with transition density because the EoS with and cannot reproduce the masses of this event.
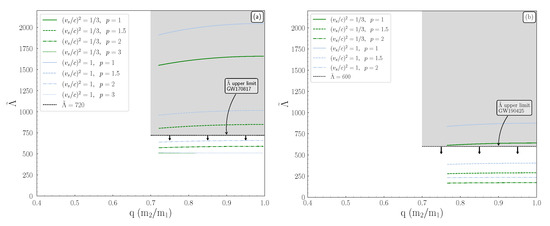
Figure 3.
The effective tidal deformability as a function of the binary mass ratio q for the event (a) GW170817 and (b) GW190425. The measured upper limits for are also indicated, with the grey shaded region corresponding to the excluded area. The green (blue) curves correspond to the () case.
Beyond the useful constraints that we obtained so far by the study of the EoSs through the observed upper limit of , a more direct connection between this quantity and the speed of sound bounds is still needed. This idea, which lies at the very heart of our study, was the main motive. Such a direct relation between the referred quantities can be accomplished if we treat the variation of in Figure 3 as a function of the transition density , i.e., the and relations.
In Figure 4, we display the relation between the effective tidal deformability and the transition density at the maximum mass configuration for the two bounds of the speed of sound, and , and the two events GW170817 (Figure 4a) and GW190425 (Figure 4b). The corresponding upper measured limits for , as well as the compatible lower transition density values, are also indicated. The predictions on the bound of the speed of sound which are considered between the two referred limits correspond to the middle region.
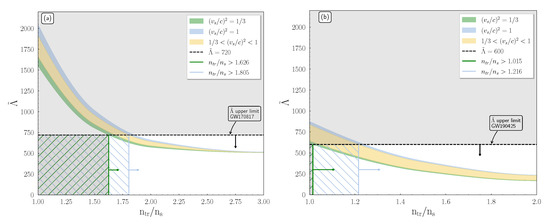
Figure 4.
as a function of the transition density (in units of saturation density ) at the maximum mass configuration for the two speed of sound bounds and and for the events (a) GW170817 and (b) GW190425. The measured upper limits for [14,98] as well as the corresponding lower values of transition density are also indicated for both events. The green (blue) arrow marks the accepted region of transition density for the () case. The green lower (blue upper) curved shaded region corresponds to the () limit. The yellow shaded area indicates the region between the two cases of bounds of the speed of sound.
The main remarks from the observation of Figure 4 are the following
- The overall thickness decreases as the transition density reaches higher values. This behavior can be explained by the variation of the radius presented in the M-R diagram (see Figure 2).
- The thickness of each shaded region decreases as the reaches higher values.
According to our findings, for the GW170817 event, the lower limit for the transition density is 1.626 for and 1.805 for . In the case of the second event, GW190425, the corresponding limits are 1.015 for and 1.216 for . Therefore, the first event imposes more stringent constraints on the EoS. In particular, the value of the speed of sound must be lower than , at least up to density 1.626 (so the EoS is soft enough to predict the tidal deformability). Furthermore, the EoS must remain casual at least up to density 1.805. In addition, according to the Fermi liquid theory (FLT), the speed of sound must be for [122], meaning that the EoS cannot exceed this value for , which is in agreement with our finding of the lower limit for the case of .
We notice that so far we used the upper limit on to impose stringent constraints on the . The existence of a lower limit on could provide further information. Indeed, for the GW170817 event, such a lower limit is provided both by the gravitational wave data [24,98] and the electromagnetic (EM) counterpart of the merger [123,124,125,126,127,128]. Most et al. [129] used the bound of Reference [123] and demonstrated its significance in order to further constrain the tidal deformability and the radius of a neutron star. For our case of interest and especially for the GW170817 event, a lower limit on similar to the proposed values, could not provide any further constraint, even if we consider the more optimistic boundary of .
On the contrary, for the second event GW190425, its higher component masses lead to smaller values of . Hence, there is an inability for the upper limit of to provide further constraints. We speculate that the existence of a lower limit on would be able to provide constraints, especially leading to an upper limit for . Hence, binary neutron stars coalescences with heavy masses would be helpful to constrain the upper limit of via the lower limit of as provided by the EM counterpart. Unfortunately, an EM counterpart for the GW190425 event was not detected [14,130].
Furthermore, we provide in Figure 4 an expression for the and boundary curves of the green (lower) and blue (upper) shaded regions, respectively. This expression gives the exact value of the lower limit on and , respectively. The expression is given by the following equation, and the coefficients on Table 1,

As one can observe from Figure 2, the highest mass is provided by the stiffest EoSs, i.e., the higher value of speed of sound. Therefore, the behavior of the maximum mass and the speed of sound has to be studied further.
In Figure 5, the behavior of the effective tidal deformability as a function of the maximum mass for the two speed of sound bounds and for both events is displayed. The corresponding upper observational limit for (black dashed horizontal line), the compatible maximum mass in each case (horizontal arrows), and the current observed maximum neutron star mass (vertical purple shaded region) are also indicated.
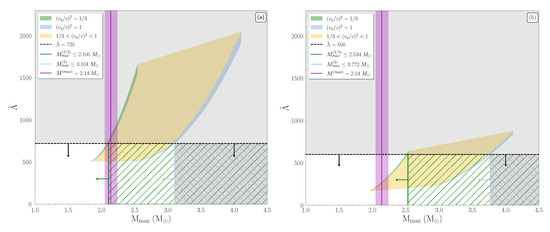
Figure 5.
The effective tidal deformability as a function of the maximum mass for the two speed of sound bounds and and for the events (a) GW170817 and (b) GW190425. The measured upper limits for (black dashed lines with arrows; see References [14,98]); the corresponding maximum mass shaded regions, for the (left green) case, for the case (right blue), and for the middle cases (yellow); and the current observed maximum neutron star mass (purple shaded vertical area; see Reference [17]) are also displayed. The green left (blue right) arrow marks the accepted region of maximum mass for () case.
At first glance in Figure 5, there is a contradiction between the maximum mass and the upper limit of the observed . For the first event shown in Figure 5a, the upper limit of is compatible with a maximum mass value for and for . Nonetheless, this bound corresponds to transition density in approximation 1.5. Experimental evidence disfavors this value. Therefore, the simultaneous derivation of the maximum mass combined with the experimental knowledge that the EoS cannot take this bound of sound speed for are in contradiction. Furthermore, the upper limit on for the case of lies roughly inside the estimation of the measured maximum mass. In the general perspective, we notice that two different points of view antagonize each other. The constraints derived by the upper limit on lead to softer EoSs, contrary to the observational estimations of the maximum mass of neutron stars, which lead to stiffer EoSs. As we move to higher values of the speed of sound, this contrast decreases, with the causal scenario of leading to a very wide area for the maximum mass.
In the case of the second event GW190425 displayed in Figure 5b, the constraints provided by the measured are less stringent than the GW170817 event, with a maximum mass value of for and for . However, the presence of a lower limit on , especially in the case of events with heavy components (such as GW190425), could constrain the lower maximum mass.
In addition, we provide an expression that describes the as a function of the maximum mass . The expression is given by the following equation and the coefficients in Table 1,
The expression in this form means that . Moreover, the adoption of an upper limit on the maximum mass in Figure 5 could provide an additional constraint on the behavior of the speed of sound. Specifically, by applying the estimated upper limit [131], the case of in Figure 5a for the GW170817 event should be excluded. On the contrary, the estimated upper limit for the bound, is a more tight constraint. Additionally, an upper limit such as imposes a general upper bound on the possible intermediate values of speed of sound (intermediate shaded area in the figure). Concerning the second event in Figure 5b, a strict upper limit on could constrain even the case.
Another interesting relation is the as a function of the radius of a neutron star, for both events, which is displayed in Figure 6. First of all, the upper limit on leads to a limitation on the maximum values of the radius, especially in the case of . Furthermore, there is a trend between and , which was also remarked on by Raithel et al. [132], mentioning that the effective tidal deformability depends strongly on the radii of the stars rather on the component masses. This strong dependence can be observed in Figure 6.
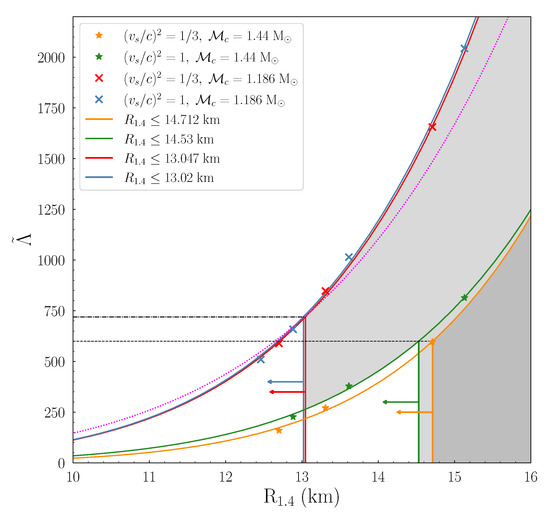
Figure 6.
The effective tidal deformability as a function of for both events and all the bounds of the speed of sound. The dashed and dash-dotted horizontal black lines correspond to the upper limit on for the GW190425 and GW170817 events, respectively, taken from References [14,98]. The grey shaded regions correspond to the excluded areas. The horizontal arrows indicate the allowed area for in each case. The purple dotted curve demonstrates the proposed expression by References [133,134].
In particular, for the GW170817 event, the curves of the two limited cases, red and blue for the and bounds, respectively, of the speed of sound are almost identical. The cross marks correspond to the specific values for each case. In our study, we considered four cases of transition density ; therefore, eight marks are expected in total, but in the diagram, only seven can be seen. This is because of the identical values for the case that the two bounds provide. This is clear from their behavior in Figure 2 in which, for the mass range of GW170817 event, their M-R curves are identical.
Moreover, as the effective tidal deformability shows higher values, the distance between them also increases. The same behavior is present in the curves of Figure 3a, in which their in-between distance increases for higher values of . This increment is related to the , meaning that the differentiation for small values of is more obvious. Hence, in these cases, the effect of each bound of the speed of sound is easier to be manifested.
The dotted purple line corresponds the approximate relation of References [133,134]. We notice that this approximate relation is valid only for the first event and for specific assumptions on the components’ radii. In particular, the main assumption of this approximation consists on the relation. From the comparison of Figure 6 with the M-R diagram of Figure 2, it follows that for smaller values of (i.e., more stiff EoSs), (a) the inclination of the curves increases and (b) the difference between the M-R curves of boundary cases also increases. Therefore, these remarks, combined with the strong dependence of to R (see Equation (20)), show the inability of the proposed expression to accurately reproduce the values of in the high-values region can be explained.
The grey shaded area indicates the excluded area due to the upper limit on , provided by Reference [98]. The upper limit of leads to constraints on the radius , especially for the bound and for the bound. These upper limits are consistent with other analyses [24,124,128,129,132,134,135,136,137].
For the second event (GW190425), we notice that the exact range of the component masses is not determinant [130]. The orange and green lines and marks correspond to the and bounds, respectively, of the speed of sound. The shaded grey region indicates the excluded region by the upper limit of [14]. The orange and green arrows indicate the allowed region for each case. For , the constraint on the radius is , while for is . These are more stringent constraints compared to the and of Reference [14]. We notice that recently it was found in Reference [138] that the joint contribution of gravitational waves and NICER data favors the violation of the conformal limit . In particular, this analysis suggests the violation of the conformal limit around density, where is the nuclear saturation density.
In addition, one can observe the similarity of the curves’ behavior between the two events. For higher values of , the distance between the points grows. One of the main differences is that for the second event, the curves and the points are shifted to smaller values of because of the higher chirp mass of the system. Another observation is that the fitting lines are more distinct from each other, contrary to the GW170817 event, in which they were almost identical; nevertheless, there is a common trend (see also Reference [132]). For this reason, we applied the following expression
where is in , similar to the proposed relations of References [133,134]. The coefficients for each case are given in Table 2.

Table 2.
Coefficients of Equation (62) for the two bounds of the speed of sound.
4.2. GW190814: A Postulation of the Most Massive Neutron Star
The GW190814 event that arose from the merger of a ∼ black hole with a ∼ compact object has provided various scenarios for the nature of the second component. In particular, the possibilities for the second merger component are that of (a) the lightest black hole, (b) the most compact neutron star, (c) a rapidly rotating neutron star, and (d) an exotic compact object. We note that in the present review, we consider only the scenarios where the compact object is a nonrotating (most compact) neutron star or is a rapidly rotating one [66].
In Figure 7, we display the gravitational mass as a function of the Kerr parameter for the pure MDI-APR EoS. In addition, we note the universal relation
where is the Kerr parameter at the mass-shedding limit, for two limiting cases: (a) and (b) [139]. The limiting cases correspond to the minimum and maximum possible mass for a neutron star [139], along with the maximum value of the Kerr parameter (considering the minimum possible mass) [139]. The area marked by the intersection of the gravitational mass, , with the Kerr parameter, [139], notes the area where the compact object can exist. Figure 1 and Figure 7 show that the pure MDI-APR EoS, which is well-defined in the above limits, is a suitable hadronic EoS to describe the ∼2.6 compact object.
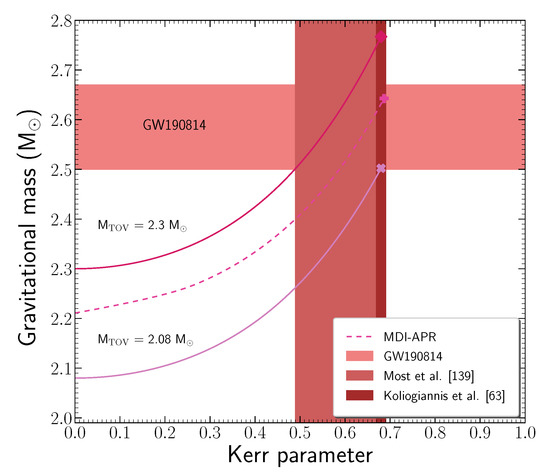
Figure 7.
Dependence of the gravitational mass on the Kerr parameter. The lower solid line represents Equation (63) with , while the upper solid line represents Equation (63) with . The dashed line corresponds to the MDI-APR EoS. In addition, the horizontal shaded region notes the mass of the second component of GW190814 event, and the vertical wide shaded region marks the Kerr parameter, , according to Reference [139]. Furthermore, the narrow vertical shaded region indicates the Kerr parameter, , extracted from Reference [63] by assuming that the low mass component was rotating at its mass-shedding limit. The cross, the plus sign, and the diamond show the maximum mass configuration at the mass-shedding limit.
Furthermore, by assuming that the second merger component is rotating at its mass-shedding limit, possible constraints are available through the Kerr parameter, the equatorial radius, and the central energy/baryon density. Specifically, by employing the relation found in Reference [63]
for the observable gravitational mass, the maximum Kerr parameter is evaluated in the range , a feature that is also noted in Figure 7. Moreover, taking into consideration the relation from Reference [64] that connects the Kerr parameter with the compactness parameter at the mass-shedding limit, namely
the equatorial radius is calculated in the range .
Finally, we focused on the central energy/baryon density, a property that is connected to the time evolution of pulsars and the appearance of a possible phase transition. The above dependence is presented in Figure 8 as the dependence of the maximum gravitational mass on both the central energy density and the central baryon density. Specifically, Figure 8 contains a wide range of hadronic EoSs (23 EoSs) [63] both at the nonrotating and maximally rotating configurations, the analytical solution of Tolman VII, Equation (66), denoted as
according to Reference [63], the calculation data from Cook et al. [140] and Salgado et al. [141], and the recent data for the nonrotating and maximally rotating configurations both in the cases of and with the corresponding transition densities.
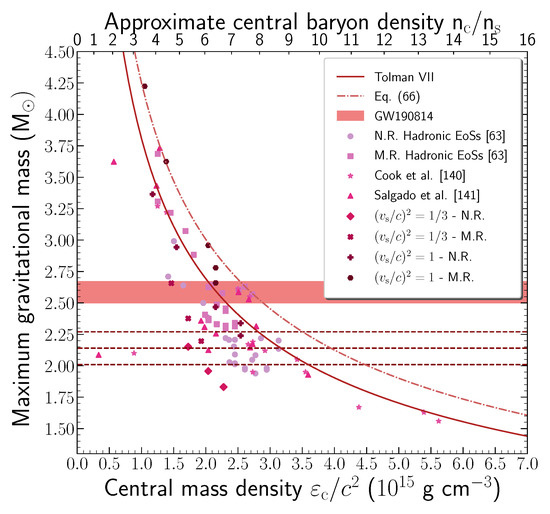
Figure 8.
Dependence of the maximum gravitational mass on the central energy/baryon density both at nonrotating and rapidly rotating with the Kepler frequency configurations. Circles and squares correspond to 23 hadronic EoSs [63] at the nonrotating (N.R.) and maximally-rotating (M.R.) cases, respectively, and stars and triangles correspond to data of Cook et al. [140] and Salgado et al. [141], respectively. Furthermore, diamonds and plus signs note the nonrotating configuration, while crosses and polygons show the maximally-rotating one, in the cases of the two limiting values of the sound speed. The horizontal dashed lines mark the current observed neutron star mass limits ( [16], [17], and [18]). Equation (66) is noted with the dashed-dotted line, while for comparison, the Tolman VII analytical solution [63] is added with the solid line. The horizontal shaded region notes the mass range of the second component of GW190814 event.
In addition, via Equation (66), which is used for the description of the upper bound for the density of cold baryonic matter [63], the central energy density can be constrained in the narrow range . The latter indicates that neutron stars with higher values of central energy density cannot exist. Furthermore, Figure 8 provides us the tools to extract the corresponding region for the central baryon density, which is . It is worth mentioning that the cases in this review meet the limit for the central energy/baryon density as they are included in the region described under Equation (66).
4.3. The Case of a Very Massive Neutron Star
4.3.1. Isolated Non-Rotating Neutron Star
In this study, we extended our previous work in Reference [65] for an isolated nonrotating neutron star by using two transition densities and eight values of speed of sound bounds [66]. The values of transition density were taken to be close to the constraints of Reference [65]. By solving numerically the system of TOV equations, combined with the previous bounds for the speed of sound, we obtained the M-R diagram, displayed in Figure 9a.
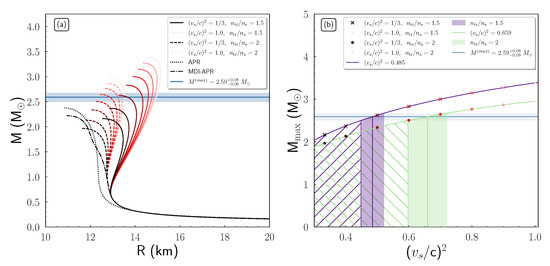
Figure 9.
(a) Mass vs. radius for an isolated nonrotating neutron star, for each transition density and all speed of sound cases. The darker curves’ color corresponds to the lower values of speed of sound. The blue horizontal line and region indicate the mass estimation of the massive compact object of Reference [19]. The dashed-dotted and dotted curves correspond to the MDI-APR and APR EoS, respectively. (b) The maximum mass of a nonrotating neutron star as a relation to the bounds of the speed of sound for each transition density (in units of saturation density ). The purple vertical shaded region corresponds to the case, while the green one corresponds to the case. The purple (green) vertical line indicates the corresponding value of the speed of sound for a massive object with .
At first sight, there are two main branches in Figure 9a related to the transition density. The solid (dashed) curves correspond to the () case. Depending on each value for the bound of the speed of sound, there are bifurcations in the families of EoSs. As we move to higher values for the speed of sound, the color of the curves lightens. The blue solid horizontal line, with the accompanying shaded region, represents the estimation of the recently observed massive compact object of Reference [19]. In general, the branch of EoSs with provides stiffer EoSs compared to the branch. Hence, the EoSs of the case are more likely to provide such a massive nonrotating neutron star than the case in which three EoSs lie outside of the shaded region. Specifically, between the same kind of transition density the EoSs with higher bounds of the speed of sound lead to higher values of neutron star mass and radius. Therefore, a generally high bound of the speed of sound (as the transition density has higher values, the speed of sound would be closer to the causal scenario) is needed for the description of such a massive compact object.
As one can observe in Figure 9a, there is a trend across the maximum masses. In order to study this behavior, we constructed the diagram of Figure 9b. The cross and star marks represent the maximum masses of and cases, respectively. The color of the marks is lighter for higher values of the speed of sound. The blue solid horizontal line, with the accompanying shaded region, indicates the estimation of the recently observed massive compact object of Reference [19]. The purple and green curves represent the following expression for the and cases, respectively, given below
where . The coefficients are given in Table 3.

By applying the formula mentioned above, we were able to obtain estimations of the speed of sound values for each transition density . In particular, for a nonrotating massive neutron star with the speed of sound must be (a) (), and (b) (). The exact values’ interval is given in Table 3. We note that in the case of higher values of transition density , the fitted expression and marks are shifted downwards; i.e., the higher the point of the transition in density, the smaller the provided maximum mass. In addition, as one can see in Figure 9b, the higher values of the speed of sound are better able to predict such massive neutron stars, until a specific boundary value of transition density (higher than those we adopted in our study), in which even the causality could not lead to such a massive neutron star.
Hence, a very massive nonrotating neutron star favors higher values of the speed of sound than the limit. Based on our previous work, the current observation of neutron star mergers leads to a lower bound on the transition density [65]. At this point, a contradiction arises; the transition density must be above a specific lower value but not big enough to predict very massive masses.
In Figure 10, we display the tidal parameters for the single neutron star case that we study as a function of the mass. The vertical blue shaded region and line indicate the mass estimation for the second compact object of Reference [19].
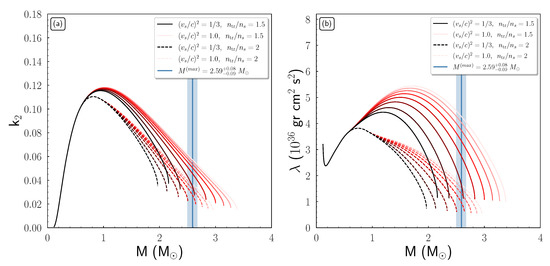
Figure 10.
Tidal parameters (a) and (b) as a function of an neutron star’s mass. The blue vertical line and shaded region indicate the estimation of the recently observed massive compact object of Reference [19]. The solid (dashed) curves correspond to the () case. The lower values of the speed of sound correspond to the darker-colored curves.
One can observe that in both diagrams there are two main families of EoSs, distinguished by the transition density . The EoSs with higher speed of sound bounds lead to bigger values on both tidal parameters. This means that a neutron star with a higher speed of sound value is more deformable than a more compact one (with a lower speed of sound value). Moreover, the EoSs with smaller transition density and higher values are more likely to predict a very massive neutron star of .
We notice that taking into consideration cases with higher transition density could lead to smaller values of tidal parameters, i.e., more compact and less deformable stars. Hence, a very high value of the speed of sound, close to the causality, would be necessary to provide such a massive nonrotating neutron star.
4.3.2. A Very Massive Neutron Star in a Binary Neutron Stars System
Beyond the hypothetical scenario of a single nonrotating neutron star, it is of particular interest to consider the binary case of two neutron stars, with the heavier having a mass of and letting the secondary lighter neutron star fluctuate within the range . By subtracting the component masses in Equation (18), we obtain the corresponding values of . Then, since the masses are defined, from the Equations (19) and (20), the effective tidal deformability can be determined.
In Figure 11a, we display the effective tidal deformability as a function of the chirp mass of the system, for all the possible binary neutron star systems with such a massive neutron star component. We have to underline that from all the EoSs that we studied in the single-neutron star case previously, in the binary case, we used only those that can provide a neutron star with mass. As one can see in Figure 11, there are two families of EoSs, distinguished by the transition density . For each family of EoSs, the EoSs with higher values of the speed of sound predict higher values of . We notice that for a binary system with and , the chirp mass is . Another remark is that binary neutron star systems with both heavy components, meaning higher , lead to smaller values of . In this case, a possible lower limit on might provide useful constraints on the EoS.
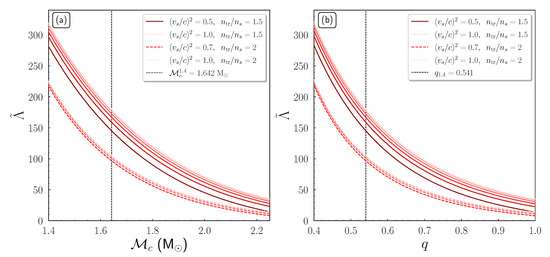
Figure 11.
The effective tidal deformability as a function of (a) the chirp mass and (b) binary mass ratio q, in the case of a very massive neutron star component, identical to Reference [19]. The darker colored curves correspond to lower values of speed of sound. The black dashed vertical line shows (a) the corresponding chirp mass and (b) mass ratio q, of a binary neutron star system with and , respectively.
In Figure 11b, we display the dependence of on the corresponding binary mass ratio q.
We have to underline that this kind of diagram is different from the usual ones (see in comparison Figure 3) because the chirp mass has no specific value. In particular, in this work, the is treated as a variable, and each point of Figure 11b corresponds to a different binary neutron star system with the heavier component in all cases being a very massive neutron star with mass . Similarly to Figure 11a, there are two main families for the curves, and the EoSs with higher speed of sound provide higher values of . The more symmetric binary neutron star systems () lead to smaller values of . On the contrary, the highest values of correspond to the most asymmetric binary neutron star systems. We notice that for a binary system with and , the asymmetry ratio is .
Moreover, we studied the effective tidal deformability and the case of an secondary component neutron star, with the heavier component neutron star taken to be . In Figure 12, we display this dependence. To be more specific, the EoSs are in five main groups, characterized by the transition density . Our study has been expanded to transition densities so that the calculations could be more accurate The higher speed of sound values correspond to lighter color. In analog to the observations of the previous Figure 11, the high speed of sound bounds lead to higher and .
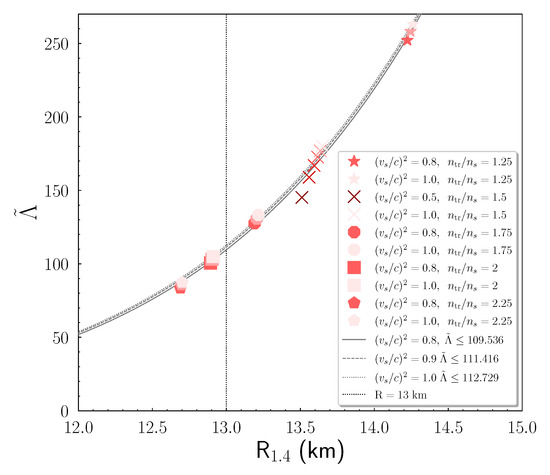
Figure 12.
The effective tidal deformability as a function of the radius of an neutron star. The heavier component of the system was taken to be . The darker colors correspond to lower values of speed of sound bounds. The grey lines show the expression of Equation (68). The black dotted vertical line indicates the proposed upper limit of Reference [132].
In addition, we applied a fitting formula to the cases. The formula was taken to be in the kind of the proposed relations of References [133,134],
where the coefficients for each case are given in Table 4. According to a recent study, a similar power-law relation connects the tidal deformability of a single neutron star to the [142]. The significance of the tidal deformability and in order to obtain information about microscopic quantities was studied in Reference [143]. By imposing an upper limit on , one can obtain an upper limit on . Hence, by adopting the general limit of Reference [132], we obtained the constraints of Table 4.
4.4. Finite Temperature Effects on Rapidly Rotating Neutron Stars
4.4.1. Sequences of Constant Baryon Mass
A way to study the effects of finite temperature on the rapidly rotating remnant after a binary neutron star merger is the sequences of constant baryon mass. The sequences provide us with information about the evolution and instabilities of hot neutron stars. In particular, in the case of the isothermal EoSs, we considered the same baryon mass configuration for the EoSs and constructed a sequence related to the cooling of a hot neutron star [64].
Figure 13a displays the Kepler frequency as a function of the temperature for four baryon masses in the range . Specifically, in the range , the Kepler frequency decreases sharply with the temperature, while for higher temperatures, a smoother behavior is presented. This dependence can be described as
where f and T are in units of Hz and MeV, respectively, and the coefficients with i = 0–3 are given in Table 5.
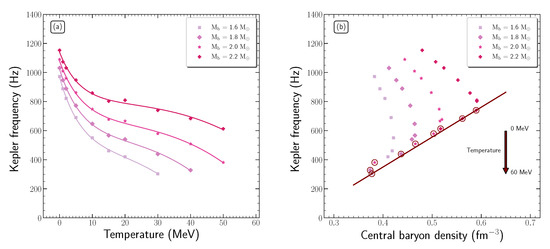
Figure 13.
Dependence of the Kepler frequency on (a) the temperature and (b) the central baryon density for baryon masses in the range . (a) Solid lines represent the fits originated from Equation (69). (b) The solid line represents Equation (70), while open circles note the high-temperature region ().

Table 5.
Coefficients with i = 0–3 for the empirical relation (69) and baryon masses in the range [1.6–2.2] .
This behavior suggests that the effects of temperature are more pronounced in the range , leading to significant lower Kepler frequencies, where for higher temperatures than , the effects are moderated.
Afterwards, in Figure 13b, the dependence of Kepler frequency on the central baryon density is presented, for four baryon masses in the range . While for low values of temperature the central baryon density increases with increasing temperature, for high values of temperature, a reduction in the values of the central baryon density is noted. In addition, for low values of temperature there is the appearance of a linear relation between the Kepler frequency and the central baryon density, assuming always a constant temperature. The significance of Figure 13b is focused on temperatures higher than , where a linear relation described as
with f and given in units of Hz and , respectively, interprets the dependence of the Kepler frequency on the central baryon density independent from the specific baryon mass. Henceforth, Equation (70) defines the allowed region that a neutron star can exist with rotation at its mass-shedding limit for a specific central baryon density and vice versa.
4.4.2. Moment of Inertia, Kerr Parameter, and Ratio
Figure 14 displays the dimensionless moment of inertia as a function of the compactness parameter for neutron stars at the mass-shedding limit in (a) isothermal and (b) isentropic profile. In both cases, the increase of the temperature or the entropy per baryon (assuming a constant lepton fraction) leads to lower values of moment of inertia and lesser compact stars than the cold star. However, for low values of temperature or low values of entropy per baryon with and , the dimensionless moment of inertia and the compactness parameter exceed the values of the cold neutron star.
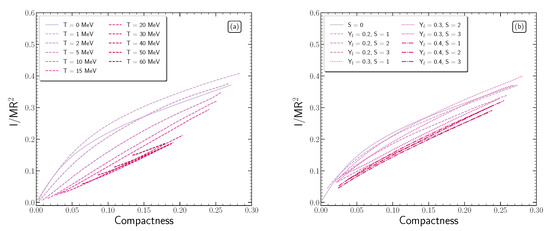
Figure 14.
Dependence of the dimensionless moment of inertia on the compactness parameter at the mass-shedding limit in the case of (a) isothermal and (b) isentropic profiles. Dashed lines note the hot configurations, while the solid line notes the cold configuration.
Afterwards, in Figure 15 we present the Kerr parameter as a function of the gravitational mass for neutron stars at the mass-shedding limit in (a) isothermal and (b) isentropic profile. In addition, we display the constraints for the Kerr parameter of neutron stars with the shaded region [64] and the Kerr bound for astrophysical Kerr black holes [97]. As the temperature or the entropy per baryon increases in the neutron star, the Kerr parameter decreases, except for high values of temperature where a slightly increase is observed. Furthermore, Figure 15c displays the Kerr parameter as a function of the temperature for constant gravitational mass in the isothermal profile. After , it is observed that the Kerr parameter creates a plate, meaning that the increase in temperature does not affect the Kerr parameter.
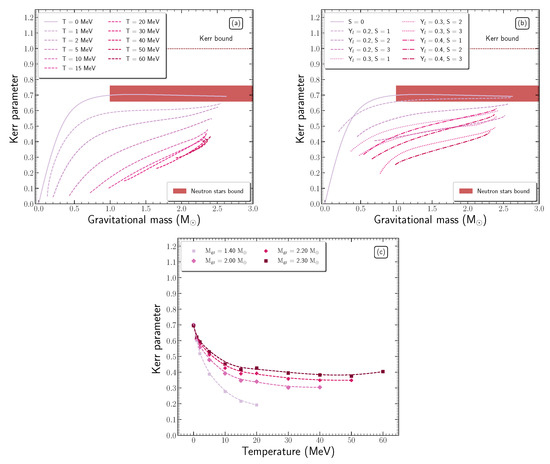
Figure 15.
Dependence of the Kerr parameter on the gravitational mass at the mass-shedding limit in the case of (a) isothermal and (b) isentropic profiles. Dashed lines note the hot configurations, while the solid line notes the cold configuration. The horizontal dotted line corresponds to the Kerr bound for astrophysical Kerr black holes, [144], while the shaded region corresponds to the neutron star limits from Reference [64]. (c) Dependence of the Kerr parameter on the temperature for gravitational masses in the range and in the case of isothermal profile.
The introduction of temperature in neutron stars cannot violate the proposed limit for Kerr black holes [97] and the one from cold neutron stars [64]. Therefore, the gravitational collapse of a hot and uniformly rotating neutron star, constrained to mass–energy and angular momentum conservation, cannot lead to a maximally rotating Kerr black hole.
In addition, it is worth mentioning that, while in the cold neutron star, for , the Kerr parameter is almost independent of the gravitational mass, in hot configurations, Kerr parameter is an increasing function of the gravitational mass. The latter leads to the conclusion that while the interplay between the angular momentum and the gravitational mass in cold neutron stars is imperceptible, that is not the case in hot neutron stars, where a significant dependence is suggested.
Finally, Figure 16 displays the angular velocity as a function of the ratio of kinetic to gravitational binding energy for neutron stars at the mass-shedding limit in (a) isothermal and (b) isentropic profile. Gravitational waves can be produced from neutron stars through the nonaxisymmetric perturbations. The vertical dotted line notes the limit for nonaxisymmetric instabilities from gravitational radiation, located at for models with [145]. The introduction of temperature leads to the conclusion that nonaxisymmetric instabilities cannot exist in hot neutron stars. However, for cases with low values of temperature ( and with ), the nonaxisymmetric instability would set in before the mass-shedding limit is reached. The latter indicates that both the maximum gravitational mass and the angular velocity will be lowered.
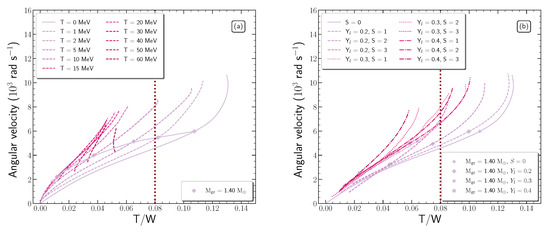
Figure 16.
Dependence of the angular velocity on the ratio of rotational kinetic to gravitational binding energy at the mass-shedding limit in the case of (a) isothermal and (b) isentropic profiles. Dashed lines note the hot configurations, while the solid line notes the cold configuration. Markers correspond to the configuration. The vertical dotted line notes the critical value, , for gravitational radiation instabilities.
The aftermath from the analysis on the compactness parameter, Kerr parameter, and ratio is the insight for the hot and rapidly rotating remnant after a neutron star merger. Actually, the remaining object is a compact object consisting of neutron star matter. By assuming a remnant with at least for isothermal neutron stars and with for isentropic ones, rotating at its mass-shedding limit, possible constraints are available through the mentioned quantities. In particular,
- compactness parameter: and ,
- Kerr parameter: and ,
- ratio : and ,
where the superscripts “iso” and “ise” correspond to isothermal and isentropic profiles [for more details see Reference [64]. Specifically, in the case that the remnant follows the isothermal profile, the remaining object is a lesser compact object than the cold neutron star, with lower values of maximum gravitational mass and frequency, and stable toward the dynamical instabilities. In the case that the remnant follows the isentropic profile, the remaining object is comparable to the cold neutron star.
5. Concluding Remarks
In this review we have presented a suitable EoS parameterized to reproduce specific values of the speed of sound and gravitational mass of neutron stars. In addition, we introduced the effects of finite temperature both in isolated neutron stars and in matters of merging. In particular, we have constructed equilibrium sequences of both nonrotating and rapidly rotating with the Kepler frequency neutron stars and paid special attention to the gravitational and baryon mass, the radius, the transition baryon density, the Kerr parameter, the moment of inertia, the ratio , and the tidal deformability. This study is applied in several gravitational wave events, GW170817, GW190425, and GW190814, and possible constraints for the EoS are extracted.
Firstly, we studied the EoS and especially imposed constraints on the speed of sound (which affects the stiffness of the EoS) and the transition density by using recent observations of two binary neutron stars mergers (GW170817 and GW190425 events). The implemented method that we developed was based on the upper limits of the effective tidal deformability (derived from the mentioned events), combined with measurements of the maximum neutron star mass. As a base in our study, we used the MDI-APR EoS, for two cases of speed of sound bounds [63,74]; the conformal case and the causal one of .
The treatment of the effective tidal deformability as a function of the transition density allowed us to extract constraints on the bounds of the speed of sound. Specifically, for the GW170817 event, we found that the speed of sound must be lower than the value , at least up to densities , and lower than up to densities . For the GW190425 event, the respective values are for the lower speed of sound bound and for the upper one. These constraints are less rigorous than those derived from the GW170817 event.
Moreover, we studied the effective tidal deformability as a function of the maximum mass for both cases of speed of sound bounds. For the GW170817, we obtained that the maximum mass should be for the bound and for the upper bound . We notice that the limit of corresponds to a transition density equal to . Hence, according to this finding, the conformal limit is in contradiction with the observational estimations of the of neutron stars. Therefore, it must be violated in order to be able to simultaneously describe small values of the effective tidal deformability and high values for neutron star mass. The reason for this contradiction is based on two different points of view that antagonize one another: the upper limit on favors softer EoSs (higher values of ), while the maximum mass observations require stiffer EoSs (smaller values of ). For higher values of the speed of sound, this contradiction becomes less severe (i.e., for the case ). We notice that the GW190425 was not able to offer further information.
Furthermore, from the study of the effective tidal deformability and the radius of a neutron star, we observed that all the EoSs follow a common trend. This trend is affected mainly by the chirp mass of the binary system. To be more specific, as the chirp mass reaches higher values, the trend moves downwards. From the event GW170817 we obtained an upper limit for both cases, which is consistent with other estimations. The event GW190425 provided an upper limit for the bound and for the bound.
We postulate that the discovery of future events of binary neutron stars mergers will provide rich information and further constraints on the bound of the speed of sound. In particular, the detection of future events could lead to more stringent constraints on the upper limit of and therefore more rigorous constraints on and bounds of the sound speed. Based on our approach, the more useful events for the lower limit of would be those with lighter component masses. Moreover, it would be of great interest to probe the lower limit of . Such a lower limit might lead to an upper value of the transition density . We make the assumption that heavier neutron star mergers would be suitable in the direction of a possible upper limit on . In any case, further detection of neutron stars mergers will assist in these open problems.
The baryon mass of the postmerger remnant is considered approximately conserved, a feature that gives rise to the significance of the temperature. In particular, in the case of hot neutron stars, the baryon mass is lower than the cold ones. As remnants are considered rapidly rotating, we study them at the mass-shedding limit. Specifically, in the cold case, the baryon mass is , while for a hot one at is and for one at is . By considering that the merger components have approximately equal masses, the above limits correspond to merger components with ∼1.5425, ∼1.2135, and ∼1.525 baryon masses, respectively. Furthermore, the immediate aftermaths of GW170817 [13] and GW190425 [14] events created hot and rapidly rotating remnants probably at the mass-shedding limit. In the case of GW170817 event, the remnant with ∼2.7 can be supported under the uniform rotation of cold and isentropic neutron stars with respect to the baryon mass of MDI+APR1 EoS. In contrast, isothermal neutron stars cannot support these values of mass. As far as the GW190425 event, the assumption of uniform rotation cannot be used to interpret the remnant of ∼3.7 . It has to be noted that the postmeger remnant is assumed to rotate differentially. However, uniform rotation is a valid candidate to provide us with useful information about neutron stars.
In the GW190814 event [19], a compact object with a mass of ∼2.6 was observed as a merger component. It is believed to be either the lightest black hole or the most massive neutron star [139]. Nonetheless, Most et al. [139] suggest that the compact object could be a neutron star rapidly spinning with in the range . In this case, the relevant postulation is in accordance with this study. More specifically, the values of the gravitational mass and Kerr parameter coincide with the ones from the MDI+APR1 EoS in both cold catalyzed matter and isentropic matter with and . Following the latter conclusion, there is a possibility that the observed star was rotating close to or at its mass-shedding limit and provide us additional constraints on the high density region of the nuclear EoS. In addition, possible constraints can be extracted for the corresponding equatorial radius. The Kerr parameter at the mass-shedding limit of the MDI+APR1 EoS lies in the region of . This region also includes the upper limit of the relevant region from Reference [139] in a narrow range. Furthermore, by exploiting the relation between the Kerr parameter and the compactness parameter, a possible tight region for the equatorial radius of the star is implied as .
The Kerr parameter also has the role of an indicator of the collapse to a black hole. In hot neutron stars, the Kerr parameter decreases as the temperature inside the neutron star increases and never exceeds that of the cold neutron star. In conclusion, thermal support cannot lead a rapidly rotating star to collapse into a maximally rotating Kerr black hole. In addition, after ∼1 , while the Kerr parameter is almost constant for the cold neutron stars, for hot neutron stars, the Kerr parameter is increasing with respect to the gravitational mass. The latter leads to a specific maximum value.
The ratio is explicitly linked to the gravitational collapse to a black hole and the existence of stable supramassive neutron stars. We consider in the present study only the first scenario. Instabilities originating from the gravitational radiation, in which the critical value is at for the configuration [145], do not exist for hot neutron stars. Nonetheless, for low values of temperatures, as the ratio exceeds the critical value, this limit sets the upper value for the maximum gravitational mass and angular velocity. It has to be noted that studies concerning the Kerr parameter as well as the ratio and the corresponding effect of the temperature are very rare. The existence of the latter studies may open a new window in neutron star studies.
A way to manifest the significance of the thermal support in neutron stars is the evolutionary sequences of constant baryon mass. In this configuration, the dependence of the Kepler frequency on the central baryon density presents a linear relation for temperatures higher than . The existence of such a relation, independent of the baryon mass, can define the allowed region of the pair of the central baryon density and corresponding Kepler frequency for a rotating hot neutron star at its mass-shedding limit.
Central baryon/energy density can also be of great interest in cold neutron stars, as it is connected with the evolution of the neutron star and the possible appearance of a phase transition. The end point from our study is that the central energy density must be lower than the values in the range , while for the central baryon density, the corresponding range is . The latter can inform us about the stability of the neutron star, as a neutron star with higher values of central energy/baryon density cannot exist, as well as can the appearance of the back-bending process.
Moreover, we examined the hypothetical scenario of a very massive neutron star with mass equal to ∼, such as the secondary component of the GW190814 system [19]. The study of the maximum mass of each EoS as a function of the speed of sound bounds (for each value of transition density ), provide us constraints in the speed of sound. To be more specific, the case leads to , while the case leads to . We postulate that as the transition density is getting higher values, it is more difficult to achieve such a massive nonrotating neutron star. In particular, above a specific high-transition-density value, the speed of sound should be close to the causality to provide such a massive neutron star.
By studying the tidal parameters for the single case, we observed that the lower transition densities lead to higher tidal parameters. Hence, the transition density corresponds to a more compact neutron star (less deformation). Furthermore, between the same kind of transition density , the EoSs with higher bounds on the speed of sound predict higher tidal parameters. Therefore, for the same transition density, the higher speed of sound bound means that the neutron star is less compact (more deformation).
Moving on to the binary neutron star system case, we adopted the hypothesis of a very massive component with , allowing us to investigate a variety of hypothetical binary neutron star systems with such a heavy component neutron star. In the case of heavy components of binary neutron star systems, meaning high value for the system’s chirp mass , the effective tidal deformability has smaller values (smaller deformation). This behavior was noticed also in the diagram, in which the increasing binary mass symmetric ratio q leads to smaller values of . For a binary neutron system with the heavier component equal to and the lighter one equal to , the chirp mass and the ratio q were estimated to be and , respectively.
Lastly, we studied the case of a binary neutron star system with with a secondary component . We especially concentrated on the radius . A general remark is that the transition density provides higher values of and than the case. We extended our study to further transition densities , which confirmed this general behavior. Additionally, the higher bounds of the speed of sound provide higher values on both parameters. By imposing an upper limit on the radius, we extracted some upper limits on the for each value of the speed of sound. In particular, this upper limit on shifts to higher values as the bound of the speed of sound increases.
This hypothetical scenario of a very massive neutron star demonstrated the key role of a microscopic quantity of the EoS, the speed of sound, which dramatically affects the EoS in combination with the changes in the transition density. We notice that the existence of such a massive nonrotating neutron star would mean a significant difference from all the cases known so far, which is a challenge for physics.
The underlying physics of neutron star mergers and the hot, rapidly rotating remnant should be investigated by considering differential rotation and cooling mechanisms, as these are the main features in the early postmerger phase. In addition, special emphasis should be given in the phase transition region, the existence of exotic degrees of freedom in the interior of neutron stars, as well as the accurate measurement of the tidal deformability. Finally, the observation of binary neutron star mergers and black-hole–neutron-star mergers, combined with the above studies, may provide significant constraints for the construction of the EoS.
Author Contributions
Conceptualization, P.S.K., A.K.-P. and C.C.M.; Methodology, P.S.K. and A.K.-P.; Software, P.S.K. and A.K.-P.; Validation, P.S.K., A.K.-P. and C.C.M.; Formal Analysis, P.S.K. and A.K.-P.; Investigation, P.S.K., A.K.-P. and C.C.M.; Data Curation, P.S.K. and A.K.-P.; Writing—Original Draft Preparation, P.S.K., A.K.-P. and C.C.M.; Writing—Review and Editing, P.S.K., A.K.-P. and C.C.M.; Visualization, P.S.K., A.K.-P. and C.C.M.; Supervision, C.C.M. All authors contributed equally to this work. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors would like to thank K. Kokkotas for their constructive comments and insight during the preparation of the manuscript and also L. Rezzolla for useful correspondence and clarifications. The authors also thank B. Farr and Chatziioannou for their assistance providing computational tools regarding the kernel density estimation of the sample data and D. Radice, N. Stergioulas, and N. Minkov for the useful correspondence. We also acknowledge P. Meszaros and A. Sedrakian for their useful comments regarding the hot equations of state. In addition, the authors wish to thank the Bulgarian Academy of Science and the organizers of the International Workshop “Shapes and Dynamics of Atomic Nuclei: Contemporary Aspects” (SDANCA-21) for the their hospitality while this was completed. We would like to thank the financial support of the Bulgarian National Science Fund under contracts No. KP-06-N48/1 and No. KP-06-N28/6.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| EoS | Equation of state |
| MDI | Momentum dependent interaction |
| APR | Akmal, Pandharipande, and Ravenhall |
| SNM | Symmetric nuclear matter |
| ANM | Asymmetric nuclear matter |
| PNM | Pure neutron matter |
| NM | Nuclear model |
| TOV | Tolman-Oppenheimer-Volkoff |
| N.R. | Non-rotating configuration |
| M.R. | Maximally-rotating configuration |
References
- Shapiro, S.; Teukolsky, S. Black Holes, White Dwarfs, and Neutron Stars; John Wiley and Sons: New York, NY, USA, 1983. [Google Scholar]
- Glendenning, N. Compact Stars: Nuclear Physics, Particle Physics, and General Relativity; Springer: Berlin, Germany, 2000. [Google Scholar]
- Haensel, P.; Potekhin, A.; Yakovlev, D. Neutron Stars 1: Equation of State and Structure; Springer: New York, NY, USA, 2007. [Google Scholar]
- Weinberg, S. Gravitational and Cosmology: Principle and Applications of the General Theory of Relativity; Wiley: New York, NY, USA, 1972. [Google Scholar]
- Zel’dovich, Y.B. The equation of state at ultrahigh densities and its relativistic limitations. Sov. Phys. JETP 1962, 14, 1143–1147. [Google Scholar]
- Zel’dovich, Y.; Novikov, I. Stars and Relativity; Dover Publications, Inc.: Mineapolis, MN, USA; New York, NY, USA, 1971. [Google Scholar]
- Hartle, J.B. Bounds on the mass and moment of inertia of non-rotating neutron stars. Phys. Rep. 1978, 46, 201–247. [Google Scholar] [CrossRef]
- Bedaque, P.; Steiner, A.W. Sound Velocity Bound and Neutron Stars. Phys. Rev. Lett. 2015, 114, 031103. [Google Scholar] [CrossRef]
- Moustakidis, C.C.; Gaitanos, T.; Margaritis, C.; Lalazissis, G.A. Bounds on the speed of sound in dense matter, and neutron star structure. Phys. Rev. C 2017, 95, 045801. [Google Scholar] [CrossRef]
- Reed, B.; Horowitz, C.J. Large sound speed in dense matter and the deformability of neutron stars. Phys. Rev. C 2020, 101, 045803. [Google Scholar] [CrossRef]
- Van Oeveren, E.D.; Friedman, J.L. Upper limit set by causality on the tidal deformability of a neutron star. Phys. Rev. D 2017, 95, 083014. [Google Scholar] [CrossRef]
- Ma, Y.L.; Rho, M. Sound velocity and tidal deformability in compact stars. Phys. Rev. D 2019, 100, 114003. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; et al. GW190425: Observation of a Compact Binary Coalescence with Total Mass ∼ 3.4 M ⊙. Astrophys. J. 2020, 892, L3. [Google Scholar] [CrossRef]
- Arzoumanian, Z.; Brazier, A.; Burke-Spolaor, S.; Chamberlin, S.; Chatterjee, S.; Christy, B.; Cordes, J.M.; Cornish, N.J.; Crawford, F.; Cromartie, H.T.; et al. The NANOGrav 11-year Data Set: High-precision Timing of 45 Millisecond Pulsars. Astrophys. J. Suppl. Ser. 2018, 235, 37. [Google Scholar] [CrossRef]
- Antoniadis, J.; Freire, P.; Wex, N.; Tauris, T.; Lynch, R.; van Kerkwijk, M.H.; Kramer, M.; Bassa, C.; Dhillon, V.S.; Driebe, T.; et al. A massive pulsar in a compact relativistic binary. Science 2013, 340. [Google Scholar] [CrossRef]
- Cromartie, H.; Fonseca, E.; Ransom, S.; Demorest, P.B.; Arzoumanian, Z.; Blumer, H.; Brook, P.R.; DeCesar, M.E.; Dolch, T.; Ellis, J.A.; et al. Relativistic Shapiro delay measurements of an extremely massive millisecond pulsar. Nat. Astron. 2020, 4, 72–76. [Google Scholar] [CrossRef]
- Linares, M.; Shahbaz, T.; Casares, J. Peering into the Dark Side: Magnesium Lines Establish a Massive Neutron Star in PSR J2215+5135. Astrophys. J. 2018, 859, 54. [Google Scholar] [CrossRef]
- Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; Agathos, M.; et al. GW190814: Gravitational Waves from the Coalescence of a 23 Solar Mass Black Hole with a 2.6 Solar Mass Compact Object. Astrophys. J. 2020, 896, L44. [Google Scholar] [CrossRef]
- Tan, H.; Noronha-Hostler, J.; Yunes, N. Neutron Star Equation of State in Light of GW190814. Phys. Rev. Lett. 2020, 125, 261104. [Google Scholar] [CrossRef]
- Datta, S.; Phukon, K.S.; Bose, S. Recognizing black holes in gravitational-wave observations: Challenges in telling apart impostors in mass-gap binaries. arXiv 2021, arXiv:gr-qc/2004.05974. [Google Scholar]
- Alsing, J.; Silva, O.H.; Berti, E. Evidence for a maximum mass cut-off in the neutron star mass distribution and constraints on the equation of state. Mon. Not. R. Astron. Soc. 2018, 478, 1377. [Google Scholar] [CrossRef]
- Farr, W.M.; Chatziioannou, K. A Population-Informed Mass Estimate for Pulsar J0740+6620. Res. Not. Am. Astron. Soc. 2020, 4, 65. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170817: Measurements of Neutron Star Radii and Equation of State. Phys. Rev. Lett. 2018, 121, 161101. [Google Scholar] [CrossRef]
- Bethe, H.; Brown, G.; Applegate, J.; Lattimer, J. Equation of state in the gravitational collapse of stars. Nucl. Phys. A 1979, 324, 487–533. [Google Scholar] [CrossRef]
- Brown, G.; Bethe, H.; Baym, G. Supernova theory. Nucl. Phys. A 1982, 375, 481–532. [Google Scholar] [CrossRef]
- Lamb, D.Q.; Lattimer, J.M.; Pethick, C.J.; Ravenhall, D.G. Hot Dense Matter and Stellar Collapse. Phys. Rev. Lett. 1978, 41, 1623–1626. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Ravenhall, D.G. Neutron star matter at high temperatures and densities. I. Bulk properties of nuclear matter. Astrophys. J. 1978, 223, 314–323. [Google Scholar] [CrossRef]
- Lattimer, J.M. The Equation of State of Hot Dense Matter and Supernovae. Ann. Rev. Nucl. Part. Sci. 1981, 31, 337–374. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Swesty, F.D. A generalized equation of state for hot, dense matter. Nucl. Phys. A 1991, 535, 331–376. [Google Scholar] [CrossRef]
- Shen, H.; Toki, H.; Oyamatsu, K.; Sumiyoshi, K. Relativistic equation of state of nuclear matter for supernova and neutron star. Nucl. Phys. A 1998, 637, 435–450. [Google Scholar] [CrossRef]
- Shen, G.; Horowitz, C.J.; O’Connor, E. Second relativistic mean field and virial equation of state for astrophysical simulations. Phys. Rev. C 2011, 83, 065808. [Google Scholar] [CrossRef]
- Wellenhofer, C.; Holt, J.W.; Kaiser, N. Thermodynamics of isospin-asymmetric nuclear matter from chiral effective field theory. Phys. Rev. C 2015, 92, 015801. [Google Scholar] [CrossRef]
- Constantinou, C.; Muccioli, B.; Prakash, M.; Lattimer, J.M. Thermal properties of supernova matter: The bulk homogeneous phase. Phys. Rev. C 2014, 89, 065802. [Google Scholar] [CrossRef]
- Constantinou, C.; Muccioli, B.; Prakash, M.; Lattimer, J.M. Thermal properties of hot and dense matter with finite range interactions. Phys. Rev. C 2015, 92, 025801. [Google Scholar] [CrossRef]
- Sammarruca, F.; Machleidt, R.; Millerson, R. Temperature effects on the neutron matter equation of state obtained from chiral effective field theory. Mod. Phys. Lett. A 2020, 35, 2050156. [Google Scholar] [CrossRef]
- Nicotra, O.E.; Baldo, M.; Burgio, G.F.; Schulze, H.-J. Protoneutron stars within the Brueckner-Bethe-Goldstone theory. Astrophys. J. 2006, 451, 213–222. [Google Scholar] [CrossRef]
- Burgio, G.F.; Schulze, H.-J. The maximum and minimum mass of protoneutron stars in the Brueckner theory. Astron. Astrophys. 2010, 518, A17. [Google Scholar] [CrossRef]
- Baldo, M.; Burgio, G. The nuclear symmetry energy. Prog. Part. Nucl. Phys. 2016, 91, 203–258. [Google Scholar] [CrossRef]
- Fortin, M.; Taranto, G.; Burgio, G.F.; Haensel, P.; Schulze, H.J.; Zdunik, J.L. Thermal states of neutron stars with a consistent model of interior. Mon. Not. R. Astron. Soc. 2018, 475, 5010–5022. Available online: https://academic.oup.com/mnras/article-pdf/475/4/5010/24056722/sty147.pdf (accessed on 24 September 2021). [CrossRef]
- Lu, J.J.; Li, Z.H.; Burgio, G.F.; Figura, A.; Schulze, H.J. Hot neutron stars with microscopic equations of state. Phys. Rev. C 2019, 100, 054335. [Google Scholar] [CrossRef]
- Li, F.; Lu, J.J.; Li, Z.H.; Chen, C.Y.; Burgio, G.F.; Schulze, H.J. Accurate nuclear symmetry energy at finite temperature within a Brueckner-Hartree-Fock approach. Phys. Rev. C 2021, 103, 024307. [Google Scholar] [CrossRef]
- Figura, A.; Lu, J.J.; Burgio, G.F.; Li, Z.H.; Schulze, H.J. Hybrid equation of state approach in binary neutron-star merger simulations. Phys. Rev. D 2020, 102, 043006. [Google Scholar] [CrossRef]
- Shang, X.L.; Li, A.; Miao, Z.Q.; Burgio, G.F.; Schulze, H.J. Nucleon effective mass in hot dense matter. Phys. Rev. C 2020, 101, 065801. [Google Scholar] [CrossRef]
- Wei, J.B.; Burgio, G.F.; Schulze, H.J.; Zappalà, D. Cooling of hybrid neutron stars with microscopic equations of state. Mon. Not. R. Astron. Soc. 2020, 498, 344–354. Available online: https://academic.oup.com/mnras/article-pdf/498/1/344/33710758/staa1879.pdf (accessed on 24 September 2021). [CrossRef]
- Raithel, C.A.; Özel, F.; Psaltis, D. Finite-temperature Extension for Cold Neutron Star Equations of State. Astrophys. J. 2019, 875, 12. [Google Scholar] [CrossRef]
- Pons, J.A.; Reddy, S.; Prakash, M.; Lattimer, J.M.; Miralles, J.A. Evolution of Proto–Neutron Stars. Astrophys. J. 1999, 513, 780–804. [Google Scholar] [CrossRef]
- Prakash, M.; Lattimer, J.; Pons, J.; Steiner, A.; Reddy, S. Evolution of a Neutron Star From its Birth to Old Age. Lect. Not. Phys. 2001, 578, 364–423. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Prakash, M. The equation of state of hot, dense matter and neutron stars. Phys. Rep. 2016, 621, 127–164. [Google Scholar] [CrossRef]
- Perego, A.; Bernouzzi, S.; Radie, D. Thermodynamics conditions of matter in neutron star mergers. Eur. Phys. J. A 2019, 55, 124. [Google Scholar] [CrossRef]
- Bauswein, A.; Janka, H.T.; Oechslin, R. Testing approximations of thermal effects in neutron star merger simulations. Phys. Rev. D 2010, 82, 084043. [Google Scholar] [CrossRef]
- Kaplan, J.D.; Ott, C.D.; O’Connor, E.P.; Kiuchi, K.; Roberts, L.; Duez, M. The Influence of Thermal Pressure on Equilibrium Models of Hypermassive Neutron Star Merger Remnants. Astrophys. J. 2014, 790, 19. [Google Scholar] [CrossRef]
- Tsokaros, A.; Ruiz, M.; Shapiro, S.L.; Sun, L.; Uryū, K.b.o. Great Impostors: Extremely Compact, Merging Binary Neutron Stars in the Mass Gap Posing as Binary Black Holes. Phys. Rev. Lett. 2020, 124, 071101. [Google Scholar] [CrossRef]
- Yasin, H.; Schäfer, S.; Arcones, A.; Schwenk, A. Equation of State Effects in Core-Collapse Supernovae. Phys. Rev. Lett. 2020, 124, 092701. [Google Scholar] [CrossRef]
- Radice, D.; Bernuzzi, S.; Perego, A. The Dynamics of Binary Neutron Star Mergers and GW170817. Ann. Rev. Nucl. Part. Sci. 2020, 70, 95–119. [Google Scholar] [CrossRef]
- Sarin, N.; Lasky, P.D.; Ashton, G. Gravitational waves or deconfined quarks: What causes the premature collapse of neutron stars born in short gamma-ray bursts? Phys. Rev. D 2020, 101, 063021. [Google Scholar] [CrossRef]
- Soma, S.; Bandyopadhyay, D. Properties of Binary Components and Remnant in GW170817 Using Equations of State in Finite Temperature Field Theory Models. Astrophys. J. 2020, 890, 139. [Google Scholar] [CrossRef]
- Sen, D. Nuclear matter at finite temperature and static properties of proto-neutron star. J. Phys. G 2020, 48, 025201. [Google Scholar] [CrossRef]
- Gale, C.; Bertsch, G.; Das Gupta, S. Heavy-ion collision theory with momentum-dependent interactions. Phys. Rev. C 1987, 35, 1666–1671. [Google Scholar] [CrossRef]
- Prakash, M.; Bombaci, I.; Prakash, M.; Ellis, P.J.; Lattimer, J.M.; Knorren, R. Composition and structure of protoneutron stars. Phys. Rep. 1997, 280, 1–77. [Google Scholar] [CrossRef]
- Li, B.A.; Schröder, W.U. Isospin Physics in Heavy-Ion Collisions at Intermediate Energies; Nova Science: New York, NY, USA, 2001. [Google Scholar]
- Li, B.A.; Chen, L.W.; Ko, C.M. Recent progress and new challenges in isospin physics with heavy-ion reactions. Phys. Rep. 2008, 464, 113–281. [Google Scholar] [CrossRef]
- Koliogiannis, P.S.; Moustakidis, C.C. Effects of the equation of state on the bulk properties of maximally rotating neutron stars. Phys. Rev. C 2020, 101, 015805. [Google Scholar] [CrossRef]
- Koliogiannis, P.S.; Moustakidis, C.C. Thermodynamical Description of Hot, Rapidly Rotating Neutron Stars, Protoneutron Stars, and Neutron Star Merger Remnants. Astrophys. J. 2021, 912, 69. [Google Scholar] [CrossRef]
- Kanakis-Pegios, A.; Koliogiannis, P.S.; Moustakidis, C.C. Speed of sound constraints from tidal deformability of neutron stars. Phys. Rev. C 2020, 102, 055801. [Google Scholar] [CrossRef]
- Kanakis-Pegios, A.; Koliogiannis, P.S.; Moustakidis, C.C. Probing the Nuclear Equation of State from the Existence of a ∼2.6 M⊙ Neutron Star: The GW190814 Puzzle. Symmetry 2021, 13, 183. [Google Scholar] [CrossRef]
- Sieniawska, M.; Bejger, M. Continuous Gravitational Waves from Neutron Stars: Current Status and Prospects. Universe 2019, 5, 217. [Google Scholar] [CrossRef]
- Glampedakis, K.; Gualtieri, L. Gravitational Waves from Single Neutron Stars: An Advanced Detector Era Survey. In The Physics and Astrophysics of Neutron Stars; Rezzolla, L., Pizzochero, P., Jones, D.I., Rea, N., Vidaña, I., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 673–736. [Google Scholar] [CrossRef]
- Andersson, N.; Kokkotas, K.D. The r-mode instability in rotating neutron stars. Int. J. Mod. Phys. D 2001, 10, 381–441. [Google Scholar] [CrossRef]
- Özel, F.; Freire, P. Masses, Radii, and the Equation of State of Neutron Stars. Annu. Rev. Astron. Astrophys. 2016, 54, 401–440. [Google Scholar] [CrossRef]
- Chatziioannou, K. Neutron-star tidal deformability and equation-of-state constraints. Gen. Relativ. Gravit. 2020, 52, 109. [Google Scholar] [CrossRef]
- Moustakidis, C.C. Effects of the nuclear equation of state on the r-mode instability and evolution of neutron stars. Phys. Rev. C 2015, 91, 035804. [Google Scholar] [CrossRef]
- Akmal, A.; Pandharipande, V.R.; Ravenhall, D.G. Equation of state of nucleon matter and neutron star structure. Phys. Rev. C 1998, 58, 1804–1828. [Google Scholar] [CrossRef]
- Margaritis, C.; Koliogiannis, P.S.; Moustakidis, C.C. Speed of sound constraints on maximally rotating neutron stars. Phys. Rev. D 2020, 101, 043023. [Google Scholar] [CrossRef]
- Rhoades, C.E.; Ruffini, R. Maximum Mass of a Neutron Star. Phys. Rev. Lett. 1974, 32, 324–327. [Google Scholar] [CrossRef]
- Kalogera, V.; Baym, G. The maximum mass of a neutron star. Astrophys. J. 1996, 470, L61. [Google Scholar] [CrossRef]
- Koranda, S.; Stergioulas, N.; Friedman, J.L. Upper Limits Set by Causality on the Rotation and Mass of Uniformly Rotating Relativistic Stars. Astrophys. J. 1997, 488, 799. [Google Scholar] [CrossRef]
- Chamel, N.; Haensel, P.; Zdunik, J.; Fantina, A. On the Maximum Mass of Neutron Stars. Int. J. Mod. Phys. E 2013, 22, 1330018. [Google Scholar] [CrossRef]
- Podkowka, D.M.; Mendes, R.F.P.; Poisson, E. Trace of the energy-momentum tensor and macroscopic properties of neutron stars. Phys. Rev. D 2018, 98, 064057. [Google Scholar] [CrossRef]
- Xia, C.; Zhu, Z.; Zhou, X.; Li, A. Sound velocity in dense stellar matter with strangeness and compact stars. Chin. Phys. C 2021, 45, 055104. [Google Scholar] [CrossRef]
- Tews, I.; Carlson, J.; Gandolfi, S.; Reddy, S. Constraining the Speed of Sound inside Neutron Stars with Chiral Effective Field Theory Interactions and Observations. Astrophys. J. 2018, 860, 149. [Google Scholar] [CrossRef]
- Feynman, R.; Metropolis, N.; Teller, E. Equations of State of Elements Based on the Generalized Fermi-Thomas Theory. Phys. Rev. 1949, 75, 1561. [Google Scholar] [CrossRef]
- Baym, G.; Pethik, C.; Sutherland, P. The Ground State of Matter at High Densities: Equation of State and Stellar Models. Astrophys. J. 1971, 170, 299. [Google Scholar] [CrossRef]
- Moustakidis, C.C. The stability of relativistic stars and the role of the adiabatic index. Gen. Rel. Grav. 2017, 49, 68. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Prakash, M. Neutron Star Structure and the Equation of State. Astrophys. J. 2001, 550, 426–442. [Google Scholar] [CrossRef]
- Postnikov, S.; Prakash, M.; Lattimer, J.M. Tidal Love numbers of neutron and self-bound quark stars. Phys. Rev. D 2010, 82, 024016. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Prakash, M. Ultimate Energy Density of Observable Cold Baryonic Matter. Phys. Rev. Lett. 2005, 94, 111101. [Google Scholar] [CrossRef] [PubMed]
- Lattimer, J.M.; Prakash, M. Nuclear matter and its role in supernovae, neutron stars and compact object binary mergers. Phys. Rep. 2000, 333–334, 121–146. [Google Scholar] [CrossRef]
- Baiotti, L. Gravitational waves from neutron star mergers and their relation to the nuclear equation of state. Prog. Part. Nucl. Phys. 2019, 109, 103714. [Google Scholar] [CrossRef]
- Flanagan, E.E.; Hinderer, T. Constraining neutron-star tidal Love numbers with gravitational-wave detectors. Phys. Rev. D 2008, 77, 021502. [Google Scholar] [CrossRef]
- Hinderer, T. Tidal Love Numbers of Neutron Stars. Astrophys. J. 2008, 677, 1216–1220. [Google Scholar] [CrossRef]
- Damour, T.; Nagar, A. Relativistic tidal properties of neutron stars. Phys. Rev. D 2009, 80, 084035. [Google Scholar] [CrossRef]
- Hinderer, T.; Lackey, B.D.; Lang, R.N.; Read, J.S. Tidal deformability of neutron stars with realistic equations of state and their gravitational wave signatures in binary inspiral. Phys. Rev. D 2010, 81, 123016. [Google Scholar] [CrossRef]
- Fattoyev, F.J.; Carvajal, J.; Newton, W.G.; Li, B.A. Constraining the high-density behavior of the nuclear symmetry energy with the tidal polarizability of neutron stars. Phys. Rev. C 2013, 87, 015806. [Google Scholar] [CrossRef]
- Lackey, B.D.; Wade, L. Reconstructing the neutron-star equation of state with gravitational-wave detectors from a realistic population of inspiralling binary neutron stars. Phys. Rev. D 2015, 91, 043002. [Google Scholar] [CrossRef]
- Takátsy, J.; Kovács, P. Comment on “Tidal Love numbers of neutron and self-bound quark stars”. Phys. Rev. D 2020, 102, 028501. [Google Scholar] [CrossRef]
- Thorne, K.S. Tidal stabilization of rigidly rotating, fully relativistic neutron stars. Phys. Rev. D 1998, 58, 124031. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Properties of the Binary Neutron Star Merger GW170817. Phys. Rev. X 2019, 9, 011001. [Google Scholar] [CrossRef]
- Friedman, J.L.; Stergioulas, N. Rotating Relativistic Stars; Cambridge Monographs on Mathematical Physics, Cambridge University Press: Cambridge, UK, 2013. [Google Scholar] [CrossRef]
- Takami, K.; Rezzolla, L.; Yoshida, S. A quasi-radial stability criterion for rotating relativistic stars. Mon. Not. R. Astron. Soc. Lett. 2011, 416, L1–L5. Available online: https://academic.oup.com/mnrasl/article-pdf/416/1/L1/6140636/416-1-L1.pdf (accessed on 24 September 2021). [CrossRef]
- Weih, L.R.; Most, E.R.; Rezzolla, L. On the stability and maximum mass of differentially rotating relativistic stars. Mon. Not. R. Astron. Soc. Lett. 2017, 473, L126–L130. Available online: https://academic.oup.com/mnrasl/article-pdf/473/1/L126/24841378/slx178.pdf (accessed on 24 September 2021). [CrossRef]
- Stergioulas, N. 1996. Available online: http://www.gravity.phys.uwm.edu/rns/ (accessed on 24 September 2021).
- Stergioulas, N.; Friedman, J.L. Comparing Models of Rapidly Rotating Relativistic Stars Constructed by Two Numerical Methods. Astrophys. J. 1995, 444, 306. [Google Scholar] [CrossRef]
- Komatsu, H.; Eriguchi, Y.; Hachisu, I. Rapidly rotating general relativistic stars. I-Numerical method and its application to uniformly rotating polytropes. Mon. Not. R. Astron. Soc. 1989, 237, 355. [Google Scholar] [CrossRef]
- Cook, G.; Shapiro, S.; Teukolsky, S. Rapidly rotating polytropes in general relativity. Astrophys. J. 1994, 422, 227. [Google Scholar] [CrossRef]
- Goodstein, D.L. States of Matter; Dove: New York, NY, USA, 1985. [Google Scholar]
- Fetter, A.L.; Walecka, J.D. Quantum Theory of Many-Particle Systems; Dover: Mineola, NY, USA, 2003. [Google Scholar]
- Prakash, M. The Equation of State and Neutron Star; unpublished; 1994. [Google Scholar]
- Burgio, G.F.; Baldo, M.; Nicotra, O.E.; Schulze, H.J. A microscopic equation of state for protoneutron stars. Astrophys. J. Suppl. 2007, 308, 387–394. [Google Scholar] [CrossRef][Green Version]
- Xu, J.; Chen, L.W.; Li, B.A.; Ma, H.R. Effects of isospin and momentum dependent interactions on liquid–gas phase transition in hot asymmetric nuclear matter. Phys. Lett. B 2007, 650, 348–353. [Google Scholar] [CrossRef]
- Moustakidis, C.C. Temperature and momentum dependence of single-particle properties in hot asymmetric nuclear matter. Phys. Rev. C 2008, 78, 054323. [Google Scholar] [CrossRef]
- Moustakidis, C.C.; Panos, C.P. Equation of state for β-stable hot nuclear matter. Phys. Rev. C 2009, 79, 045806. [Google Scholar] [CrossRef]
- Tan, N.H.; Loan, D.T.; Khoa, D.T.; Margueron, J. Mean-field study of hot β-stable protoneutron star matter: Impact of the symmetry energy and nucleon effective mass. Phys. Rev. C 2016, 93, 035806. [Google Scholar] [CrossRef]
- Takatsuka, T.; Nishizaki, S.; Hiura, J. Particular Properties of Dense Supernova Matter. Prog. Theor. Phys. 1994, 92, 779–802. Available online: https://academic.oup.com/ptp/article-pdf/92/4/779/5358408/92-4-779.pdf (accessed on 24 September 2021). [CrossRef][Green Version]
- Takatsuka, T. Hot Neutron Stars at Birth and Related Problems*). Prog. Theor. Phys. 1996, 95, 901–912. Available online: https://academic.oup.com/ptp/article-pdf/95/5/901/5280763/95-5-901.pdf (accessed on 24 September 2021). [CrossRef]
- Friedman, J.L.; Ipser, J.R.; Sorkin, R.D. Turning Point Method for Axisymmetric Stability of Rotating Relativistic Stars. Astrophys. J. 1988, 325, 722. [Google Scholar] [CrossRef]
- Sorkin, R.D. A Stability Criterion for Many Parameter Equilibrium Families. Astrophys. J. 1982, 257, 847. [Google Scholar] [CrossRef]
- Goussard, J.O.; Haensel, P.; Zdunik, J.L. Rapid uniform rotation of protoneutron stars. Astron. Astrophys. 1997, 321, 822–834. Available online: http://aa.springer.de/papers/7321003/2300822.pdf (accessed on 24 September 2021).
- Marques, M.; Oertel, M.; Hempel, M.; Novak, J. New temperature dependent hyperonic equation of state: Application to rotating neutron star models and I–Q relations. Phys. Rev. C 2017, 96, 045806. [Google Scholar] [CrossRef]
- LORENE. LORENE: Langage Objet pour la RElativité NumériquE. 1998. Available online: https://lorene.obspm.fr/ (accessed on 24 September 2021).
- Miller, M.C.; Lamb, F.K.; Dittmann, A.J.; Bogdanov, S.; Arzoumanian, Z.; Gendreau, K.C.; Guillot, S.; Harding, A.K.; Ho, W.C.G.; Lattimer, J.M.; et al. PSR J0030+0451 Mass and Radius from NICER Data and Implications for the Properties of Neutron Star Matter. Astrophys. J. 2019, 887, L24. [Google Scholar] [CrossRef]
- Greif, S.K.; Raaijmakers, G.; Hebeler, K.; Schwenk, A.; Watts, A.L. Equation of state sensitivities when inferring neutron star and dense matter properties. Mon. Not. R. Astron. Soc. 2019, 485, 5363–5376. Available online: https://academic.oup.com/mnras/article-pdf/485/4/5363/28262089/stz654.pdf (accessed on 24 September 2021). [CrossRef]
- Radice, D.; Perego, A.; Zappa, F.; Bernuzzi, S. GW170817: Joint Constraint on the Neutron Star Equation of State from Multimessenger Observations. Astrophys. J. 2018, 852, L29. [Google Scholar] [CrossRef]
- Tews, I.; Margueron, J.; Reddy, S. Critical examination of constraints on the equation of state of dense matter obtained from GW170817. Phys. Rev. C 2018, 98, 045804. [Google Scholar] [CrossRef]
- Radice, D.; Dai, L. Multimessenger parameter estimation of GW170817. Eur. Phys. J. A 2019, 55, 50. [Google Scholar] [CrossRef]
- Kiuchi, K.; Kyutoku, K.; Shibata, M.; Taniguchi, K. Revisiting the Lower Bound on Tidal Deformability Derived by AT 2017gfo. Astrophys. J. 2019, 876, L31. [Google Scholar] [CrossRef]
- Coughlin, M.W.; Dietrich, T.; Doctor, Z.; Kasen, D.; Coughlin, S.; Jerkstrand, A.; Leloudas, G.; McBrien, O.; Metzger, B.D.; O’Shaughnessy, R.; et al. Constraints on the neutron star equation of state from AT2017gfo using radiative transfer simulations. Mon. Not. R. Astron. Soc. 2018, 480, 3871–3878. Available online: https://academic.oup.com/mnras/article-pdf/480/3/3871/33043575/sty2174.pdf (accessed on 24 September 2021). [CrossRef]
- Coughlin, M.W.; Dietrich, T.; Margalit, B.; Metzger, B.D. Multimessenger Bayesian parameter inference of a binary neutron star merger. Mon. Not. R. Astron. Soc. Lett. 2019, 489, L91–L96. Available online: https://academic.oup.com/mnrasl/article-pdf/489/1/L91/30032497/slz133.pdf (accessed on 24 September 2021). [CrossRef]
- Most, E.R.; Weih, L.R.; Rezzolla, L.; Schaffner-Bielich, J. New Constraints on Radii and Tidal Deformabilities of Neutron Stars from GW170817. Phys. Rev. Lett. 2018, 120, 261103. [Google Scholar] [CrossRef]
- Foley, R.J.; Coulter, D.A.; Kilpatrick, C.D.; Piro, A.L.; Ramirez-Ruiz, E.; Schwab, J. Updated parameter estimates for GW190425 using astrophysical arguments and implications for the electromagnetic counterpart. Mon. Not. R. Astron. Soc. 2020, 494, 190–198. Available online: https://academic.oup.com/mnras/article-pdf/494/1/190/32982848/staa725.pdf (accessed on 24 September 2021). [CrossRef]
- Rezzolla, L.; Most, E.R.; Weih, L.R. Using Gravitational-wave Observations and Quasi-universal Relations to Constrain the Maximum Mass of Neutron Stars. Astrophys. J. 2018, 852, L25. [Google Scholar] [CrossRef]
- Raithel, C.A.; Özel, F.; Psaltis, D. Tidal Deformability from GW170817 as a Direct Probe of the Neutron Star Radius. Astrophys. J. 2018, 857, L23. [Google Scholar] [CrossRef]
- Zhao, T.; Lattimer, J.M. Tidal deformabilities and neutron star mergers. Phys. Rev. D 2018, 98, 063020. [Google Scholar] [CrossRef]
- De, S.; Finstad, D.; Lattimer, J.M.; Brown, D.A.; Berger, E.; Biwer, C.M. Tidal Deformabilities and Radii of Neutron Stars from the Observation of GW170817. Phys. Rev. Lett. 2018, 121, 091102. [Google Scholar] [CrossRef]
- Annala, E.; Gorda, T.; Kurkela, A.; Vuorinen, A. Gravitational-Wave Constraints on the Neutron-Star-Matter Equation of State. Phys. Rev. Lett. 2018, 120, 172703. [Google Scholar] [CrossRef]
- Fasano, M.; Abdelsalhin, T.; Maselli, A.; Ferrari, V. Constraining the Neutron Star Equation of State Using Multiband Independent Measurements of Radii and Tidal Deformabilities. Phys. Rev. Lett. 2019, 123, 141101. [Google Scholar] [CrossRef]
- Fattoyev, F.J.; Piekarewicz, J.; Horowitz, C.J. Neutron Skins and Neutron Stars in the Multimessenger Era. Phys. Rev. Lett. 2018, 120, 172702. [Google Scholar] [CrossRef]
- Landry, P.; Essick, R.; Chatziioannou, K. Nonparametric constraints on neutron star matter with existing and upcoming gravitational wave and pulsar observations. Phys. Rev. D 2020, 101, 123007. [Google Scholar] [CrossRef]
- Most, E.R.; Papenfort, L.J.; Weih, L.R.; Rezzolla, L. A lower bound on the maximum mass if the secondary in GW190814 was once a rapidly spinning neutron star. Mon. Not. R. Astron. Soc. Lett. 2020, 499, L82–L86. [Google Scholar] [CrossRef]
- Cook, G.; Shapiro, S.; Teukolsky, S. Rapidly Rotating Neutron Stars in General Relativity: Realistic Equations of State. Astrophys. J. 1994, 424, 823. [Google Scholar] [CrossRef]
- Salgado, M.; Bonazzola, S.; Gourgoulhon, E.; Haensel, P. High precision rotating neutron star models 1: Analysis of neutron star properties. Astron. Astrophys. 1994, 291, 155. [Google Scholar]
- Tsang, C.; Tsang, M.; Danielewicz, P.; Fattoyev, F.; Lynch, W. Insights on Skyrme parameters from GW170817. Phys. Lett. B 2019, 796, 1–5. [Google Scholar] [CrossRef]
- Weih, J.B.; Lu, J.J.; Burgio, G.F.; Li, Z.H.; Schulze, H.J. Are nuclear matter properties correlated to neutron star observables? Eur. Phys. J. A 2020, 56, 63. [Google Scholar] [CrossRef]
- Thorne, K.S. Disk-Accretion onto a Black Hole. II. Evolution of the Hole. Astrophy. J. 1974, 191, 507–520. [Google Scholar] [CrossRef]
- Morsink, S.M.; Stergioulas, N.; Blattnig, S.R. Quasi-normal Modes of Rotating Relativistic Stars: Neutral Modes for Realistic Equations of State. Astrophys. J. 1999, 510, 854–861. [Google Scholar] [CrossRef][Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).