The Frequency Fluctuation Model for the van der Waals Broadening
Abstract
:1. Introduction
2. Description of the Method
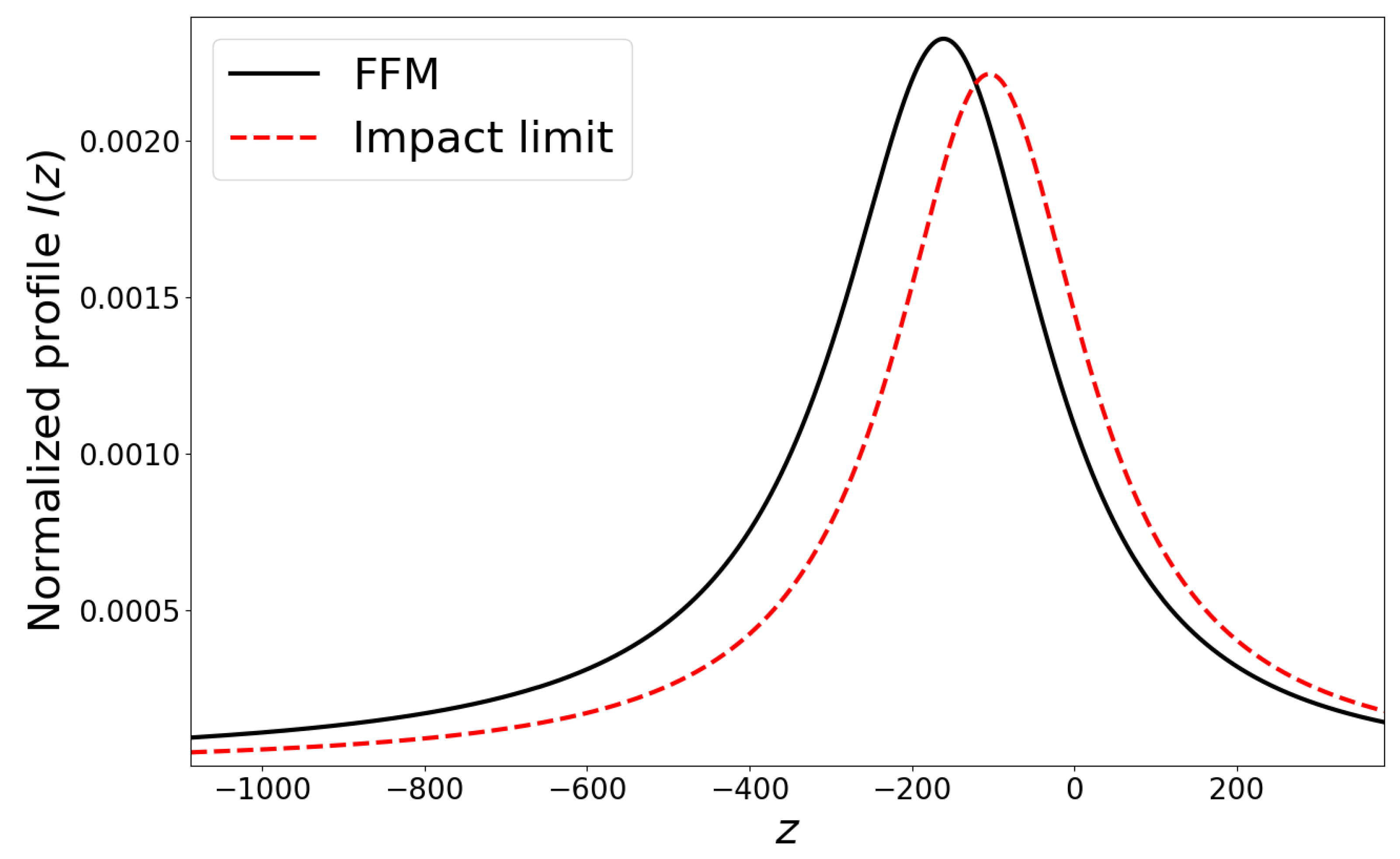
3. The Results of Numerical Calculations
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Abbreviations
| FFM | Frequency Fluctuation Model |
| MD | Molecular Dynamics |
| CT | Chen and Takeo |
References
- Griem, H.; Baranger, M.; Kolb, A.; Oertel, G. Stark broadening of neutral helium lines in a plasma. Phys. Rev. 1962, 125, 177. [Google Scholar] [CrossRef]
- Kogan, V. Broadening of spectral lines in high-temperature plasma. Plasma Phys. Probl. Control Fusion 1958, 4, 305. [Google Scholar]
- Stambulchik, E.; Maron, Y. Plasma line broadening and computer simulations: A mini-review. High Energy Density Phys. 2010, 6, 9–14. [Google Scholar] [CrossRef]
- Brissaud, A.; Frisch, U. Theory of Stark broadening—II exact line profile with model microfield. J. Quant. Spectrosc. Radiat. Transf. 1971, 11, 1767–1783. [Google Scholar] [CrossRef]
- Alexiou, S. Implementation of the Frequency Separation Technique in general lineshape codes. High Energy Density Phys. 2013, 9, 375–384. [Google Scholar] [CrossRef]
- Ferri, S.; Calisti, A.; Mossé, C.; Rosato, J.; Talin, B.; Alexiou, S.; Gigosos, M.A.; González, M.A.; González-Herrero, D.; Lara, N.; et al. Ion Dynamics Effect on Stark-Broadened Line Shapes: A Cross-Comparison of Various Models. Atoms 2014, 2, 299–318. [Google Scholar] [CrossRef]
- Talin, B.; Calisti, A.; Godbert, L.; Stamm, R.; Lee, R.; Klein, L. Frequency-fluctuation model for line-shape calculations in plasma spectroscopy. Phys. Rev. A 1995, 51, 1918. [Google Scholar] [CrossRef] [PubMed]
- Mossé, C.; Calisti, A.; Stamm, R.; Talin, B.; Bureyeva, L.; Lisitsa, V. A universal approach to Rydberg spectral line shapes in plasmas. J. Phys. At. Mol. Opt. Phys. 2004, 37, 1343. [Google Scholar] [CrossRef]
- Calisti, A.; Bureyeva, L.; Lisitsa, V.; Shuvaev, D.; Talin, B. Coupling and ionization effects on hydrogen spectral line shapes in dense plasmas. Eur. Phys. J. D 2007, 42, 387–392. [Google Scholar] [CrossRef]
- Calisti, A.; Mossé, C.; Ferri, S.; Talin, B.; Rosmej, F.; Bureyeva, L.; Lisitsa, V. Dynamic Stark broadening as the Dicke narrowing effect. Phys. Rev. E 2010, 81, 016406. [Google Scholar] [CrossRef] [PubMed]
- Ferri, S.; Calisti, A.; Mossé, C.; Mouret, L.; Talin, B.; Gigosos, M.A.; González, M.A.; Lisitsa, V. Frequency-fluctuation model applied to Stark-Zeeman spectral line shapes in plasmas. Phys. Rev. E 2011, 84, 026407. [Google Scholar] [CrossRef] [PubMed]
- Stambulchik, E.; Maron, Y. Quasicontiguous frequency-fluctuation model for calculation of hydrogen and hydrogenlike Stark-broadened line shapes in plasmas. Phys. Rev. E 2013, 87, 053108. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Letunov, A.; Lisitsa, V. The Coulomb Symmetry and a Universal Representation of Rydberg Spectral Line Shapes in Magnetized Plasmas. Symmetry 2020, 12, 1922. [Google Scholar] [CrossRef]
- Bureeva, L.; Kadomtsev, M.; Levashova, M.; Lisitsa, V.; Calisti, A.; Talin, B.; Rosmej, F. Equivalence of the method of the kinetic equation and the fluctuating-frequency method in the theory of the broadening of spectral lines. JETP Lett. 2010, 90, 647–650. [Google Scholar] [CrossRef]
- Takeo, M.; Chen, S. Broadening and shift of spectral lines due to the presence of foreign gases. Rev. Mod. Phys. 1957, 29, 20. [Google Scholar]
- Anderson, P.; Talman, J. Proceedings of the Conference on Broadening of Spectral Lines, Murray Hill, NJ, USA, 3 May 1956.
- Astapenko, V.; Letunov, A.; Lisitsa, V. From the Vector to Scalar Perturbations Addition in the Stark Broadening Theory of Spectral Lines. Universe 2021, 7, 176. [Google Scholar] [CrossRef]
- Chandrasekhar, S.; von Neumann, J. The Statistics of the Gravitational Field Arising from a Random Distribution of Stars. Astrophys. J. 1942, 95, 489–531. [Google Scholar] [CrossRef] [Green Version]
- Sobelman, I.I. Introduction to the Theory of Atomic Spectra: International Series of Monographs in Natural Philosophy; Elsevier: Amsterdam, The Netherlands, 2016; Volume 40. [Google Scholar]
- Demura, A.; Umanskii, S.Y.; Scherbinin, A.V.; Zaitsevskii, A.V.; Demichenko, G.V.; Astapenko, V.A.; Potapkin, B.V. Evaluation of Van der Waals Broadening Data. Int. Rev. At. Mol. Phys. 2011, 2, 109–150. [Google Scholar]
- Omar, B.; González, M.Á.; Gigosos, M.A.; Ramazanov, T.S.; Jelbuldina, M.C.; Dzhumagulova, K.N.; Zammit, M.C.; Fursa, D.V.; Bray, I. Spectral line shapes of He I line 3889 Å. Atoms 2014, 2, 277–298. [Google Scholar] [CrossRef] [Green Version]
- Margenau, H. Theory of pressure effects of foreign gases on spectral lines. Phys. Rev. 1935, 48, 755. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Letunov, A.; Lisitsa, V.; Astapenko, V. The Frequency Fluctuation Model for the van der Waals Broadening. Foundations 2021, 1, 200-207. https://doi.org/10.3390/foundations1020015
Letunov A, Lisitsa V, Astapenko V. The Frequency Fluctuation Model for the van der Waals Broadening. Foundations. 2021; 1(2):200-207. https://doi.org/10.3390/foundations1020015
Chicago/Turabian StyleLetunov, Andrei, Valery Lisitsa, and Valery Astapenko. 2021. "The Frequency Fluctuation Model for the van der Waals Broadening" Foundations 1, no. 2: 200-207. https://doi.org/10.3390/foundations1020015
APA StyleLetunov, A., Lisitsa, V., & Astapenko, V. (2021). The Frequency Fluctuation Model for the van der Waals Broadening. Foundations, 1(2), 200-207. https://doi.org/10.3390/foundations1020015







