A Game-Theoretic Analysis of Cooperation Among Autonomous Systems in Network Federations

Abstract

This paper investigates cooperative behavior among Autonomous Systems (ASs) within a federated network environment designed to support collaborative shared-technology deployment. It makes use of the concept of an AS federation, where independently managed systems adhere to a shared standard while maintaining implementation flexibility. Using a systematic game-theoretic framework, the study models various coalition structures—including full cooperation, partial coalitions, and defection—across several canonical cooperative games. The analysis evaluates the effects of different cooperation strategies and resource-sharing schemes on payoff distribution and coalition stability. Simulation results over short- and medium-to-long-term horizons demonstrate that cooperative coalition formation, especially with fair payoff allocation, consistently outperforms solitary strategies. The study also identifies key thresholds affecting partial coalition viability and explores the impact of defection on overall federation performance. By linking theoretical game models with practical deployment challenges in heterogeneous networked systems, this work offers valuable insights for designing mechanisms that promote effective cooperation in complex, resource-constrained environments.

1. Introduction

Cooperation among participants in complex technological and infrastructural systems is increasingly recognized as a critical factor for enhancing efficiency and achieving mutual benefits. However, identifying the conditions under which cooperative behavior yields superior outcomes compared to operating independently remains a significant challenge. This is particularly true in heterogeneous settings where participants differ in resources, objectives, and strategic incentives. Addressing this challenge requires a systematic analytical framework capable of capturing the dynamics of collaboration across diverse environments.

This paper employs cooperative game theory to investigate coalition formation and the strategic interactions of participants within integrated technological infrastructures. A range of canonical cooperative games—including the Prisoner’s Dilemma, Stag Hunt, Public Goods, Gift Exchange, and Dinner’s Dilemma—is used to simulate different cooperative scenarios. These encompass full coalition formation, complete defection, and partial coalitions with mixed cooperation and defection strategies, thus enabling a comprehensive examination of collaboration under varying configurations.

Game theory is a mathematical framework analyzing strategic interactions among rational agents operating within defined rules and potential outcomes [1]. It examines how each participant anticipates others’ actions to formulate optimal strategies, considering the interdependence of decisions [2]. By evaluating costs, benefits, and payoffs across possible scenarios, game theory identifies strategies that maximize individual or collective gains, whether interests align, conflict, or overlap [3]. Its versatile methodology spans disciplines such as economics, political science, sociology, and computer science, with applications in areas like wireless resource allocation, cybersecurity, and cloud service optimization [4,5,6]. Cooperative game theory focuses on coalition formation, enabling participants to achieve mutually beneficial, non-zero-sum outcomes through coordination. In contrast, constant-sum (zero-sum) games preclude cooperation, as one agent’s gain equals another’s loss, making coordination ineffective [2].

This paper employs the concept of an Autonomous System federation—an alliance of ASs collaborating to deploy blockchain technology across their networks—introduced in [7,8]. A federation represents a collective that adheres to a shared standard while allowing members flexibility to adapt the standard to their internal needs. ASs joining the federation commit to integrating blockchain within their managed networks, creating an interconnected environment that supports homogeneous blockchain deployment. This integration enables distributed infrastructure management and fosters collaboration among ASs in both implementing and leveraging blockchain functionalities.

The purpose of this study is to examine the feasibility and efficiency of cooperative arrangements within federations, where members collaborate to integrate technologies that require substantial infrastructural resources. Blockchain technology, which serves as the case study in this paper, exemplifies such an integration challenge. Through joint collaboration and resource pooling, federation members can adopt new technologies within their infrastructures while distributing the associated costs of resource allocation. Given the complexity of these interactions, it is essential to investigate the dynamics of inter-member cooperation in order to better understand and address the challenges of such collaborative frameworks.

Blockchain technology, considered integral to heterogeneous AS infrastructures in this paper, is a data structure comprising an ordered, backward-linked sequence of transaction blocks [9]. Operating on a decentralized, resilient peer-to-peer (P2P) network, all nodes hold equal status without privileged roles, enabling them to both consume and provide services, though they may assume varying functions within the ecosystem. Transactions, the basic data units, cryptographically encode value or information transfers and are publicly recorded to maintain a complete ownership history. These transactions are broadcast to the network, validated by full nodes, relayed, and temporarily stored in memory pools pending confirmation and inclusion in blocks.

Most studies that apply game theory typically adopt an evolutionary approach, employ incentive mechanisms to enhance the attractiveness of cooperation, or combine both strategies. The current paper has a different approach, and it proposes to demonstrate through simulations that the collaboration between the ASs in implementing technologies that have rigorous infrastructure requirements, such as blockchain technology, provides the best outcome. The approach used here does not have an evolutive character, but a comparative one, so the objective was to compare a set of cooperative games that the game theory provides, in order to determine how often and in which cases the collaboration represents the best option in order to achieve the highest benefit.

Analyses are conducted over both short-term and medium-to-long-term time horizons to observe how cooperative benefits and coalition stability evolve. The study also explores different payoff distribution schemes, comparing proportional allocation based on resource contribution with equal sharing among coalition members. This comparison provides insights into how resource heterogeneity affects fairness, coalition stability, and incentive alignment.

By simulating these varied scenarios, the research aims to deepen the understanding of cooperative mechanisms in multi-agent systems. The insights gained are intended to inform the design of protocols and mechanisms that support effective cooperation in distributed and resource-constrained technological environments.

The paper’s original contributions are:

• It develops a comprehensive analytical approach employing multiple canonical cooperative games to model and simulate varying cooperation dynamics among federation members, including full coalitions, partial coalitions, and defection.
• It investigates the formation and stability of partial coalitions within federations, identifying critical thresholds and conditions under which partial cooperation either sustains or undermines collective benefits.
• It compares proportional versus equal payoff allocation methods in heterogeneous federations, demonstrating how resource-based proportional sharing enhances fairness, coalition stability, and long-term cooperation incentives.
• Extends analysis across multiple time horizons to capture the cumulative impact of coalition strategies on performance, confirming that cooperation yields sustained advantages over solo participation.
• It provides novel insights linking theoretical cooperative game models with practical challenges in blockchain-enabled distributed network management, offering guidance for designing mechanisms that foster effective collaboration among autonomous entities.

The paper is organized as follows: Section 2 provides background and related work regarding collaboration approaches in game theory regarding blockchain and federated network environments. Section 3 presents the cooperative games used and describes the implementation of the scenario proposed to be modeled. The simulation results are presented and analyzed in Section 4. Section 5 concludes the paper.

2. Background

The selected games fall under the category of cooperative games, where multiple actors collaborate by forming coalitions that participants may join or leave based on their individual payoffs or rewards.

Liu et al. [10] provide a comprehensive survey of game theory applications in blockchain networks, encompassing both cooperative and non-cooperative frameworks and bridging the gap between extensive blockchain research and limited game-theoretic exploration. It reviews blockchain fundamentals—including decentralized ledger structures, consensus mechanisms, and data organization—and distinguishes between permissionless and permissioned blockchains with their respective protocols. The survey introduces game theory concepts relevant to blockchain, focusing on strategic interactions among rational nodes aiming to maximize utility. It categorizes applications into security, mining management, and blockchain-based services, highlighting the strengths of game-theoretic models in capturing strategic behavior and designing incentive-compatible protocols, while acknowledging challenges related to model complexity, scalability, and rationality assumptions.

An evolutionary game theory framework to model cooperation dynamics in blockchain networks was developed by Zhang et al. [11], where rational participants weigh resource costs (computing power, stakes, bandwidth) against rewards (block validation incentives) in repeated strategic interactions. Using replicator dynamics, the framework demonstrates that cooperation stabilizes when long-term rewards surpass short-term exploitation gains, with strategy evolution influenced by cost-reward ratios, malicious actor prevalence, and network growth expectations. Early intervention via reputation-based mechanisms is proposed to isolate malicious participants during network bootstrapping. Simulations confirm cooperation dominates when the reward-to-cost ratio exceeds 1.5, malicious actors represent less than 15% of the network, and future growth exceeds 20%. The framework also informs design principles for incentive structures, such as penalizing free-riders and favoring historically cooperative participants in reward allocation.

Singh et al. [12] introduced a continuous-time dynamic game model analyzing Bitcoin mining, where miners strategically consume electricity to maximize profits, highlighting the tension between individual incentives and collective sustainability. Three strategic frameworks are considered: the social optimum (cooperative), which maximizes joint profits and balances resource use for long-term sustainability; the Nash equilibrium (non-cooperative), where miners act selfishly, causing overconsumption and reduced long-term profits; and the myopic Nash equilibrium, with miners maximizing immediate gains, accelerating resource depletion. The model demonstrates that cooperative strategies conserve electricity stocks and yield higher collective profits, while non-cooperative strategies lead to faster depletion and suboptimal gains. The authors propose Pigovian taxes to internalize external costs and align selfish behavior with social optimum. Although focused on Bitcoin, the framework applies broadly to Proof-of-Work blockchains, emphasizing cooperation’s critical role in mitigating energy waste under the assumption of honest miners without adversarial actions.

A blockchain-integrated federated learning framework that leverages game theory to create a fair data-trading ecosystem was proposed by Zhang et al. [13], addressing trust and incentive misalignments in traditional FL. Using Shapley value-based mechanisms, participant data contributions are quantified, with rewards proportional to data quality and utility. A two-stage Stackelberg game models interactions between data owners (sellers) and model trainers (buyers), establishing a Nash equilibrium that maximizes both parties’ utilities. The framework ensures transaction auditability via immutable ledgers, employs homomorphic encryption for privacy-preserving model aggregation, and uses zero-knowledge proofs to validate data authenticity without revealing raw data. Blockchain eliminates centralized vulnerabilities and enables trust minimization, while game theory dynamically adapts rewards to real-time data utility, enhancing incentives beyond conventional federated learning.

Li et al. [14] addressed the challenge of designing incentive mechanisms for blockchain systems in non-cryptocurrency contexts, where traditional cryptocurrency rewards are unsuitable. It proposes a game theory-based mechanism aligned with consensus protocols—specifically Practical Byzantine Fault Tolerance (PBFT)—to predict and influence validator behavior, mitigating misbehaviors such as free-riding and dishonest validation. The model incorporates two reward schemes: a final payoff after consensus completion and an expected payoff distributed during consensus based on anticipated outcomes. Modeled as strategic games between validators and the system, these schemes ensure honest participation maximizes utility. Mathematical proofs and simulations confirm the mechanism’s effectiveness in promoting honesty and system stability. Additionally, repeated game models, including the infinitely repeated prisoner’s dilemma, discourage free-riding and enforce cooperation, establishing a robust, game-theoretic framework for incentivizing validator integrity in non-cryptocurrency blockchains.

Pu and Lam [15] developed a game-theoretic model to determine optimal blockchain adoption timing among competing ship operators responding to customer demands for blockchain solutions. The model treats operators as rational players influenced by costs, competition, network externalities, and customer substitution policies. It compares fixed pricing—constant adoption costs—and mixed pricing—variable costs decreasing as adoption grows. Using a Nash equilibrium algorithm, the study finds mixed pricing accelerates and expands adoption by leveraging network effects and cost-sharing. This framework quantitatively elucidates how competitive and pricing dynamics drive blockchain diffusion in maritime transport, emphasizing the critical roles of cost-effectiveness and network externalities, and is adaptable to analogous technology adoption scenarios in other industries.

A game-theoretic Pay-For-Gain (PFG) incentive mechanism for Delay-Tolerant Networks (DTNs) was introduced by Yin et al. [16] to mitigate selfish node behavior. Grounded in loan-credit theory, the scheme motivates nodes to share buffer resources by rewarding message forwarding with credits redeemable for future transmissions. A credit loan system fosters mutual dependency, allowing nodes to borrow resources during scarcity. The model demonstrates that cooperation maximizes long-term payoffs and establishes conditions under which cooperative strategies are optimal. Selfish nodes that refuse to forward messages incur debt penalties, reducing their transmission priority, while highly cooperative nodes gain preferential message delivery, effectively incentivizing cooperative participation.

Kovacs et al. [7] proposed a cooperative game-theoretic framework modeling the feasibility of shared blockchain infrastructure deployment across federated Autonomous Systems (ASs). By conceptualizing AS collaboration as a non-zero-sum coalitional game, the framework analyzes incentive structures that encourage rational, self-interested ASs to jointly adopt blockchain technology while preserving operational autonomy. Incorporating a Pay-For-Gain (PFG) incentive system—adapted from delay-tolerant networks—that rewards resource sharing and penalizes free-riding, the model captures AS decisions to join or leave coalitions based on payoff-driven strategies. Evolutionary simulations demonstrate that coalition stability improves when resource-sharing benefits surpass individual costs and defection penalties outweigh short-term gains. This work establishes a foundation for trust-minimized cooperation in decentralized multi-AS infrastructure deployment.

A comparative table summarizing the main differences between the referenced works and the current paper is presented in

Table 1. Related work and proposed approach summary.

Reference	Focus and Context	Methodology/Model	Technology/Domain	Cooperation Modeling	Unique Contribution Compared to Current Paper
Liu et al. [10]	Survey of game theory in blockchain (cooperative and non-cooperative); incentive mechanisms and protocols	Comprehensive literature survey	Blockchain (various)	Both types; strategic focus	Broad overview, does not simulate federations
Zhang et al. [11]	Evolutionary cooperation mechanisms in blockchain; role of costs/rewards; impact of malicious actors	Evolutionary game theory, replicator dynamics	Blockchain networks (PoW, PoS)	Evolutionary and coalition	Dynamic modeling of defender vs. attacker
Singh et al. [12]	Dynamic game of electricity consumption in mining; social optimum vs. Nash equilibrium	Continuous-time dynamic game	Bitcoin mining (PoW blockchain)	Social optimum (cooperative)	Focused on mining sustainability and resource use
Zhang et al. [13]	Fair data trading using federated learning and blockchain; Shapley value and Stackelberg games for incentives	Shapley value, Stackelberg game	Blockchain-supported federated learning	Cooperative pricing/reward	Data trade incentives; privacy-preserving design
Li et al. [14]	Incentive mechanisms for non-cryptocurrency blockchains; validator honesty and PBFT	Repeated/prisoner’s dilemma game	Blockchain (PBFT and non-crypto)	Repeated coalition games	Focus on validator incentives without currency
Pu and Lam [15]	Optimal adoption timing of blockchain among competing operators; cost and network externality effects	Nash equilibrium, adoption games	Blockchain tech in maritime transport	Adoption (coordination)	Adoption timing; network effects on incentives
Yin et al. [16]	Incentive mechanisms for cooperation in delay-tolerant networks (DTNs); buffer and credit sharing	Loan-credit based game mechanisms	Delay-tolerant networks	Buffer/credit-based coalition	Applies to DTNs, not infrastructural blockchain
Kovacs et al. [7]	Cooperative feasibility for shared blockchain across federated Autonomous Systems (ASs); incentive schemes	Non-zero-sum coalitional games, evolutionary simulations, PFG	Inter-AS blockchain infrastructure	Coalition formation, PFG	Focused on multi-AS blockchain infrastructure
Current work	Quantitative assessment of coalition-based vs. independent action in federations integrating resource-heavy technologies (e.g., blockchain); average fitness gaps and scenario evaluation over short and medium-to-long term	Quantitative simulations of full and partial coalition, across synergy levels and timescales	Federations integrating infrastructure-demanding technologies (blockchain case)	Coalition, partial coalition, independent action	Provides scenario-comparative, empirical simulation with explicit fitness gap metrics; analyzes coalition stability across full/partial membership and synergy, directly quantifying numerical benefits over various timescales

. The table covers research focus, methodology, technology context, cooperation modeling, and unique contributions.

3. Game Theory Approaches and Algorithms

Due to the behavior of the parties involved (Autonomous Systems) and the similarities between the decision-making process and real-life decision-making, cooperation can be analyzed through game theory. Considering that cooperation occurs in non-zero-sum games—since in this type of game the participants can achieve additional gains through collaboration—we can thus employ such games to describe and model the situation.

An illustrative example used to model this problem is the Prisoner’s Dilemma. In its classical form, two participants, having committed a crime, aim to minimize their punishment. Each must choose either to testify or remain silent, with outcomes as follows: both testify results in moderate sentences; both remain silent yields light sentences; if one testifies while the other remains silent, the testifier receives no sentence, and the silent party receives a heavy sentence. Rationally, testifying is the dominant strategy, as it avoids the worst-case outcome. Thus, both testifying and receiving moderate sentences is the equilibrium. Paradoxically, mutual cooperation (both remaining silent) provides the best collective outcome, minimizing total punishment.

The paradox lies in the fact that selfish decisions worsen outcomes compared to cooperative behavior. When the game is repeated iteratively, participants can learn that cooperation maximizes long-term gains. Defection by one player can be punished by the other in subsequent rounds, resulting in sustained suboptimal outcomes until cooperation is restored. However, in finitely repeated games, this dynamic unravels—players anticipate no future retaliation in the final round and may choose to defect. This reasoning propagates backward, leading to defection in all rounds by backward induction. Consequently, cooperation emerges as the optimal strategy only in infinitely or indefinitely repeated games, where the end point is uncertain [2].

Besides the Prisoner’s Dilemma, which is the most popular and widely used game in such cases (including in computer science), there exist other games that could be employed to model the problem at hand. In the following section, several examples will be mentioned.

In the Pure Coordination game, two companies simultaneously select a technology standard for compatible products. Divergent standards result in sales losses, while adopting a common standard increases sales. Consumers typically favor one technology, so aligning with the preferred standard maximizes profits. This game features multiple Nash equilibria, making coordination on a single equilibrium the primary challenge. Consumer preference often serves as a focal point, guiding companies toward consensus. Communication mechanisms, such as industry consortia, help reduce uncertainty and facilitate coordination [17,18,19]. In this context, if ASs successfully join the federation and integrate blockchain technology within their network architectures, cooperation would enhance their gains beyond independent operation by leveraging positive network effects and minimizing coordination risks.

The Stag Hunt game models a scenario in which two hunters independently choose their prey. Mutual cooperation to hunt the stag yields the highest joint payoff. However, if one defects to hunt the hare, the cooperating hunter receives nothing, while the defector secures a smaller but guaranteed reward. This game presents two pure strategy Nash equilibria: the payoff-dominant equilibrium (Stag, Stag), which maximizes collective benefit, and the risk-dominant equilibrium (Hare, Hare), which minimizes individual risk amid uncertainty but also reduces overall gains. The central challenge is overcoming the trust dilemma, as players must rely on mutual cooperation to attain the superior outcome. Communication and credible commitments can enhance coordination toward this equilibrium. As the number of participants increases, establishing trust and coordination becomes more complex, rendering cooperation more difficult to sustain. Unlike the Prisoner’s Dilemma, the Stag Hunt admits multiple stable outcomes, mirroring real-world situations where cooperation hinges on mutual expectations and risk tolerance [20,21,22]. In the context of autonomous systems, cooperation within the proposed federation can yield greater benefits than typical individualistic strategies, provided sufficient trust and coordination mechanisms exist.

The Gift-Exchange game, a key model in behavioral economics, illustrates the principle of reciprocity. In this framework, an employer may offer wages exceeding contractual obligations, while the employee can respond by exerting higher effort. Mutual engagement in this reciprocal exchange—higher wages balanced by increased effort—yields superior outcomes for both parties. Empirical studies consistently demonstrate that higher wages elicit greater effort, underscoring the importance of trust and trustworthiness in economic interactions [23,24,25]. Applied to autonomous systems, if ASs cooperatively invest effort and resources within the federation, they can collectively benefit through positive reciprocity. Conversely, insufficient effort or resource allocation motivated by short-term self-interest undermines both collective federation output and individual gains, as mutual generosity—and its associated benefits—is forfeited.

The Diner’s Dilemma, an n-player cooperative game, involves individuals sharing a meal with an equally split bill. Each diner chooses between a more expensive and a cheaper dish. Although the expensive dish is superior, its personal cost is unjustifiable when paid individually. However, since costs are shared, ordering the expensive dish becomes a strictly dominant strategy, reducing individual marginal cost. When all diners opt for the expensive dish, the group incurs higher costs and lower collective utility than if all chose the cheaper option, exemplifying the conflict between individual rationality and group welfare [26,27]. In the context of blockchain integration, this game models the risk of resource overconsumption by providers sharing federation costs without proper coordination and incentives. While the basic model assumes linear cost increases with participants, real-world factors like economies of scale or caps can mitigate this effect. Institutional mechanisms such as itemized billing or peer monitoring further align individual incentives with collective welfare.

The Public Goods game is a fundamental model in game theory that examines the conflict between individual incentives and collective welfare. Participants choose how many tokens to contribute to a common pool, which is then multiplied by a factor greater than one but less than the number of players and equally redistributed. This structure captures the classic social dilemma: although full cooperation maximizes group welfare, individuals are incentivized to free ride by contributing less while benefiting from others’ contributions. Public goods are characterized by non-excludability and non-rivalry, complicating their funding and provision without adequate incentives [28,29]. This model is highly applicable to collective action challenges, such as resource allocation among ASs within a blockchain-integrated federation, where cooperation yields shared benefits and lowers individual costs. Extensions incorporating participant heterogeneity and complex network effects offer deeper insights into cooperative behavior.

This study employs simplified cooperative game theory models to analyze a scenario involving heterogeneous Autonomous Systems (ASs) considering blockchain integration within their networks. Integration may occur individually or via coalition formation, pooling resources to support blockchain operations. Typically, simulations in cooperative game theory include incentive mechanisms to promote cooperation, maximize collective gains, and penalize undesirable behaviors, often incorporating evolutionary dynamics to optimize strategies over time.

The present work models the concept through the pure forms of previously discussed games, adapted to ensure consistent outputs and facilitate meaningful analysis. The primary aims are to assess how often cooperative behavior yields optimal outcomes, evaluate the attractiveness of cooperation, and test the robustness of the conclusion that collaboration produces superior results. Even without explicit incentives, a general tendency toward cooperation may suggest it as the preferred strategy.

The simulation model abstracts ASs as participants deciding resource allocation for blockchain operation, with resources ranging from 1 GB to 4 GB. Each AS represents a blockchain node within its Software-Defined Networking (SDN) architecture, modeled as a network device with limited accessible resources rather than specialized blockchain hardware.

Each participant processes a transaction load per round, with a round representing one day. Based on current technology and literature [7,30,31,32], normal daily transactions range from 1000 to 2000, above average is around 2500, and high demand exceeds 3000. Transaction sizes are averaged to approximate realistic loads. If the processed transactions fall below a threshold, the participant gains no benefit that round.

A maximum transaction processing capacity per round is defined (between 288 and 3000 transactions), accounting for resource limits and average transaction sizes, informed by blockchain hardware and infrastructure studies [30,31,32] and empirical benchmarks. Excess transactions overflow into subsequent rounds, potentially accumulating if demand remains high. The maximum theoretical processing capacity in optimal conditions is 5760 transactions per round. For individual ASs, an overflow threshold of 2880 transactions is set. For coalitions, the threshold scales with coalition size, average resources, and resource distribution; for example, a coalition of five ASs has a threshold of 9000 transactions. Transactions exceeding these thresholds carry over as overflow.

In simulations, the required transactions per round are fixed at 2000 to represent typical demand. Coalitions benefit from a synergy factor applied to operational capacity, modeled at four levels: no synergy (factor 1.0), low (1.1), medium (1.3), and high (1.5). Each simulation initializes the number of ASs and rounds, with participants randomly assigned resource allocations (1–4 GB) and transaction loads (288–3000 per round). Participants choose to process transactions solo (defect) or as part of a coalition, which apportions the total transaction load accordingly. Overflow thresholds are calculated per participant and coalition.

At the start of each simulation round, coalition resources and the total transactions to be processed are calculated, including any overflow from previous rounds. The coalition payoff is then determined, subject to meeting minimum requirements: the coalition’s total resources must be at least the minimum resource allocation per participant multiplied by the number of participants, and the total transactions must meet a predefined minimum threshold. If these conditions are unmet, the coalition payoff is zero. Otherwise, the payoff is calculated using the formula:

$$payof f_C = synergyFactor \times \left({\displaystyle \frac{resource{s}_C }{\max PosResource{s}_C}} \times transaction{s}_C\right),$$

(1)

where $synergyFactor$ represents the coalition’s synergy boost, $resource{s}_C$ is the coalition’s available resources, $\max PosResource{s}_C$ is the coalition’s maximum possible resources, and $transaction{s}_C$ the transaction load for the round.

If transactions overflow into the next round, a penalty is applied to the coalition payoff as follows:

$$payof f_C = payof f_C \times \left(1 - {\displaystyle \frac{overflo{w}_C}{\mathrm{10,000}}}\right),$$

(2)

where $overflo{w}_C$ represents the coalition’s transactions that overflow into the next round.

Once the coalition payoff is established, individual member payoffs are computed based on the specific game model. Similarly, solo participant payoffs are determined, accounting for overflow and verifying if individual resource and transaction thresholds are met. Failure to meet these conditions results in zero payoff. If criteria are fulfilled, solo payoffs are calculated as per the game’s framework, subject to the same overflow penalty formula:

$$payof f_S = payof f_S \times \left(1 - {\displaystyle \frac{overflo{w}_S}{\mathrm{10,000}}}\right),$$

(3)

where $overflo{w}_S$ represents the single participant’s transactions that overflow.

Partial coalitions, where some participants cooperate and others act independently, are also considered. Subcases reduce coalition size incrementally by one member each time, providing insight into coalition robustness relative to membership. For partial coalitions, resources, transaction loads, and overflow are computed similarly. Payoff calculations and penalties align with those for full coalitions, with formulas presented in (1) and (2), while individual payoffs depend on the specific game.

The fitness of each participant is computed as:

$$fitness = payof f_C - payof f_S,$$

(4)

where $payof f_C$ represents the (partial) coalition’s payoff, and $payof f_S$ represents the solo participants’ payoff.

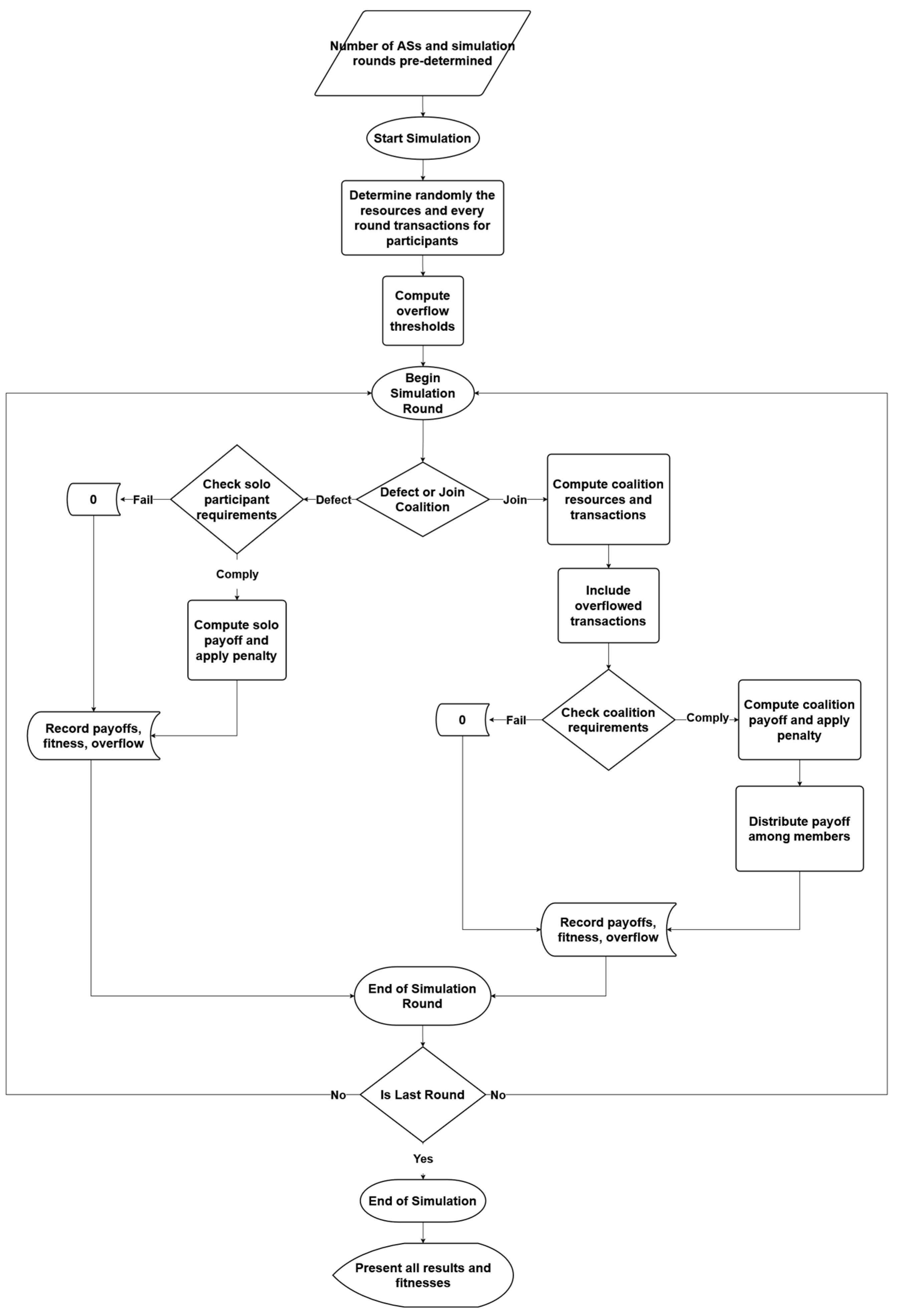
These steps repeat for every simulation round. After completion, round-wise coalition, solo, and fitness payoffs are presented, alongside aggregated total fitness for each participant. Results for partial coalitions, including payoffs and fitness, are also reported, as well as transaction overflow per participant and coalition. The simulation workflow is illustrated in Figure 1.

It should be noted that the simulation rounds are not evolutionary; multiple rounds simulate temporal progression and diverse operational conditions. This approach broadens the range of transaction loads analyzed, improving insight into cooperative dynamics and benefits. Including partial and non-cooperative scenarios enriches the dataset, enabling more robust conclusions.

Based on the outlined simulation steps, cooperative games are implemented to model the scenario, each with specific characteristics. For the Prisoner’s Dilemma, key factors influencing payoffs include: a cooperation factor (1.5 boost), defect factor (neutral, 1.0), temptation factor (1.75 boost applied to defectors in partial coalitions), and sucker factor (0.75 penalty applied to cooperators betrayed by defectors). The coalition payoff is computed as per the general formula, with individual participant payoffs calculated as:

$$payof f_{AS} = {\displaystyle \frac{resource{s}_{AS}}{resource{s}_C}} \times payof f_C \times cooperationPayof fFactor,$$

(5)

where $resource{s}_{AS}$ represents the coalition participant’s (AS) resources, and $cooperationPayoffFactor$ represents the factor that boosts the payoff.

Solo participant payoff follow:

$$payof f_S = {\displaystyle \frac{resource{s}_S}{\max Resources}} \times transaction{s}_S \times defectPayof fFactor,$$

(6)

where $resource{s}_S$ represents the solo participant’s resources, $\max Resources$ represents the maximum resources possible, and $defectPayof fFactor$ represents the factor that boosts the payoff.

In partial coalitions, cooperative participants’ payoffs are penalized by the sucker factor, while defectors gain the temptation factor:

$$payof f_{AS} = {\displaystyle \frac{resource{s}_{AS}}{resource{s}_{PC}}} \times payof f_{PC} \times suc\ker Payof fFactor,$$

(7)

where $resource{s}_{AS}$ represents the partial coalition participant’s resources, $resource{s}_{PC}$ represents the partial coalition’s resources, and $suc\ker Payof fFactor$ represents the factor that decreases the payoff;

$$payof f_{SPC} = payof f_S \times temptationPayof fFactor,$$

(8)

where $payof f_S$ represents the solo participant’s payoff and $temptationPayof fFactor$ represents the factor that boosts the payoff.

For the Pure Coordination game, payoff computations mirror those of the Prisoner’s Dilemma (5), (6), but exclude boost factors, and partial cooperation is not modeled due to the game’s nature.

The Stag Hunt game closely resembles Pure Coordination in payoff calculations yet includes partial coalition scenarios. Partial coalition payoffs use the coalition Formula (7) without Prisoner’s Dilemma-specific factors, while defectors’ payoffs align with the solo case.

The Public Goods game computes participant payoffs proportionally to resources and coalition size:

$$payof f_{AS} = {\displaystyle \frac{resource{s}_C}{numberOfMembers}} ÷ resource{s}_C \times payof f_C,$$

(9)

where $numberOfMembers$ represents the number of participants in the coalition.

Partial coalition payoffs use an analogous formula to (9), with defectors’ payoffs matching those in the Stag Hunt and Pure Coordination games for both coalition cases.

In the Gift-Exchange game, a diminishing factor (0.5) and average participant resource (calculated to be 2.5 in the current setup) are introduced. Payoffs for coalition members follow the Public Goods Formula (9). Solo participants’ payoffs are computed as in the Public Goods game. Partial coalition payoffs incorporate a diminishing adjustment accounting for non-cooperators:

$$payof f_{AS} = payof f_{AS} \times \left(1 - \left(numberOfNonCoopParticipants \times {\displaystyle \frac{averageResource{s}_{AS}}{\max PosResources}} \times \dim i nishingFactor\right)\right),$$

(10)

where $numberOfNonCoopParticipants$ represents the number of participants that defect, $\max PosResources$ represents the maximum value possible for the resources of a participant.

Finally, the Diner’s Dilemma calculates coalition member payoffs as:

$$payof f_{AS} = {\displaystyle \frac{payof f_C}{numberOfMembers}}$$

(11)

Solo and partial coalition defectors’ payoffs follow the Gift-Exchange game’s method. Partial coalition member payoffs scale similarly to Formula (11), using partial coalition parameters.

All unspecified simulation steps adhere to the general methodology described earlier. The following chapter presents and discusses the simulation results for the cooperative games considered.

4. Results

The proposed scenario was modeled and simulated using the cooperative games presented in the section above. This section holds the details of the simulation flow presented and the important aspects. Also, the results are presented and analyzed in order to help form conclusions.

As outlined in the previous chapter, the simulation involved five participants to ensure sufficient case diversity while maintaining clarity in results analysis. The simulation modeled participant behavior and interactions over discrete time intervals, represented by simulation rounds. Two temporal scenarios were examined: a short-term operation comprising 30 rounds aimed at assessing immediate benefits, and a medium-to-long-term operation spanning 365 rounds to evaluate benefits over an extended period with greater variability.

Four simulation modes, defined by varying levels of synergy within participant coalitions, were considered to examine their impact on cooperative benefits. Synergy represents the enhancement resulting from resource integration within the coalition. The modes included: (1) no synergy, without benefit enhancement; (2) low synergy, with a modest increase (factor 1.1); (3) medium synergy, providing a moderate boost (factor 1.3); and (4) high synergy, yielding a substantial benefit increase. These modes simulated different efficiencies of integration and cooperation, thereby influencing coalition gains.

To ensure comparability across modes, participant configurations were held constant. This was achieved by predefining each participant’s resources and the transactions they process per round, allowing direct quantification of benefits attributable solely to synergy effects.

The simulations focus on the cooperative games’ implementations. The primary scenario evaluates the outcomes associated with full cooperation, where all participants form a coalition, contrasted with the outcomes when participants act independently. Additionally, the results include the fitness function values, which quantify the relative gains between cooperative and non-cooperative behaviors. Beyond these metrics, the analysis reports the cumulative fitness accrue over multiple rounds and the transaction overflow experienced by the participants. Due to the absence of an evolutionary component in this simulation, the benefits do not exhibit any systematic increase or decrease over successive rounds. For the low-, medium- and high-synergy cases, since the simulations were conducted using the same dataset and do not incorporate an evolutionary component to modify values across rounds, the primary difference lies in the increase in payoff values corresponding to the higher synergy factors.

For Prisoner’s dilemma game, a detailed summary of the resources utilized by each participant is provided in

Table 2. Participants’ resources for Prisoner’s dilemma game.

AS	GB
AS1	2 GB
AS2	4 GB
AS3	3 GB
AS4	2 GB
AS5	1 GB

.

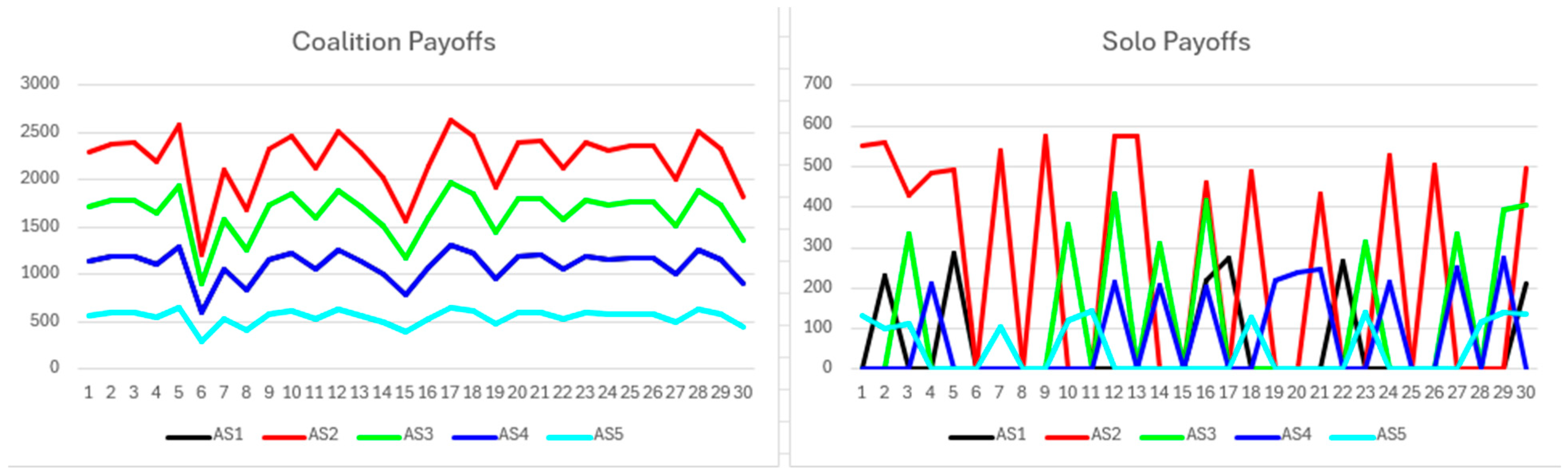
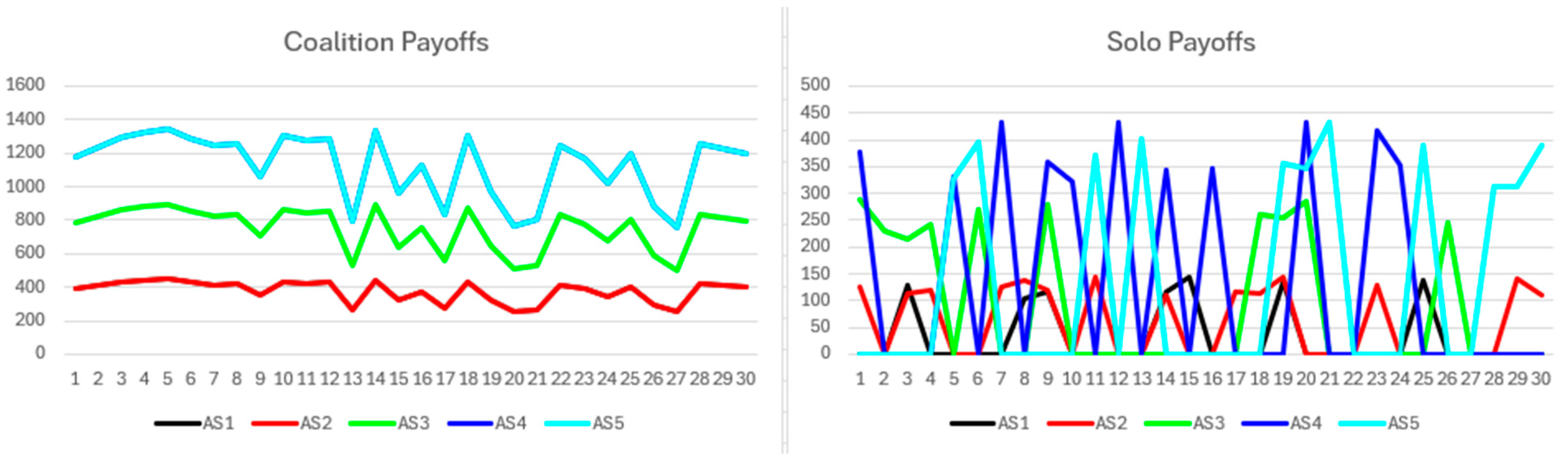
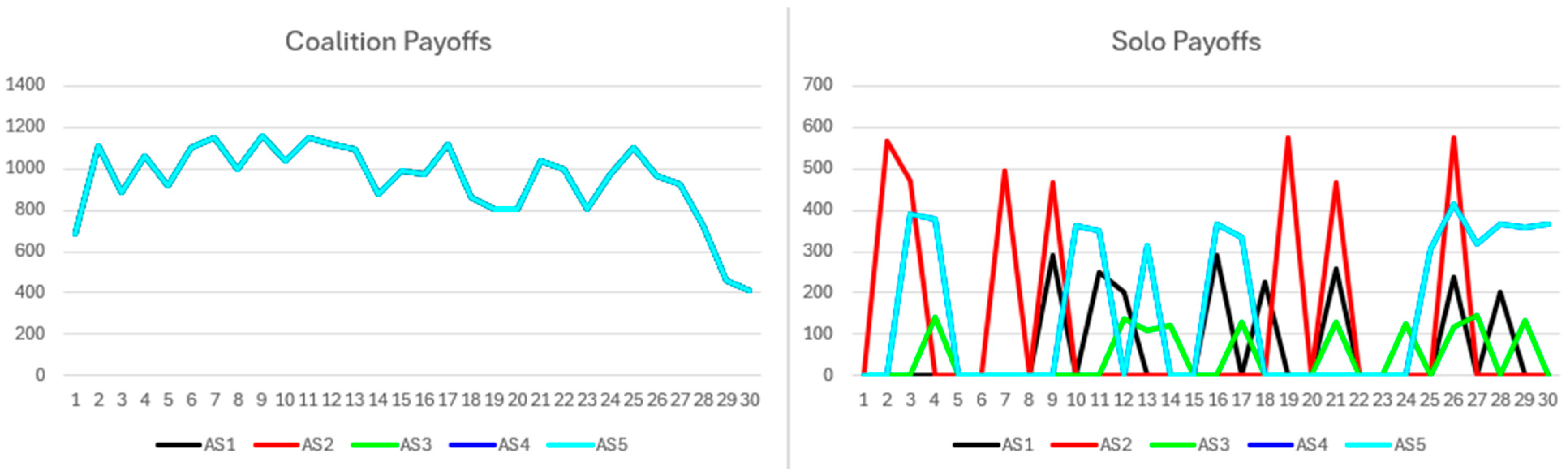
The simulation results are presented as follows. First, the short-term no-synergy scenario is analyzed, with coalition and solo payoffs shown in Figure 2. Participants allocating greater resources consistently achieve higher benefits, directly reflecting the resource distributions detailed in Table 2. Coalition payoffs remain relatively stable across rounds, with minor variations driven by transaction volume fluctuations. Participants with equal resources receive similar payoffs. By contrast, solo payoffs exhibit significant volatility and occasionally drop to zero when processing demands fall below the threshold. Solo payoffs are consistently and substantially lower than those within coalitions.

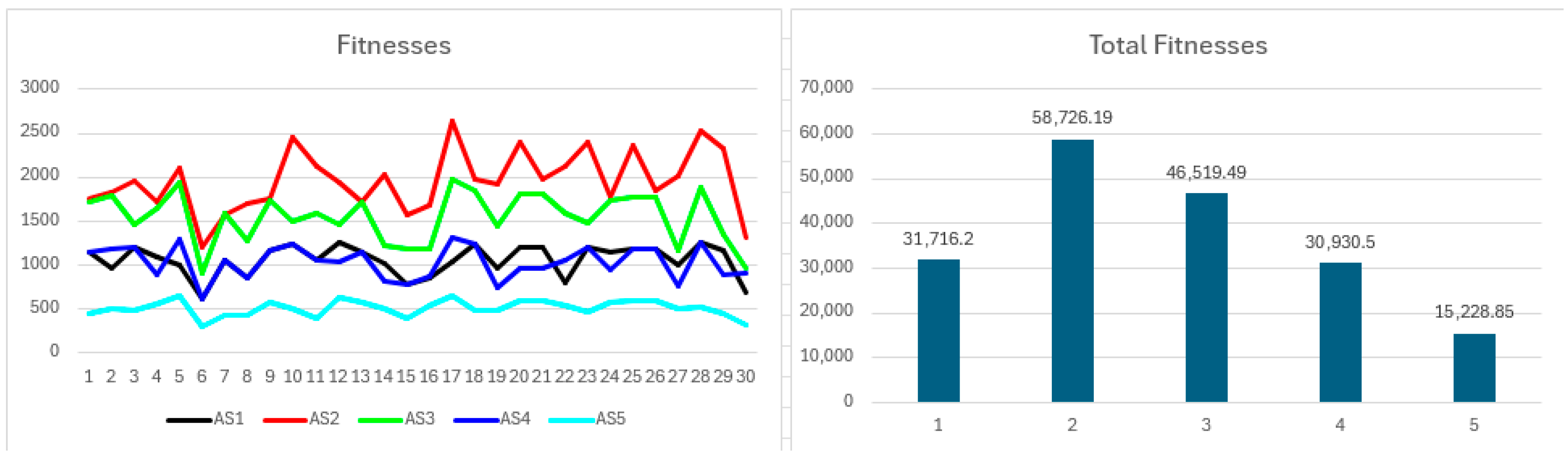
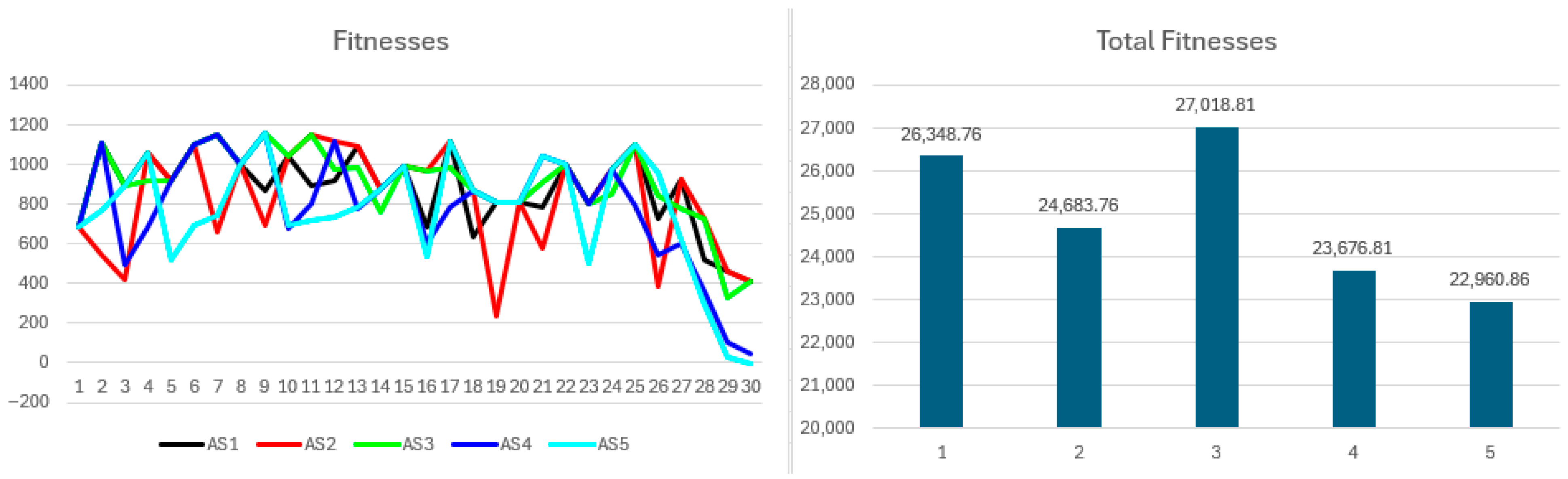
Figure 3 depicts fitness values per round and cumulative fitness at the simulation end. Fitness, defined as the difference between cooperative and non-cooperative payoffs, remains positive throughout. Periods of zero solo benefits produce pronounced fitness spikes exceeding payoff fluctuations. Fitness rankings correspond closely to the payoff patterns from Figure 2. Cumulative fitness correlates positively with resource levels; participants contributing more resources attain superior outcomes.

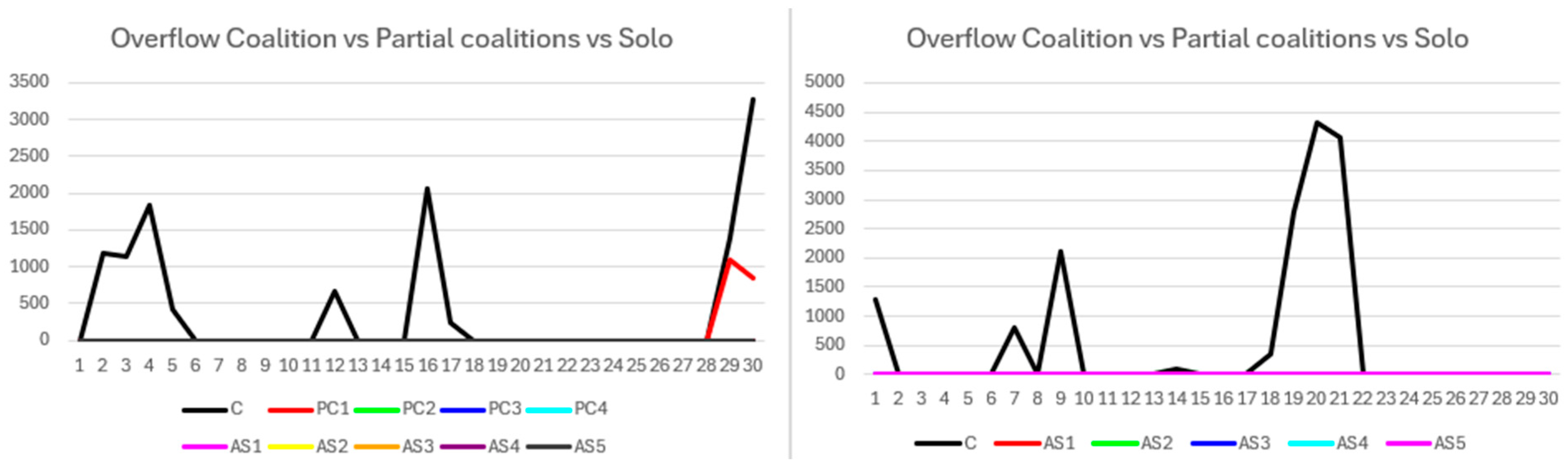
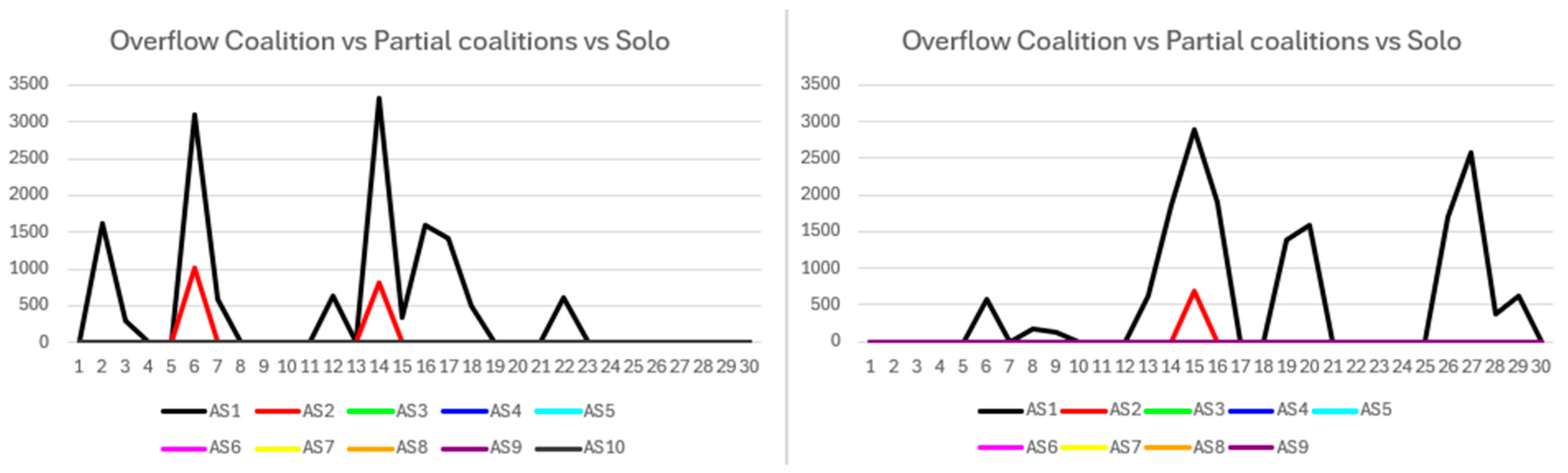
Transaction overflow is illustrated in Figure 4, categorized as coalition (C), partial coalition (PC), and solo (AS). Overflow penalties arise when transaction volumes exceed processing capacity. While overflow correlates with lower payoffs in certain instances, it does not fully account for all payoff reductions, indicating other factors influence results.

Although the Prisoner’s Dilemma framework inherently encourages cooperation, benefitting coalition payoffs, results suggest that cooperation alone does not fully explain coalition success. Coalition formation significantly elevates payoffs beyond non-cooperative levels, with cooperation further enhancing gains.

For the Pure Coordination game, a summary of the resources utilized by each participant is provided in

Table 3. Participants’ resources for Pure coordination game.

AS	GB
AS1	1 GB
AS2	1 GB
AS3	2 GB
AS4	3 GB
AS5	3 GB

.

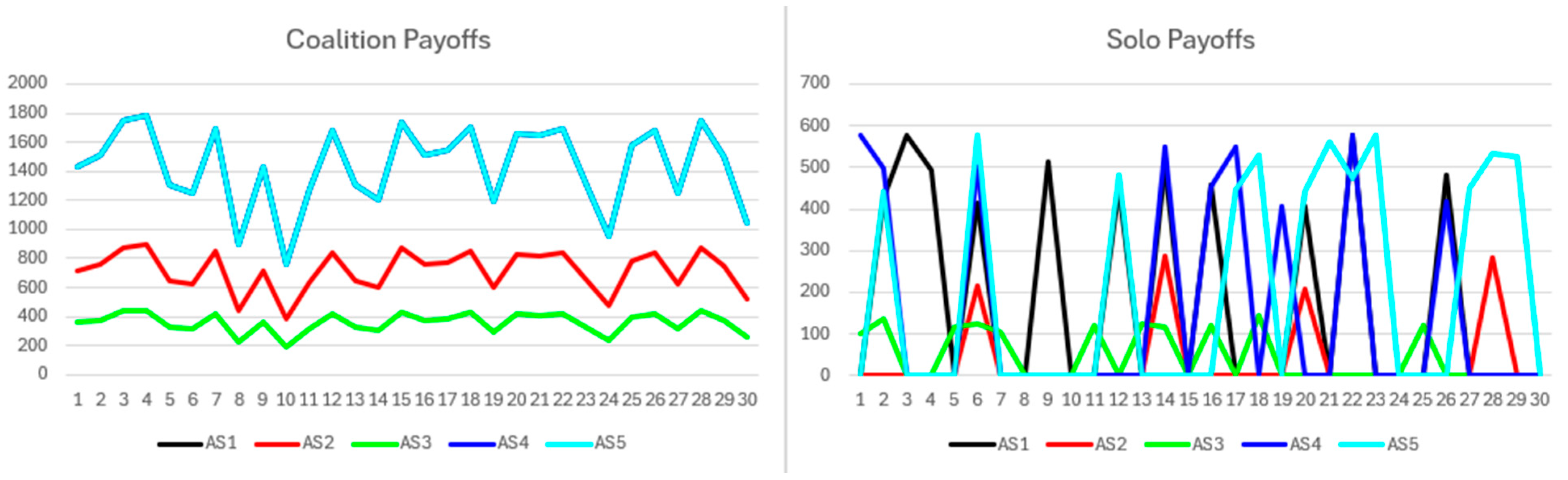
The simulation results begin with the short-term no-synergy scenario. Figure 5 presents coalition and solo payoffs. Coalition payoffs consistently exceed solo payoffs and exhibit smoother trends, reflecting the coalition’s ability to maintain stable benefits within a narrow range, thereby minimizing fluctuations. Participants with equal resources receive identical coalition payoffs proportional to their contributions. In contrast, solo payoffs show greater variability due to intermittent benefit receipt but remain proportional to participant resources when awarded.

Figure 6 shows fitness results, indicating minor variations where participants with equal coalition payoffs differ based on their solo payoffs. Elevated fitness values confirm coalition benefits surpass those of non-cooperation. Cumulative fitness aligns with payoff trends and resource contributions, with minimal variation among participants of equal resources driven primarily by non-cooperative performance.

Figure 4 details transaction overflow, which occurs solely within the coalition. A significant overflow between rounds 17 and 22 temporarily impairs coalition performance but is effectively managed, allowing stabilization afterward.

For the Stag Hunt game, a summary of the resources utilized by each participant is provided in

Table 4. Participants’ resources for Stag hunt game.

AS	GB
AS1	4 GB
AS2	2 GB
AS3	1 GB
AS4	4 GB
AS5	4 GB

.

The simulation results begin with the short-term no-synergy scenario. Figure 7 shows coalition and solo payoffs, with coalition payoffs consistently exceeding solo payoffs and exhibiting smoother trends. This reflects the coalition’s ability to maintain stable benefits within a narrow range each round, reducing fluctuations. Participants with equal resources receive proportionally identical coalition payoffs. In contrast, solo payoffs are more variable, as non-cooperative participants receive benefits intermittently. When awarded, solo payoffs fall within a narrow range and scale with participant resources, although many rounds yield no payoff.

Figure 8 presents fitness values, showing minor variations where participants with equal coalition payoffs differ according to their solo payoffs. Consistently high fitness confirms the superiority of cooperative benefits compared to the variability in solo outcomes. Cumulative fitness aligns closely with payoffs and resource contributions, with minimal variation among equal-resource participants, primarily driven by differences in solo payoff consistency and magnitude.

Figure 9 depicts transaction overflow, revealing significant events within the coalition. However, these spikes have minimal overall impact, as backlogs are efficiently resolved within short periods, reflected in stable payoff and fitness trends.

For the Public Goods game, the resources utilized by each participant are summarized in

Table 5. Participants’ resources for Public goods game.

AS	GB
AS1	1 GB
AS2	1 GB
AS3	3 GB
AS4	3 GB
AS5	1 GB

.

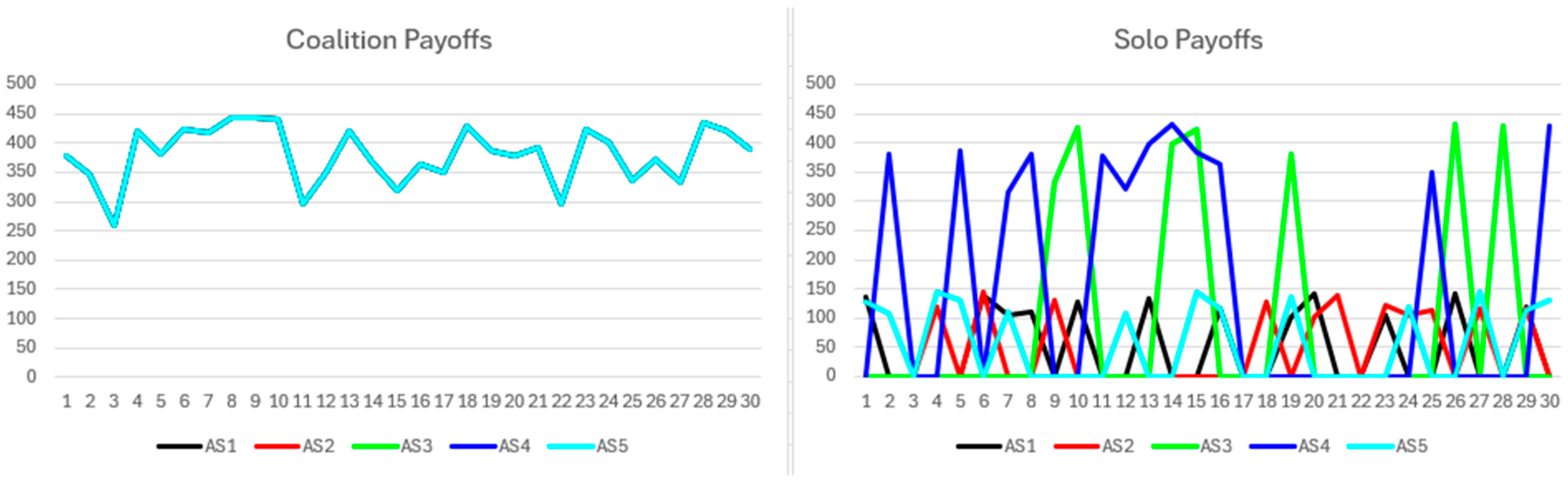
The simulation results begin with the short-term no-synergy scenario. Figure 10 shows coalition and solo payoffs, with coalition payoffs closely aligning with but exhibiting smoother trends than solo payoffs, reflecting the coalition’s ability to secure stable benefits within a narrow range each round. All coalition participants receive identical payoffs regardless of resource contribution. Conversely, solo payoffs are less consistent, with some rounds yielding no benefits; when awarded, they fall within a narrow range and scale with participant resources. Participants with the highest solo payoffs tend to approximate coalition payoffs.

Figure 11 presents fitness values differentiating coalition payoffs among participants. Due to similar coalition and solo payoffs, rounds with high solo payoffs produce fitness near zero, indicating a cancelation effect. Occasionally, fitness dips below zero when solo payoffs exceed coalition returns. Cumulative fitness mirrors payoff patterns, with participants bearing coalition performance burdens—typically those with greater resources—showing greater divergence. This is the first case where cooperation matches high-resource non-cooperation; total fitness confirms coalition robustness, as consistent coalition payoffs surpass episodic, inconsistent solo gains. However, uniform coalition payoffs favor low-resource participants and limit high-resource returns, equalizing payoffs and aligning them with solo outcomes. Scenarios with more high-resource participants would likely amplify differences between coalition and solo payoffs.

Figure 9 depicts transaction overflow occurring exclusively within the coalition, with three significant episodes spanning multiple rounds before mitigation. Despite overflow, coalition payoffs remain stable. Conversely, solo payoffs suggest overflow periods coincide with favorable outcomes for high-resource solo participants. Fitness data reveal these participants are disadvantaged, as their payoffs might equal or exceed coalition returns if they defect.

For the Gift Exchange game, the resources allocated by each participant are summarized in

Table 6. Participants’ resources for Gift exchange game.

AS	GB
AS1	2 GB
AS2	1 GB
AS3	3 GB
AS4	4 GB
AS5	2 GB

.

The simulation results begin with the short-term no-synergy scenario. Figure 12 presents coalition and solo payoffs. Coalition payoffs surpass solo payoffs and display smoother trajectories, reflecting the coalition’s capacity to deliver consistent benefits within a narrow range each round, thus reducing fluctuations. All coalition participants receive identical payoffs. Solo payoffs show greater variability, as non-cooperative participants do not earn payoffs every round. When awarded, solo payoffs fall within a limited range and scale proportionally with participant resources. The highest solo payoffs partially overlap with the lowest coalition payoffs, indicating relatively strong solo performance.

Figure 13 displays fitness values, revealing variation among participants with equal coalition payoffs based on their solo payoffs. Overall, fitness values are high, confirming the advantage of coalition participation. However, participants with greater resources achieve solo payoffs close to coalition levels, reducing their fitness in some rounds. Cumulative fitness, also shown in Figure 13, reflects individual fitness patterns and is relatively independent of resource contributions. Participants with the largest resource endowments tend to receive slightly lower net benefits due to uniform coalition payoffs and proximities in solo payoffs, which diminish their cooperative advantage.

Transaction overflow data in Figure 14 indicate coalition overflow between rounds 12 and 16. Despite a temporary surge in transaction volume, coalition payoffs remain largely stable. Fitness values show a more noticeable decline but remain positive. The coalition effectively manages this overflow, mitigating its impact and stabilizing performance in subsequent rounds.

For the Dinner’s Dilemma game, the resources allocated by each participant are summarized in

Table 7. Participants’ resources for Dinner’s dilemma game.

AS	GB
AS1	2 GB
AS2	4 GB
AS3	1 GB
AS4	3 GB
AS5	3 GB

.

The simulation results begin with the short-term no-synergy scenario. Figure 15 displays coalition and solo payoffs, with coalition payoffs consistently higher and exhibiting smoother trends, reflecting the coalition’s ability to maintain stable benefits within a narrow range each round, thereby minimizing fluctuations. All coalition participants receive identical payoffs regardless of individual resource contributions. Notably, payoffs decline in the final rounds; subsequent analysis explores potential causes. In contrast, solo payoffs are less consistent, as non-cooperative participants receive payoffs intermittently. When awarded, solo payoffs remain within a limited range and scale proportionally with resource contributions.

Figure 16 presents fitness values, showing that while coalition payoffs are uniform, fitness varies according to participants’ solo performance. Overall fitness remains high, confirming the coalition’s advantage. The late-stage fitness decline parallels the reduction in coalition payoffs as they converge with solo values. Cumulative fitness reflects payoff outcomes and resource contributions, with participants of similar resources achieving comparable benefits. The data indicate an inverse relationship between resource endowment and benefit, where low-resource participants attain higher returns at the expense of high-resource ones.

Transaction overflow data in Figure 14 reveal overflow exclusively within the coalition. A substantial overflow emerges in the final rounds, persisting until the simulation’s end without effective mitigation. This overflow adversely affects coalition payoffs and fitness, accounting for the observed decline. Nonetheless, the coalition’s strong prior performance ensures overall benefits remain superior to those of solo participants.

Across all examined games—Prisoner’s Dilemma, Pure Coordination, Stag Hunt, Public Goods, Gift Exchange, and Dinner’s Dilemma—simulations for low- and medium-synergy scenarios preserve the qualitative characteristics observed in no-synergy cases, with coalition payoffs, fitness values, and cumulative fitness consistently improving due to synergy enhancements. Solo payoffs remain stable and unaffected, as synergy influences only cooperative outcomes. Fitness patterns maintain their form, differing primarily in magnitude, with medium synergy typically producing the most favorable results, including the elimination of negative fitness values from the Public Goods game onward. High-synergy cases are not explicitly detailed to avoid redundancy but follow analogous trajectories with proportionally greater coalition benefit amplifications, underscoring a consistent, scalable impact of synergy on coalition performance across diverse game-theoretic models.

Across all six games—Prisoner’s Dilemma, Pure Coordination, Stag Hunt, Public Goods, Gift Exchange, and Dinner’s Dilemma—the medium-to-long-term simulations reveal that coalition payoffs generally remain stable and comparable to short-term results, particularly at the upper range, despite occasional fluctuations and short periods of negative payoffs. Solo payoffs consistently exhibit greater variability and lower values, reflecting intermittent failure to meet processing thresholds. Fitness values confirm the persistent advantage of cooperation, with cumulative fitness positively correlated with resource contributions; however, participants with higher resources often experience reduced relative benefits due to uniform coalition payoffs for specific games. Transaction overflow occurs predominantly within coalitions, with several significant spikes that correspond to temporary declines in payoff and fitness, though coalitions effectively manage most overflow events without lasting disruption. Low- and medium-synergy scenarios maintain established patterns, showing improved coalition performance and fitness proportional to synergy level, yet synergy does not entirely mitigate the impact of major overflow spikes or negative fitness events. High-synergy cases, though not explicitly detailed, follow analogous trends with greater magnitude improvements but retain similar vulnerabilities. Overall, synergy consistently enhances coalition outcomes across all games while cooperation remains the dominant strategy despite transient challenges posed by transaction overflows and participant heterogeneity.

The study extends the analysis of coalition formation by introducing a partial coalition scenario, where only a subset of participants cooperate while others act independently, using the same parameters as the full coalition for consistent comparison. Partial coalitions range from four cooperators versus one defector down to a single cooperator, varying by game. Results reveal that as coalition size decreases, cooperative payoffs generally decline and fluctuations increase, though cooperation typically remains preferable to solo action. In the Prisoner’s Dilemma, defectors benefit from payoff multipliers, increasing volatility, and cooperation loses dominance when coalition size is too small; however, cooperation still yields higher total fitness in most configurations. In contrast, the Stag Hunt and Public Goods games show stable cooperation gains despite smaller coalitions, with the Public Goods game occasionally benefiting from lower-resource defectors reducing collective burden. Games like Gift Exchange and Dinner’s Dilemma exhibit more pronounced payoff declines with defection but maintain cooperative superiority. Notably, certain games prohibit effective coalitions with minimal members. Medium-to-long-term simulations confirm that even partial cooperation significantly improves cumulative outcomes over time, establishing partial coalition cooperation as a consistently superior strategy across diverse game-theoretic contexts.

To provide a more concrete understanding of the results, the average total fitness per game was aggregated and is presented in Figure 17, highlighting the advantages of cooperation over independent action. The figure illustrates the additional gains achieved through coalition formation, measured relative to the benefits obtained by acting independently. Average gains were calculated for each game across the first three synergy levels, considering both short-term and medium-to-long-term scenarios. The results consistently show that coalitions outperform independent strategies under all conditions, with higher synergy levels further amplifying cooperative benefits. These advantages become even more pronounced in the medium-to-long-term simulations, where the performance gap between coalition and independent outcomes increases substantially in favor of cooperation.

Similarly, Figure 18 presents the outcomes for partial coalitions, considering both short-term and medium-to-long-term scenarios. While a reduction in cooperative members leads to decreased benefits for the coalition, the results still generally surpass those of independent action. The only exception appears in the prisoner’s dilemma with a two-member coalition, where cooperative members were penalized and non-cooperators gained due to the specific rules of the game. However, in the medium-to-long-term simulations, partial coalitions—even those with an increased number of missing members—clearly outperform independent strategies by a significant margin. Overall, these findings provide strong evidence that cooperation within federations maximizes outcomes and ensures increasing long-term benefits, thereby reinforcing the value of coalition strategies and dispelling concerns about potential declines over time.

This chapter presented the results of simulations conducted for the proposed approaches and scenarios, accompanied by an analysis and discussion of the findings. Various degrees of collaboration, implemented through coalition formation, were examined and compared against the strategy of acting independently. The scenarios were modeled using a range of cooperative games, with particular emphasis placed on evaluating the performance outcomes associated with cooperative behavior.

5. Conclusions

In this study, we developed a streamlined yet comprehensive framework to evaluate the benefits of cooperation within federations, focusing on the joint integration of technologies that require substantial infrastructural resources. Through this framework, we addressed a wide range of scenarios and game types, each characterized by different cooperative rules and strategies, thereby fulfilling the study’s objective of assessing the dynamics and value of collaborative approaches in such contexts.

The simulations considered a comprehensive set of scenarios, including full cooperation, complete defection, and mixed strategies where partial coalitions coexisted with independent actors, while also accounting for different levels of coalition efficiency and synergy. By analyzing both short-term and medium-to-long-term outcomes across six game-theoretic models, the results consistently demonstrated that cooperative strategies—particularly when participants formed coalitions—tended to yield superior outcomes compared to independent action. Even in mixed configurations, coalition members generally benefited more than defectors, highlighting the strategic and practical advantages of collaboration in addressing the infrastructural demands of technology integration. These findings not only confirm the feasibility of cooperative approaches but also emphasize their long-term efficiency and potential to create sustained value within federations.

The results strongly confirm the quantitative superiority of cooperation over independent action. On average across all games, coalitions achieved a total fitness that was 26,592 points higher in the short term, corresponding to a substantial relative improvement, and 323,444 points higher in the medium-to-long term, representing an even greater proportional gain as cooperation effects accumulate. Partial coalitions also delivered consistent advantages, outperforming independent strategies by 8362 points in the short term and by 84,199 points in the medium-to-long term, again reflecting significant relative improvements in overall fitness. While some isolated cases were observed—such as specific scenarios in which coalition outcomes were low or even negative—these exceptions were rare and did not alter the overall pattern. The comprehensive set of simulations demonstrated that, both in the short and medium-to-long term, coalition strategies consistently outperformed independent action. Even partial coalitions, despite occasional isolated underperformances, ultimately proved more effective and reliable, achieving better results across nearly all cases. These findings demonstrate not only the immediate but also the compounding long-term benefits of coalition strategies and provide robust evidence that cooperative behavior, whether embraced by all or only a subset of participants, is the most effective and beneficial strategy for federations integrating resource-intensive technologies.

The cooperative games considered for simulation fall into two categories. Games that share the payoffs obtained to the participants based on the resources the participants bring to the coalition, and games that share the payoffs obtained equally to each participant without taking into consideration the difference in resources. Based on the results obtained and the analysis, the first category of games provides better results for the modeled scenario. Every participant receives a share of the total payoffs in relation to the resources they contributed with, which provides a fair and equal treatment. Also, because the payoffs sharing is flexible, it permits the members of the coalition to better react to the processing fluctuations. The second category of games mentioned here, on the other hand, puts a lot of pressure on the members with more resources, making the absorption of the processing fluctuations felt more heavily. Because the payoffs are fixed and equal for all of the members, the result obtained is that the members with more resources are affected on the fitness side, with participants with fewer resources having a clear advantage and difference in the obtained results. This occurs because members with greater resources use increased effort to compensate for the processing demands that low-resource members are unable to meet. This leads to an unbalanced effort-to-benefit ratio, which directly impacts the fitness calculation. As a result, the ease with which low-resource members can accumulate payoffs becomes unfair and may even lead to inefficient outcomes in certain rounds. In conclusion, the results are more favorable and stable when payoffs are aligned with the resources invested, leading to improved coalition performance as well.

Typically, the study of cooperative behavior involves employing evolutionary approaches with varying incentive structures, allowing researchers to analyze behavioral trends and assess the feasibility, preference, and efficiency of cooperation. In contrast, the primary objective of the present work is to investigate whether similar conclusions can be drawn by applying a classical game theory framework without introducing additional incentives to promote cooperation. This study aimed to demonstrate that cooperation can emerge naturally and become the optimal strategy. Moreover, if cooperation arises as the preferred course of action in the absence of external incentives or evolutionary mechanisms, it validates the feasibility and effectiveness of cooperation within the context of the proposed shared-technology adoption and implementation scenario.

The current findings demonstrate that cooperative strategies consistently yield substantial quantitative benefits over independent action in federated environments integrating resource-intensive technologies. When applied to practical settings—such as commercial Autonomous Systems (ASes), Internet Service Providers (ISPs), or academic federations—these results suggest that forming coalitions to jointly deploy and manage shared infrastructure (e.g., blockchain networks or other advanced services) leads to increased overall efficiency, resource optimization, and long-term sustainability. In real-world networks, this translates into reduced operational costs, enhanced service reliability, and improved ability to address large-scale integration challenges that would be difficult or economically unviable for single entities acting alone. Even partial cooperation—where only some participants join a coalition—offers marked advantages, indicating that network operators and institutions have incentive to pursue collaborative frameworks. While isolated cases of suboptimal performance might occur, the overwhelming evidence supports coalition-building as the most effective approach to maximize both immediate and compounding long-term benefits in complex, multi-stakeholder network environments.

Future research could extend this work by applying the proposed framework to blockchain and other resource-intensive technologies, by examining larger-scale federations, and exploring how external factors such as regulation, interoperability requirements, and market dynamics influence the stability, scalability, and long-term success of cooperative strategies.

For the current study, overall, a comprehensive analysis of numerous observations consistently indicates that cooperative behavior yields superior outcomes, even in circumstances where environmental factors diminish the effectiveness of collaboration.