Contrastive Geometric Cross-Entropy: A Unified Explicit-Margin Loss for Classification in Network Automation

Abstract

As network automation and self-organizing networks (SONs) rapidly evolve, edge devices increasingly demand lightweight, real-time, and high-precision classification algorithms to support critical tasks such as traffic identification, intrusion detection, and fault diagnosis. In recent years, cross-entropy (CE) loss has been widely adopted in deep learning classification tasks due to its computational efficiency and ease of optimization. However, traditional CE methods primarily focus on class separability without explicitly constraining intra-class compactness and inter-class boundaries in the feature space, thereby limiting their generalization performance on complex classification tasks. To address this issue, we propose a novel classification loss framework—Contrastive Geometric Cross-Entropy (CGCE). Without incurring additional computational or memory overhead, CGCE explicitly introduces learnable class representation vectors and constructs the loss function based on the dot-product similarity between features and these class representations, thus explicitly reinforcing geometric constraints in the feature space. This mechanism effectively enhances intra-class compactness and inter-class separability. Theoretical analysis further demonstrates that minimizing the CGCE loss naturally induces clear and measurable geometric class boundaries in the feature space, a desirable property absent from traditional CE methods. Furthermore, CGCE can seamlessly incorporate the prior knowledge of pretrained models, converging rapidly within only a few training epochs (for example, on the CIFAR-10 dataset using the ViT model, a single training epoch is sufficient to reach 99% of the final training accuracy.) Experimental results on both text and image classification tasks show that CGCE achieves accuracy improvements of up to 2% over traditional CE methods, exhibiting stronger generalization capabilities under challenging scenarios such as class imbalance, few-shot learning, and noisy labels. These findings indicate that CGCE has significant potential as a superior alternative to traditional CE methods.

1. Introduction

Network automationand self-organizing networks (SONs) increasingly rely on on-device classifiers for real-time traffic identification, intrusion detection, and fault diagnosis. Because of its simplicity and low-latency footprint, cross-entropy (CE) loss remains the default optimisation objective for such edge-deployed models [1,2,3,4,5,6,7,8,9,10,11,12,13,14]. A standard CE pipeline maps features to class scores with a linear layer and then applies asoftmax. Although effective, this routine only implicitlystores class information in the weight matrix and imposes no explicit geometric structure on the feature space [15,16,17]. As a result, learned representations may lack intra-class compactness and clear inter-class margins, ultimately limiting generalisation under the dynamic, noisy conditions typical of large-scale automated networks [18,19,20,21,22,23,24].

Several avenues have been explored to overcome these limitations. Margin-based lossessuch as ArcFace [18] and CosFace [16] explicitly enlarge geometric margins in feature space, while contrastive learningapproaches like SimCLR [25] and MoCo [26] pull positive pairs together and push negatives apart. Although both lines of work improve discrimination, margin losses are highly sensitive to hyper-parameters and label noise [27,28,29,30,31,32], whereas contrastive methods often require large batches, complex hard-negative mining, or auxiliary memory banks [33,34,35,36,37,38,39]. These extra costs clash with the tight latency and memory budgets of edge devices embedded in SON infrastructures.

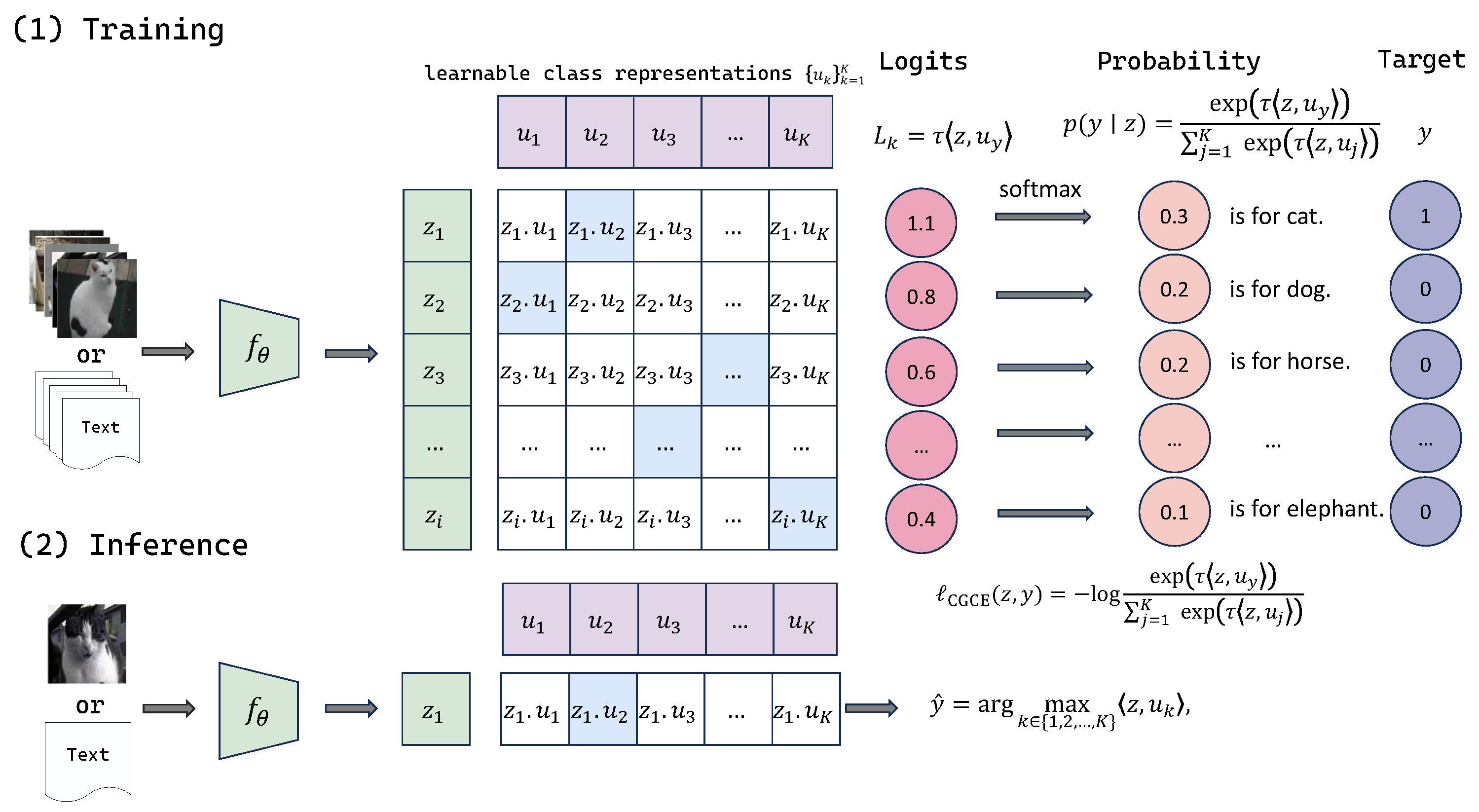
To retain CE’s efficiency while meeting the geometric demands of reliable classification, we propose Contrastive Geometric Cross-Entropy (CGCE). CGCE assigns each class a trainable representation vector and defines the loss via dot-product similarity between features and these vectors, simultaneously tightening intra-class clusters and widening inter-class gaps—yet without large batches, negative mining, or extra memory. At inference time, a sample is classified simply by its similarity to the learned class vectors, streamlining deployment on resource-constrained network nodes.

Because class information is explicit, CGCE can seamlessly absorb priors from powerful pretrained encoders: class vectors may be initialised with class-wise feature means or semantic embeddings derived from label text, enabling rapid convergence and resilience to class imbalance, few-shot regimes, and noisy labels—conditions frequently observed in operational networks.

Compared with vanilla CE, CGCE (i) establishes quantifiable geometric margins that sharpen decision boundaries, (ii) integrates pretrained priors for fast online model updates essential to self-optimising network functions, and (iii) keeps computation and memory on par with CE, preserving the low-latency footprint required by large-scale SON deployments. Experiments across vision, NLP, and code-analysis datasets demonstrate up to a 2% absolute accuracy gain over CE together with superior robustness, positioning CGCE as a practical loss for next-generation network-automation pipelines.

2. Related Work

Cross-entropy loss has been widely adopted in classification tasks due to its optimization stability and ease of implementation [1,2,3,4,5,6,7,40,41]. However, this loss function primarily models class information implicitly, lacking explicit constraints on intra-class compactness and inter-class separation, which may restrict a model’s discriminative capability in complex tasks [18,19,20,21,22,23,24]. To overcome these limitations, several studies have introduced improvements based on geometric margins—such as ArcFace and CosFace—that explicitly enlarge the inter-feature distance [16,18,42,43,44,45]. These methods typically require meticulous hyperparameter tuning and exhibit limited performance in the presence of label noise or class imbalance [27,28,29,30,31,32]. Contrastive learning has demonstrated significant advantages in enhancing feature discriminativeness, particularly under unsupervised settings, but it often relies on large training batches and effective sample mining strategies [25,26,33,34,36,37,38,39,46,47,48]. Although supervised contrastive learning mitigates some of these issues by leveraging label information to construct sample pairs, it still incurs high training costs [35]. In this work, we propose the CGCE method, which synergistically integrates the strengths of cross-entropy and contrastive learning. By introducing class representation vectors, our approach explicitly constructs geometric boundaries without additional computational overhead, thereby simultaneously enhancing model discrimination, training efficiency, and generalization ability.

3. Methods

In this section, we introduce the proposed Contrastive Geometric Cross-Entropy (CGCE) framework, which enhances classification by enforcing explicit geometric constraints via learnable class representation vectors. We first define the CGCE loss and its optimization objective. Then, we provide a theoretical analysis showing that minimizing CGCE naturally induces clear geometric margins. Finally, we discuss its connections to traditional cross-entropy and supervised contrastive learning.

3.1. Problem Definition

Consider a multi-class classification task with a given training dataset ${\left\{(z_i,y_i)\right\}}_{i=1}^N$, where each sample has a feature representation $z_i=f_{\theta }\left(x_i\right)\in {\mathbb{R}}^d$ obtained via a feature extractor $f_{\theta }$, and a corresponding class label $y_i\in \{1,2,\dots ,K\}$. In contrast to traditional CE approaches, we explicitly introduce a set of learnable class representation vectors ${\{u_k\in {\mathbb{R}}^d\}}_{k=1}^K$ to directly characterize each class.

Specifically, for a single sample $(z,y)$, the CGCE loss is defined as follows:

$${\ell }_{\mathrm{CGCE}}(z,y)=-log{\displaystyle \frac{exp\left(\tau \langle z,u_y\rangle \right)}{{\sum }_{k=1}^{K}exp\left(\tau \langle z,u_k\rangle \right)}},$$

(1)

where $\tau >0$ is a temperature hyperparameter and $\langle ·,·\rangle$ denotes the dot-product operation. For the entire training dataset, the average CGCE loss is as follows:

$$R_{\mathrm{CGCE}}\left(\left\{u_k\right\}\right)={\displaystyle \frac{1}{N}}\sum _{i=1}^N{\ell }_{\mathrm{CGCE}}(z_i,y_i).$$

(2)

This definition explicitly embodies the core idea of contrastive learning: during training, the model optimizes both the feature extractor and the class representation vectors, pulling sample features closer to their corresponding class representations and pushing them away from the representations of other classes, thereby explicitly forming a measurable geometric margin in the feature space.

At inference time, classification decisions become straightforward: for a new sample x, we first compute its feature representation $z=f_{\theta }\left(x\right)$, and then select the class whose representation vector has the highest similarity (dot product) to z:

$$\widehat{y}=arg\underset{k\in \{1,2,\dots ,K\}}{max}\langle z,u_k\rangle .$$

(3)

Figure 1 provides an overview of the proposed CGCE framework.

3.2. Theoretical Analysis

To demonstrate theoretically that minimizing CGCE loss naturally leads to clear geometric class boundaries, we analyze a representative case for a single training sample.

First, we introduce the following notations:

$$L_k=\tau \langle z,u_k\rangle ,L_y=\tau \langle z,u_y\rangle ,L_{\max }^{-}=\underset{k\ne y}{max}{L}_k.$$

(4)

The geometric margin for a sample $(z,y)$ is then defined as follows:

$$\Delta (z,y)={\displaystyle \frac{L_y-L_{\max }^{-}}{\tau }}.$$

(5)

Clearly, the sample is classified correctly if and only if $\Delta (z,y)>0$.

We now rigorously derive a lower bound on this geometric margin. Consider the case when the CGCE loss satisfies the following:

$${\ell }_{\mathrm{CGCE}}(z,y)\le ϵ,ϵ<log(K-1).$$

(6)

Under this condition, we derive the following chain of inequalities:

$$\begin{array}{cc}\hfill & exp(-ϵ)\le p\left(y\right|z)={\displaystyle \frac{exp\left(L_y\right)}{{\sum }_{k=1}^{K}exp\left(L_k\right)}}\hfill \\ \hfill & \le {\displaystyle \frac{exp\left(L_y\right)}{exp\left(L_y\right)+(K-1)exp\left(L_{\max }^{-}\right)}}\hfill \\ \hfill & ⟹exp(-ϵ)\left[exp\left(L_y\right)+(K-1)exp\left(L_{\max }^{-}\right)\right]\le exp\left(L_y\right)\hfill \\ \hfill & ⟹exp(-ϵ)\left[1+(K-1)exp(L_{\max }^{-}-L_y)\right]\le 1\hfill \\ \hfill & ⟹(K-1)exp(L_{\max }^{-}-L_y)\le exp\left(ϵ\right)-1\hfill \\ \hfill & ⟹exp(L_{\max }^{-}-L_y)\le {\displaystyle \frac{exp\left(ϵ\right)-1}{K-1}}\hfill \\ \hfill & ⟹L_{\max }^{-}-L_y\le log{\displaystyle \frac{exp\left(ϵ\right)-1}{K-1}}\hfill \\ \hfill & ⟹L_y-L_{\max }^{-}\ge -log{\displaystyle \frac{exp\left(ϵ\right)-1}{K-1}}\ge log(K-1)-ϵ.\hfill \end{array}$$

(7)

Thus, we obtain a rigorous lower bound for the geometric margin:

$$\Delta (z,y)={\displaystyle \frac{L_y-L_{\max }^{-}}{\tau }}\ge {\displaystyle \frac{log(K-1)-ϵ}{\tau }}>0.$$

(8)

This theoretical result shows that, once the CGCE loss is sufficiently small, the model naturally forms a clear, measurable decision boundary in the feature space. This property can be extended to the entire dataset: if the average CGCE loss across all training samples is low, then the model’s overall class separability is guaranteed.

Traditional CE methods lack this explicit geometric margin guarantee because they implicitly encode class information only within the linear classification layer parameters (weights and biases), without explicitly defining or optimizing class representation vectors. Therefore, minimizing the traditional CE loss does not directly imply an explicit measurable geometric margin, but rather merely improves class probabilities indirectly. In contrast, CGCE’s explicit introduction and optimization of trainable class vectors enable this rigorous theoretical guarantee, enhancing the discriminative power of the learned feature space.

4. The Relationship and Differences Between CGCE, Cross-Entropy, and Supervised Contrastive Loss

We propose the Contrastive Geometric Cross-Entropy (CGCE) framework, which introduces learnable class representation vectors and utilizes the similarity between sample features and class vectors as the scoring metric. This approach naturally fuses classification with contrastive learning. In essence, CGCE is closely related to the traditional Cross-Entropy (CE) loss and can be viewed as a special case of Supervised Contrastive Loss (SCL) at the class level.

Traditional CE loss is computed based on the logits produced by a linear classifier. It is typically defined as follows:

$${\ell }_{CE}=-log{\displaystyle \frac{exp\left({\mathrm{logit}}_y\right)}{{\sum }_{j}exp\left({\mathrm{logit}}_j\right)}},$$

(9)

where the logits are usually obtained by multiplying the weights of a linear layer with the input features.

In contrast, CGCE explicitly defines the logits as the dot product similarity between the sample features and the class representation vectors, scaled by a temperature factor $\tau$, and then normalized via the softmax function. This modification preserves the probabilistic interpretation of CE while effectively extracting the class information from the model weights into learnable class vectors, thereby constructing explicit geometric decision boundaries in the feature space.

While SCL emphasizes constructing positive and negative sample pairs at the individual sample level—maximizing similarity among samples of the same class and minimizing similarity among samples of different classes—this method typically incurs high computational complexity due to the maintenance of numerous pairs within each batch. CGCE simplifies this contrastive mechanism to the class level: each sample is matched only with its corresponding class vector as a positive example, with all other class vectors treated as negatives. In this configuration, if the class vectors are considered as the “positive samples” in the SCL framework, the CGCE loss is equivalent to SCL under the setting of “one anchor, one positive, and the rest negatives”. This reduction not only diminishes the dependency on batch size but also enhances scalability and efficiency.

In summary, CGCE integrates the stability of CE with the discriminative advantages of contrastive learning. It inherits the classification capability of CE while incorporating the clear separation in feature space offered by SCL, all while avoiding the computational overhead associated with constructing extensive positive-negative pairs. This design, characterized by its geometric interpretability and contrastive enhancement, enables CGCE to achieve superior generalization and training efficiency.

5. Experiments

5.1. Experimental Settings

In this section, we provide a detailed description of the overall experimental plan and implementation details. To evaluate the effectiveness of CGCE relative to the traditional CE method, we conducted both image classification and text classification experiments using the CE and CGCE loss functions under identical experimental conditions. The traditional CE method is implemented using a classic linear classification layer; that is, a fully connected layer is appended after the feature extractor to map the extracted features to class scores, followed by a softmax function to compute class probabilities and cross-entropy loss for optimization. In contrast, the CGCE method explicitly introduces a set of trainable class representation vectors, directly computes the dot product between the sample embeddings and the class representation vectors, scales the dot product with a temperature parameter $\tau$, and then computes the softmax probabilities to construct the contrastive geometric cross-entropy loss. The length of the class vectors is set to match the model’s output feature dimension—for text tasks, it uses the hidden state of the first token from a RoBERTa model (typically 768 dimensions), and, for image tasks, it is determined by the model (2048 dimensions for ResNet-50 or the hidden_size, e.g., 768, for Vision Transformer).

To ensure a fair and rigorous comparison between the two methods, we strictly controlled the experimental conditions. These include the selection of datasets, the choice of feature extractor models, data preprocessing methods (e.g., random cropping, random horizontal flipping, color jittering, and normalization for image tasks; tokenization and encoding for text tasks), batch size, number of training epochs, learning rate, mixed precision training, early stopping strategy, and learning rate scheduling (e.g., cosine annealing). All experiments were conducted on a uniform hardware platform using an NVIDIA RTX 4090D GPU. Moreover, each experiment was repeated with five different random seeds to ensure the stability and reliability of the results, and the average accuracy along with the corresponding confidence intervals was reported.

Specifically, for image classification tasks, we employed the CIFAR-10 [49], CIFAR-100 [49], and ImageNet [50] datasets and used ResNet-50 [51] and Vision Transformer (ViT) [52] as the feature extractors; for text classification tasks, we utilized the SST-2 [53], SST-5 [53], IMDB [54], AG News [55], Devign [56], and Big-Vul [57] datasets, with feature extractors including BERT [58], RoBERTa [59], CodeBERT [60], and UniXcoder [61]. Through these carefully designed and strictly controlled experimental conditions, we ensured that any performance differences between CGCE and the traditional CE method can be solely attributed to the design of the loss function, rather than to other external factors.

5.2. Evaluation Under Standard Conditions

In the standard setting, we primarily investigate the performance of CGCE in scenarios where data availability is ample, class distributions are balanced, and label quality is high. As shown in

Table 1. Accuracy (%) with confidence intervals of image classification models on datasets using traditional CE and CGCE. Both Top1 and Top5 accuracies are reported; the “Avg.” column indicates the average performance gain (in percentage points) of CGCE over CE across these metrics.

Model	Dataset	Top1 Acc (%)			Top5 Acc (%)
		CE	CGCE	Avg.	CE	CGCE	Avg.
ResNet-50	CIFAR-10	97.00 ± 0.12	97.08 ± 0.15	+0.08	99.97 ± 0.01	99.99 ± 0.00	+0.01
	CIFAR-100	83.86 ± 0.20	84.48 ± 0.22	+0.62	97.30 ± 0.08	97.40 ± 0.06	+0.10
	ImageNet	78.68 ± 0.25	79.27 ± 0.30	+0.57	92.81 ± 0.12	93.01 ± 0.08	+0.20
ViT	CIFAR-10	98.91 ± 0.08	99.15 ± 0.06	+0.24	99.96 ± 0.01	99.99 ± 0.01	+0.03
	CIFAR-100	91.92 ± 0.15	92.68 ± 0.18	+0.76	99.20 ± 0.02	99.32 ± 0.03	+0.12
	ImageNet	82.43 ± 0.18	83.01 ± 0.24	+0.58	95.95 ± 0.05	96.03 ± 0.11	+0.08

, we first compare the proposed CGCE with traditional CE on the CIFAR-10, CIFAR-100, and ImageNet datasets using ResNet-50 and Vision Transformer (ViT) as feature extractors. The results indicate that CGCE consistently achieves higher overall accuracy than CE. This suggests that CGCE effectively pulls sample features closer to their corresponding class representations, while simultaneously pushing them away from other classes in the feature space, thereby forming a clearer geometric boundary and enhancing both intra-class compactness and inter-class separability.

Moreover, we observe that, for relatively simple tasks (e.g., CIFAR-10 and the Top-5 accuracy metric), the improvements offered by CGCE are modest, likely because CE already performs exceptionally well under these conditions. In contrast, as dataset complexity increases (e.g., CIFAR-100 and ImageNet), the advantages of CGCE become more pronounced. A possible explanation lies in CGCE’s built-in contrastive learning mechanism: during training, positive samples are explicitly “pulled” toward the target class vector, while negative samples are “pushed” away from other class vectors. When the task grows more complex—thus increasing the number of classes and negative samples—CGCE can better exploit the abundant negative samples, refining the feature representation and constructing a more distinct geometric boundary that facilitates more accurate discrimination across classes.

The experimental results on text classification tasks, reported in

Table 2. Top-1 accuracy (%) with confidence intervals on various datasets using traditional CE and CGCE. The “Avg.” column indicates the average performance gain (in percentage points) of CGCE over CE.

Model	Dataset	CE	CGCE	Avg.
BERT	SST-2	92.66  ±  0.13	92.89  ±  0.08	+0.23
	SST-5	52.86  ±  0.35	53.32  ±  0.33	+0.46
	IMDB	93.20  ±  0.22	93.37  ±  0.20	+0.17
	AG News	94.11  ±  0.18	94.29  ±  0.16	+0.18
RoBERTa	SST-2	95.07  ±  0.25	95.64  ±  0.23	+0.57
	SST-5	54.59  ±  0.30	55.22  ±  0.18	+0.63
	IMDB	95.34  ±  0.16	95.42  ±  0.22	+0.08
	AG News	94.46  ±  0.18	94.60  ±  0.10	+0.14
CodeBERT	Devign	63.64  ±  0.40	65.28  ±  0.28	+1.64
	Big-Vul	98.14  ±  0.10	98.97  ±  0.16	+0.83
UniXcoder	Devign	67.74  ±  0.25	69.74  ±  0.33	+2.00
	Big-Vul	98.66  ±  0.08	99.27  ±  0.07	+0.61

, further corroborate the superior performance of CGCE compared to CE. We conjecture that CGCE capitalizes more effectively on the rich semantic information in pretrained language models: by introducing trainable class representation vectors, which can be semantically initialized via natural language label descriptions or class-average embeddings, CGCE is able to capture finer-grained semantic distinctions. During training, CGCE’s contrastive mechanism explicitly pulls each sample’s features closer to the appropriate semantic class vector, while pushing them away from irrelevant classes. This semantic contrast allows the model to more fully exploit the intrinsic semantic features of the pretrained model, thereby achieving higher accuracy and robustness in text classification scenarios.

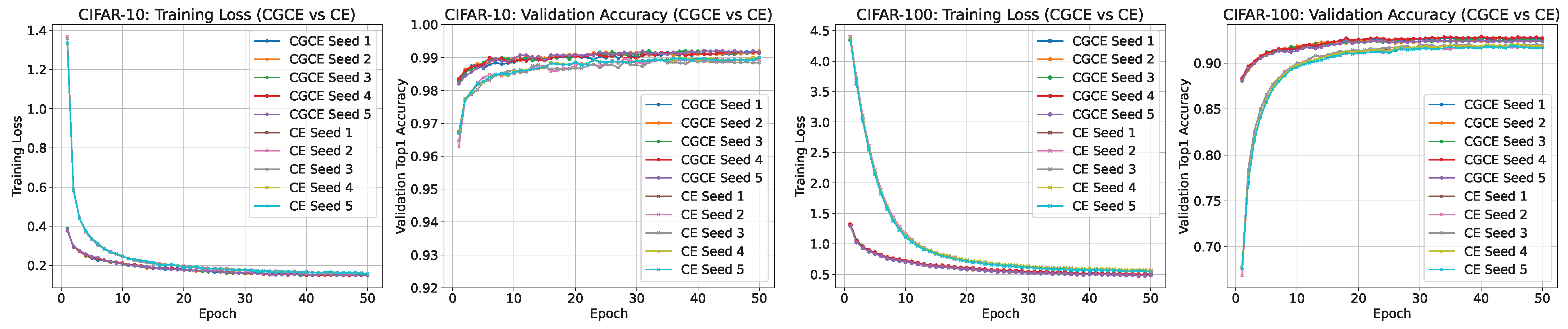
Rapid Convergence Property: One of the key practical advantages of the CGCE method is its rapid convergence capability. As shown in Figure 2, the training loss curve on the CIFAR-100 and CIFAR-10 dataset clearly indicates that, compared with the traditional Cross-Entropy method, the loss for CGCE decreases more rapidly in the initial training epochs. Specifically, for the same number of epochs, the CGCE method not only achieves a significantly lower training loss but also attains higher validation accuracy more quickly, approaching optimal performance within fewer epochs.

This rapid convergence property can be attributed to two main factors. First, the explicit geometric constraint mechanism in CGCE, which, through learnable class representation vectors, effectively pulls the sample features closer to their corresponding class vectors while pushing them away from others, rapidly establishing clear and stable decision boundaries early in training. Second, the use of class-average features from a pretrained model as the initial values for the class representation vectors ensures that these vectors are closer to the true data distribution, further accelerating early convergence.

5.3. Performance Evaluation Under Complex Conditions

To evaluate the applicability of CGCE under more complex conditions, we designed three sets of experiments to assess its performance in scenarios involving data scarcity, class imbalance, and label noise.

Data Scarcity: In the CIFAR-10, CIFAR-100, ImageNet, and SST-2 datasets, we progressively reduced the number of samples per class (e.g., from 200 samples down to 1 sample) to evaluate the generalization capability of CGCE under limited data conditions. The results, as shown in

Table 3. Accuracy (%) with confidence intervals: comparison of traditional CE and CGCE across datasets and sample sizes (N: samples per class). The “Avg.” column shows the mean improvement (in percentage points) of CGCE over CE.

Dataset	Method	N = 200	N = 100	N = 50	N = 20	N = 10	N = 5	N = 2	N = 1	Avg.
CIFAR-10	CE	97.06 ± 0.47	95.98 ± 0.53	95.18 ± 0.42	91.49 ± 0.67	73.87 ± 1.12	63.20 ± 1.65	53.15 ± 2.43	45.63 ± 3.25	-
	CGCE	98.09 ± 0.52	97.91 ± 0.38	97.50 ± 0.33	96.48 ± 0.45	93.59 ± 0.80	86.41 ± 2.10	75.82 ± 1.80	61.75 ± 2.40	+11.50
CIFAR-100	CE	90.02 ± 0.68	88.57 ± 0.47	86.47 ± 0.41	83.69 ± 0.95	78.05 ± 1.35	66.70 ± 1.85	44.14 ± 2.62	25.10 ± 3.10	-
	CGCE	91.42 ± 0.42	89.96 ± 0.52	88.75 ± 0.65	86.28 ± 0.70	81.12 ± 0.92	72.97 ± 1.45	51.24 ± 2.33	36.30 ± 3.31	+4.42
ImageNet	CE	79.13 ± 0.38	78.27 ± 0.35	77.26 ± 0.62	72.55 ± 0.92	68.85 ± 1.60	55.55 ± 2.26	11.60 ± 2.26	1.41 ± 1.20	-
	CGCE	81.03 ± 0.45	80.63 ± 0.42	80.35 ± 0.48	79.73 ± 1.08	78.80 ± 1.42	76.66 ± 1.41	68.68 ± 2.80	57.70 ± 3.28	+19.87
SST-2	CE	86.58 ± 0.63	64.56 ± 0.78	62.39 ± 0.56	49.32 ± 1.05	49.54 ± 1.30	49.08 ± 1.32	49.08 ± 1.84	49.08 ± 1.80	-
	CGCE	88.99 ± 0.38	89.68 ± 0.25	88.07 ± 0.85	77.06 ± 1.10	55.05 ± 1.41	53.56 ± 1.05	55.50 ± 1.23	57.80 ± 1.45	+13.26

, indicate that, even under extreme data scarcity, CGCE maintains high accuracy and effectively mitigates the risk of overfitting.

Class Imbalance: In this experiment, we divided all classes into two groups by designating half of the classes as majority classes (with a larger number of samples) and the other half as minority classes (with fewer samples). We then manually adjusted the sample ratio between the majority and minority classes to simulate extreme imbalance. As presented in

Table 4. Accuracy (%) with confidence intervals for CE and CGCE across datasets and imbalance ratios (IRs).

Method	SST-2			CIFAR-100			ImageNet			Avg.
	IR = 0.05	IR = 0.1	IR = 0.5	IR = 0.05	IR = 0.1	IR = 0.5	IR = 0.05	IR = 0.1	IR = 0.5
CE	88.07 ± 0.37	91.28 ± 0.23	92.43 ± 0.31	59.72 ± 0.55	80.78 ± 0.45	90.71 ± 0.65	53.31 ± 0.43	75.94 ± 0.35	81.68 ± 0.55	–
CGCE	88.30 ± 0.42	91.06 ± 0.27	92.66 ± 0.20	82.39 ± 0.48	88.22 ± 0.42	92.10 ± 0.35	73.58 ± 0.62	76.66 ± 0.52	81.87 ± 0.48	+5.88

, the results demonstrate that CGCE is better able to preserve the features of minority classes, thereby improving overall classification performance and significantly alleviating the performance degradation caused by class bias.

Label Noise: In the SST-2, CIFAR-100, and ImageNet datasets, we introduced erroneous labels at rates of 20%, 30%, and 50%, respectively, to assess the robustness of CGCE against label noise. As shown in

Table 5. Accuracy (%) with confidence intervals for CE and CGCE across datasets and noise ratios (NRs).

Method	SST-2			CIFAR-100			ImageNet			Avg.
	NR = 0.5	NR = 0.3	NR = 0.2	NR = 0.5	NR = 0.3	NR = 0.2	NR = 0.5	NR = 0.3	NR = 0.2
CE	50.69 ± 0.45	89.79 ± 0.23	91.51 ± 0.27	48.38 ± 0.62	59.46 ± 0.38	62.42 ± 0.65	82.23 ± 0.47	82.19 ± 0.33	82.32 ± 0.56	–
CGCE	53.33 ± 0.38	89.68 ± 0.18	91.86 ± 0.34	50.88 ± 0.45	60.03 ± 0.52	63.47 ± 0.40	82.68 ± 0.55	82.61 ± 0.42	82.61 ± 0.48	+0.91

, although the presence of noise reduces overall accuracy, the performance drop in CGCE is noticeably smaller than that observed with traditional CE, confirming its stronger noise resilience.

In summary, these experiments under complex scenarios thoroughly validate the stability and superiority of CGCE when addressing challenges such as data scarcity, class imbalance, and label noise, thereby demonstrating its broad applicability in practical applications.

6. Discussion

Although CGCE demonstrates excellent classification performance and generalization ability, its practical deployment is still influenced by several factors. To comprehensively evaluate its feasibility and applicability, this paper conducts an in-depth analysis of CGCE from three perspectives: computational complexity and resource overhead, the impact of temperature coefficient $\tau$ adjustment, and the initialization strategies of class representation vectors. This analysis aims to reveal the design trade-offs of CGCE and provide practical insights for future applications.

6.1. Computational Complexity and Memory Footprint Analysis

To evaluate the computational efficiency of the proposed CGCE method in practical applications, we performed a comprehensive analysis of its computational complexity and memory consumption, comparing it with the traditional cross-entropy method combined with a linear classifier.

In our theoretical analysis, assuming a batch size N, feature dimensionality d, and number of classes K, the traditional cross-entropy approach processes each sample feature $\mathbf{z}\in {\mathbb{R}}^d$ with a linear classifier by computing the class scores as $s_k={\mathbf{w}}_k^{\top }\mathbf{z}+b_k$ for $k=1,\dots ,K$, where $\mathbf{W}\in {\mathbb{R}}^{K\times d}$ and $\mathbf{b}\in {\mathbb{R}}^K$ are used. Since each $s_k$ involves d multiply-add operations, the per-sample complexity is $O(K·d)$ and the batch complexity is $O(N·K·d)$. The storage requirement, given by $K·d+K$, is approximately $O(K·d)$ for large d relative to K.

In contrast, the CGCE method introduces trainable class vectors ${\mathbf{u}}_k\in {\mathbb{R}}^d$ (for $k=1,\dots ,K$) and computes the similarity $L_k=\tau \langle \mathbf{z},{\mathbf{u}}_k\rangle$ (with temperature $\tau$) during the forward pass. This computation also takes d multiply-add operations per class, resulting in per-sample and batch complexities of $O(K·d)$ and $O(N·K·d)$, respectively, with a memory footprint of $K\times d$ parameters, i.e., $O(K·d)$.

Thus, both methods exhibit a forward computational complexity of $O(N·K·d)$ and similar memory requirements of $O(K·d)$ without additional overhead. We further validated these conclusions experimentally;

Table 6. Comparison of training time (T (s)) and peak GPU memory usage (Mem (MB)) for different loss functions across multiple dataset–model combinations.

Dataset & Model	Loss	T (s)	Mem (MB)
CIFAR-100, ResNet-50	CE	43	7033
	CGCE	43	7049
ImageNet, ViT	CE	1 817	20,751
	CGCE	1817	20,605
SST-2, BERT	CE	311	12,077
	CGCE	311	12,077

shows the per-epoch runtime (in seconds) and memory usage (in MB) for both methods under identical conditions. The experimental results confirm that both methods have nearly identical per-epoch runtime and memory consumption, consistent with our theoretical analysis.

6.2. Impact of the Temperature Coefficient $\tau$ on Classification Accuracy

In the CGCE framework, the temperature coefficient $\tau$ modulates the dot product $\langle \mathbf{z},{\mathbf{u}}_y\rangle$ between the feature embedding $\mathbf{z}=f_{\theta }\left(x\right)$ and the class representation vector ${\mathbf{u}}_y$, thereby affecting both the contrastive loss and the softmax distribution. When $\tau$ is small, the model accentuates differences between classes, resulting in a “peaked” output distribution that clearly separates positive and negative examples in the embedding space, which is beneficial for simpler tasks (e.g., CIFAR-10); however, excessive separation may lead to training instability or overfitting. Conversely, an excessively large $\tau$ yields overly smooth class distinctions, weakening decision boundaries and degrading classification performance.

As shown in

Table 7. Impact of different temperature coefficients $\tau$ on classification accuracy (%) across various datasets.

Dataset	Model	Temperature Coefficient $\mathit{\tau }$
		$\mathbf{\tau }=\mathbf{0}.\mathbf{01}$	$\mathbf{\tau }=\mathbf{0}.\mathbf{05}$	$\mathbf{\tau }=\mathbf{0}.\mathbf{07}$	$\mathbf{\tau }=\mathbf{0}.\mathbf{1}$	$\mathbf{\tau }=\mathbf{0}.\mathbf{2}$	$\mathbf{\tau }=\mathbf{0}.\mathbf{3}$	$\mathbf{\tau }=\mathbf{0}.\mathbf{5}$	$\mathbf{\tau }=\mathbf{1}.\mathbf{0}$
CIFAR-10	ResNet-50	97.07 ± 0.17	96.93 ± 0.14	97.03 ± 0.16	97.08 ± 0.15	96.84 ± 0.13	96.73 ± 0.18	96.61 ± 0.22	96.30 ± 0.21
	ViT	99.15 ± 0.06	99.08 ± 0.06	99.05 ± 0.07	99.08 ± 0.06	98.96 ± 0.07	98.82 ± 0.08	96.60 ± 0.11	96.40 ± 0.13
CIFAR-100	ResNet-50	84.19 ± 0.32	84.48 ± 0.28	84.12 ± 0.33	82.79 ± 0.37	82.86 ± 0.29	78.34 ± 0.42	68.84 ± 0.48	58.36 ± 0.55
ImageNet	ResNet-50	78.80 ± 0.42	79.27 ± 0.30	79.13 ± 0.39	78.77 ± 0.38	76.04 ± 0.43	72.55 ± 0.47	69.23 ± 0.53	66.18 ± 0.57
	ViT	82.29 ± 0.31	82.89 ± 0.26	82.79 ± 0.28	83.01 ± 0.24	81.40 ± 0.32	79.62 ± 0.37	78.03 ± 0.41	77.63 ± 0.42
Devign	UniXcoder	67.44 ± 0.43	69.01 ± 0.38	69.15 ± 0.37	69.67 ± 0.32	69.74 ± 0.33	69.23 ± 0.38	68.20 ± 0.42	67.65 ± 0.47

, our experiments on CIFAR-10, CIFAR-100, ImageNet, and Devign reveal a single-peaked trend in accuracy as $\tau$ increases. For datasets with many classes and higher complexity (e.g., CIFAR-100 and ImageNet), a moderate $\tau$ helps capture subtle inter-class differences without collapsing similar classes, while for simpler tasks a smaller $\tau$ accelerates convergence. Moreover, different network architectures exhibit varying sensitivity to $\tau$; for instance, ResNet performs well with a slightly lower $\tau$ due to its strong spatial priors, whereas ViT benefits from a moderate $\tau$ that balances contrastive separation and generalization.

Overall, we recommend using $\tau =0.1$ as an initial value, with further tuning based on dataset complexity and network architecture to achieve the optimal balance between training stability and generalization.

6.3. Impact of Class Representation Initialization

This section aims to investigate the effect of different initialization methods for the class representation vectors in the CGCE framework on model convergence speed and overall performance. According to the design of CGCE, the class representation vectors can be initialized in three ways: (1) in the absence of prior information, the vectors can be initialized using a random normal distribution to ensure generality and robustness; (2) when a pretrained model is available, the average feature vectors of samples from each class, as extracted by the pretrained model, can be used as the initial values to better align with the true feature distributions; and (3) when abundant semantic information is present, the natural language description of the labels can be fed into the pretrained feature extractor to obtain corresponding semantic embeddings as the initial class representations.

We conducted experiments on text classification tasks (using the SST-2 dataset with the RoBERTa-base model) and image classification tasks (using the CIFAR-100 and ImageNet datasets with the ViT model) to compare the effects of these three initialization methods on model performance.

As shown in

Table 8. Final accuracy of CGCE with different class representation initializations.

Dataset	Initialization Method	Accuracy (%)
CIFAR-100	Category Average Vector	$\mathbf{92}.\mathbf{68}\pm \mathbf{0}.\mathbf{18}$
	Random Normal Distribution	$92.52\pm 0.16$
ImageNet	Category Average Vector	$\mathbf{83}.\mathbf{01}\pm \mathbf{0}.\mathbf{24}$
	Random Normal Distribution	$82.95\pm 0.23$
SST-2	Label Text Description	$94.61\pm 0.27$
		$\mathbf{95}.\mathbf{64}\pm \mathbf{0}.\mathbf{23}$
		$95.42\pm 0.26$
	Category Average Vector	$95.30\pm 0.19$
	Random Normal Distribution	$95.30\pm 0.21$

, in image classification, using category average vectors for initialization modestly boosts final accuracy by better capturing true feature distributions and offering a more informative start. Although the performance gap with random initialization narrows over time, the category average method still provides a significant advantage when training time or resources are limited.

For text classification, initializing class representations with label text descriptions generally achieves the highest accuracy by directly embedding rich semantic information. However, the effectiveness of these descriptions can vary, and determining the optimal phrasing remains a challenging issue.

Overall, the choice of initialization strategy critically impacts both the training dynamics and final performance of the CGCE framework. Under limited training conditions, category average or label text description initialization can significantly improve accuracy, while with ample training, even random initialization can eventually yield comparable results. These findings underscore the robustness and flexibility of CGCE across different initialization methods, offering practical options for diverse applications.

7. Conclusions

This work proposes a novel classification framework—Contrastive Geometric Cross-Entropy (CGCE)—which explicitly enhances both intra-class compactness and inter-class separability in the feature space by introducing learnable class representation vectors, all without incurring additional computational or memory overhead. Theoretically, CGCE naturally forms clear and measurable decision boundaries as the loss converges, and empirical results indicate that it achieves excellent discriminative performance and rapid convergence under standard conditions, while also exhibiting strong robustness in challenging scenarios such as data scarcity, class imbalance, and label noise.

Nonetheless, CGCE does have certain limitations in practice. In large-scale image tasks, the computation of class averages introduces extra overhead, and in text tasks, reliance on semantic label descriptions may lead to additional computational cost or semantic deviations. Future work could explore integrating multimodal priors, adapting CGCE to incremental or online learning, and employing large-scale pretrained models to automatically generate label descriptions, thereby further enhancing its practicality and extensibility.

Overall, CGCE offers a simple and efficient alternative for multi-class classification by bridging geometric representation learning and probabilistic modeling. Its fast convergence, strong performance, and extensibility make it a promising direction for future research in both academic and practical domains.