A Comprehensive Review of Satellite Orbital Placement and Coverage Optimization for Low Earth Orbit Satellite Networks: Challenges and Solutions
Abstract
1. Introduction
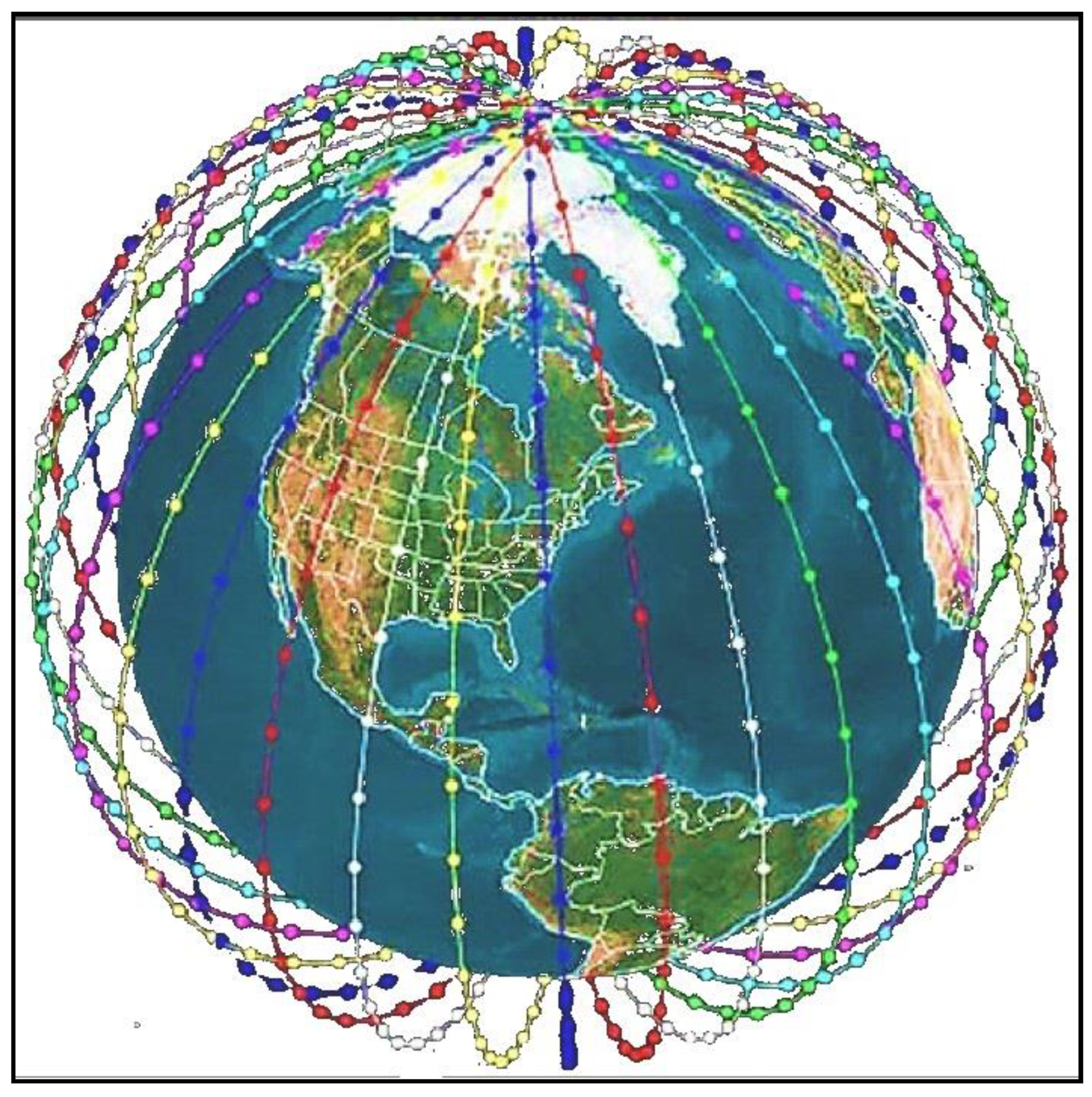
1.1. Satellite Constellation Architecture
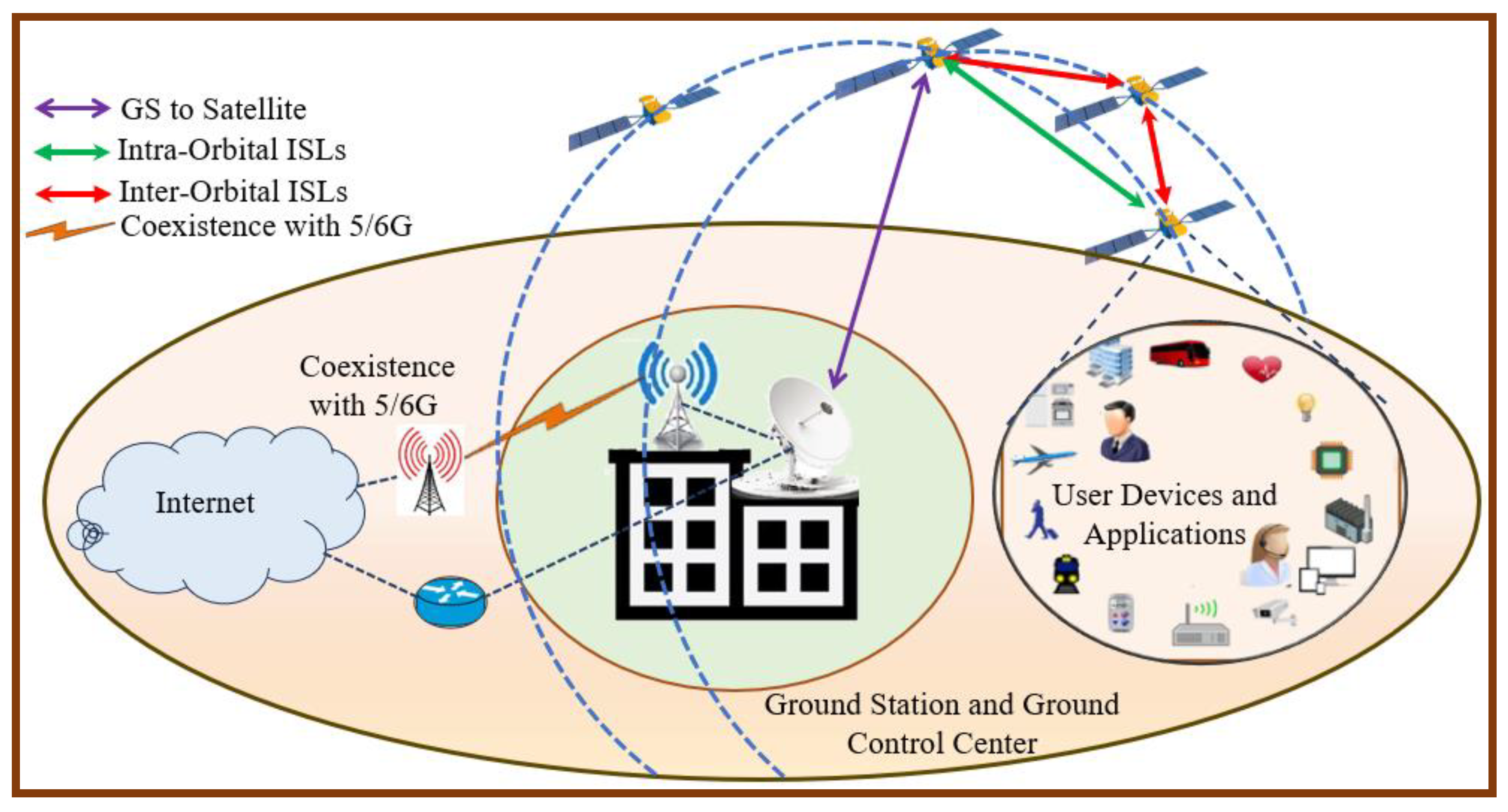
1.2. Operation of LEO Satellite Networks
- Direct Connection: The user device connects directly to the satellites that cover the user device’s area.
- Satellite Relay: The satellites are equipped with an onboard LTE/5/6G modem (eNodeB) which acts like a cell tower in space that can receive from and transmit to user devices.
- Inter-Satellite Links (ISLs): The satellite uses laser ISLs to transmit the signal across the satellite network toward the satellite that is positioned over a GS.
- Ground Station Link: The signal is then downlinked to a GS connected to terrestrial networks that can provide an internet backbone.
1.3. Problem Statement and Research Motivation
1.4. Research Contribution
- It reviews the optimization methods of SOP and coverage for LEO networks. It highlights the main parameters that have been considered in increasing internet connectivity, coverage area, and reliability.
- It analyses the LEO parameters that can mitigate the effect of signal impairments and space debris, and it enhances the swath width for the LEO satellite network.
- It suggests two solutions for SOP and coverage optimization for LEO networks based on effective machine learning algorithms.
2. Related Works
2.1. Related Work on Satellite Orbital Placement
2.2. Related Work on Optimization of LEO Coverage Area
2.3. Related Work on LEO Orbital Signal Impairments
3. Analysis of Satellite Orbital Placement and Coverage Optimization for LEO
3.1. Orbital Parameters and Their Impact
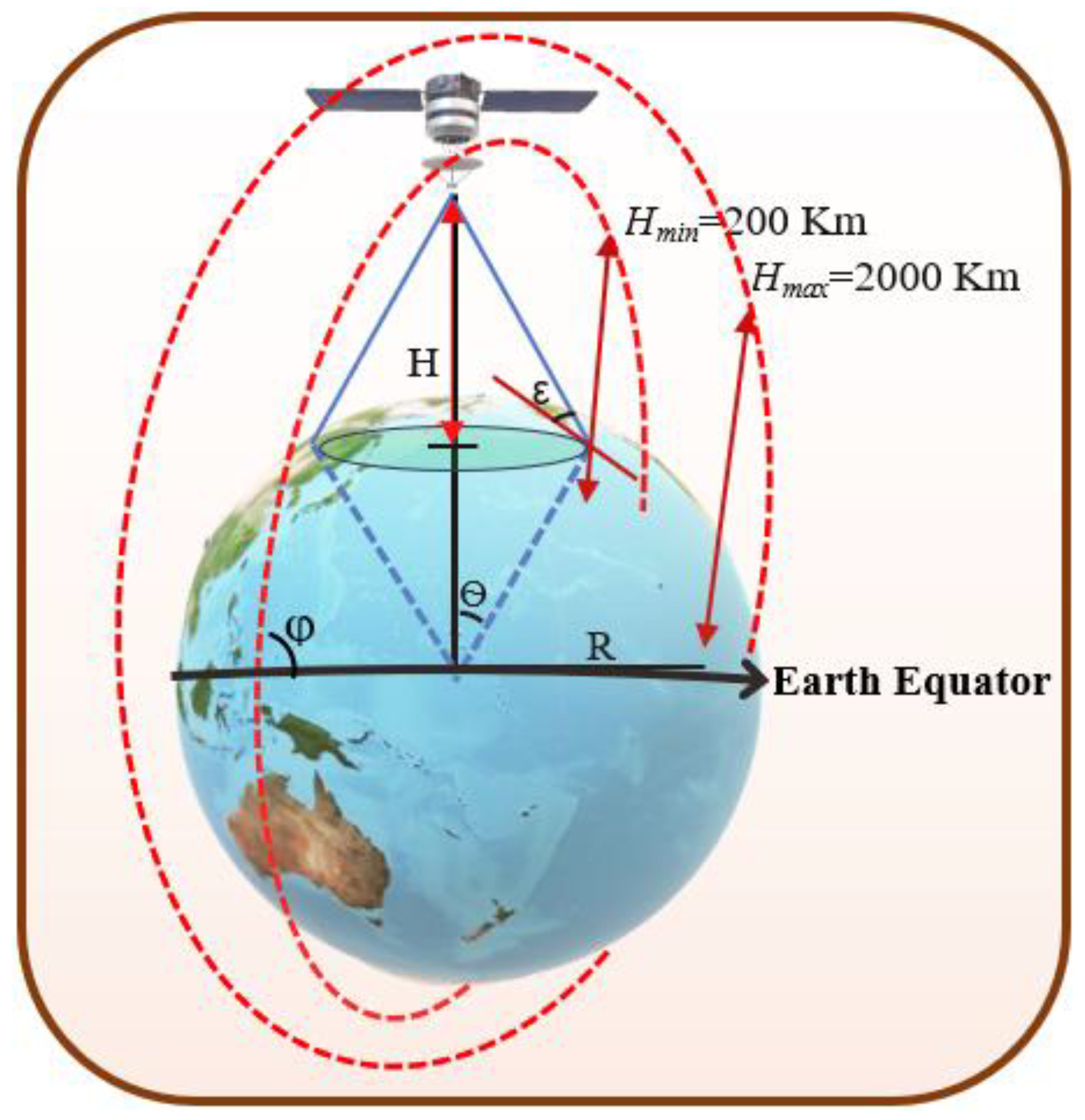
3.1.1. Satellite Coverage Area
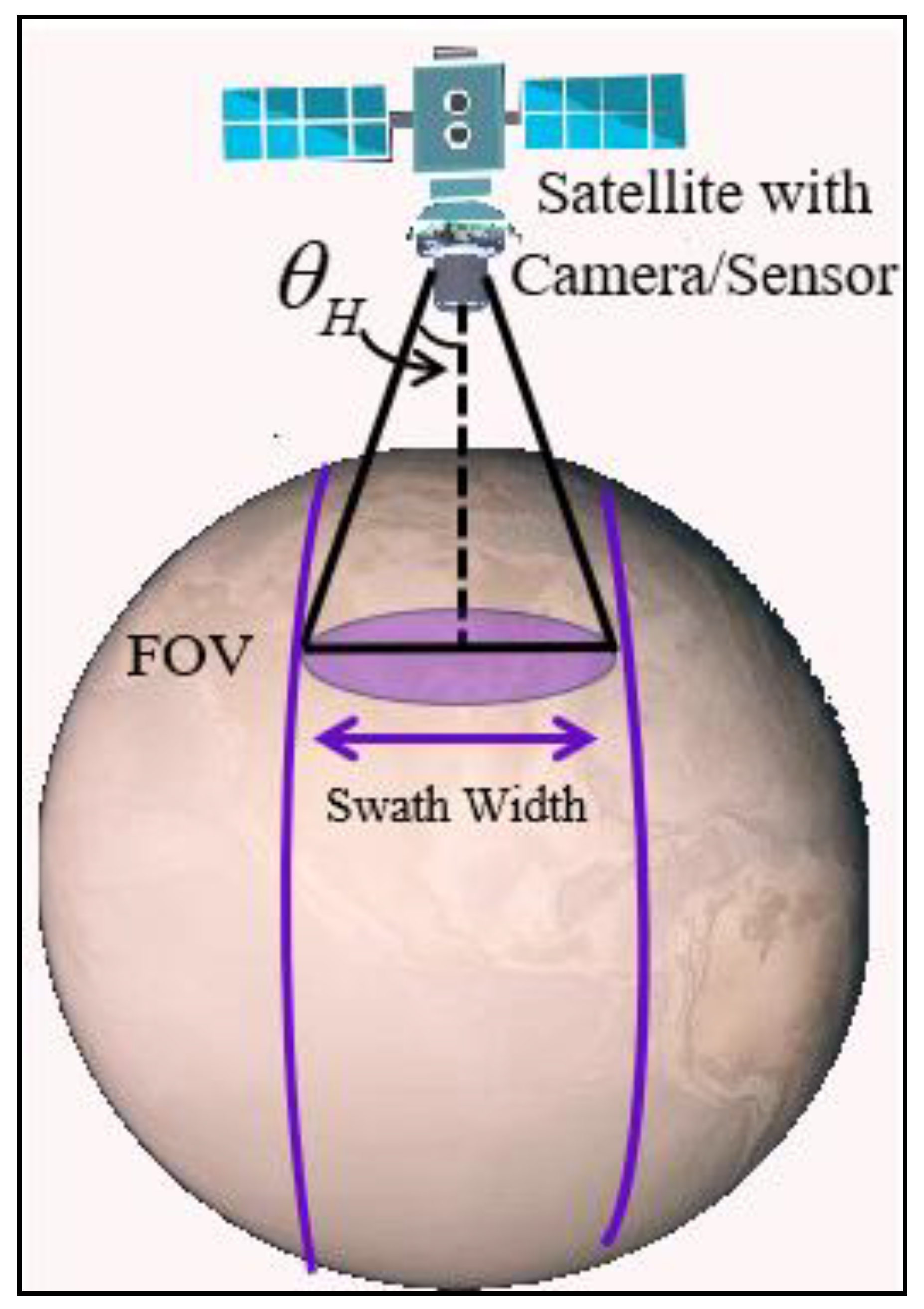
3.1.2. Satellite Swath Width
3.1.3. LEO Space Debris
3.1.4. LEO Signal Impairments
- Intra-System Interference: Beams from adjacent satellites can overlap, which causes interference for users on the ground.
- Inter-System Interference: Interference from satellites in different LEO constellations or from satellites in higher orbits (MEO/GEO) that use adjacent frequency bands.
- Terrestrial Interference: Signals from ground-based systems such as 5G towers, Wi-Fi networks, and microwave signals are a major source of interference.
- Space Weather: Solar flares and geomagnetic storms cause signal attenuation or noise.
- Intentional Interference (Jamming): Malicious attempts to transmit powerful signals at a satellite to disrupt its communication link.
- Multipath and Doppler Effects: Caused by fast satellite movement and terrain-based signal reflection.
4. Discussion of Satellite Orbital Placement Proposed Solutions
4.1. Satellite Orbital Placement Proposed Solution
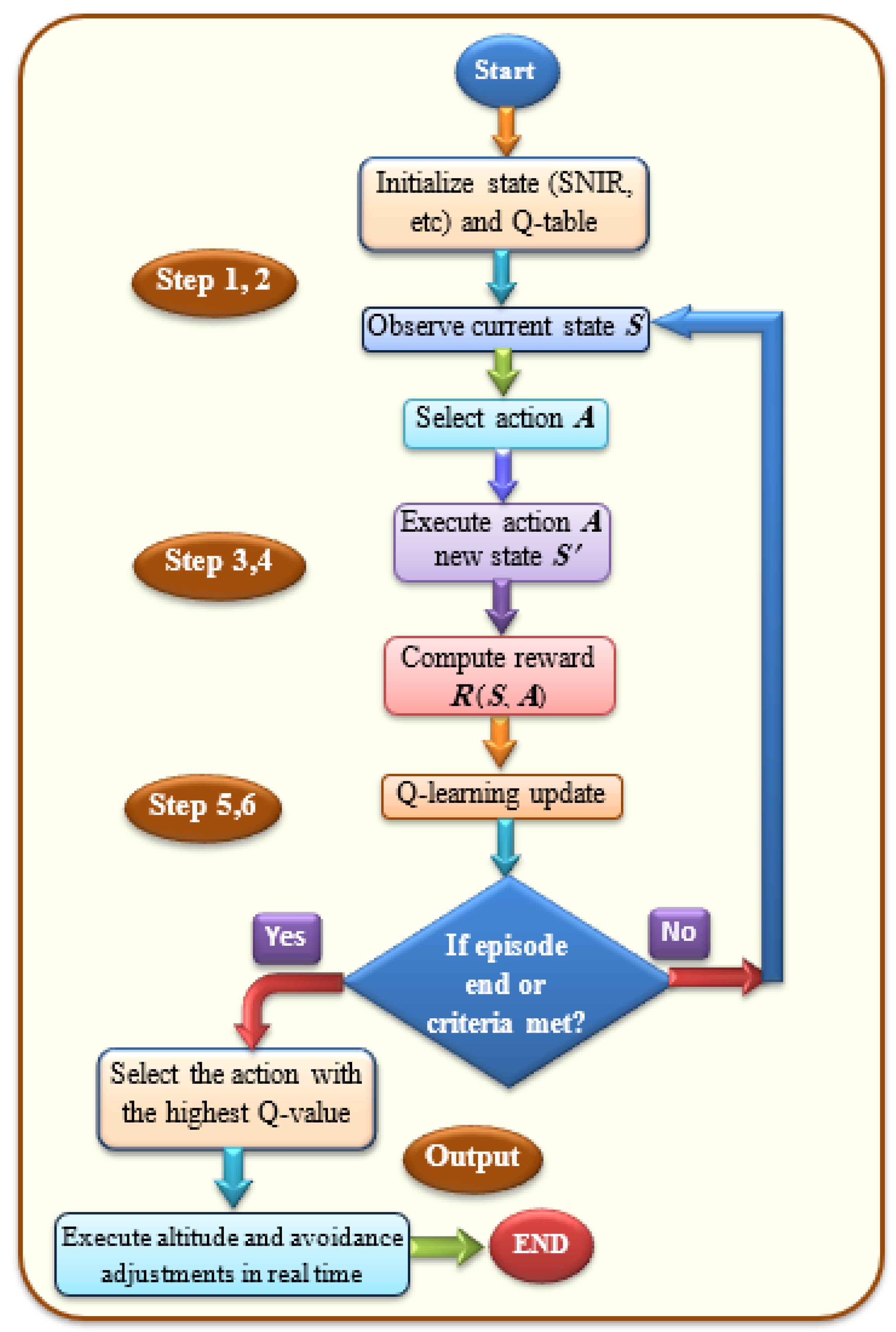
- Step 1: Define state and action.States include current altitude, SINR, latency, debris encounter rates, and estimated collision probability.Actions consist of discrete or continuous orbital actions such as altitude adjustments, inclination shifts, and short collision avoidance.
- Step 2: Initialize the matrix Q of DRL.The Q-matrix must be constructed and initialized to 0. The columns represent all possible actions, while the rows represent the states for each action.
- Step 3: Select and perform action.For each episode, an agent takes an action (e.g., adjust altitude or perform collision avoidance), transitions to the next state , and receives a reward .
- Step 4: Reward estimation.The reward in Equation (7) is computed.
- Step 5: Q-value update and evaluation.
- Step 6: Integrated collision avoidance.Collision avoidance is embedded within the action space and reward function. Consequently, an AI system with an advanced detection system should be applied for each satellite to perform real-time orbital adjustments.
- A learned Q-table that maps each state (including current altitude, debris count, SINR, etc.) to action values.
- A policy that chooses the action with the highest Q-value in each state. This translates to recommended orbital placement and operation commands for each satellite agent.
- Select optimal action via the learned policy.
- Execute altitude and avoidance adjustments in real time.
4.2. Coverage Optimization Proposed Solution
- Step 1: Obtain the value of SOP.The latitude (H) should be estimated from the previous algorithm of orbital placement because it is an important parameter in the coverage area equation.
- Step 2: Determine the weightage for each involved parameter.The satellite should autonomously adjust values of inclination angle, elevation angle, and swath width. The number of satellites in each orbit is determined to reliably cover the whole ground. Weights for each parameter are calculated based on their relative impact on communication and coverage performance.
- Step 3: Use optimization function.We suggest using heuristic or metaheuristic algorithms such as Genetic Algorithms (GAs), Particle Swarm Optimization (PSO), Simulated Annealing (SA), and Ant Colony Optimization (ACO) for real-time optimization of satellite coverage. Heuristic and metaheuristic algorithms have several advantages compared to exact or gradient-based methods in satellite coverage optimization because they show outstanding performance in managing complex, high-dimensional, and nonlinear search spaces without requiring derivative information [50,51,52,53,54,55,56,57,58]. Also, they show a critical advantage for real-time satellite operations because they are computationally efficient and scalable, delivering near-optimal solutions much faster than exact methods. Their flexibility allows them to easily incorporate additional constraints or objectives such as geological models, communication quality, or collision avoidance, while balancing global exploration with local exploitation.
- Step 4: Communication evaluation.The link quality and reliable internet connectivity should be evaluated for each coverage optimization selection.
- Step 5: Select optimal coverage area parameters.After evaluation of each selection, the most optimal value of inclination angle, elevation angle, and swath width are determined based on the latitude value that is estimated in Equations (3) and (5).
4.3. Expected Results
- Orbital Placement Based on DRL Solution
- ○
- Improve collision avoidance efficiency by dynamically selecting altitudes and inclinations with lower debris density and risk.
- ○
- Achieve a higher long-term SINR and lower end-to-end delay through learning-based altitude and position adjustment.
- ○
- Maximize a multi-objective reward that balances signal quality, latency, collision risk, and debris avoidance.
- ○
- Enable satellites to adapt in real time to orbital decay, space weather effects, and traffic density, which will reduce the need for manual control.
- Coverage Optimization Based on Metaheuristic Methods
- ○
- Increase total coverage area per satellite or constellation through dynamic adjustment of inclination and swath width.
- ○
- Enhance link reliability and throughput, especially in high-demand areas, by optimizing elevation and footprint overlap.
- ○
- Provide scalable and near-optimal coverage planning that can adapt to different orbital altitudes or regional requirements.
- ○
- Enable autonomous satellite configuration, reducing ground control workload and improving operational flexibility.
5. Limitations and Future Works
- Computational Cost and Energy Consumption: DRL training requires large-scale computation, typically performed on high-performance GPUs or distributed cloud servers. Although the optimization phase occurs at the ground station, frequent retraining for changing orbital dynamics could require significant energy and cost resources.
- Communication Delays and Bandwidth Constraints: Real-time orbital adjustments depend on timely uplink/downlink between satellites and ground stations. The latency of transmitting control commands, especially during high-traffic periods can degrade the responsiveness of AI-driven placement decisions.
- Security and Cyber-Resilience Risks: The use of AI-driven autonomous decision-making increases vulnerability to cyberattacks, data spoofing, or adversarial manipulation of state inputs. Such attacks could lead to unsafe orbital maneuvers or degraded coverage performance if not addressed with robust authentication and encryption mechanisms.
- Explainability and Regulatory Compliance: Regulatory bodies often require transparent decision-making processes for orbital maneuvers. Black-box models like DRL pose challenges for interpretability, which may slow down approval processes or raise trust issues among operators and policymakers.
- Scope of Evaluation: This study primarily focuses on orbital placement and coverage optimization. It does not yet fully integrate power management, inter-satellite routing, or payload optimization, which are critical for comprehensive LEO network performance.
6. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Çelikbilek, K.; Lohan, E.S.; Praks, J. Optimization of a LEO-PNT Constellation: Design Considerations and Open Challenges. Int. J. Satell. Commun. Netw. 2025, 43, 272–292. [Google Scholar] [CrossRef]
- Prol, F.S.; Bhuiyan, M.Z.H.; Kaasalainen, S.; Lohan, E.S.; Praks, J.; Çelikbilek, K.; Kuusniemi, H. Simulations of Dedicated LEO-PNT Systems for Precise Point Positioning: Methodology, Parameter Analysis, and Accuracy Evaluation. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 6499–6516. [Google Scholar] [CrossRef]
- Liu, J.; Hao, J.; Yang, Y.; Xu, Z.; Liu, W.; Wu, R. Design optimisation of low earth orbit constellation based on BeiDou Satellite Navigation System precise point positioning. IET Radar, Sonar Navig. 2022, 16, 1241–1252. [Google Scholar] [CrossRef]
- Nardin, A.; Dovis, F.; Fraire, J.A. Empowering the Tracking Performance of LEO-Based Positioning by Means of Meta-Signals. IEEE J. Radio Freq. Identif. 2021, 5, 244–253. [Google Scholar] [CrossRef]
- Frąckiewicz, M. Sky-Fi Revolution: How Starlink Is Reshaping Global Internet Access. Available online: https://ts2.tech/en/sky-fi-revolution-how-starlink-is-reshaping-global-internet-access (accessed on 29 May 2025).
- Wu, Z.; Ni, S.; Xiao, W.; Li, Z.; Liu, H. Study on the Feasibility and Performance Evaluation of High-Orbit Spacecraft Orbit Determination Based on GNSS/SLR/VLBI. Remote Sens. 2024, 16, 4214. [Google Scholar] [CrossRef]
- Page, P.S.; Bhargao, K.S.; Baviskar, H.V.; Kasbekar, G.S. Distributed probabilistic congestion control in LEO satellite networks. In Proceedings of the 2023 15th International Conference on Communication Systems & Networks (COMSNETS), Bangalore, India, 3–8 January 2023; pp. 335–339. [Google Scholar]
- Ekici, E.; Akyildiz, I.F.; Bender, M.D. Datagram routing algorithm for LEO satellite networks. In Proceedings of the IEEE INFOCOM 2000. Conference on Computer Communications. Nineteenth Annual Joint Conference of the IEEE Computer and Communications Societies (Cat. No. 00CH37064), Tel Aviv, Israel, 26–30 March 2000; Volume 2, pp. 500–508. [Google Scholar]
- The Many Locations for Space Science Missions, Satellite Orbits. Available online: https://www.teledyne.com/digital-imaging-space-science-monthly/satellite-orbits (accessed on 25 April 2025).
- Wang, R.; Kishk, M.A.; Alouini, M.-S. Stochastic Geometry-Based Low Latency Routing in Massive LEO Satellite Networks. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 3881–3894. [Google Scholar] [CrossRef]
- Guo, J.; Rincon, D.; Sallent, S.; Yang, L.; Chen, X.; Chen, X. Gateway placement optimization in LEO satellite networks based on traffic estimation. IEEE Trans. Veh. Technol. 2021, 70, 3860–3876. [Google Scholar] [CrossRef]
- Fontanesi, G.; Ortíz, F.; Lagunas, E.; Baeza, V.M.; Vázquez, M.; Vásquez-Peralvo, J.A.; Minardi, M.; Vu, H.-N.; Honnaiah, P.J.; Lacoste, C.; et al. Artificial Intelligence for Satellite Communication and Non-Terrestrial Networks: A Survey. arXiv 2023, arXiv:2304.13008. [Google Scholar] [CrossRef]
- Shang, Z. Towards Future Communication: AI-Based Satellite Constellation Orbit Optimization and Design for Underserved Areas. TechRxiv 2025. [Google Scholar] [CrossRef]
- Prol, F.S.; Ferre, R.M.; Saleem, Z.; Valisuo, P.; Pinell, C.; Lohan, E.S.; Elsanhoury, M.; Elmusrati, M.; Islam, S.; Celikbilek, K.; et al. Position, navigation, and timing (PNT) through low earth orbit (LEO) satellites: A survey on current status, challenges, and opportunities. IEEE Access 2022, 10, 83971–84002. [Google Scholar] [CrossRef]
- Ge, H.; Li, B.; Nie, L.; Ge, M.; Schuh, H. LEO constellation optimization for LEO enhanced global navigation satellite system (LeGNSS). Adv. Space Res. 2020, 66, 520–532. [Google Scholar] [CrossRef]
- Çelikbilek, K.; Saleem, Z.; Ferre, R.M.; Praks, J.; Lohan, E.S. Survey on optimization methods for LEO-satellite-based networks with applications in future autonomous transportation. Sensors 2022, 22, 1421. [Google Scholar] [CrossRef] [PubMed]
- Guo, J.; Wang, Y.; Xie, X.; Sun, C. A fast satellite selection algorithm for positioning in LEO constellation. Adv. Space Res. 2024, 73, 271–285. [Google Scholar] [CrossRef]
- Ghoniem, I.F.; Mousa, A.E.-K.; El-Fiky, G. GNSS-RO LEO satellite orbit optimization for Egypt and the Middle East region. Alex. Eng. J. 2020, 59, 389–397. [Google Scholar] [CrossRef]
- Imoto, Y.; Satoh, S.; Obata, T.; Yamada, K. Optimal constellation design based on satellite ground tracks for Earth observation missions. Acta Astronaut. 2023, 207, 1–9. [Google Scholar] [CrossRef]
- Xue, W.; Hu, M.; Ruan, Y.; Wang, X.; Yu, M. Research on Design and Staged Deployment of LEO Navigation Constellation for MEO Navigation Satellite Failure. Remote Sens. 2024, 16, 3667. [Google Scholar] [CrossRef]
- Cakaj, S. The coverage belt for low earth orbiting satellites. In Proceedings of the 39th International Convention on Information and Communication Technology, Electronics and Microelectronics (ICICTEM), Opatija, Croatia, 30 May 2016; pp. 554–557. [Google Scholar]
- Cakaj, S.; Kamo, B.; Lala, A.; Rakipi, A. The coverage analysis for low earth orbiting satellites at low elevation. Int. J. Adv. Comput. Sci. Appl. 2014, 5, 6–10. [Google Scholar] [CrossRef]
- Zhu, T.G.; Solosa, S.S.; Maniani, P. Modeling and optimization of multi-altitude leo satellite networks using cox point processes: Towards efficient coverage and performance analysis. Int. J. Enterp. Model. 2023, 17, 35–44. [Google Scholar] [CrossRef]
- Silvirianti, X.; Kaddoum, G. Quantum Adaptive Learning for Coverage Optimization in LEO Satellite Network. TechRxiv 2025. [Google Scholar] [CrossRef]
- Shin, J.; Park, S.-Y.; Son, J.; Song, S.-C. Design of regional coverage low earth orbit (LEO) constellation with optimal inclination. J. Astron. Space Sci. 2021, 38, 217–227. [Google Scholar] [CrossRef]
- Lluch, I.; Golkar, A. Satellite-to-satellite coverage optimization approach for opportunistic inter-satellite links. In Proceedings of the 2014 IEEE Aerospace Conference, Big Sky, MT, USA, 1–8 March 2014; pp. 1–13. [Google Scholar]
- Lee, M.; Kim, S.; Kim, M.; Jung, D.-H.; Choi, J. Analyzing downlink coverage in clustered low earth orbit satellite constellations: A stochastic geometry approach. IEEE Trans. Commun J. 2025. [Google Scholar] [CrossRef]
- Zong, P.; Kohani, S. Optimal satellite LEO constellation design based on global coverage in one revisit time. Int. J. Aerosp. Eng. 2019, 2019, 4373749. [Google Scholar] [CrossRef]
- Hassan, S.S.; Park, Y.M.; Tun, Y.K.; Saad, W.; Han, Z.; Hong, C.S. SpaceRIS: LEO satellite coverage maximization in 6G sub-THz networks by MAPPO DRL and whale optimization. IEEE J. Sel. Areas Commun. 2024, 42, 1262–1278. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhu, Q. Autonomous and resilient control for optimal leo satellite constellation coverage against space threats. arXiv 2022, arXiv:2203.02050. [Google Scholar] [CrossRef]
- Pinell, C.; Prol, F.S.; Bhuiyan, M.Z.H.; Praks, J. Receiver architectures for positioning with low earth orbit satellite signals: A survey. EURASIP J. Adv. Signal Process. 2023, 2023, 60. [Google Scholar] [CrossRef]
- Ning, Q.; Yang, X.; Chen, B.; Zhou, X. The performance analysis of NOMA in LEO satellite rain attenuation and fading hybrid channel. Int. J. Satell. Commun. Netw. 2021, 40, 256–267. [Google Scholar] [CrossRef]
- Jia, M.; Meng, S.; Guo, Q.; Gu, X. Analysis of inter-system interference of large-scale LEO satellite constellation. J. Terahertz Sci. Electron. Inf. Technol. 2022, 20, 34–39. [Google Scholar]
- Liu, J.; Wang, K.; El-Mowafy, A.; Yang, X. PCO and hardware delay calibration for LEO satellite antenna downlinking navigation signals. Meas. Sci. Technol. 2024, 35, 086314. [Google Scholar] [CrossRef]
- Dwivedi, A.K.; Chaudhari, S.; Varshney, N.; Varshney, P.K. Performance analysis of LEO satellite-based IoT networks in the presence of interference. IEEE Internet Things J. 2023, 11, 8783–8799. [Google Scholar] [CrossRef]
- Miteva, R.; Samwel, S.W.; Tkatchova, S. Space Weather Effects on Satellites. Astronomy 2023, 2, 165–179. [Google Scholar] [CrossRef]
- Radojkovic, I.; Anastasov, J.; Milic, D.N.; Ivaniš, P.; Djordjevic, G.T. Secrecy Analysis of LEO Satellite-to-Ground Station Communication System Influenced by Gamma-Shadowed Ricean Fading. Electronics 2025, 14, 293. [Google Scholar] [CrossRef]
- Beidas, B.F. Low cost per bit for LEO satellite systems: Radio-frequency impairments compensation. In Non-Geostationary Satellite Communications Systems; The Institution of Engineering and Technology: London, UK, 2022. [Google Scholar] [CrossRef]
- Ma, J.; Kang, R.; Li, R.; Zhang, Q.; Liu, L.; Wang, X. Uncertainty Theory-Based Resilience Analysis for LEO Satellite Communication Systems. Symmetry 2022, 14, 1568. [Google Scholar] [CrossRef]
- Zhang, Z. ChirpPair: Packet acquisition in uncoordinated access channels of Low Earth Orbit (LEO) satellite networks. EURASIP J. Wirel. Commun. Netw. 2024, 2024, 47. [Google Scholar] [CrossRef]
- Sun, Y.; Rao, P.; Hu, T. Parameter Design and Performance Evaluation of a Large-Swath and High-Resolution Space Camera. Sensors 2021, 21, 4106. [Google Scholar] [CrossRef]
- National Research Council. 3 Debris Population Distribution. In Orbital Debris: A Technical Assessment; The National Academies Press: Washington, DC, USA, 1995. [Google Scholar] [CrossRef]
- National Academies of Sciences, Engineering, and Medicine. Limiting Future Collision Risk to Spacecraft: An Assessment of NASA’s Meteoroid and Orbital Debris Programs; The National Academies Press: Washington, DC, USA, 2011. [Google Scholar] [CrossRef]
- ESA’S Annual Space Environment Report. Available online: https://www.sdo.esoc.esa.int/environment_report/Space_Environment_Report_latest.pdf (accessed on 5 May 2025).
- Astromaterials Research & Exploration Science, NASA Orbital Debris Program Office. Available online: https://orbitaldebris.jsc.nasa.gov/faq/ (accessed on 5 May 2025).
- Space Safety, About Space Debris. Available online: https://www.esa.int/Space_Safety/Space_Debris/About_space_debris (accessed on 5 May 2025).
- Ahmed, A.A.; Malebary, S.J.; Ali, W.; Barukab, O.M. Smart Traffic Shaping Based on Distributed Reinforcement Learning for Multimedia Streaming over 5G-VANET Communication Technology. Mathematics 2023, 11, 700. [Google Scholar] [CrossRef]
- Ahmed, A.A. An effective handover management based on SINR and software-defined network over urban vehicular ad hoc networks. Trans. Emerg. Telecommun. Technol. 2019, 30, e3787. [Google Scholar] [CrossRef]
- Ahamed, A. A real-time routing protocol with adaptive traffic shaping for multimedia streaming over next-generation of Wireless Multimedia Sensor Networks. Pervasive Mob. Comput. 2017, 40, 495–511. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiang, D.; Shao, F.; Wu, T.; Liang, X.; Chen, J. Metaheuristic-Based Beam Scheduling Strategies for LEO Multibeam Satellite: A Comparison. IEEE Commun. Lett. 2025, 29, 1166–1170. [Google Scholar] [CrossRef]
- Tomar, V.; Bansal, M.; Singh, P. Metaheuristic Algorithms for Optimization: A Brief Review. Eng. Proc. 2023, 59, 238. [Google Scholar] [CrossRef]
- Li, F.; Wan, Q.; Wen, F.; Zou, Y.; He, Q.; Li, D.; Zhong, X. Multi-Satellite Imaging Task Planning for Large Regional Coverage: A Heuristic Algorithm Based on Triple Grids Method. Remote Sens. 2024, 16, 194. [Google Scholar] [CrossRef]
- Zeng, L.; Qin, P.; Zhou, Y.; Liu, H.; Cai, Y. A Heterogeneous Multi-Satellite Dynamic Mission Planning Method Based on Metaheuristic Algorithms. Electronics 2024, 13, 4353. [Google Scholar] [CrossRef]
- Xu, J.; Kishk, M.A.; Alouini, M.-S. Space-air-ground-sea integrated networks: Modeling and coverage analysis. IEEE Trans. Wirel. Commun. 2023, 22, 6298–6313. [Google Scholar] [CrossRef]
- Zhao, D.; Qin, H.; Xin, N.; Song, B. Flexible resource management in high-throughput satellite communication systems: A two-stage machine learning framework. IEEE Trans. Commun. 2023, 71, 2724–2739. [Google Scholar] [CrossRef]
- Wang, S.; Zhuang, X.; Wu, C.; Fan, G.; Li, M.; Xu, T.; Zhao, X. Multi-Layer LEO Constellation Optimization Based on D-NSDE Algorithm. Remote Sens. 2025, 17, 994. [Google Scholar] [CrossRef]
- Wu, S.; Wang, W.; Wen, J.; Wu, Y. Review on development of LEO Internet constellation. J. Beijing Univ. Aeronaut. Astronaut. 2024, 50, 1–11. [Google Scholar]
- Houssein, E.H.; Saeed, M.K.; Hu, G.; Al-Sayed, M.M. Metaheuristics for Solving Global and Engineering Optimization Problems: Review, Applications, Open Issues and Challenges. Arch. Comput. Methods Eng. 2024, 31, 4485–4519. [Google Scholar] [CrossRef]
| Research Work (Year) | Tools/Methods | Problem Solved | Effects Achieved | Limitation (Analytical) |
|---|---|---|---|---|
| Z. Shang [13] (2024) | Deep reinforcement learning | Optimization of satellite constellation for communication coverage in remote zones | Increased link throughput (~500 Mbps) and improved coverage in challenging regions | Region-specific optimization constrains scalability; the model may require substantial retraining when applied to different orbital inclinations, latitudes, or ground infrastructure conditions. |
| F.S. Prol et al. [14] (2023) | NSGA-III multi-objective GA | Reduced satellite count for BeiDou enhancement while maintaining coverage | Achieved hybrid constellations (177 and 186 sats) with improved GDOP and positioning | Limited simulation datasets risk overfitting to idealized scenarios, making performance uncertain under variable environmental or operational conditions. |
| G. Haibo et al. [15] (2025) | Literature review of LEO-PNT systems | Identification of system design and signal requirements for LEO-PNT | Compiled a comprehensive design framework | The absence of environmental factor modeling (e.g., atmospheric interference, orbital debris) limits applicability for dynamic and unpredictable real-world orbital conditions. |
| Kaan et al. [16] (2022) | Orbital parameter analysis | Promoted uniform satellite distribution for GNSS constellations | Improved constellation uniformity across latitudes | Focuses on parameter-driven uniformity but does not integrate emerging AI/heuristic optimization methods, potentially missing more adaptive deployment strategies. |
| L. Jing et al. [3] (2021) | Geometric satellite selection algorithm | Fast selection of optimal satellites for constellation deployment | Higher computational efficiency in selection | Prioritizes computational speed, which may sacrifice redundancy and robustness, especially in fault-tolerant or mission-critical applications. |
| G. Junqi et al. [17] (2023) | Comparative optimization methods | Evaluated tools and metrics across communication, navigation, and sensing domains | A broader understanding of method suitability | Lack of validation under real-world signal degradation scenarios weakens confidence in long-term operational reliability. |
| Kaan et al. [1] (2023) | Regional orbital optimization (100+ orbital cases) | GNSS-LEO optimization for the Middle East | Identified an optimal regional orbit set (altitude 1500 km, inclination 0°) | Constrained to Middle Eastern regional parameters, performance in other regions may vary significantly due to different orbital dynamics and coverage demands. |
| I.F. Ghoniem et al. [18] (2020) | Metaheuristic optimization | Constellation design for interferometric applications | Found effective solutions for interferometric performance | Geographic specialization restricts broader adoption; the algorithm may require significant adaptation for diverse orbital regimes. |
| Yuta et al. [19] (2010) | Deployment-phase aware design | Optimization based on constellation deployment stages | Tailored designs to mission requirements across deployment stages | Metaheuristic complexity imposes high computational demands, which may hinder real-time decision-making in dynamic mission environments. |
| W. Xue et al. [20] (2024) | Deep reinforcement learning | Optimization of satellite constellation for communication coverage in remote zones | Increased link throughput (~500 Mbps) and improved coverage in challenging regions | Limited testing under performance degradation scenarios leaves uncertainty about resilience in adverse signal and environmental conditions. |
| Research Work (Year) | Tools/Methods | Problem Solved | Effects Achieved | Limitation (Analytical) |
|---|---|---|---|---|
| S. Cakaj [21,22] (2016, 2014) | Analytical modeling of LEO belt coverage | Identification of optimal altitude (5633–8177 km) and elevation angles (2–10°) | Defined parameter ranges that maximize the ground coverage area | Static analytical assumptions overlook dynamic environmental and operational constraints, which can lead to deviations from predicted coverage performance in real-world deployments. |
| Z. Titus et al. [23] (2023) | Cox point process + GA-based optimization | Multi-altitude constellation design optimizing coverage probability, capacity | Derived performance metrics (coverage probability, interference) and optimized altitude allocations | High computational complexity may hinder real-time adaptability and scalability, especially for large-scale constellations or rapidly changing traffic patterns. |
| Silvirianti et al. [24] (2025) | Quantum adaptive learning (QAL) + stochastic geometry | Coverage optimization in stochastic LEO network configurations | Promising adaptive coverage enhancement leveraging quantum algorithms | Reliance on emerging quantum computing technologies limits near-term applicability due to hardware immaturity and high integration costs. |
| J. Shin et al. [25] (2021) | Analytical constellation design + inclination search | Regional, discontinuous LEO coverage specific to target regions | Improved regional coverage through optimal inclination selection | Regional focus limits the applicability to global systems; the approach lacks mechanisms for rapid reconfiguration to respond to shifting coverage demands. |
| I. Lluch et al. [26] (2014) | Satellite-to-satellite link modeling | Determination of optimal inter-satellite link range at LEO altitudes | Showed diminishing returns beyond ~6000 km link ranges | Does not incorporate advances in laser or phased-array inter-satellite communications, potentially underestimating achievable link distances in future systems. |
| Miyeon et al. [27] (2025) | SIR/LOS threshold modeling + mathematical analysis | Enhancing coverage probability in clustered satellite networks | Identified optimal SIR/LOS thresholds to boost effective coverage | Requires extensive empirical data for calibration; may struggle to adapt to fast-changing link quality in dynamic orbital environments. |
| Peng Zong et al. [28] (2019) | Genetic Algorithm (GA) | Single-revisit regional coverage optimization | Demonstrated pole coverage using inclinations > 90° with minimal satellites | Optimizes revisit frequency but does not fully address trade-offs between coverage persistence, latency, and system resource allocation. |
| Hassan et al. [29] (2024) | RIS-enabled 6G + sub-THz networks | Integration of LEO with terrestrial 6G to maximize joint coverage | Theoretical gains in coverage enhancement using RIS technology | Dependent on RIS technology readiness and its seamless integration into heterogeneous satellite–terrestrial network architectures. |
| Zhao et al. [30] (2022) | Autonomous self-healing framework | Maximizing coverage while minimizing control effort and system resilience | Showed resilient coverage adaptation under perturbations | Limited validation across diverse operational scenarios; scalability and interoperability with existing network control frameworks remain uncertain. |
| Research Work (Year) | Tools/Methods | Problem Solved | Effects Achieved | Limitation (Analytical) |
|---|---|---|---|---|
| Christina et al. [31] (2023) | Receiver design survey, augmentation methods (e.g., STL services) | Doppler shift, signal attenuation in LEO downlink | Identified common challenges and potential STL-based mitigation strategies | STL services inherently offer lower accuracy than GNSS, and their limited geographic availability restricts global applicability of the proposed augmentation solutions. |
| Qian Ning et al. [32] (2022) | Hybrid channel modeling (rain + shadow fading) + NOMA techniques | Rain and shadow fading impact on LEO downlink capacity | NOMA improved ergodic capacity under fading; lower altitude and power usage increased efficiency | Gains are highly dependent on accurate channel state information; real-time estimation may be challenging, and implementation complexity could hinder large-scale adoption. |
| JIA Min et al. [33] (2022) | Simulation of inter-satellite interference in LEO | Signal interference across large LEO constellations | Demonstrated significant interference in high-frequency inter-satellite links | Exclusively simulation-based, which may fail to capture hardware imperfections, atmospheric effects, and operational variability observed in real deployments. |
| Jiawei Liu et al. [34] (2024) | In-orbit calibration of phase-center offsets (PCOs) and hardware delays | Downlink signal accuracy degraded by hardware/phase-center offsets | Calibration approach enhanced signal precision via ground tracking | Requires dense ground station networks and continuous observational data; precision may degrade in regions with sparse tracking infrastructure. |
| A.K. Dwivedi et al. [35] (2023) | Analytical outage probability modeling + SIC/CM decoding schemes | Ground station decoding under interference and high SNR | Derived formulas for outage probability, enabling optimized system design | Assumes perfect synchronization, which is rarely achievable in real-world scenarios; asynchronous transmissions could reduce decoding reliability. |
| R. Miteva et al. [36] (2023) | Space weather survey (geomagnetic storms, solar events) | Atmospheric drag and operational resilience during space weather events | Highlighted cumulative weather effects potentially causing major service disruption | Focuses primarily on cumulative long-term impacts; immediate, short-term mitigation strategies for active satellite operations are not fully addressed. |
| Radojkovic et al. [37] (2025) | Secrecy capacity modeling under gamma-shadowed Ricean fading | Secure LEO downlink under complex fading and eavesdropping threats | Quantified secrecy capacity reductions under specialized fading channel | Assumes a narrow set of fading models, potentially limiting applicability to environments with mixed or non-stationary channel conditions. |
| Bassel F. Beidas [38] (2022) | Digital frequency offset compensation, I/Q-imbalance correction | Frequency offset and I/Q errors in LEO analog frequency converters | Improved signal fidelity through digital algorithms | Algorithm effectiveness may degrade under hardware variability and temperature drift; integration requires complex calibration procedures. |
| Ji Ma et al. [39] (2022) | Uncertainty theory-based resilience modeling | Network resilience against multiple impairments | Proposed belief-based availability measure and evolution model | Requires extensive, high-quality datasets to accurately calibrate uncertainty models; data scarcity in certain operational contexts could limit reliability. |
| Zhenghao Zhang [40] (2024) | Chirp-based packet detection under weak signals | Packet detection in low-SNR LEO environments | More reliable packet acquisition with reduced peak-to-average power | Performance sensitivity to varying noise profiles and Doppler rates may reduce consistency; compatibility with existing receiver architectures needs assessment. |
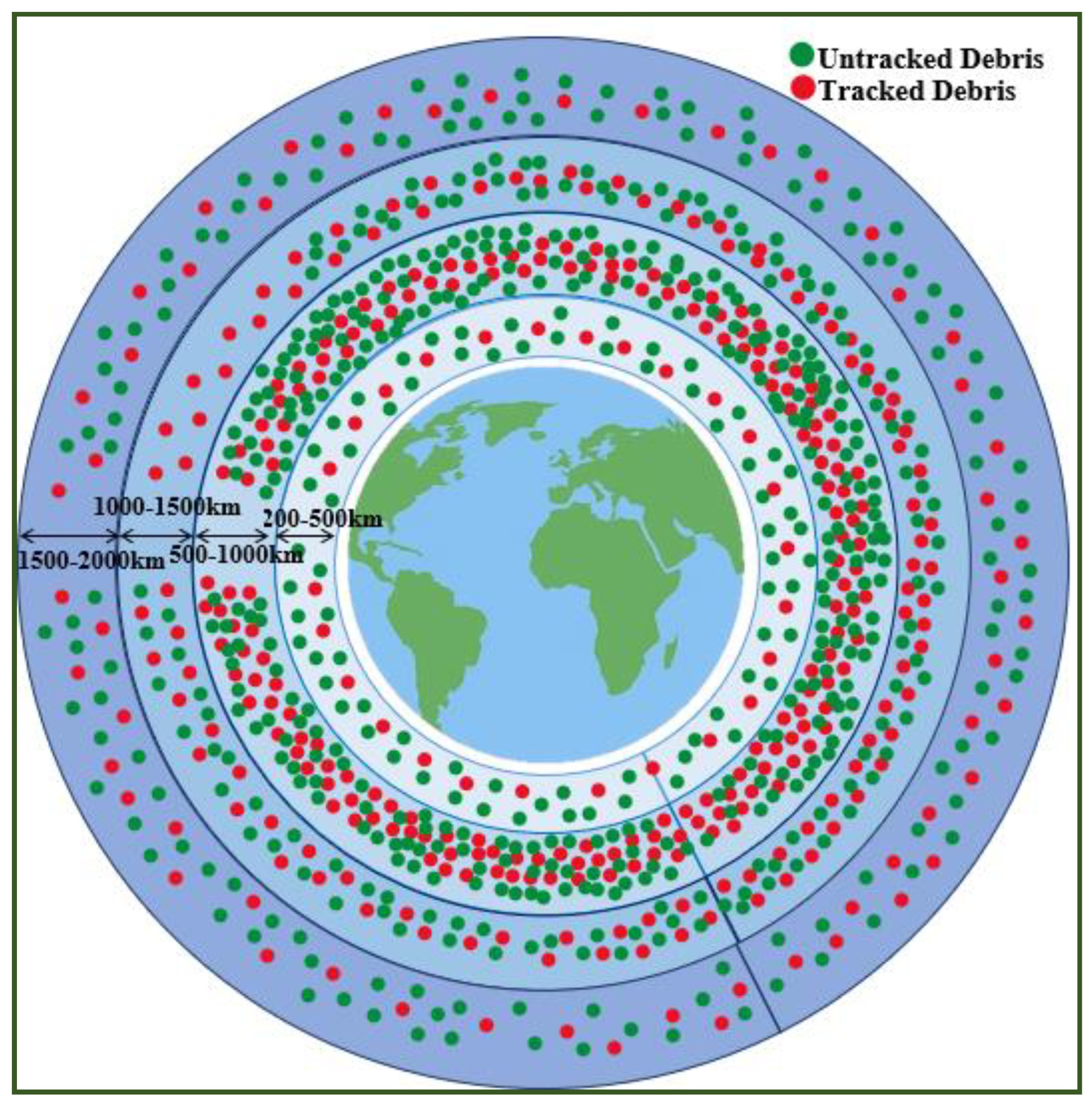
| Altitude Range (km) | Tracked Debris (>10 cm) | Estimated Untracked Debris (1 mm–10 cm) | Description |
|---|---|---|---|
| 200–500 | ~1200 | ~60,000 | Lower density; frequent orbital decay due to atmospheric drag. Debris typically re-enters within years. |
| 500–800 | ~4500 | ~150,000 | Moderate density; long-lived orbits. Popular for remote sensing missions. |
| 800–1000 | ~6800 | ~200,000 | Densest zone, called “congested LEO belt”. Site of several breakup events (e.g., Iridium–Cosmos collision). |
| 1000–1500 | ~3000 | ~80,000 | Includes old satellites and upper stages. Low drag means that the debris remains for centuries. |
| 1500–2000 | ~1000 | ~30,000 | Sparse compared to lower LEO, but debris is persistent due to low atmospheric influence. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmed, A.A. A Comprehensive Review of Satellite Orbital Placement and Coverage Optimization for Low Earth Orbit Satellite Networks: Challenges and Solutions. Network 2025, 5, 32. https://doi.org/10.3390/network5030032
Ahmed AA. A Comprehensive Review of Satellite Orbital Placement and Coverage Optimization for Low Earth Orbit Satellite Networks: Challenges and Solutions. Network. 2025; 5(3):32. https://doi.org/10.3390/network5030032
Chicago/Turabian StyleAhmed, Adel A. 2025. "A Comprehensive Review of Satellite Orbital Placement and Coverage Optimization for Low Earth Orbit Satellite Networks: Challenges and Solutions" Network 5, no. 3: 32. https://doi.org/10.3390/network5030032
APA StyleAhmed, A. A. (2025). A Comprehensive Review of Satellite Orbital Placement and Coverage Optimization for Low Earth Orbit Satellite Networks: Challenges and Solutions. Network, 5(3), 32. https://doi.org/10.3390/network5030032







