1. Introduction
Today’s information societies depend deeply on optical networks to handle massive flows of data between data centers, cloud computing platforms, telecom networks, and end users, ensuring fast and reliable information exchange. Optical networks are communication infrastructures that utilize light for transmitting, processing, and switching information, relying on optical fibers as the transmission medium [
1]. Since the proposal of using optical fibers for communications purposes by Charles Kao in 1966 [
2], the evolution of optical networks has been marked by many breakthroughs [
3]. Among the most significant ones is the development of WDM (wavelength division multiplexing) technology.
WDM can significantly increase the capacity of optical transmission by simultaneously transmitting multiple optical signals, often referred to as optical channels, through a single optical fiber, with each channel utilizing its own wavelength. Therefore, the problem of designing optical networks is markedly different from designing electrical networks in the sense that it involves, besides finding a path for each traffic demand (routing), also assigning a wavelength to that path (wavelength assignment). The routing and wavelength assignment (RWA) problem is a well-studied topic in the field of optical networking. This problem can be formulated using integer linear programming (ILP) with the objective of minimizing the number of wavelengths, leading to optimal solutions [
4]. However, since the problem is NP-complete (nondeterministic polynomial-time complete), it requires intensive computation, limiting its applicability to small and medium-sized networks. For large networks, one must rely on suboptimal heuristics to speed up the calculations. (see [
5] for an overview). More recently, machine learning techniques have also been explored to obtain near-optimal RWA solutions with a significant reduction in computation time [
6].
The RWA problem can be static or dynamic [
5]. In static RWA, all traffic demands are known in advance, and the goal is to minimize the number of wavelengths needed to route all of them. All decisions are made offline, before any traffic is actually sent. In dynamic RWA, traffic demands arrive over time in a random way. The number of available wavelengths is fixed, and the goal is to route the demands while minimizing the blocking of requests. Decisions are made online, as the demands arrive. A drawback of dynamic RWA is that it requires a very advanced control plane, such as SDN (Software-Defined Networking), which increases the complexity and sophistication of the network.
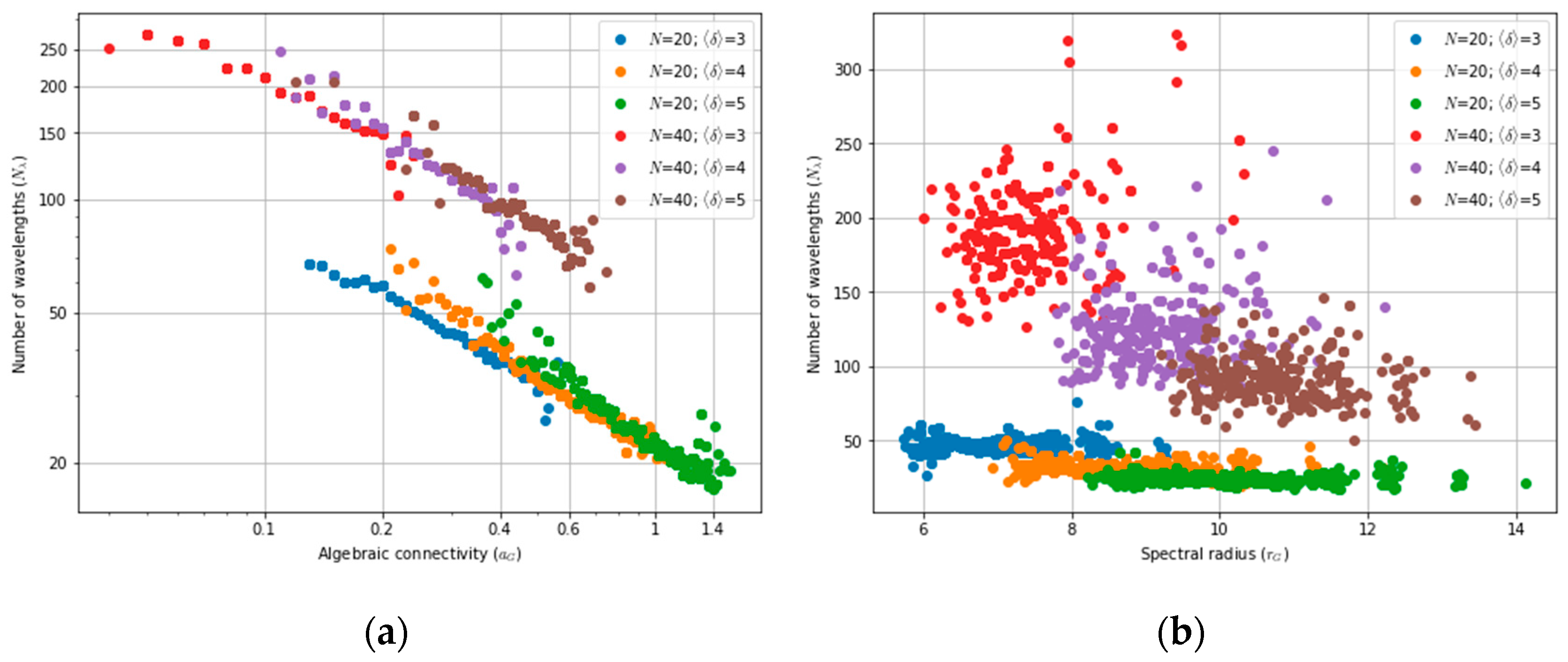
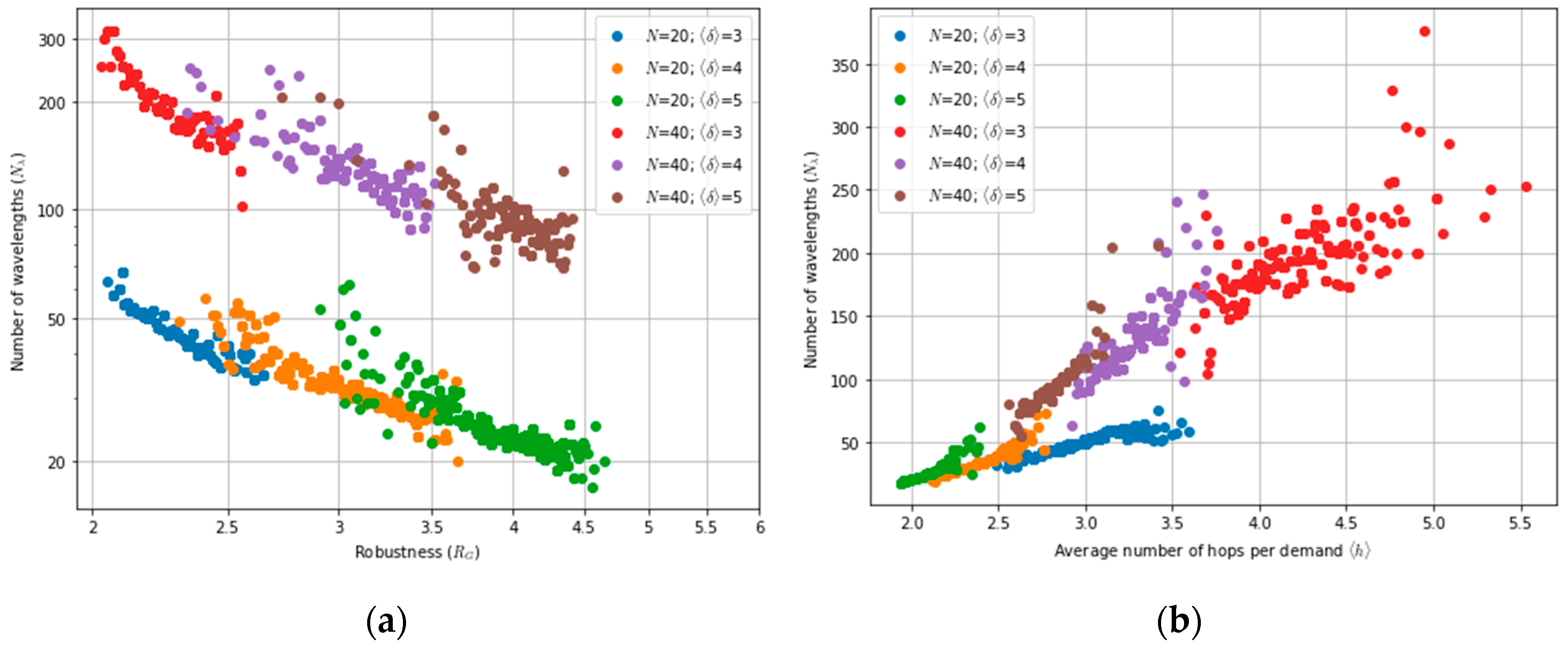
Another closely related topic that is paramount for network designers is understanding how the number of required wavelengths, also denoted wavelength usage, to accommodate a given traffic demand relates to parameters associated with network’s physical topology and identifying general trends in this relationship. This problem has been the focus of many studies. To the best of our knowledge [
7,
8] were the first works to study that interdependency, considering topological parameters such as node degree and its variance, physical connectivity, internodal distance, and the number of spanning trees, using statistical analysis that required the generation of large number of random networks. Furthermore, ref. [
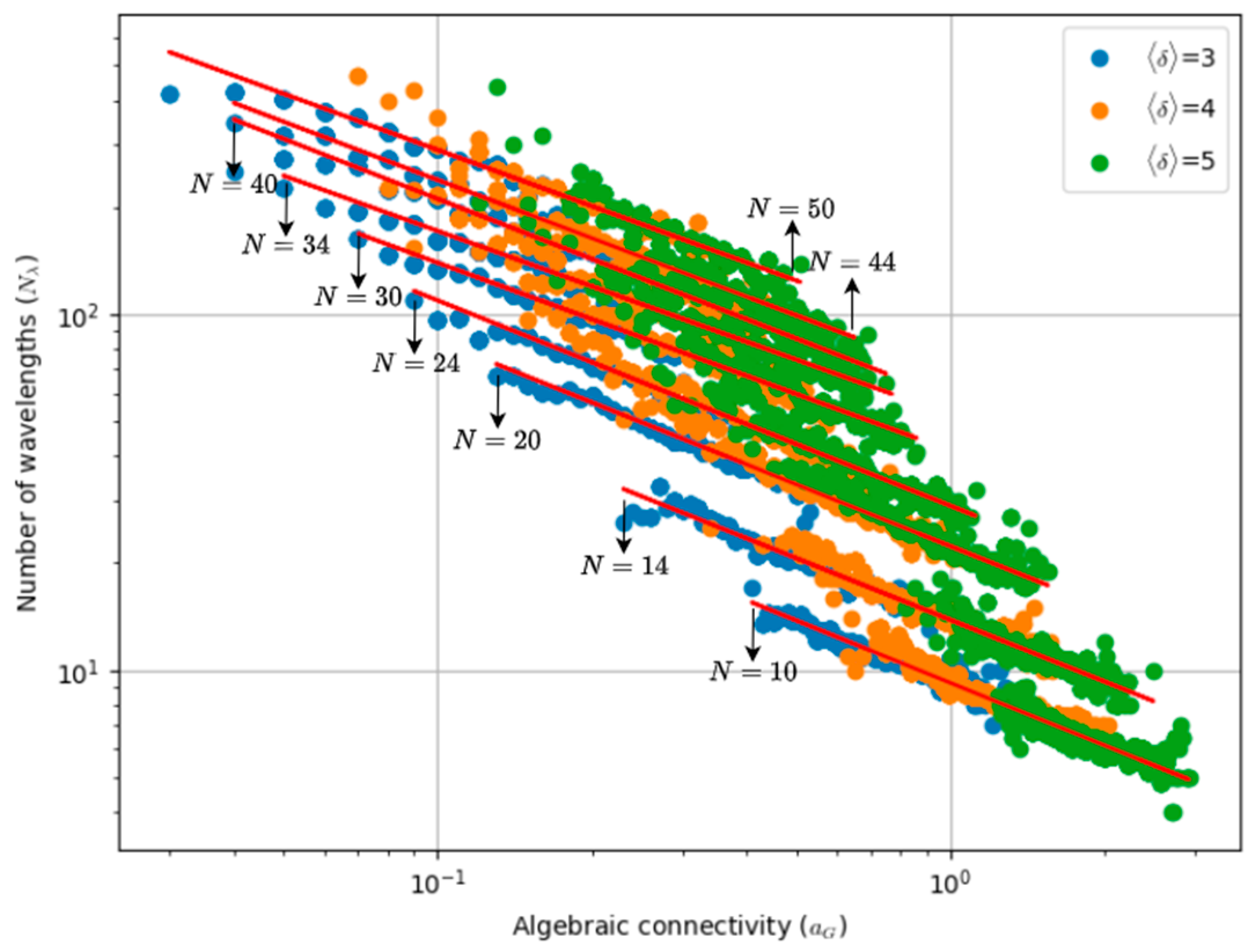
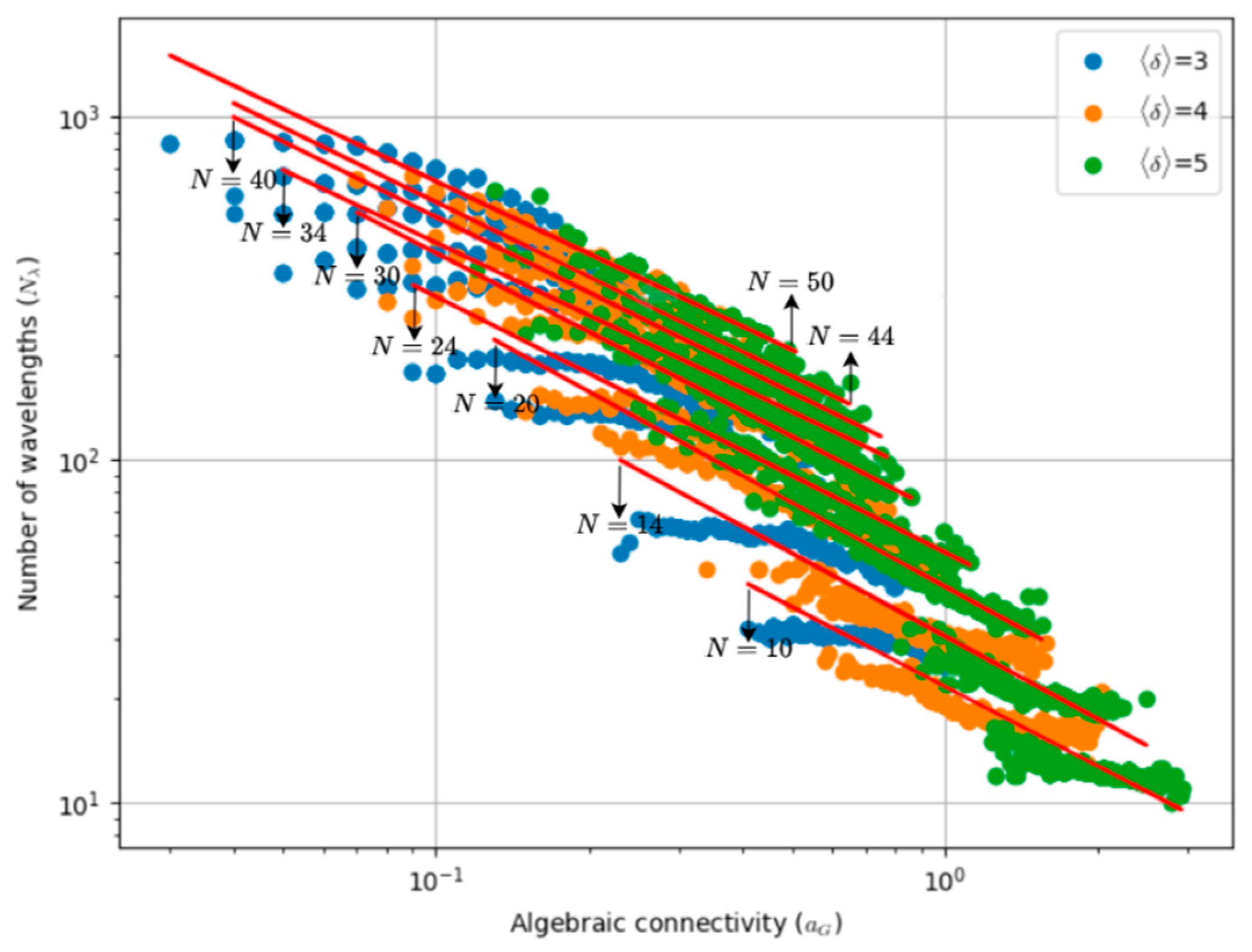
9] adds algebraic connectivity to the modelling and shows that this parameter provides the most accurate estimate of wavelength usage among those studied by the authors. Interestingly, ref. [
10] also showed that algebraic connectivity is strongly correlated with other network metrics like capacity and robustness. While these studies rely on general random networks, ref. [
11] addresses the wavelength usage problem but focuses on other networks models, such as small-world and scale-free networks, considering parameters like the average shortest paths length.
Survivability has become a critical feature of modern optical networks, particularly in backbone segments, due to the huge volume of traffic they handle. This involves a set of techniques that enables networks to remain fully operational during outages, typically caused by link failures due to fiber cuts or equipment failures at the network nodes. To ensure survivability, networks rely on two main approaches: protection and restoration techniques [
12]. The former uses deployed backup resources (e.g., optical channels, wavelengths, etc.) that are automatically activated when a failure occurs, while the latter dynamically discovers and allocates resources after a failure is detected.
A commonly used protection technique operating in the optical domain is known as 1 + 1 Optical Channel (OCh) protection [
13]. In this scheme, the source node transmits two identical optical signals over two physically disjoint optical channels. As a consequence, both signals must use the same wavelength, which increases overall wavelength consumption and adds complexity to the wavelength assignment strategies.
An important question to address is how survivability affects wavelength requirements and how it depends on topological parameters. As far as we know, this problem has received limited attention in literature. For instance, in [
8,
14], the authors analyzed the impact of a link restoration technique on wavelength requirements using lower bounds and heuristics, respectively. Similarly, ref. [
15] investigated the issue using ILP (integer linear programming) and heuristic formulations to assess dedicated and shared path protection, as well as shared link protection. However, none of these studies have considered the influence of topological parameters in their analysis.
In this paper, we revisit the problem of wavelength assignment in optical backbone networks to understand the dependency of wavelength requirements on topological parameters, while also considering survivability features. Although great emphasis has been placed on algebraic connectivity, additional topological parameters not previously considered by other authors, such as spectral radius and robustness, are also examined. Furthermore, by relying on regression techniques, simple formulas are derived to predict wavelength requirements and the wavelength increment factor, assuming a 1 + 1 OCh protection scheme, with this factor being defined as the ratio between the number of wavelengths required with protection to the number without protection.
The paper is organized in five sections.
Section 2 describes the model used to characterize the optical network, defines the topological parameters considered in the study, and defines the protection strategy adopted in this work. In
Section 3, we describe the algorithms employed, with emphasis on the problem of computing disjoint node paths.
Section 4 presents the methodologies for generating synthetic data sets and provides a discussion of the results, also focusing on the derivation of formulas to estimate wavelength requirements. Finally,
Section 5 summarizes and concludes the paper.
2. Network Aspects and Survivability
2.1. Network and Topological Parameters Characterization
Transparency has been a widely accepted assumption in the design of optical networks, particularly in backbone segments, since the advent of optical amplifiers and WDM technologies [
16]. In line with this our analysis, assumes that optical networks are transparent, meaning that optical signals are transmitted from the source to the destination without optoelectronic conversion, maintaining their optical nature throughout the entire path. Therefore, in these networks, all node functionalities (such as multiplexing, switching, etc.) take place in the optical domain, and the node structure is based on reconfigurable optical add-drop multiplexers (ROADMs) [
1]. A ROADM is responsible not only for locally adding and dropping optical channels but also for enabling optical bypass by switching optical channels from incoming to outgoing optical links. An optical link represents a physical interconnection between two nodes and is implemented using a pair optical fibers and optical amplifiers adequately spaced to compensate for the fiber losses. Each optical fiber supports WDM signals, meaning it carries a specific number of optical channels, with each channel being characterized by its own wavelength. As a result, the number of optical channels is determined by the number of wavelengths
per link.
In this work, we also assume that optical networks are static, which is a common assumption in optical backbone networks. In such networks, optical channels are pre-established offline according to a fixed traffic, matrix and remain unchanged during operation.
The physical topology of an optical network can be described as an undirected graph where } represents the set of ROADM nodes and } represents the set of optical links, with being the number of nodes and the number of links (also called edges). Another way to describe the physical topology is through the adjacency matrix. This is an square matrix , where each element = 1 if there is a link between and and 0 otherwise. The degree matrix is also fundamental for network characterization, as it provides additional structural information. It is an diagonal matrix , where each element is equal to the node degree if , and 0 otherwise. Note that the node degree of node corresponds to the number of links incident to
Besides
and
, other topological parameters can be used to properly characterize a network. These topological parameters can be classified into spectral and non-spectral categories [
9]. The spectral parameters are the eigenvalues of the graph Laplacian matrix, defined as
. In this work, we consider two spectral parameters: the algebraic connectivity
and the spectral radius
. The former corresponds to the second smallest eigenvalue of matrix
and measures how well the graph is connected, while the latter corresponds to the largest eigenvalue of matrix
and quantifies how node degree imbalance is structured across the network.
The non-spectral parameters considered in this work include the average node degree
, the average number of hops per demand
and the robustness
. The first parameter is defined as
The number of hops per demand corresponds to the number of links traversed by a given traffic demand, after it has been mapped to a path using a specific routing strategy. Assuming a shortest path routing strategy, the hop matrix
is an
matrix, where all diagonal elements are zero, and each elements
denotes the minimum number of hops traversed by the traffic demand between nodes
and
. Considering a full-mesh logical topology the average minimum number of hops per demand is given by
A full-mesh logical topology means that each node is logically connected to every other node in the network. This corresponds to a uniform traffic pattern, where there is one traffic demand between each pair nodes, a general assumption in this work.
The starting point for evaluating network robustness is computing the redundancy matrix
. This is a
matrix, where each element is defined as the node disjoint pairwise connectivity and corresponds to the maximum number of nodes disjoint paths between nodes
and
[
17]. This value is crucial for designing protection paths in optical networks [
18], a topic that will be addressed in the following subsection. The robustness is defined as the average node-disjoint pairwise connectivity and is given by [
10]
To perform statistical analysis, large data sets are essential. One effective way of obtaining such data sets is to generate numerous network topologies, which can be done using random graphs designed to adequately describe the characteristics of real-world networks, as explained in
Section 4.1.
2.2. Network Survivability
Due to the massive volumes of data transported by optical networks, ensuring network survivability is paramount. To achieve this, these networks must implement mechanisms to recover traffic in the event of failures. Such failures can occur at either the node or link level. The former are primarily caused by equipment failures, particularly transponders (see [
1] for an explanation of their role), while the latter are mainly due to fiber cuts. To guarantee resilience against failures in the working transponder (i.e., the one used to support service traffic), redundant transponders can be used. These transponders can be provided in either a dedicated or shared manner [
14]. In the dedicated solution, each working transponder is duplicated, while in the shared solution, a single redundant transponder can protect multiple working transponders.
To protect against link failures, additional backup resources need to be provided. Similarly, these resources can also be dedicated or shared. In the first case, each working channel has a fully reserved backup channel, while in the second, multiple working channels share the same backup resources. Furthermore, dedicated protection can be applied at the path, or link level. In the first case, the entire end-to-end path (or connection) between the source and destination nodes is protected, while in the second case, only individual links in the path are considered. A requirement of dedicated path protection is that the working and the backup path must be node- and link-disjoint. Although shared protection schemes are more efficient in terms of resource utilization, they are not advisable in the context of backbone segments, as they involve complex coordination and may not guarantee the stringent recovery time requirements expected in these segments.
A commonly used path-dedicated protection technique operating in optical domain is designated as 1 + 1 OCh protection [
13]. In this scheme, the source node transmits identical signals over two physically disjoint optical channels (working and backup), and the destination node receives both signals, selecting the one with the highest quality. This scheme is operationally simple and ensures fast protection switching because the decision is local and does not require signaling between nodes. However, since the working and backup paths use the same wavelength, this increases the complexity of wavelength assignment strategies and overall wavelength consumption. The determination of the additional wavelength consumption inherent in this scheme will be a central topic of this work.
3. Routing and Wavelength Assignment
The wavelength requirements in a network depends on both the physical topology, described by the adjacency matrix and the logical topology which defines the profile of traffic demands between nodes. This profile is represented by a traffic matrix, where each entry specified the demand between a pair of nodes. As noted previously, in this work we assume a uniform traffic profile where each pair of nodes has one unit of traffic demand, corresponding to a full-mesh logical topology.
For each traffic demand between a pair of nodes, a path must be found in the physical topology, and a wavelength must be assigned to it. This process is known as routing and wavelength assignment (RWA) problem. Since multiple paths exist between each pair of nodes, the routing objective is to determine the shortest path using a heuristic such as Dijkstra’s algorithm. Furthermore, in the presence of 1 + 1 OCh protection, two node-disjoint paths must be computed. Finding such paths is a well-known problem in graph theory. A common approach to deal with this problem is Suurballe’s algorithm [
19] or Bhandari’s algorithm [
18]. However, these algorithms compute only two shortest node-disjoint paths, and, therefore, cannot be applied to determine the robustness parameter
, which requires computing the maximum number of node-disjoint paths between each pair of nodes. To address this limitation, this work uses a solution based on the Ford-Fulkerson algorithm, transforming the node-disjoint path problem into a maximum-flow problem [
20], and subsequently using Depth-First Search (DFS) to extract the required paths. This solution is implemented using Algorithm 1.
| Algorithm 1: Node disjoint paths |
| | Input: network undirected graph: node source; destination node |
| | Output: all node-disjoint paths from to |
| 1: | Make a copy of the network graph G. Initialize ,with |
| 2: | Convert the graph into a directed graph by replacing each undirected edge with two directed edges, one in each direction |
| 3: | for each node in do |
| 4: | | Replace with two nodes and |
| 5: | | Assign all incoming edges of to and all outgoing edges of to |
| 6: | | A directed edge from to is added with unit capacity |
| 7: | end for |
| 8: | Execute the Ford-Fulkerson algorithm on to find the maximum flow from to |
| 9: | Save the max-flow value in |
| 10: | for do |
| 11: | | Perform DFS on the residual graph, considering only edges with flow equal to 1
When is reached, retrieve the path and decrement the flow of all edges in it by 1
Merge nodes and back into the original node |
| | |
| 12: | |
| | |
| 13 | |
| 14 | end for |
The wavelength assignment problem consists of assigning one wavelength to each path associated with a traffic demand, subject to two constraints:(i) each path must use the same wavelength on all links along its route from the source to the destination (wavelength continuity constraint); (ii) different paths that traverse the same link must be assigned different wavelengths (wavelength conflict constraint). This problem can be solved using ILP techniques, graph coloring approaches, or heuristics (e.g., first fit, most used, etc.) [
5]. ILP techniques provide exact results but are computationally intensive, making them impractical for large networks. Graph coloring is faster than ILP but does not guarantee optimal results. Finally, heuristics are the fastest methods but only provide approximate solutions. As a compromise, between accuracy and computational complexity we used graph coloring in our work.