Advancements in Indoor Precision Positioning: A Comprehensive Survey of UWB and Wi-Fi RTT Positioning Technologies
Abstract
1. Introduction
- (1)
- Comparative analysis of UWB and Wi-Fi RTT-based positioning: we first comparatively analyze the signal characteristics of UWB and Wi-Fi signals, which are the root cause of differences in performance such as bandwidth, multipath effects.
- (2)
- NLOS identification and ranging error mitigation methods: a critical aspect of improving ranging and positioning accuracy involves the detection, identification, and correction of NLOS errors in UWB and Wi-Fi RTT ranging measurements.
- (3)
- Advanced positioning methodologies: A variety of advanced positioning methodologies are reviewed, including methods for enhancing positioning accuracy and continuity, and practical considerations for efficient field deployment. Multi-sensor fusion is highlighted as a fundamental approach in this context.
- (4)
- Advantages and disadvantages: We thoroughly discuss the strengths and limitations of UWB and Wi-Fi RTT high-precision indoor positioning technologies, providing a balanced perspective on their applicability, potential challenges, and future development.
2. Overview of Positioning Principles Using UWB and Wi-Fi RTT Radio Signals
2.1. TOF-Based Positioning Principle
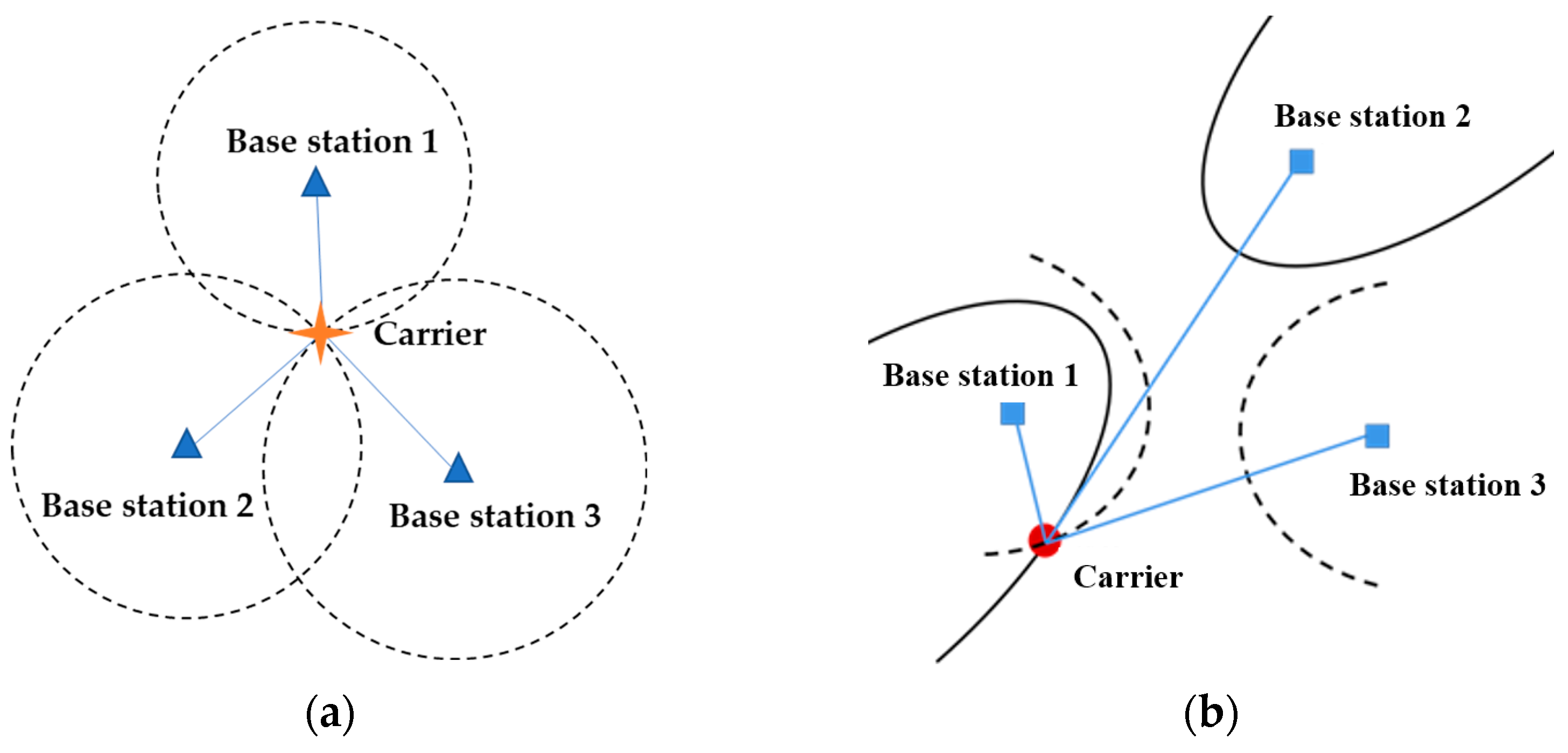
2.2. TOA/TDOA-Based Positioning Principle
2.3. Ranging Error Optimization
2.4. Comparison of UWB and Wi-Fi RTT Positioning Technologies
3. NLOS Ranging Error and Correction Methods of UWB and Wi-Fi RTT Signals
3.1. NLOS Signal and Identification
3.2. NLOS Ranging Error Mitigation
4. Advanced Positioning Methodologies Using UWB and Wi-Fi RTT Signals
4.1. Integrated Positioning of Data Fusion
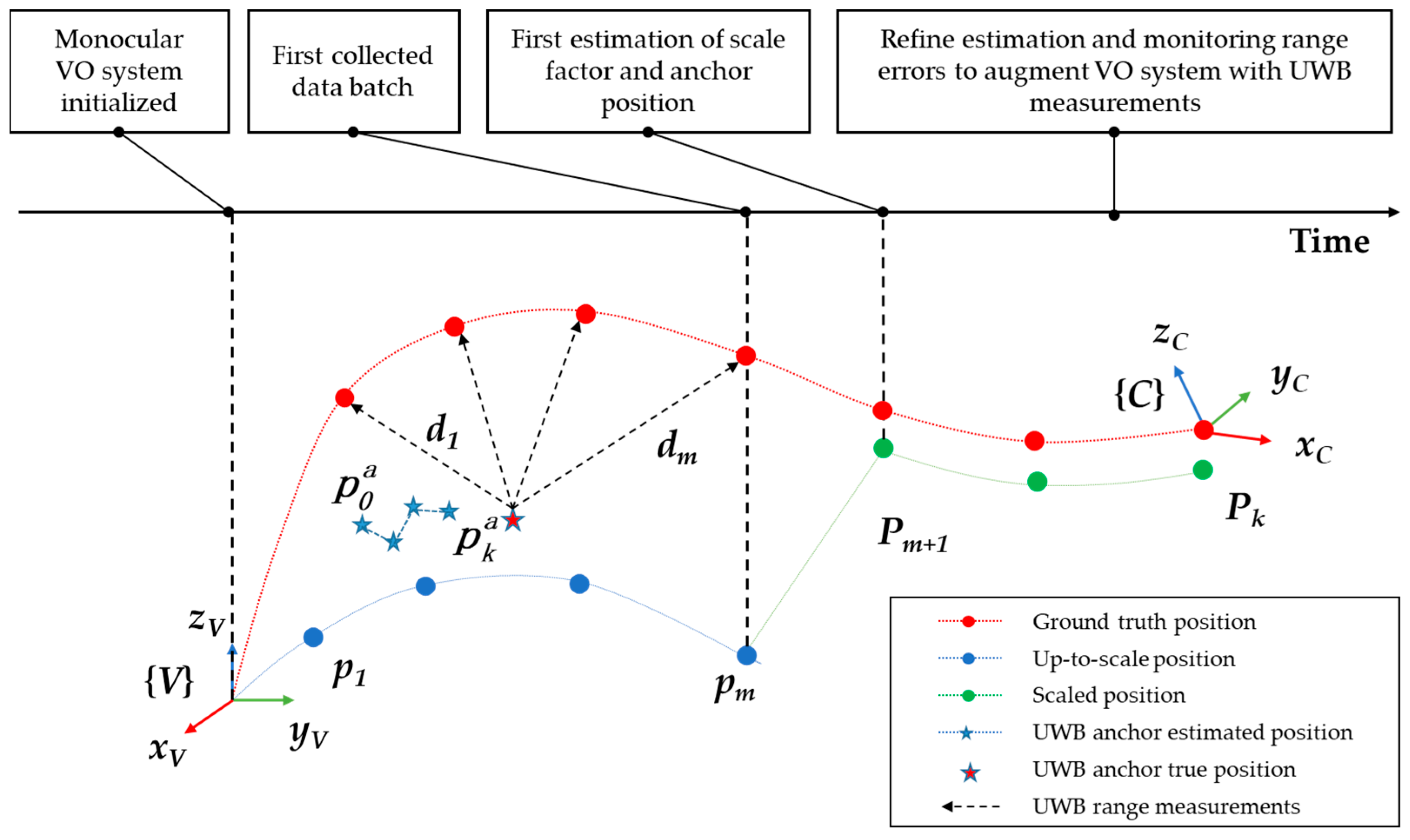
4.2. Autonomous Calibration of Base Station Coordinates
5. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, C.; Zhen, J.; Chang, K.; Xu, A.; Zhu, H.; Wu, J. An indoor positioning and tracking algorithm based on angle-of-arrival using a dual-channel array antenna. Remote Sens. 2021, 13, 4301. [Google Scholar] [CrossRef]
- Nie, J.; Liu, Y.; Hu, Y.; Wang, Y.; Xia, S.; Preindl, M.; Jiang, X. SPIDERS+: A light-weight, wireless, and low-cost glasses-based wearable platform for emotion sensing and bio-signal acquisition. Pervasive Mob. Comput. 2021, 75, 101424. [Google Scholar] [CrossRef]
- El-Sheimy, N.; Li, Y. Indoor navigation: State of the art and future trends. Satell. Navig. 2021, 2, 7. [Google Scholar] [CrossRef]
- Qorvo UWB Solutions with Apple’s U1 & U2 Chip. Available online: https://www.qorvo.com/innovation/ultra-wideband/products/uwb-solutions-compatible-with-apple-u1 (accessed on 4 September 2024).
- Jathe, N.; Lütjen, M.; Freitag, M. Indoor positioning in car parks by using Wi-Fi round-trip-time to support finished vehicle logistics on port terminals. IFAC-Pap. Online 2019, 52, 857–862. [Google Scholar] [CrossRef]
- Mazhar, F.; Khan, M.G.; Sällberg, B. Precise indoor positioning using UWB: A review of methods, algorithms and implementations. Wirel. Pers. Commun. 2017, 97, 4467–4491. [Google Scholar] [CrossRef]
- Alarifi, A.; Al-Salman, A.; Alsaleh, M.; Alnafessah, A.; Al-Hadhrami, S.; Al-Ammar, M.A.; Al-Khalifa, H.S. Ultra wideband indoor positioning technologies: Analysis and recent advances. Sensors 2016, 16, 707. [Google Scholar] [CrossRef]
- Wu, P. Comparison between the Ultra-wide Band based indoor positioning technology and other technologies. J. Phys. Conf. Ser. 2022, 2187, 012010. [Google Scholar] [CrossRef]
- Dong, Y.; Arslan, T.; Yang, Y. Real-time NLOS/LOS identification for smartphone-based indoor positioning systems using Wi-Fi RTT and RSS. IEEE Sens. J. 2021, 22, 5199–5209. [Google Scholar] [CrossRef]
- Coppens, D.; Shahid, A.; Lemey, S.; Van Herbruggen, B.; Marshall, C.; De Poorter, E. An overview of UWB standards and organizations (IEEE 802.15.4, FiRa, Apple): Interoperability aspects and future research directions. IEEE Access 2022, 10, 70219–70241. [Google Scholar] [CrossRef]
- Inpixon Solutions. Available online: https://www.inpixon.com/solutions (accessed on 4 September 2024).
- Navigine Solutions. Available online: https://navigine.com/webinar-uwb-positioning-and-its-industrial-applications-noccela-and-navigine-solutions/ (accessed on 4 September 2024).
- Ubisense Solutions. Available online: https://ubisense.com/ (accessed on 4 September 2024).
- Jung, B.G.; Chung, B.C.; Yim, J.; Yoo, Y.S.; Park, H. Learning based Wi-Fi RTT range estimation. In Proceedings of the 2021 International Conference on Information and Communication Technology Convergence (ICTC), Jeju Island, Republic of Korea, 20–22 October 2021; pp. 1030–1032. [Google Scholar] [CrossRef]
- Qiu, S.; Allan, R.; Nilavalan, R.; Ivey, J.; Butterfield, S.; Li, M. Performance analysis of a fail-safe wireless communication architecture for IoT based fire alarm control panels. SN Appl. Sci. 2021, 3, 379. [Google Scholar] [CrossRef]
- Makki, A.; Siddig, A.; Saad, M.; Bleakley, C. Survey of WiFi positioning using time-based techniques. Comput. Netw. 2015, 88, 218–233. [Google Scholar] [CrossRef]
- Oguntala, G.; Abd-Alhameed, R.; Jones, S.; Noras, J.; Patwary, M.; Rodriguez, J. Indoor location identification technologies for real-time IoT-based applications: An inclusive survey. Comput. Sci. Rev. 2018, 30, 55–79. [Google Scholar] [CrossRef]
- Ridolfi, M.; Kaya, A.; Berkvens, R.; Weyn, M.; Joseph, W.; Poorter, E.D. Self-calibration and collaborative localization for UWB positioning systems: A survey and future research directions. ACM Comput. Surv. CSUR 2021, 54, 1–27. [Google Scholar] [CrossRef]
- Elsanhoury, M.; Mäkelä, P.; Koljonen, J.; Välisuo, P.; Shamsuzzoha, A.; Mantere, T. Precision Positioning for Smart Logistics Using Ultra-Wideband Technology-Based Indoor Navigation: A Review. IEEE Access 2022, 10, 44413–44445. [Google Scholar] [CrossRef]
- Liu, J.; Zhao, Z.; Hu, N.; Huang, G.; Gong, X.; Yang, S. Summary and Prospect of Indoor High-Precision Positioning Technology. Geomat. Inf. Sci. Wuhan Univ. 2022, 47, 997–1008. [Google Scholar] [CrossRef]
- Chen, R.; Guo, G.; Chen, L.; Niu, X. Application Status, Development and Future Trend of High-Precision Indoor Navigation and Tracking. Geomat. Inf. Sci. Wuhan Univ. 2023, 48, 1591–1600. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, S.; Han, Y.; Zhu, P. Research Progress of Indoor Positioning Technology and Its Application in Seamless Navigation. Comput. Syst. Appl. 2023, 32, 29–40. [Google Scholar]
- Che, F.; Ahmed, Q.Z.; Lazaridis, P.I.; Sureephong, P.; Alade, T. Indoor positioning system (IPS) using ultra-wide bandwidth (UWB)-for industrial internet of things (IIoT). Sensors 2023, 23, 5710. [Google Scholar] [CrossRef]
- Qu, J. A review of UWB indoor positioning. J. Phys. Conf. Ser. IOP Publ. 2023, 2669, 012003. [Google Scholar] [CrossRef]
- Wang, F.; Tang, H.; Chen, J. Survey on NLOS Identification and Error Mitigation for UWB Indoor Positioning. Electronics 2023, 12, 1678. [Google Scholar] [CrossRef]
- Dai, J.; Wang, M.; Wu, B.; Shen, J.; Wang, X. A Survey of Latest Wi-Fi Assisted Indoor Positioning on Different Principles. Sensors 2023, 23, 7961. [Google Scholar] [CrossRef]
- Lin, Y.; Yu, K.; Zhu, F.; Bu, J.; Dua, X. The State of the Art of Deep Learning-Based Wi-Fi Indoor Positioning: A Review. IEEE Sens. J. 2024, 24, 27076–27098. [Google Scholar] [CrossRef]
- Martin-Escalona, I.; Zola, E. Ranging estimation error in Wi-Fi devices running IEEE 802.11mc. In Proceedings of the 2020 IEEE Global Communications Conference, Taipei, China, 7–11 December 2020; pp. 1–7. [Google Scholar] [CrossRef]
- Guo, G.; Chen, R.; Ye, F.; Peng, X.; Liu, Z.; Pan, Y. Indoor smartphone localization: A hybrid Wi-Fi RTT-RSS ranging approach. IEEE Access 2019, 7, 176767–176781. [Google Scholar] [CrossRef]
- Ibrahim, M.; Liu, H.; Jawahar, M.; Nguyen, V.; Gruteser, M.; Howard, R.; Yu, B.; Bai, F. Verification: Accuracy evaluation of Wi-Fi fine time measurements on an open platform. In Proceedings of the 24th Annual International Conference on Mobile Computing and Networking, New York, NY, USA, 15 October 2018; pp. 417–427. [Google Scholar] [CrossRef]
- Zhao, Y.; Zou, J.; Guo, J.; Huang, G.; Cai, L. A Novel Ultra-Wideband Double Difference Indoor Positioning Method with Additional Baseline Constraint. ISPRS Int. J. Geo. Inf. 2021, 10, 634. [Google Scholar] [CrossRef]
- Peng, Y.; Li, G.; Wang, L.; Li, M. UWB indoor positioning station layout PDOP value analysis. J. Navig. Position. 2017, 5, 103–106. [Google Scholar]
- Yang, D.; Wang, J.; Wang, M.; Zhang, Y. Analysis of the impact of base station deployment on positioning accuracy in emergency environments. Surv. Mapp. Bull. 2020, 90–94. [Google Scholar] [CrossRef]
- Bharadwaj, R.; Alomainy, A.; Parini, C. Study of ultra wideband localization techniques using various monitoring configurations. In Proceedings of the 2012 6th European Conference on Antennas and Propagation (EUCAP), Prague, Czech Republic, 26–30 March 2012; pp. 2035–2038. [Google Scholar] [CrossRef]
- Bharadwaj, R.; Parini, C.; Alomainy, A. UltrawidebandBased 3-D Localization Using Compact Base-Station Configurations. IEEE Antennas Wirel. Propag. Lett. 2014, 13, 221–224. [Google Scholar] [CrossRef]
- Wang, J. Optimization Method of UWB Base Station Layout for Underground Parking Lot. Shanghai Highw. 2021, 4, 78–84. [Google Scholar]
- Li, J.; Xiu, C.; Yang, D. An Optimal Deployment Method of UWB positioning base station. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2022, X-3/W1-2022, 85–91. [Google Scholar] [CrossRef]
- Android Devices that Support Wi-Fi RTT. Available online: https://developer.android.com/develop/connectivity/wifi/wifi-rtt#supported-aps (accessed on 4 September 2024).
- Zebra FTM RTT. Available online: https://docs.zebra.com/us/en/mobile-computers/software/zebra-ftm-wi-fi-location-ig/c-zebra-ftm-wi-fi-location-integrator-guide.html (accessed on 4 September 2024).
- Google. WiFiRttScan. Available online: https://play.google.com/store/apps/details?id=com.google.android.apps.location.rtt.wifirttscan (accessed on 4 September 2024).
- Compulab. WILD Minimal. Available online: https://github.com/Compulab-WILD/WILD-minimal (accessed on 4 September 2024).
- Google. WifiRttLocator. Available online: https://play.google.com/store/apps/details?id=com.google.android.apps.location.rtt.wifirttlocator (accessed on 4 September 2024).
- Google Play FTMRTT App. 2022. Available online: https://play.google.com/store/apps/details?id=com.welwitschia.ftmrtt (accessed on 4 September 2024).
- FTMRTT. 2022. Available online: https://people.csail.mit.edu/bkph/FTMRTT_app (accessed on 4 September 2024).
- WifiRttScanX. Available online: https://play.google.com/store/apps/details?id=com.welwitschia.wifirttscanX (accessed on 4 September 2024).
- Ogawa, M.; Choi, H. Measurement accuracy of Wi-Fi FTM on actual devices. IEICE Commun. Express 2020, 9, 567–572. [Google Scholar] [CrossRef]
- Yu, K.; Wen, K.; Li, Y.; Zhang, S.; Zhang, K. A novel NLOS mitigation algorithm for UWB localization in harsh indoor environments. IEEE Trans. Veh. Technol. 2019, 68, 686–699. [Google Scholar] [CrossRef]
- Jiokeng, K.; Jakllari, G.; Tchana, A.; Beylot, A.L. When FTM discovered MUSIC: Accurate Wi-Fi-based ranging in the presence of multipath. In Proceedings of the 2020 IEEE Conference on Computer Communications, Toronto, ON, Canada, 6–9 July 2020; pp. 1857–1866. [Google Scholar] [CrossRef]
- Si, M.; Wang, Y.; Xu, S.; Sun, M.; Cao, H. A Wi-Fi FTM-based indoor positioning method with LOS/NLOS identification. Appl. Sci. 2022, 10, 956. [Google Scholar] [CrossRef]
- Choi, J.; Choi, Y.S.; Talwar, S. Unsupervised learning techniques for trilateration: From theory to android app implementation. IEEE Access 2019, 7, 134525–134538. [Google Scholar] [CrossRef]
- Horn, B.K.P. Doubling the accuracy of indoor positioning: Frequency diversity. Sensors 2020, 20, 1489. [Google Scholar] [CrossRef] [PubMed]
- Chai, C.; Liu, B.; Pan, J. Indoor positioning optimization algorithm based on threshold filtering. Comput. Mod. 2022, 4, 79–85. [Google Scholar]
- Yan, L.; Lu, Y.; Zhang, Y. Improved least-squares algorithm for TDOA/AOA-based localization. Chin. J. Radio Sci. 2016, 31, 394–400. [Google Scholar]
- Zhang, C.; Wang, W.; Xu, C.; Sun, X.; Guo, J.; Tu, Z.; Mao, Y. A TOA-based optimization positioning algorithm for non-line-of-sight errors. J. Nanjing Univ. Posts Telecommun. Nat. Sci. Ed. 2022, 42, 56–63. [Google Scholar]
- Cao, H.; Wang, Y.; Bi, J.; Xu, S.; Si, M.; Qi, H. Indoor positioning method using Wi-Fi RTT based on LOS identification and range calibration. ISPRS Int. J. Geo. Inf. 2020, 9, 627. [Google Scholar] [CrossRef]
- Gentner, C.; Ulmschneider, M.; Kuehner, I.; Dammann, A. Wi-Fi-RTT indoor positioning. In Proceedings of the 2020 IEEE/ION Position, Location and Navigation Symposium (PLANS), Portland, OR, USA, 20–23 April 2020; pp. 1029–1035. [Google Scholar] [CrossRef]
- Wann, C.D.; Yeh, Y.J.; Hsueh, C.S. Hybrid TDOA/AOA indoor positioning and tracking using extended kalman filters. In Proceedings of the 2006 IEEE 63rd Vehicular Technology Conference, Melbourne, Australia, 7–10 May 2006; pp. 1058–1062. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, Y.; Nie, R.; Cheng, Q.; Zhu, G. Optimal location method of spontaneous data fusion based on TDOA/AOA. In Proceedings of the 2021 OES China Ocean Acoustics, Harbin, China, 14–17 July 2021; pp. 885–889. [Google Scholar] [CrossRef]
- Wei, Z.; Chen, X.; Fang, L.; Zhao, N.; Guo, S.; Li, X. Joint positioning technique based on TOF and TDOA. In Proceedings of the 2018 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Houston, TX, USA, 14–17 May 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Zeng, Z.; Liu, S.; Lei, W. NLOS detection and mitigation for UWB/IMU fusion system based on EKF and CIR. In Proceedings of the 2018 IEEE 18th International Conference on Communication Technology (ICCT), Chongqing, China, 8–11 October 2018; pp. 376–381. [Google Scholar] [CrossRef]
- Yu, Y.; Chen, R.; Chen, L.; Xu, S.; Li, W.; Wu, Y.; Zhou, H. Precise 3-D indoor localization based on Wi-Fi FTM and built-in sensors. IEEE Internet Things J. 2020, 7, 11753–11765. [Google Scholar] [CrossRef]
- Choi, J.; Choi, Y.-S. Calibration-free positioning technique using Wi-Fi ranging and built-in sensors of mobile devices. IEEE Internet Things J. 2021, 8, 541–554. [Google Scholar] [CrossRef]
- Han, K.; Yu, S.M.; Kim, S.L.; Ko, S.W. Exploiting user mobility for Wi-Fi RTT positioning: A geometric approach. IEEE Internet Things J. 2021, 8, 14589–14606. [Google Scholar] [CrossRef]
- Xu, S.; Chen, R.; Yu, Y.; Guo, G.; Huang, L. Locating smartphones indoors using built-in sensors and Wi-Fi ranging with an enhanced particle filter. IEEE Access 2019, 7, 95140–95153. [Google Scholar] [CrossRef]
- Yu, Y.; Chen, R.; Chen, L.; Guo, G.; Ye, F.; Liu, Z. A robust dead reckoning algorithm based on Wi-Fi FTM and multiple sensors. Remote Sens. 2019, 11, 504. [Google Scholar] [CrossRef]
- Dvorecki, N.; Bar-Shalom, O.; Banin, L.; Amizur, Y. A machine learning approach for Wi-Fi RTT ranging. In Proceedings of the 2019 International Technical Meeting of the Institute of Navigation, Reston, VA, USA, 28–31 January 2019; pp. 435–444. [Google Scholar] [CrossRef]
- Choi, J. Enhanced Wi-Fi RTT ranging: A sensor-aided learning approach. IEEE Trans. Veh. Technol. 2022, 71, 4428–4437. [Google Scholar] [CrossRef]
- Marano, S.; Gifford, W.M.; Wymeersch, H.; Win, M.Z. NLOS identification and mitigation for localization based on UWB experimental data. IEEE J. Sel. Areas Commun. 2010, 28, 1026–1035. [Google Scholar] [CrossRef]
- Bregar, K.; Mohorčič, M. Improving indoor localization using convolutional neural networks on computationally restricted devices. IEEE Access 2018, 6, 17429–17441. [Google Scholar] [CrossRef]
- Chen, Y.-Y.; Huang, S.-P.; Wu, T.-W.; Tsai, W.-T.; Liou, C.-Y.; Mao, S.-G. UWB System for Indoor Positioning and Tracking With Arbitrary Target Orientation, Optimal Anchor Location, and Adaptive NLOS Mitigation. IEEE Trans. Veh. Technol. 2020, 69, 9304–9314. [Google Scholar] [CrossRef]
- Djosic, S.; Stojanovic, I.; Jovanovic, M.; Nikolic, T.; Djordjevic, G.L. Fingerprinting-assisted UWB-based localization technique for complex indoor environments. Expert. Syst. Appl. 2021, 167, 114188. [Google Scholar] [CrossRef]
- Wang, Q.; Li, Z.; Zhang, H.; Yang, Y.; Meng, X. An indoor UWB NLOS correction positioning method based on anchor LOS/NLOS map. IEEE Sens. J. 2023, 23, 30739–30750. [Google Scholar] [CrossRef]
- Zheng, S.; Li, Z.; Liu, Y.; Zhang, H.; Zou, X. An optimization-based UWB-IMU fusion framework for UGV. IEEE Sens. J. 2022, 22, 4369–4377. [Google Scholar] [CrossRef]
- Cheng, L.; Huang, S.; Xue, M.; Bi, Y. A robust localization algorithm based on NLOS identification and classification filtering for wireless sensor network. Sensors 2020, 20, 6634. [Google Scholar] [CrossRef] [PubMed]
- Gao, Z.; Jiao, Y.; Yang, W.; Li, X.; Wang, Y. A method for UWB localization based on CNN-SVM and hybrid locating algorithm. Information 2023, 14, 46. [Google Scholar] [CrossRef]
- Shao, W.; Luo, H.; Zhao, F.; Tian, H.; Yan, S.; Crivello, A. Accurate indoor positioning using temporal–spatial constraints based on Wi-Fi fine time measurements. IEEE Internet Things J. 2020, 7, 11006–11019. [Google Scholar] [CrossRef]
- Sun, M.; Wang, Y.; Xu, S.; Qi, H.; Hu, X. Indoor positioning tightly coupled Wi-Fi FTM ranging and PDR based on the extended Kalman filter for smartphones. IEEE Access 2020, 8, 49671–49684. [Google Scholar] [CrossRef]
- Liu, X.; Zhou, B.; Huang, P.; Xue, W.; Li, Q.; Zhu, J. Kalman Filter-Based Data Fusion of Wi-Fi RTT and PDR for Indoor Localization. IEEE Sens. J. 2021, 21, 8479–8490. [Google Scholar] [CrossRef]
- Liu, X.; Zhou, B.; Wu, Z.; Liang, A.; Li, Q. An Indoor 3-D Quadrotor Localization Algorithm Based on Wi-Fi RTT and MEMS Sensors. IEEE Internet Things J. 2022, 9, 20879–20888. [Google Scholar] [CrossRef]
- Zhou, B.; Wu, Z.; Chen, Z.; Liu, X.; Li, Q. Wi-Fi RTT/Encoder/INS-Based Robot Indoor Localization Using Smartphones. IEEE Trans. Veh. Technol. 2023, 72, 6683–6694. [Google Scholar] [CrossRef]
- Guo, G.; Chen, R.; Niu, X.; Yan, K.; Xu, S.; Chen, L. Factor Graph Framework for Smartphone Indoor Localization: Integrating Data-Driven PDR and Wi-Fi RTT/RSS Ranging. IEEE Sens. J. 2023, 23, 12346–12354. [Google Scholar] [CrossRef]
- Lee, G.T.; Seo, S.B.; Jeon, W.S. Indoor Localization by Kalman Filter Based Combining of UWB-Positioning and PDR. In Proceedings of the 2021 IEEE 18th Annual Consumer Communications & Networking Conference (CCNC), Las Vegas, NV, USA, 9–12 January 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Shi, Q.; Cui, X.; Li, W.; Xia, Y.; Lu, M. Visual-UWB navigation system for unknown environments. In Proceedings of the 31st International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS+ 2018), Miami, FL, USA, 24–28 September 2018; pp. 3111–3121. [Google Scholar] [CrossRef]
- Cai, Q.; Jiang, B.; Wu, Y.; Xu, H. A distributed SLAM with UWB-VIO fusion framework for enhanced elative localization of multi-UAVs system. In Proceedings of the 2023 4th International Conference on Computer Vision, Image and Deep Learning (CVIDL), Zhuhai, China, 12–14 May 2023; pp. 284–290. [Google Scholar] [CrossRef]
- Brovko, T.; Chugunov, A.; Malyshev, A.; Korogodin, I.; Petukhov, N.; Glukhov, O. Complex Kalman Filter Algorithm For Smartphone-based Indoor UWB/INS Navigation Systems. In Proceedings of the 2021 Ural Symposium on Biomedical Engineering, Radio electronics and Information Technology (USBEREIT), Yekaterinburg, Russia, 13–14 May 2021; pp. 0280–0284. [Google Scholar] [CrossRef]
- Shin, S.; Lee, E.; Choi, J.; Myung, H. MIR-VIO: Mutual information residual-based visual inertial odometry with UWB fusion for robust localization. In Proceedings of the 21st International Conference on Control, Automation and Systems (ICCAS), Jeju, Republic of Korea, 12–15 October 2021; pp. 91–96. [Google Scholar] [CrossRef]
- Ziegler, T.; Karrer, M.; Schmuck, P.; Chli, M. Distributed formation estimation via pairwise distance measurements. IEEE Robot. Autom. Lett. 2021, 6, 3017–3024. [Google Scholar] [CrossRef]
- Nguyen, T.H.; Nguyen, T.M.; Xie, L. Range-focused fusion of camera-IMU-UWB for accurate and drift-reduced localization. IEEE Robot. Autom. Lett. 2021, 6, 1678–1685. [Google Scholar] [CrossRef]
- Jung, K.; Shin, S.; Myung, H. U-VIO: Tightly coupled UWB visual inertial odometry for robust localization. In Proceedings of the Robot Intelligence Technology and Applications RiTA 2021, Daejeon, Republic of Korea, 16–17 December 2021; pp. 272–283. [Google Scholar] [CrossRef]
- Wang, R.; Jiang, H.; Zhang, Q.; Liu, G.; Yu, F.R. Real-Time UWB and IMU Fusion Positioning System for Urban Rail Transit with High Mobility. In Proceedings of the 2024 IEEE 99th Vehicular Technology Conference (VTC2024-Spring), Singapore, 24–27 June 2024; pp. 1–7. [Google Scholar] [CrossRef]
- Jiang, P.; Hu, C.; Wang, T.; Lv, K.; Guo, T.; Jiang, J.; Hu, W. Research on a Visual/Ultra-Wideband Tightly Coupled Fusion Localization Algorithm. Sensors 2024, 24, 1710. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Wu, Z.; Li, J.; Sun, W.; Wang, J. A novel adaptive Kalman filter based NLOS error mitigation algorithm. IFAC Pap. 2015, 48, 1118–1123. [Google Scholar] [CrossRef]
- He, J.; Geng, Y.; Liu, F.; Xu, C. CC-KF: Enhanced TOA Performance in Multipath and NLOS Indoor Extreme Environment. IEEE Sens. J. 2014, 14, 3766–3774. [Google Scholar] [CrossRef]
- Xiao, Z.; Wen, H.; Markham, A.; Trigoni, N.; Blunsom, P.; Frolik, J. Identification and mitigation of non-line-of-sight conditions using received signal strength. In Proceedings of the International Conference on Wireless and Mobile Computing, Networking and Communications, Lyon, France, 7–9 October 2013; pp. 667–674. [Google Scholar] [CrossRef]
- Wen, W.; Bai, X.; Kan, Y.C.; Hsu, L.T. Tightly coupled GNSS/INS integration via factor graph and aided by fish-eye camera. IEEE Trans. Veh. Technol. 2019, 68, 10651–10662. [Google Scholar] [CrossRef]
- Nguyen, T.H.; Nguyen, T.M.; Xie, L. Tightly-coupled single-anchor ultra-wideband-aided monocular visual odometry system. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 665–671. [Google Scholar] [CrossRef]
- Nguyen, T.H.; Nguyen, T.M.; Xie, L. Tightly-coupled ultra-wideband-aided monocular visual SLAM with degenerate anchor configurations. Auton. Robot. 2020, 44, 1519–1534. [Google Scholar] [CrossRef]
- Cao, Y.; Beltrame, G. VIR-SLAM: Visual, inertial, and ranging SLAM for single and multi-robot systems. Auton. Robot. 2021, 45, 905–917. [Google Scholar] [CrossRef]
- Garcia-Fernandez, M.; Hoyas-Ester, I.; Lopez-Cruces, A.; Siutkowska, M.; Banqué-Casanovas, X. Accuracy in Wi-Fi access point position estimation using round trip time. Sensors 2021, 21, 3828. [Google Scholar] [CrossRef]
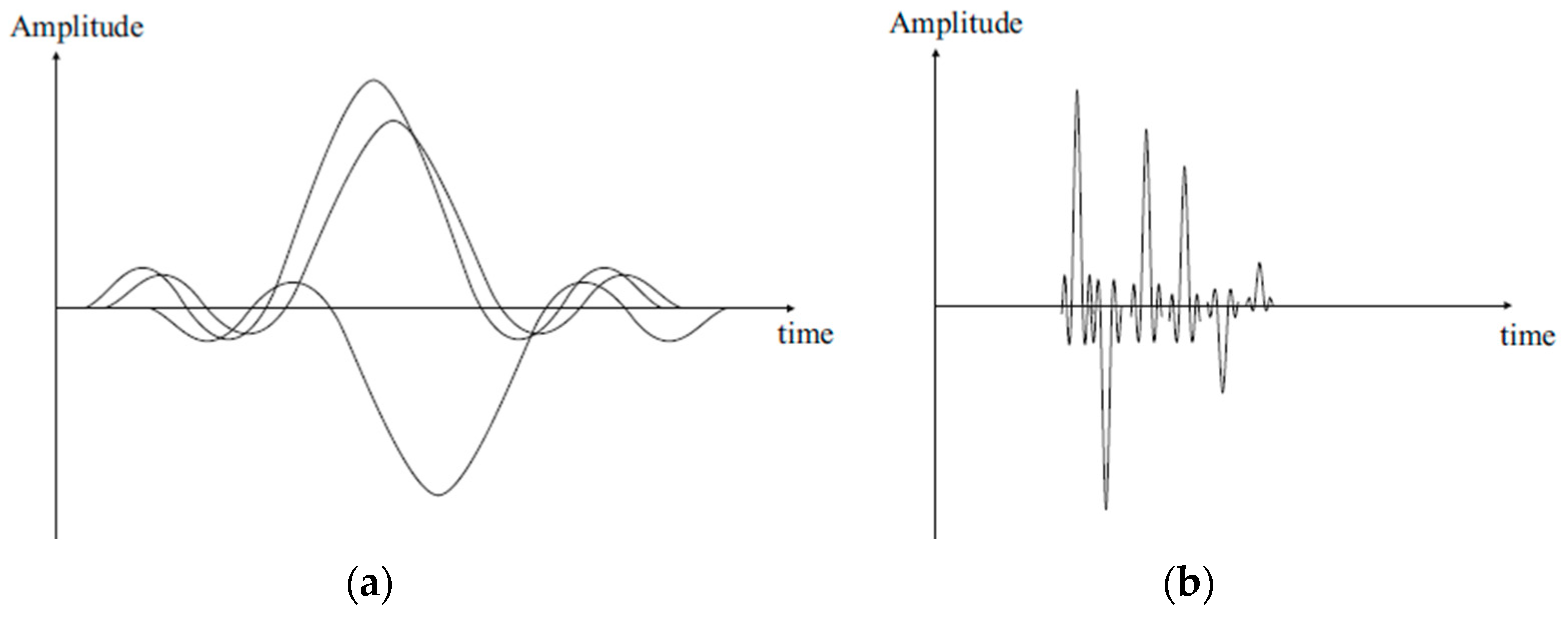
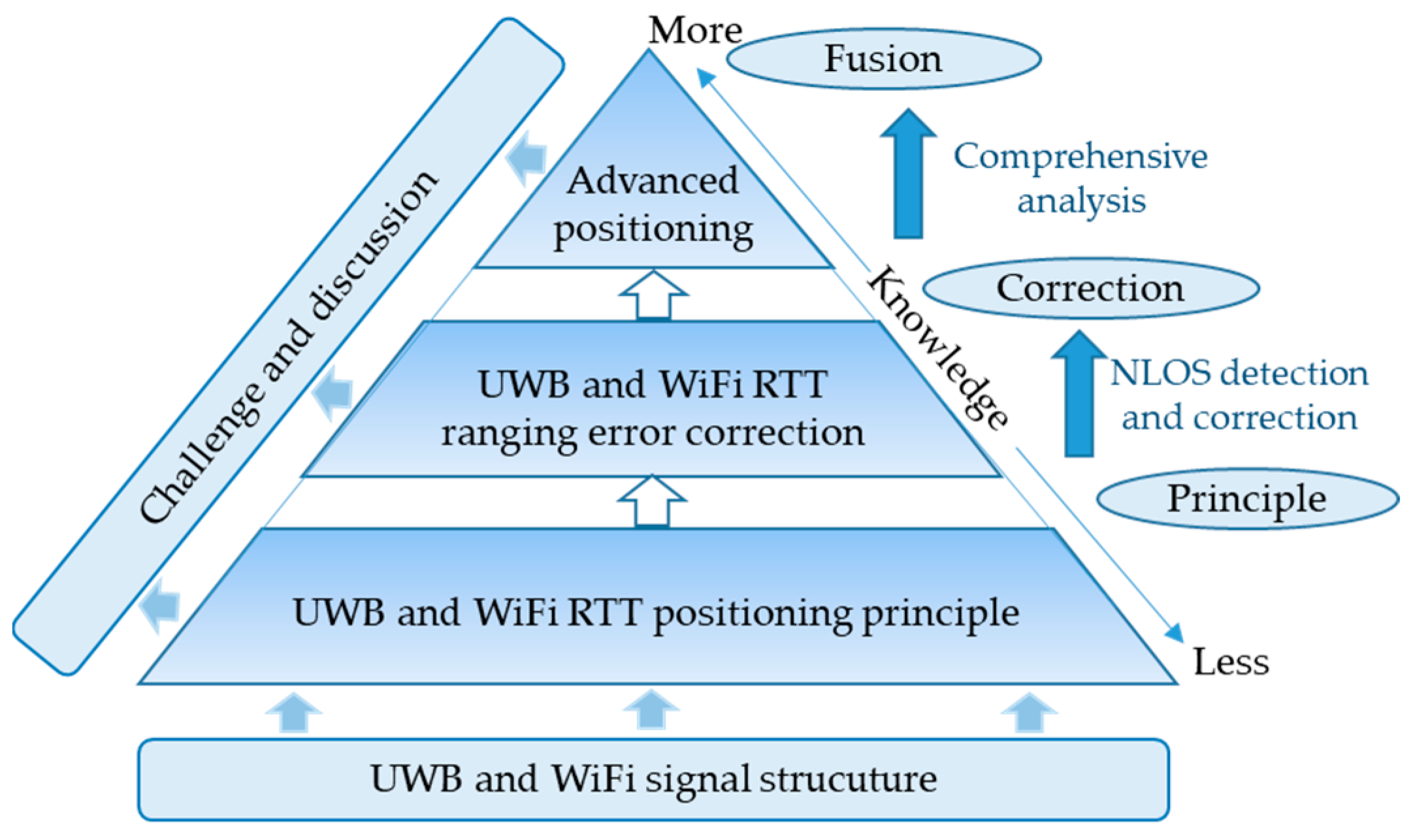
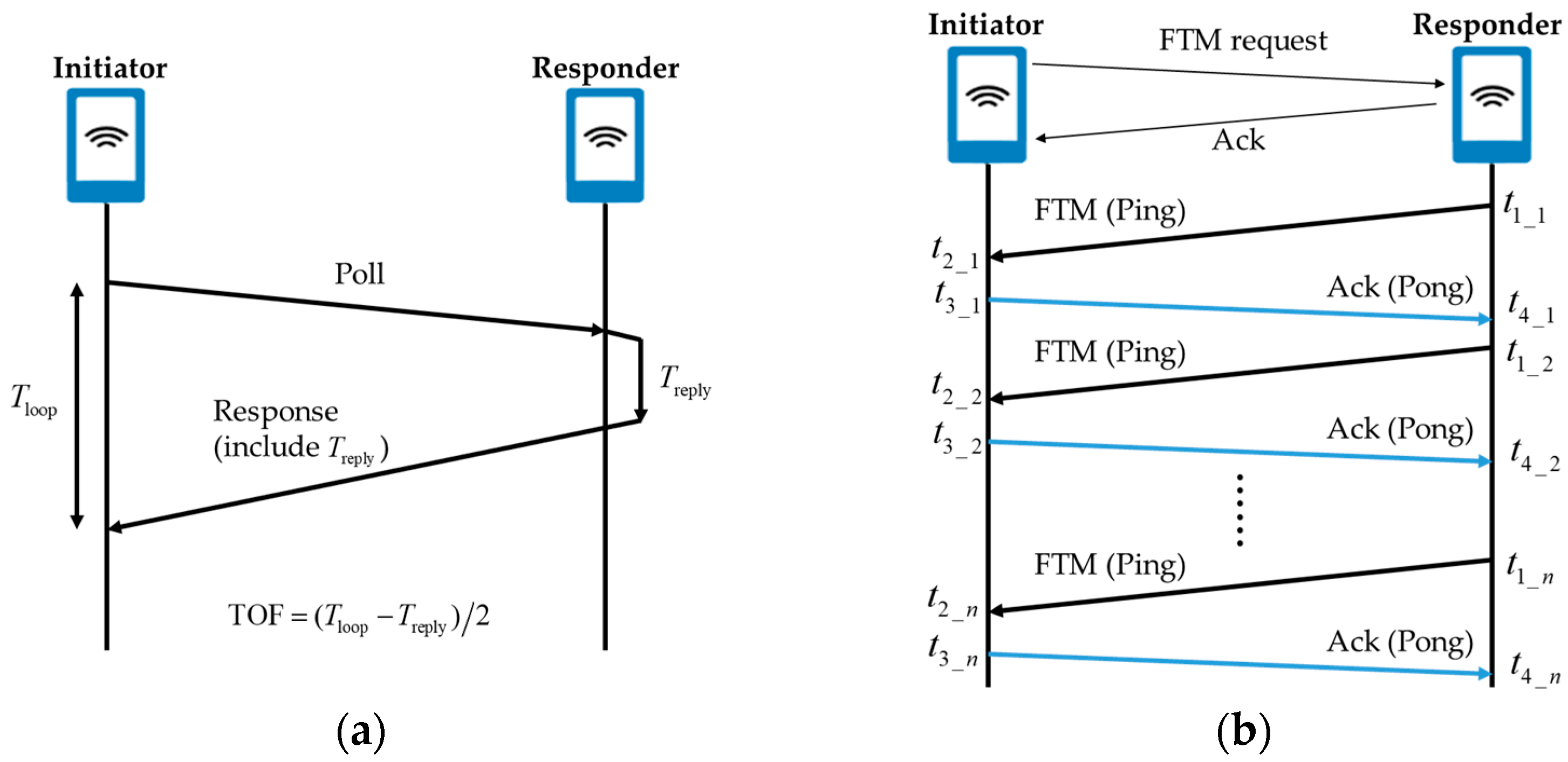
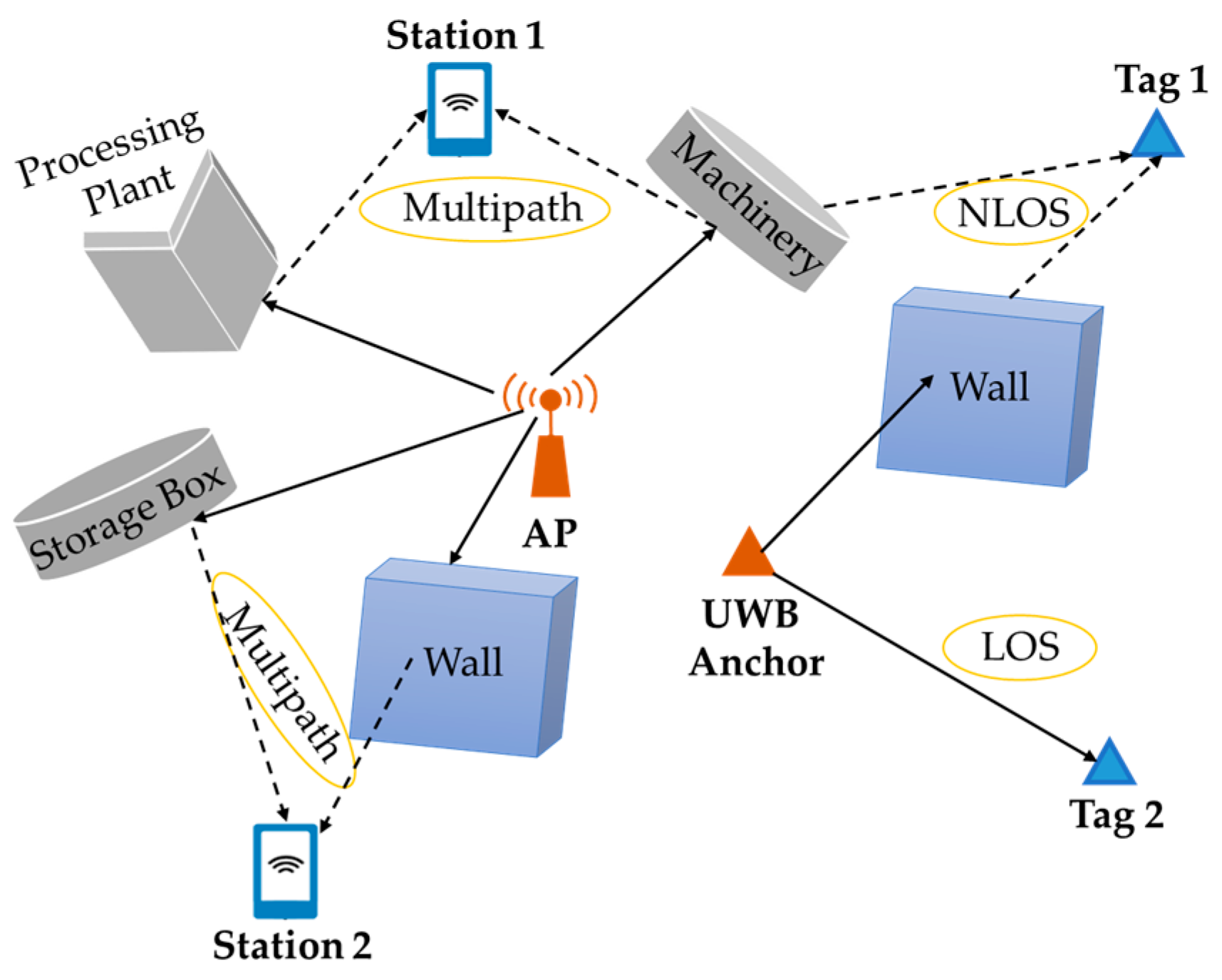
| Reference | Year | Technology |
|---|---|---|
| [16] | 2015 | Overview of the Wi-Fi Fine time measurement-based positioning principle |
| [7] | 2016 | Overview of UWB positioning principle, algorithms and challenges |
| [6] | 2017 | Overview of fundamental UWB positioning principle and algorithms |
| [17] | 2018 | Overview of indoor positioning technology |
| [18] | 2021 | Overview of UWB self-calibration and collaborative localization |
| [8] | 2022 | Overview of the main positioning algorithms in general |
| [19] | 2022 | Overview of UWB-based smart logistics |
| [20] | 2022 | Overview of indoor high-precision positioning technology |
| [21] | 2023 | Overview of indoor high-precision positioning technology |
| [22] | 2023 | Overview of indoor positioning technology |
| [23] | 2023 | Overview of the classification of NLOS error and its impact on UWB positioning accuracy |
| [24] | 2023 | Overview of fundamental UWB positioning principle and algorithms and their recent development. |
| [25] | 2023 | Overview of NLOS identification and error mitigation for UWB indoor positioning |
| [26] | 2023 | Overview of Wi-Fi assisted indoor positioning on different principles |
| [27] | 2024 | Overview of deep learning-based Wi-Fi indoor positioning |
| Category | Manufacturer | Product | Band/Version Supporting FTM RTT |
|---|---|---|---|
| Access Points | Nest Wifi Pro (Wi-Fi 6E) | up to 6 GHz | |
| Google Wi-Fi | up to 5 GHz | ||
| Google Nest Wi-Fi Router | up to 5 GHz | ||
| Google Nest Wi-Fi Point | up to 5 GHz | ||
| Aruba | AP504, AP505, AP514, AP515, AP518, AP503H, AP505H, AP534/AP535, AP555, AP565, AP575 | up to 5 GHz | |
| AP61x | up to 6 GHz | ||
| Cisco | 9130, 9136, 9164, 9166 | up to 6 GHz | |
| Compulab | Compulab WILD AP | up to 5 GHz | |
| Phones | Google Pixel | 6, 6 pro, 5, 5a, 5a 5G, 4 XL, 4, 4a, 3 XL, 3, 3a XL, 3a, 2 XL, 2, 1XL, 1 | Android 9.0+ |
| Xiaomi Mi | 10 Pro, 10, 9T, 9, Note 10, Note 10 Lite, CC9 Pro | Android 9.0+ | |
| Xiaomi Redmi | Mi 9T Pro, Note 9S, Note 9 Pro, Note 8T, Note 8, K30 Pro, K20 Pro, K20, Note 5 Pro | Android 9.0+ | |
| LG | G8X ThinQ, V50S ThinQ, V60 ThinQ, V30 | Android 9.0+ | |
| Samsung Galaxy | Note 10+ 5G, S20+ 5G, S20+, S20 5G, S20 Ultra 5G, S20, Note 10+, Note 10 5G, Note 10, A9 Pro | Android 9.0+ | |
| POCO | X2 | Android 9.0+ | |
| Sharp Aquos | R3 SH-04L | Android 9.0+ | |
| Retail, Warehousing and Distribution Center Devices | Zebra Handhelds | TC52, TC52x, TC72, TC57, TC57x, TC77, TC83. EC30, EC50, EC55, MC3300x, MC9300, PS20 TC52ax, MC3300ax, TC52-HC, TC52x-HC TC52ax-HC | up to 5 GHz, Android 10.0+ |
| Zebra Wearables | WT6300 | up to 5 GHz, Android 10.0+ | |
| Zebra Tablets | ET51, ET56, L10A *ET40, *ET45 *ET40-HC, *ET45-HC | up to 5 GHz, Android 10.0+ | |
| Zebra Vehicle Mounted and Concierge | VC8300, CC600, CC6000 | up to 5 GHz, Android 10.0+ | |
| Zebra Handhelds | TC53, TC53e, TC53e-RFID, TC73, TC58, TC58e, TC78, MC3400, MC9400, MC9450, PS30 *TC22, *TC27, HC50, *HC20 | up to 6 GHz, Android 10.0+ | |
| Zebra Wearables | WT6400, WT5400 | up to 6 GHz, Android 10.0+ | |
| Zebra Tablets | ET60, ET65 | up to 6 GHz, Android 10.0+ | |
| Skorpio | X5 | Android 10.0+ |
| Year | Sensors | Fusion Category | Algorithm | Platform | Experiment | Accuracy (m) | Limitations |
|---|---|---|---|---|---|---|---|
| 2019 [64] | IMU, Wi-Fi RTT | Loose coupling | Enhanced particle filter | Smartphone | An office room of 11 m × (12.4 m/10 m) × 3 m | <1 m in 86.7% of the cases | Large amount of calculation and poor stability |
| 2019 [65] | IMU, Wi-Fi RTT | Loose coupling | PDR and Wi-Fi RTT are integrated by UKF | Smartphone | An office room of 12 m × 12 m; A shopping mall | <2 m | Long-term localization performance needs to be improved |
| 2020 [77] | IMU, Wi-Fi RTT | Tight coupling | Weighted least squares method and EKF | Smartphone | An office room of 20 m × 6 m | 0.68 m in 80% of the cases | The method is unstable when the Wi-Fi RTT measurements change drastically caused by multipath |
| 2021 [78] | IMU, Wi-Fi RTT | Loose coupling | A fusion-tracking federated filter | Smartphone | The two areas of 10 m × 10 m and 6 m × 4 m; An office room of 32 m × 21 m | <1 m in about 80% of the cases | Poor performance in large scenes |
| 2022 [79] | IMU, Wi-Fi RTT | Tight coupling | Error-state Kalman filter; Rauch–Tung–Striebel smoothing for localization optimization | UAV with IMU of the smartphone | An office room of 5 m × 4 m; A U-shaped public area with length of 13 m | 1.36 m in office room; 0.92 m in public area | Unknown performance in large scenes |
| 2023 [80] | IMU, Wi-Fi RTT | Tight coupling | Adaptive extended Kalman filter | Robot with IMU of the smartphone | An office building with LOS and NLOS experiments | 0.8 m in 80% of LOS cases; 1.04 m in 80% of NLOS cases | The robot speed is unknown |
| 2023 [81] | IMU, Wi-Fi RTT/RSS | Tight coupling | Factor graph optimization | Smartphone | Two real areas of 126 m2 | 0.39 m | Three pre-set phone modes |
| 2024 [9] | Wi-Fi RTT, Wi-Fi RSS | Loose coupling | A nonparametric regression | Smartphone | A passage and a classroom environment of 112.5 m2 | 1.15 m in 90% of the cases | Further validation of the method across diverse experimental settings is needed |
| Year | Sensors | Fusion Category | Algorithm | Platform | Experiment | Accuracy (m) | Limitations |
|---|---|---|---|---|---|---|---|
| 2018 [82] | Monocular camera, UWB | Tight coupling | Joint nonlinear optimization on Lie-Manifold | Vehicle | The EuRoC MAV datasets | 0.036 | The cost of generating global maps is high |
| 2021 [83] | IMU, UWB | Loose coupling | Deep learning-based speed estimation; KF-based position integration | Smartphone | An area of 5 m × 31 m | 0.21 m | The design trajectory is simple |
| 2021 [84] | IMU, UWB | Tight coupling | A complex Kalman filter for integration | Smartphone | A closed area of 9 m × 18 m | / | No NLOS impact |
| 2021 [85] | Camera, IMU, UWB | Tight coupling | Mutual-information-based residual optimization | Robot | An indoor environment with the dimension about 2.70 m × 1.80 m using a mobile robot | 0.16 | The environment is relatively simple with fixed UWB anchors |
| 2021 [86] | mono-VIO, UWB | Tight coupling | Residual-based optimization | UAV | Simulates the UAV flights using Gazebo and RotorS | <0.2 | Pursuing real-world experiments |
| 2021 [87] | VIO, UWB | Tight coupling | Residual-based optimization | Robot | “Loop” tests tin a 6 m × 6 m indoor area; “Open” tests in a 30 m × 10 m outdoor area | 0.06~0.14 | Only-one-robot scenarios, and multi-robots scenarios need to be extended |
| 2021 [88] | VIO, UWB | Tight coupling | Graph optimization | Robot | An indoor environment with the dimensions of about 2.70 m × 1.80 m using a mobile robot | <0.2 | The method considers an ideal environment considering only a situation where the UWB signal is a LOS |
| 2023 [89] | UWB, Visual-inertial odometry (VIO) | Loose coupling | Distributed pose graph optimization | UAV | An indoor environment with dimensions of 5 m × 4 m × 2.5 m using two UAVs | 0.2 | The cost of generating global maps online is unacceptable. The bandwidth for communication is high |
| 2024 [90] | IMU, UWB | Loose coupling | An Error-State-Kalman-Filter-based real-time fusion | Electric vehicle | A tunnel of 140 m × 5 m × 4 m | <0.4 m in LOS cases with a moving speed of 36 km/h | No experiment in the NLOS cases |
| 2024 [91] | Vision SLAM, UWB | Tight coupling | EKF with threshold detection and adaptive measurement noise estimator | Robot | Obstacle-free and obstacle-rich environments | 0.076~0.082 | The method overlooks the small spatial offset generated using the UWB label device on the mobile platform. The experiments are conducted in a small field, leading to fewer accumulated errors |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiao, J.; Yang, F.; Liu, J.; Huang, G.; Zhang, W.; Li, M. Advancements in Indoor Precision Positioning: A Comprehensive Survey of UWB and Wi-Fi RTT Positioning Technologies. Network 2024, 4, 545-566. https://doi.org/10.3390/network4040027
Qiao J, Yang F, Liu J, Huang G, Zhang W, Li M. Advancements in Indoor Precision Positioning: A Comprehensive Survey of UWB and Wi-Fi RTT Positioning Technologies. Network. 2024; 4(4):545-566. https://doi.org/10.3390/network4040027
Chicago/Turabian StyleQiao, Jiageng, Fan Yang, Jingbin Liu, Gege Huang, Wei Zhang, and Mengxiang Li. 2024. "Advancements in Indoor Precision Positioning: A Comprehensive Survey of UWB and Wi-Fi RTT Positioning Technologies" Network 4, no. 4: 545-566. https://doi.org/10.3390/network4040027
APA StyleQiao, J., Yang, F., Liu, J., Huang, G., Zhang, W., & Li, M. (2024). Advancements in Indoor Precision Positioning: A Comprehensive Survey of UWB and Wi-Fi RTT Positioning Technologies. Network, 4(4), 545-566. https://doi.org/10.3390/network4040027







