Abstract
The escalating demand for high-quality video streaming poses a major challenge for communication networks today. Catering to these bandwidth-hungry video streaming services places a huge burden on the limited spectral resources of communication networks, limiting the resources available for other services as well. Large volumes of video traffic can lead to severe network congestion, particularly during live streaming events, which require sending the same content to a large number of users simultaneously. For such applications, multicast transmission can effectively combat network congestion while meeting the demands of all the users by serving groups of users requesting the same content over shared spectral resources. Streaming services can further benefit from multi-connectivity, which allows users to receive content from multiple base stations simultaneously. Integrating multi-connectivity within multicast streaming can improve the system resource utilization while also providing seamless connectivity to multicast users. Toward this end, this work studied the impact of using multi-connectivity (MC) alongside wireless multicast for meeting the resource requirements of video streaming. Our findings show that MC substantially enhances the performance of multicast streaming, particularly benefiting cell-edge users who often experience poor channel conditions. We especially considered the number of users that can be simultaneously served by multi-connected multicast systems. It was observed that about of the users that are left unserved under single-connectivity multicast are successfully served using the same resources by employing multi-connectivity in multicast transmissions. We prove that the optimal resource allocation problem for MC multicast is NP-hard. As a solution, we present a greedy approximation algorithm with an approximation factor of . Furthermore, we establish that no other polynomial-time algorithm can offer a superior approximation. To generate realistic video traffic patterns in our simulations, we made use of traces from actual videos. Our results clearly demonstrate that multi-connectivity leads to significant enhancements in the performance of multicast streaming.
1. Introduction
The rapid growth of video streaming applications has been the primary driver of innovation in cellular networks. As of 2023, video traffic constituted over of all mobile data traffic [1]. While revolutionizing the way media are consumed online, video streaming has also created several challenges for telecommunication networks. Video streams are resource-intensive services that require a significant amount of bandwidth. As a result, the exponential increase in demands for video streaming can quickly overload the network infrastructure leading to network congestion, which leads to slower speeds, network outages, and degraded quality of service.
A large portion of video traffic is made up of live streaming from social media and streaming platforms with millions of users watching the same content simultaneously. These live streams pose additional challenges for the network due to their high data rate, low latency, and overall quality of service requirements [2]. Using traditional one-to-one or unicast communications, such applications involves transmitting the same content separately to each user, thus consuming a large portion of the available bandwidth. Multicast transmissions are an efficient means of catering to such services by serving users that need the same content simultaneously [3,4]. Multi-connectivity allows users to receive content from multiple base stations simultaneously. Therefore, when a video is being streamed by several base stations, allowing multi-connectivity within multicast transmissions can further improve the performance of multicast streaming services. We use the term Multi-Connectivity (MC) multicasting to refer to such a system where multi-connectivity is used alongside multicast transmissions. In this MC multicast system, users are capable of multi-connectivity and can, therefore, receive multicast content from multiple base stations simultaneously.
This paper proposes the use of MC multicasting for catering to the simultaneous demands of bandwidth-hungry video streams. Integrating MC with multicast transmission not only boosts cell capacity, but also diminishes the reliance of good multicasting performances from the weakest users in the system. While MC has received considerable attention for its impact on throughput and handover improvements [5,6,7,8], its unexplored integration with multicast transmissions presents a promising avenue for further research.
MC multicasting allows users to potentially connect to and receive content from multiple base stations and over various Radio Access Technologies (RATs) simultaneously. It can address the demanding requirements of 5G, including high data rates, ultra-reliable low latency, and high mobility [9]. By enabling users to receive content from multiple base stations concurrently, it serves a larger user base and enhances the performance for cell-edge users. The procedures for establishing multi-connectivity within the Third Generation Partnership Project (3GPP) multicast architecture and the associated control-signaling requirements were defined in [10].
1.1. Contributions
This work studied the integration of multi-connectivity in multicast transmissions for meeting the bandwidth demands of video streaming services. We address the problem of resource allocation in a multi-connected multicast system with the aim of maximizing the number of users that can be simultaneously served using multicast transmissions. The analyses, discussions, and simulations in this work provide conclusive evidence that multi-connectivity significantly improves the performance of multicast streaming systems. The main contributions of this paper are summarized as follows:
- We propose a multi-connected multicast system specifically designed for video streaming. This system utilizes the existing 3GPP Multimedia Broadcast Multicast Services (MBMS) framework, enabling multicast users to receive streaming content from multiple base stations seamlessly and with minimal signaling overhead. The resulting MC multicast system serves as a low-overhead alternative to the MBMS Single Frequency Network (MBSFN) operations within 3GPP multicast systems.
- We formulate the resource allocation problem in the MC multicast system with the aim of maximizing the number of multicast users served simultaneously. Since the MC multicast system is tailored for handling concurrent demands for bandwidth-intensive video streams with limited resources, we employed the metric of the number of users simultaneously served to measure its performance.
- We prove that the resource allocation problem in MC multicast systems is NP-hard, which means that there are no polynomial-time algorithms that can find the optimal solution. Therefore, we propose a centralized greedy approximation algorithm with an approximation factor of . We establish that this algorithm offers the most accurate approximation achievable for the problem.
- The centralized algorithm necessitates a central server to dictate resource allocation across all base stations within a region. Such a coordination may become impractical with an increasing number of base stations. Therefore, we also propose a distributed resource allocation algorithm for MC multicasting, allowing base stations to autonomously make resource allocation decisions.
- Extensive simulations clearly demonstrate the performance enhancements attained by incorporating MC in wireless multicasting, particularly for video streaming applications. We employed traces from actual video streams sourced from [11,12] to generate realistic video traffic patterns in our simulations.
In the following section, we provide an overview of the current research across the various facets of multi-connectivity and multicasting in cellular mobile networks.
1.2. Related Literature
Multicasting has been recognized as an effective means of catering to bandwidth-hungry video transmissions [3] in cellular mobile networks. Resource allocation algorithms designed for multicast streaming have been shown to serve significantly more users while minimizing the impact of multicast streaming on other services [4,13]. Further improvements in the performance of multicast video streaming have been achieved by exploiting the inherent loss-tolerant nature of video streams [14].
The use of MC has been studied for mitigating radio link failures in ultra-dense intra-frequency 5G network deployments [15], demonstrating substantial reductions in failures and throughput improvements for cell-edge users. Additionally, proportional fair allocation policies have been designed [16], tailored for multi-connected ultra-dense networks, prioritizing users based on load balancing and signal characteristics. MC has also been shown to enhance network availability for ultra-reliable low latency communication (URLLC) applications in 5G [17], where network availability is crucial. MC also optimizes the system resource utilization in URLLC through load-aware cell selection [18].
Numerous architectures have been proposed for implementing MC in 5G [19]. The comparative evaluations in [20] assessed throughput performance in distributed and cloud-based heterogeneous network architectures, favoring cloud-based networks for superior throughput. In [21], a 5G architecture integrating multiple RATs was proposed, facilitating seamless inter-RAT MC with LTE and Wireless Local Area Networks (WLANs). A control-and-user-plane split architecture for MC in 5G NR was introduced in [22], bypassing macro-cells for the user plane transmissions of multi-connected users. It wasn shown in [23] that MC exhibits significant reductions in transmit power compared to single-connected systems, resulting in improved outage probability and spectral efficiency. MC has also been examined as a means of optimizing power consumption, particularly for 5G heterogeneous cloud radio access networks [24]. Furthermore, beyond cellular networks, MC has also found applications in vehicle-to-anything (V2X) services, playing a pivotal role in meeting Quality of Service (QoS) requirements [25].
MC, combined with guard bands, has also been shown to provide substantial improvement in millimeter-wave (mmWave) session continuity [26]. The methodologies in [27] were used to evaluate MC’s impact on ultra-dense urban mmWave networks, showcasing enhancements in denial-of-service and session drop probabilities. The trade-offs between system complexity and performance enhancement in multi-connected mmWave systems were explored in [28]. In [29], a network throughput-optimizing algorithm approaching the global optimum solution was proposed for addressing the link scheduling problem in multi-connected mmWave networks. The uplink MC frameworks presented in [30] efficiently monitor channel dynamics and link directions in mmWave transmissions, leading to efficient scheduling and session management. By mitigating radio link failures due to mobility, MC also ensures seamless connectivity for mobile users [15]. The combination of MC and network coding was studied in [31] to enable the transmission of high-quality video streaming services over mmWave networks.
Despite the wide-ranging applications of MC, its use in multicast streaming has not yet been explored in the existing literature. This work is the first to leverage MC for this crucial application and establish improvements in system performance that are achieved using MC multicasting for video streaming. We also address the problem of resource allocation in the proposed system. The rest of this paper is organized as follows. An overview of the existing 3GPP standards for multicasting and MC is provided in Section 2. This is followed by a discussion on how these two techniques can be used together within the current and future generations of wireless mobile networks in Section 2.1. The MC multicast system model and the associated resource allocation problem are discussed in Section 3. In Section 4, we prove the NP-hardness of the resource allocation problem and then provide an approximation algorithm for it in Section 5. We then examine the use of distributed resource allocation for MC multicasting in Section 6. Finally, we present the simulation results in Section 7 and conclude this paper in Section 8.
1.3. Notation
The set of natural numbers is denoted by 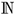 . The cardinality of a set A is denoted by . The set of integers up to n is denoted as . An overview of the most commonly used variable notations can be found in Table 1.
. The cardinality of a set A is denoted by . The set of integers up to n is denoted as . An overview of the most commonly used variable notations can be found in Table 1.
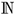 . The cardinality of a set A is denoted by . The set of integers up to n is denoted as . An overview of the most commonly used variable notations can be found in Table 1.
. The cardinality of a set A is denoted by . The set of integers up to n is denoted as . An overview of the most commonly used variable notations can be found in Table 1.
Table 1.
Notation of the most commonly used variables.
2. Multi-Connectivity in MBMS
Multicast services were first standardized as part of release 9 [32] of the 3GPP standards as MBMS [33] and later as evolved-MBMS (eMBMS) [34], which is also a part of the Fifth Generation (5G) New Radio (NR) [35] standards. Within MBMS, two modes of multicast operation are defined, namely, Single-Cell Point-To-Multipoint (SC-PTM) and MBSFN. SC-PTM, which refers to the multicast mode where content is multicast to users within a single cell. In the MBSFNs mode of operation, all the base stations within a designated MBSFN area [36] transmit the same content in strict synchronization [33]. MBSFN transmissions necessitate precise synchronization between all base stations in the MBSFN area and extended cyclic prefixes. This is crucial to enhancing service quality for cell-edge receivers, as it enables the combination of signals from various base stations, resulting in improved user experience. However, the extended cyclic prefix reduces system throughput, and the requirement for tight synchronization results in significant control overheads. MC multicast overcomes these limitations with a considerably simpler framework than MBSFN and lower transmission overheads. We discuss this in greater detail in Section 2.2.
The supporting architecture for MBMS with 5G NR is shown in Figure 1. The network elements that support MBMS services are the Broadcast Multicast Service Centre (BM-SC), the MBMS GateWay (MBMS-GW), and the Multicell/Multicast Coordination Entity (MCE) [33]. The BM-SC serves as an interface between the core network and the multicast/broadcast content providers. It is responsible for transporting MBMS data into the core network, managing group memberships and subscriptions, and charging for MBMS sessions [32]. The MCE is responsible for allocating radio resources to the base stations for MBSFN operations. The MBMS-GW uses IP multicasting to forward the MBMS session data to the base stations. The base stations can then transmit the data to the User Equipments (UEs) via wireless multicast/broadcast.
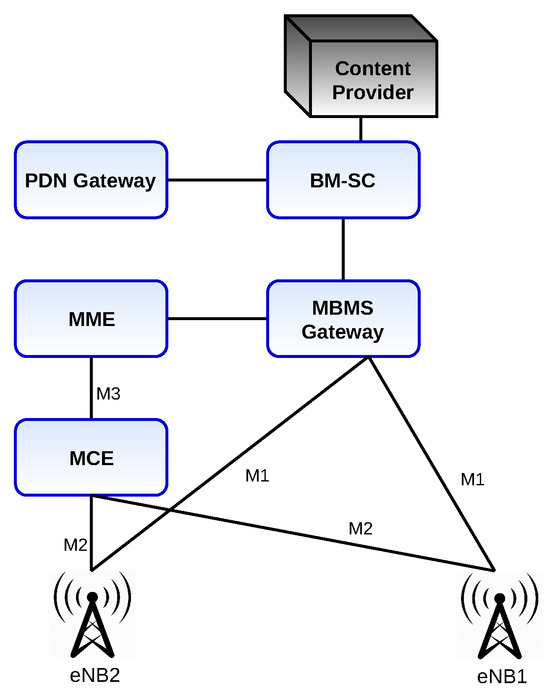
Figure 1.
MBMS architecture.
In the following section, we discuss the features of MBMS that enable the use of the proposed MC multicast operations.
2.1. Enabling Multi-Connectivity in Multicast Transmissions
The MBMS user plane protocol architecture defines a synchronization (SYNC) protocol layer on the transport network layer for content synchronization [37]. This layer carries the information needed for identifying transmission times and detecting packet loss. The SYNC protocol is terminated in the BM-SC and the base stations. As a result, the MBMS content sent to the base stations associated with the same BM-SC are synchronized. Consequently, UEs can receive and combine multiple copies of the same content received from these base stations without the need to exchange any additional control signaling. The proposed multi-connectivity multicast scheme leverages this inherent synchronization in MBMS systems, enabling UEs to obtain multicast content from multiple sources without requiring additional synchronization. Furthermore, since MBMS operates as an idle-mode procedure, UEs can use MC multicasting without establishing a Radio Resource Control (RRC) connection to a base station. The signaling procedures for enabling MC in MBMS were proposed in [10].
For enabling multi-connectivity in MBMS, we redefine the dynamic between the primary and secondary base stations of a multi-connected UE compared to what is traditionally defined for unicast transmissions [38]. Specifically, we propose the following:
- Connectivity: Firstly, depending on its capability, a UE can connect to any number of base stations and receive multicast content from all of them. A UE can also remain in the RRC idle mode if it is not connected to any base station and still receive content from any number of base stations [10].
- Primary and Secondary Base Stations: For a UE using MC multicasting in RRC idle mode, the primary base station refers to the base station that it is camped on. For a UE in RRC connected mode, the primary base station refers to the one it is connected to. All other base stations from which the UEs may receive content are called secondary base stations. Furthermore, the primary and secondary base stations of a UE do not operate in a traditional master–slave configuration in MC multicasting. Secondary base stations are not dictated by the primary base station in their interaction with the UE [10]. A multicast UE can receive relevant control information and multicast data from multiple base stations independently. Thus, there is no real distinction between primary and secondary base stations for a UE. Each base station that serves the UE under MC multicasting is equivalent from the perspective of the MC multicast transmissions.
2.2. MC Multicast versus MBSFN
5G NR uses MBSFN to enhance system efficiency by simultaneously transmitting identical content over the same radio resources within neighboring cells grouped in an MBSFN area. By leveraging the use of multi-connectivity, MC multicasting can provide the same advantages as MBSFN transmissions while employing a significantly simpler framework with reduced transmission overheads. Similar to MBSFNs, a UE can receive multicast content from multiple base stations, leading to an enhanced Signal-to-Noise Ratio (SNR), particularly for cell-edge users. However, unlike MBSFN operations, base stations under MC multicasting are not obligated to use the same Physical Resource Blocks (PRBs) for streaming multicast content. In MC multicasting, identical MBMS services are streamed through multiple base stations, and each base station independently allocates PRBs to the multicast streams. Consequently, each base station can optimize resource allocation for various services within its cell, resulting in significant frequency diversity that improves the probability of reliably receiving MBMS content. A multicast UE has the flexibility to decode any of the multiple copies of the content it receives. As demonstrated in Section 7, this diversity leads to substantial performance improvements in terms of the number of UEs served and the number of packets successfully delivered.
In the following section, we discuss the resource allocation problem in the MC multicast system.
3. Resource Allocation in MC Multicast
Consider a system of C cells, each with one base station serving it. There are M multi-connected multicast UEs in the system that can receive multicast content from any subset of the C base stations. The set denotes the set of all cells/base stations, and the set of all users is denoted by . Resource allocation decisions are made at every time slot t. In each time slot, there are N PRBs available for allocation in each cell. The set of all PRBs is denoted by . We assume that there is multicast content available in all the cells, which is being streamed by all the UEs. The multicast content is streamed at a rate of R bits per second. The UEs can potentially receive the multicast streaming content from any number of neighboring base stations in addition to their respective primary base stations. The multicast stream is allocated to one PRB in each cell, in each time slot. Resource allocation decisions are either made independently by each base station or by a central entity such as the MCE that manages the base stations within a region.
The channel states of UEs vary as a function of time t as well as the PRB . In the PRB j of cell c at time t, UE k can decode a maximum rate of bits per second, which is a function of the channel state of the UE. That is, the better the channel experienced by UE k, the higher the rate . Since the multicast content is transmitted at a rate of R bits per second, a UE may not successfully receive the multicast content from the base station that it is connected to. For instance, consider that the PRB j is allocated to the multicast stream in cell c at time t. UE k will be able to decode the content sent by c only if . On the other hand, if , UE k will not be able to successfully decode the content sent from cell c. Thus, in the absence of multi-connectivity, a UE can successfully receive data only if it can decode the content from its primary cell, whereas a multi-connected UE successfully receives data if it can decode the content from any one of the base stations that it receives content from.
Remark 1.
Note that, even though we assume a constant bit rate R, video streaming traffic typically uses a variable bit rate (VBR) encoding, which means that the amount of data to be transmitted for the video varies over time. We employed a constant rate model for the sake of simplicity in defining the resource allocation problem. However, our problem, as well as the proposed resource allocation policies, can be easily adapted to the VBR model by considering the proposed setup as a snapshot of a longer VBR video stream. More specifically, to adapt to the VBR model, the transmission rate R can be made a function of time t (denoted by ). Then, the system model discussed above essentially represents a small enough block of time during which the rate is constant. Similarly, the resource allocation problem can be defined with the time dependent rate . As we will see in the following sections, the proposed policies make allocation decisions in every time slot. Thus, the proposed policies can be used as is with the relevant rate in each time slot.
In the following, we define the resource allocation problem for this system.
Problem Definition
The resource allocation problem within the MC multicast system aims to maximize the number of UEs served in each time slot. We chose the number of UEs served as the optimization metric for this problem to capture the unique requirements of the MC multicast problem. The primary objective of the MC multicast system is to ensure that the multicast video stream is delivered to a large audience without causing network congestion. Note that our system model construction ensures that only one resource is allocated to the multicast stream in each time slot, which prevents overloading the system while serving several video streams. Therefore, we used the number of users served to illustrate the effectiveness of the resource allocation algorithms in meeting the video streaming demands of users within the limited resources.
In the system under consideration, since a UE can receive the same content from several base stations, its performance is impacted by the resource allocation decisions across multiple cells. Therefore, the resource allocation needs to be optimized over all C cells in the system. Throughout this study, we assumed that the users are static and do not change positions for the entire duration of the multicast transmissions.
For the mathematical formulation of the resource allocation problem, we first define the following sets. Assuming that every UE is trying to receive the multicast content from the base station of cell c, let us use to denote the set of users that would successfully receive the multicast content if PRB j is allocated to the multicast service in cell c, i.e., for all and all , the set is given by
The collection of all such sets corresponding to cell c is given by
Let be the collection of sets . In using these definitions, the resource allocation problem for the MC multicast system can now be stated as follows.
Definition 1
(Resource allocation problem ). Given the universal set of all users and the collection of sets , determine such that is maximized subject to the following:
Then, in each cell , the PRB assigned to the multicast stream is given by such that .
The objective of the of the resource allocation problem in Definition 1 is to maximize the cardinality of the union of sets , which is the set of users successfully served. The solution of is subject to the following constraints:
- For all , : This constraint ensures that there is precisely one set in corresponding to each cell . That is, only one PRB is assigned to the multicast stream in each cell, as required by the problem formulation.
- : This constraint ensures that there are precisely C of the sets in the solution set . Together with the constraint in Constraint 1, this guarantees that a set is chosen for every cell c, i.e., a PRB is allocated for multicast streaming in every cell.
The resource allocation decisions are a function of (a) the channel states of UEs in each of the N PRBs, (b) the number of UEs streaming the multicast content, and (c) the location of the UEs with respect to each base station.
4. Computational Complexity
We show that the resource allocation problem is NP-hard, and therefore, no polynomial-time algorithms exist for solving it. We prove this through a reduction from the Maximum Coverage Problem (MCP) [39], which is a known NP-hard problem defined as follows.
Definition 2
(Maximum Coverage Problem (MCP)). Consider a universal set , a number 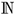 , and a collection of sets , where for all , . The objective of the MCP is to determine a sub-collection such that .
, and a collection of sets , where for all , . The objective of the MCP is to determine a sub-collection such that .
 , and a collection of sets , where for all , . The objective of the MCP is to determine a sub-collection such that .
, and a collection of sets , where for all , . The objective of the MCP is to determine a sub-collection such that . That is, given a collection of m subsets of a universal set , the objective of the MCP is to find the sub-collection of at most k subsets from that cover the maximum number of elements from the universal set .
Theorem 1.
The MC multicast resource allocation problem is NP-hard.
Proof.
The proof of the NP-hardness of can be accomplished in the following steps:
- First, we show that an instance of a known NP-hard problem (MCP in this case) can be reduced to an instance of in polynomial time. This means that we can design a polynomial-time algorithm that takes the MCP as input and results in an instance of .
- Next, we show that a solution of can be mapped to a corresponding solution for the MCP in polynomial time.
- Finally, using the results from steps 1 and 2, we prove that no polynomial-time algorithm exists for solving because such an algorithm would also provide a polynomial-time solution for the MCP, which is known to be NP-hard.
We begin by defining an algorithm to reduce an instance of MCP to an instance of in polynomial time. An instance of MCP can be reduced to an instance of as follows:
- Given an instance of the MCP in Definition 2 with the universal set , the collection of m sets with and some
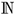 .
. - Define a MC multicast system with the set of UEs , number of cells , and the number of PRBs in each cell , and for all , the set .
- This defines a resource allocation problem of the form of in Definition 1. This reduction can be accomplished in constant time ().
The pseudo-code of the algorithm for accomplishing this reduction is given in Algorithm 1.
| Algorithm 1: Pseudo-code for reducing the MCP to |
 |
This yields a one-to-one correspondence between an instance of MCP and an instance of , which completes the first step of the proof. We now proceed to show that a solution of the resulting instance of can be mapped to a solution of MCP in polynomial time.
Let us assume that there exists a polynomial-time algorithm for solving the instance of resulting from Algorithm 1 that provides a solution . Then, the following hold true by the definition of :
- ;
- For all , ;
- maximizes .
This solution can be mapped to a solution of MCP as follows. Given the MCP in Definition 2, construct the solution set such that if , then . Since , it holds that . Therefore, by Definition 2, the constructed set is a feasible solution of the MCP. The pseudo-code for this mapping is given in Algorithm 2.
| Algorithm 2: Pseudo-code for mapping a solution of to a solution of the MCP |
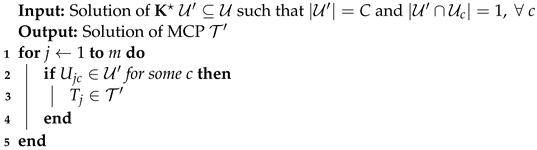 |
To complete the proof, what is left to prove is that the constructed solution is indeed the optimal solution of the MCP. We prove this by contradiction as follows.
Let us assume that is not the optimal solution of the MCP. This implies that there exists a set such that and
If (5) is true, then we can construct another solution to , using as follows. Let with and let . We construct the set as follows
Then, by Definition 1, the following hold true:
- ;
- For all , ;
- ,
This contradicts our assumption that is the optimal solution of . This implies that there does not exist any set such that and . Therefore, is indeed the optimal solution of the MCP.
Algorithm 2 maps a solution of to a solution of the MCP in constant time ( assignments). Thus, a polynomial-time solution for also provides a polynomial-time solution for the MCP. This is not possible unless P = NP. This implies that no polynomial-time algorithm exists for solving , and therefore, is an NP-hard problem. □
Since the MC multicast resource allocation problem is NP-hard, we cannot construct a polynomial-time algorithm to determine its optimal solution. Therefore, in the following section, we construct approximation algorithms that provide some performance guarantees.
5. Centralized Greedy Approximation Algorithm
We propose a greedy approximation algorithm for solving the resource allocation problem . Centralized greedy approximation (CGA) works iteratively by maximizing the number of additional users served in each iteration. In the first iteration, the CGA chooses the set of the form in (1) from that has the largest number of elements. In the subsequent steps, it picks a that serves the maximum number of yet unserved users. In each step, the set chosen is from a different sub-collection , i.e., c in the subscript of the chosen sets is different for each set picked by the algorithm. The collection of sets chosen after C iterations is the output of the algorithm.
The steps involved in the decision making of the CGA policy are explained below. To begin, we have an empty solution set .
- In the first step of CGA, the algorithm finds the largest set , i.e., .
- The solution set is updated to . This implies that PRB is allocated to the multicast stream in cell .
- Next, for all , the sets are removed from the set . This step ensures that the algorithm finds a feasible solution that satisfies the constraint (4) in Definition 1.
- In the next step, CGA picks the set that contains the maximum number of UEs that were not present in any set picked in the previous iterations and assigns PRB to the multicast stream in cell . Following this, steps 2, 3, and 4 are repeated times to determine the solution.
At the end of C iterations of CGA, the output set contains exactly C sets of the form . The PRB assigned to the multicast stream in cell c is given by such that .
The pseudo-code for this algorithm is given in Algorithm 3.
| Algorithm 3: Centralized Greedy Approximation Algorithm for |
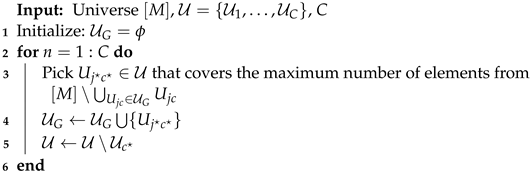 |
In the following theorem, we prove that the solution to given by CGA has an approximation factor of . This means that the solution provided by this approximation algorithm serves at least of the number of users that would be served by the optimal algorithm.
To state this result, we first define the following notation. Let denote the optimal solution to the resource allocation problem , i.e., the optimal algorithm would serve UEs in the system. Let denote the number of UEs served up to the nth iteration by the CGA algorithm. The gap between the optimal solution and the intermediate solution of the CGA algorithm after the nth iteration is given by
Therefore, , and the total number of UEs served by the CGA algorithm at the end of C iterations is given by . Using these notations, the following theorem presents the approximation factor for the CGA algorithm.
Theorem 2.
The CGA algorithm (Algorithm 3) is a approximation for the resource allocation problem . That is,
In fact, no other algorithm can achieve a better approximation unless P = NP.
To prove Theorem 2, we first prove the following two results. First, in Lemma 1, we determine the lower bound on the incremental improvements in the solution achieved in the intermediate steps of the CGA algorithm. This result will quantify the rate at which the CGA algorithm approaches the optimal solution. Then, in Lemma 2, we provide an upper bound on that quantifies the gap between the optimal solution and the intermediate solution of the CGA algorithm at the nth iteration, . Finally, using these two results, we can prove that the solution of the CGA algorithm is at least within of the optimal solution.
Lemma 1.
Under the CGA algorithm, the number of additional UEs served from iteration n to is lower bounded by . That is, for all , it holds that
where C is the total number of cells in the system, and is in (7).
Proof.
Let be the optimal solution of the resource allocation problem , where for all , the set is the set of UEs served by the base station of cell c. Let denote the set of users served at the end of the nth iteration of CGA, and is the set of users not yet covered at the end of the nth iteration. Then, it holds that
Due to multi-connectivity, the sets are not disjoint, which implies the inequality in (10). The quantity on the right hand side of (10) gives the number of unserved UEs after n iterations that would be served by the optimal solution . To arrive at the inequality in (11), note that the UEs served by the CGA algorithm may not be the same UEs that the optimal algorithm serves. Therefore, is at least equal to .
From (10) and (11), it follows that
Since CGA picks the set that serves the maximum possible number of yet unserved users in each iteration, we have
From (13) and (14), it follows that
which completes the proof. □
Lemma 2.
The difference between the number of UEs served in the optimal solution and the number of users served by the at the end of iterations of the CGA algorithm is upper bounded as follows:
where denotes the total number of UEs served by the CGA algorithm up to and including the th iteration.
Proof.
We prove this result by induction. For , if
it implies that
which is true due to Lemma 1. Thus, the result holds for .
Now, we assume that
and prove the corresponding inequality for .
From the definition of , it follows that
where the inequality in (23) follows due to Lemma 1, and (24) follows from (23) due to (19). Therefore, by mathematical induction, the result holds for all n. This completes the proof. □
Using these results, we can now prove Theorem 2 as follows.
Proof.
From Lemma 2, it follows that
In the limit as , from (25), it follows that
which implies that
That is, CGA provides a approximation for .
To complete the proof of Theorem 2, it only remains to show that this is the best possible approximation for . This can be easily seen using the following arguments. Let us assume that there is an algorithm that could provide a better approximation for . Then, this algorithm would also provide a better approximation for the MCP because, as we proved in Theorem 1, a solution for can be mapped to a solution of the MCP in polynomial time using Algorithm 2. This is a contradiction since the greedy algorithm is known to be the best possible approximation for the MCP unless P = NP [40]. Therefore, no other algorithm can provide a better approximation for than the CGA algorithm.
This completes the proof. □
Comparison with Optimal Solutions
In this section, we evaluate the performance guarantees of the proposed CGA algorithm by comparing its solution with the optimal solution obtained for a smaller sized problem of the form in Definition 1. For the purposes of this comparison, we use a 3-cell MC multicast system with 5 PRBs in each cell. To obtain the optimal solution, we employ a brute force algorithm that works as follows. The brute force algorithm first lists out all the possible PRB allocations for the 3-cell system. For instance, for a system with 2 cells and 2 PRBs, denoted by and in each cell, the possible allocations would be and . Following this, the algorithm finds the total number of UEs that would be served under each of these possible allocations. Finally, the output of the algorithm is the allocation that serves the maximum number of UEs.
In Figure 2a,b, we plot the number of UEs left unserved under the CGA algorithm and the corresponding optimal value obtained using the brute force algorithm. We refer to the plot corresponding to the brute force algorithm as ‘Optimal’ in the figures. Figure 2a shows the number of UEs left unserved under the two algorithms as a function of an increasing number of UEs in the system. We observe that the solution of the CGA algorithm matches the optimal solution for up to 30 UEs in the system. As the number of UEs increases, up to 3 additional UEs are left unserved while using the CGA algorithm compared to the optimal solution. Figure 2b shows the number of UEs left unserved under the two algorithms as a function of increasing cell sizes. We observe that CGA serves just as many UEs as the optimal solution for smaller cell sizes. As the cell sizes increase, one additional UE is left unserved under the CGA algorithm compared to the optimal solution.
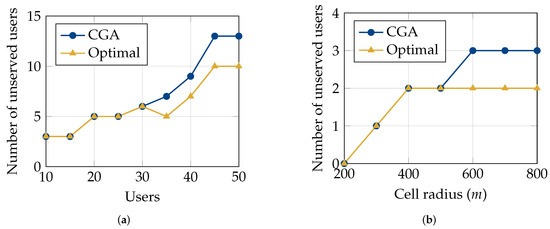
Figure 2.
Comparisons of the average number of users left unserved under CGA and the optimal resource allocation as a function of (a) an increasing number of users and (b) increasing cell radii (number of users ).
These plots show that the CGA algorithm provides optimal solutions for smaller systems. However, as the scale of the system increases, the solution provided by the CGA algorithm becomes sub-optimal.
Although the CGA algorithm provides provable approximation guarantees, it does so while requiring the presence of a central controller that can make allocation decisions for all base stations, based on the global view of the system. As the number of cells C increases, such a centralized setup may lead to large communication overheads and increased delays. In this case, a decentralized approach where base stations make allocation decisions independently might be more feasible, albeit at the cost of losing on the performance of the MC multicast streaming. In the following, we discuss the performance trade-offs between the centralized and distributed allocation for MC multicasting and propose a distributed approximation algorithm for .
6. Distributed Resource Allocation
In the absence of a centralized controller, allocation decisions are made by each base station independently based only on the knowledge of its own cell. This type of allocation does not fully reap the benefits of multi-connectivity. We illustrate this with the following example. Consider a 2-cell system containing cells and . There are two PRBs available for allocation in each cell. We denote these as and . Cell has four users, and cell has two users . All users are streaming the same multicast content. Assume that user has a good channel only in and can successfully receive content only on . Users , and have a good channel only in and can, therefore, successfully receive content only on . User has a good channel in both the PRBs and would be served on either of them. Users and are connected to both the cells and can receive content from either of them.
Let us now look at the allocations that will be conducted by a distributed policy that maximizes the number of users served in each cell independently. Cell considers the users connected to its base station and allocates PRB to the stream because it serves the maximum number of users, namely , and . Cell also optimizes independently and allocates PRB to the stream to serve users , and . Under this allocation, user remains unserved even though it was multi-connected, since it could only receive the content over PRB . On the other hand, users and receive content from both the cells. In contrast, a centralized policy would take the users of both the cells under consideration and allocate PRB to the multicast stream in and PRB to the stream in and successfully serve all the users in the system.
Any centralized allocation policy, even if it is sub-optimal, will always do better in terms of the number of users successfully served than a policy that allocates resources in a distributed manner. A centralized policy does not necessarily mean that the policy is optimizing over the entire system. Any form of centralization that looks beyond just the individual cell will reap better performances than a completely uncoordinated allocation. In the following, we propose a distributed resource allocation algorithm for a MC multicast system that can be used even in the absence of a central controller.
Distributed Greedy Allocation
In the Distributed Greedy Allocation (DGA) policy, each base station allocates resources to the multicast streams by only optimizing over their individual cells. Although allocating resources in a distributed manner will result in sub-optimal resource allocation decisions as discussed above, a distributed policy allows base stations to make allocation decisions independently. Therefore, such a policy can be used for enabling MC multicasting even in the absence of a central entity that can control all the base stations in a region. Furthermore, in case of content that is highly delay sensitive, the signaling delays due to the communication between the base stations and the central controller might not be tolerable. For such applications, the DGA policy can be used to sacrifice optimality in favor of lower delays.
The DGA policy solves the resource allocation problem for each cell independently. The distributed resource allocation problem is defined as follows. As in Section 3, denotes the set of users that would successfully receive the multicast content if PRB j is allocated to the multicast service in cell c. Set is the collection of such sets for cell c. The distributed resource allocation problem within each cell c can now be stated as follows.
Definition 3
(Distributed resource allocation problem ). For all , given the collection of sets , determine such that .
To solve the distributed resource allocation problem , the DGA policy at each base station allocates a PRB to the multicast stream to maximize the number of users served by it. That is, PRB is assigned to the multicast stream in cell c if .
The pseudo-code for this algorithm is given in Algorithm 4. The variable in Algorithm 4 is an indicator random variable that is equal to 1 only when PRB j is allocated to the multicast stream in cell c.
| Algorithm 4: Distributed Greedy Allocation algorithm |
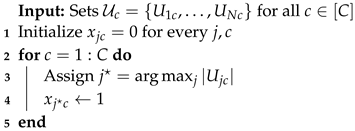 |
7. Simulations
We studied the performance of the proposed MC multicast in an MBMS system consisting of seven urban macro cells [41]. A base station was located at the center of each cell, and UEs were distributed uniformly at random in the cells. To create 5G-specific physical layer conditions, we created channels using the models recommended by 3GPP [42]. The SNR used to rate mappings was also measured according to 3GPP specifications [42]. Other relevant simulation parameters are given in Table 2. The cell-edge users in the system were multi-connected to all the base stations in the system. In all the cells, one PRB was allocated to the multicast stream in each time slot. Multi-connected users successfully received a packet if they could decode the content from at least one of the base stations. Other users only received the multicast content from their primary base stations.

Table 2.
System simulation parameters [42].
The number of packets delivered successfully and the number of UEs successfully served were used as the performance metrics in these simulations. In Figure 3, we plot the average number of packets successfully received by UEs under the CGA and the DGA resource allocation algorithms. One packet was transmitted in every sub-frame (1 ms), and we plotted the average number of packets successfully received by all the UEs in the system over a period of 10 s (10,000 packets). As expected from the discussions in Section 6, we observe that the centralized policy performs better than the distributed policy. However, despite its distributed nature, the packet loss under the DGA algorithm is at most greater than that under the CGA algorithm. Therefore, in the absence of centralized control, the DGA algorithm can provide a performance close to that of the centralized policy.
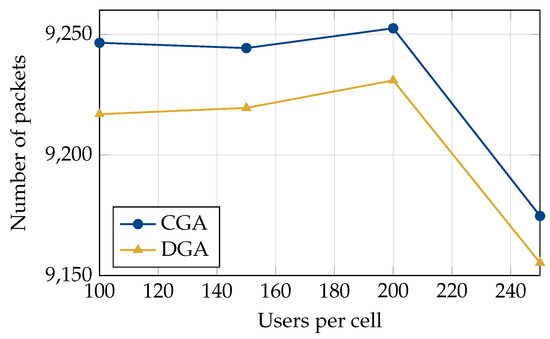
Figure 3.
Average number of packets successfully delivered using MC multicasting as a function of an increasing number of users under centralized (Algorithm 3) and distributed (Algorithm 4) resource allocation algorithms.
In Figure 4, Figure 5 and Figure 6, we compare the performance of MC multicasting with that of the conventional Single-Connectivity (SC) multicast transmission scheme. For resource allocation in SC multicasting, we used the DGA algorithm from Section 6, and the CGA algorithm was used in the resource allocation for MC multicasting. Note that since users are connected to a single base station in SC multicasting, the DGA algorithm provides the optimal solution for maximizing the number of users served. For the plots in Figure 4 and Figure 5, data were transmitted at a fixed rate in each sub-frame. The points in these plots were obtained by averaging over 10,000 sub-frames.
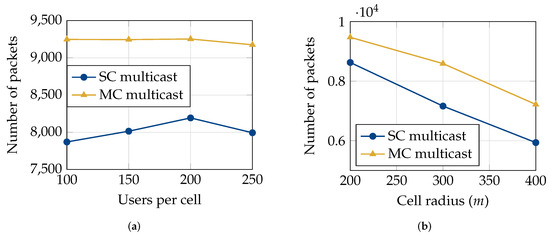
Figure 4.
Comparisons of the average number of packets (out of 10,000) successfully delivered under SC and MC multicasting. Resource allocation was performed using the proposed CGA algorithm (Algorithm 3), and the results are plotted as a function of (a) an increasing number of users and (b) increasing cell radii.
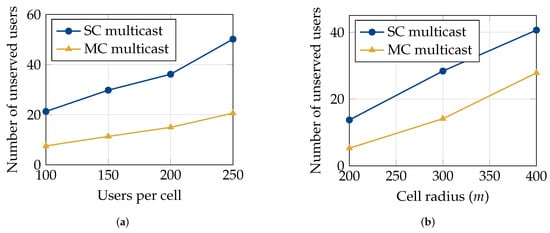
Figure 5.
Comparisons of the average number of users left unserved under SC and MC multicasting. Resource allocation was performed using the proposed CGA algorithm (Algorithm 3), and the results are plotted as a function of (a) an increasing number of users and (b) increasing cell radii.
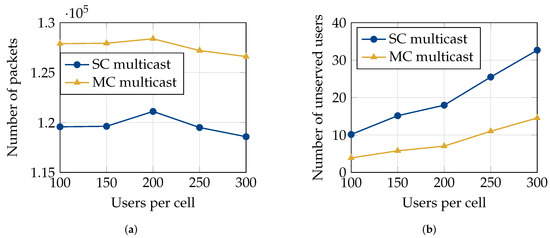
Figure 6.
Comparisons of (a) the average number of packets successfully delivered (out of 133,121) and (b) the average number of users left unserved under SC and MC multicasting while transmitting a real-time video stream. Realistic video traffic patterns were generated using traces of a video of the Tokyo Olympics [11].
Figure 4a illustrates the number of packets successfully delivered under MC and SC multicasting as the number of users increased. We observe a decline in the number of packets successfully delivered as the number of UEs increases. However, the number of packets successfully delivered under MC multicasting is much larger than that under SC multicasting. Figure 4b plots the same metric as a function of the cell radius. We observe that the number of packets successfully delivered decreases as the cell sizes increase. This is because the path loss of the cell edge users increases as the cells become larger. The key observation here is that the performance gap between MC and SC follows an increasing trend. The relative performances of MC and SC are similar to what we observe in Figure 4a.
Figure 5a,b plot the average number of users left unserved in a cell per sub-frame as a function of an increasing number of users and the cell radius, respectively. The number of users left unserved increases as the number of users and cell radius increase. The performance gap between MC and SC multicasting also increases as the number of users increases. We observe that in the absence of multi-connectivity, nearly thrice as many users are left unserved.
In Figure 6a,b, we compare the performances of MC and SC multicasting while serving a real-time video stream. To generate realistic video traffic patterns, we used traces of a video of the Tokyo Olympics that has 133,121 packets (obtained from http://trace.eas.asu.edu, (accessed on 20 March 2023)) [11]. For these simulations, the rate of transmission varied every sub-frame according to the size of the video frame being transmitted. We ran the simulations for the duration of the video stream (133,121 sub-frames) and then averaged the results over the entire duration of the transmission. From Figure 6a, we observe that MC multicasting delivers around 8000 more packets successfully than SC multicasting. From Figure 6b, we observe that 10–20 more UEs are left unserved under SC multicasting than under MC multicasting. The performance gap between the two increases as the number of UEs in the system increases.
In Figure 7a,b, we compare the performance of MC multicasting with that of MBSFN transmissions. Since MBSFN requires transmitting the content over the same PRB in all the cells, we chose the PRB that serves the maximum number of UEs in the entire system. We used traces from a real video stream (Tokyo Olympics [11]) to generate realistic video traffic patterns in these simulations as well. We observe that MC multicasting performs remarkably better than MBSFN. It succeeds in delivering a significantly greater number of packets successfully and is also able to serve many more UEs than MBSFN. These results validate our claims that MC multicasting can provide the benefits of MBSFNs while eliminating the need for strict synchronization. In fact, as observed in Figure 7, MC multicasting outperforms MBSFN by large margins.
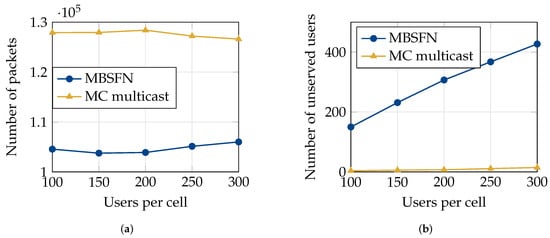
Figure 7.
Comparisons of (a) the average number of packets successfully delivered (out of 133,121) and (b) the average number of users left unserved under MC multicasting and MBSFN while transmitting a real-time video stream. Realistic video traffic patterns were generated using traces of a video of the Tokyo Olympics [11].
These simulation results clearly indicate that using multi-connectivity results in significant performance enhancements in multicast systems. The flexibility of potentially receiving content from multiple base stations results in more users being served and in reduced packet loss as well. Thus, MC multicasting has tremendous potential for use in video streaming services. It can help alleviate the burden on network resources while serving a larger number of users simultaneously.
8. Conclusions
In this paper, we propose leveraging multi-connectivity (MC) for multicast transmissions and prove that it results in significant performance enhancements for multicast streaming services. We address the resource allocation problem in MC multicasting, aiming to maximize the number of concurrently served users and prove its NP-hardness. Our proposed centralized greedy approximation (CGA) algorithm for MC multicast resource allocation achieves an approximation ratio of . For delay-sensitive applications where centralized resource allocation might become infeasible, we propose a distributed greedy allocation (DGA) algorithm that enables MC multicasting without coordination between base stations. We show that, despite its distributed nature, the DGA algorithm results in just more packet loss compared to the centralized policy. Using rigorous simulations, we conclusively demonstrate that employing multi-connectivity in multicast transmissions results in increased user coverage and reduced packet losses. Furthermore, we evaluated the efficacy of our algorithms in real-time video streaming applications, utilizing traces from authentic video streams to generate realistic traffic patterns. Performance comparisons of the CGA algorithm’s solution with the optimal solution obtained for a smaller problem size using brute force show that they match. We also demonstrated that MC multicasting outperforms MBSFN, eliminating the need for strict synchronization and extended cyclic prefixes.
9. Future Research Directions
This work provides a proof of concept for integrating MC within multicast transmissions, but several practical questions remain open for further research. For instance, we assumed that the users are static for the entire duration of the multicast transmission. The impact of user mobility on the proposed algorithms remains to be studied. Allowing for mobility will imply that the sets of users served under a certain allocation keep changing as a function of time. Therefore, new resource allocation algorithms need to be developed that can take this into consideration. Since the problem of resource allocation in MC multicasting is shown to be NP-hard, machine learning-based algorithms can also be developed for optimizing the allocation decisions. Another interesting research direction would be to consider a system where a number of different multicast streams can be simultaneously broadcast in a multicast region.
Author Contributions
Formal analysis, S.u.Z. and P.C.; software, S.u.Z.; supervision, P.C., A.K. and H.V.P.; visualization, S.u.Z.; writing—original draft, S.u.Z.; writing—review and editing, S.u.Z., P.C., A.K. and H.V.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The video traces used for the simulations in Section 7 are part of the Arizona State University Video Trace Library (http://trace.eas.asu.edu/, (accessed on 20 March 2023)) [11].
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Ericsson Mobility Report. 2023. Available online: https://www.ericsson.com/4ae12c/assets/local/reports-papers/mobility-report/documents/2023/ericsson-mobility-report-november-2023.pdf (accessed on 12 July 2023).
- Hung, Y.H.; Wang, C.Y.; Hwang, R.H. Optimizing social welfare of live video streaming services in mobile edge computing. IEEE Trans. Mob. Comput. 2019, 19, 922–934. [Google Scholar] [CrossRef]
- Zuhra, S.u.; Chaporkar, P.; Karandikar, A. Efficient Grouping and Resource Allocation for Multicast Transmission in LTE. In Proceedings of the IEEE WCNC, San Francisco, CA, USA, 19–22 March 2017; pp. 1–6. [Google Scholar]
- Zuhra, S.u.; Chaporkar, P.; Karandikar, A. Towards Optimal Grouping and Resource Allocation for Multicast Streaming in LTE. IEEE Trans. Veh. Technol. 2019, 68, 12239–12255. [Google Scholar] [CrossRef]
- Rosa, C.; Pedersen, K.; Wang, H.; Michaelsen, P.H.; Barbera, S.; Malkamaki, E.; Henttonen, T.; Sébire, B. Dual connectivity for LTE small cell evolution: Functionality and performance aspects. IEEE Commun. Mag. 2016, 54, 137–143. [Google Scholar] [CrossRef]
- Pan, M.S.; Lin, T.M.; Chiu, C.Y.; Wang, C.Y. Downlink traffic scheduling for LTE-A small cell networks with dual connectivity enhancement. IEEE Commun. Lett. 2016, 20, 796–799. [Google Scholar] [CrossRef]
- Polese, M.; Giordani, M.; Mezzavilla, M.; Rangan, S.; Zorzi, M. Improved handover through dual connectivity in 5G mmWave mobile networks. IEEE J. Sel. Areas Commun. 2017, 35, 2069–2084. [Google Scholar] [CrossRef]
- Wang, H.; Rosa, C.; Pedersen, K.I. Dual connectivity for LTE-advanced heterogeneous networks. Springer Wirel. Netw. 2016, 22, 1315–1328. [Google Scholar] [CrossRef]
- Odarchenko, R.; Aguiar, R.L.; Altman, B.; Sulema, Y. Multilink approach for the content delivery in 5G networks. In Proceedings of the International Scientific-Practical Conference Problems of Infocommunications. Science and Technology, Kharkiv, Ukraine, 9–12 October 2018; pp. 140–144. [Google Scholar]
- Karandikar, A.; Chaporkar, P.; Jha, P.K.; Zuhra, S.u. Methods and Systems for Using Multi-Connectivity for Multicast Transmissions in a Communication System. U.S. Patent 11,368,818, 21 June 2022. [Google Scholar]
- Seeling, P.; Reisslein, M. Video transport evaluation with H. 264 video traces. IEEE Commun. Surveys Tutorials 2011, 14, 1142–1165. [Google Scholar] [CrossRef]
- Van der Auwera, G.; David, P.T.; Reisslein, M. Traffic and quality characterization of single-layer video streams encoded with the H. 264/MPEG-4 advanced video coding standard and scalable video coding extension. IEEE Trans. Broadcast. 2008, 54, 698–718. [Google Scholar] [CrossRef]
- Zuhra, S.u.; Chaporkar, P.; Karandikar, A. Auction Based Resource Allocation and Pricing for Heterogeneous User Demands in eMBMS. In Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC), Marrakesh, Morocco, 15–18 April 2019; pp. 1–6. [Google Scholar]
- Zuhra, S.u.; Besser, K.L.; Chaporkar, P.; Karandikar, A.; Poor, H.V. Optimal Resource Allocation for Loss-Tolerant Multicast Video Streaming. Entropy 2023, 25, 1045. [Google Scholar] [CrossRef] [PubMed]
- Tesema, F.B.; Awada, A.; Viering, I.; Simsek, M.; Fettweis, G.P. Mobility modeling and performance evaluation of multi-connectivity in 5G intra-frequency networks. In Proceedings of the IEEE Globecom Workshops (GC Wkshps), San Diego, CA, USA, 6–10 December 2015; pp. 1–6. [Google Scholar]
- Ba, X.; Wang, Y.; Zhang, D.; Chen, Y.; Liu, Z. Effective scheduling scheme for multi-connectivity in intra-frequency 5G ultra-dense networks. In Proceedings of the IEEE International Conference on Communications Workshops, Kansas City, MO, USA, 20–24 May 2018; pp. 1–5. [Google Scholar]
- She, C.; Chen, Z.; Yang, C.; Quek, T.Q.; Li, Y.; Vucetic, B. Improving network availability of ultra-reliable and low-latency communications with multi-connectivity. IEEE Trans. Commun. 2018, 66, 5482–5496. [Google Scholar] [CrossRef]
- Ba, X.; Wang, Y. Load-aware cell select scheme for multi-connectivity in intra-frequency 5G ultra dense network. IEEE Commun. Lett. 2019, 23, 354–357. [Google Scholar] [CrossRef]
- Ravanshid, A.; Rost, P.; Michalopoulos, D.S.; Phan, V.V.; Bakker, H.; Aziz, D.; Tayade, S.; Schotten, H.D.; Wong, S.; Holland, O. Multi-connectivity functional architectures in 5G. In Proceedings of the IEEE International Conference on Communications Workshops, Kuala Lumpur, Malaysia, 23–27 May 2016; pp. 187–192. [Google Scholar]
- Michalopoulos, D.S.; Maeder, A.; Kolehmainen, N. 5G multi-connectivity with non-ideal backhaul: Distributed vs cloud-based architecture. In Proceedings of the IEEE Globecom Workshops, Abu Dhabi, United Arab Emirate, 9–13 December 2018; pp. 1–6. [Google Scholar]
- Chandrashekar, S.; Maeder, A.; Sartori, C.; Höhne, T.; Vejlgaard, B.; Chandramouli, D. 5G multi-RAT multi-connectivity architecture. In Proceedings of the IEEE International Conference on Communications Workshops, Kuala Lumpur, Malaysia, 23–27 May 2016; pp. 180–186. [Google Scholar]
- Du, L.; Zheng, N.; Zhou, H.; Chen, J.; Yu, T.; Liu, X.; Liu, Y.; Zhao, Z.; Qian, X.; Chi, J.; et al. C/U split multi-connectivity in the next generation new radio system. In Proceedings of the IEEE Vehicular Technology Conference Spring, Sydney, NSW, Australia, 4–7 June 2017; pp. 1–5. [Google Scholar]
- Wolf, A.; Schulz, P.; Dörpinghaus, M.; Santos Filho, J.C.S.; Fettweis, G. How reliable and capable is multi-connectivity? IEEE Trans. Commun. 2018, 67, 1506–1520. [Google Scholar] [CrossRef]
- Saimler, M.; Coleri, S. Multi-Connectivity Based Uplink/Downlink Decoupled Energy Efficient User Association in 5G Heterogenous CRAN. IEEE Commun. Lett. 2020, 24, 858–862. [Google Scholar] [CrossRef]
- Kousaridas, A.; Zhou, C.; Martín-Sacristán, D.; Garcia-Roger, D.; Monserrat, J.F.; Roger, S. Multi-Connectivity Management for 5G V2X Communication. In Proceedings of the IEEE International Symposium on Personal, Indoor and Mobile Radio Communications, Istanbul, Turkey, 8–11 September 2019; pp. 1–7. [Google Scholar]
- Kovalchukov, R.; Moltchanov, D.; Begishev, V.; Samuylov, A.; Andreev, S.; Koucheryavy, Y.; Samouylov, K. Improved Session Continuity in 5G NR with Joint Use of Multi-Connectivity and Guard Bandwidth. In Proceedings of the 2018 IEEE Global Communications Conference, Abu Dhabi, United Arab Emirates, 9–13 December 2018; pp. 1–7. [Google Scholar]
- Petrov, V.; Solomitckii, D.; Samuylov, A.; Lema, M.A.; Gapeyenko, M.; Moltchanov, D.; Andreev, S.; Naumov, V.; Samouylov, K.; Dohler, M.; et al. Dynamic multi-connectivity performance in ultra-dense urban mmWave deployments. IEEE J. Sel. Areas Commun. 2017, 35, 2038–2055. [Google Scholar] [CrossRef]
- Gapeyenko, M.; Petrov, V.; Moltchanov, D.; Akdeniz, M.R.; Andreev, S.; Himayat, N.; Koucheryavy, Y. On the degree of multi-connectivity in 5G millimeter-wave cellular urban deployments. IEEE Trans. Veh. Technol. 2018, 68, 1973–1978. [Google Scholar] [CrossRef]
- Tatino, C.; Malanchini, I.; Pappas, N.; Yuan, D. Maximum throughput scheduling for multi-connectivity in millimeter-wave networks. In Proceedings of the 2018 International Symposium on Modeling and Optimization in Mobile, Ad Hoc, and Wireless Networks, Shanghai, China, 7–11 May 2018; pp. 1–6. [Google Scholar]
- Giordani, M.; Mezzavilla, M.; Rangan, S.; Zorzi, M. An efficient uplink multi-connectivity scheme for 5G millimeter-wave control plane applications. IEEE Trans. Wirel. Commun. 2018, 17, 6806–6821. [Google Scholar] [CrossRef]
- Drago, M.; Azzino, T.; Polese, M.; Stefanović, Č.; Zorzi, M. Reliable video streaming over mmWave with multi connectivity and network coding. In Proceedings of the 2018 International Conference on Computing, Networking and Communications (ICNC), Maui, HI, USA, 5–8 March 2018; pp. 508–512. [Google Scholar]
- Velde, H.; Hus, O.; Baker, M. Broadcast Operation. In LTE-The UMTS Long Term Evolution From Theory to Practice, 2nd ed.; John Wiley & Sons Ltd.: Chichester, UK, 2011; pp. 293–305. [Google Scholar]
- 3GPP TS 23.246 v.17.0.0 Rel. 17. Multimedia Broadcast/Multicast Service (MBMS); Architecture and Functional Description. 2022-03. Available online: https://www.3gpp.org/ftp/Specs/archive/23_series/23.246/ (accessed on 20 December 2023).
- 3GPP TS 36.440 v.8 Rel. 8. Evolved Universal Terrestrial Radio Access Network (E-UTRAN); General Aspects and Principles for Interfaces Supporting Multimedia Broadcast Multicast Service (MBMS) Within E-UTRAN. 2017-03. Available online: https://www.3gpp.org/ftp/Specs/archive/36_series/36.440/ (accessed on 20 December 2023).
- 3GPP TR 23.757 v.1.0.0 Rel. 17. Study on Architectural Enhancements for 5G Multicast-Broadcast Services. 2020. Available online: https://portal.3gpp.org/desktopmodules/Specifications/SpecificationDetails.aspx?specificationId=3621 (accessed on 2 December 2023).
- Gimenez, J.J.; Carcel, J.L.; Fuentes, M.; Garro, E.; Elliott, S.; Vargas, D.; Menzel, C.; Gomez-Barquero, D. 5G new radio for terrestrial broadcast: A forward-looking approach for NR-MBMS. IEEE Trans. Broadcast. 2019, 65, 356–368. [Google Scholar] [CrossRef]
- 3GPP TS 36.300 v.15.5.0 Rel. 15. LTE; E-UTRA and E-UTRAN; Overall Description; Stage 2. 2019. Available online: https://www.3gpp.org/ftp/Specs/archive/36_series/36.300/ (accessed on 4 December 2023).
- 3GPP TS 37.340 v.17.6.0 Rel. 17. 5G; NR; Multi-Connectivity; Overall Description. 2023. Available online: https://www.3gpp.org/ftp/Specs/archive/37_series/37.340/ (accessed on 4 December 2023).
- Hochbaum, D.S. Approximating Covering and Packing Problems: Set Cover, Vertex Cover, Independent Set, and Related Problems. In Approximation Algorithms for NP-Hard Problems; PWS Publishing Company: New York, NY, USA, 1997; Available online: https://api.semanticscholar.org/CorpusID:118757286 (accessed on 20 December 2023).
- Feige, U. A threshold of ln n for approximating set cover. J. ACM (JACM) 1998, 45, 634–652. [Google Scholar] [CrossRef]
- 3GPP TR 38.901 v.17.0.0 Rel. 17. 5G; Study on Channel Model for Frequencies from 0.5 to 100 GHz. 2022. Available online: https://www.3gpp.org/ftp/Specs/archive/38_series/38.901/ (accessed on 30 December 2023).
- 3GPP TS 38.214: Radio Access Network; NR; Physical Layer Procedures for Data. v.17.5.0 Rel. 17. 2023. Available online: https://www.3gpp.org/ftp/Specs/archive/38_series/38.214/ (accessed on 30 December 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).